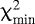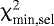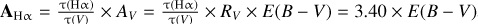| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 42 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833776 | |
| Published online | 07 February 2019 | |
Modeling ionized gas in low-metallicity environments: the Local Group dwarf galaxy IC 10★
1
Laboratoire AIM, CEA/Service d’Astrophysique, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
e-mail: fiorella.polles@obspm.fr
2
Université Paris Sud, 91400 Orsay, France
3
LERMA, Observatoire de Paris, CNRS, PSL University, Sorbonne University, 75014 Paris, France
4
University of Cincinnati, Clermont College, 4200 Clermont College Drive, Batavia, OH 45103, USA
5
Institut für theoretische Astrophysik, Zentrum für Astronomie der Universität Heidelberg, Albert-Ueberle Str.2, 69120 Heidelberg, Germany
6
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
7
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
Received:
4
July
2018
Accepted:
18
September
2018
Context. Star formation activity is an important driver of galaxy evolution and is influenced by the physical properties of the interstellar medium. Dwarf galaxies allow us to understand how the propagation of radiation and the physical conditions of the different ISM phases are affected by the low-metallicity environment.
Aims. Our objective is to investigate the physical properties of the ionized gas of the low-metallicity dwarf galaxy, IC 10, at various spatial scales: from individual H II regions to the entire galaxy scale and examine whether diagnostics for integrated measurements introduce bias in the results.
Methods. We modeled the ionized gas combining the mid- and far-infrared fine-structure cooling lines observed with Spitzer/IRS and Herschel/PACS, with the photoionization code CLOUDY. The free parameters of the models are the age of the stellar cluster, the density, and the ionization parameter of the ionized gas as well as the depth of the cloud. The latter is used to investigate the leakage of the ionizing photons from the analyzed regions of IC 10. We investigated H II regions in the main star-forming body, on scales of ~25 pc, three in the main star-forming region in the center of the galaxy and two on the first arc. We then considered larger sizes on the scale of ~200 pc.
Results. Most clumps have almost-identical properties, density ~102–102.6 cm−3, ionization parameter between 10−2.2 and 10−1.6, and age of the stellar cluster ~5.5 Myr. All of them are matter-bounded regions, allowing ionizing photons to leak. The relatively uniform physical properties of the clumps suggest a common origin for their star formation activity, which could be related to the feedback from stellar winds or supernovae of a previous generation of stars. The properties derived for ~200 pc size “zones” have similar properties as the H II regions they encompass, but with the larger regions tending to be more radiation bounded. Finally, we investigated the fraction of [CII] 157.7 μm, [SiII] 34.8 μm and [FeII] 25.9 μm emission arising from the ionized gas phase and we find that most of the emission originates from the neutral gas, not from the ionized gas.
Key words: HII regions / ISM: lines and bands / galaxies: ISM / galaxies: individual: IC 10 / techniques: spectroscopic
The reduced images and spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/622/A119
© ESO 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The interstellar medium (ISM) plays a key role in understanding star formation (SF) process, as it is at the same time the reservoir of gas and dust and the repository of stellar ejecta, enriched by the elements produced by nucleosynthesis in massive stars. While it is still difficult to assess the details of the ISM properties at high redshifts, galaxies in the Local Group offer the opportunity to study several “chemically young”, meaning metal-poor, dwarf galaxies. Metal-poor dwarf galaxies are not genuinely young (i.e., they are at least older than ~1 Gyr) and consequently they cannot be directly compared to high-redshift galaxies. Nevertheless, these unevolved nearby dwarf galaxies remain the best laboratories to examine SF and physical conditions in the metal-poor ISM.
Some irregular dwarf galaxies harbour super star clusters (e.g., 30 Doradus in the Large Magellanic Cloud, Hunter 1999) and some of them host Wolf-Rayet (WR) stars (e.g., IC 10, Massey & Holmes 2002), hinting at intense SF activity within the last 10 Myr. The combination of a young massive stellar population which produces hard ultraviolet (UV) photons and a dust-poor ISM (more transparent) can result in a hard radiation field extending over galaxy-wide scales. Observations are consistent with the above picture, with ionized gas tracers detected throughout these galaxies (e.g., Kawada et al. 2011; Lebouteiller et al. 2012a; Cormier et al. 2015).
The gas tracers, that is, the cooling lines, provide access to the gas properties of the ISM, such as elemental abundances (e.g., Garnett 1990; Stasińska 2007; Kewley et al. 2010), temperatureand density, and reveal the nature of the heating mechanism of the gas (UV, X-rays, shocks, etc.; e.g., Baldwin et al. 1981; Osterbrock & Ferland 2005; Kaufman et al. 2006; Dimaratos et al. 2015; Lee et al. 2016; Lebouteiller et al. 2017). The mid- and far-infrared (MIR and FIR) lines – the focus of this paper – are less affected by the dust and gas attenuation compared to optical lines, and are therefore potentially ideal tracers of the ISM parameters deeper into star forming clouds.
The Herschel Dwarf Galaxy Survey (DGS, Madden et al. 2013) enabled the observations of many such cooling lines in some of the most metal-poor dwarf galaxies in the nearby Universe. It provided FIR and submillimeter (submm) photometric and spectroscopic observations of 48 low-metallicity dwarf galaxies. The spectroscopic data from the Herschel telescope (Pilbratt et al. 2010), together with Spitzer (Werner et al. 2004) MIR spectroscopic data, provide ~20 MIR and FIR fine-structure cooling lines to study the ionized, atomic and molecular gas in dwarf galaxies. Analysis on global galaxy-wide scales of the DGS by Cormier et al. (2012, 2015) shows that the physical properties of the ISM of these galaxies are different compared to those of the more metal-rich (starburst, spiral, IR-bright) galaxies. The Cormier et al. (2015) study highlights, for example, that the brightest FIR line for these galaxies on global scales, is the [OIII] 88.4 μm line, while it is [CII] 157.7 μm in more metal-rich galaxies. The emission of the [OIII] 88.4 μm line requires photons with energy greater than 35 eV, thus the strength of [OIII] 88.4 μm emission is indicativeof the presence of a significant Lyman continuum flux, and the extent of [OIII] 88.4 μm emission is a consequence of the low dust abundance.
An important next step is to connect integrated galaxy scale analyses to resolved region studies (e.g., Lebouteiller et al. 2012a; Chevance et al. 2016; Lee et al. 2016; Fahrion et al. 2017), by examining the ISM properties of a nearby galaxy that can be resolved and fully mapped. Performing an analysis at different spatial scales can help to develop a more consistent picture of the ISM characteristics. The challenge is to take into account the variations in signal-to-noise ratio of the diagnostic tracers and their spatial coverage, compelling us to select specific combinations of tracers at the different scales. Since the modeling strategy depends on what tracers are available, it is important to extract the best possible constraints on the physical properties as a function of the spatial scales used and identify the potential corresponding biases.
The proximity of the dwarf irregular galaxy IC 10 (~715 kpc; Sakai et al. 1999; Sanna et al. 2009; Kim et al. 2009) makes it an opportune object to investigate the relation between the local properties of the different gas phases and the larger scales characteristics in a low metallicity environment and to understand which combinations of emission lines provide useful diagnostics as a function of the spatial scale considered. Moreover, IC 10 has been mapped in all of the tracers available with Spitzer and Herschel, providing larger data cubes than currently available in the optical. Combinations of ionic and atomic tracers should provide the constraints necessary to build a self-consistent model of the ISM and thus assess the physical properties (e.g., density, filling factor) of the different ISM phases.
In this paper we perform a study of the ionized gas: the dense H II regions as well as the diffuse ionized gas of IC 10. The best solutions in this study will then set a reference model of the ionized gas distribution and characteristics that will be used to further model the associated neutral and molecular gas components, in a subsequent paper.
This paper is organized as follows. First, we present an overview of IC 10 (Sect. 2) and the dataset used in this study (Sect. 3). Next, in Sect. 4 we describe our modeling strategy. Modeling the MIR and FIR line emission we determine the physical properties of the ionized gas in the H II regions as well as at larger scales (Sect. 5). Finally, we discuss the results obtained (Sect. 6) and we summarize our conclusions in Sect. 7.
 |
Fig. 1. Three-color image of IC 10 (main body) with polycyclic aromatic hydrocarbon (PAH) emission (Spitzer/IRAC4, 8 μm) in red, H α (1.8 m Perkins Telescope; Hunter & Elmegreen 2004) in green, and stars (Spitzer/IRAC1, 3.6 μm) in blue. The tracers highlight the bright star-forming region in the center and two arcs with extended Hα and PAH emission. |
2. Overview of IC 10
The irregular dwarf galaxy IC 10 has a metallicity of 12+log(O/H) = 8.26 (Lequeux et al. 1979; Garnett 1990; Richer et al. 2001; Magrini & Gonçalves 2009), ≈2.7 times lower than the solar metallicity (12+log(O/H) = 8.69; Asplund et al. 2009) and between that of the Small and Large Magellanic Clouds. It was identified as an external object by Mayall (1935) and as a member of the Local Group by Hubble (1936). The estimated distance is uncertain because of the location of this galaxy close to the Galactic plane (b = −3.3°). The distance has been determined to be from 500 kpc to 3 Mpc (Sandage & Tammann 1974; Sakai et al. 1999; Borissova et al. 2000; Hunter 2001). In this paper we adopt 715 kpc (Kim et al. 2009; Lim & Lee 2015), the distance calculated by Kim et al. (2009) using the tip of the red giant branch (TRGB) method. This distance is close to 700 kpc, a value frequently adopted in the recent literature (e.g., Lebouteiller et al. 2012a; Heesen et al. 2018). At this distance 1′′ ≡ 3.5 pc. Thus, IC10 is close enough for its SF regions to be resolved and far enough to be fully mapped.
The IC 10 galaxy consists of a main body and several star forming arcs (Fig. 1). These components are sitting in an extended and complex H I envelope whose diameter is 7 times larger than the optical diameter (Huchtmeier 1979; Wilcots & Miller 1998; Ashley et al. 2014). H I holes are prominent throughout the body of IC 10, the origin of which has been interpreted to be cumulative effects of stellar winds (Wilcots & Miller 1998; Nidever et al. 2013). The velocity field of the ionized gas closely matches the HI velocity field (Thurow & Wilcots 2005). Supernova remnants and winds from WR stars have been identified asthe main driver of the gas kinematics (Thurow & Wilcots 2005). The hard radiation from the WR stars, together with photons leaking from the H II regions, are the sources of such extended ionized gas emission (Hidalgo-Gámez 2005).
Several parameters suggest that IC 10 is undergoing a starburst phase. The star formation rate is ~0.2 M⊙ yr−1 and Hodge & Lee (1990) discovered a large number (144) of H II regions, which is relatively high for a galaxy with stellar mass of 4 × 108 M⊙. The starburst nature of the galaxy is confirmed by the stellar component of the galaxy. The well-studied stellar population of IC 10 highlights young stellar clusters (≤10 Myr) located in the Hα emitting regions (Vacca et al. 2007; Sanna et al. 2009; Yin et al. 2010), while the old clusters are distributed over a wide area of the disk (Lim & Lee 2015). Moreover, WR stars abound in IC 10 (e.g., Massey & Holmes 2002)1. IC 10 shows high SF activity considering the low molecular gas surface density, determined from CO observation (e.g., Wilson & Reid 1991; Leroy et al. 2006), although a large quantity of H2 (100 times the mass of molecular gas present in the CO core) has been inferred from the CO-dark gas tracer [CII] 158 μm (Madden et al. 1997). Finally, the gas-to-dust mass ratio (G/D) is estimated to be 240–475 (Rémy-Ruyer 2013; G/D ~160 for the Milky Way), lower than that expected based on a linear relation between gas-to-dust ratio and metallicity (~ 103; Rémy-Ruyer et al. 2014).
3. Data
As part of the DGS sample, IC 10 has been observed with the Herschel/PACS (Photodetector Array Camera and Spectrometer; Poglitsch et al. 2010) instrument, and it has also been observed in the MIR with the IRS (Infrared Spectrograph; Houck et al. 2004) onboard Spitzer, providing access to a wide range of gas tracers. In this section, we present the data used in our study.
3.1. Spitzer/IRS spectroscopy
IC 10 was mapped with the low-resolution modules (R = λ∕Δλ ≈ 60–127) of the IRS with the Spitzer Space Telescope: two Short-Low (SL; λ = 5.7–14.5 μm) and two Long-Low (LL; λ = 14–38 μm). The SL map consists of 8 × 58 slit positions while the LLmap consists of 2 × 20 slit positions. Five additional pointings were observed toward bright knots with the high-resolution modules (R ≈600) Short-High (SH; λ = 9.9–19.6 μm) and Long-High (LH; λ = 18.7– 37.2 μm). Figure 2 shows the area covered by the low-resolution modules and the positions of the high-resolution pointings. Table 1 provides observational parameters. The integrated rest-frame spectrum (Δv = 348) together with the modeled spectral energy distribution (SED) for one of the selected zones (Sect. 4.1) of size ~ (174 pc × 226 pc) in the center of IC 10 is shown for illustration in Fig. 3 while a magnification of individual lines is displayed in Fig. 4.
We refer to Lebouteiller et al. (2012b) for the general principles on the reduction of the IRS data and map reconstruction, while here we present an updated reduction. The data was first reduced with CUBISM (Smith et al. 2007)and the bad pixels in the detector were identified and ignored using the backtracking tools before projecting and exporting the datacube. The SL and LL data cubes were projected independently with different map parameters (different sampling), moreover the SL maps exhibit gaps, which can result in some discrepancy in the continuum flux level for a given spatial region. The amplitude of this discrepancy was estimated by calculating the stitching factor between the SL and LL continuum for the overlap wavelength window around 14–15 μm. The ratio is close to one with a standard deviation σst of about 15% per pixel of 4′′. A Monte-Carlo method was used to produce the spectral maps and estimate the associated uncertainties. For each of 100 realisations, our method was as follows:
- 1.
the gaps in the SL map were filled using a b-spline fit in the direction perpendicular to the slits;
- 2.
a median filtering was applied in the dispersion direction to accommodate the lower spatial resolution due to the incomplete sampling in that direction;
- 3.
each plane was convolved to a resolution of either 4′′ (SL) or 12′′ (SL and LL);
- 4.
each plane was resampled to a pixel size of either 4′′ (SL) or 12′′ (SL and LL);
- 5.
each spectral line and the continuum of a plane were simultaneously fitted with a Gaussian and a second-order polynomial, respectively.
The final line flux and associated uncertainties were calculated using the median and median absolute deviation of the line flux distribution among the 100 outcomes. In Fig. 5, we show the line maps prior to convolution and resampling (points 3 and 4), and Table 2 reports the general properties of those lines.
The individual high-resolution pointings (Fig. B.1) were retrieved from the CASSIS spectral database (Lebouteiller et al. 2011, 2015). For some pointings, the emission is extended, and, as a consequence, the SH and LH spectra do not align because both modules have different slit sizes (4.7′′ × 11.3′′ for SH, 11.1′′ × 22.3′′ for LH). For such cases, we used the wavelength-dependent extended source flux calibration available in CASSIS, and applied a scaling factor to match SH to LH in the overlapping wavelength range of 19.0– 19.5μm. Some pointings are dominated by a point source, and in such cases the SH and LH spectra, after using a point-source flux calibration (a factor between 1.5 and 4.5), aligned fairly well. The final fluxes obtained with the high-resolution modules for each pointing arepresented in the Table B.1.
The line fluxes are not corrected for possible attenuation due to the silicate absorption bands at ≈10 and ≈20 μm (Galliano et al. 2018). The [ArIII] and [SIV] lines, located at 9.0 and 10.5 μm respectively are the most likely to be attenuated by the silicate dust (the silicate absorption band at ≈ 20μm is comparatively weaker). The silicate absorption optical depth at 10 μm in IC 10 is about τ ≈ 0.2 on average across the main body, with peaks around 0.4 toward the clumps (Lebouteiller et al. 2012a). From τ we calculated the extinction A10 μm < 1.086 × 0.4 ~ 0.4 mag. This value is an upper limit, since our line measurements correspond to spatial scales larger than those used for which the silicate absorption optical depth peaks were determined. If we wish to calculate the attenuation of the [ArIII] and [SIV] lines, we need to assume a geometry, which can be either “screen” (assuming that the gas is located behind the dust) or “mixed” (assuming the gas is mixed with the dust). Iν/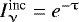 is the solution of the transfer of radiation through dust, where Iν is the observed intensity and
is the solution of the transfer of radiation through dust, where Iν is the observed intensity and 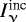 is the incident intensity. For a homogeneous mixture of gas and dust, the equation becomes Iν/
is the incident intensity. For a homogeneous mixture of gas and dust, the equation becomes Iν/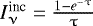 (Mathis 1972). If we assume that the gas and dust are well mixed, the silicate absorption measured toward IC 10 clumps corresponds to an attenuation of less than 50% with lower values expected for the large zones (τ ≈ 0.2 on average across the main body, while 50% is calculated assuming τ ≈ 0.4). Overall, we consider that the infrared lines are little affected by extinction, thus we do not correct for this in the line emission.
(Mathis 1972). If we assume that the gas and dust are well mixed, the silicate absorption measured toward IC 10 clumps corresponds to an attenuation of less than 50% with lower values expected for the large zones (τ ≈ 0.2 on average across the main body, while 50% is calculated assuming τ ≈ 0.4). Overall, we consider that the infrared lines are little affected by extinction, thus we do not correct for this in the line emission.
 |
Fig. 2. Hα map. Contours and boxes show the areas covered by the Herschel/PACS map of [OIII] 88.4 μm (in red), Spitzer/IRS SL maps (in magenta, SL1 and SL2), and Spitzer/IRS LL maps (in blue, LL1 and LL2). The yellow crosses show the positions of the high-resolution pointings. |
 |
Fig. 3. SED ofa region of ~(174 pc × 226 pc) in IC 10 (Main zone, see Fig. 6). The black dots with error bars represent the WISE, Herschel/PACS and Herschel/SPIRE photometry. The photometry data come from the DustPedia database (Clark et al. 2018), and will be interpreted in Lianou et al. (in prep.). The black emission lines are from the Spitzer/IRS and Herschel/PACS spectrometers. The data uncertainties are shown in the gray area. These observations have been fitted by the model of Galliano (2018). The total dust component is shown as the red area, stellar contribution as the yellow area, and the blue line represents the total model. The brightest emission features are labeled in green, including the main aromatic features (A.F.), commonly called PAH. |
Main properties of the IRS modules and the AORs of the IRS observations of IC 10.
3.2. Herschel/PACS spectroscopy
IC 10 was observed with PACS in [OIII] 88.4 μm, [NII] 121.9 μm, [CII] 157.7 μm, [OI] 63.2 μm and [OI] 145.5 μm as part of the Herschel DGS. Table 2 reports the general properties of those emission lines.
The PACS array consists of 5 × 5 spatial pixels covering a total field of view 47′′ × 47′′. The velocity resolution is ~90 km s−1 at 60 μm, ~ 125 km s−1 at 90 μm and ~ 295 km s−1 at 120 μm (PACS Observer’s Manual 2013). The observations have been done in unchopped mode, in which an offset position is observed before and after the IC 10 observation. The data cubes have been reduced with Herschel Interactive Processing Environment (HIPE, Ott 2010) v12.0.0 and then processed with PACSman (Lebouteiller et al. 2012a) for the line fit and map construction. To estimate the uncertainty on the fit parameters, a Monte-Carlo approach was used. Details of the observations, the reduction of the PACS data and uncertainties can be found in Cormier et al. (2015). Figure 3 shows the lines for the Main zone (M; Fig. 6) together with the corresponding SED and the Spitzer spectra. The individual lines are displayed in Fig. 4. The maps of [OIII] 88.4 μm and [NII] 121.9 μm are shown in Fig. 5.
 |
Fig. 4. Individual Spitzer/IRS and Herschel/PACS spectral lines observed in the Main zone (defined in Fig. 6). |
Properties of the infrared fine-structure cooling lines used in this study.
3.3. Ancillary data: Hα
Another tracer of the ionized gas is the optical line Hα. IC 10 has been observed in Hα with the 1.8 m Perkins Telescope at Lowell Observatory at a resolution of 2.3′′ (Hunter & Elmegreen 2004). The data is calibrated but not extinction-corrected. The map was convolved to the Spitzer/IRS SL resolution (3.7′′) using a Gaussian kernels. In this way the Hα image is consistent with the highest resolution available for the MIR line maps. Since Hα suffers from significant extinction from Galactic dust along the line of sight toward IC 10 (Galactic latitude of IC 10 ~3.3°) and from dust internal to IC 10, we have not used Hα as a constraint in the analysis. Instead, we used the model unattenuated predictions for Hα and the observed value in order to estimate the extinction a posteriori (see Sect. 6.3).
 |
Fig. 5. Spectral maps from Herschel/PACS and Spitzer/IRS of IC 10 used in this study in W m−2 sr−1. All of the tracers show bright clumps in the southeast region (Main zone; defined in Fig. 6) and in the northwest (Arc1 zone; defined in Fig. 6). |
3.4. Morphology
The maps of MIR and FIR emission lines (Fig. 5) show bright compact clumps distributed in the main star-forming region and in two arcs. The emission of these lines peak in the same clumps as Hα.
The MIR fine-structure lines [ArIII] 8.9 μm, [SIV] 10.5 μm and [NeIII] 15.5 μm have high critical density, ≥5 × 104 cm−3 (Table 2), and high ionization potential, 27.6, 34.7, and 41 eV, respectively. These lines are good diagnostics of the dense ionized gas, that is, the younger H II regions. Other MIR tracers, such as [ArII] 6.9 μm and [NeII] 12.8 μm, in addition to the compact clumps also show prominent extended emission, which likely arises in relatively more diffuse medium. The corresponding ions exist for lower energies, thus they better trace the outer shell of H II regions as well as relatively diffuse low-ionization gas (Cormier et al. 2012; Dimaratos et al. 2015). The S2+ ion with ionization potential of 23.3 eV has been observed at two wavelengths, 18.7 and 33.5 μm, which have critical densities for collisionswith electrons of 2 × 104 and 7 × 103 cm−3, respectively.Hence, we have access to the useful density tracer of the ionized gas, [SIII] 33.5 μm/[SIII] 18.7 μm (Osterbrock & Ferland 2005).
The FIR fine-structure lines [OIII] 88.4 μm and [NII] 121.9 μm are characterized by much lower critical densities than the MIR tracers. Both lines arise from more diffuse ionized gas (Table 2). In particular, the extended [OIII] 88.4 μm emission, which has an ionization potential of 35.1 eV and a critical density 500 cm−3, suggests a high filling factor of diffuse ionized gas. The low-metallicity ISM seems to be very porous, allowing hard photons such as those creating the O2+ ion to penetrate over large distances, even extending to galaxy scales (e.g., Cormier et al. 2015).
Our study focuses on the physical conditions of the compact, dense H II regions as well as the diffuse, ionized gas of IC 10. Thus, we will use the lines from all species that trace mostly the ionized gas: N+, O2+, Ne+, Ne2+, S2+, S3+, Ar+, and Ar2+. We do not use species with ionization potentials lower than 13.6 eV in our models since they may be ionized in regions where hydrogen remains neutral; these include C+, Si+, or Fe+ and the corresponding prominent emission lines in the infrared, [CII] 157.7 μm, [FeII] 25.9 μm [FeII] 17.9 μm and [SiII] 34.8 μm. Because [CII], [FeII] and [SiII] are important constraints for the neutral atomic and molecular gas, we estimate their fractions arising in the ionized gas component, as predicted by the model, in Sect. 6.2.
 |
Fig. 6. Outlines of the various zones and clumps investigated are overlaid on the Hα background image. |
4. Method to derive the ionized gas properties
4.1. Various spatial scales
Three spatial scales have been selected to analyse the ionized gas properties: clumps, zones, and body.
4.1.1. Clumps
The smallest spatial scale accessible is limited by the spatial resolution of the instruments. The best resolution is achieved with the Spitzer/IRS SL observations (4′′, corresponding to 14 pc at the distance of IC 10). With this resolution we can disentangle the clumps from the more extended gas component. Although many clumps could, in principle, be investigated, we focused the analysis on the brightest clumps of the galaxy in MIR and FIR lines. We identified five such clumps in the body of IC 10: three in the central main star-forming region (M#1, M#2, and M#3), and two in the first star-formingarc (A1#1 and A1#2). Figure 6 shows the clump locations.
We used a 2D Gaussian fit to disentangle the clumps and an underlying background component, and to calculate the integrated flux of each of them. For all tracers, the minimum Gaussian width was set by the resolution of the instrument, 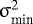 = (FWHM/2.35)2. The flux uncertainties were calculated using a Monte-Carlo method. Each map was perturbed 100 times based on the line fit uncertainties and for each iteration the integrated flux was calculated. Since the spatial resolution of SL and LL models are different, we treated these data differently. For tracers with spatial resolution better than 12′′ (SL-IRS maps: [ArII] 6.9 μm, [ArIII] 8.9 μm, [SIV] 10.5 μm and [NeII] 12.8 μm; PACS maps: [OIII] 88.4 μm and [NII] 121.9 μm), some degree of freedom on the position, (maximum) size, and asymmetry was allowed. The asymmetry of the Gaussian, described by the parameter Rab = σa/σb (with σa and σb measured in the two axes of the Gaussian), was constrained to be between 0.5 and 2. For the tracers with low spatial resolution (>12′′; [SIII] 18.7 μm, [SIII] 33.5 μm and [NeIII] 15.5 μm) the clumps are not spatially resolved. In fact, we computed intrinsic dimensions of the clumps that were similar to or lower than 12′′. Hence we fixed the width of the Gaussian to the resolution of the maps and the reference positions were fixed based on the Hα peaks (convolved to the Spitzer resolution).
= (FWHM/2.35)2. The flux uncertainties were calculated using a Monte-Carlo method. Each map was perturbed 100 times based on the line fit uncertainties and for each iteration the integrated flux was calculated. Since the spatial resolution of SL and LL models are different, we treated these data differently. For tracers with spatial resolution better than 12′′ (SL-IRS maps: [ArII] 6.9 μm, [ArIII] 8.9 μm, [SIV] 10.5 μm and [NeII] 12.8 μm; PACS maps: [OIII] 88.4 μm and [NII] 121.9 μm), some degree of freedom on the position, (maximum) size, and asymmetry was allowed. The asymmetry of the Gaussian, described by the parameter Rab = σa/σb (with σa and σb measured in the two axes of the Gaussian), was constrained to be between 0.5 and 2. For the tracers with low spatial resolution (>12′′; [SIII] 18.7 μm, [SIII] 33.5 μm and [NeIII] 15.5 μm) the clumps are not spatially resolved. In fact, we computed intrinsic dimensions of the clumps that were similar to or lower than 12′′. Hence we fixed the width of the Gaussian to the resolution of the maps and the reference positions were fixed based on the Hα peaks (convolved to the Spitzer resolution).
For the analysis at this scale (~25 pc) we used the absolute line fluxes of the SL tracers ([ArII] 6.9 μm, [ArIII] 8.9 μm, [NeII] 12.8 μm and [SIV] 10.5 μm) and the PACS tracers [OIII] 88.4 μm and [NII] 121.9 μm. With only these lines, however, the density is not well constrained so we added the LL line ratio [SIII] 33.5 μm/[SIII] 18.7 μm (Sect. 3.4). Whilethe lower spatial resolution of the LL tracers introduces systematic uncertainties when their absolute fluxes are considered together with SL tracers, the LL line ratio [SIII] 33.5 μm/[SIII] 18.7 μm does not affect the determination of other parameters (U, age,...). Furthermore, although other line ratios, such as [SIV] 10.5 μm/[SIII] and [NeIII] 15.5 μm/[NeII] 12.8 μm (or the combination of the two) can be used in principle to trace some model parameters, we decide not to use them because they involve linesfrom different modules or instruments and, most importantly, because our strategy relies on absolute fluxes whenever possible. The final fluxes are presented in Table 3.
4.1.2. Zones
We selected large areas of the galaxy (few hundreds pc), that are expected to exhibit different local physical conditions (Fig. 6). This allows us to consider integrated emission to improve the signal-to-noise ratio (S/N) of faint areas. Some zones enclose the clumps described above (M and A1) and structures visible in Hα (Arc2 (A2), Central (C), Diffuse2 (D2), and Diffuse3 (D3)) while the Diffuse1 (D1) zone was selected in order to examine the most diffuse phase possible. A single spectrum was produced by stacking spectra in the cube for all pixels of the zone. Line fluxes and errors were propagated through a Monte-Carlo simulation. For each Monte-Carlo iteration a zone spectrum was produced and one set of line fluxes was calculated. The fluxes and the associated errors were calculated using the median and the standard deviation of the flux distribution. For each PACS line, instead, we simply summed the line flux over the pixels in each zone, and propagated errors accordingly. The HIPE pipeline does not provide uncertainties on the measurements. Instead, empirical errors were calculated from the dispersion of the data cloud at every wavelength bin, and the line flux and errors were then inferred from each projected pixel (see Lebouteiller et al. 2012a). Table 4 presents the fluxes and errors measured for each zone. Figure 3 shows as an example the set of lines corresponding to the integrated M zone of ~(174 pc × 226 pc). By increasing the spatial scale from clumps to zones, we are able to use in the analysis the absolute fluxes of all of the tracers, including the IRS LL tracers ([NeIII] 15.5 μm [SIII] 18.7 μm and [SIII] 33.5 μm).
Final fluxes (× 10−16 W m−2) for each clump.
4.1.3. Body (B)
The largest scale corresponds to most of the star-forming body of the galaxy, encompassing a region of 545 pc × 743 pc and includes most of the zones examined individually and described above. It is the largest region available in IC 10 with all of the Spitzer spectroscopic observations. The integrated fluxes of this area were calculated with the same method used for the other zones. We omitted the PACS tracers from the analysis of the Body region, because the observations do not cover the full map.
4.2. Cloudy setup
To model the ionized gas, we used the spectral synthesis code CLOUDY c13.03 (Ferland et al. 2013). CLOUDY is a 1D spectral synthesis code which computes the physical and chemical structure and predicts the resulting spectrum of a region of gas and dust exposed to an ionizing radiation field. Our calculation is a constant pressure model2. The code requires the following input parameters:
- 1.
the shape of the source spectrum of the radiation field striking the cloud. We only consider a radiation field from a stellar population as a source, using the assumption of an instantaneous burst (age of the burst, tburst, which is varied);
- 2.
the intensity of the input radiation field. In our case we use the dimensionless ionization parameter (U, which is varied);
- 3.
the hydrogen density at the illuminated face of the cloud (nH, which is varied);
- 4.
the chemical composition and grain properties (which are fixed);
- 5.
the cloud depth (which is varied).
The model parameters are described in detail below.
4.2.1. Shape of the source spectrum
We used the spectral synthesis code STARBURST99 (Leitherer et al. 2010) to create the stellar ionizing continuum that serves as input for the CLOUDY models. Specifically, we choose a Salpeter initial mass function (α = 2.35) with an upper mass limit, Mup, of 100 M⊙ as done in López-Sánchez et al. (2011) and Padova asymptotic giant branch tracks with a metallicity of 0.008. We assume a single-burst star formation event. A continuous star formation rate may be envisaged, but the shape of the UV spectrum below 912 Å (i.e., for energies above 13.6 eV) is almost age-independent in this case, making this scenario difficult to test based on ionized gas tracers alone.
Several papers present studies of the stellar population of IC 10 (e.g., Vacca et al. 2007; Sanna et al. 2009; Yin et al. 2010). Motivated by these studies, the age of the cluster is varied within the range of 2.5–7 Myr (steps of 0.1 Myr between 2.5 and 3.5 Myr and between 5 and 6 Myr, and steps of 0.5 Myr between 3.5 and 5 Myr and between 6 and 7 Myr3).
4.2.2. Intensity of the radiation field
We used the ionization parameter U, to constrain the source brightness. U is the dimensionless ratio of the hydrogen-ionizing photons to total hydrogen density, characterizing the intensity of the radiation field:
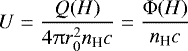 (1)
(1)
where r0 is the distance from the source to the inner edge of the cloud, nH is the total hydrogen density, c is the speed of light, Q(H) is the number of hydrogen-ionizing photons emitted by the central source and Φ(H) is the surface flux of ionizing photons. In our model, logU ranges from −4 to −1 with steps of 0.2.
4.2.3. Hydrogen density
The hydrogen density at the illuminated face of the cloud of our model grid covers the range of 10–104 cm−3 with steps of 0.2 dex. In pressure equilibrium, which is the case of our models, the density in the H II region stays almost constant, since the temperature remains stable.
4.2.4. Chemical composition
We set the elemental abundances of oxygen, nitrogen, neon, argon and sulfur to observed values, based on Magrini & Gonçalves (2009) and López-Sánchez et al. (2011). We adopted the abundance values for the clumps in Table 5, which are compatible with the values found in those works and the dispersion between the values in the different studies. For the other elements, we chose the solar abundances scaled to the metallicity of IC 10, Z = 0.3 Z⊙. For the analysis at larger scales, we considered the values reported for the clumps in the M zone (second column of Table 5), the abundance values for the individual clumps are the same within uncertainties. Uncertainties on the elemental abundances were taken into account when modeling the line fluxes (Sect. 4.3).
The dust grain properties of IC 10 are not well known. We chose to use the grain properties of the Small Magellanic Cloud. We adopted the grain size distribution presented in Weingartner & Draine (2001) which consists of graphites and silicates. The total dust abundance is scaled to the metallicity of IC 10.
Elemental abundances used to model the clumps of IC 10 with CLOUDY.
 |
Fig. 7. Hydrogen density (solid line) and ionization fraction (ne/nH; dashed line) as a function of the depth of the cloud for a model with log U = −2, nH = 2.2 cm−3 and tburst = 5.5 Myr. The depth is normalized to the depth at the ionization front. |
4.2.5. Cloud depth and stopping criterion
We are interested in the ionized gas properties. The maximum depth into the model cloud that we consider corresponds to the ionization front. The ionization front is defined as the depth where the hydrogen ionization fraction H+/H drops below 1%. Calculating the model until the ionization front is equivalent to calculating a radiation-bounded H II region, in other words, a cloud which is optically thick to ionizing radiation from which no photons with energies above 13.6 eV will escape. Models that are stopped at lower depth correspond to matter-bounded H II regions (sometimes called density-bounded) from which a significant fraction of the ionizing photons escape. Figure 7 shows an example of the total hydrogen density and the ionization fraction (ne/nH) as a function of the depth.
The regions investigated in this work are small compared to the extent of the ionized gas emission observed in IC 10. Thus, it is possible that a large fraction of the ionizing photons escapes from the individual regions. In order to simulate matter-bounded as well as radiation-bounded regions, we treat the depth of the cloud as a free parameter. In this study the normalized depth into the cloud is expressed as d∕dIF where d is the depth at which the calculation is stopped and dIF is the ionization front depth. If the region is radiation-bounded, the observed lines will be better reproduced at the ionization front (cloud depth of 1). Otherwise, if the H II region is matter-bounded, a better model can be found with a smaller depth.
The depth at which the calculation is stopped is an important parameter for those lines with relatively low ionization potentials, such as [ArII] 6.9 μm and [NII] 121.9 μm with ionization potentials of 15.7 and 14.5 eV, respectively. This is because these lines are predominantly emitted in the outer parts of the H II region (see Fig. 8). If some of the observed regions do indeed have a significant escape fraction, the matter-bounded models will better reproduce the faintness of those lines. We keep in mind that the derived value of the depth corresponds to the depth for a single modeled cloud. In reality, multiple H II regions may contribute to the observed emission lines. In that case depth represents an averaged property, which is related to the fraction of matter- vs. radiation-bounded clouds.
 |
Fig. 8. Cumulative intensity (Icum) of the lowest ionization potential lines used in this study as function of the depth of the cloud for a model with log U = −2, nH = 2.2 cm−3 and tburst = 5.5 Myr. The intensities and the depth are normalized to the values reached at the ionization front. Both [NeII] 12.8 μm and [ArIII] 8.9 μm achieve the maximum emission at 50% of the depth of the cloud, while [NII] 121.9 μm and [ArII] 6.9 μm reach the total emission at the ionization front. |
4.3. Optimization
In order to derive the physical properties of the ionized gas, we compared the fluxes calculated (Sect. 4.1) with the grid of models presented in Sect. 4.2. We want to compare the observed line luminosities to the values predicted by CLOUDY (similar to the method used by, e.g., Cormier et al. 2012;Dimaratos et al. 2015). Since our CLOUDY calculations are performed using intensities (erg cm−2 s−1; Sect. 4.2) we convert predicted intensities to absolute luminosities, which requires a scaling factor defined as the ratio between the observed line luminosity, O, and the modeled line intensity, M. Ideally, we would like to use the observed line-to-bolometric luminosity ratio as a constraint in the models, but this proved difficult since we only had access to the infrared luminosity with the Herschel and Spitzer photometry measurements and not to the bolometric luminosity. We should convert the infrared luminosity to the bolometric luminosity, but since we are studying resolved star-forming regions and zones we do not have enough informations to provide an infrared-to-bolometric conversion factor. Instead of using a reference line that would be used to normalize the models to the observations, sglobal is an additional parameter in our models. In this way there is no a priori selection of the best line for the normalization.
The correlated uncertainties of the tracers are accounted for by building a covariance matrix between all tracers. For each model, the goodness of the fit is calculated with the χ2 as
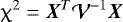 (2)
(2)
where X is a N-dimensional vector (N is the total number of the observed lines used as constraints). For each line j, Xj = Oj − (Mj × sglobal). Oj is the observed emission of line j, Mj is the model-predicted emission and sglobal is the global scaling factor described above. 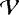 is the covariance matrix (N × N) with Vij = ρij σi σj, where σi and σj are the uncertainties related to the lines i and j, respectively, and ρij is the correlation coefficient between σi and σj. The uncertainties taken into account to calculate the matrix are the calibration uncertainties (5% for IRS and 12% for PACS), the uncertainties on the line fit (Tables 3 and 4), the uncertainties on the elemental abundances (Table 5), and the uncertainties due to the SL/LL stitching (15% for IRS LL; Sect. 3.1). We populate the covariance terms (uncertainties and correlation coefficient) using a Monte Carlo simulation with 106 iterations. The best model is found by minimizing the χ2 value.
is the covariance matrix (N × N) with Vij = ρij σi σj, where σi and σj are the uncertainties related to the lines i and j, respectively, and ρij is the correlation coefficient between σi and σj. The uncertainties taken into account to calculate the matrix are the calibration uncertainties (5% for IRS and 12% for PACS), the uncertainties on the line fit (Tables 3 and 4), the uncertainties on the elemental abundances (Table 5), and the uncertainties due to the SL/LL stitching (15% for IRS LL; Sect. 3.1). We populate the covariance terms (uncertainties and correlation coefficient) using a Monte Carlo simulation with 106 iterations. The best model is found by minimizing the χ2 value.
In order to understand the relationship and possible degeneracy between free parameters, we calculate the probability density function (PDF), which, for each physical parameter p = (p1,..., pn), is calculated as
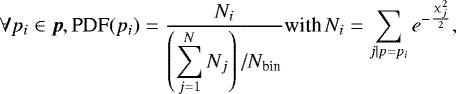 (3)
(3)
where the sum is performed over all of the j-models for which the free parameter p is equal to p1, p2,...,pn. The PDF is normalized by 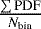 , where Nbin is the number of the bins. With this normalization, the PDFs can be easily compared even if they have a different number of bins.
, where Nbin is the number of the bins. With this normalization, the PDFs can be easily compared even if they have a different number of bins.
We computed the PDFs of each free parameter individually as well as the 2D PDFs for each pair of parameters, in order to highlight potential degeneracies between parameters in the parameter space. We also computed the histograms of each parameter for the best models only. The best models are those with a χ2 value lower than 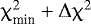 , where Δχ2 = 5.89 is the 1σ confidence interval with five free parameters (Press et al. 1992), i.e., nH, U, tburst, depth and s.
, where Δχ2 = 5.89 is the 1σ confidence interval with five free parameters (Press et al. 1992), i.e., nH, U, tburst, depth and s.
5. Results
5.1. Model results for clumps
5.1.1. Results
The best model solutions for each clump are listed in Table 6. Most clumps have nearly identical properties except A1#1, which has lower density and higher ionization parameter, but with larger error bars.
The density, nH, of the clumps is well constrained, with values between 100 and 400 cm−3. As a separate approach we use the theoretical ratio of [SIII] 33.5 μm/[SIII] 18.7 μm as a tracer of thedensity. The high spectral resolution IRS pointings give us access to the [SIII] line ratio at higher resolution (e.g., Dudik et al. 2007). Since the high-resolution observations are pointings with relatively small apertures, there is no spatial information. Hence, we can use these observations (Table B.1) only for clumps that coincide with the positions of the high-resolution pointings: M#3, A1#1, and A1#2. Using the calculation of a two-level system, as opposed to a full model, we find densities of 102.1, 102.5, and 102.5 cm−3, respectively. These results are compatible, within the uncertainties, with the values that we found with the model grids.
The physical depth is lower than one (between 0.55 and 0.90), which can be interpreted either as one cloud around the stellar cluster being matter bounded, or some fraction of the clouds around the stellar cluster being matter bounded and some fraction being radiation bounded. However, this parameter shows large uncertainties. The depth is mostly constrained by [ArII] 6.9 μm and [NII] 121.9 μm, and both lines have large error bars compared to most of the other tracers. For all of the clumps, the [ArII] 6.9 μm S/N is overall lower than two while [NII] 121.9 μm is not only faint but it also carries a relatively large calibration uncertainty (12%) because it is observed with PACS, unlike most of the other lines observed with IRS (5% calibration uncertainty).
The derived age of the burst and the ionization parameter are rather homogeneous across the galaxy, with ages ranging from 5.3 to 5.7 Myr and ionization parameters from 10−2.2 to 10−1. These two parameters also show large uncertainties. We calculated the PDFs and the histograms of the best models to estimate uncertainties. Figure A.1 shows the results for the clump M#1. The PDFs and the histograms of the other clumps are shown in Figs. C.1–C.4. Only the density seems to be tightly constrained by our tracers. All the other parameters do not have a well-defined solution. For a given clump, many models have similar χ2 values, close to the minimum χ2. Hence the PDFs are almost flat and the histograms include many models, providing parameter values distributed over the entire parameter range used in the model grid. Thus, we cannot provide a useful error estimate. The large uncertainties on the ionization parameter and the starburst age are related to the degeneracy between these two parameters, which can be clearly seen in the 2D PDF parameters. A model with a young stellar population combined with a low ionization parameter produces a similar spectrum as a model with older starburst and a high ionization parameter (Morisset et al. 2016).
Results of the best model parameters with 1σ uncertainties and the 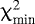 for the clumps.
for the clumps.
5.1.2. Constraining the age range
The PDFs of tburst show two peaks at ≈3 and ≈5.5 Myr. Since we do not have enough information on the age of the stellar population, we explored the effect of restricting the starburst age to either one of the two peaks, in order to witness the effects on the PDFs of the other parameters. Figure A.2 shows the results for the clump M#1. The figure shows the PDFs when constraining tburst between 2.8 and 3.4 Myr (i.e., the WR stage), and the PDFs for constraining tburst between 5.2 and 5.8 Myr (i.e., the typical H II region age for an instantaneous burst hypothesis; Sect. 4.2). The comparisons for the other clumps are shown in Figs. C.5–C.8. As expected the PDFs for the ionization parameter change. This is due to the well known degeneracy described above. The PDFs for the physical depth also change, which can be easily understood since the ionization parameter, the starburst age, and the physical depth all depend on the relative intensity of high- vs. low-ionization tracers. In the case of the physical depth, this is because higher ionization species are located closer to the ionizing sources. The density parameter, instead, is not affected by the range of starburst age.
For all of the clumps, the starburst age around 5.5 Myr is preferred by the models (higher probability), which is consistent with the model solution for the zones (Sect. 5.2). The subset of the models with an age around 5.5 Myr (Fig. A.2) corresponds to a relatively low physical depth parameter for the clumps (0.7–0.9), U between 10−2.5 and 10−1, and density consistently around ≥250 cm−3, except for the clump A1#1 with a lower density around 100 cm−3. Hence, these experiments show that well constrained solutions can be found if the degeneracy between U, the starburst age, and the physical depth parameters can be lifted, for instance by forcing the age around 5.5 Myr.
The best age solution equal to 5.5 Myr for all of the clumps (as well as for the zones) is probably driven by the detection of appreciable amounts of highly ionized species such as S3+ together with the hypothesis of an instantaneous burst. Such highly-ionized species are produced by energetic photons from short-lived stars (≲ 6 Myr). Therefore, for ages much larger than ≈6 Myr, we should not be able to detect [SIV] (or [NeIII]). A continuous SF could also be considered as an alternative to the instantaneous burst, but with our tracers we cannot investigate this case (Sect. 4.2.1).
The H II regions that we have analyzed are all distributed along the edge of a large H I and Hα hole. This hole is probably the result of the combined effect of stellar winds or supernovae over several Myrs. Wilcots & Miller (1998) calculated that the expanding bubble shell ought to become gravitationally unstable within 107 yr, implyingthat a second SF event, after the one that created the hole, is likely to be triggered. Hence, the young stellar population that we found with our modeling could be the second SF event triggered by stellar winds of the first stellar generation. An additional support of this scenario is given by the identification of several giant molecular clouds (GMCs) around the H I bubbles throughout IC 10 (Leroy et al. 2006). This is reminiscent of studies of Milky Way GMCs, which are formed at the overlapping interface between several Galactic H I supershells produced by previous episodes of stellar feedback, such as stellar winds or supernovae (Dawson et al. 2015; Inutsuka et al. 2015). Hence, the age found is consistent with a scenario of overlapping interfaces between several H I supershells that can trigger new episodes of SF and explain the location of GMCs in IC 10. However, this scheme is in contradiction with other studies that found that stellar feedback is not the dominant trigger of molecular cloud formation (e.g., Dawson et al. 2013). Another scenario that could explain this young stellar population is the interaction between the extended H I envelope and the galaxy. The gas infalling from the large reservoir may have driven the present star formation in the galaxy (Wilcots & Miller 1998).
5.1.3. Comparison with previous optical studies
The properties of the H II regions have been already investigated in previous studies using optical lines. It is interesting to compare our results with previous results. However, the comparison between our results and those obtained with optical spectroscopy should be regarded with caution. In fact, infrared lines probe deeper within the galaxy or within individual clouds than optical lines, possibly reaching regions with different physical conditions (Sect. 6.3).
López-Sánchez et al. (2011) analyzed a region that corresponds to M#1. For the whole area, they derived densities between 100 and 400 cm−3 and stellar population ~3.3 Myr. This bright H II region has been also studied by Arkhipova et al. (2011), which investigated the properties of the brightest H II regions of IC 10. Combining optical line ratios with CLOUDY models, they found densities between 30 and 200 cm−3, stellar age between 2.5 and 5 Myr and an ionization parameter between 10−3.6 and 10−2.5.
Both optical studies found a stellar age ~3 Myr. These solutions for stellar ages correspond to one of our PDF peaks we find for stellar age (Figs. A.1 and C.1–C.4). However, it does not correspond to our best solutions which have older stellar ages (~5.5 Myr), higher U (10−2.2–10−1) and are matter-bounded clouds. The smaller ages derived in the optical study also have consequences in that they derive lower U due to the stellar age-U degeneracy already discussed (Sect. 5.1.2). A younger stellar age would require a lower U value. Regarding the density, our results are in agreement with the densities derived by López-Sánchez et al. (2011) and with the highest values obtained by Arkhipova et al. (2011).
Results of the best-model parameters with the relative bounds of 1σ uncertainties, the absolute minimum χ2 and the number of line ratios available to constrain the solution, for each zone and Body areas.
5.2. Model results for zones and the Body
Table 7 summarizes the model solutions with 1σ uncertainties for the zones and the Body. The final column of Table 7 provides the reduced χ2 for those zones with more constraints than their number of free parameters (which was not the case for the clump analysis). Overall, the physical depth parameter is larger for the zones, between 0.7 and 1, compared to the individual clumps (0.55–0.9). As the volume increases, a larger fraction of ionizing photons is absorbed by the gas and the ionized gas component becomes globally almost radiation bounded. Interestingly, the depth of the largest area analyzed, B, is clearly below 1 and peaks at 0.85, which implies that even on the scale of the entire body, a significant fraction of ionizing radiation may escape. One would need the observations of the MIR and FIR ionized gas lines over the entire IC 10 galaxy scale to infer if ionizing photons manage to escape the galaxy outside its large H I halo extension. The stellar age we determine is almost the same for most of the zones, at ≈5.5 Myr, and it coincides with the most likely age of the stellar population of the clumps. Similar values of U and nH are found for the integrated M zone and the star-forming clumps M#1, M#2, and M#3 which are the brightest components in M (Tables 6 and 7). The same conclusion is reached for the arc zone A1 and the clumps A1#1 and A1#2, and for the zone B that is dominated by the bright regions associated with SF. This suggests that the properties estimated at the ~200 pc scale (zones) are dominated by the brightest compact clumps (~25 pc scales).
The results concerning the ionization parameter and the density highlight important differences between the regions in IC 10. Indeed, the zone M has log U = −1.4 and nH = 102.2 cm−3, while the zone A2 has log U = −2.4 and nH = 102.0 cm−3. These differences could be due to more stars, or to the fact that SF might be embedded in denser and more compact regions.
As for the clump analysis, we show in Fig. A.4 the PDFs and histograms of the best models (defined by the minimum χ2) of the zone M.Each parameter shows a well-defined peak in the PDF and the histograms of the best models occupy narrow ranges, implying that reliable values have been determined. This shows that with a suite of well-detected lines from different species with a range of critical densities and ionization potentials, and with an adequate method for finding the best model, one can derive several of the physical parameters at once and break the degeneracies, in particular between the starburst age and the ionization parameter. Even the depth parameter is well constrained (≈0.80) due to the robust detection of [ArII] when integrating over the zone M.
The PDFs and the histograms for the other zones are presented in the Appendix (Figs. D.1–D.7). One can see that depending on the S/N of the tracers used, it becomes impossible to constrain some parameters. This is particularly evident for the physical depth, due to lack of sufficient S/N of [ArII] as well as the density, since the [SIII] 33.5 μm line also has low S/N. The zone C is a star-forming region fainter than zones M or A1 and it was not observed in the [OIII] 88.4 μm line. The ionization parameter in the zone C is lower than in zone M and the best model of the zone C prefers high depth values (>0.85), however the large uncertainty of the [ArII] 6.9 μm line prevents a reliable determination of the physical depth for this zone. The zone D1 is the region with the lowest surface brightness and [ArII] 6.9 μm, [SIV] 10.5 μm, and [SIII] 18.7 μm were not detected. There were not enough constraints to solve for the free parameters. The low S/N of [ArII] 6.9 μm has a direct impact on the depth determination, while the low S/N of [SIII] 18.7 μm has a direct impact on the density determination. Even the starburst age or the ionization parameter cannot be determined, which is in part due to the nondetection of [SIV] 10.5 μm. For zone B (the main body of the galaxy), all of the tracers are available except [OIII] 88.4 μm, whose spatial coverage over the main body is incomplete. Results are shown in Fig. D.7. The parameters are well constrained, with a density around 100 cm−3, a large ionization parameter (log U > −2), and depth around 0.85.
Ratios of observed over best fit model integrated fluxes for each clumps.
5.3. Comparison between observations and best predicted emission
We compared the observed and predicted absolute line fluxes to quantify how observations are reproduced by our model. Tables 8 and 9 present the observed fluxes over the best-fit model fluxes for each clump and zone, respectively.We also computed the PDFs of the ratios between observed and predicted absolute line fluxes. Results for clump M#1 are shown in Fig. A.3 (for the other clumps see Figs. C.9–C.12). Most PDFs peak around 0 in log scale, meaning that the observations are well reproduced, most often within a factor of between two and three. There are some exceptions: [OIII] 88.4 μm in M#1, and [OIII] 88.4 μm and [NII] 121.9 μm in M#3 and A1#2. The best solution obtained underestimates by several factors these line fluxes. This suggests that only a small fraction of the observed emission originates from the dense H II regions. This is not surprising since [OIII] 88.4 μm and [NII] 121.9 μm originate from more diffuse ionized gas due to their low critical densities (5×102 cm−3 and 3×102 cm−3, respectively). The best models tend to fit the dense component because most of the lines that we used to constrain the solutions arise from a dense component and those tracers of the diffuse ionized gas have a larger calibration uncertainty. They thus carry less weight than the other lines in the calculation of the χ2. Unfortunately, we do not have enough tracers to constrain a model that combines both components. We also notice some systematic biases: [ArII] 6.9 μm and [ArIII] 8.9 μm are always overestimated by the models by a factor of about two. This result may indicate that the assumed argon elemental abundance in the models is too high, which seems reasonable considering the large uncertainty on the argon abundance (Table 5).
We computed the PDFs of the constraints (observation/model) also for the zones. Figure A.5 shows the PDFs for the zone M. Although the model parameters are well constrained, we can see that some lines, such as [NeII] and [OIII] are under-predicted by a factor of between three and four. Thus, we argue that these two lines are likely to arise in the relatively diffuse ionized gas ([NeII] because Ne+ exists for a large range of relatively low photon energies: 22–41 eV).
In summary, for the clumps as well as for the zones, most of the lines are reproduced within a factor of two. The cases for which the predicted fluxes are several factors away from the observed value would need to be investigated, but we tentatively describe the discrepancy due to the mix of the diffuse and dense ionized gas. While the denser phase related to the young clusters seems to be well constrained by a model with a single component at any spatial scale, such a model misses and ignores other phases that may be important.
Ratios of observed over best fit model integrated fluxes for the zones.
6. Discussion
6.1. Porosity of the ISM
Our models consider a single central ionizing source fully surrounded by a ionized gas cloud (Sect. 4.2). In reality, multiple clouds may contribute to the observed emission-lines, potentially not covering all of the lines of sight from the ionizing source (i.e., some radiation may escape). These clouds may be a combination of matter- and radiation-bounded clouds. Therefore, as for other parameters, the physical depth parameter represents some kind of average property.
Still, our results for the clump depth, between 0.75 and 0.90, imply that a significant portion of ionizing photons is able to escape the clumps. Such results are compatible with the investigation of Hidalgo-Gámez (2005), which shows that the photons leaking fromH II regions, in addition to the ionization provided by the WR stars, are responsible for the extended diffuse ionized gas in IC 10.This has implication for the photodissociation regions (PDRs), which are the neutral zones bordering only the radiation-bounded clouds. Thus, the estimated fraction of escaping ionizing photons may be used to infer a covering factor of radiation-bounded clouds around the ionizing source, which, in turn, sets important constraints when comparing PDR model predictions with the observations.
The depth parameter is larger when considering larger zones. However, some zones still require a depth parameter less than one. This implies that the larger zones are getting close to a radiation-bounded case, but not fully. The fact that the ISM is porous over large spatial scales is related to the abundance of dust in the galaxy, and therefore to the metallicity. Several studies show that the ISM at low metallicity is relatively more porous than more metal-rich environments (e.g., Madden et al. 2006; Kawada et al. 2011; Lebouteiller et al. 2012a; Cormier et al. 2015). IC 10 shows extended H I structures, and it is likely that the fraction of ionizing photons escaping IC 10 is close to zero when considering the entire galaxy. Direct measurements of the Lyman continuum in external galaxies suggest a small fraction of escaping ionizing photons (e.g., Cowie et al. 2009; Bridge et al. 2010; Leitet et al. 2013).
The importance of the ISM porosity at low metallicity is also suggested by the extended spatial distribution of [OIII] 88.4 μm line, which traces the diffuse ionized gas. It is shown to extend over large spatial scales in nearby giant H II regions in the Magellanic Clouds (Kawada et al. 2011; Lebouteiller et al. 2012a). IC 10 also shows an extended [OIII] 88.4 μm line emission throughout the main body of the galaxy (Fig. 5). Another observational tracer of the porosity is the ratio [OIII] to [CII], that mostly measures the amount of PDR vs the amount of low density ionized gas. It is observed that [OIII] 88.4 μm is the brightest infrared line in low-metallicity galaxies (while [CII] is relatively brighter in more metal-rich environments, Cormier et al. 2015). In IC 10 the [OIII] to [CII] ratio varies from 0.6 toward the more diffuse regions up to 4.5 toward the brightest H II regions. These characteristics of [OIII] 88.4 μm line emission in low metallicity environments suggest a high filling factor of diffuse highly ionized gas due to the lower abundance of dust which, in turn, can cause enhanced disruption of the natal molecular cloud resulting in a lower covering factor of dense clouds around young stellar clusters.
The depth parameter and [OIII]/[CII] are two signs of the ISM porosity. The way we have introduced the depth parameter in the model suggests a promising avenue for quantifying the ISM porosity. Understanding how the porosity changes as a function of metallicity requires applying this method developed for IC 10 to other spatially-resolved objects.
6.2. Origins of [CII], [FeII], and [SiII]
The C+, Fe+, and Si+ ions have ionization potentials lower than that of hydrogen (11.3, 7.9 and 8.2 eV, respectively), while the potential of the next ionization stage is above 13.6 eV. Therefore, the origin of these lines is ambiguous. They may arise from the neutral and from the ionized gas. In the neutral gas, the collision partners are mostly H0, H2, and free electrons (coming from the ionization of species with ionization potentials below 13.6 eV or from cosmic ray and soft X-ray photoionization of H). In the ionized gas, the collision partners are e− coming from the ionization of H by Lyman Continuum photons. Observationally, [CII] 157.7 μm is found to be a strong emission line originating in the surface layers of PDRs illuminated by the radiation field of massive stars (e.g., Negishi et al. 2001), but it can also arise from the ionized gas phase (Madden et al. 1993; Abel et al. 2005; Cormier et al. 2012).
For this reason we did not use [CII] 157.7 μm, [FeII] 25.9 μm and [SiII] 34.8 μm to constrain the physical conditions of the ionized gas. Instead we calculated the [CII], [FeII], and [SiII] emissions predicted by the models in the ionized gas, which we then compare to the observed values. Because of the low spatial resolution of [CII] and low S/N of [FeII] and [SiII] we only make this comparison for the integrated zones (Table 4).
The ratios of the observed over predicted values are shown in Figs. A.6 and D.8. Except forthe case of the zone D1, all of the other histograms show that the observed line is systematically larger than that predicted, in the range from about 30 to 150. From this we can conclude that those ambiguous lines in the M and arc zones do not arise from the ionized gas in the H II regions. The PDF of [SiII] 34.8 μm for the zone D1, instead, has a much broader distribution and the value of the observed [SiII] 34.8 μm emission over the best model solution is at the low end cutoff of the PDF, preventing a definite conclusion on the origin of the observed [SiII] for this zone. However, as discussed in Sect. 5.2, there is no satisfactory solution for the zone D1 so the “best” solution considered should be regarded with caution. Hence, using the model solutions to compare to the observed [CII], [SiII], and [FeII], we find that these lines seem to originate either in the PDR or in a potentially diffuse ionized gas component (which is not accounted for in the models).
Alternatively, [NII] 121.9 μm can be used to estimate the [CII] 157.7 μm coming fromthe ionized gas. With an ionization potential of 14.5 eV it originates only in the ionized phase. Knowing the elemental abundance and the ionization fractions C+/C and N+/N, the theoretical ratio [CII]/[NII] 122μm is then a function of gas density and temperature (Heiles 1994; Abel 2006; Oberst et al. 2006). Temperature plays a minor role and the ratio mostly depends on density. We have calculated the observed [CII]/[NII] pixel-by-pixel (for each pixel with good S/N) and we have found that only a tenth of the observed [CII] can be explained as originating in the ionized gas, for any density. The difference is due to the presence of [CII] in the neutral gas.
We conclude that [CII] does not arise from H II regions nor from a diffuse ionized gas phase but it arises from neutral gas/PDRs. We can, therefore, use [CII] with little or no correction for the future PDR modeling effort.
6.3. Extinction
The dwarf galaxy IC 10 lies close to the Galactic plane (Galactic latitude b = −3.3°), which implies a significant foreground reddening in addition to the internal reddening. Assuming the models are well constrained by the suite of infrared lines, we can compare the predicted intrinsic Hα emission to the observed value (not corrected for extinction; Sect. 3) and infer the extinction. The relation between the observed and the emitted Hα, assuming screen extinction, is given by the relation
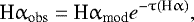 (4)
(4)
where Hαobs and Hαmod are the observed and the predicted emission, respectively, and τ(Hα) is the optical depth, τ(Hα) = C × k(Hα). The k(Hα) is the opacity curve used in CLOUDY (grain properties of the Small Magellanic Cloud from Weingartner & Draine 2001) and C is the reddening factor. Knowing C (thus τ(Hα)), then the extinction is AHα = 1.086 τ(Hα). Finally, using the reddening relation AHα = 3.404 E(B − V), we calculate the reddening. The values obtained with this method are presented in Table 10. We estimate for the clumps E(B − V) between 1.6 and 2.0 mag.
For an independent estimate, we also calculated the extinction using the HI recombination line Huα 12.3 μm observed with the Spitzer/IRS high-resolution pointings (Table B.1). From Hummer & Storey (1987), we estimated the theoretical ratio Hα/Huα expected for case B recombination, assuming a temperature 10 000 K and density of 100 cm−3, resulting in a value of ≈294. We thus computed τ(Hα) using the relation:
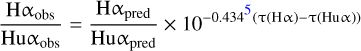 (5)
(5)
where both τ(Hα) and τ(Huα) are estimated using the opacity curve of CLOUDY. Then we calculate the E(B − V) values, following the procedure described before. The values are reported in Table 10. We estimate E(B − V) ~2 mag, that is, quite similar to the values obtained from the CLOUDY model predictions. Both methods provide high extinction values compared to previous works. This is not surprising since in our calculations we are using MIR and FIR lines to predict the emitted unreddened Hα (either the metallic species used for the CLOUDY predictions or the HI recombination line Huα), which allow us to probe deeper into dusty regions. However, the fact that we estimate consistently large values, even from clumps that are located far away from each other, suggests that the extinction is due to a uniform absorption component rather than from the star-forming region.
Previous studies report reddening values between 0.7 and 1.0 mag, depending on the method used. Using Cepheid variable stars, for example, Sakai et al. (1999) calculated E(B − V) = 1.16 mag, while Massey & Armandroff (1995) estimated E(B − V) = 0.75–0.80 mag based on WR stars and the blue stellar population. Table 10 summarizes the extinction values from the literature6. These measurements correspond to various regions and various spatial scales, so the comparison with our model estimates toward the clumps is not trivial. Borissova et al. (2000) investigated several regions used in our study (Table 10). The values we find with our methods are similar to those measured by Borissova et al. (2000) using the NIR to optical line ratio Brγ/Hα. Both studies used IR/optical line to estimate E(B − V), probing deeper into the dust than the methods based on optical observations alone.
The measurement of the visual extinction seen by the gas enables the potential use of many optical lines as constraints to the models. These new constraints complement the infrared tracers, by giving access to lines of different species, with different critical densities. Some remaining degeneracies between physical parameters may be broken using this combination.
E(B–V) in IC 10 fromseveral works, including this study.
7. Summary
We have presented the Spitzer/IRS and Herschel/PACS spectroscopic observations of the infrared cooling lines tracing the ionized gas in the nearby irregular dwarf galaxy IC 10. The proximity of this galaxy allows us to investigate the multiphase ISM on different spatial scales. We have focused our investigation on the nature of ionizing sources as well as the physical properties of the ionized gas, based on the observational constraints and the CLOUDY modeling solutions.
Firstly we have modeled the brightest H II regions in MIR and FIR emission lines. Three of these regions are located on the main star-forming regions of the galaxy (M) and two regions on the first arc (A1). We found tburst between 5.3 and 5.7 Myr, U between 10−2.2 and 10−1, density between 102 and 102.6 cm−3 and depth between 0.55 and 0.9. Thus, the physical properties of the clumps (tburst, log U and nH) are quite uniform, suggesting a common origin for their SF activity. The origin of the ionizing sources in the H II regions analyzed in this study could be related to the feedback from stellar winds or supernovae of a previous generation of stars. Using [ArII] 6.9 μm and [NII] 121.9 μm we determined that all of the clumps are matter-bounded clouds (depth between 0.55 and 0.9), with a significant fraction of ionizing photons escaping the nebula.
At this scale, we have also estimated the total extinction in each clumps with two different methods: (1) comparing the observed Hα with that predicted by our CLOUDY model, and 2) using the ratio of Hα(3-2)/Huα(7-6). The values obtained with the two methods are similar, with E(B − V) between 1.6 and 2 mag.
Secondly modeling larger areas (~200 pc; zones), which were expected to exhibit different local physical conditions, we found that overall, the physical depth parameter is larger for the zones, between 0.7 and 1, than for the clumps. The estimated stellar age is almost the same for most of the zones, at ~5.5 Myr, and the results are in agreement with the stellar age determined for the clumps. Instead, the results concerning the ionization parameter and the density highlight differences between the regions in IC 10. Modeling the zones with a single component model, we found that similar physical conditions are obtained for various spatial scales as long as bright components dominate the emission in the integrated zone. The depth solutions for larger spatial scales suggest that the clouds are almost radiation bounded. The matter-bounded nature at almost any spatial scale indicates that the ISM is quite porous, which is possibly due to the low metallicity of the environment.
In the case of the clumps, the method seems to fail in constraining well the model parameters and we had to include additional constraints ([SIII] line ratio or fixing the age of the starburst) to narrow down the range of parameters. However, when all of the tracers are available and the S/N is sufficient, the method provides satisfactory solutions with reasonable reduced χ2 values, with few biases and with the possibility of breaking degeneracies between parameters. The comparison between the observations and the best predicted emission reveals that at all of the spatial scales analyzed, a single component model is not enough to reproduce all of the tracers. Indeed, another diffuse ionized gas component may be necessary.
Finally we have investigated the origin of the [CII] 157.7 μm, [FeII] 25.9 μm and [SiII] 34.8 μm emission to determine the fraction of the emission arising from the ionized gas phase. We find that most of the emission of the [CII], [FeII], and [SiII] arises in the PDR component.
This investigation of the physical properties of IC 10 confirms the importance of the ionized gas in a porous ISM which seems to characterize low-metallicity environments (Cormier et al. 2012, 2015; Lebouteiller et al. 2012a; Chevance et al. 2016). As a consequence of the low dust abundance, the hard photons from the star-forming sites leak from the H II regions and traverse the larger scales. We find in this study that photon leakage seems to decrease with the increasing size of the region considered, suggesting that on the global scale, the galaxy appears to behave more like a radiation-bounded object. However, in order to verify this hypothesis of local to global scales, a thorough modeling at full global scales is required.
This work also suggests that a large-scale simple single-component model cannot reproduce well all of the observed line emission, in particular the [NeII] and [OIII]. A diffuse ionized component may be appropriate for the largest scales. A multicomponent CLOUDY model would be useful to determine the properties of this diffuse phase. Cormier et al. (2012) have also demonstrated that for the case of the more distant, unresolved, starburst galaxy Haro 11, an additional low-ionization component reproduces better the [NeII] 12.8 μm emission without affecting the other ionic tracers. Cormier et al. (in prep.) constructs two-component CLOUDY models to explain the global emission lines in the arising in the dense and diffuse ionized components in the DGS.
Acknowledgements
The authors would like to thank the anonymous referee for providing comments that help to improve the paper. We also thank Deidre Hunter for constructive feedback. We acknowledge support from the DAAD/PROCOPE projects 57210883/35265PE and the SYMPATICO grant (ANR-11- BS56-0023) of the French Agence Nationale de la Recherche. The authors acknowledge support by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. D.C. is supported by the European Union’s Horizon 2020 research and innovation programe under the Marie Skłodowska-Curie grant agreement No. 702622. N.P.A. acknowledges funding from NASA and SOFIA through grant program SOF 05-0084. S.H. acknowledges financial support from DFG program HO 5475/2-1. M.Y.L. acknowledges support from the DIM ACAV of the Région Île de France. M.C. gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG) through an Emmy Noether Research Group, grant number KR4801/1-1. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including University of Lethbridge (Canada); NAOC (China); CEA, LAM(France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, University of Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). Thisdevelopment has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA).
Appendix A: Additional figures
 |
Fig. A.1. Results for the clump M#1. Top panels: PDFs for nH, log U, tburst (Age), and physical depth. The blue histograms show the PDF for each single parameter. The 2D PDFs are shown as density plots(black ~1, to white ~0) at the intersection between two parameters. The blue horizontal and vertical lines indicate the parameter value corresponding to the best model solution, with the corresponding parameter value given in blue. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. A.2. PDFs for the clump M#1. The blue histograms show the PDFs from Fig. A.1, with the best model ( |
 |
Fig. A.3. PDFs of observed vs. predicted constraint values (absolute line fluxes and the [SIII] line ratio) for the clump M#1. We also show the PDF for [ArIII] 8.9 μm/[ArII] 6.9 μm as an a posteriori check. The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the right corner. |
 |
Fig. A.4. Results for the zone M (Main). Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. A.5. PDFs of the observed vs. predicted constraint values for the M (Main). See Fig. A.3 for the plot description. |
 |
Fig. A.6. PDFs of the observed over predicted [SiII] 34.8 μm (left panel) and [CII] 157.7 μm (middle panel) for the zone M (top panels) and of the [SiII] 34.8 μm (left panel) and [FeII] 25μm (right panel), for the D2 zone. The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the corner. |
Appendix B: HR-IRS pointings
Fluxes (× 10−16 W m−2) obtained with high-resolution (HR) modules for each pointing used in this work.
Five bright knots throughout IC 10 were mapped with high-resolution modules (R ≈ 600) Short-High (SH; λ = 9.9–19.6 μm) and Long-High (LH; λ = 18.7– 37.2 μm), as it has been presented in Sect. 3.1. Figure B.1 shows the position of the high-resolution slits, while the fluxes are provided in Table B.1. We used these data as independent calculation of the density (Sect. 5.1) and the reddening values (Sect. 6.3) for some of the clumps.
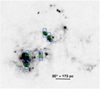 |
Fig. B.1. Hα map of IC 10. The Spitzer/IRS high-resolution slits are overlaid, the long wavelength module is shown in blue and the short wavelength module in green. |
Appendix C: Clump solutions
Here we present the modeling solutions obtained for the clumps M#2, M#3, A1#1, and A1#2 (see Sect. 5.1). Figures C.1–C.4 show, in the upper rows, the PDFs of each of the four physical properties individually and the 2D PDFs for each pair of parameters. While, on the bottom row, the corresponding statistical histograms of the parameters of the clump are shown.
Figures C.5–C.8 show the effect on the solutions if we selected only the model solutions with tburst between 2.8 and 3.3 Myr (top) and tburst between 5.2 and 5.8 Myr (bottom).
Finally, we compute the PDFs of the ratios between observed and predicted line emission. Results for the M#2, M#3, A1#1, and A1#2 are shown in Figs. C.9–C.12.
 |
Fig. C.5. PDFs for the clump M#2. The blue histograms show the PDFs from Fig. C.1, with the best model ( |
 |
Fig. C.9. PDFs of observed vs. predicted constraint values for the clump M#2. See Fig. A.3 for the plot description. |
 |
Fig. C.10. PDFs of observed vs. predicted constraint values for clump M#3. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
 |
Fig. C.11. PDFs of observed vs. predicted constraint values for the clump A1#1. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
 |
Fig. C.12. PDFs of observed vs. predicted constraint values for the clump A1#2. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
Appendix D: Zone solutions
 |
Fig. D.1. Results for the A1 (Arc1) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.2. Results for the A2 (Arc2) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.3. Results for the C (Central) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.4. Results for the D2 (Diffuse2) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.5. Results for the D3 (Diffuse3) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.6. Results for the D1 (Diffuse1) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.7. Results for the B (Body) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
 |
Fig. D.8. PDFs of the observed over predicted [SiII] 34.8 μm (left panels) and [CII] 157.7 μm (right panels) for the zones A1 (top panels) A2 (middle panel) and D1 (bottom panels). The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the corner. |
References
- Abel, N. P. 2006, MNRAS, 368, 1949 [NASA ADS] [CrossRef] [Google Scholar]
- Abel, N. P., Ferland, G. J., Shaw, G., & van Hoof P. A. M. 2005, ApJS, 161, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhipova, V. P., Egorov, O. V., Lozinskaya, T. A., & Moiseev, A. V. 2011, Astron. Lett., 37, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ashley, T., Elmegreen, B. G., Johnson, M., et al. 2014, AJ, 148, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borissova, J., Georgiev, L., Rosado, M., et al. 2000, A&A, 363, 130 [NASA ADS] [Google Scholar]
- Bridge, C. R., Teplitz, H. I., Siana, B., et al. 2010, ApJ, 720, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Madden, S. C., Lebouteiller, V., et al. 2016, A&A, 590, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Ford, H. C., & Neill, J. D. 1989, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, C. J. R., Verstocken, S., Bianchi, S., et al. 2018, A&A, 609, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Lebouteiller, V., Madden, S. C., et al. 2012, A&A, 548, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowie, L. L., Barger, A. J., & Trouille, L. 2009, ApJ, 692, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Drissen, L., Abbott, J. B., Royer, P., & Smartt, S. J. 2003, A&A, 404, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, J. R., McClure-Griffiths, N. M., Wong, T., et al. 2013, ApJ, 763, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, J. R., Ntormousi, E., Fukui, Y., Hayakawa, T., & Fierlinger, K. 2015, ApJ, 799, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Demers, S., Battinelli, P., & Letarte, B. 2004, A&A, 424, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dimaratos, A., Cormier, D., Bigiel, F., & Madden, S. C. 2015, A&A, 580, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dudik, R. P., Weingartner, J. C., Satyapal, S., et al. 2007, ApJ, 664, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fahrion, K., Cormier, D., Bigiel, F., et al. 2017 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Galliano, F. 2018, MNRAS, 476, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 1990, ApJ, 363, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Rafferty, D. A., Horneffer, A., et al. 2018, MNRAS, 476, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1994, ApJ, 436, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Hidalgo-Gámez, A. M. 2005, A&A, 442, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodge, P., & Lee, M. G. 1990, PASP, 102, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1936, Realm of the Nebulae (Connecticut: Yale University Press) [Google Scholar]
- Huchtmeier, W. K. 1979, A&A, 75, 170 [NASA ADS] [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A. 1999, in New Views of the Magellanic Clouds, eds. Y.-H. Chu, N. Suntzeff, J. Hesser, & D. Bohlender, IAU Symp., 190, 217 [NASA ADS] [Google Scholar]
- Hunter, D. A. 2001, ApJ, 559, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. a., & Elmegreen, B. G. 2004, AJ, 128, 2170 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-i., Inoue, T., Iwasaki, K., & Hosokawa, T. 2015, A&A, 580, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., & Hollenbach, D. J. 2006, ApJ, 644, 283 [Google Scholar]
- Kawada, M., Takahashi, A., Yasuda, A., et al. 2011, PASJ, 63, 903 [NASA ADS] [Google Scholar]
- Kewley, L. J., Rupke, D., Zahid, H. J., Geller, M. J., & Barton, E. J. 2010, ApJ, 721, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, M., Kim, E., Hwang, N., et al. 2009, ApJ, 703, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Barry, D. J., Spoon, H. W. W., et al. 2011, ApJS, 196, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Cormier, D., Madden, S. C., et al. 2012a, A&A, 548, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Sloan, G. C., Groenewegen, M. A. T., et al. 2012b, A&A, 546, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Barry, D. J., Goes, C., et al. 2015, ApJS, 218, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Péquignot, D., Cormier, D., et al. 2017, A&A, 602, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M.-Y., Madden, S. C., Lebouteiller, V., et al. 2016, A&A, 596, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitet, E., Bergvall, N., Hayes, M., Linné, S., & Zackrisson, E. 2013, A&A, 553, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [Google Scholar]
- Leroy, A., Bolatto, A., Walter, F., & Blitz, L. 2006, ApJ, 643, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, S., & Lee, M. G. 2015, ApJ, 804, 123 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R., Mesa-Delgado, A., López-Martín, L., & Esteban, C. 2011, MNRAS, 411, 2076 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Geis, N., Genzel, R., et al. 1993, ApJ, 407, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Poglitsch, A., Geis, N., Stacey, G. J., & Townes, C. H. 1997, ApJ, 483, 200 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., & Gonçalves D. R. 2009, MNRAS, 398, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., & Armandroff, T. E. 1995, AJ, 109, 2470 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., & Holmes, S. 2002, ApJ, 580, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1972, ApJ, 176, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Mayall, N. U. 1935, PASP, 47, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Morisset, C., Delgado-Inglada, G., Sánchez, S. F., et al. 2016, A&A, 594, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negishi, T., Onaka, T., Chan, K.-W., & Roellig, T. L. 2001, A&A, 375, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nidever, D. L., Ashley, T., Slater, C. T., et al. 2013, ApJ, 779, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Oberst, T. E., Parshley, S. C., Stacey, G. J., et al. 2006, ApJ, 652, L125 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Osterbrock, D., & Ferland, G. 2005, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Herndon, VA: University Science Books) [Google Scholar]
- Ott, S. 2010, Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser. (San Francisco: Astronomical Society of the Pacific), 2010, 434, 139 [Google Scholar]
- PACS Observer’s Manual 2013, http://herschel.esac.esa.int/Docs/PACS/html/pacs_om.html [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Rémy-Ruyer,A. 2013, Ph.D. Thesis, Université Paris 11, France. [Google Scholar]
- Rémy-Ruyer,A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richer, M. G., Bullejos, A., Borissova, J., et al. 2001, A&A, 370, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, S., Madore, B. F., & Freedman, W. L. 1999, ApJ, 511, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Tammann, G. A. 1974, ApJ, 194, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, N., Bono, G., Stetson, P. B., et al. 2009, ApJ, 699, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Armus, L., Dale, D. A., et al. 2007, PASP, 119, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Stasińska, G. 2007, The Emission Line Universe (Cambridge: Cambridge University Press) [Google Scholar]
- Thurow, J. C., & Wilcots, E. M. 2005, AJ, 129, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Sheehy, C. D., & Graham, J. R. 2007, ApJ, 662, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wilcots, E. M., & Miller, B. W. 1998, AJ, 116, 2363 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D., & Reid, I. N. 1991, ApJ, 366, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Magrini, L., Matteucci, F., et al. 2010, A&A, 520, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Crowther et al. (2003) identified in total 25 WR, 14 WC (WR star whose spectrum is dominated by lines of carbon) and 11 WN (WR star whose spectrum is dominated by lines of nitrogen), which is an unusually high WC/WN for a metal-poor galaxy. Observed WC/WN as a function of the metallicity for different galaxies of the Local Group is shown in Massey & Holmes (2002) and in Crowther et al. (2003).
CLOUDY can compute the propagation of the radiation assuming constant density or constant pressure. This is important when the model is computed beyond the ionized phase. In constant pressure setup the density is adjusted such that the total pressure is constant throughout the cloud. Total pressure includes thermal pressure, turbulent, ram, and magnetic pressures and radiation pressure, both from the stellar continuum and internally generated light.
The steps are smaller between 2.5 to 3.5 Myr and between 5 to 6 Myr because the PDFs of our solutions show the peaks in these two ranges (Sect. 5.1), thus we want to have a finer grid to investigate these ranges more accurately.
0.434 = log10(2.7), see Eq. (4).
For more references see Demers et al. (2004).
All Tables
Main properties of the IRS modules and the AORs of the IRS observations of IC 10.
Results of the best model parameters with 1σ uncertainties and the 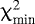 for the clumps.
for the clumps.
Results of the best-model parameters with the relative bounds of 1σ uncertainties, the absolute minimum χ2 and the number of line ratios available to constrain the solution, for each zone and Body areas.
Fluxes (× 10−16 W m−2) obtained with high-resolution (HR) modules for each pointing used in this work.
All Figures
 |
Fig. 1. Three-color image of IC 10 (main body) with polycyclic aromatic hydrocarbon (PAH) emission (Spitzer/IRAC4, 8 μm) in red, H α (1.8 m Perkins Telescope; Hunter & Elmegreen 2004) in green, and stars (Spitzer/IRAC1, 3.6 μm) in blue. The tracers highlight the bright star-forming region in the center and two arcs with extended Hα and PAH emission. |
| In the text | |
 |
Fig. 2. Hα map. Contours and boxes show the areas covered by the Herschel/PACS map of [OIII] 88.4 μm (in red), Spitzer/IRS SL maps (in magenta, SL1 and SL2), and Spitzer/IRS LL maps (in blue, LL1 and LL2). The yellow crosses show the positions of the high-resolution pointings. |
| In the text | |
 |
Fig. 3. SED ofa region of ~(174 pc × 226 pc) in IC 10 (Main zone, see Fig. 6). The black dots with error bars represent the WISE, Herschel/PACS and Herschel/SPIRE photometry. The photometry data come from the DustPedia database (Clark et al. 2018), and will be interpreted in Lianou et al. (in prep.). The black emission lines are from the Spitzer/IRS and Herschel/PACS spectrometers. The data uncertainties are shown in the gray area. These observations have been fitted by the model of Galliano (2018). The total dust component is shown as the red area, stellar contribution as the yellow area, and the blue line represents the total model. The brightest emission features are labeled in green, including the main aromatic features (A.F.), commonly called PAH. |
| In the text | |
 |
Fig. 4. Individual Spitzer/IRS and Herschel/PACS spectral lines observed in the Main zone (defined in Fig. 6). |
| In the text | |
 |
Fig. 5. Spectral maps from Herschel/PACS and Spitzer/IRS of IC 10 used in this study in W m−2 sr−1. All of the tracers show bright clumps in the southeast region (Main zone; defined in Fig. 6) and in the northwest (Arc1 zone; defined in Fig. 6). |
| In the text | |
 |
Fig. 6. Outlines of the various zones and clumps investigated are overlaid on the Hα background image. |
| In the text | |
 |
Fig. 7. Hydrogen density (solid line) and ionization fraction (ne/nH; dashed line) as a function of the depth of the cloud for a model with log U = −2, nH = 2.2 cm−3 and tburst = 5.5 Myr. The depth is normalized to the depth at the ionization front. |
| In the text | |
 |
Fig. 8. Cumulative intensity (Icum) of the lowest ionization potential lines used in this study as function of the depth of the cloud for a model with log U = −2, nH = 2.2 cm−3 and tburst = 5.5 Myr. The intensities and the depth are normalized to the values reached at the ionization front. Both [NeII] 12.8 μm and [ArIII] 8.9 μm achieve the maximum emission at 50% of the depth of the cloud, while [NII] 121.9 μm and [ArII] 6.9 μm reach the total emission at the ionization front. |
| In the text | |
 |
Fig. A.1. Results for the clump M#1. Top panels: PDFs for nH, log U, tburst (Age), and physical depth. The blue histograms show the PDF for each single parameter. The 2D PDFs are shown as density plots(black ~1, to white ~0) at the intersection between two parameters. The blue horizontal and vertical lines indicate the parameter value corresponding to the best model solution, with the corresponding parameter value given in blue. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. A.2. PDFs for the clump M#1. The blue histograms show the PDFs from Fig. A.1, with the best model ( |
| In the text | |
 |
Fig. A.3. PDFs of observed vs. predicted constraint values (absolute line fluxes and the [SIII] line ratio) for the clump M#1. We also show the PDF for [ArIII] 8.9 μm/[ArII] 6.9 μm as an a posteriori check. The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the right corner. |
| In the text | |
 |
Fig. A.4. Results for the zone M (Main). Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. A.5. PDFs of the observed vs. predicted constraint values for the M (Main). See Fig. A.3 for the plot description. |
| In the text | |
 |
Fig. A.6. PDFs of the observed over predicted [SiII] 34.8 μm (left panel) and [CII] 157.7 μm (middle panel) for the zone M (top panels) and of the [SiII] 34.8 μm (left panel) and [FeII] 25μm (right panel), for the D2 zone. The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the corner. |
| In the text | |
 |
Fig. B.1. Hα map of IC 10. The Spitzer/IRS high-resolution slits are overlaid, the long wavelength module is shown in blue and the short wavelength module in green. |
| In the text | |
 |
Fig. C.1. Results for the clump M#2. See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. C.2. Results for the clump M#3. See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. C.3. Results for the clump A1#1. See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. C.4. Results for the clump A1#2. See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. C.5. PDFs for the clump M#2. The blue histograms show the PDFs from Fig. C.1, with the best model ( |
| In the text | |
 |
Fig. C.6. PDFs for the clump M#3. See Fig. C.5 for the plot description. |
| In the text | |
 |
Fig. C.7. PDFs for the clump A1#1. See Fig. C.5 for the plot description. |
| In the text | |
 |
Fig. C.8. PDFs for the clump A1#2. See Fig. C.5 for the plot description. |
| In the text | |
 |
Fig. C.9. PDFs of observed vs. predicted constraint values for the clump M#2. See Fig. A.3 for the plot description. |
| In the text | |
 |
Fig. C.10. PDFs of observed vs. predicted constraint values for clump M#3. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
| In the text | |
 |
Fig. C.11. PDFs of observed vs. predicted constraint values for the clump A1#1. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
| In the text | |
 |
Fig. C.12. PDFs of observed vs. predicted constraint values for the clump A1#2. For this clump [NII] 121.9 μm is an available constraint. See Fig. A.3 for the plot description. |
| In the text | |
 |
Fig. D.1. Results for the A1 (Arc1) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.2. Results for the A2 (Arc2) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.3. Results for the C (Central) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.4. Results for the D2 (Diffuse2) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.5. Results for the D3 (Diffuse3) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.6. Results for the D1 (Diffuse1) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.7. Results for the B (Body) zone. Top panels: PDFs, see Fig. A.1 for the plot description. Bottom panels: histograms of parameter distributions for the best models (see text for details). |
| In the text | |
 |
Fig. D.8. PDFs of the observed over predicted [SiII] 34.8 μm (left panels) and [CII] 157.7 μm (right panels) for the zones A1 (top panels) A2 (middle panel) and D1 (bottom panels). The vertical red lines indicate the observed vs. predicted values for the best model (lowest χ2), with the corresponding value shown in the corner. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.