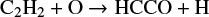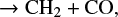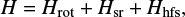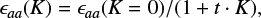| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201834419 | |
| Published online | 15 January 2019 | |
Rotational spectroscopy of the HCCO and DCCO radicals in the millimeter and submillimeter range⋆
1
Center for Astrochemical Studies, Max-Planck-Institut für extraterrestrische Physik, Gießenbachstraße 1, 85748 Garching, Germany
e-mail: chantzos@mpe.mpg.de
2
Ural Federal University, Ekaterinburg, Russia
3
Visiting Leading Researcher, Engineering Research Institute “Ventspils International Radio Astronomy Centre” of Ventspils University of Applied Sciences, Inženieru 101, Ventspils 3601, Latvia
Received:
12
October
2018
Accepted:
27
November
2018
Context. The ketenyl radical HCCO has recently been detected in the interstellar medium (ISM) for the first time. Further astronomical detections of HCCO will help us understand its gas-grain chemistry, and subsequently revise the oxygen-bearing chemistry towards dark clouds. Moreover, its deuterated counterpart DCCO has never been observed in the ISM. A broad spectroscopic investigation is still lacking for both HCCO and DCCO, although they exhibit a significant astrophysical relevance.
Aims. In this work we aim to measure the pure rotational spectra of the ground state of HCCO and DCCO in the millimeter and submillimeter region, considerably extending the frequency range covered by previous studies.
Methods. The spectral acquisition was performed using a frequency-modulation absorption spectrometer between 170 and 650 GHz. The radicals were produced in a low-density plasma generated from a select mixture of gaseous precursors. We were able to detect and assign more than 100 rotational lines for each isotopolog.
Results. The new lines have significantly enhanced the previous data set allowing the determination of highly precise rotational and centrifugal distortion parameters. In our analysis we took into account the interaction between the ground electronic state and a low-lying excited state (Renner–Teller pair) which enables the prediction and assignment of rotational transitions with Ka up to 4.
Conclusions. The present set of spectroscopic parameters provides highly accurate, millimeter, and submillimeter rest-frequencies of HCCO and DCCO for future astronomical observations. We also show that towards the pre-stellar core L1544, ketenyl peaks in the region where c-C3H2 peaks, suggesting that HCCO follows a predominant hydrocarbon chemistry, as already proposed by recent gas-grain chemical models.
Key words: molecular data / methods: laboratory: molecular / techniques: spectroscopic / radio lines: ISM
The full list of transitions is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/621/A111
© ESO 2019
1. Introduction
The evolution of organic molecules from dark clouds to planetary systems is of fundamental importance to shed light on the astrochemical heritage of life on Earth (Caselli & Ceccarelli 2012). However, interstellar organic chemistry is still not fully understood (Herbst & van Dishoeck 2009). Complex organic species (COMs) have been widely detected in hot cores embedded in high-mass star forming regions (Cummins et al. 1986; Blake et al. 1987) and low-mass hot corinos (Cazaux et al. 2003; Bottinelli et al. 2004). Their formation towards warm sources is well reproduced by the so-called “warm-up scenario” (Garrod & Herbst 2006; Garrod 2008), wherein COMs form on the surface of dust grains through radical-radical reactions and are eventually ejected to the gas-phase via thermal desorption during the warm-up phase of the protostar. Organic species, such as CH3OCH3, H2CCO, and CH3OCHO have also been detected in cold, pre-stellar cores (Cernicharo et al. 2012; Bacmann et al. 2012; Vastel et al. 2014; Jiménez-Serra et al. 2016) but other formation processes are needed to justify their presence in the gas phase, since there is no rise in temperature toward a starless or a pre-stellar core (T < 20 K). Pre-stellar cores are the initial phase of star formation immediately before gravitational collapse sets in, which ultimately leads to the birth of a protostar.
So far, there have been several chemical models (Vasyunin & Herbst 2013; Reboussin et al. 2014; Ruaud et al. 2015; Chang & Herbst 2016) that try to reproduce the observed abundances of COMs toward pre-stellar cores. All of them include grain-surface reactions and nonthermal desorption processes. One of these studies was carried out by Vasyunin et al. (2017), in which organic species are formed on dust grains through ion-molecule as well as radiative association reactions, and released in the gas phase through reactive desorption. With a multilayer treatment of ice chemistry and a special approach to reactive desorption based on experimental studies of Minissale et al. (2016), Vasyunin et al. (2017) were able to reproduce the abundance of many COMs, like CH3OH and HCOOCH3, toward the pre-stellar core L1544. Recent work by Shingledecker et al. (2018) has shown that taking into account cosmic-ray proton bombardment of icy dust grain mantles in gas-grain chemical models also boosts the formation of some COMs. Despite the progress that has been made in the last few years, there are still some important pieces of the puzzle missing to understand the interstellar organic chemistry taking place in dark clouds.
One of the missing pieces in oxygen-bearing chemistry has been ketenyl, HCCO, a possible building block of oxygen-containing COMs. HCCO was detected for the first time by Agúndez et al. (2015) in two sources, Lupus-1A and L483. After including all known formation and destruction reactions of HCCO from the literature and the chemical databases, it was found that the main formation mechanism for HCCO is the reaction between OH and C2H. Nevertheless, a discrepancy of three orders of magnitude between the observed and the predicted HCCO abundance implies that there is an effective formation mechanism of HCCO that is still unknown and which can compete against its depletion by reactions with neutral atoms (Agúndez et al. 2015). Previous studies (Hudson & Loeffler 2013; Maity et al. 2014) had shown that ketene, H2CCO, can be formed in ices after UV and electron irradiation, representing a possible formation path for HCCO as an intermediate product. In Wakelam et al. (2015a), the rate coefficient of the main HCCO formation pathway was increased by almost an order of magnitude based on the comparison to similar reactions. In doing so, their chemical model was able to reproduce the observed abundances of HCCO towards the sources Lupus-1A and L483. However, the reaction of interest, OH + C2H → HCCO + H, has never been studied before, either theoretically or experimentally, and there remains a large uncertainty surrounding HCCO chemistry. From the above considerations, it is evident that further observations are needed to revise the gas-grain chemistry of HCCO. Moreover, deuterated ketenyl, DCCO, has never been detected in the ISM and its spectral line catalog is not yet available in the online databases. The interstellar detection of DCCO would give information about possible deuteration routes of HCCO, and put more constraints on current gas-grain chemical models.
The laboratory spectrum of HCCO was first measured by photoionisation mass spectroscopy (Jones & Bayes 1972) targeting the reactions
where channel (1) is more than two times faster than reaction (2) throughout a broad range of temperatures (Michael & Wagner 1990). Follow-up work was done by Endo & Hirota (1987), where pure rotational lines of HCCO (N = 15−18) and DCCO (N = 17−20) were measured in the 320–390 GHz range. Their analysis showed a considerable interaction between the ground state and a low-lying excited state (Renner–Teller pair), which leads to a strong perturbation of the spin-rotation splitting. In another work done by Ohshima & Endo (1993), HCCO was studied in the microwave spectral region in a supersonic jet expansion. In particular, the fine and hyperfine components of the N = 1 – 0 transition were measured at around 21 GHz, enabling the determination of the hyperfine coupling constants ascribed to the hydrogen nucleus. A further study by Szalay et al. (1996) involved the ab initio calculations of rotational constants, equilibrium geometries, and excitation energies of the ground and excited electronic states of HCCO. Their results are in good agreement with the values obtained from the microwave and millimeter measurements.
In this work we have recorded the pure rotational spectra of HCCO and DCCO between 170 and 650 GHz, substantially extending the frequency range compared to the previous studies mentioned above. More than 100 lines were recorded and assigned for each isotopolog, reducing the errors of the rotational and centrifugal distortion constants down by a factor of ∼40. With this new data set we are able to provide highly accurate rest frequencies for future astronomical millimeter observations.
2. Laboratory experiments
In the present work, the rotational spectra were taken with the frequency-modulation mm/sub-mm Absorption Cell spectrometer developed at the Center for Astrochemical Studies (CASAC) in Garching. A full description of the experiment can be found in Bizzocchi et al. (2017). This instrument consists of an absoprtion cell made of a Pyrex tube (3 m long and 5 cm in diameter), which serves as the main flow cell. Each end is equipped with one stainless steel electrode in order to apply a high voltage and ignite a discharge, creating a plasma from the appropriate mixture of gaseous precursors. To stabilize the plasma and minimize the collisions between the species, the outer walls of the cell are cooled with liquid nitrogen.
As a radiation source we use an active multiplier chain (Virginia Diodes, Inc.) which is coupled to a synthesizer (Keysight E8257D) operating at centimeter wavelengths. By applying additional frequency multipliers, the radiation source can cover the 82–1100 GHz frequency range continuously. High phase accuracy is achieved by phase locking the synthesizer with an external 10 MHz rubidium clock (Stanford Research Systems). For the detection of the molecular signal we use a liquid-He-cooled InSb hot electron bolometer (QMC Instruments Ltd.). The signal is frequency-modulated with a sine wave of 15 kHz, while the output detector signal is demodulated at 2f (where f denotes the modulation frequency) by a lock-in amplifier (Standford Research Systems SR830), meaning that we record the second derivative of the actual absorption line.
HCCO and DCCO were produced by a DC high-voltage plasma (∼11 mA, ∼0.6 kV) of a 2:1 mixture of O2 and C2H2/C2D2 diluted in a buffer gas of Ar (total pressure ∼28 mTorr). The freezing point of acetylene C2H2 provides a lower limit to the cooling temperature of the cell at around 190 K.
 |
Fig. 1. Left panel: recording of the JKa, Kc = 230,23 – 220,22 transition of HCCO. Total integration time is 309 s with a time constant of 3 ms. Right panel: recording of the JKa, Kc = 120,12 – 110,11 transition of DCCO. Total integration time is 127 s with a 3 ms time constant. The red curves represent our modeled 2f Voigt profiles (see text). |
3. Results and data analysis
HCCO and DCCO have a 2A″ ground electronic state with one unpaired electron at the carbon nucleus and show a paramagnetic nature1. Both species show a rich rotational spectrum with fine (spin-rotation interaction) and hyperfine structure (H/D nuclear spin). In addition, the ground state rotational constants determined in Endo & Hirota (1987) led to inertia defects of 0.155(15) and 0.120(4) amu Å for HCCO and DCCO, respectively, confirming the planarity of the species. The dipole moment along the a axis has been determined by Szalay et al. (1996) to be 1.59D and by Jerosimić (2007) to be 1.68D. We have adopted the second value for the predictions of the line intensities. The total dipole moment is only marginally larger than its a component. We detected 114 and 138 new lines for HCCO and DCCO, respectively. These are a-type rotational transitions, with N ranging from 8 to 27 for HCCO and with N = 9−33 for DCCO with a maximum Ka of 4. We have modeled the frequency-modulated absorption lines using an in-house code that implements the 2f Voigt profiles presented by Dore (2003). The estimated accuracy on the central frequency depends on the signal-to-noise ratio, the line width, and the baseline (mainly caused by standing waves formed between the two windows placed at each end of the absorption cell), and ranges between 25 and 75 kHz by our estimates. In Fig. 1 we show plots of HCCO and DCCO lines, as well as the corresponding fitted profiles.
The initial prediction for new rotational transitions of HCCO and DCCO was done based on the spectroscopic constants determined previously by Endo & Hirota (1987). The spectral analysis was done using the Pickett SPFIT/SPCAT suite of programs (Pickett 1991), applying an S-reduced, asymmetric rotor Hamiltonian (Watson 1977):
where Hrot describes the rotational energy of the molecule, Hsr the spin-rotation interaction, and Hhfs the hyperfine coupling. The spin-rotation interaction arises from the spin dipole moment of the unpaired electron that interacts with the magnetic field generated by the rotation of the molecule. The hyperfine coupling was only included for HCCO, since its hyperfine splitting was already resolved in Ohshima & Endo (1993), unlike DCCO. The hyperfine coupling involves two constants: the Fermi contact interaction bF and the dipolar interaction c. The Fermi contact interaction describes the magnetic coupling between the unpaired electron and the hydrogen nucleus, indicating the overlap of the unpaired spin on the nucleus. The dipolar coupling depends only on the orientation of the unpaired electron with respect to the hydrogen nucleus, meaning that constant c is structure dependent (Ohshima & Endo 1993).
The previous study by Endo & Hirota (1987) had shown that the observed spin splittings of the Ka = 2 and Ka = 3 lines are much smaller than those expected from the Ka = 1 lines. This peculiar behavior is caused by the Renner–Teller coupling (see Appendix A), whereby a special case of vibronic coupling is canceling the degeneracy of the electronic state 2Πu, which subsequently splits to an excited, linear component, 12A′(12Π), and a ground, bent component, 12A″(12Π). The low-lying excited state interacts with the ground state, which leads to a non-negligible perturbation of the rotational levels. As a result, a conventional power series of the spin-rotation constant ϵaa(K) is not sufficient to reproduce the anomalous K-dependence. In order to include this distortion in the analysis, Endo & Hirota (1987) adopted a Pade-type formula given by
allowing the prediction and assignment of transitions with Ka up to 4. The parameter t corresponds to ω/ΔE, where ω describes the bending vibration frequency and ΔE the electronic energy of the excited state (see work from Endo & Hirota 1987 for further explanation). In order to take into account the energy perturbation mentioned above, we calculated one effective spin-rotation constant ϵaa(K) for every K transition according to Eq. (4), using the t value inferred by Endo & Hirota (1987). Thus, we defined five separate ϵaa constants in the input file of the fitting program, where ϵaa(K = 0) is applied to all transitions with Ka = 0, ϵaa(K = 1) is applied to all transitions with Ka = 1, and so on. After including all the lines, we were able to fit ϵaa(K = 0) and ϵaa(K = 1) while keeping the remaining epsilon parameters fixed. We also set the relation between ϵaa(K = 0) and the other epsilon parameters for K = 2,3,4 constant. This means that ϵaa(K = 2,3,4) are changed with respect to the fitted ϵaa(K = 0) parameter, following Eq. (4). The application of the Pade-type expansion for ϵaa(K) allows us to fit and predict rest frequencies for transitions with Ka up to 4 and an accuracy well suited for astrophysical needs. Without this approach we were only able to predict lines up to Ka = 2.
Spectroscopic parameters determined for HCCO and DCCO.
The final fits include our new measured lines as well as those measured in the previous studies mentioned above. In case of HCCO, there were two transitions, JKa, Kc = 153,12 – 143,11 and JKa, Kc = 163,13 – 153,12, measured by Endo & Hirota (1987), which were considerably deviating from the predicted frequencies (∼300 kHz). For this reason, we have re-measured these two lines in the laboratory to search for possible misassignments. However, since the discharge of acetylene and oxygen leads to the production of numerous species (other than HCCO), the resulting spectra had various lines that were partially blended with the HCCO features, making the line assignment rather difficult. In the end, we were able to measure and assign the JKa, Kc = 163,13 – 153,12 transition, which is in better agreement with the prediction than the one measured by Endo & Hirota (1987).
For both species, the final fits allowed us to determine all the quartic centrifugal distortion constants, one sextic parameter, HKN, as well as all the quartic and one sextic spin-rotation constant, 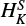 2. The resulting parameters are listed in Table 1. For the HCCO spectral analysis, in addition to those included in the previous fit done by Endo & Hirota (1987), we added one sextic constant HK, one octic, LKKN, and one decadic constant, PKKKN, along with one sextic spin-rotation parameter,
2. The resulting parameters are listed in Table 1. For the HCCO spectral analysis, in addition to those included in the previous fit done by Endo & Hirota (1987), we added one sextic constant HK, one octic, LKKN, and one decadic constant, PKKKN, along with one sextic spin-rotation parameter, 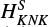 . Adding these extra parameters has considerably improved the fit, resulting in a root mean square (rms) deviation of 59 kHz, which is an improvement of a factor of approximately two compared to the previous fit by Endo & Hirota (1987 rms =125 kHz).
. Adding these extra parameters has considerably improved the fit, resulting in a root mean square (rms) deviation of 59 kHz, which is an improvement of a factor of approximately two compared to the previous fit by Endo & Hirota (1987 rms =125 kHz).
Spin-rotation constants ϵaa(K) determined for HCCO and DCCO.
Strong correlations between HK, LKKN, PKKKN and other constants modify the final values of some rotational parameters with respect to Endo & Hirota (1987). In particular, the introduction of LKKN, PKKKN has a significant impact on the constants  , (ϵab + ϵba)/2,
, (ϵab + ϵba)/2, 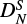 , HKN and DNK, with correlation coefficients ranging from 82% to 99%. This also results in a sign change for DNK, d2, and
, HKN and DNK, with correlation coefficients ranging from 82% to 99%. This also results in a sign change for DNK, d2, and 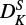 compared to the previous published results (Endo & Hirota 1987). Nevertheless, these high-order centrifugal distortion corrections are critical to reproduce our spectral data within the experimental accuracy: by using a smaller set of constants, the obtained rms is increased up to several megahertz. An accurate determination of the rotational constants would require a full analysis of both interacting states (12A′(12Π) and 12A″(12Π)), which is beyond the scope of this work.
compared to the previous published results (Endo & Hirota 1987). Nevertheless, these high-order centrifugal distortion corrections are critical to reproduce our spectral data within the experimental accuracy: by using a smaller set of constants, the obtained rms is increased up to several megahertz. An accurate determination of the rotational constants would require a full analysis of both interacting states (12A′(12Π) and 12A″(12Π)), which is beyond the scope of this work.
The spectral analysis of DCCO resulted in a root mean square deviation of 64 kHz. Also, here the rotational parameters are more strongly constrained in our fit (see e.g., constants (ϵab + ϵba)/2 and 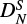 ) compared to Endo & Hirota (1987). In addition, we were able to determine DK, unlike Endo & Hirota (1987), where the constant had previously been kept fixed to 5000 MHz. In case of
) compared to Endo & Hirota (1987). In addition, we were able to determine DK, unlike Endo & Hirota (1987), where the constant had previously been kept fixed to 5000 MHz. In case of 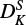 we note a considerable difference of a factor of ∼500 between ours and the previous study. Since there is a correlation between the constants DK and
we note a considerable difference of a factor of ∼500 between ours and the previous study. Since there is a correlation between the constants DK and 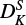 of ∼50%, we do expect a change in
of ∼50%, we do expect a change in 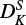 by fitting DK.
by fitting DK.
Spectroscopic parameters of DCCO transitions relevant at low temperatures (∼10 K).
 |
Fig. 2. Map of the H2 column density derived from far-infrared images taken by Herschel (Spezzano et al. 2016). The dashed squares cover 40″ in the x- and y- direction and indicate the regions where the molecules c-C3H2 and CH3OH peak. The white circle represents the beam of the Herschel/SPIRE instrument. On the left part of the figure we show the resulting spectra of the JKa, Kc = 40,4 – 30,3 transition of HCCO averaged over the dashed squares. The red line plots the CLASS Gaussian fit. |
Table 2 shows a summary of the ϵaa(K) constants for HCCO and DCCO determined in this work. A list with all the experimental frequencies is available at the CDS.
4. Astrochemical relevance
In cold environments with a gas temperature of 10 K or lower (such as Lupus-1A and L483, where HCCO has been detected), the Boltzmann distribution for HCCO and DCCO peaks at around 100 GHz. With the present results we are able to reduce the predicted uncertainties down to 5–14 kHz at this frequency range (for HCCO and DCCO, respectively), opening the possibility for astronomical observations towards cold sources, such as starless and pre-stellar cores, which are characterized by narrow emission lines. Table 3 lists five DCCO transitions with Ka = 0 that could be relevant for observations of cold sources in the 3 mm range.
Further HCCO detections towards cold sources will help us clarify the gas-grain chemistry of this species in the early phase of star formation. As already mentioned in the introduction, HCCO is believed to be formed mainly in the gas-phase, via the reaction of C2H with OH. A first step towards understanding the HCCO interstellar chemistry would be to search for a correlation between HCCO and its main precursor C2H. An ideal candidate for this purpose is the well-studied, evolved pre-stellar core, L1544. The chemical structure of the source L1544 was studied in Spezzano et al. (2017) through molecular maps. In particular, the authors investigated the spatial distribution of 22 different molecules, and came to the conclusion that different parts of the source favor the formation of either carbon-, nitrogen-, or oxygen-bearing molecules. c-C3H2 and other carbon-chain molecules like H2CCC and C3H, have their emission peak in the southeast part of the core, while oxygen-bearing species, such as CH3OH, HCO, and SO peak towards the northeast part of the dust continuum peak. In addition, HNCO (as well as CH3CCH, CH2DCCH and CH3CCD) peaks towards the northwest part of the core. The right part of Fig. 2 shows the H2 column density map in L1544, which was derived by the far-infrared images taken with Herschel/SPIRE (Spezzano et al. 2016). We used the data by Spezzano et al. (2017) to search for an HCCO line at 86.6 GHz. For the data processing we employed the software CLASS from the GILDAS3 package (Pety et al. 2005). Since the HCCO detections are very weak (∼10 mK), we chose to average its spectrum over two large regions that contain either the c-C3H2 or CH3OH peak, and cover 40″ in the x- and y-directions, respectively. These regions are marked by the dashed squares in Fig. 2. The center of the map is positioned at the 1.3 mm dust peak (Ward-Thompson et al. 1999).
As can be seen on the left part of Fig. 2, HCCO peaks towards the region where c-C3H2 peaks, while the line intensity decreases by almost a factor of two towards the CH3OH peak.This is clear evidence that HCCO follows a different chemistry than other oxygen-bearing species, showing instead a predominant hydrocarbon chemistry. This favors the hypothesis that C2H is chemically related to HCCO. However, higher-sensitivity observations are needed to prove this relation and constrain the gas-grain chemical models.
5. Chemical model
The chemical model that we apply is based on the model developed by Vasyunin & Herbst (2013) with several minor updates in grain-surface chemistry (Vasyunin et al., in prep.), and includes a gas-grain chemical network with 6000 gas-phase reactions, 200 surface reactions, and 660 species. The gas-phase and grain surface chemistry are connected by accretion and desorption processes. The code numerically integrates chemical rate equations and gives a set of time-dependent abundances of all chemical species for a time span that the user chooses. We use typical conditions of a cold dark cloud with a gas and dust temperature of 10 K, a visual extinction of 30 magnitudes, a proton density of 2 × 104 cm−3, and a cosmic ionization rate of 1.3 × 1017 s−1. As initial atomic abundances we use the ones reported in Wakelam et al. (2015a). In addition, we include all the known formation and destruction reactions for HCCO available in the literature and the KInetic Database for Astrochemistry (KIDA) online database (Wakelam et al. 2015b). In order to simulate the HCCO chemistry, the model is run with steady physical conditions and integrated over 107 years. As already reported in previous studies (Agúndez et al. 2015; Wakelam et al. 2015a), we find that the main formation pathway of HCCO in the gas-phase is the reaction of C2H with OH, while the most effective reaction on grain surfaces is s − H + s − CCO → s − HCCO. For the reaction OH + C2H → HCCO + H we use a rate coefficient of 2 × 10−10 cm3 s−1, as proposed in Wakelam et al. (2015a).
In the end, our simulations are able to reproduce the observed abundance of HCCO for times between 105 and 106 year, reaching a maximum abundance of 5.6 × 10−11. Nevertheless, a theoretical and/or an experimental study of the main formation pathway OH + C2H → HCCO + H is still needed for a better interpretation of the chemical simulations.
6. Conclusions
This work describes a rotational analysis of the ketenyl radical HCCO and its deuterated counterpart DCCO. For each isotopolog we measured and assigned more than 100 lines. We extended the measurements up to ∼650 GHz, which helped us improve the determination of the spectroscopic parameters with respect to the previous study by Endo & Hirota (1987). In particular, we measured the rotational transitions with N ranging from 8 to 27 for HCCO and with N = 9 − 33 for DCCO with a maximum Ka of 4.
For both species we were able to determine all the quartic centrifugal distortion constants, one sextic parameter, HKN, and all the quartic spin-rotation constants, and one sextic spin-rotation constant,
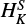 .
.We expanded the centrifugal distortion analysis of HCCO by including a sextic constant HK, an octic, LKKN, and one decadic constant, PKKKN, along with one sextic spin-rotation parameter,
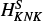 . This extended set of parameters reduced the rms deviation by a factor of approximately two with respect to the previous fit by Endo & Hirota (1987). We also decreased the uncertainty on the rotational constants by up to a factor of approximately 40.
. This extended set of parameters reduced the rms deviation by a factor of approximately two with respect to the previous fit by Endo & Hirota (1987). We also decreased the uncertainty on the rotational constants by up to a factor of approximately 40.We show that towards the pre-stellar core L1544, HCCO peaks within the region where c-C3H2 peaks, suggesting that the ketenyl formation is based predominantly on hydrocarbon chemistry.
The spectral analysis of DCCO resulted in a rms deviation of 64 kHz. The rotational parameters are more strongly constrained in our fit with respect to Endo & Hirota (1987). We provide for the first time a catalog of highly accurate frequencies for DCCO (uncertainties at 3 mm ∼ 15 kHz), which allows a future DCCO detection in cold sources, like starless and pre-stellar cores.
The ketenyl radical is a quasilinear molecule in the ground state with an ∠ HCC angle of 135° and a ∠ CCO angle of 169° (Szalay et al. 1996).
Acknowledgments
We thank the anonymous referee for his/her comments which significantly improved the present manuscript. The work by Anton Vasyunin is partially supported by the ERDF project “Physical and chemical processes in the interstellar medium”, No.1.1.1.1/16/A/213.
References
- Aarts, J. 1978, Mol. Phys., 35, 1785 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2015, A&A, 577, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Lattanzi, V., Laas, J., et al. 2017, A&A, 602, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Lefloch, B., et al. 2004, ApJ, 615, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M. 1977, J. Mol. Spectr., 68, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Q., & Herbst, E. 2016, ApJ, 819, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Cummins, S. E., Linke, R. A., & Thaddeus, P. 1986, ApJS, 60, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Dore, L. 2003, J. Mol. Spectr., 221, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Endo, Y., & Hirota, E. 1987, J. Chem. Phys., 86, 4319 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2008, A&A, 491, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Herzberg, C., & Teller, E. 1933, Z. Physik. Chem., 21, 410 [Google Scholar]
- Hudson, R. L., & Loeffler, M. J. 2013, ApJ, 773, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Jerosimić, S. V. 2007, J. Mol. Spectr., 242, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Jones, I. T. N., & Bayes, K. D. 1972, J. Am. Chem. Soc., 94, 6869 [Google Scholar]
- Lee, T. J., Fox, D. J., Schaefer, H. F. III., & Pitzer, R. M. 1984, J. Chem. Phys., 81, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Maity, S., Kaiser, R. I., & Jones, B. M. 2014, ApJ, 789, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Michael, J. V., & Wagner, A. F. 1990, J. Phys. Chem., 94, 2453 [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohshima, Y., & Endo, Y. 1993, J. Mol. Spectr., 159, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Reboussin, L., Wakelam, V., Guilloteau, S., & Hersant, F. 2014, MNRAS, 440, 3557 [NASA ADS] [CrossRef] [Google Scholar]
- Renner, R. 1934, Z. Physik., 92, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Ruaud, M., Loison, J. C., Hickson, K. M., et al. 2015, MNRAS, 447, 4004 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Tennis, J., Le Gal, R., & Herbst, E. 2018, ApJ, 861, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Bizzocchi, L., Caselli, P., Harju, J., & Brünken, S. 2016, A&A, 592, L11 [CrossRef] [EDP Sciences] [Google Scholar]
- Spezzano, S., Caselli, P., Bizzocchi, L., Giuliano, B. M., & Lattanzi, V. 2017, A&A, 606, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szalay, P. G., Stanton, J. F., & Bartlett, R. J. 1992, Chem. Phys. Lett., 193, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, P. G., Fogarasi, G., & Nemes, L. 1996, Chem. Phys. Lett., 263, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, ApJ, 842, 33 [Google Scholar]
- Wakelam, V., Loison, J.-C., Hickson, K. M., & Ruaud, M. 2015a, MNRAS, 453, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015b, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., Motte, F., & Andre, P. 1999, MNRAS, 305, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, J. K. G. 1977, J. Mol. Spectr., 65, 123 [Google Scholar]
Appendix A: Theoretical considerations: Renner–Teller effect
The coupling between the vibrational angular and the electron orbital momenta (with Λ > 0) in a linear molecule is known as the Renner–Teller interaction (Herzberg & Teller 1933; Renner). This effect occurs when the nuclei are displaced within a bending vibration, and a vibrational angular momentum with the projection number l = 0,1,2,. . . is induced. The resulting vibronic angular momentum K around the molecular axis is then equal to K = |± Λ ± l|, meaning that a doubly degenerate electronic state (with Λ > 0) is split into two components (Brown 1977; Lee et al. 1984). In the case of the ketenyl radical, the unpaired electron occupies a Π orbital that lies perpendicular to the molecular plane. When the H-atom is bent away from the linear molecular axis, the 12Πu degeneracy is canceled and split into two components: a 12A″(1 2Π) bent component described by an attractive potential with respect to the bending coordinate, and a 12A′(1 2Π) linear component described by a repulsive potential (Szalay et al. 1996; Aarts 1978). The anomalous features observed in the spectrum are ascribed to the fact that 2A′ is a low-lying excited state that interacts with the ground state 2A″ resulting to a non-negligible perturbation of the rotational levels. A small energy splitting between these two states would mean a stronger interaction of the systems, and thus a stronger perturbation. Using the spin-rotation coupling obtained from the submillimeter spectrum, Endo & Hirota (1987) predicted that the excited electronic state 12A′ lies only 777 K above the ground state 12A″, assuming that the unpaired electron is mostly localized at the carbon atom. However, Szalay et al. (1992) showed that the unpaired electron has a considerable density on both the oxygen and the carbon atom, which led finally to an energy splitting of 1727 K (Szalay et al. 1996).
All Tables
Spectroscopic parameters of DCCO transitions relevant at low temperatures (∼10 K).
All Figures
 |
Fig. 1. Left panel: recording of the JKa, Kc = 230,23 – 220,22 transition of HCCO. Total integration time is 309 s with a time constant of 3 ms. Right panel: recording of the JKa, Kc = 120,12 – 110,11 transition of DCCO. Total integration time is 127 s with a 3 ms time constant. The red curves represent our modeled 2f Voigt profiles (see text). |
| In the text | |
 |
Fig. 2. Map of the H2 column density derived from far-infrared images taken by Herschel (Spezzano et al. 2016). The dashed squares cover 40″ in the x- and y- direction and indicate the regions where the molecules c-C3H2 and CH3OH peak. The white circle represents the beam of the Herschel/SPIRE instrument. On the left part of the figure we show the resulting spectra of the JKa, Kc = 40,4 – 30,3 transition of HCCO averaged over the dashed squares. The red line plots the CLASS Gaussian fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.