| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 3 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201834321 | |
| Published online | 11 January 2019 | |
Contrast sensitivities in the Gaia Data Release 2
1
Department of Astronomy, Stockholm University, AlbaNova University Center, 10691 Stockholm, Sweden
e-mail: alexis@astro.su.se
2
Subaru Telescope, National Astronomical Observatory of Japan, 650 North Aohoku Place, Hilo, HI 96720, USA
Received:
26
September
2018
Accepted:
13
November
2018
The source detection sensitivity of Gaia is reduced near sources. To characterise this contrast sensitivity is important for understanding the completeness of the Gaia data products, in particular when evaluating source confusion in lower resolution surveys such as photometric monitoring for transits. Here, we statistically evaluate the catalogue source density to determine the Gaia Data Release 2 source detection sensitivity as a function of angular separation and brightness ratio from a bright source. The contrast sensitivity from ∼0.4″ out to 12″ ranges in ΔG = 0–14 mag. We find the derived contrast sensitivity to be robust with respect to target brightness, colour, source density, and Gaia scan coverage.
Key words: techniques: photometric / methods: data analysis / catalogs
© ESO 2019
1. Introduction
The final data products from the Gaia astrometric mission (Prusti et al. 2016) will likely be released well into the mid-2020s; in the mean time intermediate data releases provide unprecedented high quality in many areas, including astrometry, photometry, and completeness (Brown et al. 2018; Lindegren et al. 2018; Evans et al. 2018; Arenou et al. 2018). In addition to serving as a rich source for science exploitation, the Gaia data form the basis for source catalogues of current and future space missions such as the photometric monitoring missions TESS (Ricker et al. 2015), CHEOPS (Cessa et al. 2017), and PLATO (Rauer et al. 2014). One key aspect for evaluating the suitability of targets for planning purposes, or the significance of detected variability, is the potential contamination of the target by background sources inside an angular resolution element (in the range 10–20″ for the mentioned photometric missions). Having an estimate for the completeness limits of the Gaia data near the targets then becomes vitally important for understanding how bright background stars can be and still be missing from the catalogue. The contrast sensitivity (CS) is also important, for example when planning high spatial resolution surveys for multiplicity, to be able to predict expected companion yields in light of the Gaia data.
The pre-launch expected CS of Gaia has been estimated for the inner arcsecond (de Bruijne et al. 2015). Post launch, estimates of the completeness of the Gaia Data Release 2 (DR2) have been empirically made by comparing Gaia detections of multiple systems to known systems from the Washington Visual Double Star Catalogue (WDS; Mason et al. 2001). This estimate shows the fraction of WDS companions recovered in DR2 as a function of separation (Fig. 8 of Arenou et al. 2018), but not as a function of brightness contrast. Recently, Ziegler et al. (2018) made a comprehensive study of the DR2 recoverability of companions detected by a large adaptive optics survey, and derived the CS as a function of separation and brightness contrast for the inner 3.5″. Here, we devise a complementary method to empirically determine the CS out to 18″ from source density statistics. Implementing an efficient way of organising the DR2 data, we use the full catalogue to derive the CS. We also divide the sample into subsamples to study how the CS depends on brightness, colour, source density, and Gaia scan coverage.
2. Methods
2.1. Empirical contrast sensitivity
We empirically determined the CSs of the DR2 sample by counting the number of sources as a function of angular distance from a bright source (hereafter called the target), and compare that with the estimated sky density of those sources at that location in the sky. Targets are selected to be all sources within the magnitude range G = 6–12 mag with parallax and proper motion detected with at least 3σ. This magnitude range was chosen to include a sufficient number of sources for the statistics, and at the same time a wide dynamic range. For each target a field of 18″ radius is checked for background sources. The angular distance s and magnitude difference ΔG then determine the bin location (i, j) in a two-dimensional angular separation i versus brightness contrast j grid so that each background source for all targets adds 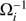 to the bin bi, j, where Ωi is the solid angle of ring i. Each bin is then normalised by mj = maxi(bi, j), the maximum accumulated background source density for each j. Then, fi, j = bi, j/mj is the fraction of sources detected as a function of angular distance and brightness ratio. The source density for a given ΔG increases sharply at a certain separation and becomes constant at larger separations. Due to contamination from physical companions, there are more sources than expected close to the target compared to the background density. To reduce the number of physical companions, we reject sources with a parallax and proper motion within 3σ of the target. This also removes duplicated sources (described in Sect. 10.2.2 of the DR2 online documentation, release 1.1). Even so, there remains a significant excess of sources near the target. This could be due to spurious detections, which are well known to be present around bright stars (Sect. 6.3 of Fabricius et al. 2016), or underestimated errors for sources near bright targets, so that actual companions show spurious parallaxes or proper motions sufficiently different from the target to not be removed. By using the maximum source density (including remaining physical companions), we effectively assume that the source density is constant within the separation of maximum background density, and that the reason for the lower observed density is the reduced sensitivity at close separation. Since the CS is a strong function of angular separation, the determined limits are robust with respect to variations in true source density. Still, this results in an uncertainty for the CS of the inner 1.5″ (briefly addressed in Sect. 4).
to the bin bi, j, where Ωi is the solid angle of ring i. Each bin is then normalised by mj = maxi(bi, j), the maximum accumulated background source density for each j. Then, fi, j = bi, j/mj is the fraction of sources detected as a function of angular distance and brightness ratio. The source density for a given ΔG increases sharply at a certain separation and becomes constant at larger separations. Due to contamination from physical companions, there are more sources than expected close to the target compared to the background density. To reduce the number of physical companions, we reject sources with a parallax and proper motion within 3σ of the target. This also removes duplicated sources (described in Sect. 10.2.2 of the DR2 online documentation, release 1.1). Even so, there remains a significant excess of sources near the target. This could be due to spurious detections, which are well known to be present around bright stars (Sect. 6.3 of Fabricius et al. 2016), or underestimated errors for sources near bright targets, so that actual companions show spurious parallaxes or proper motions sufficiently different from the target to not be removed. By using the maximum source density (including remaining physical companions), we effectively assume that the source density is constant within the separation of maximum background density, and that the reason for the lower observed density is the reduced sensitivity at close separation. Since the CS is a strong function of angular separation, the determined limits are robust with respect to variations in true source density. Still, this results in an uncertainty for the CS of the inner 1.5″ (briefly addressed in Sect. 4).
In order to efficiently retrieve background sources around targets, we implemented a hierarchical data structure to store the positions and DR2 identification numbers for all sources. To avoid singularities at the poles, the right ascension and declination of each source define a three-dimensional directional vector of unit length. An octree of hierarchical cubes is then constructed such that the outermost cube circumscribes the unit sphere, and the direction vector coordinate position of any source is located in a unique subcube. The number of levels of the octree depends on the stellar density, but is defined so that no cube contains more than a given maximum number M of sources. In our python implementation we find M = 2 × 105 to give good performance, resulting in at least 8500 cubes at the lowest level for the 1.7 × 109 sources of the DR2. The octree of cubes makes it efficient at retrieving sources within an angle of any direction, as only subcubes intersecting the viewing cone need to be considered, and directional comparisons can be made on the cube rather than the source level. By storing the data of sources near each other in the sky also close to each other on the storage medium, bottle-necking disc access and cache misses are reduced. This software was originally produced in support of observation preparation and data reduction for the CHEOPS mission, but is adapted here for the purpose of characterising the CSs of DR2.
2.2. Contrast sensitivity variability
To enable the study of how robust the derived CS is, we divide the DR2 targets into several subsamples and derive CSs for each subsample separately. For variation with target brightness we divide the sample into targets with G = 6–9 mag and G = 9 − 12 mag. The photo-electrons generated by a source are not dependent on the colour of the source, so the detection threshold in G should in principle be insensitive to the colour of the source. Since the point spread function (PSF) of the optical system is colour dependent, there may be a colour dependence for the detection threshold, in particular for the CS where the PSF of the target contributes to the background brightness. We explore the colour dependence by limiting the sample to sources with derived effective temperatures, and dividing it into “red” and “blue’ sources, respectively defined as having effective temperatures cooler and hotter than Tbreak = 5000 K. The Tbreak is chosen to produce an approximately equal number of sources in each subsample. We then compare the CS for the two cases were the target is either red or blue.
Gaia does not scan all parts of the sky equally often, and the number of scans is strongly related to the ecliptic where regions near the ecliptic pole are covered more than those close to the equator (e.g. Figs. B3 and B4 in Lindegren et al. 2018). In principle, more scans of a target could improve the CS. To test this, we divide the sample into sources inside and outside 30° of the ecliptic, corresponding to high and low scan coverage regions.
Since the CS is estimated by normalising with the background source density, there should in principle be no dependence on the source density. We test this by dividing the sample into sources inside and outside 15° of the galactic plane, representing high and low source density regions.
3. Results
The derived CS is shown in Fig. 1 as the estimated fraction of detected background sources as a function of angular separation (0.4–18″) and flux ratio (ΔG = 0–14 mag). Figure 1 adds up the count of background sources for targets in the magnitude range 6–12 mag. Table 1 tabulates separations from the target, where 1%, 10%, 50%, 90%, and 99% of nearby sources of specified contrast ΔG to the target are detected.
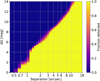 |
Fig. 1. Contrast sensitivity determined as a fraction of detected sources as a function of angular distance and magnitude difference to a target source. |
Separation as a function of ΔG and detection fraction.
The results from the CS variability study is presented in Fig. 2. In general, the CSs are consistent within ∼0.5 mag. The CSs are smooth with a discontinuity just at 1.1″. We do not know the origin of this discontinuity, but one plausible explanation is that it stems from the DR2 special processing of sources within 2″. Bright sources are assigned a scanning window of 18 pixels, corresponding to 1.06″ (Table 1.1 of the DR2 online documentation, release 1.1); sources closer to each other than this may result in one source having its scan window truncated, eliminating the source from further processing and thus systematically lowering the detection yield of such sources.
 |
Fig. 2. Contrast sensitivities as in Fig. 1, but for the range of subsamples described in Sect. 2.2. The target brightness range is in general G = 6 − 12, except for the two samples divided into G = 6 − 9 and G = 9 − 12, as noted in the panels. “Red” and “blue” targets are defined as cooler or hotter than 5000 K, respectively. The ecliptic equator sample is targets within 30° of the ecliptic plane, while the polar sample is the complement. The corresponding dividing angle for the Galactic plane samples is 15°. |
The small deviation at the faint end of the G = 9 − 12 mag sample is due to the detection limit of DR2 (at G ∼ 20 mag). The CS of red targets also seem marginally reduced within 1″, perhaps due to a broader PSF for red targets.
4. Discussion and conclusions
We find a significantly lower CS for the inner arcsecond in DR2 compared to the pre-launch expectations for the full mission (e.g. at 1″ we find ΔG ∼ 3 mag compared to their ΔG = 7 mag; de Bruijne et al. 2015), but are consistent with Ziegler et al. (2018) for the inner 3″ and ΔG = 7 they cover. This is encouraging, since their method of comparing DR2 to known close-separation sources is not vulnerable to companion contamination. The discontinuity we observe at 1.1″ is less pronounced in their sample, but it is difficult to be conclusive at this level of detail due to their limited statistical sample restricting the resolution.
The overabundance of background sources near targets, even after filtering out probable companions by parallax and proper motion, points to a systematic underestimation of errors at close separations. Since the overabundance of close sources must be due to either spurious detections or bound companions, the data could serve as a basis for a statistical study of multiplicity. Because of the special techniques employed for registering close sources, a good understanding of potential systematic biases is essential for an accurate interpretation. To find out whether the DR2 errors are biased at separations smaller than a few arcsec, comparison to a catalogue of known binary systems (e.g. Arenou et al. 2018) would likely be a good strategy.
Given the current limitations of DR2 in the detection methods applied to sources at small separations (Brown et al. 2018), future data releases will no doubt improve contrast sensitivities.
Acknowledgments
We thank the anonymous referee for the timely and constructive reports. AB was supported by the Swedish National Space Agency through contract 75/13.
References
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Brown, A. G. A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cessa, V., Beck, T., Benz, W., et al. 2017, SPIE Conf. Ser., 10563, 105631L [Google Scholar]
- de Bruijne, J. H. J., Allen, M., Azaz, S., et al. 2015, A&A, 576, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabricius, C., Bastian, U., Portell, J., et al. 2016, A&A, 595, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Prusti, T., de Bruijne, J. H. J., Brown, A. G. A., et al. 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instr. Syst., 1, 014003 [Google Scholar]
- Ziegler, C., Law, N. M., Baranec, C., et al. 2018, AJ, 156, 259 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Contrast sensitivity determined as a fraction of detected sources as a function of angular distance and magnitude difference to a target source. |
| In the text | |
 |
Fig. 2. Contrast sensitivities as in Fig. 1, but for the range of subsamples described in Sect. 2.2. The target brightness range is in general G = 6 − 12, except for the two samples divided into G = 6 − 9 and G = 9 − 12, as noted in the panels. “Red” and “blue” targets are defined as cooler or hotter than 5000 K, respectively. The ecliptic equator sample is targets within 30° of the ecliptic plane, while the polar sample is the complement. The corresponding dividing angle for the Galactic plane samples is 15°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


