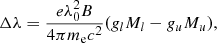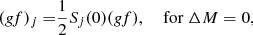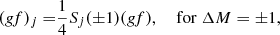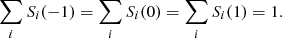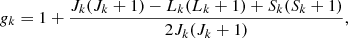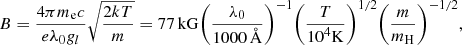EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 620 (December 2018) A&A, 620 (2018) A176 Full HTML
Free Access
Issue
A&A
Volume 620, December 2018
Article Number A176
Number of page(s) 4
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201834097
Published online 14 December 2018

© ESO 2018

1. Introduction

The surface magnetic fields of about 10% of hot spectral type A and late-B stars have strengths on the order of 0.1 − 10 kG (Aurière et al. 2007; Romanyuk 2007). In such stars, the radiative diffusion may operate in a relatively quiet environment, leading to chemical peculiarity (Vauclair 2003; Michaud 2004). Precise spectropolarimetric observations show that about the same fraction of O and early-B stars also have strong magnetic fields (Morel et al. 2015; Wade et al. 2016; Grunhut et al. 2017). In these stars the radiative force launches mass outflow, that is, the stellar wind (see Puls et al. 2008, for a review) that allows for interaction between the magnetic field and the wind.

The radiatively driven wind of hot stars is ionized, therefore it flows along the magnetic field lines. That the stellar wind is channeled along the magnetic field has numerous observational consequences (Petit et al. 2013). When the stellar wind energy density dominates the magnetic field energy density, the magnetic field opens up and the wind leaves the star (ud-Doula & Owocki 2002). The opposite case leads to relatively complex flow structures that include the inhibition of the outflow and fall-back of the wind onto the stellar surface (ud-Doula et al. 2008; Küker 2017), or the trapping of the wind in centrifugally supported clouds (Landstreet & Borra 1978; Townsend et al. 2005).

The interaction of the stellar wind with a strong magnetic field has evolutionary consequences. The wind is forced to the corotation at large distances from the star, leading to angular momentum loss and rotational braking (ud-Doula et al. 2009; Meynet et al. 2011). This effect was discovered not only on evolutionary timescales (Shultz et al. 2017), but also on human timescales (Townsend et al. 2010). Moreover, that the stellar wind is channeled by the magnetic field also affects the mass-loss rate. The local wind mass flux becomes proportional to the tilt of the magnetic field (Owocki & ud-Doula 2004). Moreover, wind may leave a star only along open magnetic field lines, but it falls back along closed magnetic field lines (Owocki et al. 2016). The resulting wind quenching leads to an additional reduction of the mass-loss rate that resembles a weakening of the wind at low metallicity. This means that magnetic stars lose less mass than their non-magnetic counterparts, and the magnetic fields provide an alternative explanation of the high mass of black hole binary merger progenitors (Petit et al. 2017).

The magnetic field affects not only wind dynamics, but also the radiative transfer, which may be important in radiatively driven winds. The Zeeman and Hanle effects lead to the polarization of the radiation in spectral lines. This might be used to detect even relatively weak magnetic fields in the winds (Ignace & Gayley 2003; Ignace et al. 2004; Gayley & Ignace 2010). Moreover, the associated line splitting affects the line force and therefore also the mass-loss rate. Stronger absorption due to line splitting may enhance the wind blanketing effect (Abbott & Hummer 1985; Krtička 2016), which contributes to the light variability that is observed in magnetic O stars (Koen & Eyer 2002; Nazé 2004).

Despite its possible evolutionary consequences, the influence of the Zeeman effect on line-driven winds has never been studied in greater detail. In general, this would require self-consistent wind models with polarized line transfer (e.g., Tichý et al. 2015) that account for the mutual radiative interaction of individual Zeeman components induced by the Doppler effect (Ignace & Gayley 2003; Gayley & Ignace 2010). Such models are not available. However, the strongest influence of the Zeeman effect on the line-driving mechanism presumably arises from the line splitting, which may modify the line force. Even including this effect, however, requires wind models for which the radiative force is calculated in a more advanced approach than with the single-line Sobolev approximation.

While the dynamical effects of the magnetic field (i.e., the magnetic field tilt and the field divergence) on the mass-loss rate have been studied in detail using magnetohydrodynamic (MHD) models (ud-Doula & Owocki 2002), the effect of the line splitting was neglected. This might have a significant effect on the reliability of evolutionary models that include magnetized mass-loss (e.g., Petit et al. 2017). To understand the influence of the Zeeman effect on the radiative force and on the wind mass-loss rate, we modified our METUJE wind models to account for Zeeman splitting. Our wind models calculate the radiative force consistently in the comoving frame (CMF) in a global approach. In this way, the models account for the interaction of individual Zeeman components and allowed us to predict the influence of magnetically split line blanketing on emergent fluxes. To pinpoint the effect of the line splitting, we neglect the dynamical effects of the magnetic field connected with wind channeling along the magnetic field lines.

2. Global wind models

Wind models with magnetically split line blanketing were calculated using the METUJE code (Krtička & Kubát 2017). The code provides global (unified) models of the stellar photosphere and radiatively driven wind. The METUJE code solves the radiative transfer equation, the kinetic (statistical) equilibrium equations, and the equations of continuity, momentum, and energy in the photosphere and in the wind. Models are calculated assuming stationary (time-independent) and spherically symmetric wind flow.

The radiative transfer equation is solved in the CMF (Mihalas et al. 1975). To solve the equation, we account for line and continuum transitions that are relevant in photospheres and winds of hot stars. The considered elements and ions are listed in Krtička & Kubát (2009).

The ionization and excitation state is calculated from the kinetic equilibrium equations (also called non-local thermal equilibrium (NLTE) equations, see Hubeny & Mihalas 2014). We account for the radiative and collisional excitation, deexcitation, ionization, and recombination. The bound-free radiative rates are consistently calculated from the CMF mean intensity, while the bound-bound rates rely on the Sobolev approximation. The ion models were either adopted from the TLUSTY model stellar atmosphere input data (Lanz & Hubeny 2003, 2007) or prepared by us. Both sources use the same strategy to construct the ionic models, that is, the data are based on the Opacity and Iron Project calculations (Seaton et al. 1992; Hummer et al. 1993) and are corrected for the observational line and level data available in the NIST database (Kramida et al. 2015). An exception is the ionic model of phosphorus, which was prepared using data described by Pauldrach et al. (2001). The ionic levels with low excitation energy are explicitly included in the calculations, while levels with higher excitation energy are merged into superlevels (see Lanz & Hubeny 2003, 2007, for details).

Depending on the location in the atmosphere, we use three different methods to solve the energy equation. The differential form of the transfer equation is applied deep in the photosphere, while the integral form of this equation is used in the upper layers of the photosphere (Kubát 1996), and the electron thermal balance method (Kubát et al. 1999) is applied in the wind. In all three cases, the individual terms in the energy equation are taken from the CMF radiative field. These terms, together with the CMF radiative force calculated accounting for line, bound-free, and free-free transitions and light scattering on free electrons, are inserted in the hydrodynamical equations. The hydrodynamical equations, that is, the continuity equation, equation of motion, and the energy equation, are solved iteratively to obtain the wind density, velocity, and temperature structure. The final model is derived by varying the base velocity to search for a smooth transonic solution with the maximum mass-loss rate (Krtička & Kubát 2017).

The output from TLUSTY model stellar atmospheres (Lanz & Hubeny 2003, 2007) was used as the initial guess of the solution in the photosphere. These TLUSTY models were calculated for the same effective temperature, surface gravity, and chemical composition as the wind models, but neglecting the magnetic field.

3. Including magnetically split line blanketing

The inclusion of the magnetic line splitting into our wind code closely follows the quantum mechanical theory of the Zeeman effect (Sobelman 1977; Landi Degl’Innocenti & Landolfi 2004). When a magnetic field is present, each atomic level k described by the total, orbital, and spin angular momentum quantum numbers Jk, Lk, and Sk is split into 2Jk + 1 sublevels with magnetic quantum numbers Mi = −Jk, …, Jk. According to the selection rules, only the transitions with ΔM = Mu − Ml = −1, 0, 1 are allowed between magnetically split upper u and lower l levels. The splitting of the energy levels leads to the wavelength shift Δλ relative to the laboratory line wavelength λ0

Δλ= e λ 0 2 B 4π m e c 2 ( g l M l − g u M u ), $$ \Delta \lambda = \frac{{e\lambda _0^2B}}{{4\pi {m_{\rm{e}}}{c^2}}}({g_l}{M_l} - {g_u}{M_u}),\ $$(1)

where e and me are the elementary charge and the electron mass, B is the field modulus, and gl and gu are the Landé factors.

In our non-magnetic models, the line force is calculated based on line data derived from the VALD database (Piskunov et al. 1995; Kupka et al. 1999) with some updates using the NIST data (Kramida et al. 2015). To account for the magnetic field, we replaced the original lines by their split components selected according to quantum-mechanical rules and with wavelength shifts given by Eq. (1). The oscillator strengths of each split line j were computed from the original oscillator strength g​f

( g f ) j = 1 2 S j ( 0 ) ( g f ) , for Δ M = 0 , $$ \begin{aligned} (g\!f)_j=&\frac{1}{2}S_j(0)(g\!f), \quad \text{ for}\;{\Delta } M=0,\end{aligned} $$(2)

( g f ) j = 1 4 S j ( ± 1 ) ( g f ) , for Δ M = ± 1 , $$ \begin{aligned} (g\!f)_j=&\frac{1}{4}S_j(\pm 1)(g\!f), \quad \text{ for}\;{\Delta } M=\pm 1, \end{aligned} $$(3)

where the relative line strengths given in Table 1 are additionally normalized to unity for each group of the Zeeman components

∑ i S i ( − 1 ) = ∑ i S i ( 0 ) = ∑ i S i ( 1 ) = 1 . $$ \begin{aligned} \sum _iS_i(-1)=\sum _iS_i(0)=\sum _iS_i(1)=1. \end{aligned} $$(4)

Table 1.

Relative strengths of magnetically split lines.

The Landé factors were mostly taken from the Kurucz line list1 using cross-matching of lines with the VALD line list. For the remaining lines, the Landé factors were computed assuming LS coupling

g k = 1 + J k ( J k + 1 ) − L k ( L k + 1 ) + S k ( S k + 1 ) 2 J k ( J k + 1 ) , $$ \begin{aligned} g_k=1+\frac{J_k(J_k+1)-L_k(L_k+1)+S_k(S_k+1)}{2J_k(J_k+1)} ,\end{aligned} $$(5)

with term designation from the Kurucz line line list, or we assumed mean Landé factors gk = 1.2 (e.g., Kochukhov et al. 2005) when the designation was not available. The number of unsplit lines in the original line list with different sources of Landé factors and the total number of magnetically split lines that are accounted for in the calculation is given in Table 2.

Table 2.

Number of lines with different sources of Landé factors and the total number of lines.

The magnetic field varies with radius according to the div B = 0 constraint. We neglected this effect and assumed a constant magnetic field throughout the whole computational domain, because the mass-loss rate is determined close to the star, where the magnetic field is nearly equal to its surface value. Moreover, the magnetic field is typically so strong that it dominates even in deep photospheric layers, therefore we can assume that the field has the same strength for great and small optical depths. This enabled us to split the lines in the external file and not in the code itself, while the effect of this assumption on our final results is negligible. Moreover, the magnetic field also varies across the stellar surface. By neglecting these variations, we provide in fact models for concentric cones, in which the surface variations of magnetic field can be neglected.

4. Hot-star wind models with Zeeman line splitting

The adopted stellar parameters, that is, the effective temperature Teff, radius R*, mass M, and luminosity L, together with derived mass-loss rates Ṁ are given in Table 3. We selected a representative sample of O-star parameters that correspond to a main-sequence star with Teff = 30 kK and to two supergiants with Teff = 37.5 kK and Teff = 42.5 kK. The stellar parameters were derived using the formulas of Martins et al. (2005). The magnetic field strengths we selected cover typical surface fields found in O stars, which are up to few kilogauss (Donati et al. 2002, 2006; Wade et al. 2012a,b; Hubrig et al. 2015). We assumed two metallicity values that correspond to that of our Sun (Asplund et al. 2009) and to that of the Large Magellanic Cloud (Z = 0.5 Z⊙). This enables us to study the metallicity effect on the magnetically split line blanketing that is due to the variation in the contribution of individual elements with metallicity (e.g., Vink et al. 2001). The mass-loss rates given in Table 3 do not account for the dynamical effects of the magnetic field. Therefore, these values in fact correspond to ṀB=0 rates that need to be further corrected to obtain the local mass flux that accounts for dynamical effects (Owocki et al. 2016).

Table 3.

Adopted stellar parameters of the studied stars and derived wind mass-loss rates.

It follows from the predicted mass-loss rates in Table 3 that Zeeman splitting has a negligible effect on the radiative force and on the wind mass-loss rates. The relative change in mass-loss rates is on the order of a few percent for magnetic field strengths of up to 10 kG. The mass-loss rate decreases by about 10% for the strongest magnetic field considered, 100 kG, which surpasses any magnetic field ever detected on the surfaces of OB stars, however (e.g., Wade et al. 2012b; Grunhut et al. 2017). The decrease can be explained as a result of line broadening, which, as shown in the case of turbulent broadening, leads to a decrease in mass-loss rate (Krtička & Kubát 2010). For the strongest magnetic fields we considered, the implicit assumption that the magnetic splitting of the energy levels is small compared to the fine-structure splitting may not be appropriate. For such fields a more general approach describing the so-called Paschen–Back effect should be used (e.g., Khalack & Landstreet 2012). This does not significantly affect the general results, however.

The magnetically split line blanketing is important only if the line shifts are comparable with the line broadening. In our models we only assume thermal broadening2, in which case Eq. (1) gives the condition for the minimum magnetic field strength,

B= 4π m e c e λ 0 g l 2kT m =77 kG ( λ 0 1000 Å ) −1 ( T 10 4 K ) 1/2 ( m m H ) −1/2 , $$ B = \frac{{4\pi {m_{\rm{e}}}c}}{{e{\lambda _0}{g_l}}}\sqrt {\frac{{2kT}}{m}} = 77\,{\rm{kG}}{\left( {\frac{{{\lambda _0}}}{{1000\,{\AA}}}} \right)^{ - 1}}{\left( {\frac{T}{{{{10}^4}{\rm{K}}}}} \right)^{1/2}}{\left( {\frac{m}{{{m_{\rm{H}}}}}} \right)^{ - 1/2}},\ $$(6)

assuming gl = gu = 1.2 and ΔM = 1. Here m is the atomic mass and mH is the hydrogen atom mass. Equation (6) shows that a magnetic field with a strength of about 100 kG is needed to affect the line force. Such a magnetic field is higher than the upper limit of magnetic fields that have been observed in nondegenerate stars. This also explains why we did not find any strong effect of the magnetic field on the line force.

The magnetic line splitting exceeds the Doppler shift that is connected with the radial wind motion for magnetic fields that are stronger than about 1 MG. Such strong fields are typically found in some white dwarfs (see Kawka 2018, for a review). In this case, the magnetically split lines behave independently and do not interact with each other. Consequently, a stronger radiative force and higher mass-loss rates can be expected. This might have implications for hot (Teff ≳ 100 kK) magnetic white dwarfs that have winds (Krtička et al., in prep.).

We did not find any strong flux variability that would be due to the magnetically split line blanketing. The typical flux changes in the optical region at 5500 Å correspond to magnitude variations of about 10−4 mag. Consequently, we do not expect any strong rotationally modulated flux variability in magnetic O stars that would be purely due to the Zeeman splitting. A similar result was obtained in magnetic main-sequence BA stars, where the magnetic field only affects emergent fluxes in strongly overabundant atmospheres (Khan & Shulyak 2006). The observed light variability in magnetic O stars (Koen & Eyer 2002; Nazé et al. 2015) is therefore due to other processes, such as wind blanketing that is modulated by the tilt of the magnetic field and stellar rotation (Krtička 2016) or due to light absorption in a magnetically confined circumstellar environment (Wade et al. 2011; Munoz et al. 2018).

5. Conclusions

We studied the effect of line splitting that is due to the magnetic field (Zeeman effect) on the wind properties in massive stars. We used our own numerical wind code with CMF radiative transfer and NLTE level populations to estimate the influence of the Zeeman splitting on the line force. We showed that for the magnetic fields that are typically found in OB stars, the Zeeman splitting has a negligible influence on the line force and also on the wind mass-loss rates and terminal velocities. The line splitting only affects the radiative force for magnetic fields that are stronger than about 100 kG. We found only very weak flux variability that is due to the magnetically split line blanketing. We conclude that only dynamical effects connected with a magnetic field have a strong effect on the mass-loss rate. These effects were deliberately neglected here because they were studied using MHD models in detail, and we aimed at understanding of the effect of the line splitting.

2

We can neglect other types of broadening for our purpose because, for example, in stars with strong magnetic fields macroturbulent broadening can be neglected because subsurface convection is likely inhibited in strong magnetic fields (Sundqvist et al. 2013).

Acknowledgments

The author thanks O. Kochukhov for discussing the problem and the anonymous referee for constructive comments. This work was supported by grant GA ČR 16-01116S. Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum provided under the program “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042) is greatly appreciated.

References

  1. Abbott, D. C., & Hummer, D. G. 1985, ApJ, 294, 286 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  5. Donati, J.-F., Howarth, I. D., Bouret, J.-C., et al. 2006, MNRAS, 365, L6 [NASA ADS] [CrossRef] [Google Scholar]
  6. Gayley, K. G., & Ignace, R. 2010, ApJ, 708, 615 [NASA ADS] [CrossRef] [Google Scholar]
  7. Grunhut, J. H., Wade, G. A., Neiner, C., et al. 2017, MNRAS, 465, 2432 [NASA ADS] [CrossRef] [Google Scholar]
  8. Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres (Princeton: Princeton University Press) [Google Scholar]
  9. Hubrig, S., Schöller, M., Kholtygin, A. F., et al. 2015, MNRAS, 447, 1885 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
  11. Ignace, R., & Gayley, K. G. 2003, MNRAS, 341, 179 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ignace, R., Nordsieck, K. H., & Cassinelli, J. P. 2004, ApJ, 609, 1018 [NASA ADS] [CrossRef] [Google Scholar]
  13. Kawka, A. 2018, Contrib. Astron. Observat. Skalnate Pleso, 48, 228 [Google Scholar]
  14. Khan, S. A., & Shulyak, D. 2006, A&A, 448, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Khalack, V., & Landstreet, J. D. 2012, MNRAS, 427, 569 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kochukhov, O., Khan, S., & Shulyak, D. 2005, A&A, 433, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2015, NIST Atomic Spectra Database (ver. 5.3) [Google Scholar]
  19. Krtička, J. 2016, A&A, 594, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Krtička, J., & Kubát, J. 2009, MNRAS, 394, 2065 [NASA ADS] [CrossRef] [Google Scholar]
  21. Krtička, J., & Kubát, J. 2010, A&A, 519, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Krtička, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kubát, J. 1996, A&A, 305, 255 [NASA ADS] [Google Scholar]
  24. Kubát, J., Puls, J., & Pauldrach, A. W. A. 1999, A&A, 341, 587 [NASA ADS] [Google Scholar]
  25. Küker, M. 2017, Astron. Nachr., 338, 868 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  27. Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophysics and Space Science Library, 307 [Google Scholar]
  28. Landstreet, J. D., & Borra, E. F. 1978, ApJ, 224, L5 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
  31. Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Meynet, G., Eggenberger, P., & Maeder, A. 2011, A&A, 525, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Michaud, G. 2004, IAU Symp., 224 173 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mihalas, D., Kunasz, P. B., & Hummer, D. G. 1975, ApJ, 202, 465 [NASA ADS] [CrossRef] [Google Scholar]
  35. Morel, T., Castro, N., Fossati, L., et al. 2015, New Windows on Massive Stars, 307, 342 [NASA ADS] [Google Scholar]
  36. Munoz, M., Wade, G. A., Nazé, Y., Bagnulo, S., & Puls, J. 2018, CoSka, 48, 149 [NASA ADS] [Google Scholar]
  37. Nazé, Y. 2004, PhD thesis, Univ. Liège [Google Scholar]
  38. Nazé, Y., Walborn, N. R., Morrell, N., Wade, G. A., & Szymański, M. K. 2015, A&A, 577, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Owocki, S.P., & ud-Doula, A. 2004, ApJ, 600, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  40. Owocki, S.P., ud-Doula, A., Sundqvist, J.O., et al. 2016, MNRAS, 462, 3830 [NASA ADS] [CrossRef] [Google Scholar]
  41. Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Petit, V., Owocki, S. P., Wade, G. A., et al. 2013, MNRAS, 429, 398 [NASA ADS] [CrossRef] [Google Scholar]
  43. Petit, V., Keszthelyi, Z., MacInnis, R., et al. 2017, MNRAS, 466, 1052 [NASA ADS] [CrossRef] [Google Scholar]
  44. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
  45. Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Romanyuk, I. I. 2007, Astrophys. Bull., 62, 62 [NASA ADS] [CrossRef] [Google Scholar]
  47. Seaton, M. J., Zeippen, C. J., Tully, J. A., et al. 1992, Rev. Mex. Astron. Astrofis., 23, 19 [NASA ADS] [EDP Sciences] [Google Scholar]
  48. Shultz, M., Wade, G., Rivinius, T., et al. 2017, IAU Symp., 329, 126 [Google Scholar]
  49. Sobelman, I. I. 1977, Introduction to the Theory of Atomic Spectra (Nauka: Moscow) [Google Scholar]
  50. Sundqvist, J. O., Petit, V., Owocki, S. P., et al. 2013, MNRAS, 433, 2497 [NASA ADS] [CrossRef] [Google Scholar]
  51. Tichý, A., Štěpán, J., Trujillo Bueno, J., & Kubát, J. 2015, Polarimetry, 305, 401 [NASA ADS] [Google Scholar]
  52. Townsend, R. H. D., Owocki, S. P., & Groote, D. 2005, ApJ, 630, L81 [NASA ADS] [CrossRef] [Google Scholar]
  53. Townsend, R. H. D., Oksala, M. E., Cohen, D. H., Owocki, S. P., & ud-Doula, A. 2010, ApJ, 714, 318 [Google Scholar]
  54. ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
  55. ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2008, MNRAS, 385, 97 [NASA ADS] [CrossRef] [Google Scholar]
  56. ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2009, MNRAS, 392, 1022 [NASA ADS] [CrossRef] [Google Scholar]
  57. Vauclair, S. 2003, Ap&SS, 284, 205 [NASA ADS] [CrossRef] [Google Scholar]
  58. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Wade, G. A., Howarth, I. D., Townsend, R. H. D., et al. 2011, MNRAS, 416, 3160 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wade, G. A., Grunhut, J., Gräfener, G., et al. 2012a, MNRAS, 419, 2459 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wade, G. A., Maíz Apellániz, J., Martins, F., et al. 2012b, MNRAS, 425, 1278 [NASA ADS] [CrossRef] [Google Scholar]
  62. Wade, G. A., Neiner, C., Alecian, E., et al. 2016, MNRAS, 456, 2 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Relative strengths of magnetically split lines.

In the text
Table 2.

Number of lines with different sources of Landé factors and the total number of lines.

In the text
Table 3.

Adopted stellar parameters of the studied stars and derived wind mass-loss rates.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.