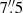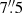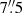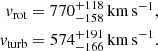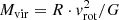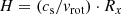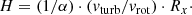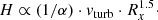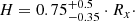| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201732081 | |
| Published online | 10 December 2018 | |
Simultaneous Hα and dust reverberation mapping of 3C 120: Testing the bowl-shaped torus geometry⋆
1
Astronomisches Institut, Ruhr–Universität Bochum, Universitätsstraße 150, 44801
Bochum, Germany
e-mail: ramolla@astro.rub.de
2
Institut für Astrophysik, Universität Göttingen, Friedrich-Hund Platz 1, 37077
Göttingen, Germany
3
Institute for Astronomy, 640 North A’ohōkū Place, Hilo, HI 96720-2700, USA
4
Instituto de Astronomía, Universidad Católica del Norte, Avenida Angamos 0610, Antofagasta, Chile
Received:
11
October
2017
Accepted:
8
August
2018
We monitored the Seyfert-1 galaxy 3C 120 between September 2014 and March 2015 at the Universitätssternwarte Bochum near Cerro Armazones in BVRIJK and a narrowband filter covering the redshifted Hα line. In addition we obtained a single contemporary spectrum with the spectrograph FAST at Mt. Hopkins. Compared to earlier epochs 3C 120 is about a factor of three brighter, allowing us to study the shape of the broad line region (BLR) and the dust torus in a high luminosity phase. The analysis of the light curves yields that the dust echo is rather sharp and symmetric in contrast to the more complex broad Hα BLR echo. We investigated how far this supports an optically thick bowl-shaped BLR and dust torus geometry. The comparison with several parameterizations of these models supports the following geometry: The BLR clouds lie inside the bowl closely above the bowl rim up to a halfcovering angle 0° < θ < 40° (measured against the equatorial plane). Then the BLR is spread over many isodelay surfaces, yielding a smeared and structured echo as observed. Furthermore, if the BLR clouds shield the bottom of the bowl rim against radiation from the nucleus, the hot dust emission comes essentially from the top edge of the bowl (40° < θ < 45°). Then, for small inclinations as for 3C120, the top dust edge forms a ring that largely coincides with a narrow range of isodelay surfaces, yielding the observed sharp dust echo. The scale height of the BLR increases with radial distance from the black hole (BH). This leads to luminosity dependent foreshortening effects of the lag. We discuss the implications and possible corrections of the foreshortening for the BH mass determination and consequences for the lag (size)–luminosity relationships and the difference from interferometric torus sizes.
Key words: galaxies: Seyfert / quasars: emission lines / infrared: galaxies / galaxies: nuclei / galaxies: structure / quasars: supermassive black holes
Tables of the lightcurve data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/A137
© ESO 2018
1. Introduction
The quasar paradigm comprises a supermassive black hole (BH), a central X-ray source, an accretion disk (AD) surrounded by a broad line region (BLR), and a molecular dusty torus farther out. These formal components serve as working frame: the AD, BLR, and torus may have smooth transitions rather than being separated entities with sharp boundaries. As the inner quasar regions cannot be resolved by conventional imaging techniques, reverberation mapping (RM) is the main tool of the trade (Bahcall et al. 1972; Peterson 1993; Horne et al. 2004). The RM technique traces the response of irradiated regions to the light fluctuations of continuum emission from the inner AD. In particular, RM studies of the BLR trace the response of line emission to continuum variations and determine the time lag, τ, between their signals, with the BLR size, RBLR ∼ cτ (c is the speed of light). Reverberation mapping can reach a spatial resolution of better than 10−5 pc, clearly surpassing the capabilities of current imaging instruments.
Line-to-continuum RM studies find that RBLR ranges from a few light days to several light months. At low redshift, a relatively tight size-luminosity relation for the Hβ-emitting region has been identified: RBLR(Hβ)∝Lα with α ≃ 0.5 and monochromatic active galactic nucleus (AGN) luminosity L at 5100Å (Kaspi et al. 2000; Bentz et al. 2013). Conversely, L may be inferred from RBLR or Rdust measurements, opening the possibility of using AGNs as standard candles for cosmological distance studies (Oknyanskij 1999; Collier et al. 1999; Watson et al. 2011, Haas et al. 2011; Czerny et al. 2013; Yoshii et al. 2014; Hönig et al. 2017).
To characterize the line profiles, various studies using the ratio full width at half maximum (FWHM) to line dispersion σv revealed a large diversity between sources with flat-topped lines (showing large FWHM/σv) and sources with narrow-peaked lines with extended wings (showing small FWHM/σv); the latter class shows a trend toward higher accretion rates as measured by Eddington ratios, while inclination appears to play a minor role in FWHM/σv (Sulentic et al. 2000; Collin & Kawaguchi 2004; Collin et al. 2006). Alternatively, BLR properties could be luminosity dependent, such that the use of σv as a proxy for vrot leads to an overestimate of MBH at high-z or high luminosity. From RM studies of individual Seyferts during phases of low and high luminosity (Kollatschny & Zetzl 2011, 2013a,b) find an indication that both the scale height above the equatorial plane and the ratio of turbulent to rotation velocity vturb/vrot of the BLR increase with luminosity. A potential explanation is that brightening of an individual AGN makes the BLR visible at larger RBLR, where vrot should be smaller (Kepler’s law); if vturb remains constant then the ratio vturb/vrot increases with RBLR.
If the height-to-radius ratio H/R is proportional to vturb/vrot, this implies a growing vertical extent of the BLR above the disk plane. It is clear that geometry has a substantial influence on the calculation of the central BH mass.
Well-sampled light curves allow us to restore information about the spatially unresolved BLR geometry (Horne et al. 1991; Maoz et al. 1991; Pancoast et al. 2012). In a nutshell, tightly localized gas distributions (e.g., nearly face-on flat disks) produce a sharp echo of the continuum light curve, while more isotropic gas configurations (e.g., spheres) lead to smoothed light curves for the line emission band. The line-integrated transfer function depends on the BLR geometry, i.e., the location of the BLR clouds at the time they respond; BLR kinematic information is not necessary. It is intriguing to check if the geometry of the visible BLR changes with luminosity (or accretion rate Ṁ) in a nonisomorphic manner.
For the archetypal Sy-1 galaxy NGC 5548, Gaskell et al. (2007) analyzed the AGN energy budget and derived crucial conclusions concerning the geometry of the BLR and dust torus: the BLR has a likely covering factor about 40%, which translates to a half-covering angle θ ≈ 40°. The BLR shields a substantial fraction of the dust torus from direct illumination by the AD, allowing for the observed relatively small near-infrared (NIR) contribution to the AGN energy budget. At the same time, the BLR obscuration also removes the problem that the dust torus covering factor is greater than the BLR covering factor, and is consistent with the observed fraction of obscured AGNs. The flux reduction at the torus also reduces the problem of AGN dust reverberation lags giving sizes smaller than the dust sublimation radii.
Near-infrared RM studies of the dusty torus find τdust ≈ 4 × τHβ between hot-dust continuum emission and optical continuum fluctuations (Koshida et al. 2014). However, Rdust = c ⋅ τdust is three times smaller than the dust sublimation radius, Rsub, inferred from the UV luminosity (Suganuma et al. 2006; Kishimoto et al. 2007). To resolve this conflict, Kawaguchi & Mori (2010, 2011) proposed a bowl-shaped dust torus that smoothly continues into the central AD. The AD emission is highest at the polar region and lowest at the equatorial region. The anisotropy of the AD emission controls the angle dependent dust sublimation radius and thus the concave rim of the bowl. For the bowl-shaped torus, assuming that the hot dust emission arises from the entire bowl surface, the dust transfer functions show about three times faster responses than for a bagel-shaped torus (see, e.g., Fig. 1 of Urry & Padovani 1995), in agreement with observations. Notably, for small inclinations (i.e., rather face-on than edge-on view) the transfer functions of the dust emission show a sharp peak. Kawaguchi & Mori’s studies pioneered the bowl-shaped dust torus, but did not yet consider the BLR. The relation between BLR and dust torus has long been debated. For instance, (Czerny & Hryniewicz 2011) proposed that the AD reaches far out until it meets the torus and that the BLR clouds are launched from the outer AD in a dusty wind at that radius, where the temperature in the AD matches the dust sublimation temperature. In this scenario, however, how far the reverberation-based BLR and dust lags should essentially be the same is an open issue contrary to the factor 3–5 larger dust lags observed so far.
Consequently, in continuation of Kawaguchi & Mori’s work, Goad et al. (2012) modeled BLRs, assuming that they are confined by a bowl-shaped torus geometry, and suggested that the BLR clouds lie above the bowl surface (see their Fig. 1). Goad et al. successfully tested the bowl-confined BLR models with reverberation data of NGC 5548. Notably, the BLR clouds may shield part of the dust from the AD radiation, bringing the hot dust covering fraction closer to that deduced by Landt et al. (2011) and Mor & Trakhtenbrot (2011). Then the hot dust emission would arise essentially from the edge, i.e., top rim, of the bowl. For the Seyfert-1 WPVS48, Pozo Nuñez et al. (2014a) found an exceptionally sharp NIR echo, which led these authors to favor the theory that the hot dust is essentially located at the edge rather than the entire rim.
 |
Fig. 1. FAST spectrum of 21 November 2014 is normalized to the maximum value and drawn as black line. The Johnson B, V, and R responses that have been folded with the KAF 16801 CCD are overplotted in in colored dashed curves. The yellow shaded area represents the 680 nm NB filter folded with the quantum efficiency of the STL-6303 CCD. All filter response functions are normalized to their maximum. |
Simultaneous BLR and dust reverberation studies might be able to shed further light on the geometry and the interplay between BLR and dust. Therefore, we have embarked on such a study of 3C 120.
The BLR galaxy 3C 120 belongs to the most frequently monitored Seyfert-1 galaxies and results from several campaigns have been reported: spectroscopic RM by Peterson et al. (1998) covering the Hβ region, velocity resolved RM covering Hγ, Hβ, and Hα by Grier et al. (2012, 2013) and Kollatschny et al. (2014). Photometric reverberation mapping (PRM) of Hβ has been reported by Pozo Nuñez et al. (2012, 2014b). During the spectroscopic campaigns before 1998 and in 2008 and 2009 (Kollatschny) the average λlog(Lλ5100) AGN luminosity at 5100Å was about 44.01 and 44.12. In 2009 and 2010 (Pozo Nuñez) this dropped to 43.84 erg s−1, similar as in 2010 and 2011 (Grier, 43.87 erg s−1). Between September 2014 and March 2015 we continued photometric monitoring; Ramolla et al. (2015) found a brightening by a factor three (44.32 erg s−1) from the B and V band light curves. The brightening occurred between January and August 2014, as revealed by a spectrum in December 2013 taken at the Asiago Observatory where λlog(Lλ5100) ≈ 43.82 erg s−1 (PhD Thesis, priv. comm., data in Berton et al. 2015).
We report on the analysis of the entire data set in BVRIJK and a narrow band (NB) at 680 nm and contemporaneous spectrum taken in November 2014. We assumed a luminosity distance of 138 Mpc for a cosmological model with Ωm = 0.27, Ωv = 0.73 and H0 = 73 km s−1 Mpc−1.
2. Observations and data reduction
We monitored 3C 120 between 27 August 2014 and 3 March 2015 at the Universitätssternwarte Bochum, which is located near Cerro Armazones, the location of the upcoming ESO Extremely Large Telescope.
The photometric data was reduced with standard IRAF1 bias, dark, and flatfield correction. Astrometric matching was performed with Scamp (Bertin et al. 2006). Before stacking multiple exposures, they were resampled onto a common coordinate grid using Swarp (Bertin et al. 2002). The photometry is performed on combined frames with a fixed  aperture, found to be the optimum in our previous studies (Haas et al. 2011; Pozo Nuñez et al. 2012, 2013, 2015; Ramolla et al. 2015).
aperture, found to be the optimum in our previous studies (Haas et al. 2011; Pozo Nuñez et al. 2012, 2013, 2015; Ramolla et al. 2015).
Our aim is to combine relative photometry in the field with absolute photometry anchored to Landolt fields. First, we selected 20 close nonvariable stars (calibrators) in the AGN field with brightnesses ranging from 0.5 to 10 times of the nuclear 3C 120 flux. Then, we performed photometry of 3C 120 and these stars using the  aperture with SExtractor (Bertin & Arnouts 1996). The calibrator light curves were normalized to their average over all days in the observation epoch. We used the scatter of the normalized ensemble of calibrators within a particular night as the relative photometric error. Dividing the flux of 3C 120 by the nightly average of the normalized ensemble resulted in the relative light curve of the target.
aperture with SExtractor (Bertin & Arnouts 1996). The calibrator light curves were normalized to their average over all days in the observation epoch. We used the scatter of the normalized ensemble of calibrators within a particular night as the relative photometric error. Dividing the flux of 3C 120 by the nightly average of the normalized ensemble resulted in the relative light curve of the target.
Absolute photometry was obtained using additional observations of suitable fields from Landolt (2009). Since there are no literature photometric fluxes for the NB and R bands2, we fit the available Landolt measurements of each source by Planck functions. We rejected the star for calibration if the largest residual of this fit was larger than 5%. Otherwise, the flux of the NB was interpolated by the Planck function. We performed airmass dependent extinction correction (Patat et al. 2011) to determine the instrument response in the 3C 120 field in units of Jy. Finally, galactic foreground extinction correction was applied based on the Schlafly & Finkbeiner (2011) extinction maps. The calibration of the relative IR fluxes in J and K band was performed in the same manner as for the optical data above. We carried out the absolute calibration using 2MASS stars (AAA flagged) in the 3C 120 maps. Supplementing our photometric data, we obtained a single epoch spectrum taken by the SAO FAST spectrograph at the Fred Lawrence Whipple Observatory (FLWO) on Mt. Hopkins.
2.1. Berlin Exoplanet Search Telescope II
The Berlin Exoplanet Search Telescope II (BEST II) is a 25 cm aperture Baker-Ritchey-Chrétien system, using a KAF16801 4096 × 4096 pixel CCD with a pixel size of 9 μm and a field of view of 1.7° ×1.7°. Since 2012, this telescope is also in service for AGN observations. More details on the instrument can be found in Kabath et al. (2009).
The BEST II telescope was used with Johnson B, V, R (λeff = 700 nm) and I bands to trace the AD continuum variations. This allows us to separate the host galaxy flux in these filters (see Ramolla et al. 2015) and to remove the AGN continuum contribution in our NB.
2.2. Robotic Bochum Twin Telescope
The 15 cm Robotic Bochum Twin Telescope (RoBoTT), previously known as the VYSOS 6 telescope, is a twin-refractor design. It consists of two Takahashi TOA 150, attached to a common German equatorial mount. Both refractors are equipped with KAF16801 CCDs, hence they provide the same quantum efficiency per wavelength as the BEST II telescope when using identical filters. The field of view is 2.7° ×2.7°. More details can be found in Haas et al. (2012).
RoBoTT Johnson V band observations serve to supplement the BEST II data by covering a gap between September and October 2014. Before and after this gap, there are numerous days at which both instruments were available to observe simultaneously. The overlap between BEST II and RoBoTT in Fig. 3 demonstrates the comparability of both instruments.
2.3. Bochum Monitoring Telescope
The Bochum Monitoring Telescope (BMT ) is a 40 cm Coudé telescope, featuring a SBIG STL-6303 CCD with 3072 × 2048 pixel, each sized 9 μm. The resulting field of view is 41.2′ × 27.5′. A more detailed description of the telescope and filters can be found in Ramolla et al. (2013).
To monitor the redshifted Hα emission line, NB observations in an Asahi 680 nm filter (12 nm FWHM) have been provided. Owing to the redshift of 0.03301 ± 0.00003 (Michel & Huchra 1988), the broad Hα emission line is redshifted into our NB filter, centered at 677.94 nm.
2.4. Infra-Red Imaging System
The Infra-Red Imaging System (IRIS) is a 80 cm Nasmyth telescope equipped with a HAWAII-1 detector. The field of view is 12.5′ × 12.5′ with a pixel size of 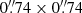 . The filter wheel is equipped with standard 2MASS J, H, K, and NB filters. Further information can be found in Hodapp et al. (2010).
. The filter wheel is equipped with standard 2MASS J, H, K, and NB filters. Further information can be found in Hodapp et al. (2010).
2.5. FAST Spectra
To supplement our new photometric data of 2014/2015 we used the FAST long-slit spectrograph of the 1.5 m Tillinghast reflector telescope at the Fred Lawrence Whipple Observatory in Arizona, USA. Spectra of 3C 120 together with the calibration star HD 19445 were taken in the night of 21 November 2014. The 300 lines mm−1 grating was used together with a 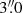 slit aperture. More details on the instrument are given in Fabricant et al. (1998). Reduction was performed using standard flatfield, wavelength, and flux calibration routines as described in Tokarz & Roll (1997). The resulting spectrum is shown in Fig. 1 together with the filter response profiles of our photometric campaign.
slit aperture. More details on the instrument are given in Fabricant et al. (1998). Reduction was performed using standard flatfield, wavelength, and flux calibration routines as described in Tokarz & Roll (1997). The resulting spectrum is shown in Fig. 1 together with the filter response profiles of our photometric campaign.
3. Results
3.1. Line coverage of the narrow band
The FAST spectrum (Fig. 1) allows us to estimate the contribution of the continuum and the narrow and broad emission lines to the photometric bands. For this purpose, we fold the filter response curves with the quantum efficiency of the KAF-16801 CCD and use this as detector response function R(λ). For each selected band we integrate the line profiles L(λ) and the (power law) continuum C(λ) separately. The fraction f of line flux of the total flux is then given in Eq. (1) as follows:
The results of the line contributions are summarized in Table 1. The contributions of Hγ and Hβ to the B band flux are on the order of our photometric uncertainty. The contribution of Hβ to the V band is only slightly above this value. The flux beyond 7400 Å was assumed to be the extrapolated power law, determined from the continuum. In the R band, the strong Hα emission causes a contribution of 18%. The 680 nm NB filter is clearly dominated by the Hα flux.
Contribution of emission lines to the photometric bands.
While spectroscopic reverberation data enables us to use the velocity information from the RMS spectra, i.e., from the variable portion of the emission lines, several attempts have been made to determine the mass of the central BH using single epoch spectra (e.g., Vestergaard 2002; Woo et al. 2007; Denney et al. 2009).
In order to calculate the velocity dispersion of the broad Hα line, we perform a decomposition of the spectrum around this feature into
-
As depicted by the dashed black line in Fig. 2, we assume the continuum in the wavelength range from 6600 Å to 7000 Å to follow a power law (it is almost linear in this range). The power law was determined through fitting in the line free spectral regions 4600 − 4800, 5300 − 6000, 6300 − 6500, and 7050 − 7200 Å.

Fig. 2. Hα line profile decomposition. The continuum is shown with a black dashed line. The narrow Hα, [N II], and [S II] features were fitted with the red curves. The yellow area shows the 680 nm NB profile. All data is normalized to the maximum. The broad Hα is represented by the black continuous curve.
-
The narrow Hα, [N II], and [S II] lines are fitted through subtraction of a line profile template of the strong 5007 Å [O III] emission line, positioned at the appropriate redshifted wavelength. To improve the fitting quality of the faint 6548 Å [N II] component, we assume its integrated flux to be 1/3.05 of the 6584 Å [N II] line, according to line intensity ratios as determined by Storey & Zeippen (2000). While it is usually more reasonable to use a template from the [S II] lines (Ho et al. 1997, due to the similar critical density as [N II]), these lines in our spectrum are weak and blended, so we approximate the shape of the narrow lines by the [O III] profile instead. The ratio of best fit narrow Hα to [N II] 6584 Å line strength is 2.96/1. These profiles are shown by the red curves in Fig. 2.
-
For the remaining broad Hα line, we use a decomposition into Gauss-Hermite polynomials similar to Woo et al. (2007). Using a fourth order polynomial produces the curve shown by the black solid line in Fig. 2. Fitting the broad line profile with two or more Gaussians does not deliver a better fit than with Gauss-Hermite polynomials.
Correcting for the spectral resolution of the FAST instrument, we determine the broad Hα dispersion of 3C 120 to be 1532 ± 201 km s−1. This is lower but still comparable to the result of 1638 ± 105 km s−1, by Kollatschny et al. (2014) using the Hobby-Eberly Telescope for spectroscopic RM in a different epoch (2008/2009). The FWHM of the broad Hα component alone is 1420 ± 129 km s−1.
3.2. Light curves
The optical light curves in Fig. 3 show significant variability features in all bands. The B, V, and R band observations, tracing the variable continuum, start with a decline in brightness from the absolute maximum values in September 2014 to the minimum in mid-November 2014. Afterward there is a rise of flux to a local maximum in mid-December 2014. Between mid-December and early January 2015, there appears to be a slight decline that changes into another rise toward end of January. Afterward, we observe a plateau phase with minor variations. The 680 nm NB flux already reveals the large contribution of Hα emission. This flux follows the behavior of the broad bands with a distinct lag, but the relative amplitude of the variations is much lower. The NB contains in addition to the strong Hα a substantial continuum contribution that has to be removed for a proper lag determination.
 |
Fig. 3. Combined optical light curves from all telescopes. Open diamonds indicate observations taken with the BMT telescope, filled circles represent BEST II and open triangles RoBoTT. All fluxes were measured inside an aperture of |
The Hα light curve was obtained by subtracting the continuum flux from the 680 nm NB as described in Sect. 3.3. Hα clearly shows similar features as the broad optical bands but shifted in time. However, compared to the average flux, the amplitude of these variations is much lower and is analyzed in Sect. 3.4.
Observations in I band between September and December 2014 trace the brightest and faintest phases, and therefore are valuable for the flux variation gradient (FVG) analysis.
3.3. Flux separation
3.3.1. AGN and host in the optical
Using the FVG method (Choloniewski 1981; Winkler et al. 1992), we disentangle the constant host from the variable AGN flux inside our aperture. This is possible since the color of the variable component is sufficiently constant. The method was already applied successfully to the B and V band data of 3C 120, covering observations from 2009 until 2015 in Ramolla et al. (2015). Owing to the large luminosity coverage of the underlying B and V band data, we adopt the determined B band host flux of (1.69 ± 0.28) mJy and the corresponding V band host flux of (3.89 ± 0.29) mJy.
The contribution in the I band is determined through the FVG diagram in Fig. 4. The continuous black lines indicate the upper and lower 1σ deviation of the flux variation of the AGN with a slope ΓBI of 0.925 ± 0.025 determined by an ordinary least square (OLS) bisector fit. The intersection of the AGN and host flux of B = (1.69 ± 0.28) mJy occurs at I = (8.97 ± 0.33) mJy, which is denoted by the red cross. The mean AGN flux in the I band is determined as the average of the remaining variable component, which is (10.34 ± 1.54) mJy. All fluxes are listed in Table 2.
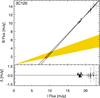 |
Fig. 4. B vs. I flux variations of 3C 120 in the |
Mean fluxes from the FVG analysis and rest-frame delays.
For comparison, the yellow filled area outlines the range of host B − V colors as determined for several Seyfert 1 galaxies by (Sakata et al. 2010) in an 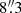 aperture. Using the B-band flux of our long-term campaign (Ramolla et al. 2015), our value lies at the lower (red) range.
aperture. Using the B-band flux of our long-term campaign (Ramolla et al. 2015), our value lies at the lower (red) range.
Through image decomposition of HST images, Bentz et al. (2009) found an S0 host morphology for 3C 120. To estimate the host fluxes in the R band, we fit the BVI spectral energy distribution (SED) with a redshifted S0 galaxy template. The best fitting spectral template was obtained with the PEGASE-3 spectral evolution modeling package for an age of 13 Gyr (Fioc et al., in prep., based on Fioc et al. 1997). Figure 5 shows the optical to infrared part of the spectrum. The spectral template is redshifted to z = 0.03301 and flux-scaled to our measured B, V, and I host fluxes indicated by the diamond symbols. Fluxes are determined by convolution of the PEGASE3 spectrum with the response function of our filters. Assuming that this template is a good approximation, the expected R-band flux of the host is then (5.90 ± 0.31) mJy, shown by the red square in Fig. 5.
 |
Fig. 5. Host galaxy template spectrum in the observed filters, scaled to match the measured fluxes in B, V, and I (red diamonds). The red square shows the fitted R-band flux. |
3.3.2. Hα emission line flux
With the estimate of host flux in the R band, we can now take a closer look at the flux variation behavior seen in the B − R FVG diagram in Fig. 6. We interpolate the expected slope of the AGN to be ΓBR = 0.953 ± 0.013 using ΓBV = 0.979 ± 0.005 (Ramolla et al. 2015) and ΓBI = 0.925 ± 0.025 as determined above and assuming a power law AGN SED between B and I. This slope is now aligned to the observed fluxes in the B and R bands. As seen in the residuals in Fig. 6, the flux variations of the continuum and Hα, as seen in the R band, show a very linear trend that suits our interpolated slope ΓBR within the majority of error margins. Some deviation of linearity may occur since the R band contains the delayed Hα variation that does not correlate directly with the variable continuum. However, the relative amplitude of the Hα variation is small (< 10 %), as seen in Fig. 3. The R band host flux is indicated by a red cross in Fig. 6. Clearly, the AGN slope does not intersect our measured B-band flux (dotted line) at this position. This is due to the contribution of the Hα emission line in the R band. The average Hα flux can then be determined from this FVG diagram considering the constant R-band host flux estimate of 5.90 mJy (Sect. 3.3.1). Then the average Hα flux3 in the R band is (2.57 ± 0.42) mJy. The corresponding flux contribution of Hα in the R band is then (13.7 ± 2.2) %. This is less than estimated from the smaller slit aperture of the spectroscopic data (see Table 1). Becasue of the smaller aperture, more flux of the spatially extended host is lost in the spectrum.
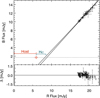 |
Fig. 6. B vs. R flux variations of 3C 120 in the |
Because the central wavelength of the NB filter lies close to λeff of the R band, we can assume that the host to AGN ratio in the continuum is roughly the same in both filters. This allows us to subtract the R-band light curve directly from the NB light curve in order to obtain the variable signal of Hα alone. The resulting Hα light curve is depicted at the bottom of Fig. 3, showing a minimum in Feb. 2015, and hence a clear delay relative to the AGN continuum variation seen in the broad bands.
3.4. Delay of the Hα broad line region
The large three month decline and two month rise is seen in all the broad bands. It is followed by a plateau phase during which the flux is almost constant, close to the average flux of the epoch. Any long-term secular variation is masked within the structure of the long-term feature. Its response can be clearly seen in the Hα light curve. The shift of this signal is about 70 days, which is about half of our total observation campaign. Linear detrending as proposed by Welsh (1999) would cause a bias toward short delays and is therefore not performed.
To determine the Hα delay, we apply the discrete correlation function (DCF; Edelson & Krolik 1988) analysis between B, Hα and other optical light curves. A binning of one day is chosen since this represents the median sampling of our data set. Figure 7 shows for B-Hα a clear broad maximum ranging from 55 to 95 days. To estimate the uncertainty, the flux randomization/random subset selection (FR/RSS) method is used as described by Peterson et al. (1998). This leads to a result of 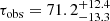 days for the delay of Hα in the observers frame. All delays are finally corrected for redshift dependent time dilation and listed in Table 2.
days for the delay of Hα in the observers frame. All delays are finally corrected for redshift dependent time dilation and listed in Table 2.
 |
Fig. 7. Discrete correlation functions between B and the optical data. The correlation of B with V band is colored blue; the uncorrected R-band correlation is shifted −0.5 and shown in green; the line flux corrected R band is shifted −1.0 and shown in red; the I-band correlation is shifted −1.5 and shown in orange; the correlation between B and Hα is shown in black. Dotted lines represent the 1σ uncertainties. |
Notably, the width of the cross correlation (from 55 to 95 days, i.e., 40 days, Fig. 7) is significantly larger than indicated by the τobs uncertainty of 1-σ ≈ 13 days derived by the FR/RSS method. This plateau-like cross correlation indicates even a substructure in the form of a sharp bright peak at 60 days. Figure 8 shows the histogram of the FR/RSS statistics in more detail. It clearly reveals a sharp peak around 60 days, in addition to the broad plateau between 55 and 95 days. This suggests a complex transfer function, if the input variation is a delta function.
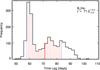 |
Fig. 8. B − Hα cross correlation (DCF) statistics obtained from 2000 FR/RSS runs. The vertical red solid line denotes the median. The vertical red dotted area indicates the range inside the 68% confidence, and the blue vertical dotted lines give the formal 1σ uncertainty around the median. We note the low-τ peak, i.e., the strong signal at lag 60 days, about 20% shorthand of the median. |
3.5. Inter-band continuum delays
The dense (one day) median sampling of the data allows us to search for delays that increase with increasing wavelength and are associated with reprocessing of emission in the AD, as was reported for several other Seyfert 1s by Sergeev et al. (2005). Compared to the measured Hα and Hβ BLR sizes of 3C 120 of several light weeks, the size of the AD is expected to be much smaller, on the order of light days.
As seen in the spectrum (Fig. 1), the V band is slightly polluted by Hβ while Hα has 18% contribution in the R band. Our photometric analysis (Sect. 3.4) shows that the contribution of Hα to R in the photometry is even weaker (13.7% in R) and that the amplitude of the line variation is much smaller than that of the continua. To verify that the Hα contribution to the broad bands does not introduce a significant bias toward larger delays, we also compute an Rs band light curve from our R band minus the Hα light curve.
The correlation functions between B, R, Rs, and I are shown in Fig. 7. The results of the FR/RSS analysis between B band and other continuum light curves are summarized in Table 2. The errors are consistent with a very low delay close to τ ≈ 0. A bias toward higher delays, potentially introduced by the Hβ contribution, is not seen.
3.6. Dust torus variability
The infrared J and K light curves are shown in Fig. 9. In the period from September until December 2014 one observes a slight decline in the J band similar to the slope in the optical, but different from the optical bands (Fig. 3), there is no clear rise in the January to March data. The light curve minimum is reached in February 2015. The K-band flux also has its lowest flux values in February 2015, but in contrast to all other bands there is no adequate decline in late 2014, instead the flux is rising. The variations in both bands show a significant delay. The trough of the large variable feature seen in the optical at November 2014 is now seen at the end of February 2015.
 |
Fig. 9.
|
We perform the DCF analysis on the IR data. The result is shown in Fig. 10. In analogy to the analysis in the optical we apply the FR/RSS method to estimate the errors in the time delays. The results, corrected for redshift dependent time dilation, are listed in Table 24.
 |
Fig. 10. Discrete correlation functions between B and IR data. The correlation of B with K band is shown in blue; B to J band correlation is shifted down by −1 and shown in green. Dotted lines represent the 1σ uncertainties. |
In Fig. 10, B-band to J- and K-band correlation functions are shown, shifted by 1.0 for visibility. This allows us to see two important aspects of the correlation between optical and IR. First, the peak of the maximum correlation remains within the FR/RSS error margins in Table 2. Second, the autocorrelation contribution of AD continuum in the IR fluxes becomes visible at τ = 0. This effect is stronger in the J band, which can be explained by the flux composition in the filters. The K band is almost completely dominated by the warm dust, while the contribution of the AD continuum adds a measurable autocorrelation contribution in the uncorrected J band data. However, the lag of the dust emission is clearly seen in the peak between 80 and 110 days. This is further corroborated by the DCF FR/RSS statistics shown for B − J and B − K in Fig. 11. We note the strong symmetry in contrast to the asymmetric B − Hα DCF FR/RSS statistics (Fig. 8)5.
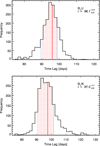 |
Fig. 11. B − J and B − K DCF statistics obtained from 2000 FR/RSS runs. The colored lines indicate median, confidence range, and uncertainty as in Fig. 8. We note the pronounced symmetry of the B − J and B − K distributions compared to the asymmetry of B − Hα in Fig. 8. |
3.7. Dust lag versus luminosity
The dust lag determined with our B − K cross-correlation analysis places 3C 120 on the lower side of the τ − MV distribution when compared with a larger sample by Suganuma et al. (2006). This is depicted in Fig. 12, based on data by Koshida et al. (2014). Kishimoto et al. (2007) found that the measured average dust lag (solid black line) was a factor of 3 lower than the expected sublimation radius Rsub (Barvainis 1987; dashed line), which is defined for a sublimation temperature of 1500 K. The solution to this problem might be found in the geometric shape of the torus as proposed by Kawaguchi & Mori (2010, 2011). We consider this further in Sect. 4.
 |
Fig. 12. Absolute visual magnitude MV and measured cross-correlation delay of the hot dust. The host-subtracted AGN luminosity, corrected for galactic foreground extinction, is MV (Schlafly & Finkbeiner 2011). Black points are based on the data of Suganuma et al. (2006), as tabulated in Koshida et al. (2014), and labeled s06 and ko14. The continuous line is the best fit determined by s06. The black dashed line corresponds to the light travel time to the expected sublimation radius determined by Kishimoto et al. (2007). Blue pn14 data is WVPS 48 taken from Pozo Nuñez et al. (2014a) and green (pn15) is PGC 50427 measured in Pozo Nuñez et al. (2015). Our new measurement for 3C 120 is shown in red. |
Notably, the four most luminous sources (MV < −21 mag) lie clearly below the average (solid line in Fig. 12). For 3C 120 at the given MV = −21.8 mag Fig. 12 suggests that the sublimation radius Rsub corresponds to a lag τCCF of about 434 days (rest frame, i.e., 450 days observed frame), hence even a factor of 5 larger than measured. One reason could be that after the strong brightening of 3C 120 in 2013, the dust torus did not expand within the one year until 2014 when our observations were performed. Then it would have still a rather small size, controlled by the past 1.4 mag lower luminosity state. For instance, at MV = −20.4 mag the corresponding lag of Rsub would be about 300 days, consistent with the average line (dashed line in Fig. 12). A slow receding of the dust torus on a timescale of several years also appears consistent with the observations of NGC 4151 by Kishimoto et al. (2013). Laor (2004) discussed the timescales of the dust sublimation and dust reformation followed by the time variation of the illumination, and he noted the possibility of hysteresis effects. We return to that point in Sect. 4.1.
4. Comparison with bowl-shaped geometries
The B-Hα cross correlation shows a broad maximum plateau ranging from 55 to 95 days (Fig. 7), while the B-NIR cross correlations are more peaked ranging from 80 to 110 days (Fig. 10). Thus, at first glance, the BLR lies closer to the AD than the dust torus, in agreement with the AGN unified model; the BLR may overlap with or transition into the dust torus. However, the striking feature is that the dust echo is sharper than the Hα echo. This is clearly not consistent with a bagel-shaped dust torus, and therefore special geometries have to be considered. We compare our data with the bowl-shaped geometry as proposed by Kawaguchi & Mori (2010; 2011; Sect. 4.1) and the variant bowl model proposed by Goad et al. (2012; Sect. 4.2). A comprehensive modeling is beyond the scope of this paper, but we compare the data with a few model cases in this work.
Because the inclination for the disk equatorial plane of 3C 120 is small, we first consider the models with a face-on view, i.e., i = 0°. Thereafter we discuss the effects of inclination, adopting an inclination of i = 16°, based on the radio jet orientation found by Agudo et al. (2012). We note that for a moderately inclined bowl, the face-on models roughly hold for the left and right part of the inclined bowl, and that essentially only the tilted top and bottom parts of the bowl contribute to altering the transfer function.
In addition, we incorporate gas clouds and the Hα BLR inside the bowl with an estimated covering half-angle of 40.75°. We derive this by assuming a dust covering fraction of ∼10% (average between Landt et al. 2011 and Mor & Trakhtenbrot 2011) with a torus half-opening angle of 45°, which is consistent with the Sy1/2 number counts (Huchra & Burg 1992).
A common feature of the bowl geometry is that the height of the BLR above the equatorial plane increases strongly with equatorial radius Rx. In Sect. 4.3 we consider how far this fits the H/Rx estimates derived, if one applies the line profile analysis proposed by Kollatschny & Zetzl (2011, 2013a,b).
4.1. Kawaguchi-Mori-Bowl
We use the dust torus model by Kawaguchi & Mori (2010) (henceforth called KM model), where the rim of the torus is given by the sublimation radius under the assumption of anisotropic illumination by the AD (their Eq. (3)). We start adopting an inclination i = 0° and sublimation radius Rsub in polar direction of 450 ld (observed frame), as inferred from Fig. 12 (Sect. 3.7). We adopt the model with θmin = 45° and θmax = 89°. In addition, we incorporate gas clouds and the Hα BLR inside the bowl with a tentative covering half-angle of 40°. Guided by the locally optimized emitting clouds (LOC) model of Baldwin et al. (1995), we place the BLR at a distance of rLOC ≈ 160 − 200 ld from the BH, which corresponds to about 1/2–1/3 of Rsub. We consider this choice as reasonable because it is derived from average ratios between simultaneous dust and Hα BLR lag measurements (see, e.g., Pozo Nuñez et al. 2014a, 2015); given a typical ratio lag(Hα )/lag(Hβ) ≈ 1.54 (Bentz et al. 2010), this choice is also consistent with the findings of τdust ≈ 4 × τHβ between hot-dust continuum emission and optical continuum fluctuations (Koshida et al. 2014).
With regard to the LOC model, however, we mention the following caveat: For simplicity, the BLR region is placed at the same distance from the BH for various angles, i.e., not taking into account an angle-dependent illumination of the BLR clouds by the AD. For comparison, an angle-dependent illumination would result in a larger BLR distance toward the polar direction (compared to the equatorial direction). Nevertheless, the BLRs adopted in this work fill only a small angle range between about 20 and 40 degrees from the equatorial plane (indicated by the blue shaded areas in Figs. 13– 16) and therefore this simplification does not alter the basic results and conclusions obtained here.
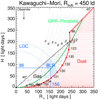 |
Fig. 13. Geometric properties of the dust torus model by Kawaguchi & Mori when seen face-on. In three dimensions, the model is rotationally symmetric around the y-axis and mirrored on the x-axis. The BH is located at the origin (0,0). The adopted sublimation radius Rsub is 450 ld in polar direction. The thick red line indicates the border of the dust, and the volume filled by dust is shaded in red. The dust distribution is cut at a half-opening angle of 45°. For later comparison, the green line (labeled GKR-Parabola) indicates the slightly different bowl shape as given by Goad et al. (2012). The black curves show the isodelay surfaces with numbers giving the delay in days. The large black numbers along the bowl rim list the delay at that place. The black solid line at angle 40° to the equatorial plane indicates the potential distribution of the gas clouds (small black dots). The blue hatched area indicates Hα BLR that we see, adopting the LOC model of Baldwin et al. (1995). The thick blue lines indicate the average height (86 ld) and equatorial radius (156 ld) of the BLR. |
Figure 13 shows the bowl-shaped dust torus and the BLR clouds located inside the bowl. The main features are as follows:
-
A large portion of the bowl rim coincides with the isodelay surfaces of 120–130 days6.
-
If all the dust along the bowl rim contributes to the measured varying dust emission, then the expected lag lies between 99 and 132 days, hence about 20 days larger than the observed range of 80–110 days (Fig. 10).
-
The BLR matches a broad range of isodelay surfaces. However, the lags between 60 and 130 days are larger than the observed range of 55–95 days (Fig. 7). To match the observed range, the BLR has to be located closer to the BH, for example, at a LOC radius of about rLOC ≈ 50 ld, but this leads to an exceptionally small rLOC/Rsub ≈ 0.1.
In conclusion, the model with Rsub = 450 ld provides qualitatively a good approach but fails in detail too much to agree with the data. Therefore, we consider a similar model but with smaller Rsub = 350 ld and smaller rLOC ≈ 150 ld, as shown in Fig. 14. The main features are as follows:
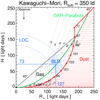 |
Fig. 14. Similar as Fig. 13, but for a smaller sublimation radius Rsub of 350 ld in polar direction. Also, the radius of the LOC has been slightly diminished to 150 ld, and the covering half-angle of the gas clouds has been enlarged to 45°. This places the BLR within the isodelay surfaces between 40 and 100 days as indicated by the B − Hα cross correlation (Fig. 7). |
-
A large portion of the bowl rim coincides with the isodelay surfaces of 80–110 days, consistent with the data (Fig. 10).
-
Likewise, the BLR matches the range of isodelay surfaces between 50 and 100 days, consistent with the data (Fig. 7).
While this model choice appears satisfying, we did not yet account for the inclination of i = 16° which broadens the BLR and dust transfer functions. Kawaguchi & Mori (2011) presented dust transfer functions for a range of inclinations (θobs, see their Fig. 5). Already at inclinations 10° < i < 20° the dust transfer function broadens, with a centroid at about 0.3–0.4 Rsub, which translates to a lag of 105–140 days for 3C 120, hence larger than what our data measure. In addition, the dust transfer function becomes asymmetric with a pronounced maximum at the long delay end and a tail toward the short delay end. Our observational data, however, show very symmetric B/J and B/K cross correlations (Figs. 10 and 11), suggesting rather a symmetric dust transfer function.
Figure 15 shows the Kawaguchi-Mori model with even smaller Rsub = 300 ld, which may bring the observed and predicted lag ranges at 10° < i < 20° to an agreement. However, it does not solve the discrepancy of the observed symmetric cross correlation of the light curves and the predicted asymmetric transfer function. Therefore, we suggest that other bowl profiles are required or that the varying hot dust emission does not arise from all along the entire bowl rim, rather only from a small portion of the rim. We discuss further details in Sect. 5.
4.2. Goad-Korista-Ruff Model
Goad et al. (2012) modeled the BLR, assuming that it is confined by a bowl-shaped torus geometry and suggesting that the BLR clouds lie above and next to the bowl surface. In this model (henceforth called GKR model), the BLR clouds may shield part of the dust rim from the AD radiation, reducing the hot dust covering fraction and bringing it closer to that of ∼10% deduced by Landt et al. (2011) and Mor & Trakhtenbrot (2011). Then the hot dust emission would arise essentially from the edge, i.e., the top rim of the bowl. We use this model with the proposed parabola-shaped bowl rim, whereby the bowl goes up to a half-opening angle of 45°. We note that this bowl shape is less convex than the Kawaguchi-Mori-Bowl (cf. the green line labeled GKR–Parabola in Figs. 13–15). This less pronounced convexity may be interpreted as physical manifestation of the dust shielding by the gas clouds. We assume further that the gas clouds (and the BLR) are located within a half-covering angle θ of 40°, so that the edge lies at 40° < θ < 45°. We started with an inclination i = 0°. We adjusted the bowl size, so that the edge essentially coincides with the isodelay contour of 100 days.
Figure 16 shows the bowl-shaped dust torus at inclination i = 0° and the BLR clouds located inside the bowl. The main features of the dust and BLR echoes are as follows:
 |
Fig. 16. Bowl-shaped torus model with parabolic dust rim, as proposed by Goad et al. (2012). The lines, colors, and labels are similar as for Fig. 13. The very thick red line labeled “Edge” indicates the dust rim above θ = 40°. The thick blue long-dashed line indicates a potential BLR gas distribution close to the bowl rim; Goad et al. also assumed a LOC controlled BLR gas distribution in their calculation of the BLR transfer function. |
-
Dust: Below the edge, the lag decreases steadily for the inner parts of the bowl rim. The rim crosses many isodelay surfaces. If all the dust along the bowl rim contributes to the measured varying dust emission, then the expected dust lag lies between about 61 and 102 days. We note that for an inclined bowl (say at i = 16°; see Agudo et al. 2012) the transfer function becomes broader than at i = 0°. Then the expected dust lags disagrees with the sharp NIR echo observed. This argues for a scenario in which the gas clouds shield the inner bowl rim below the edge and in which the edge provides the bulk of the varying hot dust emission, as proposed by Goad et al.
-
BLR: The BLR (blue shaded area, estimated by the LOC principle) matches the isodelay contours at i = 0°, which appears consistent with the observed range of 55-95 days (see Fig. 7). If the bowl is inclined at i = 16°, this range of lags holds for the left and right part of the inclined bowl, while the tilted top and bottom smears out the lag range as illustrated in Fig. 17. We now consider this effect further. In their Fig. 1, Goad et al. assumed a gas distribution rather close to the bowl rim, similar to that marked by the long dashed blue line in Fig. 16. While at i = 0° the expected BLR lag range appears then very narrow, it broadens with increasing inclination. Goad et al. (2012) show calculated BLR transfer functions (response functions Ψ(τ)) for a grid of parameters and inclinations in their Fig. 5; their BLR calculations took the LOC principle into account. For the parabola (exponent α = 2) they find: At i = 10°: Ψ(τ) is symmetric with clear τ peak and extended wings. At i = 30°: Ψ(τ) shows a strong asymmetry, with a pronounced peak at low τ (with a value of about 20% of the median of the τ range). By eye-balled linear interpolation, we estimate that at i = 16° the asymmetry shows up as well with a low-τ peak at about 80% of the median of the τ range, exactly as seen in the data (58/72, see Fig. 11). Thus, the GKR BLR model appears nicely consistent with our 3C 120 data.

Fig. 17. Scheme of the low-τ peak response and the smeared echo for a bowl rim observed at inclination i ≈ 16°. The dust torus is shaded in gray. The bowl rim has been adopted as a “parabola” with exponent α = 2.2, slightly more convex than in Fig. 16. The long dashed lines indicate the isodelay contours. That part of the rim for which the lag matches the data is defined in red; it leads to a sharp low-τ peak response. On the other hand, the entire part of the rim on the left-hand side (marked by the blue arrow) leads to a broad response that is more delayed and smeared out over time.
To summarize, the GKR model has the interesting property that–by shielding the dust rim by the gas clouds–places the hot dust emission to the edge, i.e., a spatially confined region, allowing for a rather sharp and symmetric dust transfer function at small inclinations as well; this is consistent with the 3C 120 observations. At the same time, the GKR model predicts a broad transfer function for the BLR with a low-τ peak, which is again consistent with the 3C 120 observations.
4.3. FWHM/sigma and the scale height of the BLR
In a bowl geometry the scale height H of the BLR above the equatorial plane increases strongly with equatorial radius Rx. We consider how far this fits the H/Rx estimates derived from FWHM/sigma7, if one applies the line profile analysis proposed by Kollatschny & Zetzl (2011, 2013a,b). In particular, this analysis separates rotational and turbulent velocities (vrot and vturb, resp.), allowing us to derive an improved BH mass using a proper vrot. We begin with a few introductory explanations.
While the BLR kinematics is widely believed to be gravitationally dominated by the BH (e.g., Gaskell 1988; Peterson & Wandel 1999), a thin disk-like geometry with a pure Keplerian velocity profile is not able to explain most of the observed AGN spectra. Osterbrock (1978) already noted that some vertical extension is required for the BLR and consequently some significant vertical motion to maintain its thickness. Fitting the statistics of line widths, he found a typical rotational velocity of 5000 km s−1 and a turbulent velocity of 2000 km s−1 for the BLR gas.
It is well known that the FWHM/sigma line ratio of the broad emission lines in the best reverberation studied Seyfert-1 galaxies and quasars shows a large dispersion (Peterson et al. 2004). Collin et al. (2006) investigated the FWHM/sigma line ratio of that sample. These authors showed that this ratio is anticorrelated with the Eddington ratio and with line widths; broader emission lines (Population 1) tend to have relatively flat-topped profiles and narrower lines (Population 2) have more extended wings (see also Sulentic et al. 2000; Collin & Kawaguchi 2004). Collin et al. tentatively suggested that the difference between the two populations is due to the relative strength of a disk-wind component, which is stronger in Population 1. These authors discuss the possible role of self-gravity as the physical driver controlling the strength of the disk wind. They find a stronger wind is expected for larger Eddington ratios, which is consistent with the smaller FWHM/sigma line ratios found for Population 1 objects8.
In a different approach,Kollatschny & Zetzl (2011, 2013a) analyzed broad emission line profiles of CIV , helium, and Balmer lines of the above sample presented by Peterson et al. (2004). They considered emission line profiles (Gaussian, Lorentzian, logarithmic, and exponential) resulting from various kinematical and dynamical models. For instance, turbulent motions result in Lorentzian profiles, inflow or outflow motions lead to logarithmic profiles and electron scattering to exponential profiles; all three profiles yield FWHM/sigma ≈ 1 and therefore they are further commonly denoted as turbulence. Assuming that these motions are superimposed by the Keplerian motion of the gas clouds, Kollatschny & Zetzl computed the rotational convolution of Lorentzian profiles and derived the FWHM and sigma values of these newly generated convolved profiles. Finally, they compared FWHM/sigma and FWHM for the data and model profiles. This way, they used the FWHM/sigma line ratio versus FWHM diagram for separating rotational and turbulent velocities. Their studies so far indicate that inclination plays a minor role and is limited to a few outlier sources, similar to what Collin et al. (2006) found in another study9.
4.3.1. Disentangling rotational and turbulent velocities
Figure 18 shows the FWHM/sigma versus FWHM measurements of 3C 120 from previous campaigns (see Fig. 22 in Kollatschny et al. 2014) together with the Hα result of our new epoch, determined through the spectral decomposition in Sect. 2.5. The dotted and dashed lines represent the grid of computed theoretical rotational and turbulent Lorentzian profiles following Kollatschny & Zetzl (2011, 2013a)10.
 |
Fig. 18. Ratio of FWHM/σ with our observed value and measurements of previous studies of 3C 120 and other lines; p04: Peterson et al. (2004); g12: Grier et al. (2012); k14: Kollatschny et al. (2014). Dashed lines indicate theoretical ratios of rotationally broadened Lorentzian profiles. |
From this diagram we determined the rotational and turbulent velocities to be
Compared to the Hα value in Kollatschny et al. (2014), the rotational component has decreased from 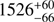 km s−1 (i.e., by a factor 2), while the turbulent component remains unchanged within the errors or has marginally increased from
km s−1 (i.e., by a factor 2), while the turbulent component remains unchanged within the errors or has marginally increased from 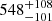 km s−1 (Table 3).
km s−1 (Table 3).
Virial masses, i.e., BH masses adopting f = 1, in units of 106 M⊙ computed for several methods, as well as input parameters derived from several campaigns.
If vrot manifests the Keplerian motion of the clouds, the decrease of vrot is qualitatively consistent with the increase of the Hα BLR radius: if the BLR lies in the equatorial plane, the radius R would increase by a factor 2.4 from 28.5 ld to 68.9 ld (Table 3). For a BLR in the equatorial plane, however, the virial mass
would then decrease by a factor 22/2.4 = 1.67, which is quantitatively incompatible with the obvious requirement of Mvir being constant. The value Mvir times a geometric scaling factor f is equal to the BH mass MBH. This suggests that a special geometry is required to resolve the discrepancy. Such a geometry could be a bowl shape with foreshortening effect. We discuss that topic further in Sect. 5.2.
4.3.2. BLR scale height and radius
In theoretical studies of ADs around a compact central mass, Pringle (1981) found that the disk scale height H at equatorial radius Rx is given by
with the sound speed cs and the Keplerian velocity vrot (see his Eq. 3.16). For an ensemble of particles, cs and vrot denote the average of the particle distributions. Using this relation, Kollatschny & Zetzl (2013a) made the further assumptions that vturb < cs, vturb = α′cs, where α′ is close to the usual viscosity parameter α ≤ 1 (e.g., Shakura & Sunyaev 1973). If the BLR gas clouds are distributed in such an AD-like configuration, then we can compute the scale height of the BLR as
For Keplerian orbits (with 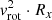 = constant) this yields
= constant) this yields
This is a flared disk in which the height increases over-proportionally with radius11. Furthermore, the gravitational potential of the central mass decreases with increasing R, so that–for constant α and vturb–the clouds at large Rx can lift up to larger height above the equatorial plane.
For our new Hα data of 3C 120, the usage of Eq. (5), with values and errors from Eq. (2) and assuming the viscosity parameter α to be unity, yields
We compare this spectroscopically obtained value with that geometrically derived for the bowl-shaped BLRs in Fig. 16. If the BLR clouds lie at the intersection of the 70 d isodelay contour with the bowl rim, then H/Rx ≈ 50/100 = 0.5. For the blue shaded BLR area H = 82 ld and Rx = 123 ld we obtain H/Rx = 82/123 ≈ 0.67 (see the thick blue lines with labels). Given the uncertainties for both the spectroscopic and geometric method, the H/Rx values agree surprisingly well.
5. Discussion
The simultaneous BLR and dust reverberation data of 3C 120 after strong brightening by a factor 3 allows us to check for luminosity dependent effects. One such effect is the geometry of the BLR–torus system. We discuss a bowl-shaped geometry in this section.
5.1. Change of bowl size with varying luminosity
When the luminosity increases, we expect that the dust torus size increases owing to sublimation of the innermost dust and vice versa (receding torus model; Lawrence 1991). However, the timescale on which this increase/decrease happens is not yet known. It is likely that the receding of the torus is slow, lasting longer than one year. Indications for a yearlong timescale come from the observations of NGC 4151 by Kishimoto et al. (2013). For 3C 120 the ratios of lag(dust) to lag(BLR) and lag(dust) to MV are small compared to other AGN. This suggests that 3C 120 is overluminous for the current bowl size and that the torus rim has not yet receded in accord with the current high luminosity.
The AD luminosity of a Seyfert AGN changes typically by 10%–30% within a few weeks. While the bowl size appears to stay essentially constant or to change slowly over at least several months, the gas clouds obviously react fast (within days or hours) to a change in luminosity. According to the LOC model of Baldwin et al. (1995), the gas clouds do not instantaneously move away or toward the illumination source, rather only their excitation and ionization states change, depending on the distance from the illuminating compact AD. This change can be instantaneous and those clouds fulfilling the locally optimized conditions shine as BLR. Then at a low luminosity state the BLR consists essentially of clouds in the bottom of the bowl with small H/Rx, but at a high luminosity state the BLR is preferably located at larger distance, hence at larger H/Rx. In other words, the BLR swings inside the bowl with the systematic trend that H/Rx increases with increasing luminosity due to the bowl rim. It is possible to further speculate that the BLR covering angle increases with increasing luminosity as well. We discuss these issues further in Sect. 5.4.
5.2. Black hole mass calculation
We consider potential effects of the bowl-shaped geometry on the BH mass calculation.
Reverberation based BH masses are commonly computed using
where Δv is a measure for the velocity, R = c ⋅ τ and f is the geometric scaling factor that is still under debate. From a statistical analysis of 16 AGN, Onken et al. (2004) determined f = 5.5, but also other values 3 < f < 9 have been reported; the gravitational redshift measured for Mrk 110 indicates f = 7.8 in this source if the BLR is an inclined ring at i = 21° (Kollatschny 2003). To be independent of f, we consider the virial mass Mvir (Eq. (3)), i.e., MBH adopting f = 1.
Table 3 lists virial masses from previous reverberation campaigns of 3C 120 and our new data. For intercomparison, the virial masses are calculated using several parameter sets: standard velocity estimates (FWHM, σv) and vrot as determined from the FWHM/sigma analysis (Sect. 4.3.1). Likewise, two versions of the orbit radius are used: the standard R = c ⋅ τ (middle block, rows 7–9 in Table 3) and the radius Rcorr = c ⋅ τ/ffs corrected for the foreshortening factor ffs of the measured lag c ⋅ τ (last block, rows 10–14 in Table 3). The calculation of ffs requires knowledge of H/Rx. For the correction we tentatively adopt the H/Rx ∝ vturb/vrot values from the FWHM/sigma analysis (Sect. 4.3.2). We further adopt a face-on view, i = 0, which roughly holds for the left and right side on an inclined bowl and therefore allows us to estimate a mean ffs. Then ffs = 1 − sin(θ) with θ = atan(H/Rx). For the parameters in the last block the errors are very uncertain and therefore not listed; nevertheless the numbers allow us to recognize trends. Thus, Table 3 lists viral masses obtained for four different methods (rows 7–9, 14).
We begin with considering the previous data, first at low luminosity for Hβ, then at intermediate luminosity for Hα and Hβ, and finally the new data at high luminosity.
-
1)
Columns 2–4 list the results for Hβ obtained at three low luminosity campaigns. For each method the virial masses agree notably well. Fig. 16 indicates that at a lag of about 25–38 days the Hβ BLR lies presumably in the bottom of the bowl at small Rx < 50 ld where the scale height and potential foreshortening effects might play a minor role. Thus the differences in the viral masses between different methods are due to the different kinds of velocity measures used.
-
2)
Columns 5–6 list results obtained for Hα and Hβ from the 2008/2009 campaign by Kollatschny et al. (2014) at 10–25% larger luminosity (row 1 in Table 3). For each of the four methods the virial mass of Hα agrees notably well with the previous estimates obtained with the same method. For Hβ, however, all four methods yield a larger virial mass than the previous campaigns; within the uncertainties the virial mass may be considered consistent12.
-
3)
Column 7 list results obtained for Hα with the new data. The parameters differ significantly by about a factor 2 from previous parameters: the lag τ is larger, and the velocities FWHM and vrot are smaller. Using the standard R = c ⋅ τ this leads to smaller virial masses compared to previous values, in particular for vrot (row 9). To solve the discrepancy of Mvir, we suggest that the lags do not linearly translate into orbit radius, i.e., distance from the BH. In a bowl-shaped geometry, Hα is emitted at largest distance, hence at largest scale height H, and thus suffers from the largest foreshortening. When correcting for the foreshortening factor using the FWHM/sigma analysis, the virial mass using Rcorr agrees well with that obtained in the previous campaigns (row 14). However, for this spectroscopically derived Rcorr we obtain a large θ = 37° close to adopted maximal half-covering angle θ = 40°. Therefore we consider the two geometric alternative H/Rx estimates from Fig. 16: (1) if the BLR lies at the bowl rim, where it cuts the isodelay surface, then H/Rx ≈ 70/140 = 0.5. (2) If we adopt the shaded BLR, then H/Rx ≈ 82/123 = 0.67. These values are smaller than 0.75 and lead to a more moderate correction and a slightly smaller virial mass: Rcorr = 124.6 ld, Mvir = 14.3 × 106 M⊙, and Rcorr = 154.7 ld, Mvir = 17.8 × 106 M⊙, respectively. Both values agree well with previous Mvir estimates.
To summarize, in a bowl-shaped geometry the calculation of Mvir may be affected by the foreshortening of the observed BLR lag, which leads to an underestimation of the BLR distance from the BH. The foreshortening effect increases with increasing distance of the BLR from the BH. For the 3C 120 data, a tentative correction of the foreshortening effect by spectroscopic or geometric H/Rx estimates yields consistent Mvir values for different Balmer lines (Hα, Hβ ) and different AGN luminosities.
5.3. Evidence favoring a bowl-shaped BLR & dust geometry
The cross correlations of the respective light curves B–Hα and B-NIR yield that the Hα echo is broad with a pronounced low-τ peak (Fig. 8) and the dust echo is symmetric and sharper than the BLR echo (Fig. 11). To make these results consistent, we compared the data with bowl-shaped BLR–torus models by KM and GKR. We adopted an inclination i = 16°. The KM bowl is more convex than the GKR bowl.
The comparison shows that, if the hot dust emission comes from the entire rim, then both the KM and GKR models yield no good fit of the lag to the data. The predicted asymmetries in the transfer functions and CCFs are not consistent with the symmetry of the data. This led us to the conclusion that the hot varying dust seen in the J and K bands is located only at the edge of the bowl. This could be achieved if the BLR gas clouds shield most of the dust rim below a covering angle of about 40° (measured from the equatorial plane). The BLR gas clouds are located in the bowl, along and above the rim, but not entirely up to the edge. Then the predicted broad transfer function with low-τ peak is consistent with the cross-correlation function of the data (B−Hα ). Regarding the precise parameterization of the bowl rim, we cannot exclude the KM model by our eyeball comparison of the data with a few Rsub cases. We also mention the caveat that no angle dependency is considered in the BLR LOC model here. Nevertheless, the fact that a large portion of the rim below the edge has to be shielded argues in favor of the GKR bowl.
Thus, a bowl-shaped BLR–torus model leads to a consistent view of the light curve data.
We checked this model further by comparison with previous RM results of the BLR at much (up to factor 3) lower luminosity (Grier et al. 2013; Pozo Nuñez et al. 2012; Kollatschny et al. 2014): in all these RM campaigns between 2008 and 2011 rather small Hβ lags (24–28 days) and a symmetric CCF have been found; Pozo et al. even found an extremely sharp CCF. If interpreted in the picture of a GKR bowl with a dust rim like that shown in Fig. 16 (i.e., where the edge lies at Rx ≈ 220 ld), then the isodelay surfaces indicate that the BLR was located at small Rx ≤ 50 ld. There the height H of the bowl rim is small (H/Rx < 15/50 ≈ 1/3, see blue long-dashed line in Fig. 16). The same holds for the Hα BLR in 2008, with a lag similar to Hβ (Kollatschny et al. 2014). Finally, a bowl-shaped BLR-dust torus geometry provides a natural way to obtain–after correction for the foreshortening effects – consistent Mvir estimates for different Balmer lines and AGN luminosities.
Because it appears hard to achieve such an overall consistent picture for other geometric configurations, we think that our new data together with the previous data provide clear evidence favoring a bowl-shaped BLR and dust geometry for 3C 120.
5.4. Consequences for the size/lag–luminosity relationships
Two important size/lag–luminosity relationships are known: one between the size of the BLR and the AGN luminosity (Kaspi et al. 2000; Bentz et al. 2013), and one between the lag of the inner dust torus and the AGN luminosity (Oknyanskij et al. 1999; Koshida et al. 2014). We note that the first relation assumes that the BLR size can be estimated by c ⋅ τ. This assumption holds if the BLR is spherical or located in the equatorial plane. However, it does not hold in a simple manner for a bowl-shaped BLR and torus geometry because then foreshortening effects play a role. Therefore, these relations should actually be considered as lag–luminosity relations and the transformation of lag to physical size should be carried out taking the geometry into account.
The relation between dust lag and AGN luminosity shows a scatter by a factor 2 around the average (solid line in Fig. 12). To understand the scatter, we assume that all sources in Fig. 12 exhibit a bowl-shaped torus geometry and that the hot dust emission occurs primarily from the edge of the bowl-shaped torus (Fig. 16). Then the scatter of the relation may naturally be explained by a hysteresis effect. If the AGN quickly brightens but the torus does not respond quickly enough, then the source moves to the left of the average relation (as 3C 120). On the other hand, if the AGN quickly dims, we can speculate that the torus dimension shrinks slowly with a hysteresis, leading to a right-hand shift of the position of the source in the dust lag–AGN luminosity diagram.
Furthermore, Koshida et al. (2014) compared the reverberation based inner torus size adopted as Rdust = c ⋅ τ with the size from interferometric measurements. The interferometric radius in the K band was found to be systematically larger than the dust reverberation radius in the same band by about a factor of two. Koshida et al. (2014) proposed that this might be interpreted by the difference between the flux-weighted radius and the response-weighted radius of the innermost dust torus. We point out that a straightforward natural explanation of this difference is also provided by the foreshortening effect. If the hot dust emission occurs primarily from the edge of the bowl-shaped torus (Fig. 16), then the lag is about a factor 2–3 shorter than simply inferred from the distance of the edge from the BH. The importance of the foreshortening effect was already noted by Pozo Nuñez et al. (2014a) for Sy-1 galaxy WPVS48 (blue source in Fig. 12).
Likewise the BLR lag depends on where the BLR is located in the bowl, for example, further in the bottom or further along the rim at increased scale height. As pointed out in Sect. 5.1, the bowl size may stay roughly constant, while the luminosity changes by 30% but the lag may suffer from foreshortening. Then, for a sample of AGN, this introduces a scatter in the R − L relationship.
So far it is not yet clear whether this effect applies mainly the Hα line or whether it also affects Hβ or other broad emission lines. Certainly, Hα requires rather a low excitation potential and therefore the Hα BLR is more extended than other emission lines typically used for RM. Therefore, the effects of the bowl-shaped geometry might be strongest for Hα. On the other hand, Hα is the brightest broad AGN emission line at optical wavelengths and as such well suited for PRM. Future coordinated dust and BLR reverberation campaigns will provide further insight.
6. Summary
We carried out a BVRIJK and 680 nm NB PRM campaign of 3C 120 during the epoch 2014–2015. The Hα line was completely covered by our NB, as verified by a contemporaneous spectrum. By applying the FVG method, we separate host and AGN flux in our filters. We compare the BLR and dust reverberation data with a range of bowl-shaped dust geometries as first invoked by Kawaguchi & Mori (2010), which were subsequently refined by Goad et al. (2012) including the BLR. In this view, the BLR clouds are seen only on that side of the bowl facing the observer. The simultaneous BLR and dust reverberation data allow us to draw the following conclusions:
-
During our epoch, 3C 120 has passed a high brightness state with log(λLλ5100) = 44.32 erg s−1, which is three times brighter than in 2009/2010.
-
The CCF between B and Hα yields a mean rest-frame delay of
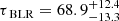 ld. The CCF is broader than indicated by the rather small uncertainties; it shows a broad plateau between 55 and 95 days and a clear substructure peak at 60 days. This indicates that the BLR is spread over a large range of isodelay surfaces.
ld. The CCF is broader than indicated by the rather small uncertainties; it shows a broad plateau between 55 and 95 days and a clear substructure peak at 60 days. This indicates that the BLR is spread over a large range of isodelay surfaces. -
The NIR J and K band light curves allow us to measure a dust emission delay (
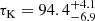 ld), which is unusually short compared to the BLR delay. Likewise the CCF between B and the NIR bands is surprisingly sharper than between B and Hα. This indicates that the hot dust emission arises from a confined volume, which is covered by a narrow range of isodelay surfaces.
ld), which is unusually short compared to the BLR delay. Likewise the CCF between B and the NIR bands is surprisingly sharper than between B and Hα. This indicates that the hot dust emission arises from a confined volume, which is covered by a narrow range of isodelay surfaces. -
Our data reach good consistency with the model by Goad et al. (2012), where the BLR clouds shield the bowl-shaped dust rim up to a half-covering angle of θ ≈ 40° from the nuclear radiation. Such a BLR reproduces the observed structured broad B–Hα CCF with a pronounced low-τ peak predicted from the models. In parallel, the hot dust emission arises from the small part of the rim at 40° < θ < 45° facing the observer, reproducing the sharp and symmetric B–NIR CCF; because this hot dust edge lies closer to the observer than the equatorial plane this also explains the short lag by foreshortening of the light travel time.
-
In a bowl-shaped geometry the calculation of the viral black hole mass Mvir may be affected by the foreshortening of the observed BLR lag, which leads to an underestimate of the BLR distance from the BH and of Mvir. The foreshortening effect increases with increasing distance of the BLR from the BH. For the 3C 120 data, a tentative correction of the foreshortening effect by spectroscopic or geometric H/Rx estimates yields consistent Mvir values for different Balmer lines (Hα, Hβ ) and different AGN luminosities.
-
If AGN in general exhibit a bowl-shaped BLR-dust torus geometry, the foreshortening effects naturally contribute to the scatter in the relationship between AGN luminosity and lag-inferred BLR size. The foreshortening effects may also explain why reverberation-based torus sizes are on average about a factor two smaller compared with interferometric torus sizes. Hysteresis effects may also contribute to the scatter in the relationship between AGN luminosity and dust lag.
Combined with spectral and infrared data, our analysis indicates a vertically extended BLR region that can be explained as an envelope of a thick dust torus with a bowl-shaped inner border.
Further light curves and emission line spectra for a sample of objects are required to corroborate this approach. The monitoring of the BLR emission lines should ideally cover distinct luminosity epochs of a single source, which will reveal how the vertical structure of a particular emission line grows with luminosity. This is especially interesting for the strong and thus easily measurable Hα emission line that likely has the largest variation in scale height.
Including the NB emission lines as in Fig. 2.
There are small peaks at the lag of about 33 days in both B − K and B − J correlations (Fig. 10). We think that broad emission lines like Paschen are not able to explain these small peaks because the line strengths are too small (cf. Landt et al. 2008 for typical Sy-1 galaxies) and any Paschen delay would be much larger than 33 days, when compared/similar to Hα lags. Instead, we suspect that the small peaks are caused by the two (probably too high) noisy data points in the J and K light curves at end of January 2015 (Fig. 9), which interfere with the local maximum of the B band light curve in December 2014 (Fig. 3). The small peaks in the B − K and B − J correlations essentially disappear, when we omit the two J and K data points at end of January 2015 from the light curves.
We have tentatively disentangled the contributions of host and AD to the NIR light curves, but this requires an uncertain extrapolation of host and AD from the optical to the NIR bands. Therefore, we here use the NIR light curves as observed. Nevertheless, in our tests the DCF results for the host and AD subtracted NIR light curves become sharper and do not show any indication for a substructure as seen for the B − Hα DCF FR/RSS statistics in Fig. 8.
Collin et al. (2006) considered FWHM/sigma versus sigma (see their Fig. 3), which is a 1/x versus x dependency (x = sigma) and as such somewhat difficult to interpret. In contrast, Kollatschny & Zetzl (2011) analyzed FWHM/sigma versus FWHM, which evidently reveals a clear and smooth deviation from a linear x vs. x trend (x = FWHM) and finally puts the suggested existence of two distinctly separated populations into question. One may speculate that the sources with relatively large turbulent velocities by Kollatschny & Zetzl are exactly those Population 1 sources by Collin et al., but this is beyond the scope of this paper.
The grid in Fig. 18 will soon become publicly available (Kollatschny et al., in prep.). A preliminary version of the grid can be found at http://www.astro.physik.uni-goettingen.de/~zetzl/blrvelo/
For α ≪ 1, say α = 0.1, H/Rx may become larger than unity, hence the assumption of a geometrically thin AD does no longer hold. Therefore, Kollatschny & Zetzl (2013a) assumed α′≈α = 1, which is a conservative estimate providing a lowest possible H/Rx.
Acknowledgments
We are grateful to Emilio E. Falco and Marco Berton for supporting us with recent spectroscopy. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This publication is supported as a project of the Nordrhein-Westfälische Akademie der Wissenschaften und der Künste in the framework of the academy program by the Federal Republic of Germany and the state Nordrhein-Westfalen. This work is supported by the DFG programs Ha 3555/12-1, Ko 857/32-2, and Ko 857/33-1. The observations on Cerro Armazones benefited from the care of the guardians Hector Labra, Gerardo Pino, Roberto Munoz, and Francisco Arraya. We thank the referee for critical and constructive comments.
References
- Agudo, I., Gómez, J. L., Casadio, C., Cawthorne, T. V., & Roca-Sogorb, M. 2012, ApJ, 752, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Kozlovsky, B.-Z., & Salpeter, E. E. 1972, ApJ, 171, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J., Ferland, G., Korista, K., & Verner, D. 1995, ApJ, 455, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2010, ApJ, 716, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [NASA ADS] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., & Radovich, M. 2002, Astronomical Data Analysis Software and Systems XI, ASP Conf. Ser., 281, 228 [NASA ADS] [Google Scholar]
- Berton, M., Foschini, L., Ciroi, S., et al. 2015, A&A, 578, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choloniewski, J. 1981, Acta Astron., 31, 293 [NASA ADS] [Google Scholar]
- Collier, S., Horne, K., Wanders, I., & Peterson, B. M. 1999, MNRAS, 302, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., & Kawaguchi, T. 2004, A&A, 426, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2011, A&A, 525, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., Hryniewicz, K., Maity, I., et al. 2013, A&A, 556, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denney, K. D., Peterson, B. M., Dietrich, M., Vestergaard, M., & Bentz, M. C. 2009, ApJ, 692, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Cheimets, P., Caldwell, N., & Geary, J. 1998, PASP, 110, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, in The Impact of Large Scale Near-IR Sky Surveys, eds. F. Garzon, N. Epchtein, A. Omont, B. Burton, & P. Persi, Astrophys. Space Sci. Lib., 210, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 1988, ApJ, 325, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., Klimek, E. S., & Nazarova, L. S. 2007, ArXiv e-prints [arXiv:0711.1025] [Google Scholar]
- Goad, M. R., Korista, K. T., & Ruff, A. J. 2012, MNRAS, 426, 3086 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012, ApJ, 755, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Peterson, B. M., Horne, K., et al. 2013, ApJ, 764, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Haas, M., Chini, R., Ramolla, M., et al. 2011, A&A, 535, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haas, M., Hackstein, M., Ramolla, M., et al. 2012, Astron. Nachr., 333, 706 [NASA ADS] [Google Scholar]
- Ho, L. C., Filippenko, A. V., Sargent, W. L. W., & Peng, C. Y. 1997, ApJS, 112, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Hodapp, K. W., Chini, R., & Reipurth, B. 2010, in Proc. SPIE, 7735, 77351A [CrossRef] [Google Scholar]
- Hönig, S. F., Watson, D., Kishimoto, M., et al. 2017, MNRAS, 464, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., Welsh, W. F., & Peterson, B. M. 1991, ApJ, 367, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., Peterson, B. M., Collier, S. J., & Netzer, H. 2004, PASP, 116, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J., & Burg, R. 1992, ApJ, 393, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kabath, P., Erikson, A., Rauer, H., et al. 2009, A&A, 506, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, T., & Mori, M. 2010, ApJ, 724, L183 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, T., & Mori, M. 2011, ApJ, 737, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Beckert, T., & Weigelt, G. 2007, A&A, 476, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2013, ApJ, 775, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Kollatschny, W. 2003, A&A, 412, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2011, Nature, 470, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2013a, A&A, 549, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2013b, A&A, 558, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., Ulbrich, K., Zetzl, M., Kaspi, S., & Haas, M. 2014, A&A, 566, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koshida, S., Minezaki, T., Yoshii, Y., et al. 2014, ApJ, 788, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 2009, AJ, 137, 4186 [NASA ADS] [CrossRef] [Google Scholar]
- Landt, H., Bentz, M. C., Ward, M. J., et al. 2008, ApJS, 174, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Landt, H., Elvis, M., Ward, M. J., et al. 2011, MNRAS, 414, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A. 2004, ASP Conf. Ser., 311, 169 [NASA ADS] [Google Scholar]
- Lawrence, A. 1991, MNRAS, 252, 586 [NASA ADS] [Google Scholar]
- Maoz, D., Netzer, H., Mazeh, T., et al. 1991, ApJ, 367, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, A., & Huchra, J. 1988, PASP, 100, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., & Trakhtenbrot, B. 2011, ApJ, 737, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Oknyanskij, V. L. 1999, Odessa Astronomical Publications, 12, 99 [NASA ADS] [Google Scholar]
- Oknyanskij, V. L., Lyuty, V. M., Taranova, O. G., & Shenavrin, V. I. 1999, Astron. Lett., 25, 483 [NASA ADS] [Google Scholar]
- Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1978, Proc. Natl. Acad. Sci., 75, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2012, ApJ, 754, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., & Wandel, A. 1999, ApJ, 521, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pozo Nuñez, F., Ramolla, M., Westhues, C., et al. 2012, A&A, 545, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozo Nuñez, F., Westhues, C., Ramolla, M., et al. 2013, A&A, 552, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozo Nuñez, F., Haas, M., Chini, R., et al. 2014a, A&A, 561, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozo Nuñez, F., Haas, M., Ramolla, M., et al. 2014b, A&A, 568, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozo Nuñez, F., Ramolla, M., Westhues, C., et al. 2015, A&A, 576, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ramolla, M., Drass, H., Lemke, R., et al. 2013, Astron. Nachr., 334, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Ramolla, M., Pozo Nuñez, F., Westhues, C., Haas, M., & Chini, R. 2015, A&A, 581, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakata, Y., Minezaki, T., Yoshii, Y., et al. 2010, ApJ, 711, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sergeev, S. G., Doroshenko, V. T., Golubinskiy, Y. V., Merkulova, N. I., & Sergeeva, E. A. 2005, ApJ, 622, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Suganuma, M., Yoshii, Y., Kobayashi, Y., et al. 2006, ApJ, 639, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000, ApJ, 536, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Tokarz, S. P., & Roll, J. 1997, ASP Conf. Ser., 125, 140 [NASA ADS] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M. 2002, ApJ, 571, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D., Denney, K. D., Vestergaard, M., & Davis, T. M. 2011, ApJ, 740, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, W. F. 1999, PASP, 111, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, H., Glass, I. S., van Wyk, F., et al. 1992, MNRAS, 257, 659 [NASA ADS] [Google Scholar]
- Woo, J.-H., Treu, T., Malkan, M. A., Ferry, M. A., & Misch, T. 2007, ApJ, 661, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshii, Y., Kobayashi, Y., Minezaki, T., Koshida, S., & Peterson, B. A. 2014, ApJ, 784, L11 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Virial masses, i.e., BH masses adopting f = 1, in units of 106 M⊙ computed for several methods, as well as input parameters derived from several campaigns.
All Figures
 |
Fig. 1. FAST spectrum of 21 November 2014 is normalized to the maximum value and drawn as black line. The Johnson B, V, and R responses that have been folded with the KAF 16801 CCD are overplotted in in colored dashed curves. The yellow shaded area represents the 680 nm NB filter folded with the quantum efficiency of the STL-6303 CCD. All filter response functions are normalized to their maximum. |
| In the text | |
 |
Fig. 2. Hα line profile decomposition. The continuum is shown with a black dashed line. The narrow Hα, [N II], and [S II] features were fitted with the red curves. The yellow area shows the 680 nm NB profile. All data is normalized to the maximum. The broad Hα is represented by the black continuous curve. |
| In the text | |
 |
Fig. 3. Combined optical light curves from all telescopes. Open diamonds indicate observations taken with the BMT telescope, filled circles represent BEST II and open triangles RoBoTT. All fluxes were measured inside an aperture of |
| In the text | |
 |
Fig. 4. B vs. I flux variations of 3C 120 in the |
| In the text | |
 |
Fig. 5. Host galaxy template spectrum in the observed filters, scaled to match the measured fluxes in B, V, and I (red diamonds). The red square shows the fitted R-band flux. |
| In the text | |
 |
Fig. 6. B vs. R flux variations of 3C 120 in the |
| In the text | |
 |
Fig. 7. Discrete correlation functions between B and the optical data. The correlation of B with V band is colored blue; the uncorrected R-band correlation is shifted −0.5 and shown in green; the line flux corrected R band is shifted −1.0 and shown in red; the I-band correlation is shifted −1.5 and shown in orange; the correlation between B and Hα is shown in black. Dotted lines represent the 1σ uncertainties. |
| In the text | |
 |
Fig. 8. B − Hα cross correlation (DCF) statistics obtained from 2000 FR/RSS runs. The vertical red solid line denotes the median. The vertical red dotted area indicates the range inside the 68% confidence, and the blue vertical dotted lines give the formal 1σ uncertainty around the median. We note the low-τ peak, i.e., the strong signal at lag 60 days, about 20% shorthand of the median. |
| In the text | |
 |
Fig. 9.
|
| In the text | |
 |
Fig. 10. Discrete correlation functions between B and IR data. The correlation of B with K band is shown in blue; B to J band correlation is shifted down by −1 and shown in green. Dotted lines represent the 1σ uncertainties. |
| In the text | |
 |
Fig. 11. B − J and B − K DCF statistics obtained from 2000 FR/RSS runs. The colored lines indicate median, confidence range, and uncertainty as in Fig. 8. We note the pronounced symmetry of the B − J and B − K distributions compared to the asymmetry of B − Hα in Fig. 8. |
| In the text | |
 |
Fig. 12. Absolute visual magnitude MV and measured cross-correlation delay of the hot dust. The host-subtracted AGN luminosity, corrected for galactic foreground extinction, is MV (Schlafly & Finkbeiner 2011). Black points are based on the data of Suganuma et al. (2006), as tabulated in Koshida et al. (2014), and labeled s06 and ko14. The continuous line is the best fit determined by s06. The black dashed line corresponds to the light travel time to the expected sublimation radius determined by Kishimoto et al. (2007). Blue pn14 data is WVPS 48 taken from Pozo Nuñez et al. (2014a) and green (pn15) is PGC 50427 measured in Pozo Nuñez et al. (2015). Our new measurement for 3C 120 is shown in red. |
| In the text | |
 |
Fig. 13. Geometric properties of the dust torus model by Kawaguchi & Mori when seen face-on. In three dimensions, the model is rotationally symmetric around the y-axis and mirrored on the x-axis. The BH is located at the origin (0,0). The adopted sublimation radius Rsub is 450 ld in polar direction. The thick red line indicates the border of the dust, and the volume filled by dust is shaded in red. The dust distribution is cut at a half-opening angle of 45°. For later comparison, the green line (labeled GKR-Parabola) indicates the slightly different bowl shape as given by Goad et al. (2012). The black curves show the isodelay surfaces with numbers giving the delay in days. The large black numbers along the bowl rim list the delay at that place. The black solid line at angle 40° to the equatorial plane indicates the potential distribution of the gas clouds (small black dots). The blue hatched area indicates Hα BLR that we see, adopting the LOC model of Baldwin et al. (1995). The thick blue lines indicate the average height (86 ld) and equatorial radius (156 ld) of the BLR. |
| In the text | |
 |
Fig. 14. Similar as Fig. 13, but for a smaller sublimation radius Rsub of 350 ld in polar direction. Also, the radius of the LOC has been slightly diminished to 150 ld, and the covering half-angle of the gas clouds has been enlarged to 45°. This places the BLR within the isodelay surfaces between 40 and 100 days as indicated by the B − Hα cross correlation (Fig. 7). |
| In the text | |
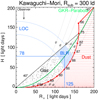 |
Fig. 15. Similar as Fig. 14, but for a smaller sublimation radius Rsub of 300 ld in polar direction. |
| In the text | |
 |
Fig. 16. Bowl-shaped torus model with parabolic dust rim, as proposed by Goad et al. (2012). The lines, colors, and labels are similar as for Fig. 13. The very thick red line labeled “Edge” indicates the dust rim above θ = 40°. The thick blue long-dashed line indicates a potential BLR gas distribution close to the bowl rim; Goad et al. also assumed a LOC controlled BLR gas distribution in their calculation of the BLR transfer function. |
| In the text | |
 |
Fig. 17. Scheme of the low-τ peak response and the smeared echo for a bowl rim observed at inclination i ≈ 16°. The dust torus is shaded in gray. The bowl rim has been adopted as a “parabola” with exponent α = 2.2, slightly more convex than in Fig. 16. The long dashed lines indicate the isodelay contours. That part of the rim for which the lag matches the data is defined in red; it leads to a sharp low-τ peak response. On the other hand, the entire part of the rim on the left-hand side (marked by the blue arrow) leads to a broad response that is more delayed and smeared out over time. |
| In the text | |
 |
Fig. 18. Ratio of FWHM/σ with our observed value and measurements of previous studies of 3C 120 and other lines; p04: Peterson et al. (2004); g12: Grier et al. (2012); k14: Kollatschny et al. (2014). Dashed lines indicate theoretical ratios of rotationally broadened Lorentzian profiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} f = \frac{ \int \! R(\lambda ) L(\lambda ) \, \mathrm{d} \lambda }{\int \! R(\lambda ) \left[ L(\lambda )+C(\lambda ) \right] \, \mathrm{d} \lambda }\cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa32081-17/aa32081-17-eq5.gif)