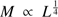| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834109 | |
| Published online | 30 October 2018 | |
Letter to the Editor
Revisiting the mass-luminosity relation with an effective temperature modifier
1
Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing, 100101 PR China
e-mail: wjf@zihexin.com
2
School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing, 100049, PR China
e-mail: zhzhong@nao.cas.cn
Received:
19
August
2018
Accepted:
27
September
2018
The mass-luminosity relation (MLR) is commonly used to estimate the stellar mass. The classical MLR can hardly fit data of all the stellar mass range, thus researchers have generally adopted piecewise MLRs based on the classical MLR with different exponents for different mass ranges. However, varying turning points for the piecewise MLRs and for the exponent of each segment were used, and the estimated stellar masses are not always as good as those obtained by dynamical methods. We suggest an alternative way to improve the mass estimation accuracy: adding an effective temperature modifier to modify every segment MLR. We use a corresponding estimating equation for G- and K-type main-sequence stars, and verify this equation on two eclipsing binary catalogs. We compare the estimated results with those from a classical MLR and several piecewise MLRs. We find that the new estimates are significantly more accurate than those from the classical MLR and some piecewise MLRs, and they are not inferior to the stellar masses from other piecewise MLRs. This indicates that the temperature modifier can effectively help improve the estimation accuracy. In addition, we discuss the effect of adding the temperature modifier on the practicability of estimating stellar masses.
Key words: binaries: eclipsing / stars: fundamental parameters
© ESO 2018
1. Introduction
As a fundamental physical quantity, stellar mass plays an important role in stellar physics and the dynamics of stellar systems, for instance. However, the vast majority of stellar masses are difficult to measure directly and are often estimated using the mass-luminosity relation (MLR). Determining the MLR requires accurate and reliable data on stellar mass, mainly from binary star systems, especially detached eclipsing binaries (Andersen 1991; Torres et al. 2010). Asteroseismology can also help in obtaining precise stellar masses (North et al. 2007, 2009), but so far, there are only few data sets. In addition, the total luminosity is needed, but we were unable to directly observe the total luminosity of a star. Some researchers have therefore replaced the total luminosity with a single-band absolute magnitude, and drew the mass-magnitude relation. For example, Henry & McCarthy (1993) obtained the mass-magnitude relation of 0.08–2 solar-mass stars for the V, J, H, K bands. Benedict et al. (2016) used astrometry combined with radial velocity data to obtain the mass-magnitude relation of 0.08–0.62 solar-mass stars for the V, K bands. In addition, if the effective temperature Teff and radius R of a star are known, the total luminosity L of the star can be calculated directly, using the equation 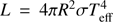 (σ is the Stefan-Boltzmann constant). Otherwise, the star’s apparent magnitude can be converted into bolometric magnitude to calculate the stellar luminosity by means of bolometric correction (Flower 1996).
(σ is the Stefan-Boltzmann constant). Otherwise, the star’s apparent magnitude can be converted into bolometric magnitude to calculate the stellar luminosity by means of bolometric correction (Flower 1996).
In the early stage, classical MLR, such as L ∝ Mα is used to fit the observed data M means stellar mass and α represents the fitting exponent). One single logarithmic linear MLR can hardly fit the stellar mass with luminosity of the entire mass range, however, because the internal structure and the main way of producing energy may not be the same for stars of different masses. In this case, piecewise MLRs are adopted to solve this problem. For each segment of a piecewise MLR, the form of the classical MLR is commonly used, but with diverse exponents. However, various turning points have been used for the piecewise MLRs and also for exponents of different mass ranges. Table 1 shows three piecewise MLRs from different works. Griffiths et al. (1988) reselected the binary samples from Popper (1980), and drew their piecewise MLR in three sections. Demircan & Kahraman (1991) discussed MLRs from models and from empirical data; Table 1 only shows the empirical MLR. Eker et al. (2015) used 268 high-precision data of detached eclipsing binaries to study the MLR. They split the MLR into four sections. This shows that not only the mass ranges and exponents, but also the number of segments may be different among researchers. For low-mass main-sequence stars, the exponent α is currently commonly around 4.
List of piecewise MLRs from different works (of the form L ∝ Mα)
The most important application of the MLR is to quickly compute the mass of a single star. However, the accuracy of estimated masses from one single classical MLR or piecewise logarithmic linear MLRs is often poor. We therefore revisit the MLR and attempt to improve the accuracy of the mass-estimating equation from the MLR. In our view, a piecewise equation seems to be necessary, but the logarithmic linear equations are not. Modifying every segment MLR by adding Teff modifiers based on the classical MLR might yield good results as well. We used data of two eclipsing binary catalogs to test this approach. In Sect. 2 we introduce the data selection. Section 3 displays the modifier and presents a comparison of different stellar mass estimations. We conclude in Sect. 4.
2. Data selection
To fit an MLR, stars with relatively reliable masses, radii, and effective temperatures are required. The most commonly used such stars are the eclipsing binary systems, and we took the detached double-line eclipsing binaries of the Milky Way (Eker et al. 2014) and DEBcat (Southworth 2015) as a primary sample.
The detached double-line eclipsing binaries of the Milky Way, also namely catalog of stellar parameters from detached double-line eclipsing binaries in the Milky Way (EKE14; Eker et al. 2014), is a catalog of 472 stars (236 binaries) with mass and luminosity parameters. The mass range is 0.18 M⊙ ~ 32.60 M⊙, the radius range is 0.21 R⊙ ~ 21.19 R⊙, and the temperature range is 2750 K ~ 43 000 K.
The full name of the DEBcat is catalog of the physical properties of well-studied eclipsing binaries. It is constantly updated over the years. As of February 28, 2018, the catalog contains 398 stars (199 binaries). The ranges of mass, radius, and the temperature are 0.11 M⊙ ~ 27.27 M⊙, 0.21 R⊙ ~ 67.62 R⊙ , and 2851 K ~ 38 019 K, respectively.
First we selected the main-sequence stars from the primary sample. Habets & Heintze (1981) used the precise stellar parameters of their double-line spectroscopic binaries for a luminosity classification, and they showed the log g− log M relationship at different luminosity classes, as displayed in Table 2 (g represents the surface gravity). The luminosity classifications EV⊙, V⊙ − V, V − IV express the boundaries of the extreme zero-age main sequence (ZAMS), between the ZAMS and the main sequence, and between the main sequence and giants, respectively, while V⊙ and V express the linear least-squares fitting of ZAMS stars and main-sequence stars in the sample of Habets & Heintze (1981). We placed the stellar log M in our sample into the corresponding function, and calculated the theoretical log g, then we compared it with the real value of the sample. When log gV−IV ≤ log g ≤ log gEV⊙, we can select the main-sequence stars in the primary sample. Figure 1 displays the picture of log g vs log M of the main-sequence star sample. The lines are functions of EV⊙, V⊙, V⊙ − V, V − IV, and V in Table 2. Black solid points in (a) are stars from EKE14 ( MWEB stands for Milky Way eclipsing binaries), and blue circles in (b) are stars from DEBcat.
 |
Fig. 1. Main-sequence stars selected from (panel a) EKE14 (black solid points) and (panel b) DEBcat (blue circles) according to the luminosity classification of Habets & Heintze (1981). The straight lines from top to bottom are functions of EV⊙, V⊙, V⊙ − V, V − IV, and V in Table 2. |
Luminosity classification and corresponding fitting functions between log g and log M (Habets & Heintze 1981).
The logarithmic MLR of the sample stars is displayed in Fig. 2. In this figure, the MLR of this sample has several turning points, but they are not obvious, and it is difficult to obtain a uniform linear MLR. Although the exponent α remains around 4, it does change in different mass ranges. Because of the relatively many G- and K-type stars in the sample, we only discuss the modification equations of G- and K-type main-sequence stars. According to Table 7 in Habets & Heintze (1981), the effective temperature range of G- and K-type stars is 3700 K < Teff < 6050 K. We used this condition to select the G- and K-type main-sequence stars in Fig. 2. There are 92 stars from EKE14 and 70 stars from DEBcat. There is some overlap of G- and K-type main-sequence stars between EKE14 and DEBCat, but the differences in their parameters are very small. Since we cannot be sure which catalog is more accurate, we did not remove the overlap stars. Our final sample therefore contains 162 stars from EKE14 and DEBCat.
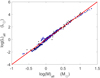 |
Fig. 2. Logarithmic MLR of main-sequence stars. Black solid points show stars from EKE14 and blue circles show stars from DEBcat. The red straight line represents one kind of classical MLR, |
3. Modified estimation and accuracy comparison
We aim to improve the accuracy of the mass-estimating equation from the MLR. An alternative way might be to add a modifier based on the classical mass-estimating equation. According to the stellar luminosity equation 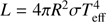 , L is proportional to the fourth power of Teff and the square of R, which means that it is more sensitive to changes in Teff. In addition, in actual observations, the measurement of R depends on an accurate distance measurement, but the measurement of Teff does not, which is more practical. Therefore, adding a Teff modifier may lead to a better mass-estimating equation without losing practicability.
, L is proportional to the fourth power of Teff and the square of R, which means that it is more sensitive to changes in Teff. In addition, in actual observations, the measurement of R depends on an accurate distance measurement, but the measurement of Teff does not, which is more practical. Therefore, adding a Teff modifier may lead to a better mass-estimating equation without losing practicability.
For the classical MLR we set = 4, combined with the stellar luminosity equation. We can easily derive the following Eq. (1), where M0 represents the classically estimated stellar mass,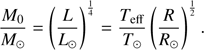 (1)
(1)
We envision building a simple enough modifier to modify Eq. (1). After some trials, we found one kind of appropriate modifier, β, and the modification equation is as bellow, where Mβ represents the modified estimated mass: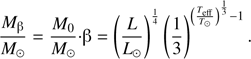 (2)
(2)
We used Eq. (2) to estimate the modification stellar masses of G- and K-type main-sequence stars, and the results are shown in Fig. 3, which displays the accuracy of classical and β modification estimations that vary with Teff. Mt represents the dynamical stellar mass of the sample, substituting the true stellar mass for comparison. Then M/Mt can indicate the accuracy of the estimation. In this figure, compared with M0, most Mβ are obviously more accurate for Teff < 5300 K, except for a few points. These stars are also poorly fit from other mainstream MLRs in Fig. 4. This is probably not the fault of modifier, but these stars do not seem to satisfy any MLRs, probably because they have relative large observational errors. On the whole, the modifier β can indeed increase the accuracy of the classical estimating equation for α = 4. However, changing exponents of a piecewise MLR can also lead to a more accurate result. Therefore, the next step is to compare the accuracy of the estimated masses obtained by piecewise MLRs with our temperature modification MLR.
 |
Fig. 3. Ratios of M0/Mt and Mβ/Mt varying with Teff. Blue solid points show classically estimated masses, and magenta asterisks represent β modification estimations. |
 |
Fig. 4. Ratios of different estimated stellar masses to sample dynamical masses varying with Teff (Mβ is shown as magenta asterisks, MG88 as green triangles, MD91 as yellow pluses, MM07 as blue squares, and ME15 as indigo crosses). |
Malkov (2007) has studied the MLR of intermediate-mass stars, from which the mass estimating equation is log m = 0.00834+0.213log L+0.0107log2L, for −1.2 < log L/L⊙ < 5.3. We used the MLR of Malkov (2007) and three piecewise MLRs from Table 1 (Griffiths et al. 1988; Demircan & Kahraman 1991; Eker et al. 2015) to estimate stellar masses of our final sample, and then labeld these estimated masses MG88, MD91, MM07, and ME15, respectively. The comparison result is displayed in Fig. 4. As can see in this figure, the accuracies of MG88 and MD91 are relatively low, and the accuracies of MM07 and ME15 are roughly similar to Mβ.
For quantitative comparison, Table 3 shows the average values, standard deviations of ratios of M0, Mβ, MG88, MD91, MM07, and ME15 to sample masses, and the percentages of stars within the corresponding relative error (RE) range. According to this table, although average value of Mβ/Mt is not the best, its standard deviation is the lowest and has the highest percentage of stars within any of the corresponding RE ranges. In addition, the percentages of stars for MG88 and MD91 are both relatively low, while the percentages of stars for MM07 and ME15 are slightly lower than for Mβ in every RE range. To summarize, we are conservative in thinking that the accuracy of our β modification estimating equation is obviously higher than those of Griffiths et al. (1988) and Demircan & Kahraman (1991), and is not inferior to those of Malkov (2007) or Eker et al. (2015). All the above indicates that the modifier β can effectively help improve the accuracy of the stellar mass-estimating equation, which is an alternative way to changing exponents of a piecewise MLR. We also considered the practicability, and adding the temperature modifier does not affect the practicability of estimating the masses of stars (see Appendix A).
Average values, standard deviations of the ratios of M0, Mβ, MG88, MD91, MM07, and ME15 to sample masses, and the percentages of stars within the corresponding relative error ranges.
4. Conclusions
The MLR is one of the most basic properties of stars, and it can be used to estimate the mass of a single star when it is combined with a photometry measurement. One single classical MLR fitting cannot accomodate the entire mass range, which is the reason why logarithmic linear piecewise equations with different exponents have been adopted to improve the mass estimation accuracy. We suggest that adding the Teff modifier on the basis of the classical MLR can be an alternative way to improve estimation accuracy. We presented a new mass-estimating equation with the temperature modifier β for G- and K-type mainsequence stars, and verified this approach on samples in two eclipsing catalogs, the EKE14 and DEBCat. We compared the β modification estimations with the classical mass estimations and those from some mainstream MLRs. The results show that modification estimations have the lowest standard deviation and the highest percentages of stars within any of the corresponding RE ranges. This shows that the accuracy of the β modification estimating equation is obviously higher than those of some mainstream MLRs, and is not inferior to the other MLRs. This means that using the temperature modifier to revise the massestimating equation can effectively improve the accuracy of stellar mass estimations. We also discussed methods for measuring the effective temperature of a star (see Appendix A). Choosing the right approach can help to quickly compute stellar effective temperatures in different situations. Therefore, we do not consider that the addition of temperature modifier would affect the practicability of estimating stellar mass.
We still think piecewise MLR should be adopted, but their turning points are still not agreed among researchers. More to the point, how many turning points are needed? It also remains debated whether they are necessary or if the trend of the MLR changes continuously and slowly, without specific turning points. In addition, the modifier we obtained can improve the accuracy of estimating the G- and K-type main-sequence stars, but for other spectral type stars, the modifier should be different. Furthermore, even with the G- and K-type main-sequence stars, the modifier β may not be the best form. We suspect, however, that the Teff modifier may be related to the physical processes of the early stage of main-sequence stars, and may help to establish a more sophisticated physical model of ZAMS stars.
Acknowledgments
We thank Zhao Gang, Liu Jifeng, Jiang Xiaojun, and Wu Zhenyu for useful discussions.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Andersen, J. 1991, A&ARv, 3, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., Henry, T. J., Franz, O. G., et al. 2016, AJ, 152, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Petford, A. D., Arribas, S., Haddock, D. J., & Selby, M. J. 1990, A&A, 232, 396 [NASA ADS] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012b, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demircan, O., & Kahraman, G. 1991, Ap&SS, 181, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Eker, Z., Bilir, S., Soydugan, F., et al. 2014, PASA, 31, e024 [NASA ADS] [CrossRef] [Google Scholar]
- Eker, Z., Soydugan, F., Soydugan, E., et al. 2015, AJ, 149, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J.I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffiths, S. C., Hicks, R. B., & Milone, E. F. 1988, JRASC, 82, 1 [NASA ADS] [Google Scholar]
- Habets, G. M. H. J., & Heintze, J. R. W. 1981, A&AS, 46, 193 [NASA ADS] [Google Scholar]
- Henry, T. J., & McCarthy, Jr., D. W. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Pichon, B., et al. 2008, A&A, 488, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malkov, O. Y. 2007, MNRAS, 382, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- North, J. R., Davis, J., Bedding, T. R., et al. 2007, MNRAS, 380, L80 [NASA ADS] [CrossRef] [Google Scholar]
- North, J. R., Davis, J., Robertson, J. G., et al. 2009, MNRAS, 393, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Popper, D. M. 1980, ARA&A, 18, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2015, in Living Together: Planets, Host Stars and Binaries, eds. S. M. Rucinski, G. Torres, & M. Zejda, ASP Conf. Ser., 496, 164 [NASA ADS] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
Appendix A: Effect of the Teff modifier on practicability
When the modification equation is used to estimate the mass of stars, it is most important to measure the effective temperature of the star. There are many methods for measuring temperature, such as direct, indirect, and semi-direct methods. First, the direct method is not directly measuring the temperature, but directly measuring the stellar radius. Interferometry is one of the most important ways to do this (Kervella et al. 2004, 2008). Combined with the stellar luminosity, we can use the stellar radius as obtained from interferometry to compute the stellar effective temperatures. Unfortunately, the number of stars in interferometry is too small, and for large data samples, it is impossible to measure the radii of all stars with an interferometric approach. It is therefore necessary to combine interferometric measurements with the color or spectral types of stars and to establish empirical formulas for calculating effective temperatures. Boyajian et al. (2012) measured the radii of 44 A-, F-, and G-type stars by interferometry, and obtained their effective temperatures by combining the results with bolometric flux measurements. Based on these stellar parameters, they obtained the empirical equations of spectral-type–Teff and color–Teff for these stars. In the same way, Boyajian et al. (2012) measured the radii and effective temperatures of 21 K- and M-type stars by interferometry and bolometric flux measurements. They also obtained the empirical relation of Teff–color–[Fe/H] for these stars. These empirical equations can be used to calculate the effective temperature of the stars in other samples.
Second, effective temperatures can be indirectly measured using the stellar spectral lines. The more common methods are the excitation equilibrium of the Fe lines, or fitting Balmer lines. The advantage of these two methods is that they are not affected by reddening, and the disadvantage is that they strongly depend on the model assumptions. In actual measurements, if there is a spectrum with a high signal-to-noise ratio (S/N), the temperature of the star can be measured by the above two methods, and the modification equations can be used to obtain the stellar mass.
In addition to directly measuring radius or indirectly using spectral lines, a so-called semi-direct method has often been used, called infrared flux method (IRFM), to calculate the effective temperature. The IRFM was first used by Blackwell & Shallis (1977), and after 13 years of development, the theory was finally completed by Blackwell et al. (1990). The advantage of the this method is that it can simultaenously measure the angular diameter and the effective temperature of the star. The IRFM has frequently been used to measure the temperature of stars of different spectral types, and the Teff–color–[Fe/H] relations of the stars were obtained accordingly (Alonso et al. 1996; Ramírez & Meléndez 2005a,b; Casagrande et al. 2006, 2010; González Hernández & Bonifacio 2009). The relations in these works are in the form of Eq. (A.1),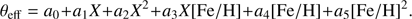 (A.1)
(A.1)
Here, θeff = 5040/Teff, and X represents the color of a star, and ai(i = 0, …, 5) are the fitting factors. Equation (A.1) can be used to calculate the stellar effective temperature as long as the photometry color and the [Fe/H] data are known. Because the fitting factors ai are generally small, the error of [Fe/H] has little effect on the error of the effective temperature. Even if the spectral S/N is not high, if the accuracy of the photometry is high, the calculated effective temperature error will be relatively small.
In general, there are many ways to measure the effective temperature. For a spectrum with high S/N, the stellar temperature can be measured by the excitation equilibrium of the Fe lines, or by fitting Balmer lines. If only photometry and [Fe/H] can be used, we can take advantage of the Teff–color–[Fe/H] relations to calculate the effective temperature. Even if photometry alone is available, using the empirical color–Teff relation can also help to calculate effective temperature. The greatest advantage in estimating stellar mass using the MLR is that a large sample of stars can be computed fast, and the methods we described above are all applicable to the rapid computing of large samples of stars, so that the addition of a temperature modifier does not affect the practicability of estimating the stellar masses.
All Tables
Luminosity classification and corresponding fitting functions between log g and log M (Habets & Heintze 1981).
Average values, standard deviations of the ratios of M0, Mβ, MG88, MD91, MM07, and ME15 to sample masses, and the percentages of stars within the corresponding relative error ranges.
All Figures
 |
Fig. 1. Main-sequence stars selected from (panel a) EKE14 (black solid points) and (panel b) DEBcat (blue circles) according to the luminosity classification of Habets & Heintze (1981). The straight lines from top to bottom are functions of EV⊙, V⊙, V⊙ − V, V − IV, and V in Table 2. |
| In the text | |
 |
Fig. 2. Logarithmic MLR of main-sequence stars. Black solid points show stars from EKE14 and blue circles show stars from DEBcat. The red straight line represents one kind of classical MLR, |
| In the text | |
 |
Fig. 3. Ratios of M0/Mt and Mβ/Mt varying with Teff. Blue solid points show classically estimated masses, and magenta asterisks represent β modification estimations. |
| In the text | |
 |
Fig. 4. Ratios of different estimated stellar masses to sample dynamical masses varying with Teff (Mβ is shown as magenta asterisks, MG88 as green triangles, MD91 as yellow pluses, MM07 as blue squares, and ME15 as indigo crosses). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.