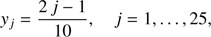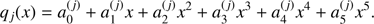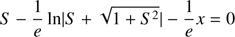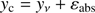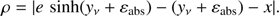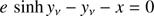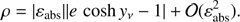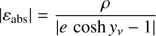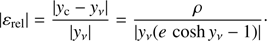| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201833563 | |
| Published online | 16 November 2018 | |
An efficient code to solve the Kepler equation
Hyperbolic case⋆
Space Dynamics Group-Technical University of Madrid, 28040 Madrid, Spain
e-mail: v.raposo.pulido@upm.es, j.pelaez@upm.es
Received:
4
June
2018
Accepted:
6
September
2018
Context. This paper introduces a new approach for solving the Kepler equation for hyperbolic orbits. We provide here the Hyperbolic Kepler Equation–Space Dynamics Group (HKE–SDG), a code to solve the equation.
Methods. Instead of looking for new algorithms, in this paper we have tried to substantially improve well-known classic schemes based on the excellent properties of the Newton–Raphson iterative methods. The key point is the seed from which the iteration of the Newton–Raphson methods begin. If this initial seed is close to the solution sought, the Newton–Raphson methods exhibit an excellent behavior. For each one of the resulting intervals of the discretized domain of the hyperbolic anomaly a fifth degree interpolating polynomial is introduced, with the exception of the last one where an asymptotic expansion is defined. This way the accuracy of initial seed is optimized. The polynomials have six coefficients which are obtained by imposing six conditions at both ends of the corresponding interval: the polynomial and the real function to be approximated have equal values at each of the two ends of the interval and identical relations are imposed for the two first derivatives. A different approach is used in the singular corner of the Kepler equation – |M| < 0.15 and 1 < e < 1.25 – where an asymptotic expansion is developed.
Results. In all simulations carried out to check the algorithm, the seed generated leads to reach machine error accuracy with a maximum of three iterations (∼99.8% of cases with one or two iterations) when using different Newton–Raphson methods in double and quadruple precision. The final algorithm is very reliable and slightly faster in double precision (∼0.3 s). The numerical results confirm the use of only one asymptotic expansion in the whole domain of the singular corner as well as the reliability and stability of the HKE–SDG. In double and quadruple precision it provides the most precise solution compared with other methods.
Key words: methods: numerical / celestial mechanics / space vehicles
A copy of the C code model is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/619/A129
© ESO 2018
1. Introduction
The hyperbolic Kepler equation (HKE) is
and it must be solved to obtain the value of the hyperbolic anomaly H in terms of the mean anomaly M and the eccentricity e of the orbit: H = H(M, e) or y = y(x, e). In this paper we use the following notation: the hyperbolic anomaly is denoted by H or y without distinction. Equally, the mean anomaly is denoted M or x.
Solving Kepler’s equation – in its elliptic or hyperbolic version – is not a new problem. For approximately the last three centuries many scientists have been interested in this resolution and many papers related to this topic have been published in each decade from the mid-seventeenth century. By 1960 problems of celestial mechanics and orbit determination were being reformulated, and indeed new fields, including astronautics and astrodynamics, were being built to study them (Colwell 1993). The introduction of rocket thrusters for space flight presented possibilities of encountering trajectories with osculating orbits whose character changes significantly during the period of interest. In that sense, a low-acceleration escape trajectory might start in a nearly circular orbit and finish on a hyperbolic path. This aspect motivated researchers to employ a formulation free from the possibilities of indeterminateness, no matter what form the orbit takes, elliptic, parabolic, hyperbolic, or possibly a circular or linear limit (Pitkin 1965).
As a consequence, during that time there were efforts in several directions to reformulate laws of orbital motion, and in particular the Kepler equation, into universal variables which incorporated all eccentricities and allow rapid, accurate computation of positions and velocities. Some of these approaches can been found in Battin (1964), Goodyear (1965), Stumpff (1968), Herrick (1971), Gooding (1987), Sarnecki (1988), Sharaf & Sharaf (2003), Beust et al. (2016), or Wisdom & Hernandez (2015). Even analytical solutions have been found using universal variables (see Tokis 2014).
However, the interest for the hyperbolic version of the Kepler equation is based on many different reasons. First of all, the solution of any highly transcendental equation is interesting, in itself, from the point of view of applied mathematics. In the field of numerical analysis some powerful techniques have been devoted to solve transcendental equations; for example, the homotopy continuation methods (see Sharaf et al. 2007; Alhindi & Sharaf 2014).
Obviously the HKE is most important in the fields of astronomy, celestial mechanics, and astrodynamics. In their paper Wisdom & Holman (1991) strongly underlined the important role that long-term integrations play in investigations in dynamical astronomy. A clear example is the LONGSTOP project Milani et al. (1986), an international cooperative program with the purpose of investigating the stability of our solar system. In these kinds of integrations, it is of paramount interest to take care of the errors involved (see Milani & Nobili 1987). The imperfect convergence of an iterative algorithm – especially when we solve transcendental equations such as the Kepler equation – is a well known source of error. To minimize such errors is always an interesting issue that helps to achieve the main objective of the research. The Kepler equation must be solved in symplectic integration codes as for example in the Wisdom–Holman method (Wisdom & Holman 1991), where the orbital elements experience small changes at every step. It can be used for long-term gravitational simulations (Rein & Tamayo 2015), or for the collisional gravitational N-body problem (Hernandez & Bertschinger 2015; Dehnen & Hernandez 2016). Beyond this, the correct determination of position and velocity in perturbed cometary orbits, which depends on the fast and accurate solution of the HKE, became an important issue. The introduction of computing machines gave impetus to the generation of algorithms that help in tasks of this kind from the very beginning. One example can be found in Davidson (1932), Smiley (1934), Davidson (1934) where a method is introduced in order to calculate the true anomaly and the time of perihelion passage for hyperbolic orbits. The authors gave an approximate solution of the HKE without explicitly mentioning it. Another example of algorithms designed to be used in a computing machine can be found in Sitarski (1968).
Some comets are originated outside of the solar system. Such comets enter the solar system coming from the interstellar space and may exit the solar system through hyperbolic trajectories. Recently the object 1I/2017 U1 reached its perihelion (0.2483 ua) following one of these hyperbolic trajectories. Frequently, the HKE is used to describe the hyperbolic anomaly of the comet. The determination of the radial distance – or the Cartesian coordinates – of such a comet requires somewhat accurate knowledge of the hyperbolic anomaly. Faintich (1972) shows how a near-parabolic comet in the Oort cloud can be perturbed by a passing star. The description of the perturbed comet orbit requires us to consider the hyperbolic motion of both stars around its common centre of mass and the time evolution of the whole system leads to a solution of the HKE.
There are, however, other fields in which the HKE plays a significant role. For example, Rauh & Parisi (2011) faces the problem of deriving macroscopic properties from the Hamiltonian of the hydrogen atom considering possible hyperbolic orbits. By using the Kustaanheimo–Stiefel (KS) transformation a pseudo-time σ is introduced into the problem. However, the relation between σ and the real time t is given by a particular version of the HKE. Thus in some quantum mechanics problems the HKE appears naturally.
Stellar dynamics is another field where the HKE also appears (see, for example; Kurth 1978). In Yabushita (1971) plan investigation is made of the possibility of a capture process in which a planet of negligible mass, initially in Keplerian orbit about a star, is perturbed by a passing star with hyperbolic velocity at great distance and becomes a planet of the star escaping to infinity with it. In order to integrate the governing equations, the HKE needs to be solved for each integration step. Since they did not have a fast and reliable solver the authors opt to integrate an additional differential equation.
Thus in many integration processes the solution of the Kepler equation – elliptic or hyperbolic – could jeopardize the procedure as indicated in Balaraman & Vrinceanu (2007). It follows, from here, the need for an efficient, fast and accurate calculation method to solve the HKE.
The HKE has been studied by several authors to develop optimal methods. In this regard, the main aspects to take into account are the accuracy and the computational performance, which are related to the method for determining the starting estimate H. The approaches in the paragraphs below represent some of the current methods used to solve (2).
The Gooding 1988 approach described in Gooding & Odell (1988): The starter is based on Lagrange’s theorem, where the equation is rewritten as a function of S = sinhH instead of H. First, Halley’s method is applied to obtain the corrector of S as well as of the function and its derivative. With these values, the Newton-Rhapson method is applied to determine the solution of the equation. It is an iterative method which requires several transcendental function evaluations.
The Fukushima 1997 approach described in Fukushima (1997): Several intervals of L = M/e are defined to select where the solution should be determined. The different methods and approximations chosen for each interval depend on the expected size solution. First, four cases in which the solution is large are selected. For these cases an asymptotic form of the main equation is considered and an approximate solution is found. Next, four other for which the solution is small cases are selected. In these latter case an iterative procedure is applied to solve the approximate forms of Kepler’s equation. In the remaining case, for which the solution interval becomes finite, a discretized Newton method is applied as well as a Newton method in which the functions are evaluated by Taylor series expansions. In that case, the starter value is the minimum of some upper bound of the solution prepared by using the Newton correction formula. This approach, depending on the case, uses or does not use an iterative method that requires several transcendental function evaluations.
The Avendaño 2015 approach described in Avendano et al. (2015): The equation is rewritten as a function of S = sinhH instead of H, such that the starter S is a piecewise-defined function involving several linear expressions and one with cubic and square roots. Once the seed is estimated, a Newton’s method is applied, by using Smale’s α-theory to decide whether the starter gives the claimed convergence rate. It is an iterative method which requires several transcendental function evaluations.
The goal of the present study is the determination of a suitable seed to initialize the numerical method for solving the Kepler equation. For that we consider the optimization already tested of the Newton–Raphson method and extend the method described in Raposo-Pulido & Peláez (2017) for the elliptical Kepler equation to the HKE. Following previous work, the Maple symbolic manipulator is chosen to obtain the code in the C programming language. The code developed is called HKE–SDG. As a result we obtain a simple way to provide fast and accurate solutions.
2. Hyperbolic Kepler equation
The Kepler equation for the hyperbolic case
determines a nonlinear function y = y(x, e) where y is the hyperbolic anomaly related with the true anomaly θ by means of
and x is the equivalent to the mean anomaly in the elliptic motion:
The eccentricity is larger than one. As a consequence x and y have the same sign, that is, y > 0 ⇔ x > 0. Since the right hand side of (2) is an odd function, for negative values of x the following change of variables leads to
where 𝔵 and 𝔶 are positives. Therefore, we focus the analysis in the resolution of Eq. (2) for positive values: (x, y)∈[0, ∞[×[0, ∞[.
The solution of the Kepler equation can be seen as a root finder problem of the function
for given values of e and x. In such a case, the Kepler equation univocally determines a bijective function y = y(x, e) which is defined on ℝ+. This property can be deduced from Bolzano’s theorem and the fact that function f(y) in Eq. (7) is strictly increasing. Indeed, f(y) is a continuous function on the closed interval ![$ [{y}_{1}, {y}_{2}] = \left[0, \frac{x}{e-1}\right] $](/articles/aa/full_html/2018/11/aa33563-18/aa33563-18-eq8.gif) and it takes values of the opposite sign at the extremes
and it takes values of the opposite sign at the extremes
Applying Bolzano’s theorem to function f(y), there exist an intermediate value y* ∈ [y1, y2] which verifies f(y*)=0. Therefore f(y) vanishes at least once in the stated interval. However, the derivative of f(y), f′(y), is always positive
That is, ∀y2 > y1 with y1, y2 ∈ [0, ∞[, f(y2) ≥ f(y1) and f(y) is strictly increasing. Consequently, f(y) is zero for only one value of y ∈ [y1, y2]. In summary, for given x, ∃ ! y such that f(y)=0.
3. Newton–Raphson algorithms
Following the procedure developed and validated in Raposo-Pulido & Peláez (2017), we use the Newton–Raphson algorithms to solve the HKE. The root searched is solution of Eq. (7). To find this root we wish to establish a successive approximation method starting from a seed y0. If yn is one of the terms of the sequence, the next term will be yn + 1 = yn + Δyn, where Δyn is given by applying a root-finding method of Laguerre (1834–1886) to the solution of the HKE (Conway 1986)
in which the sign ( + ) is selected when f′(yn) is positive; if f′(yn)< 0 the sign ( − ) must be chosen. The introduction of absolute value in the Eq. (11) is useful to avoid failures when the square root is a complex number. It does not affect the convergence of the algorithm which is practically independent of m, the degree of the polynomial.
Three different algorithms are be considered in this study: the classical Newton–Raphson (CNR) algorithm (m = 1); the modified Newton–Raphson (MNR) algorithm (m = 2); and the Conway algorithm (m = 5).
All of three algorithms use an initial seed to initialize the convergent sequence. However, its behavior, related with the reliability, is going to mark the difference. While the MNR method always converges to the real solution independently of the quality of the seed, the CNR is less stable. Therefore CNR method is more correlated with the initial value than the Conway or the MNR methods. A way to escape from this disadvantage and assure the reliability of the method is by using a very good seed as initial point. In that case the CNR and the MNR algorithms converge quickly to the real solution, as is shown in Raposo-Pulido & Peláez (2017) for the elliptic Kepler equation.
4. Seed value
As we briefly explain in the introduction, the core of this work is to generate a very good initial seed in all possible cases. If this is satisfied, then we can benefit from the convergent property of the Newton–Raphson algorithms (CNR, MNR, or Conway) to determine the right solution of the Kepler equation. This approach has been used with success in the elliptic case (see Raposo-Pulido & Peláez 2017). In this paper, we show that in the hyperbolic case too, improving the initial seed to feed a Newton–Raphson algorithm is much more cost-effective than searching for new algorithms better than the classic Newton–Raphson algorithms.
We must take into account that the accuracy of the Newton–Raphson algorithms is jeopardized when x = M ≪ 1 and e − 1 ≪ 1; This region of the plane (e, M) is called the singular corner. In such a region y is also small, and the expansion of the equation for small values of y provides
that is, the solution is badly determined from a numerical point of view since it is the ratio of two infinitesimals.
In order to determine the optimal seed, we need to introduce two different scenarios, depending on whether we are inside or outside of the singular corner. From a practical point of view we define the singular corner as the region in which x = M < 0.15 and e < 1.25. These values have been chosen arbitrarily: firstly inside the singular corner (x = M < 0.15 and e < 1.25): three regions (inner, intermediate and outer) are defined in terms of the size of x and y. In these regions we estimate the starter through an asymptotic expansion. And secondly outside the singular corner (x = M ≥ 0.15 or e ≥ 1.25): two regions are defined in terms of the infinite y-domain [0, ∞[ to estimate the starter. In the finite interval [0, 5[ the seed is determined through a fifth degree polynomial, while in the infinite interval [5, ∞[ the seed is estimated through an asymptotic approximation.
As we see below, the polynomial approximation works very well in most cases, especially when x = M is close to the ends of the interval where the polynomial is defined. In such a case the seed practically leads to the solution of the Kepler equation. However, the singular behavior of the Kepler equation makes the approximation of y(x) through this procedure ineffective and a special analysis should be implemented.
5. Inside the singular corner
To describe the solution inside the singular corner we introduce the value ε = e − 1 assuming that ε ≪ 1:
The objective is to obtain an approximation to the exact solution yν(x) of Eq. (13) with enough accuracy to be the seed used to start the Newton–Raphson convergent process. To this end, an asymptotic expansion in power of the small parameter ε will be introduced.
However we must distinguish between several regimes inside the singular corner:
-
the inner region, where x ≈ 𝒪(ε2) and y ≈ 𝒪(ε). In this inner region the most important term on the right hand side of Eq. (13) is εsinhy.
-
the intermediate region, where
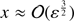 and
and 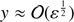 . In this intermediate region both terms on the right hand side of Eq. (13) are of the same order: sinhy − y ≈ ε sinhy.
. In this intermediate region both terms on the right hand side of Eq. (13) are of the same order: sinhy − y ≈ ε sinhy. -
the outer region, where
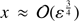 and
and 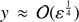 . In this outer region the most important term on the right hand side of Eq. (13) is sinhy − y.
. In this outer region the most important term on the right hand side of Eq. (13) is sinhy − y.
5.1. Inner region
In the inner region we use new variables given by the following relations:
and where (ξ, η) are both positive amounts. In Eq. (13) we introduce the expansion
The coefficients ai, i = 1, 2, … can be obtained expanding appropriately the right hand side of Eq. (13). The solution is
We must invert this solution to obtain η as a function of ξ; to this end we introduce the expansion
To calculate the coefficients bi, i = 1, 2, …, which are functions of ξ, we introduce this expansion in (16) and require that the different coefficients of each order match. The result is
Figure 1 shows the behavior of the asymptotic solution (Eqs. (14)–(18)) in the inner region. The agreement with the exact solution is excellent for very small values of x.
 |
Fig. 1. Exact solution of the Kepler equation and the asymptotic solution – up to sixth order – obtained in the inner region of the singular corner. The agreement is excellent for very small values of x. Here four values of ε have been considered: ε = 0.001, 0.101, 0.201, 0.301. |
5.2. Outer region
In the outer region we introduce the following change of variables:
We note that (ν, μ) are both positive amounts. We look for a solution of Eq. (13) given by
where the coefficients ai, i = 1, 2, … can be obtained by appropriately expanding the right hand side of Eq. (13). The solution is
Let μ0 > 0 be the real and positive solution of the cubic equation
This root always exists and is univocally defined because ν is always positive. It takes the value
Once the value of μ0 is known it is possible to invert the solution (21) to obtain μ as a function of ν; to do that we introduce the expansion
where the coefficients bi, i = 1, 2, … are functions of μ0 that must be calculated. Introducing this expansion into Eq. (21) and requiring that the different coefficients of each order match it is possible to obtain the values of bi, i = 1, 2, … The result is
5.3. Intermediate region
In the intermediate region we introduce the following change of variables:
We note that ( χ, σ) are both positive amounts. We look for a solution of Eq. (13) given by
where the coefficients ai, i = 1, 2, … can be obtained expanding appropriately the right hand side of Eq. (13). The solution is
The next step is to invert this solution to obtain σ as a function of χ. Let σ0 > 0 be the real and positive solution of the cubic equation
This root always exists; in effect, the function f(σ) verifies
therefore in the interval [0, χ] there is a root of f(σ)=0 at least. But there is only one root, because the derivative
is always positive in that interval. That root is given by
where 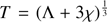 and
and 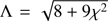 . It should be noticed that expression (33) can present a rounding-error defect when
. It should be noticed that expression (33) can present a rounding-error defect when 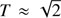 (σ0 ≪ 1). In order to minimize this error, we develop an alternative procedure to provide σ0. We rewrite the cubic Eq. (29) as
(σ0 ≪ 1). In order to minimize this error, we develop an alternative procedure to provide σ0. We rewrite the cubic Eq. (29) as
such that σ is replaced by (33) on the right hand side of the equation, obtaining
which provides a smaller rounding-error when χ ≪ 1, that is, when 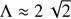 .
.
Once the value of σ0 is known it is possible to invert the solution (28) to obtain σ as a function of χ; to do that we introduce the expansion
where the coefficients bi, i = 1, 2, … are functions of σ0 that must be calculated. Introducing this expansion in (28) and requiring that the different coefficients of each order match it is possible to obtain the values of bi, i = 1, 2, … The result is
5.3.1. Matching with the inner region
A detailed insight of the solution in this region shows that when (χ, σ) take small values the asymptotic solution tends to the inner solution obtained previously. In effect, when
the solution enters in the domain of the inner solution. For that values the parameter σ0 given by (35) takes the value
If this value is introduced into Eq. (37) provides
and this expression coincides with Eq. (18) corresponding to the inner solution. This is the reason why the asymptotic solution given by Eq. (37) also provides the solution in the inner region where x is in the domain of the inner solution.
5.3.2. Matching with the outer region
When (χ, σ) take large values the asymptotic solution tends to the outer solution obtained previously. In effect, when
the solution enters in the domain of the outer solution. For those values the parameter σ given by Eq. (37) takes the value
and this expression coincides with Eq. (25) corresponding to the outer solution. This is the reason why the asymptotic solution given by Eq. (37) also provides the solution in the outer region where x is in the domain of the outer solution.
5.4. Summary of the singular corner
The analysis carried out above shows that the asymptotic expansion Eq. (37) corresponding to the intermediate region also describes the solution in the inner and outer regions of the singular corner. Figure 2 shows the exact solution of the HKE and the asymptotic solution – up to the fourth order – obtained in the intermediate region of the singular corner. The agreement is exceptional in the whole range of values of x = M. These numerical results confirm the theoretical analysis. The main consequence is that, from a practical point of view, the asymptotic expansion Eq. (37) can be used in the whole domain of the singular corner.
 |
Fig. 2. Exact solution of the Kepler equation and the asymptotic solution – up to the fourth order – obtained in the intermediate region of the singular corner. The agreement is excellent for whole range. Here four values of ε have been considered: ε = 0.001, 0.101, 0.201, 0.301. |
Therefore, only one asymptotic expansion is considered in HKE–SDG: that corresponding to the intermediate region. This approximate solution permits us to generate a very good seed to feed the Newton–Raphson convergent process for values of (e, M) inside the singular corner.
6. Outside the singular corner
We begin by performing the following change of variable
which transforms the Kepler equation into the relation
with the variable S defined in the interval [0, ∞[. Due to the infinite domains of both variables (x, y), the range of y is divided in two intervals: [0, 5[ and [5, ∞[ such that for each interval a different treatment will be applied. The limit value of five has been chosen arbitrarily; we note that the corresponding value of S ≈ 74.2 is large compared with unity. In the interval [0, 5[ the seed will be generated with polynomials. In the interval [5, ∞[ the seed will be generated with the help of an asymptotic solution of the Eq. (44) for large values of S ≫ 1 which correspond, basically, to large values of M.
6.1. Polynomial approximation
If y ∈ [0, 5[, the interval is divided into 25 even intervals; the lower ends of such intervals are given by
where the corresponding Si is obtained from (43) and Mi ≡ xi is obtained from (44) (values attached in the code). This way, we define twenty five intervals [xi, xi + 1], i = 1, …, 25. In each of these intervals we introduce a fifth degree polynomial pi(x, e), i = 1, …, 25 to interpolate the hyperbolic sine of the hyperbolic anomaly, that is, S.
We note that the coefficients of the polynomials considered in the method depend on the eccentricity. In order to simplify the reading of the equation, we abuse notation by writing the coefficients only as a function of i,
The polynomial pi(x) is only valid inside the interval [xi, xi + 1], i = 1, …, 25, where the function is approximated by the polynomial: S(x) ≈ pi(x). To do that we follow the procedure developed in Raposo-Pulido & Peláez (2017) by imposing six boundary conditions to determine the six coefficients of pi(x). These conditions assure that the function S(x) and the polynomial pi(x) share the same values and the same first and second derivatives at the ends of the interval [xi, xi + 1].
Modern symbolic manipulators such as Maple or Mathematica allow us to obtain the polynomials pi(x), i = 1, …, 25, easily and only once. Moreover, they provide the FORTRAN or C code of the polynomials that will be appropriately stored in one module to be used later. In the HKE–SDG we use the version 18.02 of Maple (Raposo-Pulido & Peláez 2017) to perform this task.
6.2. Asymptotic approximation
We note that the HKE (44) can be expressed as follows:
where f is a function of the variable S; the values of (x, e) appear as parameters. The derivative of f turns out to be
If y = H ∈ [5, ∞[, the corresponding interval for S is given by [74.203, ∞[, where the value of x could be very large. In this range x and S tend to infinite, in a first approximation.
The derivative given by Eq. (48) is, obviously, lower than unity, when y = H ∈ [5, ∞[ because S > > 1 and e > 1. As a consequence the function f(S, x, e) given by Eq. (47) is a contraction mapping. The Banach fixed-point theorem can be applied and f(S, x, e) admits a unique fixed-point S* which verify: S* = f(S*, x, e). This fixed-point is the root we are looking for.
The mathematical analysis shows that the following sequence Sn defined by
which starts in the value S0 = x/e, is convergent and it tends to the limit S*, that is, to the unique fixed-point.
The speed of convergence of this sequence is larger than usual because of the large values of S in the interval y ∈ [5, ∞[. However, a detailed analysis shows that there are faster algorithms which are also reliable.
In effect, the second term of the right hand side of Eq. (44) becomes, with respect to the first term, very small. As a consequence we can consider the logarithm as a small parameter 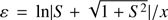 , obtaining S by applying an asymptotic expansion in power of ε. Equation (44) takes now the expression
, obtaining S by applying an asymptotic expansion in power of ε. Equation (44) takes now the expression
In the case ε = 0 the solution of Eq. (50) is 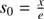 This function is known by the a priori data and therefore it is possible to obtain an asymptotic solution of Eq. (50) in the limit when ε tends to zero but for ε ≠ 0
This function is known by the a priori data and therefore it is possible to obtain an asymptotic solution of Eq. (50) in the limit when ε tends to zero but for ε ≠ 0
where the remaining coefficients si, i = 1, 2, … can be easily obtained by introducing this expansion in (50) and requiring that the resulting series vanishes for every order in ε. The asymptotic solution obtained is
We have now to obtain φ as a function of the known parameters x and e. Replacing Eqs. (52) into (44)
and taking into account that φ ≪ 1 when x tends to infinite, we compute the first order series expansion of the previous expression with respect to the variable φ
such that
Replacing (55) in (52) we obtain S as a function of x and e
In order to increase the accuracy of S, we can expand (52) by
where ξ should now be determined as a function of the known parameters x, e and φ. Replacing (57) into (44)
and repeating the process for φ, we obtain
The final expression for S, replacing (59), is given by
Now we can assess the accuracy of this asymptotic solution just studying the order of magnitude of the variables we have approximated. We note that φ and ξ decrease when e increases. Therefore e = 1 marks the lowest accuracy of solution (60), being better when e > 1 (see Table 1). If M ≥ 50, then φ is smaller than 10−1 and ξ is smaller in absolute value than 10−4. If y ≥ 5, we obtain M ≥ 69.2 when e = 1, which assures small values for φ and ξ.
Order of magnitude of φ and ξ as a function of M when e = 1.
6.3. Improving the code
The interval [0, 5[ of the hyperbolic anomaly H ≡ y has been discretized in 25 intervals. However, this number, related with the number of polynomials, can be modified having a significant impact on the accuracy of the algorithm but not jeopardizing the speed of the code. If we plot the residual ρ caused by the polynomial pi(x) associated to the interval [yi, yi + 1], we observe that it follows a Gaussian-like function reaching the maximum, approximately, at the centre of the interval (see Fig. 3). One option, to decrease the residual and obtain a better initial seed, is to increase the number of polynomials. But if we decrease the size of the intervals they become too small and the polynomials, which depend on the eccentricity e, can become numerically unstable. However, we can define a new group of polynomials qj(x) whose ends are defined by the mean points of the initial intervals [yi, yi + 1], i = 1, …, 25, by keeping the same size (see Fig. 3), that is
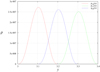 |
Fig. 3. Residual ρ versus the hyperbolic anomaly y, when the solution is determined by the polynomials p16(x), p17(x) and q16(x). |
where the corresponding Sj is obtained from Eq. (43) and Mj ≡ xj is obtained from Eq. (44) (values attached in the code). This way, we define twenty-four intervals [xj, xj + 1], j = 1, …, 24 and in each one of these intervals we introduce a fifth-degree polynomial qj(x), j = 1, …, 24 to interpolate the hyperbolic sine of the hyperbolic anomaly
The introduction of these new polynomials qj(x) is not necessary, that is, the algorithm functions normally with the original polynomials pi(x). However, the tools elaborated to create the polynomial pi(x) permit to generate the new polynomial qj(x) without additional effort. The benefit is that the accuracy and reliability of the code is increased.
7. The HKE–SDG algorithm
Given the values of M and e, to solve the hyperbolic Kepler equation we use the following algorithm.
7.1. Seed estimation
Inside the singular corner (M < 0.15 and e < 1.25). Use the sequence associated with Eq. (37) to estimate the starter value y0. The seed S0 is obtained from the relation: S0 = sinhy0.
Outside the singular corner (M ≥ 0.15 or e ≥ 1.25). The value of M permits to detect the ends xk, xk + 1 of the right interval – one of the intervals related to the polynomials pi(x) – which contains M, that is, M ∈ [xk, xk + 1]. We note that the corresponding values [Sk, Sk + 1] are known and the seed S0 satisfies: S0 ∈ [Sk, Sk + 1]. If the right interval is the last one: [x26, x27], the algorithm uses the sequence associated with Eq. (60) to estimate the starter value S0 (asymptotic approximation). If the right interval is not the last one, the algorithm identifies a new interval from the intervals related to the polynomials qj(x) containing M. Then it chooses the interval that has M closest to one of their ends. The seed S0 is given by the corresponding polynomial (46) or (62) (polynomial approximation).
7.2. Root estimation
The seed S0 is used to solve the equation
by using the Newton–Raphson algorithm. The output of this algorithm provides, through the change in variable (43), the desired value of the hyperbolic anomaly y(x).
A compact version of HKE–SDG has been made available to the reader in the way indicated by the journal under the license GPL Version 3.
8. Analysis of results
A full analysis of the algorithm was performed by considering two main aspects: speed and accuracy. The numerical analysis of HKE–SDG takes into account the ease of codification or the robustness of the procedure too. All these considerations are detailed below. The calculations have been carried out in a computer with an Intel(R) Xeon(R) E3-1535M v6 at 3.10 GHz microprocessor and the executables have been prepared with the version 17.0 of the Intel® C++ Compiler, under the Windows 10 operative system 64 bits.
8.1. Speed of the process
The Kepler equation for the hyperbolic case has been solved ≈4 × 106 times with the algorithm proposed in this paper by using a tolerance εtol. The eccentricity ranges in the interval e ∈ ]1, 10] and the values of M ≡ x range in the interval M ∈ [0, 100] (rad) (see Appendix A).
In each run we count the number of iterations needed to reach a solution with a residual ρ = |e sin h y − y − x| lower than the tolerance εtol. This number is taken as a gross measure of the speed of the procedure. Figures 4 and 5 show, in the plane (e, M), the number of iterations associated with HKE–SDG when using the MNR scheme for double and quadruple precision. Notice that in the color code of the figures, green color corresponds to two iterations, white color to one iteration and black color to zero iterations. The averaged value of iterations is 1.582 and 1.010 for double and quadruple precision respectively.
 |
Fig. 4. Results with HKE–SDG using the MNR iteration scheme in double precision. |
 |
Fig. 5. Results with HKE–SDG using the MNR iteration scheme in quadruple precision. |
8.2. Accuracy analysis
As we show in the next section HKE–SDG reaches its best performances when the MNR algorithm is used in iterative scheme. Therefore, this section focuses the analysis in HKE–SDG with the MNR algorithm. In HKE–SDG the iteration ends when: (i) the residual ρ = |e sin h y − y − x| is lower that the tolerance εtol, or (ii) the increment ΔSn/Sn in the n iteration of the MNR algorithm is lower than the zero of the machine. In order to assess the accuracy of our solution, we use the total absolute error εabs associated with the numerical solution (see Appendix B).
We fix the value of the eccentricity e, in the interval e ∈ ]1, 10]; then we scan the whole interval M ∈ [0, 100] calculating the residual ρ after zero iteration (the residual provided by the starting seed), after one iteration, after two iterations and so on. Let ρmax be the maximum residual that we find in the scanning of the whole interval M ∈ [0, 100] for each iteration number. These maximum residuals allow us to calculate the maximum values of the absolute error εmax for different number of iterations, and these absolute errors can be associated with the value of the eccentricity e as it can be shown in Appendix C.
The values of such maximum absolute errors can be plotted versus the eccentricity e. This picture provides a very good idea of the accuracy involved in our calculations after zero, one, two, … iterations. We note that the values plotted mark the worst accuracy of the numerical solution yc(x, e); in fact, for each value of e there are hundred of values of M where the accuracy is much better than the indicated by εmax. As we can see in Figs. 6 and 7 for double and quadruple precision, HKE–SDG saturates the capacity of the machine with a maximum of two iterations.
 |
Fig. 6. Maximum total absolute error εmax versus the eccentricity e, for different number of iterations. Calculations in double precision. |
 |
Fig. 7. Maximum total absolute error εmax versus the eccentricity e, for different number of iterations. Calculations in quadruple precision. |
9. Comparison of results
The Kepler equation for the hyperbolic case has been solved with the method proposed in this paper – HKE–SDG – by using different Newton–Raphson algorithms (see Appendix C). The results for double and quadruple precision confirm that HKE–SDG is almost insensitive to the Newton-Rhapson algorithm. The robustness of HKE–SDG is due to the strong optimization of the initial seed performed in the algorithm; this optimization prevents the convergence problems which could appear in the Newton–Raphson iteration when the initial seed is far away from the real root. Moreover, the same analysis has been performed with typical solvers of the Kepler equation which have been compared with HKE–SDG when using the MNR method. In this section we collect the method described in Avendano et al. (2015) (see Table 2), which is the closest to our code. The comparisons with the remaining solvers can be seen in Appendix C. In each case the HKE has been solved under the conditions described in Sect. 8 and in Sect. 8.1, that is, we solve equation ≈4 × 106 times.
Number of iteration (percentage) and computational time obtained with HKE–SDG and Avendaño algorithms checked in double (upper) and quadruple (lower) precision.
In double precision the HKE–SDG never requires, when using the MNR method, more than two iterations. Notice that the approach described in Avendano et al. (2015) requires more than three iterations for some particular cases, reaching a maximum value of 19 iterations. In double precision the Avendaño code requires 1.657 s with an averaged number of iterations of 2.672. In the case of HKE–SDG the average number was 1.582 with a CPU time of 1.398 s.
Table 2 also contains the results in quadruple precision. When using the MNR iteration scheme, HKE–SDG reaches the solution with only one or two iterations in the 99.950% of cases and in the 0.050% no iteration is necessary (see Fig. 5). The HKE–SDG keeps again the smallest number of iterations. In quadruple precision HKE–SDG reaches a maximum number of two iterations when applying the MNR method, while the method described in Avendano et al. (2015) reaches a maximum number of 21 iterations. The CPU time invested was 34.267 s with HKE–SDG and 31.422 s with Avendaño code. The averaged number of iterations was 1.010 and 2.976 for HKE–SDG and Avendaño respectively.
Figure 8 shows the number of significant digits obtained with the Avendaño and HKE–SDG codes when using the MNR method in double precision. Darker colors are associated with less precision as well as lighter colors with better precision. At first sight the two pictures are quite similar and only small differences can be appreciated. If we compare HKE–SDG with respect to the Avendaño approach, the results obtained with the last one show a lower precision for large values of eccentricity (e > 8) and small values of mean anomaly (M ≤ 5).
 |
Fig. 8. Number of significant figures, approximately, obtained with the code of Avendano et al. (2015) (left) and HKE–SDG (right) in double precision. |
Figure 9 shows the number of significant digits when quadruple precision is used in calculations. We note that the Avendaño approach shows radial beams with less precision than HKE–SDG. In fact, HKE–SDG provides the most precise solution with more than 33 significant digits in the whole plane (e, M) when quadruple precision is applied. As it is shown, HKE–SDG experiences an improvement of 20 significant figures for almost the complete plane when changing from double to quadruple precision. The results obtained with HKE–SDG when using different numerical methods are very similar and all of them assure the reliability and quality of the solution.
 |
Fig. 9. Number of significant figures, approximately, obtained with the code of Avendano et al. (2015) (left) and HKE–SDG (right) in quadruple precision. |
In summary, when double precision is used, HKE–SDG turns out to be the fastest method and it provides the most precise results. When quadruple precision is needed, HKE–SDG is the most accurate, stable and reliable even if it turns out to be a little slower.
10. Conclusions
Several conclusions can be drawn from the results obtained of our numerical research about the solution provided by the code HKE–SDG:
Firstly, convergence is always assured – as confirmed the thorough the analysis carried out in our computers – when the initial seed of the Newton–Raphson algorithm is optimized.
Secondly, the algorithm used in HKE–SDG is stable and reliable regardless of the Newton–Raphson algorithm used in the numerical solution. We note that – with double precision – the classical Newton–Raphson provides the solution in the 99.866% of cases with only one or two iterations. This remarkable result has not been found in other algorithms used in the Astrodynamics community. Improving the algorithm by using the Conway or the modified Newton–Raphson permits to obtain the right solution with only one or two iterations in the 99.868% and 99.874% of cases respectively. The reliability is also improved. Gooding, Fukushima, and Avendaño codes require more than three iterations in 0.088%, 100% and ∼63%–92% of cases respectively.
Thirdly, if a very precise answer is needed, HKE–SDG can be used with quadruple precision due to the low number of iterations required. HKE–SDG gives the maximum precision, it combines stability and reliability and the speed of the calculations is not jeopardized. Therefore, we obtain the benefit of a greater accuracy with a minimal cost.
Fourthly, if quadruple precision is used, the absolute error of the numerical solution provided by HKE–SDG is clearly under 10−24 after one iteration. In any case, after two iterations the error is always lower than 10−31, including the region e < 1.25 (the singular corner).
Finally, the algorithm has a global reach since it successfully solves the Kepler equation in the singular corner, M < 0.15 and e < 1.25. The asymptotic expansions used to generate the initial seed assure the reliability and convergence of the Newton–Raphson iterative scheme. The convergence in this special region not always is assured by some of the algorithms usually considered in the literature. Gooding code shows a deterioration in a small region of the singular corner.
Acknowledgments
This work is part of the project entitled Dynamical Analysis of Complex Interplanetary Missions with reference ESP2017-87271-P, supported by Spanish Agencia Estatal de Investigación (AEI) (Spanish Research Agency) of Ministerio de Economía, Industria y Competitividad (MINECO) (Ministry of Economy, Industry and Competitiveness) and by European Found of Regional Development (FEDER). Authors thank to the referee for the constructive comments and suggestions which helped to improve the paper.
References
- Alhindi, F. A., & Sharaf, M. 2014, J. Adv. Math., 10, 3457 [Google Scholar]
- Avendano, M., Martín-Molina, V., & Ortigas-Galindo, J. 2015, Celest. Mech. Dyn. Astron., 123, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Balaraman, G., & Vrinceanu, D. 2007, Phys. Lett. A, 369, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Battin, R. 1964, Astronautical Guidance (New York: McGraw Hill) [Google Scholar]
- Beust, H., Bonnefoy, M., Maire, A.-L., et al. 2016, A&A, 587, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colwell, P. 1993, Solving Kepler’s Equation over three Centuries (Richmond, Virginia: Willmann-Bell) [Google Scholar]
- Conway, B. A. 1986, Celest. Mech., 39, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, M. 1932, MNRAS, 93, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, M. 1934, MNRAS, 95, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Hernandez, D. M. 2016, MNRAS, 465, 1201 [Google Scholar]
- Faintich, M. B. 1972, Celest. Mech., 6, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, T. 1997, Celest. Mech. Dyn. Astron., 68, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gooding, R. 1987, Universal Procedures for Conversion of Orbital Elements to and from Position and Velocity (unperturbed orbits), Tech. rep., Royal Aircraft Establishment [Google Scholar]
- Gooding, R., & Odell, A. 1988, Celest. Mech., 44, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Goodyear, W. H. 1965, AJ, 70, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, D. M., & Bertschinger, E. 2015, MNRAS, 452, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Herrick, S. 1971, Astrodynamics: Orbit Correction, Perturbation Theory, Integration (New York: Van Nostrand Reinhold) [Google Scholar]
- Kurth, R. 1978, Q. Appl. Math., 36, 325 [CrossRef] [Google Scholar]
- Milani, A., & Nobili, A. M. 1987, Celest. Mech., 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Nobili, A., Fox, K., & Carpino, M. 1986, Nature, 319, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Pitkin, E. T. 1965, AIAA J., 3, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Raposo-Pulido, V., & Peláez, J. 2017, MNRAS, 467, 1702 [NASA ADS] [Google Scholar]
- Rauh, A., & Parisi, J. 2011, Phys. Rev. A, 83, 042101 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Sarnecki, A. 1988, Acta Astronaut., 17, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Sharaf, M., Banajh, M., & Alshaary, A. 2007, JApA, 28, 9 [NASA ADS] [Google Scholar]
- Sharaf, M. A., & Sharaf, A. A. 2003, Celest. Mech. Dyn. Astron., 86, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Sitarski, G. 1968, Acta Astron., 18, 197 [NASA ADS] [Google Scholar]
- Smiley, C. 1934, MNRAS, 95, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpff, K. 1968, On the Application of Spinors to the Problem of Celestial Mechanics, Tech. rep., National Aeronautics and Space Administration [Google Scholar]
- Tokis, J. N. 2014, Int. J. Astron. & Astrophys., 4, 683 [CrossRef] [Google Scholar]
- Wisdom, J., & Hernandez, D. M. 2015, MNRAS, 453, 3015 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Yabushita, S. 1971, MNRAS, 153, 97 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
By applying the MNR algorithm we have carried out the calculations in standard double precision and quadruple precision with a tolerance equal to: εtol = 2.22 × 10−16 and εtol = 1.0 × 10−32 respectively. The method used in this study is a numerical procedure based on successive approximations. It means if the tolerance considered is close to the zero of the machine, the method could experience artificial numerical chaos. A way to avoid this problem is by using an appropriate tolerance.
Figure 4 shows some black points; most of them on the axis M = 0. The red color (three iterations) does not appear in the figure.
Figure 5 shows the equivalent picture obtained with quadruple precision. Practically the code performs one iteration everywhere except in two zones where two iterations are needed: the singular corner and the zone with large values of M and small values of e. In both zones the seed is generated with asymptotic expansions. The algorithm never enters dead loops or any other kind of nonconvergent phase after many millions of runs. This fact confirms the reliability of the algorithm.
Appendix
Let yν(x, e) be the true solution for given values of e and the mean anomaly M ≡ x. Let yc(x, e) be the numerical solution provided by HKE–SDG for these particular values. Due to truncation and round-off errors, both solutions are related by the equation
where εabs is the total absolute error associated with the numerical solution yc(x, e). This absolute error is closely related with the residual ρ. In effect, for the numerical solution yc(x, e) the residual is given by
Since εabs is small and taking into account that the true solution verifies
the residual takes the form
Therefore the absolute error can be approximated by
and depends on the residual ρ. Something similar happens with the total relative error:
Figure 6 shows the decimal logarithm of the maximum absolute error versus the eccentricity e. The initial seed – 0 iterations – provides an error which, in the worst cases, ranges from 10−5 to 10−8. Since the calculations associated with Fig. 6 have been carried out in double precision, the residual obtained after one iteration practically saturates the capacity of the machine providing the solution with 14 or 15 significant figures. We emphasize that one additional iteration does not improve the accuracy of the numerical solution; figure shows that the lines corresponding to one, two, and three iterations are, practically, the same.
Figure 7 is similar to Fig. 6 but with the calculations carried out in quadruple precision. It is clear that with one iteration we obtain more than 31 significant figures except for values of e close to unity, where the number of significant digits is about 24–31. With two iterations HKE–SDG saturates the precision capacities of the machine, providing more than 31 significant figures. It should be underlined that one additional iteration does not improve the accuracy of the numerical solution; figure shows that the lines corresponding to two and three iterations are, practically, the same.
Appendix
Three different Newton–Raphson algorithms have been performed in the study to analyze the quality of the algorithm: the MNR method, the Conway method, and the CNR method.
Table C.1 summarizes the behavior of HKE–SDG in double precision by using these algorithms as well as the CPU time invested in the ≈4 × 106 of times that we solved the Kepler equation. When the MNR was used, in the 99.874% of cases we reach the solution with only one or two iterations and in the 0.126% no iteration is necessary. With the Conway or the CNR in a very small number of cases three iterations are needed; the averaged number of iterations was 1.583 for both methods. With any of the Newton–Raphson algorithms and using double precision, it took 1.3 s approximately to solve the whole set. The CPU time was 1.398 s when using the most reliable scheme: the MNR.
Number of iteration (percentage) and computational time obtained with HKE–SDG by using different Newton–Raphson methods checked in double (upper) and quadruple (lower) precision.
Table C.1 summarizes as well the behavior of HKE–SDG in quadruple precision. HKE–SDG reaches a maximum number of two iterations when applying the MNR method and three iterations (≤0.1%) when working with the Conway and CNR methods. The CPU time invested was 34.267 s (MNR), 38.677 s (Conway) and 35.733 s (CNR), while the averaged number of iterations was 1.010, 1.995 and 1.996 respectively.
In addition to the Avendaño approach, two different solvers of the Kepler equation have been performed in the study by using the MNR method. Firstly the method described in Gooding & Odell (1988), and secondly the method described in Fukushima (1997).
In double precision the approaches described in Gooding & Odell (1988) and Fukushima (1997) require more than three iterations for some particular cases, reaching a maximum value of 43 and 20 respectively. In the case of HKE–SDG the maximum is two. In double precision the Gooding code requires 1.808 s, while the Fukushima code requires 28.669 s. The averaged number of iterations was 2.014 and 6.117 respectively. In the case of HKE–SDG the average number was smaller than two as well as the CPU time (see Table C.2). The reason why the Fukushima code takes much more time than the rest of the codes is the very strict tolerance that we use: the zero of the machine. The Fukushima algorithm has been developed to work in double precision by evaluating the Kepler equation by a Taylor series expansion with the appropriate number of terms. Due to that truncation, to reach the precision associated to the εtol turns out to be difficult and it requires more time than habitual. With not-so-strict tolerances the differences are much smaller.
Number of iteration (percentage) and computational time obtained with HKE–SDG, Gooding and Fukushima algorithms checked in double (upper) and quadruple (lower) precision.
Table C.2 also contains the results in quadruple precision. We note that the Fukushima code does not include quadruple precision. The use of quadruple precision would imply to extend the original series, however, the authors prefer to keep the algorithm as it is explained in Fukushima (1997). When using the MNR iteration scheme HKE–SDG reaches the solution with a maximum of two iterations. The method described in Gooding & Odell (1988) does not experiment almost any change, keeping the same percentages as in double precision. In quadruple precision the Gooding code reaches a maximum number of 94 iterations with a CPU time of 24.684 s and an averaged number of iterations of 2.035.
Figure C.1 shows the number of significant digits obtained with the Gooding and Fukushima codes when using the MNR method in double precision. If we compare HKE–SDG with respect to the other approaches, the results obtained with the Gooding code show a lower precision in a small region inside the singular corner. The number of digits in Fukushima is very similar to HKE–SDG, however, for some specific points in the yellow region (M ≤ 5) the Fukushima code reaches less precision.
 |
Fig. C.1. Number of significant figures, approximately, obtained with the code of Gooding & Odell (1988; left) and Fukushima (1997; right) in double precision. |
Figure C.2 shows the number of significant digits when quadruple precision is used in calculations. We note that the Gooding approach shows again a significant deterioration in the singular corner.
 |
Fig. C.2. Number of significant figures, approximately, obtained with the code of Gooding & Odell (1988) in quadruple precision. |
All Tables
Number of iteration (percentage) and computational time obtained with HKE–SDG and Avendaño algorithms checked in double (upper) and quadruple (lower) precision.
Number of iteration (percentage) and computational time obtained with HKE–SDG by using different Newton–Raphson methods checked in double (upper) and quadruple (lower) precision.
Number of iteration (percentage) and computational time obtained with HKE–SDG, Gooding and Fukushima algorithms checked in double (upper) and quadruple (lower) precision.
All Figures
 |
Fig. 1. Exact solution of the Kepler equation and the asymptotic solution – up to sixth order – obtained in the inner region of the singular corner. The agreement is excellent for very small values of x. Here four values of ε have been considered: ε = 0.001, 0.101, 0.201, 0.301. |
| In the text | |
 |
Fig. 2. Exact solution of the Kepler equation and the asymptotic solution – up to the fourth order – obtained in the intermediate region of the singular corner. The agreement is excellent for whole range. Here four values of ε have been considered: ε = 0.001, 0.101, 0.201, 0.301. |
| In the text | |
 |
Fig. 3. Residual ρ versus the hyperbolic anomaly y, when the solution is determined by the polynomials p16(x), p17(x) and q16(x). |
| In the text | |
 |
Fig. 4. Results with HKE–SDG using the MNR iteration scheme in double precision. |
| In the text | |
 |
Fig. 5. Results with HKE–SDG using the MNR iteration scheme in quadruple precision. |
| In the text | |
 |
Fig. 6. Maximum total absolute error εmax versus the eccentricity e, for different number of iterations. Calculations in double precision. |
| In the text | |
 |
Fig. 7. Maximum total absolute error εmax versus the eccentricity e, for different number of iterations. Calculations in quadruple precision. |
| In the text | |
 |
Fig. 8. Number of significant figures, approximately, obtained with the code of Avendano et al. (2015) (left) and HKE–SDG (right) in double precision. |
| In the text | |
 |
Fig. 9. Number of significant figures, approximately, obtained with the code of Avendano et al. (2015) (left) and HKE–SDG (right) in quadruple precision. |
| In the text | |
 |
Fig. C.1. Number of significant figures, approximately, obtained with the code of Gooding & Odell (1988; left) and Fukushima (1997; right) in double precision. |
| In the text | |
 |
Fig. C.2. Number of significant figures, approximately, obtained with the code of Gooding & Odell (1988) in quadruple precision. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



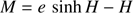
![$$ \begin{aligned} x = e\, \sinh {y} -{y}, \quad x \in ]-\infty ,\infty [, \quad {y} \in ]-\infty ,\infty [, \quad e > 1 \end{aligned} $$](/articles/aa/full_html/2018/11/aa33563-18/aa33563-18-eq2.gif)
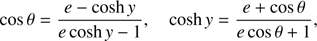
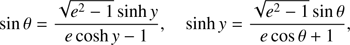
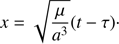
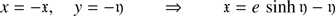
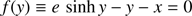
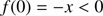
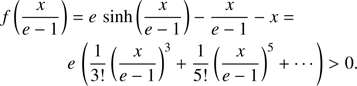
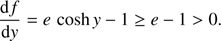
![$$ \begin{aligned} \Delta {y_n} = \frac{{ - mf({y_n})}}{{f^{\prime }({y_n}) \pm \sqrt{\left| {(m - 1)[(m - 1){{f^{\prime }}^2}({y_n}) - mf({y_n})f^{\prime \prime }({y_n})]} \right|} }} \end{aligned} $$](/articles/aa/full_html/2018/11/aa33563-18/aa33563-18-eq12.gif)
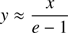

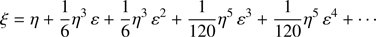
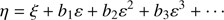
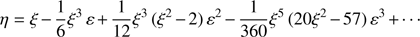

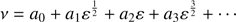
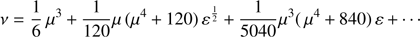
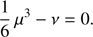
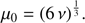
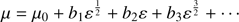
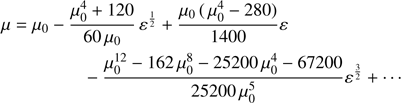

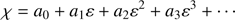
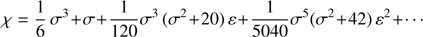
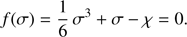
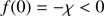
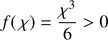
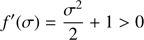
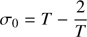
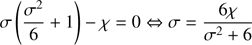
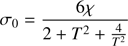
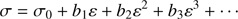
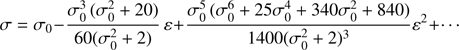

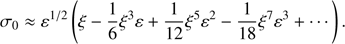
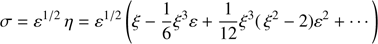

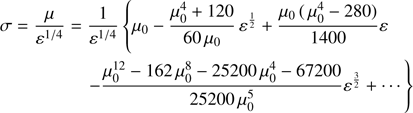
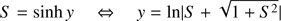
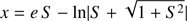
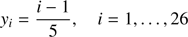
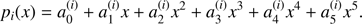
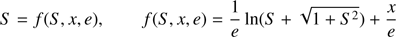
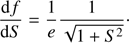
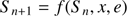
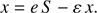
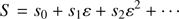
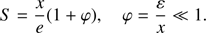
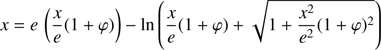
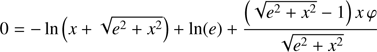
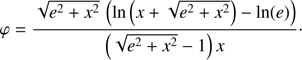
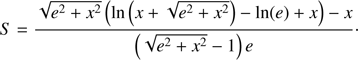
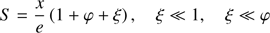
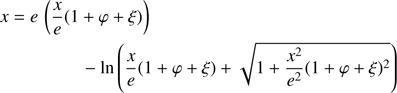
![$$ \begin{aligned} \xi = -\frac{1}{2\,x^3}\left[\ln (\dfrac{e}{2x}) \right]^2 \cdot \end{aligned} $$](/articles/aa/full_html/2018/11/aa33563-18/aa33563-18-eq70.gif)
![$$ \begin{aligned} S&=\frac{1}{2\,ex^2\left(\sqrt{e^2+x^2}-1\right)}\Big [\sqrt{e^2+x^2}\left(2\,x^2\,\ln \left(x+\sqrt{e^2+x^2}\right)\right.\nonumber \\&\left.-2\,x^2\,\ln (e)\right)+\left(\sqrt{e^2+x^2}-1\right)\left(2\,x^3-\left(\ln (e)-\ln (x)\right)^2\right.\nonumber \\&+\ln (2)\left(2\,\ln (e)-2\,\ln (x)-\ln (2)\right)\big )\Big ]. \end{aligned} $$](/articles/aa/full_html/2018/11/aa33563-18/aa33563-18-eq71.gif)