| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832640 | |
| Published online | 08 November 2018 | |
The γ-ray spectrum of the core of Centaurus A as observed with H.E.S.S. and Fermi-LAT
1 Centre for Space Research, North-West University, Potchefstroom 2520, South Africa
2 Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149, 22761 Hamburg, Germany
3 Max-Planck-Institut für Kernphysik, PO Box 103980, 69029 Heidelberg, Germany
4 Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
5 National Academy of Sciences of the Republic of Armenia, Marshall Baghramian Avenue, 24, 0019 Yerevan, Republic of Armenia
6 Instytut Fizyki Jądrowej PAN, ul. Radzikowskiego 152, 31-342 Kraków, Poland
7 Department of Physics, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima-ku, Tokyo 171-8501, Japan
8 Laboratoire d’Annecy de Physique des Particules, Université Savoie Mont-Blanc, CNRS/IN2P3, 74941 Annecy-le-Vieux, France
9 LUTH, Observatoire de Paris, PSL Research University, CNRS, Université Paris Diderot, 5 Place Jules Janssen, 92190 Meudon, France
10 University of Namibia, Department of Physics, Private Bag, 13301 Windhoek, Namibia
11 GRAPPA, Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
12 Department of Physics and Electrical Engineering, Linnaeus University, 351 95 Växjö, Sweden
13 Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
14 DESY, Platanenallee 6, 15738 Zeuthen, Germany
15 Institut für Astro-und Teilchenphysik, Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck, Austria
16 School of Physical Sciences, University of Adelaide, Adelaide 5005, Australia
17 Sorbonne Universités, UPMC Université Paris 06, Université Paris Diderot, Sorbonne Paris Cité, CNRS, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), 4 place Jussieu, 75252 Paris Cedex 5, France
18 Laboratoire Univers et Particules de Montpellier, Université Montpellier, CNRS/IN2P3, CC 72, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France
19 Université Bordeaux, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan, 33175 Gradignan, France
20 IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
21 Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen Centre for Astroparticle Physics, Erwin-Rommel-Str. 1, 91058 Erlangen, Germany
22 Astronomical Observatory, The University of Warsaw, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
23 Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
24 Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS/IN2P3, 91128 Palaiseau, France
25 School of Physics, University of the Witwatersrand, 1 Jan Smuts Avenue, Braamfontein, Johannesburg 2050, South Africa
26 Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center, 10691 Stockholm, Sweden
27 Wallenberg Academy Fellow, 103 22 Stockholm, Sweden
28 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10, rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
29 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warsaw, Poland
30 Institut für Physik und Astronomie, Universität Potsdam, KarlLiebknecht-Strasse 24/25, 14476 Potsdam, Germany
31 Aix Marseille Université, CNRS/IN2P3, CPPM, Marseille, France
32 Landessternwarte, Universität Heidelberg, Königstuhl, 69117 Heidelberg, Germany
33 Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
34 Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15, 12489 Berlin, Germany
35 Obserwatorium Astronomiczne, Uniwersytet Jagielloński, ul. Orla 171, 30-244 Kraków, Poland
36 Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University, Grudziadzka 5, 87-100 Torun, Poland
37 Japan Aerpspace Exploration Agency (JAXA), Institute of Space and Astronautical Science (ISAS), 3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 229-8510, Japan
38 Department of Physics, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa
39 Kavli Institute for Particle Astrophysics and Cosmology, Department of Physics and SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94305, USA
40 The School of Physics, The University of New South Wales, Sydney 2052, Australia
41 Department of Physics and Astronomy, The University of Leicester, University Road, Leicester LE1 7RH, UK
42 GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of High-Energy Physics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
43 Heisenberg Fellow (DFG), ITA Universität, Heidelberg, Germany
44 Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036 Yerevan, Armenia
45 Instituto de Física de Sąo Carlos, Universidade de Sąo Paulo, Av. Trabalhador Sąo-carlense, 400 -CEP 13566-590, Sąo Carlos, SP, Brazil
46 Department of Physics and Department of Astronomy, University of Maryland, College Park, MD 20742, USA
47 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
48 NASA Postdoctoral Program Fellow, USA
49 Space Science Division, Naval Research Laboratory, Washington, DC 20375-5352, USA
50 Hiroshima Astrophysical Science Center, Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan
Received:
14
January
2018
Accepted:
5
July
2018
Centaurus A (Cen A) is the nearest radio galaxy discovered as a very-high-energy (VHE; 100 GeV–100 TeV) γ-ray source by the High Energy Stereoscopic System (H.E.S.S.). It is a faint VHE γ-ray emitter, though its VHE flux exceeds both the extrapolation from early Fermi-LAT observations as well as expectations from a (misaligned) single-zone synchrotron-self Compton (SSC) description. The latter satisfactorily reproduces the emission from Cen A at lower energies up to a few GeV. New observations with H.E.S.S., comparable in exposure time to those previously reported, were performed and eight years of Fermi-LAT data were accumulated to clarify the spectral characteristics of the γ-ray emission from the core of Cen A. The results allow us for the first time to achieve the goal of constructing a representative, contemporaneous γ-ray core spectrum of Cen A over almost five orders of magnitude in energy. Advanced analysis methods, including the template fitting method, allow detection in the VHE range of the core with a statistical significance of 12σ on the basis of 213 hours of total exposure time. The spectrum in the energy range of 250 GeV–6 TeV is compatible with a power-law function with a photon index Γ = 2.52 ± 0.13stat ± 0.20sys. An updated Fermi-LAT analysis provides evidence for spectral hardening by ΔΓ ≃ 0.4 ± 0.1 at γ-ray energies above 2.8+1.0−0.6 GeV at a level of 4.0σ. The fact that the spectrum hardens at GeV energies and extends into the VHE regime disfavour a single-zone SSC interpretation for the overall spectral energy distribution (SED) of the core and is suggestive of a new γ-ray emitting component connecting the high-energy emission above the break energy to the one observed at VHE energies. The absence of significant variability at both GeV and TeV energies does not yet allow disentanglement of the physical nature of this component, though a jet-related origin is possible and a simple two-zone SED model fit is provided to this end.
Key words: gamma rays: galaxies / radiation mechanisms: non-thermal
© ESO 2018
1. Introduction
Active galaxies host a small, bright core of non-thermal emission. At a distance of d ⋍ 3.8 Mpc, Centaurus A (Cen A) is the nearest active galaxy (Israel 1998; Harris et al. 2010). Its proximity has allowed for a detailed morphological analysis over angular scales ranging from milli-arcseconds to several degrees (1° ⋍ 65 kpc). A variety of structures powered by its active galactic nucleus (AGN) have been discovered using observations in radio (e.g. Hardcastle et al. 2003, 2006; Horiuchi et al. 2006; Müller et al. 2014), infrared (e.g. Brookes et al. 2006; Meisenheimer et al. 2007), X-ray (e.g. Kraft et al. 2002; Hardcastle et al. 2003), and γ-ray (e.g. Abdo et al. 2010a, b; Yang et al. 2012) bands. These structures include a radio emitting core with a size of ≤10−2pc, a parsec-scale jet and counter-jet system, a kiloparsec-scale jet and inner lobes, up to giant outer lobes with a length of hundreds of kiloparsecs.
Based on its radio properties, Cen A has been classified as a radio galaxy of Fanaroff-Riley type I (Fanaroff & Riley 1974). According to AGN unification schemes, radio galaxies of this type are thought to correspond to BL Lacertae (BL Lac) objects viewed from the side, the latter showing jets aligned along the line of sight and corresponding to a subclass of blazars (Urry & Padovani 1995). BL Lac objects are the most abundant class of known extragalactic very-high-energy (VHE) emitters1, and exhibit double-peaked spectral energy distributions (SEDs). It is commonly thought that their low-frequency emission in the radio to ultraviolet (and X-ray, for high-peaked BL Lacs) band is synchrotron emission from relativistic electrons within a blob (zone) moving at relativistic speeds in the jet. Synchrotron self-absorption implies that the lower-frequency observed radio emission cannot be produced by a compact blob, and is likely produced by synchrotron from a larger jet component. The high-energy emission (hard X-ray to VHE γ-ray) from high-peaked BL Lac type objects has been satisfactorily modelled as synchrotron self-Compton (SSC) radiation resulting from the inverse Compton upscattering of synchrotron photons by the same relativistic electrons that produced the synchrotron radiation (Maraschi et al. 1992; Bloom & Marscher 1996), although other more complex models (involving e.g. external inverse Compton emission, hadronic interactions, or multiple zones) are conceivable (Reimer & Böttcher 2013).
At a few tens of keV to GeV photon energies, Cen A was detected by all instruments on board the ComptonGamma-Ray Observatory (BATSE, OSSE, COMPTEL, and EGRET; the acronyms are described in Appendix B.) in the period 1991–1995 revealing a high-energy peak in the SED at an energy of ∼0.1 MeV (see Kinzer et al. 1995; Steinle et al. 1998; Sreekumar et al. 1999). An earlier investigation found that it is possible to fit the data ranging from the radio band to the γ-ray band using a single-zone SSC model (Chiaberge et al. 2001), but this implies a low flux at VHE. High-energy and VHE γ-ray observations are thus important to test the validity of the SSC scenario for modelling of the SED of radio galaxies.
The discovery of Cen A as an emitter of VHE γ rays was reported on the basis of 115 h of observation (labelled data set A in this study) with the High Energy Stereoscopic System (H.E.S.S.) performed from April 2004 to July 2008 (Aharonian et al. 2009). The signal from the region containing the radio core, the parsec-scale jet, and the kiloparsec-scale jet was detected with a statistical significance of 5.0σ. In this paper, we refer to this region as the Cen A γ-ray core. Subsequent survey observations at high energies (HE; 100 MeV–100 GeV) were performed by the Large Area Telescope (LAT) on board the Fermi Gamma Ray Space Telescope(FGST) launched in June 2008 (Atwood et al. 2009). During the first three months of science operation, started on August 4, 2008, Fermi-LAT confirmed the EGRET detection of the Cen A γ-ray core (Abdo et al. 2009). Spectral analysis and modelling based on ten months of Fermi-LAT observations (Abdo et al. 2010a) suggested the high-energy γ-ray emission up to ∼10 GeV to be compatible with a single power law, yet indicated that a single-zone SSC model would be unable to account for the (non-contemporaneous) higher energy TeV emission observed by H.E.S.S. in 2004–2008. The analysis of extended Fermi-LAT data sets has in the meantime provided increasing evidence for a substantial spectral break above a few GeV (Sahakyan et al. 2013; Brown et al. 2017). This supports the conclusion that the TeV emission observed in 2004–2008 with H.E.S.S. belongs to a distinct, separate spectral component.
In this paper, we present the results of long-term observations of the Cen A γ-ray core performed both with H.E.S.S. and with Fermi-LAT. These include new (more than 100 h) VHE observations of the Cen A γ-ray core with H.E.S.S. (data set B) performed when the FGST was already in orbit. We report results of the spectral analysis of the complete H.E.S.S. data set (Sect. 2) with an exposure time that is twice that used in the previously published data set A, as well as an update (Sect. 3) of the spectrum of the Cen A γ-ray core obtained with Fermi-LAT at GeV energies. The results are discussed and put into wider context in Sect. 4.
2. H.E.S.S. observations and results
Cen A is a weak VHE source with a measured integral flux above 250 GeV of about 0.8% of the flux of the Crab Nebula2. The discovery of faint VHE γ-ray emission from Cen A motivated further observations with H.E.S.S., which were performed in 2009–2010. In this section, we report the results of the Cen A observations with H.E.S.S. taken between 2004 and 2010. It includes a re-analysis of the H.E.S.S. data taken between 2004 and 2008 using refined methods. Using the combined H.E.S.S. data set (data sets A + B), we perform a detailed study of the VHE spectrum of Cen A.
2.1. Observations and analysis
The H.E.S.S. experiment is an array of five imaging atmospheric Cherenkov telescopes3 located in the southern hemisphere in Namibia (23° 16′18″S, 16° 30′00″E) at an altitude of 1800 m above sea level (Aharonian et al. 2006). At the time of the observations used in this paper, the H.E.S.S. array consisted of four 12 m telescopes. The telescopes, arranged in a square with 120 m sides, have been in operation since 2004 (Hinton 2004). Each of these telescopes covers a field of view of 5° diameter. H.E.S.S. employs the stereoscopic imaging atmospheric Cherenkov technique (e.g. Daum et al. 1997) and is sensitive with these telescopes to γ rays above an energy threshold of ∼0.1 TeV for observations at zenith, up to energies of tens of TeV. The energy threshold increases with zenith angle. The observations of Cen A with H.E.S.S. reported in this paper were performed in wobble mode, that is with the target typically offset by about 0.5° or 0.7° from the pointing direction, allowing simultaneous background estimation in the same field of view (Berge et al. 2007). The data were recorded in 28 min exposures, called runs, which are chosen to minimise systematic changes in instrumental response. The observations of Cen A were carried out during the January-July visibility window.
Data set A was taken between April 2004 and July 2008, and 111 h of good-quality data (following a cut on the satisfactory hardware state of the cameras and good atmospheric conditions, as described in Aharonian et al. 2006) were recorded during 261 runs. The mean zenith angle of these observations is 24°. The results of a re-analysis of the data set A are presented in Sect. 2.2.1.
The new data set B was taken from 2009 to 2010 and consists of 241 runs corresponding to 102 h of additional exposure. The mean zenith angle of these observations is 23°. The total exposure time (data set A and B) adds up to 213 h. Data set A was taken prior to the launch of the FGST, while the new data set B presented here was taken after the launch of the FGST. The consistency between the results of the H.E.S.S. observations of Cen A in these two time intervals, that is, the lack of flux variability along with no change in spectral parameters, is of importance to substantiate a simultaneous spectral fit of both the HE and VHE data. The results of an analysis of data set B and of a joint analysis of the two data sets are presented in Sects. 2.2.2 and 2.2.3, respectively.
The Image Pixel-wise fit for Atmospheric Cherenkov Telescope (ImPACT) analysis (Parsons & Hinton 2014) was used to process the H.E.S.S. data. The gain of the ImPACT analysis in sensitivity is of more than a factor of 1.5 over traditional image moments-fitting (Hillas-based) analyses, used by (Aharonian et al. 2009).
The std_ImPACT cut configuration, which requires a minimum of 60 photo-electrons per image, was used. The On-source counts were taken from the circular region around the Cen A radio core. The same On-region was selected for analyses of the data sets A and B, and for a combined analysis. The reflected-region background method with multiple Off-source regions was used for spectral measurements. Given the angular resolution of H.E.S.S., the giant outer lobes are expected to negligibly affect the VHE results. Thus, the results of the H.E.S.S. data analysis for Cen A reported here are based on twice the exposure and a more sensitive analysis of data set A than that used in the publication in 2009. To cross-check the results, an independent analysis method based on a multivariate combination of discriminant variables using the physical shower properties (Becherini et al. 2011) has been applied.
2.2. Results of the observations of Cen A with H.E.S.S.
2.2.1. Results for data set A
The re-analysis of data set A yielded a γ-ray excess of 277 counts above the background (Table 1), corresponding to a firm detection with a statistical significance of 8.4σ following the method of (Li & Ma 1983). The increase in significance with respect to the published result in Aharonian et al. (2009) is related to the application of improved analysis techniques.
We derive the energy spectrum using a forward-folding technique (Piron et al. 2001). The analysis threshold, Ethr = 0.25 TeV, is given by the energy at which the effective area falls to 20% of its maximum value. The likelihood maximisation for a power-law hypothesis, dN/d E= N0 × (E/E0)−Γ, yields a photon index of Γ = 2.51 ± 0.19stat ± 0.20sys and a normalisation constant of 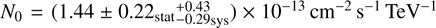 at E0 = 1 TeV. The main and cross-check analyses used in this paper provide compatible results. This ImPACT analysis leads to a smaller statistical error on the photon power-law index compared with the previously published value, Γ = 2.73 ± 0.45stat ± 0.20sys. The central value of the normalisation coeffcient obtained with the ImPACT analysis is lower by a factor of 1.7 than the previously reported value, but they are still marginally compatible within statistical and systematic errors. Accumulation of the exposure time of data set B in addition to that of the data set A allows us to refine the consistency between the current results and the previously published results by redoing a Hillas-based analysis with the latest calibration values (see Appendix A for details). The accuracy of the calibration has been considerably improved since 2009 and this in turn leads to a minimisation of the systematic uncertainty on the flux normalisation of faint VHE γ-ray sources with large exposure time, such as the Cen A core. The systematic uncertainties are conservatively estimated to be ±0.20 on the photon index and
at E0 = 1 TeV. The main and cross-check analyses used in this paper provide compatible results. This ImPACT analysis leads to a smaller statistical error on the photon power-law index compared with the previously published value, Γ = 2.73 ± 0.45stat ± 0.20sys. The central value of the normalisation coeffcient obtained with the ImPACT analysis is lower by a factor of 1.7 than the previously reported value, but they are still marginally compatible within statistical and systematic errors. Accumulation of the exposure time of data set B in addition to that of the data set A allows us to refine the consistency between the current results and the previously published results by redoing a Hillas-based analysis with the latest calibration values (see Appendix A for details). The accuracy of the calibration has been considerably improved since 2009 and this in turn leads to a minimisation of the systematic uncertainty on the flux normalisation of faint VHE γ-ray sources with large exposure time, such as the Cen A core. The systematic uncertainties are conservatively estimated to be ±0.20 on the photon index and 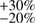 on the normalisation coeffcient.
on the normalisation coeffcient.
H.E.S.S. data and analysis results.
2.2.2. Results for data set B
The analysis of data set B yielded a γ-ray excess of 245 counts above the background (Table 1). This γ-ray excess corresponds to a firm detection with a statistical significance of 8.8σ. Thus, the Cen A γ-ray core is clearly detected as a source of VHE emission in both of the H.E.S.S. data sets. The spectral analysis of the data taken in 2009–2010 yields a photon index of Γ = 2.55 ± 0.19stat ± 0.20sys and a normalisation constant of 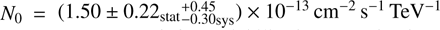 at E0 = 1 TeV.
at E0 = 1 TeV.
To search for variability between the data sets A and B, one needs to compare the intrinsic spectral properties of the source in these two time intervals. A comparison of the spectral analyses of the H.E.S.S. data sets A and B shows that the values of the power-law photon indices are compatible with each other and with that previously reported. As for the normalisations of the VHE spectrum of the Cen A γ-ray core, the best-fit normalisation values obtained with the analysis of both the data sets are compatible with each other and somewhat lower than (yet marginally compatible with) the previously reported value.
2.2.3. Results for the combined H.E.S.S. data from 2004 to 2010
Applying the ImPACT analysis to the combined data set, an excess of 522 events above the background is detected (Table 1). This excess leads to a firm detection of the Cen A γ-ray core with H.E.S.S. at a statistical significance of 12σ. The same spectral analysis as before is applied to the full data set and yields a photon index of Γ = 2.52 ± 0.13stat ±0.20sys and a normalisation constant of 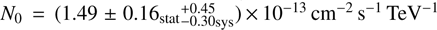 at E0 = 1 TeV. The reconstructed spectrum of the Cen A γ-ray core is shown in Fig. 1. All of the eight SED data points in the VHE range are above a 2.5σ significance level, while only one SED data point exceeds a 2σ significance level in Aharonian et al. (2009). The derived data points for each energy band in the VHE range, shown in Fig. 1, agree within error bars with those for the first and second data sets. The VHE spectrum of the Cen A core is compatible with a power-law function (χ2 = 3.9 with 6 d.o.f.).
at E0 = 1 TeV. The reconstructed spectrum of the Cen A γ-ray core is shown in Fig. 1. All of the eight SED data points in the VHE range are above a 2.5σ significance level, while only one SED data point exceeds a 2σ significance level in Aharonian et al. (2009). The derived data points for each energy band in the VHE range, shown in Fig. 1, agree within error bars with those for the first and second data sets. The VHE spectrum of the Cen A core is compatible with a power-law function (χ2 = 3.9 with 6 d.o.f.).
 |
Fig. 1. SED of Cen A γ-ray core. Fermi-LAT and H.E.S.S. data points along with a high-energy power-law extrapolation of the γ-ray spectrum measured below the break energy. Eight years of Fermi-LAT data and 213 h of H.E.S.S. data were used. Statistical error bars are shown. |
If one takes the values of the spectral parameters from the LAT four-year Point Source Catalogue (3FGL; Acero et al. 2015) obtained from the Fermi-LAT observations of Cen A between 100 MeV and 100 GeV assuming a single power-law spectrum, then one finds that N0 = (0.45 ± 0.07) × 10−13ph cm−2 s−1 TeV−1 at 1 TeV and Γ = 2.70 ± 0.03. Therefore, the differential flux at 1 TeV derived from the H.E.S.S. observations in 2004–2010 is about 3.5 times larger than that inferred from a power-law extrapolation of the 3FGL catalogue spectrum. This indicates that a deviation of the spectrum from a single power law (“hardening”) should occur at GeV energies to match the TeV data (see Sect. 3).
We searched the combined data set for evidence of time variability at the position of the Cen A core. No significant variability was found on timescales of 28 min (individual runs), months, or years. The lack of apparent flux variability along with no change in spectral parameters between the two data sets justifies combining all available data when comparing the spectrum to that of Fermi-LAT. We note that given the low flux level of the Cen A γ-ray core, a flux increase by a factor of approximately ten would be needed to allow a significant detection of variability on timescales of 28 min (corresponding to a 5σ detection in individual runs).
3. Fermi-LAT observations and results
In HE γ rays, the core of Cen A is firmly detected with the Fermi-LAT using eight years of Pass 8 data spanning over three orders of magnitude in energy. LAT analysis of Cen A involves unique challenges not present in other individual extragalactic source analyses, largely due to the massive angular extent of the Cen A non-thermal outer lobes of ∼9° and the proximity to the Galactic plane (Galactic latitude ≈ 19.4°), which is a bright source of diffuse γ-ray emission. In the following, we report corroborating evidence for the presence of an additional spectral component at γ-ray energies above a break of ⋍2.8 GeV. No significant variability either above or below this break has been detected.
3.1. Observations and analysis
LAT is a pair-conversion telescope on the FGST (Atwood et al. 2009). It has a large field of view (∼2.4 sr) and has been scanning the entire sky continuously since August 2008. The broad energy coverage and the all-sky monitoring capability make LAT observations, which bridge the gap between soft γ-ray (MeV) and TeV energy ranges, crucial to explore the spectrum of the Cen A high-energy core and to test its variability.
We selected Pass 8 SOURCE class Fermi-LAT photon data spanning eight years between August 4, 2008 and July 6, 2016 (MET 239557417 to 489507985) with energies between 100 MeV and 300 GeV. Higher energies than 300 GeV yield no detection. We performed a binned analysis by choosing a 10° × 10° square region of interest (ROI) centred at the position of the Cen A core (3FGL J1325.4-4301) as reported in the 3FGL catalogue, RA= 201°.367, Dec= −43°.030 (Acero et al. 2015), with spatial bins 0°.1 in size and initially eight energy bins per decade. We applied standard quality cuts (DATA_QUAL==1 && LAT_CONFIG==1) and removed all events with zenith angle >90° to avoid contamination from the Earth’s limb. In the following, models are compared based on the maximum value of the logarithm of the likelihood function, logℒ. The significance of model components or additional parameters is evaluated using the test statistic, whose expression is TS = 2(logℒ − logℒ0), where ℒ0 is the likelihood of the reference model without the additional parameter or component (Mattox et al. 1996).
To model the sources within the ROI, we began with sources from the 3FGL within the 15° × 15° region enclosing the ROI (the 3FGL models the Cen A lobes with a template created from 22 GHz WMAP data; see Hinshaw et al. 2009). We included the isotropic and Galactic diffuse backgrounds, iso_P8R2_SOURCE_V6_v06 and gll_iem_v06 (Acero et al. 2016), respectively. We fixed the normalisations of both the isotropic and Galactic diffuse source models to one to avoid leakage of photons from the Cen A lobes into these templates; when free, they converged to unrealistic values. The convergence to unrealistic values is due to unmodelled emission from the Cen A lobes. We introduced additional background sources in order to account for excess lobe emission. After creation of the fully developed model, freeing both these diffuse sources has a negligible effect on the results. We optimised each source in the model individually4, and then left the normalisation parameters of sources within 3° and the spectral shapes of only the core and lobes free during the final likelihood maximisation. We generated a residual TS map and residual significance map for the ROI and found several regions with data counts in excess of the model. A TS map is created by moving a putative point source through a grid of locations on the sky and maximising logℒ at each grid point, with the other, stronger, and presumably well-identified sources included in each fit. New, fainter sources may then be identified at local maxima of the TS map. Using the residual TS map as a guide for missing emission, we added ten additional background sources to the ROI model. These ten sources are most likely a surrogate for excess lobe emission and should not be considered new individual point sources. After reoptimisation and creation of a residual TS map, we observe no significant (>5σ) regions of excess counts, and a histogram of the residuals is well fit as a Gaussian distribution centred around zero.
The precise γ-ray morphology of the Cen A lobes is beyond the scope of this work and is not needed to accurately determine the SED of the core. This work on the Cen A core does not require a high-precision model for the lobes, as the angular size of the Cen A lobes is sufficiently larger than the point spread function (PSF) of the LAT, especially at higher energies where this study is focused (<1° 95% containment angle above 5 GeV)5. However, to verify this, we tested the modelling procedure above using two alternative γ-ray templates of the Cen A lobes. The first of these was a modification to the public WMAP template involving “filling in” the 2° diameter hole surrounding the core. This was accomplished by patching this area with nearby matching intensities. The second alternate lobe template tested was one made from radio data from the Parkes telescope at 6.3 cm wavelength (Junkes et al. 1993). Use of these alternate lobe templates had no significant effect on the resulting best-fit core break energy or the flux above the break energy. However, we did observe a flux deviation below the break energy, resulting in a drop in the full band energy flux of the core by up to 17% depending on which lobe template was being used. We believe this drop results from the lack of a hole (circle containing values of 0) around the core of the lobe template with the modified WMAP and the Parkes templates. We also introduced a version of the Parkes template with a hole matching the one in the WMAP and observed a flux increase of 2% instead of a drop, lending credence to our belief that the existence of the hole is the most important factor for this analysis.
3.2. Results of the observations of Cen A with Fermi-LAT
We calculated an SED over the full range by dividing the data into 14 equally spaced logarithmic energy bins and then merging the four highest energy bins into one for sufficient statistics. In each bin, the Cen A lobe and core spectral parameters were left free to optimise and within each bin these spectra were fit using a single power law. The resulting SED is plotted in Figs. 1 and 3. To plot the data point within the wide merged energy bin, we used the prescription from Lafferty & Wyatt (1995). The spectral hardening in the HE γ-ray emission from the core of Cen A above an energy break of 2.8 GeV is illustrated in Fig. 1. A broken power-law model describes well the shape of the Fermi-LAT γ-ray spectrum with a break energy of 2.8 GeV.
We optimised the break energy via a likelihood profile method. For this purpose, we fixed all parameters in the ROI model except the normalisations of sources within a 3° radius of the core to their best-fit values from the full optimisation. The logℒ profiles for the broken power-law spectral model and computed using the WMAP, modified WMAP, and Parkes templates are plotted in Fig. 2. From the position of the peak in the profile corresponding to the WMAP template, we find a best-fit break energy of  GeV. To determine the statistical preference of the broken power-law model over the single power law, we subtract the overall logℒ from the same ROI model with a single power law from the logℒ from the break energy profile at 2.8 GeV. Because these models are nested, Wilks’ theorem yields a preference of the broken power law with 4.0σ confidence (χ2 = 19.0 with 2 d.o.f.).
GeV. To determine the statistical preference of the broken power-law model over the single power law, we subtract the overall logℒ from the same ROI model with a single power law from the logℒ from the break energy profile at 2.8 GeV. Because these models are nested, Wilks’ theorem yields a preference of the broken power law with 4.0σ confidence (χ2 = 19.0 with 2 d.o.f.).
 |
Fig. 2. Fig. 2. Change in overall logℒ while fixing Cen A core break energy to values within the range 0.9–7.0 GeV, as derived from Fermi-LAT data using the WMAP, modified WMAP, and Parkes templates and compared to the logℒ value at 0.9 GeV for the WMAP template. The solid vertical line shows the best-fit value of the break energy parameter, while the dashed vertical lines show 1σ interval for the parameter. |
From this fully optimised γ-ray model of the Cen A core, we obtain a strong detection at 73σ statistical level and calculate a full-band energy flux of 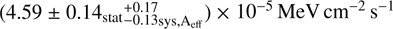 . The best-fit broken power-law prefactor6 is (3.64 ± 0.15) × 10−13 cm−2 s−1 MeV−1. In the lower-energy band, we find a photon index of
. The best-fit broken power-law prefactor6 is (3.64 ± 0.15) × 10−13 cm−2 s−1 MeV−1. In the lower-energy band, we find a photon index of 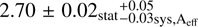 , and in the higher band,
, and in the higher band, 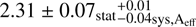 . This provides corroborating evidence for a spectral hardening by ΔΓ ∼ 0.4 above the break energy. Comparisons of these results to the Cen A core spectrum from the 3FGL catalogue (Acero et al. 2015) are not meaningful, since their analysis did not include modelling of the Cen A core spectrum as a broken power law. Using the modified WMAP template we observe a consistent photon index in the lower and upper bands, respectively, of 2.68 ± 0.03 and 2.26 ± 0.07, and using the Parkes template, 2.67 ± 0.03 and 2.29 ± 0.07. We also tested for a log-parabola spectral shape using a likelihood ratio test, analogous to Signif_Curve in the 3FGL catalogue, which Acero et al. (2015) calculated as 2.3σ, and found a TScurve = 4.5, or ∼2.1σ. The power-law index that we observe above the spectral break is consistent with the index above 10 GeV found in the 3FHL catalogue (Ajello et al. 2017).
. This provides corroborating evidence for a spectral hardening by ΔΓ ∼ 0.4 above the break energy. Comparisons of these results to the Cen A core spectrum from the 3FGL catalogue (Acero et al. 2015) are not meaningful, since their analysis did not include modelling of the Cen A core spectrum as a broken power law. Using the modified WMAP template we observe a consistent photon index in the lower and upper bands, respectively, of 2.68 ± 0.03 and 2.26 ± 0.07, and using the Parkes template, 2.67 ± 0.03 and 2.29 ± 0.07. We also tested for a log-parabola spectral shape using a likelihood ratio test, analogous to Signif_Curve in the 3FGL catalogue, which Acero et al. (2015) calculated as 2.3σ, and found a TScurve = 4.5, or ∼2.1σ. The power-law index that we observe above the spectral break is consistent with the index above 10 GeV found in the 3FHL catalogue (Ajello et al. 2017).
Finally, we tested for variability of the Cen A core both above and below the break energy (2.8 GeV) by calculating light curves using a single power-law spectral model for each. Below the break, we divided the data into 64 45 day bins and calculated flux variability using the method described in Nolan et al. (2012) Sect. 3.6, with systematic correction factor f = 0.02. Keeping the power-law index fixed to 2.70, we calculate 0.09σ (χ2 = 47.3 with 63 d.o.f.) significance for flux variability. Above the break, we divided the data into nine-month bins. Keeping the power-law index fixed to 2.31, we do not see evidence for flux variability (1.9σ, χ2 = 16.6 with 9 d.o.f.).
4. Discussion
4.1. Beyond a single-zone SSC description of the γ-ray core SED of Cen A
The proximity and the diversity of the radio structures associated with the activity of its core make Cen A an ideal laboratory to investigate radiative processes and jet physics. In this regard, an improved characterisation of its SED is important in distinguishing which emission component is likely to dominate the observed radiation. Earlier investigations (e.g. Chiaberge et al. 2001) suggested that the SED of the core of Cen A (i.e. the central source unresolved with radio, infrared, hard X-ray, and γ-ray instruments) up to sub-GeV energies appears remarkably similar to that of blazars. In a ν–νFν plot, the SED seems well represented by two broad peaks, one located in the far-infrared band and the other in the γ-ray band at energies ∼0.1 MeV. The SED as known prior to 2009 was satisfactorily described by a single zone, homogeneous SSC model assuming the jet to be misaligned (i.e. lower Doppler boosting compared to blazars). The detection of VHE and HE γ rays from Cen A by H.E.S.S. and Fermi-LAT has started to complicate this simple picture. If the available (non-contemporaneous) H.E.S.S. and Fermi-LAT data are added, a single zone SSC model is no longer able to adequately account for the overall core SED of Cen A (see also Roustazadeh & Böttcher 2011; Petropoulou et al. 2014; Abdo et al. 2010a). The SSC spectral component introduced earlier (Chiaberge et al. 2001) appears to work well only for the radio band to the MeV γ-ray band.
Moreover, the detection of VHE γ rays compatible with a power law up to ∼5 TeV raises the principal challenge of avoiding internal (i.e. on co-spatially produced synchrotron photons) γγ absorption in a one-zone SSC approach. Interferometric observations with the MID-infrared Interferometeric instrument (MIDI) at the Very Large Telescope Interferometer array (Meisenheimer et al. 2007) showed that the mid-infrared (MIR) emission from the core of Cen A is dominated by an unresolved point source <10 mas (or <0.2 pc). Abdo et al. (2010a) have argued that the MIR and VHE emission cannot originate in the same region, since the VHE emission would be strongly attenuated due to γγ interaction with mid-infrared (soft) photons. The strength of this argument depends on how well possible Doppler boosting effects can be constrained, that is, on inferences with respect to the inclination and the bulk flow Lorentz factor of the sub-parsec scale jet in Cen A. It could be shown by extending the argumentation from Section 5.2 of Abdo et al. (2010a) that the γγ-attenuation problem might be alleviated if the sub-parsec jet were inclined at 11°, that is, slightly below the lower limit of the angular range θ ∼ 12° −45° allowed by recent Tracking Active Galactic Nuclei with Austral Milliarcsecond Interferometry (TANAMI) monitoring constraints on the sub-parsec scale jet (Müller et al. 2014). Motions with the Doppler factors required to avoid γγ attenuation (δD > 5.3), however, have not yet been observed on sub-parsec scales.
The previously mentioned considerations, along with the evidence for a clear hardening of the HE spectrum of Cen A, make a single-zone SSC interpretation for its overall SED very unlikely. Alternative scenarios, where the TeV emission from the high energy Cen A core is associated with the presence of an additional emission component is instead favoured.
4.2. Characterising the overall core SED with other multi-wavelength observations
A variety of multi-wavelength data, albeit with varying angular resolution and taken non-contemporaneously, is available for Cen A and can be used to construct a characteristic core SED, an example of which is presented in Fig. 3. Observations in different broad energy ranges are shown with different symbols.
 |
Fig. 3. SED of Cen A core with model fits as described in text. The red curve corresponds to an SSC component designed to fit the radio to sub-GeV data. The blue curve corresponds to a second SSC component added to account for the highest energy data. The black curve corresponds to the sum of the two components. SED points as derived from H.E.S.S. and Fermi-LAT data in this paper are shown with open circles. Observations from the radio band to the MeV γ-ray band are from TANAMI (⋄), SEST (▴), JCMT (▹), MIDI (▽), NAOS/CONICA (◃), NICMOS (□), WFPC2 (♦), Suzaku(▵), OSSE/COMPTEL (▪). The acronyms are described in Appendix B. |
In the γ-ray regime, we combine H.E.S.S. and Fermi-LAT data to build a quasi-contemporaneous high-energy core SED. One should keep in mind, however, that given the angular resolution of H.E.S.S. and Fermi-LAT, the large-scale jet and inner lobes of Cen A could in principle also contribute to the observed γ-ray signal.
Cen A is the highest flux radio galaxy detected in hard X-ray and MeV γ-ray bands. As can be seen from Fig. 3, this energy range plays an important role in the modelling of its emission. The angular resolution at these energy bands is relatively poor compared to that at other energies (including radio, infrared, soft X-rays, GeV, and VHE γ rays). It corresponds to about 2°.5 for INTEGRAL SPI in the bandpass 18 keV–8 MeV and to about 4° in the energy range 1–30 MeV for COMPTEL (Steinle et al. 1998; Steinle 2010). We note that a recent spectral analysis of ten years of observations with INTEGRAL SPI favours a jet origin for the hard X-ray emission (Burke et al. 2014), supporting the proposal that the second peak in the SED of the Cen A core (with a maximum at ∼0.1 MeV) is jet-related and probably due to SSC radiation (Chiaberge et al. 2001; Abdo et al. 2010a). A possible X-ray contribution from accretion, however, cannot yet be excluded (for discussion, see Evans et al. 2004; Meisenheimer et al. 2007; Fürst et al. 2016). The available archival data measured in hard X-rays and MeV γ rays of Cen A have been included in Fig. 3. For the lower-energy SED part, which includes radio, mm-, infrared and optical data points, and seems well described by a synchrotron source, the available archival data are taken from Meisenheimer et al. (2007), with the exception of two data points at 8.4 GHz and 22.3 GHz measured on 2009 November 27 and 29 as part of the TANAMI programme (Ojha & Kadler 2009), replacing three consistent radio data points that were measured in the mid-1990s.
4.3. Modelling the high-energy core SED with a second emission component
The observed smooth TeV spectrum and the spectral hardening by ΔΓ ∼ 0.4 as observed with H.E.S.S. and Fermi-LAT are strongly suggestive of the contribution of a second emission component in addition to the conventionally employed single-zone SSC component under the assumption of a misaligned jet. A variety of different (not mutually exclusive) scenarios for the physical origin of this second emission component could be envisaged. Proposals in the literature for Cen A encompass
(a) magnetospheric (pulsar-like) scenarios based on leptonic inverse Compton processes in a radiatively inefficient disk environment (Rieger & Aharonian 2009; Rieger 2011);
(b) inner (parsec-and sub-parsec-scale) jet models involving for example multiple leptonic SSC-emitting components travelling at different angles to the line of sight (Lenain et al. 2008), inverse Compton interplay in a stratified jet geometry (Ghisellini et al. 2005), photo-meson pγinteractions of ultra-high-energy protons in strong (e.g. standard disk-type) photon fields (Kachelrieß et al. 2010; Sahu et al. 2012; Petropoulou et al. 2014; Fraija 2014) and elaborated lepto-hadronic modifications thereof (Reynoso et al. 2011; Cerruti et al. 2017), or γ-ray-induced pair-cascades in a strong accretion disk field (Sitarek & Bednarek 2010), a dusty torus-like region (Roustazadeh & Böttcher 2011), or a starlight photon field (Stawarz et al. 2006);
(c) extended astrophysical scenarios involving for example hadronic pp-interactions of accelerated protons with ambient matter in its kiloparsec-scale region (Sahakyan et al. 2013), the combined high-energy γ-ray contribution from a supposed population of millisecond pulsars (Brown et al. 2017), or leptonic inverse-Compton scattering off various photon fields (SSC, host galaxy starlight, cosmic microwave background, extragalactic background light) in the kiloparsec-scale jet of Cen A (Stawarz et al. 2003; Hardcastle & Croston 2011); and
(d) explanations involving physics beyond that of the Standard Model, for example the self-annihilation of dark matter (DM) particles in a putative central dark matter spike (Brown et al. 2017);
Some critical astrophysical questions arise in each of these models: near-black-hole scenarios, for example, require advectiondominated accretion disk environments to satisfy external opacity conditions, leptonic models often deviate significantly from equipartition and are affected by internal opacity constraints, hadronic scenarios usually require a very high jet power, and pulsar-population models are dependent on poorly-known density profiles, while DM models need anomalously high dark matter concentrations. However, the limited angular resolution of current γ-ray instruments and the fact that no significant statistical evidence for variability of the γ-ray emission above the break (neither at Fermi-LAT nor VHE energies) has been found, does not make it possible to strongly exclude any of these models.
We note, though, that any (future) hint of variability would likely disfavour models of type (c)–(d). The (apparent) lack of variability, on the other hand, could simply be a matter of limited statistics and therefore might still be reconciled with inner jet-related scenarios. The increased sensitivity of the Cherenkov Telescope Array (CTA; Acharya et al. 2017) will enable a deeper probe into this and may eventually distinguish between models and resolve the physical nature of this component.
Noting these limitations, we nevertheless would like to provide an illustration here that the current core SED could be satisfactorily modelled by two jet-related components where the emission below the break is attributed to the conventional (misaligned) SSC-emitting component and the emission above the break to an additional SSC-emitting jet component. We model both components as jet blobs of different size and magnetic field strength. Assuming that the conventional single-zone SSC description works well for the radio to sub-GeV part of the spectrum, we adopt the same parameters (see Table 2) for the first SSC component as reported earlier7 (Abdo et al. 2010a), apart from considering a self-consistent maximum electron Lorentz factor of γmax = 107. The SED is modelled using the numerical code SED Builder8 (Massaro et al. 2006; Tramacere et al. 2009, 2011). To account for the γ-ray spectrum above the break, we introduce a second SSC-emitting zone for which we require, amongst others, that (a) the energy density in the particles is comparable to (or less than) the energy density in the magnetic field B2/(8π) (one-sided equipartition constraint), (b) the dynamical timescale ≍R/ cis larger than the synchrotron cooling timescale at high energies (efficiency constraint), (c) the synchrotron loss timescale is longer than the gyro-timescale at γmax (acceleration constraint), and (d) the optical depth to internal γγ absorption is less than one (opacity constraint). The model given for the second SSC component (Table 2) provides an exemplary set of parameters that satisfy these constraints and that satisfactorily reproduces the observed spectrum. While not unique, this example provides an illustration that both the VHE emission measured with H.E.S.S. as well as the GeV emission measured with Fermi-LAT could be accounted for by means of a two-zone SSC scenario. If one relaxes the requirements (e.g. the one-sided equipartition constraint above), additional descriptions with for example a rather low magnetic field strength, become possible (e.g. Abdo et al. 2010a). More complex realisations might perhaps be possible if the second component were characterised by a different (blazar-like) Doppler factor δD > 1.
Parameters used for modelling overall core SED of Cen A with two SSC-emitting components.
5. Conclusions
High-energy observations of the core region in active galaxies provide important insights into the physical processes driven by a central powerhouse containing an accreting, jet-emitting super-massive black hole system. In the case of Cen A, the H.E.S.S. discovery of VHE γ-ray emission from its central region (Aharonian et al. 2009) exceeded expectations from conventional (mis-aligned) single-zone SSC scenarios, casting doubt on the appropriateness of such an interpretation. Non-simultaneous Fermi-LAT results (Sahakyan et al. 2013; Brown et al. 2017) are indeed indicative of a transition region above a few GeV in the γ-ray core spectrum of Cen A and provide evidence that the VHE emission is associated with an additional radiative component.
This paper reports results of new (more than 100 h) VHE observations of the Cen A γ-core with H.E.S.S. accumulated during the Fermi-LAT operation and provides a detailed characterisation of the complete VHE data set using advanced analysis methods. VHE γ-ray emission from the core of Cen A is detected at 12σ. No significant variability is apparent in the VHE data set. A spectral analysis of the complete data set yields a photon index of Γ = 2.52 ± 0.13stat ± 0.20sys and a normalisation constant of 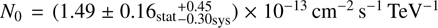 at E0 = 1 TeV. Spectral analyses of the H.E.S.S. data taken before and after the launch of the Fermisatellite give comparable results and validate the construction of a joined γ-ray spectrum based on Fermi-LAT and H.E.S.S. data. We also present an update of the Cen A core spectrum at GeV energies using eight years of Fermi-LAT Pass 8 data. The Fermi-LAT analysis provides clear evidence at a level of 4.0σ for spectral hardening by ΔΓ ≃ 0.4 at γ-ray energies above a break energy of ≃ 2.8 GeV. This hardening is suggestive of an additional γ-ray emitting component connecting the HE emission above the break energy to the one observed at VHE energies. Both the hardening of the spectrum above the break energy at a few GeV and the VHE emission excess over the power-law extrapolation of the γ-ray spectrum measured below the break energy are a unique case amongst the VHE AGNs. The results allow us for the first time to construct a representative (contemporaneous) HE-VHE SED for Cen A. While a variety of different interpretations are available, the physical origin of the additional γ-ray emitting component cannot yet be resolved due to instrumental limitations in angular resolution and the apparent absence of significant variability in both the HE and VHE data. It is possible, however, that the additional emission component is jet-related and we provide one SSC model fit to illustrate this.
at E0 = 1 TeV. Spectral analyses of the H.E.S.S. data taken before and after the launch of the Fermisatellite give comparable results and validate the construction of a joined γ-ray spectrum based on Fermi-LAT and H.E.S.S. data. We also present an update of the Cen A core spectrum at GeV energies using eight years of Fermi-LAT Pass 8 data. The Fermi-LAT analysis provides clear evidence at a level of 4.0σ for spectral hardening by ΔΓ ≃ 0.4 at γ-ray energies above a break energy of ≃ 2.8 GeV. This hardening is suggestive of an additional γ-ray emitting component connecting the HE emission above the break energy to the one observed at VHE energies. Both the hardening of the spectrum above the break energy at a few GeV and the VHE emission excess over the power-law extrapolation of the γ-ray spectrum measured below the break energy are a unique case amongst the VHE AGNs. The results allow us for the first time to construct a representative (contemporaneous) HE-VHE SED for Cen A. While a variety of different interpretations are available, the physical origin of the additional γ-ray emitting component cannot yet be resolved due to instrumental limitations in angular resolution and the apparent absence of significant variability in both the HE and VHE data. It is possible, however, that the additional emission component is jet-related and we provide one SSC model fit to illustrate this.
Despite their faintness at γ-ray energies, radio galaxies such as Cen A are emerging as a unique γ-ray source population offering important physical insight beyond what could usually be achieved in classical blazar sources. With its increased sensitivity, CTA is expected to probe deeper into this and help to eventually resolve the nature of the γ-ray emission in Cen A.
The observed integral flux of the Crab Nebula above 1 TeV is (2.26 ± 0.08stat ± 0.45sys) × 10−11 cm−2 s−1(Aharonian et al. 2006).
The power-law index, p1, of 1.8 for the first component was adopted from Abdo et al. (2010a) in order to fit the exceptionally flat Cen A spectrum, Fν ∝ ν−0.36, between 1011 and 3 × 1013 Hz (Meisenheimer et al. 2007).
Acknowledgments
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the Helmholtz Association, the Alexander von Humboldt Foundation, the French Ministry of Higher Education, Research and Innovation, the Centre National de la Recherche Scientifique (CNRS/IN2P3 and CNRS/INSU), the Commissariat à l’énergie atomique et aux énergies alternatives (CEA), the U.K. Science and Technology Facilities Council (STFC), the Knut and Alice Wallenberg Foundation, the National Science Centre, Poland grant no. 2016/22/M/ST9/00382, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the National Commission on Research, Science & Technology of Namibia (NCRST), the Austrian Federal Ministry of Education, Science and Research and the Austrian Science Fund (FWF), the Australian Research Council (ARC), the Japan Society for the Promotion of Science, and by the University of Amsterdam. We appreciate the excellent work of the technical support staff in Berlin, Zeuthen, Heidelberg, Palaiseau, Paris, Saclay, Tübingen, and in Namibia in the construction and operation of the equipment. This work benefited from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation. Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat àl’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the CentreNational d’Études Spatiales in France. This work performed in part under DOE Contract DE-AC02-76SF00515.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 700, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 719, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Science, 328, 328 [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 218 [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 223, 223 [Google Scholar]
- Acharya, B. S., Agudo, I., & Samarai, I. A. 2017, ArXiv e-prints [arXiv:1709.07997] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, ApJ, 695, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Atwood, W. B., Baldini, L., et al. 2017, ApJS, 232, 232 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Becherini, Y., Djannati-Ataï, A., Marandon, V., Punch, M., & Pita, S. 2011, Astropart. Phys., 34, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Brookes, M. H., Lawrence, C. R., Keene, J., et al. 2006, ApJ, 646, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. M., Bœhm, C., Graham, J., et al. 2017, Phys. Rev. D., 95, 063018 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, M. J., Jourdain, E., Roques, J.-P., & Evans, D. A. 2014, ApJ, 787, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Cerruti, M., Zech, A., Emery, G., & Guarin, D., 2017, AIP Conf. Proc., 1792, 050027 [CrossRef] [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 2001, MNRAS, 324, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Daum, A., Hermann, G., Heß, M., et al. 1997, Astropart. Phys., 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, D. A., Kraft, R. P., Worrall, D. M., et al. 2004, ApJ, 612, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 167P [Google Scholar]
- Fraija, N., 2014, MNRAS, 441, 441 [CrossRef] [Google Scholar]
- Fürst, F., Müller, C., Madsen, K. K., et al. 2016, ApJ, 819, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardcastle, M. J., & Croston, J. H. 2011, MNRAS, 415, 415 [Google Scholar]
- Hardcastle, M. J., Worrall, D. M., Kraft, R. P., et al. 2003, ApJ, 593, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Kraft, R. P., & Worrall, D. M. 2006, MNRAS, 368, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G. L. H., Rejkuba, M., & Harris, W. E. 2010, PASA, 27, 27 [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 180 [Google Scholar]
- Hinton J. A. 2004, New Astron. Rev., 48, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Horiuchi, S., Meier, D. L., Preston, R. A., & Tingay, S. J. 2006, PASJ, 58, 58 [CrossRef] [Google Scholar]
- Israel, F. P., 1998, A&ARv, 8, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Junkes, N., Haynes, R. F., Harnett, J. I., & Jauncey, D. L. 1993, A&A, 269, 29 [NASA ADS] [Google Scholar]
- Kachelrieß, M., & Ostapchenko, S. 2010, PASA, 27, 27 [Google Scholar]
- Kinzer, R. L., Johnson, W. N., Dermer, C. D., et al. 1995, ApJ, 449, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Forman, W. R., Jones, C., et al. 2002, ApJ, 569, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Lafferty, G. D., & Wyatt, T. R. 1995, Nucl. Instrum. Methods Phys. Res. A, 355, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Lenain, J.-P., Boisson, C., Solol, H., & Katarzyński, K. 2008, A&A, 478, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Meisenheimer, K., Tristram, K. R. W., Jaffe, W., et al. 2007, A&A, 471, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, C., Kadler, M., Ojha, R., et al. 2014, A&A, 569, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 199 [Google Scholar]
- Ojha, R., & Kadler, M., 2009 Fermi Symp., eConf Proc. C091122 [arXiv:1001.0059] [Google Scholar]
- Parsons, R. D., & Hinton, J. A. 2014, Astropart. Phys., 56, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, M., Lefa, E., Dimitrakoudis, S., & Mastichiadis, A. 2014, A&A, 562, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimer, A., & Böttcher, M. 2013, Astropart. Phys., 43, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, M. M., Medinaedina, M. C., & Romero, G. E. 2011, A&A, 531, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieger, F. M. 2011, Int. J. Mod. Phys. D, 20, 1547 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, F. M., & Aharonian, F. A. 2009, A&A, 506, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roustazadeh, P., & Böttcher, M. 2011, ApJ, 728, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Sahakyan, N., Yang, R., Aharonian, F. A., & Rieger, F. M. 2013, ApJ, 770, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Sahu, S., Zhang, B., & Fraija, N. 2012, Phys. Rev. D., 85, 043012 [NASA ADS] [CrossRef] [Google Scholar]
- Sitarek, J., & Bednarek, W. 2010, MNRAS, 409, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Hartman, R. C., Nolan, P. L., & Thompson, D. J. 1999, Astropart. Phys., 11, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, Ł., Aharonian, F., Wagner, S., & Ostrowski, M. 2006, MNRAS, 371, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, Ł., Sikora, M., & Ostrowski, M. 2003, ApJ, 597, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Steinle, H., 2010, PASA, 431, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Steinle, H., Bennett, K., Bloemen, H., et al. 1998, A&A, 330, 97 [NASA ADS] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, E., & Taylor, A. M. 2011, ApJ, 739, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 107 [Google Scholar]
- Yang, R. Z., de Ona Wilhelmie, E., Aharonian, F., & Rieger, F., 2012, A&A, 542, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A Comparison of spectral results from Hillas-based analyses
To perform a Hillas-based analysis, we applied a standard cut of θ2 < 0.0125 deg2 for the calculation of the number of ON events, where θ2 is the square of the angular separation between the reconstructed shower position and the source position. This cut is optimised to minimise the contamination by the background and is somewhat different to that used in the previous publication (θ2 < 0.03 deg2). The Hillas-based analysis performed here for the combined data set (A + B) results in a lower value of the normalisation coefficient compared with the published value. The obtained value is compatible with those derived with the main (ImPACT) and cross-check analyses. The compatibility of these results gives us confidence in the reliability of the current cross-checked analysis of the Cen A core. The comparison suggests a wider range of the systematic errors for the results of the Hillas-based analysis of data set A than that estimated in Aharonian et al. (2009). The lack of temporal variability in flux between data sets A and A + B concluded from the ImPACT analyses supports this suggestion.
Appendix B List of acronyms
SEST – 15 m Swedish-ESO Submillimetre Telescope.
JCMT –15m James Clerk MaxwellTelescope.
NAOS/CONICA – Nasmyth Adaptive Optics System/Coude Near Infrared Camera.
NICMOS – Near Infrared Camera and Multi-Object Spectrometer.
WFPC2 – Wide Field and Planetary Camera 2.
Swift-BAT – Swift-Burst Alert Telescope.
BATSE – Burst and Transient Source Experiment.
OSSE – Oriented Scintillation Spectrometer Experiment.
COMPTEL – Imaging COMPton TELescope.
EGRET – Energetic Gamma Ray Experiment Telescope.
All Tables
Parameters used for modelling overall core SED of Cen A with two SSC-emitting components.
All Figures
 |
Fig. 1. SED of Cen A γ-ray core. Fermi-LAT and H.E.S.S. data points along with a high-energy power-law extrapolation of the γ-ray spectrum measured below the break energy. Eight years of Fermi-LAT data and 213 h of H.E.S.S. data were used. Statistical error bars are shown. |
| In the text | |
 |
Fig. 2. Fig. 2. Change in overall logℒ while fixing Cen A core break energy to values within the range 0.9–7.0 GeV, as derived from Fermi-LAT data using the WMAP, modified WMAP, and Parkes templates and compared to the logℒ value at 0.9 GeV for the WMAP template. The solid vertical line shows the best-fit value of the break energy parameter, while the dashed vertical lines show 1σ interval for the parameter. |
| In the text | |
 |
Fig. 3. SED of Cen A core with model fits as described in text. The red curve corresponds to an SSC component designed to fit the radio to sub-GeV data. The blue curve corresponds to a second SSC component added to account for the highest energy data. The black curve corresponds to the sum of the two components. SED points as derived from H.E.S.S. and Fermi-LAT data in this paper are shown with open circles. Observations from the radio band to the MeV γ-ray band are from TANAMI (⋄), SEST (▴), JCMT (▹), MIDI (▽), NAOS/CONICA (◃), NICMOS (□), WFPC2 (♦), Suzaku(▵), OSSE/COMPTEL (▪). The acronyms are described in Appendix B. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


