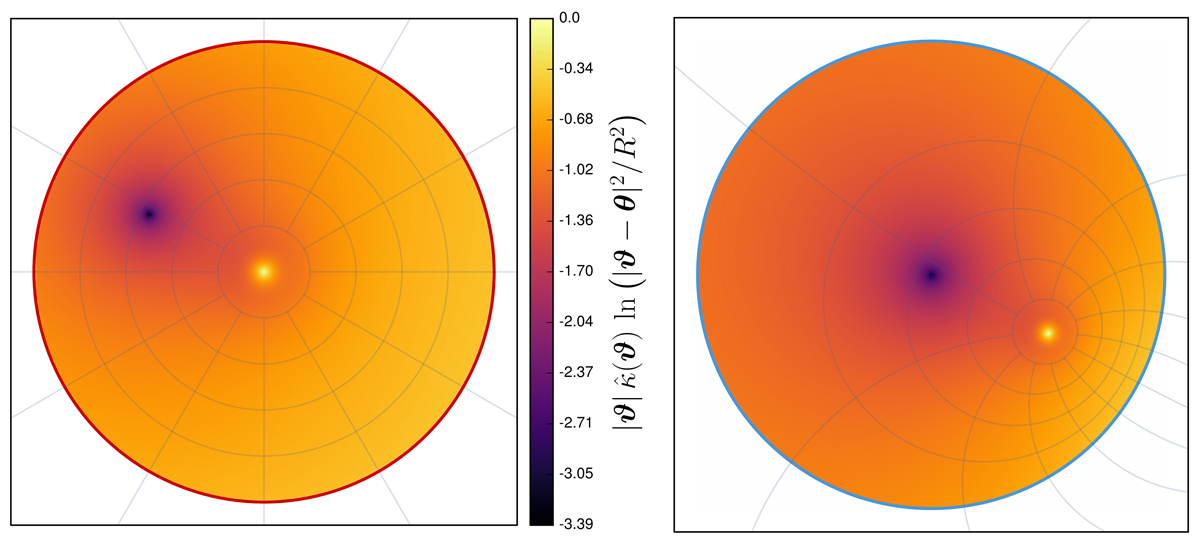
Representative example that illustrates how the integration domain 𝒰 is mapped onto the unit disk in the complex plane under a Riemann mapping. Left panel: the color coding depicts the integrand for all ϑ ∈ 𝒰. It shows a pole at ϑ = θ with θ = ( − 0.5, 0.25) θ_E and a secondary peak at the origin caused by κ(|ϑ|=0). The lens model is an NIS (θ_c = 0.1θ_E) plus external shear (γ_p = 0.1) transformed by the radial stretching with (f₀, f₂)=(0, 0.55). The red circle delimits 𝒰 with radius R. Right panel: integrand after applying the Riemann mapping described in Appendix A in Unruh et al. (2017). The pole ϑ = θ now lies at the origin of the unit (blue) circle of the complex plane. The polar grid (gray lines) allows us to visualize how the Riemann mapping acts on 𝒰. For this figure, we used the subpackage integrals that addresses both the pole and second peak.