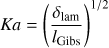| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833475 | |
| Published online | 22 October 2018 | |
Thermonuclear explosions of rapidly differentially rotating white dwarfs: Candidates for superluminous Type Ia supernovae?⋆
1
Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Emil-Fischer-Straße 31, 97074
Würzburg, Germany
2
Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Philosophenweg 12, 69120 Heidelberg, Germany
3
Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
e-mail: markus.kromer@h-its.org
4
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching, Germany
5
School of Physical, Environmental and Mathematical Sciences, University of New South Wales, Australian Defence Force Academy, Canberra, ACT 2600 Australia
6
Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611 Australia
7
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, Belfast, BT7 1NN UK
Received:
22
May
2018
Accepted:
17
July
2018
The observed sub-class of “superluminous” Type Ia supernovae lacks a convincing theoretical explanation. If the emission of such objects were powered exclusively by radioactive decay of 56Ni formed in the explosion, a progenitor mass close to or even above the Chandrasekhar limit for a non-rotating white dwarf star would be required. Masses significantly exceeding this limit can be supported by differential rotation. We, therefore, explore explosions and predict observables for various scenarios resulting from differentially rotating carbon–oxygen white dwarfs close to their respective limit of stability. Specifically, we have investigated a prompt detonation model, detonations following an initial deflagration phase (“delayed detonation” models), and a pure deflagration model. In postprocessing steps, we performed nucleosynthesis and three-dimensional radiative transfer calculations, that allow us, for the first time, to consistently derive synthetic observables from our models. We find that all explosion scenarios involving detonations produce very bright events. The observables predicted for them, however, are inconsistent with any known subclass of Type Ia supernovae. Pure deflagrations resemble 2002cx-like supernovae and may contribute to this class. We discuss implications of our findings for the explosion mechanism and for the existence of differentially rotating white dwarfs as supernova progenitors.
Key words: supernovae: general / nuclear reactions, nucleosynthesis, abundances / hydrodynamics / radiative transfer / white dwarfs
Simulation data for all models presented in this paper are available from the Heidelberg Supernova Model Archive (HESMA) at https://hesma.h-its.org.
© ESO 2018
1. Introduction
Comprehensive observational surveys of SNe Ia have revealed that, despite their relative homogeneity, several distinct subclasses exist, and the observed heterogeneity may call for different progenitors and/or explosion mechanisms. Particularly puzzling are supernovae that are very luminous and have decline rates that put them well above the Phillips relation of “normal” SNe Ia by almost one magnitude in the B-band, the prototypical examples being SN 2006gz (Hicken et al. 2007; Maeda et al. 2009) and SN 2009dc (Yamanaka et al. 2009; Tanaka et al. 2010; Silverman et al. 2011; Taubenberger et al. 2011). By now, only a few objects have been discovered that belong to this class (Taubenberger 2017). In addition to their high luminosity, two to three times that of normal SNe Ia, their lightcurves have a long rise time (> 23 days) and decline slowly (Δm15(B)∼0.8 mag). Moreover, they are characterized by low ejecta velocities, occasionally being even lower than those of normal SNe Ia, and prominent C II absorption features, while all other early-time spectral properties are not unusual.
These properties are not easy to reconcile within the framework of standard explosion models. If the luminosity at peak resulted exclusively from the decay of 56Ni, the Ni-mass produced in the event would be very close to (Howell et al. 2006) or even exceed the canonical Chandrasekhar mass of non-rotating WDs. For example, for SN 2009dc Hachinger et al. (2012) and Taubenberger et al. (2013) find about 1.5 − 1.8 M⊙ of 56Ni. This led to the suspicion that their progenitors might be super-Chandrasekhar mass WDs (Howell et al. 2006), and the name “super-Chandras” was coined for the class. Such an interpretation sounds reasonable because it is known that differentially rotating WDs, in principle, can have masses up to (or even beyond) 2.5 M⊙ (e.g., Durisen 1975). The first simulations of thermonuclear explosions of such objects (Steinmetz et al. 1992) showed that a huge amount of 56Ni is produced when they are burned in a supersonic detonation.
However, if this is true, one has to explain why their ejecta velocities are so low. Fusing 1.5 M⊙ of carbon and oxygen to iron-group and intermediate-mass elements releases roughly 2.5 × 1051 erg of nuclear binding energy and, thus, the kinetic energy of the ejecta should be around 1.5 × 1051 erg (or more), inconsistent with the observed low velocities. Also, Hachinger et al. (2012) have shown by means of “abundance tomography” that, at least for SN 2009dc, the amount of burned material at high-velocity predicted by sufficiently luminous explosion models is inconsistent with their spectra. As a way out, very asymmetric explosions with lopsided 56Ni distributions of otherwise “normal” WDs were suggested (Hillebrandt et al. 2007), but this explanation needs fine tuning. Ejecta–CSM interactions with a dense carbon–oxygen envelope were proposed as an alternative way to explain the high-luminosity of SN 2009dc (e.g. Hachinger et al. 2012; Taubenberger et al. 2013; Noebauer et al. 2016).
Here, we have revisited explosions in rapidly-rotating WDs, but in addition to the work of Pfannes et al. (2010a); Pfannes et al. (2010b) who computed pure deflagration and pure detonation models only, we also investigate deflagrations followed by a spontaneous deflagration-to-detonation transition (DDT), the more popular scenario for explosions of Chandrasekhar-mass WDs. As in Pfannes et al. (2010a); Pfannes et al. (2010b), we have constructed initial models based on the work of Yoon & Langer (2004); Yoon & Langer (2005), with minor modifications due to a slightly different equation of state (see Sect. 2.1). An improved description of the detonation front (see Sect. 3.1) constitutes a major difference to the modeling approach of Pfannes et al. (2010a); Pfannes et al. (2010b). We also relaxed their assumption of rotational symmetry in the gravitational potential. For all our models we ran a consistent pipeline in which the nucleosynthesis is determined from postprocessing the results of the hydrodynamical explosion simulations and synthetic observables are obtained from radiative transfer calculations. This enables, for the first time, a direct comparison of the rapidly-rotating model predictions with observations of superluminous SNe Ia.
This article is structured as follows. In Sect. 2 we describe the initial WD models used in our work and explain how the explosions were initiated and how the transition from the deflagration phase to a detonation was triggered for the delayed detonation models. In Sect. 3 we give a brief account of the numerical methods used for solving the reactive Euler equations, the nucleosynthesis post-processing step, and the radiative transfer. We present the results of our explosion simulations in Sect. 4. The synthetic lightcurves and spectra obtained from these in Sect. 5. A discussion and conclusions follow in Sects. 6 and 7.
2. Model setup
2.1. Rotating initial WDs
In the single-degenerate scenario of SNe Ia, an already rather massive C+O WD accretes matter from a non-degenerate companion, presumably a main sequence or subgiant star, approaches the Chandrasekhar mass limit, M ≃ 1.4 M⊙, and explodes. However, together with the matter, the WD also accretes angular momentum. If this additional angular momentum is not lost from the WD, for instance by a wind or magnetic braking, the WD will be spun up and, due to the centrifugal force, the critical mass for the final contraction and explosion will increase.
Whether this angular momentum has an important impact on the final outcome depends on the way it is redistributed in the WD. If there would be no angular momentum transport from the accreted layer into the WD a Keplerian disk would form and the accretion rate would be low. On the other hand, hydrodynamic instabilities, such as the (dynamical and secular) shear instability, will lead to angular momentum transport into the WD, as studied by Yoon & Langer (2004). They found that rapid differential rotation profiles might be established, with a maximum angular velocity somewhere at intermediate stellar mass shells, and a stable configuration would require that the angular momentum is constant on cylinders around the axis of rotation. Although their stellar evolution calculations are 1D and much of the relevant physics had to be put-in in parametrized form, WD masses of up to about 2 M⊙ seem to be possible with rather well motivated assumptions.
As in Pfannes et al. (2010a); Pfannes et al. (2010b) we have constructed initial models based on the work of Yoon & Langer (2004) and Yoon et al. (2004) and have used them to run pure detonation, delayed detonation, and pure deflagration explosion models. We have constructed the rapidly-rotating C+O WDs in hydrostatic equilibrium, and they resemble a subset of those presented in (Pfannes et al. 2010b; see Table 1 for the model parameters)1. To this end we applied the method of Eriguchi & Müller (1985) that solves the equations of hydrostatic equilibrium in integral form for a given rotation law, central density and axis ratio requator/rpole. The models AWD1, AWD4, and AWD3 (“AWD” stands for accreting white dwarf) span the range of total masses M(1.6 − 2.0 M⊙) and angular momentum J(0.9 − 2.2 × 1050 g cm2 s−1) expected for rapidly rotating WDs formed through accretion in binary systems (masses above M ∼ 2.0 M⊙ are unlikely due to the limited mass budget in single degenerate progenitor systems; Langer et al. 2000).
In the initial models, we assume equal amounts (by mass) of carbon and oxygen and no enhancement of the chemical composition due to the metallicity of the progenitors. A temperature profile as suggested by Yoon & Langer (2004) for an accreting WD was chosen similar to Pfannes et al. (2010a); Pfannes et al. (2010b) and (Pfannes 2006; see Fig. 1).
The high temperatures seen in Fig. 1 arise from the “simmering” C-burning phase prior to flame formation. Convection causes an approximately adiabatic temperature gradient in the outer layers (Piro & Chang 2008). The local maximum in the outer part of the degenerate C+O core is caused by accretion-induced heating (see Yoon & Langer 2004). In all models, a central density of ρ c = 2 × 109 g cm−3 was chosen.
The angular velocity distributions have central values Ωc between 1.6 and 4.6 rad s−1 and peak values Ωpeak ∼ 5 rad s−1. Shapes of the rotation laws and the initial density profiles are illustrated in Fig. 2.
The lower three panels show x − z-slices through the WDs along the rotational axis, which is in the z-direction, and the upper panel displays the angular velocity as a function of the radial coordinate r = (x2 + y2)1/2, where we have assumed constant angular velocity on cylinders around the axis of rotation (“barotropic rotation”). Yoon & Langer (2004) attribute the general shape of the angular velocity distribution with a maximum at around 1000–1500 km to the fact that as the mass increases toward explosion the more slowly rotating inner core contracts faster than the rapidly, nearly critically rotating surface layers and, moreover, to the limit they impose on the gain of angular momentum by accretion.
Since during the simmering phase prior to the explosion convection sets in (see, e.g., Nonaka et al. 2012), the innermost few hundred kilometers of the core may be in rigid rotation by the time the deflagration phase starts. In order to account for this effect, we assumed constant angular velocity for the inner 600 km in model AWD4. We note, however, that the influence of rapid rotation on the convective simmering phase is still unexplored.
At the highest densities, the WD cores do not deviate much from spherical symmetry, whereas at lower densities the stars show an extended “bulge” of material in equatorial direction that becomes more pronounced with increasing total angular momentum and total mass.
For completeness, Table 1 provides several additional quantities: requator and rpole are the equatorial and polar radii and the ratio requator/rpole is the eccentricity parameter. Egrav, Eint, Erot, and Ebind are the initial values of gravitational potential, internal, rotational kinetic, and effective binding energy (E bind = Egrav + Eint + Erot), respectively. Finally, β = Erot/|Egrav| is the ratio of rotational energy and gravitational binding energy.
Initial model parameters.
 |
Fig. 1. Initial temperature profile of the models as a function of density. The steep increase at high density is due to hydrostatic carbon burning and the local maximum at ρ ≃ 106 g cm−3 is caused by accretion-induced heating. |
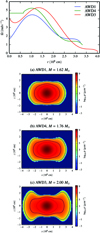 |
Fig. 2. Initial rotation laws and density distributions of all our rapidly rotating progenitor models. The lower three panels display cross-sections of the WDs with the rotational axis in z-direction. The density is color coded. Solid contours mark density levels of ρ = 105 and 107 g cm−3, corresponding to the transition densities between the main burning stages (producing iron group and intermediate mass elements, respectively, or ceasing burning) in our detonation yield tables. For comparison, the dotted contours at ρ = 1.047 × 107 and 5.248 × 107 g cm−3 show the transition densities assumed in the earlier study by Pfannes et al. (2010a). |
2.2. Explosion scenarios
For all three AWD models, we have investigated the delayed-detonation scenario, which is one of the currently favored scenarios for modeling normal SNe Ia (models AWDiddt) and which is the main subject of this article. In this scenario, it is assumed that the supernova explosion starts as a turbulent deflagration in the central core and later turns into a detonation. In addition, for the AWD3 model, we also investigated a pure deflagration (model AWD3def), which would be the outcome if the delayed detonation fails to trigger, and a centrally initiated spontaneous detonation (model AWD3det) to test the impact of the changes in the detonation scheme used in our work in comparison to (Pfannes et al. 2010a; Pfannes et al. 2010b; see also Sect. 3.1 for more details).
We begin with a discussion of the delayed-detonation models. As was done previously for the deflagration phase of non-rotating WDs (e.g. Niemeyer et al. 1996; Reinecke et al. 2002b; Röpke et al. 2006; Röpke et al. 2007) our rotating models are ignited in multiple ignition kernels around the center. Although recent studies of the pre-ignition convection phase in non-rotating Chandrasekhar-mass WDs do not support multispot ignition (Nonaka et al. 2012), the situation for rotating progenitors is less clear (Kuhlen et al. 2006). Our motivation for assuming a pronounced multispot ignition scenario is to maximize the deflagration strength and the pre-expansion when the DDT is triggered. As noted already by Steinmetz et al. (1992), pure detonations produce almost pure iron-group elements (IGEs) in the ejecta and virtually no intermediate-mass elements (IMEs), which is a potential problem for reproducing observed features of SNe Ia. This will be checked with our radiative transfer simulations. In our delayed detonation model, we aim at maximizing the IME production to test the capabilities of the model. Therefore, we put 1600 ignition kernels in a spherical volume of radius 180 km around the center at exactly the same positions as in previous studies (the model of Röpke et al. 2007 and model N1600Cdef in Fink et al. 2014; see Fig. 4). However, different kernel radii of 6 km (in between those of the two mentioned studies) are chosen.
For the transition to a supersonic detonation, a suitable criterion has to be chosen. In one-dimensional simulations, DDTs are parametrized relatively arbitrarily. A commonly used scheme is to trigger a detonation when the deflagration flame reaches fuel densities ρ
u ≲ 107 g cm−3. However, this criterion is only motivated by optimizing the agreement of synthetic with real observables of SNe Ia or, alternatively, by matching the nucleosynthesis yields (Höflich & Khokhlov 1996; Iwamoto et al. 1999). A rigorous determination of the DDT parameters from first principles is not possible, as the exact physical mechanism leading to a DDT is still unknown. An improvement in this sense is achieved by multidimensional modeling, as turbulent flame propagation is an inherently three-dimensional process. This allows a physically motivated parametrization of the DDT from properties of the flame (which itself is only a parametrization in one-dimensional modeling). There exist different DDT criteria, that are related to the onset of the distributed burning regime. The distributed burning regime is reached when at low densities the flame becomes sufficiently thick so that small eddies start to penetrate into the reaction zone and mix hot ash with cold fuel without immediately burning (cf. Peters 2000). This may lead to conditions that favor the formation of a detonation via the Zel’dovich gradient mechanism (Zel’dovich et al. 1970) or related processes (e.g. Seitenzahl et al. 2009a; Woosley et al. 2009). An equivalent condition for entering this regime is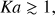 (1)
(1)
being the Karlovitz number. Here, δlam is the laminar flame width and lGibs is the Gibson scale (the size of the eddy that turns over in a laminar flame crossing time). Golombek & Niemeyer (2005) and Röpke & Niemeyer (2007) used (1) as criterion for the DDT in two- and three-dimensional simulations, following earlier suggestions by Niemeyer & Woosley (1997). However, Woosley (2007) argues that at the onset of distributed burning the first structures to form are too small to detonate and yet more mixing, lower densities, and higher Karlovitz numbers are required2. Therefore, Kasen et al. (2009) chose critical values of the Karlovitz number between 250 and 750, which causes a somewhat later transition. In this study, similar criteria are used. A DDT is initiated when at the flame the criteria are fulfilled. Consequently, transitions can (and will) happen in different locations and at different times in the exploding WD. In our models, in the final detonation phase almost all the C/O of the WD is burned to iron-group and intermediate-mass elements. However, in detail the outcome is not very sensitive to the details of the transition criterion we assume3.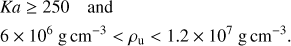 (3)
(3)
In our prompt detonation model the detonation is initiated by setting the level set function to positive values inside a small central volume with a radius of 7 km. The further evolution is computed by means of the method described in detail in Sect. 3.1 and in Sect. 6.1. The detonation scheme ensures that the detonation speed, the energy release, and the nucleosynthesis are consistently computed. Finally, in the pure deflagration model AWD3def we use identical initial conditions as in our delayed detonation model AWD3ddt, but we assume that a deflagration-to-detonation transition does not happen.
3. Numerical methods
The numerical methods we apply here are very similar to those used by Pfannes et al. (2010a); Pfannes et al. (2010b). In this section we summarize these methods and describe improvements with respect to the previous studies (see also Seitenzahl et al. 2013).
3.1. Hydrodynamics
Our simulations are carried out in three dimensions with the finite volume hydrodynamics code LEAFS (Reinecke et al. 2002a; most updates described in Seitenzahl et al. 2013 are included). We use a “hybrid” moving grid as developed by Röpke (2005); Röpke et al. (2006) with 5123 cells: while an inner uniform part of the grid (initial spatial resolution: 1.9 km) tracks the deflagration flame, an outer part with exponentially growing cell sizes tracks the overall expansion of the ejecta. All explosion models are followed until t = 100 s, when homologous expansion is reached to a good approximation.
As our initial WD models significantly depart from spherical symmetry, the gravitational potential has to be calculated more accurately than in previous studies. Here, we adopt the multipole gravity solver from Pfannes et al. (2010a); Pfannes et al. (2010b) but, in contrast to Pfannes et al. we do not assume rotational symmetry (m = 0) of the mass distribution, but include the full quadrupole term (l = 2, m ≤ l).
Reaction fronts of explosive thermonuclear burning are approximated as infinitesimally thin discontinuities between fuel and ash. These discontinuities are tracked independently for deflagrations and detonations using a level set technique (see Reinecke et al. 1999, and references therein; Golombek & Niemeyer 2005). The composition of the matter is approximated by five species: helium, carbon, oxygen and representative species for both intermediate-mass and iron-group elements. Changes in the composition and the release of nuclear binding energy are assumed to occur instantaneously behind the burning front. The final composition of the ashes and with it the reaction q-values are taken (as function of fuel density) from pre-calculated tables (CO detonation: see Fig. A.1 of Fink et al. 2010; CO deflagration: see Fig. A1 b of Fink et al. 2014) that were iteratively calibrated to our large post-processing nuclear reaction network (see Sect. 3.2). This is one of the main improvements with respect to Pfannes et al. (2010a); Pfannes et al. (2010b), who used much coarser approximations in this respect. Everywhere on the grid, the composition in nuclear statistical equilibrium (NSE) and the electron fraction Ye are adjusted according to the thermodynamic background state (see Seitenzahl et al. 2009b).
The burning speeds are also determined as functions of local quantities on the grid as described in Seitenzahl et al. (2013): an effective deflagration speed on the grid-scale is determined on the basis of a localized subgrid model (Schmidt et al. 2006a; Schmidt et al. 2006b) which takes into account turbulence on unresolved scales. The detonation speed is taken from a table as described in Fink et al. (2010): at high densities (≥107 g cm−3) the detonation is assumed to be pathological (Sharpe 1999; Gamezo et al. 1999); at low densities (< 107 g cm−3) a Chapman–Jouguet like velocity is determined for the incomplete burning regime.
3.2. Nucleosynthesis post-processing
We distribute 106 equal-mass tracer particles in the asymmetric initial WD models using a rejection method (see e.g. Press et al. 2007) to properly sample the asymmetric mass distribution. During the hydrodynamic simulations, the tracer particles are passively advected with the flow and record a Lagrangian representation of the explosion. Detailed nucleosynthetic yields are then calculated by solving a large nuclear reaction network consisting of 384 species (ranging up to 98 Mo; see Travaglio et al. 2004) for all tracer trajectories. The reaction rates we used were taken from an updated version of the REACLIB library (Rauscher & Thielemann 2000, updated 2009).
3.3. Radiative transfer
For our time-dependent 3D Monte Carlo radiative transfer calculations with the ARTIS code (Kromer & Sim 2009; Sim 2007), the final ejecta density and the detailed post-processing abundances are mapped on a 503 Cartesian grid using the scheme described in Fink et al. (2014) and Kromer et al. (2010). In each radiative transfer simulation we use 108 photon packets and follow their evolution for 111 logarithmically spaced time steps between 2 and 120 d after the explosion. We apply the atomic data set as described by Gall et al. (2012), use a gray approximation in optically thick cells (cf. Kromer & Sim 2009), and assume local thermodynamic equilibrium at early times, that is, t < 3 d.
4. Simulation results
4.1. The prompt detonation model AWD3det
As was mentioned before, this model was computed to test the impact of the changes we made in our computational scheme as compared to Pfannes et al. (2010a); Pfannes et al. (2010b).
After the central ignition, the detonation burns supersonically through the whole WD without giving it time to expand. Thus, the nucleosynthesis products of the thermonuclear burning depend only on the initial density as extracted from our detonation-yield table (see Fig. A.1 of Fink et al. 2010): IGEs are produced for ρ ≳ 107 g cm−3 and IMEs for 107 g cm−3 ≳ ρ ≳ 105 g cm−3. Due to the initial density distribution of the AWD3 model (the solid contour lines in Fig. 2 mark the transition densities), this leads to a very high mass of IGEs (1.92 M⊙, 1.44 M⊙ of it 56Ni; see Table 2 and Fig. 3) and only a low mass of IMEs (0.07 M⊙). We also note the rather high polar velocity of radioactive nickel and IMEs in this model (fourth row in Fig. 5). In general terms, our results are in fair agreement with Pfannes et al. (2010a) although there are some differences which, however, can be understood (see Sect. 6).
Results.
4.2. Delayed detonation models
Despite the roughly spherically symmetric ignition in multiple spots, the initial deflagration flame develops a pronounced anisotropy in all models. The flame propagation is much faster along the rotational axis (the z-axis) than perpendicular to it (see Fig. 4 which shows the evolution of the explosion for model AWD3ddt). This behavior has been shown to be characteristic for deflagrations in rapidly rotating WDs (Pfannes et al. 2010b). According to Pfannes et al. this has two reasons: first, the effective gravitational acceleration and with it the buoyancy force is larger along the rotational axis than perpendicular to it (due to a steeper density decline and a minimum of the centrifugal acceleration along the rotational axis); secondly, and more important, the matter flow perpendicular to the rotational axis and thus turbulence-induced flame acceleration is suppressed due to an effective angular momentum barrier.
Owing to its asymmetric propagation, the deflagration flame reaches the low-density edge of the star close to the poles while the matter in equatorial directions is still mostly unburned. Our DDT criterion Eq. (3) is first met at the trailing edges of the outer deflagration flame front, where the flame brush is wider due to the lower densities. Consequently, this is where the distributed-burning regime is reached first (cf. Röpke & Niemeyer 2007; Röpke 2007).
For all our models, the DDT occurs at times tDDT ∼ 0.80 − 0.85 s (see Table 2). Our approach allows for multiple transition points and, indeed, we find around 100 − 200 such spots where Eq. (3) is met within a time interval ΔtDDT ∼ 0.15 s. Detonations are initiated at similar times both close to the north and the south pole of the WD. From there, they propagate toward the equatorial plane and rapidly consume the remaining unburned fuel. Collisions of the leading shocks cause some enhanced compression when both detonation fronts meet close to the equatorial plane. This can still be seen in the final distribution of 28Si and 16O in Fig. 5. Moreover, since during the deflagration phase only moderate pre-expansion happened, the detonation can still produce significant amounts of IGEs. This differs from model N1600C of Seitenzahl et al. (2013), which uses the same ignition setup as our models here. However, with a non-rotating progenitor star the pre-expansion during the deflagration is much more efficient and the ensuing detonation produces mainly IMEs and O.
Our initial models form a series of increasing rotational kinetic energy Erot and total mass M of the progenitor (in the order AWD1, AWD4, AWD3). More massive models are more tightly bound and therefore start at lower initial total energy (Etot = Egrav + Eint + Ekin; see Table 2 for explosion energetics results), despite the larger Erot (see Table 1). However, due to the increasing amount of mass being burned at high densities (corresponding to an increasing nuclear energy release Enuc) within the series, all models become unbound rapidly and the more massive models even reach larger final Etot and MIGE (see also Fig. 3): MIGE ranges from 1.31 to 1.74 M⊙. Due to the rapid unbinding and expansion of the star, Ekinasymp. ≈ Etot(t = 100 s) holds for all delayed detonation (and also the pure detonation) models. The corresponding 56Ni masses are in the range 1.06 − 1.45 M⊙.
Compared to the pure detonation model AWD3det, the delayed-detonation model AWD3ddt has lower IGE mass due to the expansion of the star during the deflagration phase. Despite the chosen vigorous ignition setup, the differences are, however, relatively limited. This is in contrast to non-rotating models, in which the strength of the deflagration is distinctly anticorrelated with the mass of IGEs (Röpke & Niemeyer 2007): a weak deflagration implies that more unburned material is available for the detonation and, thus, more IGEs (and 56Ni) are produced. In the fast rotating models the deflagration wave propagates predominantly along the axis of rotation, which results always in lots of unburned fuel at the onset of the detonation. Remarkably, the AWD3ddt model even slightly surpasses AWD3det in 56Ni mass due to its lower degree of neutronization. Compared to the (rotating) pure detonation model, the delayed-detonation models produce more IMEs. However, the total IME masses are still relatively small (0.2 − 0.3 M⊙) and the exact amounts depend on the details of the initial density distributions. In all models, the amounts of unburned 12C and 16O are very small and restricted to the outermost layers.
 |
Fig. 3. Integrated nucleosynthetic yields of all explosion models. The models are (from left to right): AWD3def, AWD1ddt, AWD4ddt, AWD3ddt, and AWD3det. Black dots depict the total ejecta masses. The colored symbols are (from top to bottom): iron-group elements (IGE), 56Ni and intermediate-mass elements (IME). |
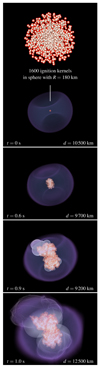 |
Fig. 4. Temporal evolution of the explosion for the AWD3ddt model. Top panel: ignition configuration (t = 0 s) with a zoom-in on the ignition kernels. Lower panels: evolution of the deflagration ash (pink) and the detonation front (light blue). The dark blue surface indicates the outer boundary of the star. d denotes the size of the computational domain. The decrease in d is due to our nested-grid approach (Röpke et al. 2006). |
4.3. The pure deflagration model AWD3def
In order to determine the observable outcome of the explosion of a rapidly rotating WD in the case that the DDT fails, we have calculated a pure deflagration version with AWD3 as the initial model. As in Pfannes et al. (2010b) the deflagration evolves preferentially along the rotation axis of the progenitor WD and leaves large fractions (∼50% of the mass) of the star unburned (cf., Fig. 5, bottom row). Compared to the other models of our sample, the energy release is relatively low and just surpasses the initial binding energy of the WD: Enuc = 1.31 × 1051 erg ≈ 1.2 |Ebind|. As discussed in detail for some of the models in Fink et al. (2014), also here significant amounts of the WD’s matter do not reach escape velocity and form a gravitationally-bound remnant object of 0.98 M⊙ after the explosion4. A cell on our numerical grid is considered as part of the remnant, if it has a negative value of the specific asymptotic kinetic energy, ϵkin,a = ϵgrav + ϵkin, at the end of the simulation. Here, ϵgrav and ϵkin are the specific gravitational and kinetic energies. The internal energy was found to be negligible for this calculation. As a result of the incomplete disruption of the star, a mere 0.353 M⊙ of 56Ni and 0.126 M⊙ of IMEs are ejected in the explosion. Remarkably, 12% of the synthesized IGEs and 9% of IMEs become part of the bound remnant. We do not find that the remnant object receives any significant kick from the explosion ejecta.
4.4. The distribution of the nucleosynthesis products in velocity space
An overview of the integrated nucleosynthetic yields of our models is given in Fig. 3 and in Table 2. In this section, we describe the details of the yield distribution in asymptotic velocity space, which is also crucial for the predictions of observables from the models described in Sect. 5.
In Fig. 5 we show in velocity space two-dimensional slices through the final abundance and density structures of the ejecta of all models (for model AWD3def, asymptotic velocities are used and thus the bound remnant is excluded). The abundance distributions were determined by mapping the final post-processing results (see Sect. 3.2) on a 2003 Cartesian grid.
Model AWD3det shows a layered abundance pattern typical for pure CO detonations. The box-shaped distribution of 56Ni and other IGEs stem from the break out of the detonation shock waves in polar direction, which occurs significantly before all material in the equatorial plane is burned (cf. Steinmetz et al. 1992).
The complex abundance patterns of model AWD3def are very similar to the pure deflagrations published by Fink et al. (2014) for non-rotating progenitor WDs. The asymmetric bipolar structure of the deflagration (visible also in the deflagration phase of the corresponding DDT model AWD3ddt in Fig. 4) is evolving to a much more symmetric structure in the free streaming phase, as the hot ashes near both poles expand significantly in all directions, while the unburned material close to the equatorial plane expands much less (this is also reflected in the high density regions close to the equatorial plane).
The delayed detonation models show complex abundance patterns from the deflagration phase in the inner regions that are surrounded by layered structures of the detonation phase in the outer parts. The deflagration ashes have a different shape compared to the pure deflagration model: they extend to higher velocities in both the z- and the −z-direction and they do not extend as far into the regions close to the equatorial plane. These structures are caused by the detonation shock waves emerging from both poles, which collide near the equatorial plane at t ∼ 1.0 s. The wave emerging from the north pole then propagates through the ashes of the large southern plume of deflagration ashes and vice versa. In this way these ashes are further accelerated in the polar direction and reach higher maximum velocities than in pure deflagration models. The former detonation shocks are still visible in the final density structures at the upper and lower edges and are the reason for the oblate shape of the outer ejecta. Asymmetric detonation initiation (away from the rotational axis) in the DDT models is the reason why these oblate structures can be tilted with respect to the equatorial plane.
Models that involve a detonation phase have significantly higher maximum ejecta velocities (∼30 000 km s−1) than the pure deflagration model (∼10 000 km s−1). This is a direct consequence of the huge explosion energies of these models, which is large compared to the initial binding energy, and consistent with results obtained for non-rotating models (see Seitenzahl et al. 2013; Seitenzahl et al. 2014).
The central high density parts of the ejecta show a prolate asymmetry in all models (also AWD3det and AWD3def). This is caused by stronger expansion toward the poles in the early explosion phases before homologous expansion is reached. For models that start with a deflagration, the asymmetric flame propagation that also causes an asymmetric expansion has already been discussed in Sect. 4.2. Another reason for stronger expansion toward the poles that applies to all models is the significantly earlier breakout of the burned matter in this direction due to the much lower polar radius of all of our progenitor WD models. This asymmetric expansion also causes a slightly asymmetric distribution of the nucleosynthetic yields in final velocity space. The velocities of the IMEs and the outer edges of the IGE-rich inner parts tend to be slightly higher along the direction of the rotational axis. The impact of these asymmetries on the observable outcomes is, however, only moderate (see Sect. 5).
 |
Fig. 5. Abundance distributions and densities of the ejecta of all models (top to bottom) at t = 100 s. Shown are slices through the x–z-plane in velocity space for 56Ni, 54Fe + 56Fe + 58Ni, 28Si, 16O, 12C and log10ρ (from left to right). |
5. Synthetic observables
We have calculated synthetic observables for all explosion models presented in Sect. 4 with our Monte Carlo radiative transfer code ARTIS as described in Sect. 3.3. The resulting lightcurves and spectra are shown in Figs. 6 and 7. For comparison, we also show observational data of normal and superluminous SNe Ia.
From the bolometric lightcurves shown in the top-left panel of Fig. 6, we conclude that our delayed and prompt detonation models are brighter than normal SNe Ia, but (at all times shown) they are still not bright enough to explain the most luminous observed SNe Ia such as SN 2009dc. This is not too surprising since none of our models reaches a 56Ni mass of 1.6 M⊙, as suggested for SN 2009dc by, for example, abundance-tomography studies of Hachinger et al. (2012). We also find that the bolometric lightcurves of these models evolve significantly faster than observed lightcurves of superluminous SNe Ia, in particular during the rise.
A similar behavior is observed for band-limited lightcurves. For example, we show B-, V- and I-band lightcurves in the other panels of Fig. 6. In particular the B-band lightcurves show a too fast past-maximum decline, but also the V-band evolution of the models is significantly faster than observed in superluminous SNe Ia. This is a result of the high ejecta velocities which, in turn, are inconsistent with observations.
Also in their synthetic spectra around maximum brightness (Fig. 7) our delayed and pure detonation models disagree with observations of superluminous SNe Ia. Most importantly, the Si II Å feature shows a significantly too large blueshift compared to observations. This is the result of the large Si velocities of all of our models discussed in Sect. 4.4. A second failure of all delayed detonation (as well as the prompt detonation) models are the missing C II 6580 Å and 7234 Å lines which are very prominent and persist up to two weeks past maximum in superluminous SNe Ia (Silverman et al. 2011; Taubenberger et al. 2011; Chakradhari et al. 2014; Parrent et al. 2016) but are not seen in our synthetic spectra. This was to be expected since the models have very little unburned material in their ejecta. Finally, the model spectra show a significant lack of flux at wavelengths shorter than 4000 Å compared to superluminous SNe Ia as, for example, SN 2009dc. This is also reflected in the B-band lightcurves in Fig. 6, where the models are systematically fainter than SN 2009dc at all epochs. This indicates too much line blanketing by IGEs in the model ejecta.
Owing to its significantly lower 56Ni mass, the pure deflagration model AWD3def is not a candidate for superluminous SNe Ia. With a bolometric peak magnitude of ∼ − 18.3 it is more than a magnitude dimmer than the delayed and pure detonation models (see Fig. 6). In fact, its bolometric peak is even fainter than that of normal SNe Ia. This is also reflected in the band-limited lightcurves, where in particular V-band and bluer lightcurves show a flux deficit compared to normal SNe Ia. The peak magnitudes in the redder bands approach those of normal SNe Ia, but the singly-peaked lightcurves of the AWD3def model do not match the observed double-peak structure in the NIR lightcurves of normal SNe Ia (see for example the I-band lightcurve in Fig. 6). Synthetic spectra of model AWD3def around maximum brightness are shown in Fig. 7. They show similar features as the spectra of previously published pure deflagration models for non-rotating progenitor WDs (see e.g. Fink et al. 2014; Kromer et al. 2015). In particular at early epochs the model spectra lack the strong features of IMEs like Si, S or Ca, which are characteristic for normal SNe Ia. Instead, the spectra resemble those of Type Iax SNe as found for deflagrations in non-rotating WDs (Kromer et al. 2013).
Despite some apparent ejecta asymmetries seen in Fig. 5 the synthetic lightcurves of all our models show generally a very moderate viewing-angle dependence (see Fig. 8), which has the tendency to decrease with time. This reflects the fact that the density structures of the models are on large-scales fairly symmetric. The strongest deviations from spherical symmetry in the density structure are present in the outer layers, which are most important at early times. In the innermost regions the ejecta show prominent asymmetries in their chemical composition. These deeper layers are not yet visible at the epochs studied here, since the ejecta are still largely optically thick. However, at later epochs, when the ejecta become optically thin, the compositional asymmetries could give rise to characteristic emission features in nebular spectra.
 |
Fig. 6. Angle-averaged synthetic lightcurves of our models, compared with the superluminous SN Ia SN 2009dc (dark gray squares) and “normal” SNe Ia SN 2005cf (gray dots), SN 2004eo (gray triangles), and SN 2003du (gray inverted triangles). |
 |
Fig. 7. Angle-averaged synthetic spectra shortly before (upper panel) and after B-band maximum (lower panel). The spectra of a normal (SN 2005cf) and a superluminous (SN 2009dc) SN Ia are shown in gray and dark gray, respectively. |
 |
Fig. 8. Bolometric and broadband lightcurves of all models for 100 different viewing angles. The magnitudes are shifted as indicated. The time is given relative to B-band maximum. As can be seen, the line-of-sight effects are small for all models. |
6. Discussion
6.1. A self-consistent detonation scheme
As mentioned already in Sect. 3.1, the main improvement of the present numerical scheme for modeling detonations over that used by Pfannes et al. (2010a) is an energy release consistent with the large post-processing nuclear network. The new scheme ensures that the detonation speed, the energy release, and the nucleosynthesis are consistent with each other. As a consequence, Pfannes et al. 2010a assumed significantly higher transition densities between the main burning stages than those that result from our self-consistent treatment (compare, e.g., the dotted and solid contours in Fig. 2). For the prompt detonation of the AWD3 rotator this results in a significantly lower total energy release Enuc of 2.65 × 1051 erg in Pfannes et al. (2010a) as compared to our value of 3.11 × 1051 erg, and a significantly lower IGE mass of 1.75 M⊙ from the post-processing as compared to our value of 1.92 M⊙.
Another major difference between our work and that of Pfannes et al. (2010a) concerns the velocity distribution of the chemical elements synthesized in the explosion. Firstly, the higher NSE transition density there naturally leads to a decrease of the velocity at the interface between IGEs and IMEs. Secondly, Pfannes et al. calculate the final abundance profile in velocity space with their reduced set of species, that is, with those used in their hydrodynamic simulations and not those from the post-processing step (corresponding to MIGE = 1.41 M⊙ – referred to as “high burning threshold” or HBT in their paper). This results in a further shift of IGEs to IMEs toward even lower velocities. Thus, in their Fig. 5b the abundances are inconsistent with their detonation speeds and the energy release. In contrast to their simulations, our model AWD3det has a maximum in the angle-averaged silicon mass distribution at around 20 000 km s−1 (see Fig. 9), whereas Pfannes et al. (2010a) find much lower values of about 10 000 km s−1 only.
We argue that our results are more realistic. Pfannes et al. (2010a) state that shear acting on the detonation front combined with the cellular instability may shift the NSE burning threshold toward higher densities and use the NSE transition densities for deflagrations (ρNSE ∼ 5 × 107 g cm−3) as plausible upper cutoff. But, there are also effects acting in the opposite direction (i.e. shifting ρNSE to lower densities) such as shock steepening in the density gradients of the WD star. Thus, in this work we use the detonation prescription from Fink et al. (2010) instead, which resembles the planar detonation case. With our improved modeling of burning in the detonation mode, we find brighter pure detonation explosions than Pfannes et al. (2010a).
6.2. Predicted observables and comparison with data
As far as their lightcurves and spectra are concerned, our rapidly rotating delayed-detonation models are not too different from the prompt detonations. They produce similar nickel masses, and also the silicon expansion velocities, as seen in the blueshifts of the Si line features in the spectra, are rather similar. This can be understood as follows. Since in our rapidly rotating delayed-detonation models the asymmetric deflagration leaves behind major parts of the WDs unburned before the DDT occurs, the explosions are always dominated by the (short) detonation phase. Therefore, compared to prompt detonation models, only slightly more IMEs are produced (due to the pre-expansion phase before the detonation sets in). Consequently, the velocity of the ejected IME material is very high as in the pure detonation case. Thus, we find both prompt- and delayed-detonation models of rapidly differentially-rotating super-MCh WDs to be incompatible with observed properties of superluminous SNe Ia. The models are not bright enough, their lightcurves decline too fast in all wavebands, and our synthetic spectra show blueshifts of the Si II 6355 Å absorption line feature that are far too high. High enough 56Ni masses and low velocities of the Si-rich ejecta cannot be realized at the same time in this kind of models. In addition, our models do not show the strong C features observed in superluminous SNe Ia, since the detonation leaves practically no unburned C in the ejecta.
This conclusion is not sensitive to the (very uncertain) DDT criterion we have used. In fact, even the prompt detonation model does not burn significantly more material than the delayed detonations. Due to the asymmetric propagation of the deflagration front and the quick expansion in polar direction, the DDT will always occur close to the poles and at a similar time after the start of the deflagration, no matter what the transition criterion is.
With a 56Ni yield of 0.353 M⊙ in the ejecta, the pure deflagration model AWD3def is much fainter than the models involving a detonation and clearly not a candidate for superluminous SNe Ia. The main purpose for including this model in the present study was to check the evolution of the thermonuclear burning if the DDT fails. Nevertheless, it is interesting to look at the synthetic observables of this model and discuss whether they may match any of the observed peculiar SNe Ia or other transients. Given that the synthetic spectra of AWD3def resemble those of the pure deflagrations in non-rotating WDs, which were found to agree fairly well with Type Iax SNe (Kromer et al. 2013; Fink et al. 2014), a potential connection to Type Iax SNe seems to be the obvious assumption. A detailed comparison to the observed sample of SNe Iax is beyond the scope of this paper, but it is interesting to point out that rotation of the progenitor stars seems to extend the possible outcomes of the pure deflagration scenario. For example, our model AWD3def yields a 56Ni mass that is very similar to the 56Ni yield of the non-rotating model N100def of (Fink et al. 2014), while the total ejecta masses differ by about 30 percent (1.02 and 1.31 M⊙, respectively). This may help in explaining some of the brighter members of the SN Iax class (e.g. Magee et al. 2016; Barna et al. 2017).
 |
Fig. 9. Angle-averaged velocity distribution of select nuclei in the ejecta of model AWD3det. The velocity bin size dv is 400 km s−1. |
7. Conclusions
The influence of rapid differential rotation of the progenitor WD on the delayed-detonation scenario has been investigated. To this end, full-star hydrodynamic explosion simulations have been carried out in three dimensions using three initial rotators that cover the expected range of rotational energies. A multispot ignition scenario was chosen for the deflagration ignition and the DDT parametrization is based on a critical Karlovitz number of 250. We simulated the flame evolution with the combustion-hydrodynamics code LEAFS and obtained detailed nucleosynthesis yields and synthetic observables in post-processing steps.
In the delayed-detonation models the deflagration quickly spreads toward the poles, before it can significantly propagate in equatorial direction. Thus, the DDT is always found to occur close to the poles (in multiple spots) and when large fractions of the star are still unburned. The pre-expansion of the remaining fuel caused by the deflagration is also found to be relatively limited. Therefore, in all models the detonation phase dominates the burning. Consequently, bright explosions ensue (M56Ni > 1 M⊙) that could be potential candidates for superluminous SNe Ia. However, the velocities of IMEs are significantly too high as compared to the low line velocities seen in early-time spectra of observed superluminous SNe Ia. Moreover, our synthetic spectra do not show the characteristic carbon lines observed in superluminous SNe Ia. We thus conclude that the delayed-detonation scenario of rapidly rotating WDs is incompatible with any of the observed SNe Ia. Despite the anisotropic flame evolution the final ejecta are on large scales close to spherical and consequently observables do not show strong viewing-angle sensitivity.
These results are robust with respect to several uncertainties that are still present in the models: (i) details of the rotation laws will not allow for much change in the explosion outcomes. Within our series of models that covers a broad range of rotational energies, the predicted spectral signatures are very similar; (ii) as the chosen ignition conditions produce a strong deflagration phase in non-rotating models, fewer ignition spots and, thus, weaker deflagrations would lead to even stronger detonations; (iii) the DDT criterion is still uncertain. However, in the models the dominant effect is the anisotropy of the deflagration. The flame will always reach the low density edge of the WD in polar directions first and the DDT has to occur close to the poles. Due to the very slow propagation of the deflagration in the equatorial plane, a somewhat later DDT will not cause much more pre-expansion of unburned fuel there.
In agreement with Pfannes et al. (2010a) we found that the problem of ejecta velocities being too high is even more severe in the case of prompt detonations. This was demonstrated in one pure detonation simulation (the AWD3 rotator) similar to one of the models of Pfannes et al. (2010a). There were some differences, though. Due to the significantly lower NSE transition density of our improved detonation scheme, much higher ejecta velocities and less IMEs than in Pfannes et al. (2010a) were found. As the delayed detonations showed too high IME velocities for the whole series of initial rotators, the same trend will also hold for the corresponding prompt detonation models. Thus, both, prompt detonations and the delayed detonations of rapidly-rotating massive progenitors cannot explain the superluminous SNe Ia. Moreover, their synthetic lightcurves and spectra do not resemble any other subclass of observed SNe Ia.
We also investigated the case of a pure deflagration for the AWD3 rotator. Owing to the rapid rotation, turbulence is suppressed perpendicular to the rotation axis, leading to an asymmetric evolution of the deflagration flame and a low release of nuclear energy. Consequently, the deflagration fails to fully unbind the progenitor WD, even for our vigorous ignition scenario. Specifically, we obtain an ejecta mass of 1.02 M⊙ (of which 0.353 M⊙ are 56Ni), while 0.980 M⊙ remain bound. The ejecta structure and synthetic observables resemble those of SNe Iax.
In summary, our results can be interpreted in two ways. The first possibility is that no detonations occur in differentially rotating super-Chandrasekhar mass WDs. In this case, deflagrations of differentially rotating super-Chandrasekhar mass WDs could contribute to the population of SNe Iax. As an alternative explanation, differentially rotating super-Chandrasekhar mass WDs may simply not exist in nature. If, for instance, a mechanism would exist which forces the WD into rigid rotation while accreting, other than those modeled in the work of Yoon & Langer (2004), the maximum mass allowed would be close to the canonical Chandrasekhar value. In fact, magnetic fields may provide such a transport mechanism as was discussed by Spruit (1999); Spruit (2004) and more recently investigated by means of numerical simulations by Wei & Goodman (2015). In principle, the argument is simple. If the WD has a poloidal magnetic field Bp, differential rotation will wind-up this field and will generate a toroidal component BΦ, increasing linearly with time until the restoring force (∝BpBΦ) stops this process and reverts it. These oscillations are damped by phase mixing (Spruit 1999) and eventually will lead to rigid rotation. However, whether or not typical magnetic fields inside the progenitors of SNe Ia are sufficiently high that the damping time is short compared with the accretion time has to be seen. Clearly, field strengths as found in polars (> 107 G) would suffice (Spruit 1999; Spruit 2004).
There are slight differences in the initial models of this study with respect to those in Pfannes et al. (2010b) due to minor differences in the equation of state used here.
The DDT criterion employed here corresponds to that used by Kasen et al. (2009) whereas the more elaborate criterion of Ciaraldi-Schoolmann et al. (2013) was used in the study of Seitenzahl et al. (2013).
In model N1600Cdef of Fink et al. (2014) the progenitor star is less tightly bound. Therefore, the deflagration fully unbinds the progenitor WD and Enuc/|Ebind|≈2.1. In our model AWD3def, the deflagration fails to unbind the WD although we use the same vigorous ignition configuration as in N1600Cdef.
Acknowledgments
We gratefully acknowledge the Gauss Centre for Supercomputing (GCS) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS share of the supercomputer JUQUEEN (Stephan & Docter 2015) at Jülich Supercomputing Centre (JSC). GCS is the alliance of the three national supercomputing centres HLRS (Universität Stuttgart), JSC (Forschungszentrum Jülich), and LRZ (Bayerische Akademie der Wissenschaften), funded by the German Federal Ministry of Education and Research (BMBF) and the German State Ministries for Research of Baden-Württemberg (MWK), Bayern (StMWFK) and Nordrhein-Westfalen (MIWF). MK, FR and RP acknowledge support from the Klaus Tschira Foundation. The research of FR was supported by the German Research Foundation (DFG) via the Collaborative Research Center SFB 881 “The Milky Way System”. RP acknowledges support by the European Research Council under ERC-StG grant EXAGAL-308037. IRS was supported by the Australian Research Council Grant FT160100028. SAS acknowledges support from STFC through grant, ST/P000312/1. This work was supported by the Deutsche Forschungsgemeinschaft via the Transregional Collaborative Research Center TRR 33 “The Dark Universe” and by the DAAD/Go8 German-Australian exchange program.
References
- Barna, B., Szalai, T., Kromer, M., et al. 2017, MNRAS, 471, 4865 [NASA ADS] [CrossRef] [Google Scholar]
- Chakradhari, N. K., Sahu, D. K., Srivastav, S., & Anupama, G. C. 2014, MNRAS, 443, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Ciaraldi-Schoolmann, F., Seitenzahl, I. R., & Röpke, F. K. 2013, A&A, 559, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durisen, R. H. 1975, ApJ, 199, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Eriguchi, Y., & Müller, E. 1985, A&A, 146, 260 [NASA ADS] [Google Scholar]
- Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fink, M., Kromer, M., Seitenzahl, I. R., et al. 2014, MNRAS, 438, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Gall, E. E. E., Taubenberger, S., Kromer, M., et al. 2012, MNRAS, 427, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Gamezo, V. N., Wheeler, J. C., Khokhlov, A. M., & Oran, E. S. 1999, ApJ, 512, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Golombek, I., & Niemeyer, J. C. 2005, A&A, 438, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachinger, S., Mazzali, P. A., Taubenberger, S., et al. 2012, MNRAS, 427, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Garnavich, P. M., Prieto, J. L., et al. 2007, ApJ, 669, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., Sim, S. A., & Röpke, F. K. 2007, A&A, 465, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höflich, P., & Khokhlov, A. 1996, ApJ, 457, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Nugent, P. E., et al. 2006, Nature, 443, 308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., & Sim, S. A. 2009, MNRAS, 398, 1809 [Google Scholar]
- Kromer, M., Sim, S. A., Fink, M., et al. 2010, ApJ, 719, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Fink, M., Stanishev, V., et al. 2013, MNRAS, 429, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Ohlmann, S. T., Pakmor, R., et al. 2015, MNRAS, 450, 3045 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhlen, M., Woosley, S. E., & Glatzmaier, G. A. 2006, ApJ, 640, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Maeda, K., Kawabata, K., Li, W., et al. 2009, ApJ, 690, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Magee, M. R., Kotak, R., Sim, S. A., et al. 2016, A&A, 589, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niemeyer, J. C., & Woosley, S. E. 1997, ApJ, 475, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Niemeyer, J. C., Hillebrandt, W., & Woosley, S. E. 1996, ApJ, 471, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Noebauer, U. M., Taubenberger, S., Blinnikov, S., Sorokina, E., & Hillebrandt, W. 2016, MNRAS, 463, 2972 [NASA ADS] [CrossRef] [Google Scholar]
- Nonaka, A., Aspden, A. J., Zingale, M., et al. 2012, ApJ, 745, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Parrent, J. T., Howell, D. A., Fesen, R. A., et al. 2016, MNRAS, 457, 3702 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, N. 2000, Turbulent Combustion (Cambridge: Cambridge University Press) [Google Scholar]
- Pfannes, J. M. M. 2006, PhD Thesis, Universität Würzburg [Google Scholar]
- Pfannes, J. M. M., Niemeyer, J. C., & Schmidt, W. 2010a, A&A, 509, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfannes, J. M. M., Niemeyer, J. C., Schmidt, W., & Klingenberg, C. 2010b, A&A, 509, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piro, A. L., & Chang, P. 2008, ApJ, 678, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes: The Art of Scientific Computing, ((Cambridge, UK: Cambridge University Press), 3 [Google Scholar]
- Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reinecke, M., Hillebrandt, W., Niemeyer, J. C., Klein, R., & Gröbl, A. 1999, A&A, 347, 724 [NASA ADS] [Google Scholar]
- Reinecke, M., Hillebrandt, W., & Niemeyer, J. C. 2002a, A&A, 386, 936 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reinecke, M., Hillebrandt, W., & Niemeyer, J. C. 2002b, A&A, 391, 1167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röpke, F. K. 2005, A&A, 432, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röpke, F. K. 2007, ApJ, 668, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., & Niemeyer, J. C. 2007, A&A, 464, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röpke, F. K., Hillebrandt, W., Niemeyer, J. C., & Woosley, S. E. 2006, A&A, 448, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röpke, F. K., Hillebrandt, W., Schmidt, W., et al. 2007, ApJ, 668, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., Niemeyer, J. C., & Hillebrandt, W. 2006a, A&A, 450, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., Niemeyer, J. C., Hillebrandt, W., & Röpke, F. K. 2006b, A&A, 450, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seitenzahl, I. R., Meakin, C. A., Townsley, D. M., Lamb, D. Q., & Truran, J. W. 2009a, ApJ, 696, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Townsley, D. M., Peng, F., & Truran, J. W. 2009b, At. Data Nucl. Data Tables, 95, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013, MNRAS, 429, 1156 [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2014, MNRAS, 444, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Sharpe, G. J. 1999, MNRAS, 310, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., Ganeshalingam, M., Li, W., et al. 2011, MNRAS, 410, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A. 2007, MNRAS, 375, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2004. in IAU Symp., 215, 356 [NASA ADS] [Google Scholar]
- Steinmetz, M., Müller, E., & Hillebrandt, W. 1992, A&A, 254, 177 [NASA ADS] [Google Scholar]
- Stephan, M., & Docter, J. 2015, J. Large-scale Res. Facil., 1, A1 [Google Scholar]
- Tanaka, M., Kawabata, K. S., Yamanaka, M., et al. 2010, ApJ, 714, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S. 2017, in Handbook of Supernovae, eds. A. Alsabti, & P. Murdin (New-York, NY: Springer), 317 [Google Scholar]
- Taubenberger, S., Benetti, S., Childress, M., et al. 2011, MNRAS, 412, 2735 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Kromer, M., Hachinger, S., et al. 2013, MNRAS, 432, 3117 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Hillebrandt, W., Reinecke, M., & Thielemann, F.-K. 2004, A&A, 425, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wei, X., & Goodman, J. 2015, ApJ, 806, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 2007, ApJ, 668, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Kerstein, A. R., Sankaran, V., Aspden, A. J., & Röpke, F. K. 2009, ApJ, 704, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Yamanaka, M., Kawabata, K. S., Kinugasa, K., et al. 2009, ApJ, 707, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zel’dovich, Y. B., Librovich, V. B., Makhviladze, G. M., & Sivashinskii, G. I. 1970, J. Appl. Mech. Tech. Phys., 11, 264 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Initial temperature profile of the models as a function of density. The steep increase at high density is due to hydrostatic carbon burning and the local maximum at ρ ≃ 106 g cm−3 is caused by accretion-induced heating. |
| In the text | |
 |
Fig. 2. Initial rotation laws and density distributions of all our rapidly rotating progenitor models. The lower three panels display cross-sections of the WDs with the rotational axis in z-direction. The density is color coded. Solid contours mark density levels of ρ = 105 and 107 g cm−3, corresponding to the transition densities between the main burning stages (producing iron group and intermediate mass elements, respectively, or ceasing burning) in our detonation yield tables. For comparison, the dotted contours at ρ = 1.047 × 107 and 5.248 × 107 g cm−3 show the transition densities assumed in the earlier study by Pfannes et al. (2010a). |
| In the text | |
 |
Fig. 3. Integrated nucleosynthetic yields of all explosion models. The models are (from left to right): AWD3def, AWD1ddt, AWD4ddt, AWD3ddt, and AWD3det. Black dots depict the total ejecta masses. The colored symbols are (from top to bottom): iron-group elements (IGE), 56Ni and intermediate-mass elements (IME). |
| In the text | |
 |
Fig. 4. Temporal evolution of the explosion for the AWD3ddt model. Top panel: ignition configuration (t = 0 s) with a zoom-in on the ignition kernels. Lower panels: evolution of the deflagration ash (pink) and the detonation front (light blue). The dark blue surface indicates the outer boundary of the star. d denotes the size of the computational domain. The decrease in d is due to our nested-grid approach (Röpke et al. 2006). |
| In the text | |
 |
Fig. 5. Abundance distributions and densities of the ejecta of all models (top to bottom) at t = 100 s. Shown are slices through the x–z-plane in velocity space for 56Ni, 54Fe + 56Fe + 58Ni, 28Si, 16O, 12C and log10ρ (from left to right). |
| In the text | |
 |
Fig. 6. Angle-averaged synthetic lightcurves of our models, compared with the superluminous SN Ia SN 2009dc (dark gray squares) and “normal” SNe Ia SN 2005cf (gray dots), SN 2004eo (gray triangles), and SN 2003du (gray inverted triangles). |
| In the text | |
 |
Fig. 7. Angle-averaged synthetic spectra shortly before (upper panel) and after B-band maximum (lower panel). The spectra of a normal (SN 2005cf) and a superluminous (SN 2009dc) SN Ia are shown in gray and dark gray, respectively. |
| In the text | |
 |
Fig. 8. Bolometric and broadband lightcurves of all models for 100 different viewing angles. The magnitudes are shifted as indicated. The time is given relative to B-band maximum. As can be seen, the line-of-sight effects are small for all models. |
| In the text | |
 |
Fig. 9. Angle-averaged velocity distribution of select nuclei in the ejecta of model AWD3det. The velocity bin size dv is 400 km s−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.