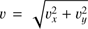| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833362 | |
| Published online | 08 November 2018 | |
Solar flares and Kelvin-Helmholtz instabilities: A parameter survey⋆
1 Centre for Mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: wenzhi.ruan@kuleuven.be
2 School of Physics and Astronomy, Yunnan University, Kunming, 650050 PR China
e-mail: chun.xia@ynu.edu.cn
Received:
4
May
2018
Accepted:
5
July
2018
Context. Hard X-ray (HXR) sources are frequently observed near the top of solar flare loops, which are also bright in soft X-ray (SXR) and extreme ultraviolet (EUV) wavebands. We revisit a recent scenario proposed by Fang et al. (2016) to trigger loop-top turbulence in flaring loops, which can help explain variations seen in SXR and EUV brightenings and potentially impact and induce HXR emission. It is conjectured that evaporation flows from flare-impacted chromospheric footpoints interact with each other near the loop top and produce turbulence via the Kelvin–Helmholtz instability (KHI).
Aims. By performing a rigorous parameter survey, in which we vary the duration, total amount, and asymmetry of the energy deposition at both footpoints, we assess the relevance of the KHI in triggering and sustaining loop-top turbulence. We synthesize SXR and EUV emission and discuss the possibility of HXR emission through bremsstrahlung or inverse Compton processes, which scatter SXR photons to HXR photons via the inverse Compton mechanism.
Methods. We performed 2.5D numerical simulations in which the magnetohydrodynamic model incorporates a realistic photosphere to coronal stratification, parametrized heating, radiative losses, and field-aligned anisotropic thermal conduction. We focus on the trigger of the KHI and the resulting turbulence, as well as identify various oscillatory patterns that appear in the evolutions.
Results. We find that a M2.2-class related amount of energy should be deposited in less than four minutes to trigger a KHI interaction. Slower deposition, or lesser energy (< 0.33 × 1029 ergs) rather leads to mere loop-top compression sites bounded by shocks, without KHI development. Asymmetry in the footpoint deposition determines whether the KHI turbulent zone gets produced away from the apex, and asymmetric cases can show a slow-mode mediated, periodic displacement of the turbulent zone. Our reference simulation further demonstrates a clear 25 s periodicity in the declining phase of the SXR light curve, wherein compressional effects dominate.
Conclusions. When turbulence is produced in the loop apex, an index of −5/3 can be found in the spectra of velocity and magnetic field fluctuations. Typical values for M-class flares routinely show KHI development. The synthesized SXR light curve shows a clear periodic signal related to the sloshing motion of the vortex pattern created by the KHI.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: flares / Sun: X-rays, gamma rays
The movies are available at https://www.aanda.org
© ESO 2018
1. Introduction
Hard X-ray (HXR) emission in solar flares has been studied for decades. In most flares HXR emission is dominated by footpoint sources, but more and more observed flares show a more complex evolution (Krucker et al. 2008). In addition to the footpoint sources, a loop-top source is reported in several flare observations (e.g. Masuda et al. 1994; Krucker et al. 2007; Su et al. 2013). The mechanism of HXR sources is widely believed to be non-thermal thick target bremsstrahlung. According to the CSHKP flare model, part of the energy released by magnetic reconnection above the flare loop is used to accelerate particles (Carmichael 1964; Sturrock 1966; Hirayama 1974; Kopp & Pneuman 1976). These accelerated electrons are guided by the magnetic field, and move from loop top to footpoints along the flare loops. Footpoint sources are generated when these energetic electrons collide with ambient ions in chromospheric footpoints and produce X-ray photons via bremsstrahlung.
Unlike foot-point sources, the loop-top source is usually not considered as a thick target. A coronal loop with a length of 109 cm and a number density of 1010 cm−3 is collisionally thin to electrons above 8 keV (Krucker et al. 2008), hence it seems difficult for the loop to stop energetic electrons with an energy of several ten keV efficiently enough to produce a loop-top HXR source. However, the efficiency of HXR photon generation increases rapidly when loop apex turbulence is taken into account. Turbulence is suggested to be an efficient trap for high energy electrons in the apex of flare loops (Fang et al. 2016). If turbulence exists in the apex, energetic electrons can effectively travel a much longer path before they leave the apex and the probability that the electrons collide or interact with ambient ions is effectively increased. Furthermore, more high energy electrons can participate in the bremsstrahlung to increase the intensity of loop-top HXR emission if the turbulence works as an efficient particle trap and accelerator. The efficiency of inverse Compton scattering (ICS) is improved by turbulence as well, since the probability that the electrons interact with soft X-ray (SXR) photons is also increased. Early on ICS was suggested, in addition to bremsstrahlung (Korchak 1967), as an alternative mechanism for HXR emission. The role of ICS can be more important than that of bremsstrahlung in HXR emission under special conditions, such as low plasma density, a hard spectrum of energetic electrons, and an anisotropic distribution of electrons (Korchak 1971; Chen & Bastian 2012). Kontar et al. (2014) suggested the spectrum of loop-top electrons to be harder than expected in studying electron transport in flare loops, and they suggested transport is affected by turbulent pitch-angle scattering. A hard loop-top electron spectrum can imply that ICS may play an important role in the HXR emission in the loop top.
The existence of turbulence in the apex of flare loops has been proved by multiple observations (e.g. Antonucci et al. 1982; Kontar et al. 2017). However, the origin of this turbulence needs further study. Fang et al. (2016) proposed a new probable turbulence source to interpret the generation of loop-top HXR emission. This new scenario suggests that Kelvin–Helmholtz instabilities (KHI) play an important role in the generation of turbulence in the apex. According to the CSHKP flare model, high speed evaporation flows are driven when high energy electrons deposit their energy into the chromospheric footpoints. The new scenario suggests that turbulence is produced via KHI when the flows go into the loop apex and interact with each other. High speed evaporation flows with a speed of 200−500 km, s −1 are frequently reported (Feldman et al. 1980; Antonucci et al. 1982; Shimizu et al. 1994; Milligan & Dennis 2009; Nitta et al. 2012; Tian et al. 2014, 2015). Nitta et al. (2012) investigated 13 flare events, 3 of which were found to have high speed flows with a velocity about 500 km s −1. Evaporating upflows with speeds higher than 500 km s−1 seem relatively rare and only a few cases are reported (e.g. Bentley et al. 1994; Tomczak 1997; Liu et al. 2006). While the evaporation flows have a speed of several hundred kilometers per second, the speed of the flows is likely comparable to the local Alfvén speed. Therefore, it is reasonable to consider the contribution of KHI. Fang et al. (2016) proved that KHI can be triggered and turbulence can be produced in the apex of flare loops. In their observational study, Antonucci et al. (1982) also found a link between high speed evaporation flows and turbulence. The turbulence in hot plasma increases and can reach a maximum turbulent velocity of 122 km s−1 when a high speed upflow with a speed of 300−400 km s−1 has been observed, while the mean turbulent velocities is of the order of 75 km s−1 in the preflare active region. We suggest that this increase of turbulent velocity is likely caused by KHI.
When the energetic particles deposit their energy into chromospheric footpoints, the energy is unlikely to be equally distributed to two footpoints. Aschwanden et al. (1999) found that the HXR emissions of two footpoints tend to be asymmetric in their survey, which indicates the asymmetry of energy deposition. The asymmetry of energy deposition is suggested to be determined by the asymmetry of the magnetic field. Figures 1–4 in Krucker et al. (2008) also indicate a result of asymmetric energy deposition, in which one footpoint is closer to the loop-top HXR or SXR sources than the other. The asymmetry of energy deposition may influence the parameters of evaporation flows and the evolution of the flare loop. In our numerical study of KHI triggering, asymmetric energy deposition strategies are adopted to make our simulations comparable with the observations.
We aim to continue the study of Fang et al. (2016) on the trigger of KHI and the generation of turbulence in flare loops. The set-up of our simulation is introduced in Sect. 2. Energy is deposited into chromospheric footpoints of a coronal loop that drives evaporation flows. The interaction of the flows, trigger of KHI, and generation of turbulence are investigated in Sect. 3. The thermodynamics and radiative evolution of the flare loop and energy cascade process of turbulence are studied with a high spatial resolution case. In addition, EUV and SXR images of the flare loop are synthesized in this section, and then the role of bremstrahlung versus the inverse Compton process in the generation of loop-top HXR sources is investigated. A parameter survey is performed to investigate important factors that influence the trigger of KHI and the generation of turbulence in Sect. 4. We summarize our work in Sect. 5.
2. Numerical set-up
We numerically solved the magnetohydrodynamics (MHD) equations with the MPI-parallelized Adaptive Mesh Refinement Versatile Advection Code MPI-AMRVAC (Keppens et al. 2012; Porth et al. 2014; Xia et al. 2018). The governing equations are written as follows: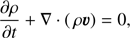 (1)
(1)
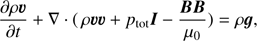 (2)
(2)
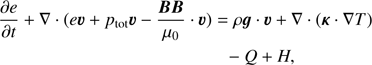 (3)
(3)
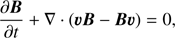 (4)where I is the unit tensor and k is the thermal conductivity tensor, and ρ, v, T, and B are density, velocity, temperature, and magnetic field, respectively. The total energy density is given by
(4)where I is the unit tensor and k is the thermal conductivity tensor, and ρ, v, T, and B are density, velocity, temperature, and magnetic field, respectively. The total energy density is given by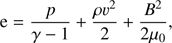 (5)and the total pressure is given by
(5)and the total pressure is given by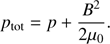 (6)
(6)
The terms Q and H in the energy Eq. (3) indicate optically thin radiative cooling and parametrized heating, respectively.
We solved the MHD equations on a Cartesian box with a domain of −40 Mm ≤ x ≤ 40 Mm and 0 Mm ≤ y ≤ 50 Mm, but vector quantities are 2.5D (i.e. they have three components). We adopted an abundance ratio of He/H = 0.1 in the calculations of density and pressure, where the plasma is assumed to be fully ionized. The gravitational acceleration is given by 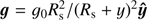 , where g0 = −274 m s−2 and Rs is the solar radius. The thermal conductivity tensor is expressed as κ = κ|| b̂b̂ where b̂ = B/B, which indicates that only thermal conduction along magnetic field lines was considered. The parallel thermal conductivity is given by κ
∥ = 8 × 10−7T5/2 erg cm−1 s−1K−7/2. We adopted a maximum heat flux
, where g0 = −274 m s−2 and Rs is the solar radius. The thermal conductivity tensor is expressed as κ = κ|| b̂b̂ where b̂ = B/B, which indicates that only thermal conduction along magnetic field lines was considered. The parallel thermal conductivity is given by κ
∥ = 8 × 10−7T5/2 erg cm−1 s−1K−7/2. We adopted a maximum heat flux 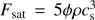 to include the saturation effect of thermal conduction (Cowie & McKee 1977), where ϕ = 1 and cs denotes the local acoustic speed. The radiative cooling function is expressed as
to include the saturation effect of thermal conduction (Cowie & McKee 1977), where ϕ = 1 and cs denotes the local acoustic speed. The radiative cooling function is expressed as 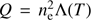 , where ne is the number density of electrons and Λ(T) is a cooling curve supplied by Colgan et al. (2008). This curve provides the radiative loss of hot and optically thin plasma; the emission from plasma with a temperature lower than 10 000 K was not considered.
, where ne is the number density of electrons and Λ(T) is a cooling curve supplied by Colgan et al. (2008). This curve provides the radiative loss of hot and optically thin plasma; the emission from plasma with a temperature lower than 10 000 K was not considered.
The initial conditions and boundary conditions are as follows. The lower boundary is located in the photosphere and the upper boundary is located in the corona. The initial distribution of temperature consists of two parts: the VAL-C temperature profile (Vernazza et al. 1981) is employed in the region between the lower boundary and htra = 2.543 Mm, and the temperature distribution in the region above htra can be written as![$$ \begin{aligned} T(y) = [3.5 F_{\rm c} (y - h_{\rm {tra}}) / \kappa + T_{\rm tra}^{7/2}]^{2/7}, \end{aligned} $$](/articles/aa/full_html/2018/10/aa33362-18/aa33362-18-eq10.gif) (7)
where Fc = 2 × 105 erg cm−2 s−1, κ = 8 × 10−7T5/2 erg cm−1 s−1 K−7/2, Ttra = 0.447 MK. There is a ghost zone below the lower boundary (y = 0) and the thickness of the ghost zone is 2 Mm. We obtained the temperature profile in the ghost zone from a linear extrapolation of the temperature profile above the lower boundary. The plasma density at the bottom of the ghost zone was set to be ne = 7.1 × 1014 cm−3. The initial plasma density in the ghost zone and the simulation region was derived from hydrostatic equilibrium ∂p/∂h = ρg. As a result, the number density at y = 0 is ne = 2.15 × 1014 cm−3. Each boundary contains two layer of ghost cells. For the left and right boundary, ρ, e, vy
, and By use a symmetric boundary, while vx, vz, Bx, and Bz employ an anti-symmetric boundary. For the upper and bottom boundaries, the velocity components also employ an anti-symmetric boundary. In the lower boundary ghost cells, ρ and e and B were fixed at their initial values. For ghost cells of the upper boundary, ρ and e were calculated according to the gravity stratification, where the value of temperature was obtained from extrapolation. The value B in the upper boundary was extrapolated assuming zero normal gradient. We imposed zero velocities at the bottom and upper boundary surface. We used the same boundary conditions for all of the simulations. We used adaptive mesh refinement to refine the mesh and increase the spatial resolution based on the spatial smoothness of density and magnetic field. The initial simulation box contains 128 × 80 cells in a domain of 80 Mm × 50 Mm, and the maximum refinement level is set to five or six. A high spatial resolution of 19.5 km is achieved inside and near the flare loop, which ensured that we could simulate the triggering of KHI and evolution of turbulence.
(7)
where Fc = 2 × 105 erg cm−2 s−1, κ = 8 × 10−7T5/2 erg cm−1 s−1 K−7/2, Ttra = 0.447 MK. There is a ghost zone below the lower boundary (y = 0) and the thickness of the ghost zone is 2 Mm. We obtained the temperature profile in the ghost zone from a linear extrapolation of the temperature profile above the lower boundary. The plasma density at the bottom of the ghost zone was set to be ne = 7.1 × 1014 cm−3. The initial plasma density in the ghost zone and the simulation region was derived from hydrostatic equilibrium ∂p/∂h = ρg. As a result, the number density at y = 0 is ne = 2.15 × 1014 cm−3. Each boundary contains two layer of ghost cells. For the left and right boundary, ρ, e, vy
, and By use a symmetric boundary, while vx, vz, Bx, and Bz employ an anti-symmetric boundary. For the upper and bottom boundaries, the velocity components also employ an anti-symmetric boundary. In the lower boundary ghost cells, ρ and e and B were fixed at their initial values. For ghost cells of the upper boundary, ρ and e were calculated according to the gravity stratification, where the value of temperature was obtained from extrapolation. The value B in the upper boundary was extrapolated assuming zero normal gradient. We imposed zero velocities at the bottom and upper boundary surface. We used the same boundary conditions for all of the simulations. We used adaptive mesh refinement to refine the mesh and increase the spatial resolution based on the spatial smoothness of density and magnetic field. The initial simulation box contains 128 × 80 cells in a domain of 80 Mm × 50 Mm, and the maximum refinement level is set to five or six. A high spatial resolution of 19.5 km is achieved inside and near the flare loop, which ensured that we could simulate the triggering of KHI and evolution of turbulence.
A background heating is employed to heat the corona, and is given by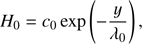 (8)where c0 = 10−4 erg cm−3 s−1 and λ0 = 80 Mm. We adopted a force-free magnetic arcade as an initial magnetic configuration,
(8)where c0 = 10−4 erg cm−3 s−1 and λ0 = 80 Mm. We adopted a force-free magnetic arcade as an initial magnetic configuration,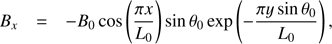 (9)
(9)
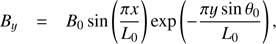 (10)
(10)
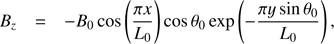 (11)where θ0 = 30∘ is the angle between the apex of the magnetic loops and the neutral line, L0 = 80 Mm is the horizontal size of the simulation box, and B0 = 80 G is the strength of magnetic field at the bottom. The resulting magnetic field strength at the loop apex is about 50 G. We performed relaxation with this initial condition and background heating to obtain a stable plasma environment during which the precise thermodynamic balance gets adjusted. When the relaxation is finished, the maximum velocity in the simulation box is smaller than 4 km s−1. The initial and the relaxed-state profiles of density and temperature at x = 0 are shown in Fig. 1.
(11)where θ0 = 30∘ is the angle between the apex of the magnetic loops and the neutral line, L0 = 80 Mm is the horizontal size of the simulation box, and B0 = 80 G is the strength of magnetic field at the bottom. The resulting magnetic field strength at the loop apex is about 50 G. We performed relaxation with this initial condition and background heating to obtain a stable plasma environment during which the precise thermodynamic balance gets adjusted. When the relaxation is finished, the maximum velocity in the simulation box is smaller than 4 km s−1. The initial and the relaxed-state profiles of density and temperature at x = 0 are shown in Fig. 1.
 |
Fig. 1. Height profiles of temperature and density before relaxation (dashed lines) and after relaxation (solid lines). |
After the relaxation, we reset the time to zero and deposited flare energy into the chromospheric footpoints of a loop to trigger evaporation flows. According to the CSHKP flare model, high energy electron flows generated in the reconnection above the loop top move along the magnetic field, heat the lower atmosphere, and trigger the evaporation flows. The observation from Ramaty High Energy Solar Spectroscopic Imager (RHESSI) suggests that the high energy electron flows have a double power law spectrum (Holman et al. 2003). The high energy particles are found to deposit most of their energy in the upper chromosphere owing to Coulomb collisions (Allred et al. 2005). This effect is incorporated and represented by an energy source H1 added in the upper chromosphere in the flare loops where the initial magnetic loops fulfil the following inequality: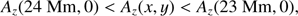 (12)
(12)
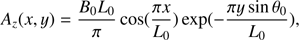 (13)where Az is a component of the magnetic vector potential A = (Ax, Ay, Az) of the force-free magnetic arcade, as we have ∇ × A = B. The Az has a maximum value at the point (x = 0, y = 0) and decreases with distance along any ray from this point. The Az(24 Mm, 0) and Az(23 Mm, 0) indicate two magnetic field lines in the x − y plane. We note that the flare energy source H1 is added only in the region given by Eq. (12). The expression of H1 is written as
(13)where Az is a component of the magnetic vector potential A = (Ax, Ay, Az) of the force-free magnetic arcade, as we have ∇ × A = B. The Az has a maximum value at the point (x = 0, y = 0) and decreases with distance along any ray from this point. The Az(24 Mm, 0) and Az(23 Mm, 0) indicate two magnetic field lines in the x − y plane. We note that the flare energy source H1 is added only in the region given by Eq. (12). The expression of H1 is written as![$$ \begin{aligned} {H_{1}} = {c_{1}} \frac{1}{\sqrt{\pi \lambda _l^2}} \exp \left[\frac{-{(y-{y_{c}})^2}}{\lambda _l^2}\right] f(t) g(x), \end{aligned} $$](/articles/aa/full_html/2018/10/aa33362-18/aa33362-18-eq17.gif) (14)where c1 denotes the total energy flux transported by energetic particles, λl2 = 0.05 Mm2, and the height yc = 1.75 Mm is located in the upper chromosphere. The function f(t), which describes the temporal evolution of energy flux, is written as follows:
(14)where c1 denotes the total energy flux transported by energetic particles, λl2 = 0.05 Mm2, and the height yc = 1.75 Mm is located in the upper chromosphere. The function f(t), which describes the temporal evolution of energy flux, is written as follows:![$$ \begin{aligned} f(t) = \frac{1}{\sqrt{\pi \lambda _t^2}} \exp \left[\frac{-{(t-2 {\lambda _{t}})^2}}{{\lambda _{t}^{2}}}\right]. \end{aligned} $$](/articles/aa/full_html/2018/10/aa33362-18/aa33362-18-eq18.gif) (15)
(15)
Obviously the energy flux has a temporal Gaussian distribution. The parameter λt denotes the time scale of heating, and the maximum energy flux is achieved at t = 2λt. The function g(x), which indicates the asymmetry of energy deposition at both footpoints, is given by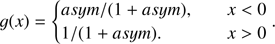 (16)
(16)
The parameter asym denotes the ratios of energy deposited at the left footpoint (x < 0) to that at the right footpoint (x > 0). We set the ratio to 0.8 in most of our simulations, since asymmetric energy deposition is more likely to happen (Aschwanden et al. 1999; Fang et al. 2016). Since the spatial distribution of the flare energy flux is static instead of dynamic, this method can not adapt to the change of density profile along the loop. The value of energy distributed per unit mass increases rapidly when a significant part of plasma leave this energy deposit area. As a result, the produced evaporation flows tend to have low densities and high speeds. However, this did not influence our research too much because the trigger of KHI is determined by Alfvén Mach number of the flows rather than the speed of the flows. In our numerical study, we tended to produce evaporation flows with Alfvén Mach numbers comparable to the observational flows, rather than produce evaporation flows that have speeds comparable to the observational flows.
3. Case study
In this section, we study a high resolution case to investigate the temporal evolution of the flare loop, the radiative evolution of the flare loop, and the energy cascade process of turbulence. In this case, we adopted a spatial resolution of 19.5 km within and near the flare loop. The value of c1 in Eq. (14) is set to 1.288 × 1013 erg cm−2, which ensures that about 1 × 1029 erg of energy is deposited into the chromospheric footpoints during the simulation. The amount of energy equals the estimated total power of non-thermal electrons (> 20 keV) in an M2.2 flare on 2003 June 10 (Milligan et al. 2006). We used a timescale λt = 60 s in Eq. (15) to deposit 90% of energy in 4 min and set the parameter asym in Eq. (16) to 0.8 to achieve asymmetric footpoint heating.
Temporal evolution of number density, speed, and temperature in this case are shown in Fig. 2. As a result of the sudden heating, the pressure in the chromospheric footpoints increases rapidly and two high speed evaporation flows are launched. Two hot, dense, and fast flows can be found at t = 43 s in the top panels of Fig. 2. The densities of the evaporation flows are about 2 × 1010 cm−3 and the speeds are about 600 km s−1. The Alfvén Mach number of the upflows seems to be comparable to that in the flare event reported by Tian et al. (2014), where the electron density is of the order of 1011 cm−3 and the blueshift is about 260 km s−1. Even though the speed of the flows reaches as high as 600 km s−1 in this case, no KHI is triggered near the boundary of the loop. The main reason is that the local Alfvén speed is also very high, as the Alfvén speed is about 600 km s−1 in the inner loop and is higher than 4000 km s−1 outside the loop. When the dense flows meet each other near t = 86 s, a shock tube problem with two slow shocks is produced in the apex. The shock tube tends to expand along the magnetic field lines in the beginning, but this tendency is prevented quickly owing to the increase of number density and velocity in the evaporation flows that continue to impinge the bounding shocks. The increase of number density and velocity in the upstream drives the slow shock surfaces to move towards the middle, and the thermal pressure in the region between the two shock surfaces becomes higher and higher because of the plasma inflow. As a result, the high pressure forces the loop to expand vertically, as shown in panels g–i in Fig. 2. Because of the expansion, the strength of the local magnetic field becomes smaller and the Alfvén speed becomes lower in the loop apex. As another result of expansion, the evaporation flows shear with the dense plasma in the apex, and the KHI can be triggered since now both the conditions of high shear velocity and low Alfvén speed are satisfied. Thereafter, turbulence is produced by KHI, as shown in panels j–l of Fig. 2. Temperature fluctuations appear in the loop apex when turbulence has been produced. This temperature feature was pointed out in observational studies by Jakimiec et al. (1998).
 |
Fig. 2. Temporal evolution of number density (left column), velocity |
We provide the synthesized AIA 131 Å emission and thermal SXR emission in 4−10 keV for comparison with observations. The intensity of the AIA 131 Å line is given by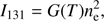 (17)where G(T) is the contribution function provided by the CHIANTI atomic database (Del Zanna et al. 2015). The method to synthesize SXR emission is provided by Pinto et al. (2015) and Fang et al. (2016). According to their method, the thermal X-ray photon flux at the photon energy hν is
(17)where G(T) is the contribution function provided by the CHIANTI atomic database (Del Zanna et al. 2015). The method to synthesize SXR emission is provided by Pinto et al. (2015) and Fang et al. (2016). According to their method, the thermal X-ray photon flux at the photon energy hν is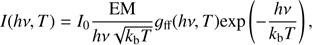 (18)where gff is the Gaunt factor for free-free bremsstrahlung emission, which is written as
(18)where gff is the Gaunt factor for free-free bremsstrahlung emission, which is written as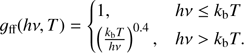 (19)
(19)
The coefficient I0 = 1.07 × 10−42 if the photon flux I(hν, T) is measured at a distance of 1 AU and is expressed in units of cm−2 s−1 keV−1. For the emission measure of a finite volume of plasma 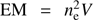 , we used the volume of a cell V = 19.5 × 19.5 × 19.5 km3. We divided the energy range 4 < hν < 10 keV equally into 60 pieces, and then estimated and added up the photon flux density in each piece to calculate the total SXR flux density of the given range. The total SXR photon flux density can be described by ISXR = ∑I(hν, T)Δhν. Integration of this emission flux along the light of sight was not performed, since our simulation data is 2D. Therefore, only the relative intensity of emission is meaningful.
, we used the volume of a cell V = 19.5 × 19.5 × 19.5 km3. We divided the energy range 4 < hν < 10 keV equally into 60 pieces, and then estimated and added up the photon flux density in each piece to calculate the total SXR flux density of the given range. The total SXR photon flux density can be described by ISXR = ∑I(hν, T)Δhν. Integration of this emission flux along the light of sight was not performed, since our simulation data is 2D. Therefore, only the relative intensity of emission is meaningful.
The evolution of SXR emission is demonstrated in Fig. 3. At t = 86 s, high intensity emission only appears near the chromospheric footpoints, even though the evaporation flows have reached the apex. This is because the footpoints have higher plasma density and temperature (∼17 MK). Later, the apex also shows high emission intensity at t = 172 s, as the temperature of plasma increases to above 20 MK via flow interaction. Thereafter, SXR emission disappears near the footpoints at t = 258 s, as the heating is finished and the local temperature decreases to about 10 MK. Meanwhile, SXR emission at the apex is still strong as the temperature of plasma is still higher than 20 MK. The flare loop has a so-called fat and bright body accompanied by a so-called slim and less bright SXR emission down the legs. This shape is similar to the spider-like structure often observed in SXR images of flares (Zhitnik et al. 2003, 2006). This spider-like shape is maintained until the end of the simulation (t ≈ 9 min).
 |
Fig. 3. Temporal evolution of synthesized AIA 131 Å emission (DN cm−5 s−1 pix−1) and SXR emission (photon cm−2 s−1). |
The total SXR flux of the flare heated loop at each time is calculated and plotted in panel a of Fig. 4. The flux decreases to about 2/3 of the maximum value when the simulation is finished at 558 s. Periodic signals are clearly demonstrated in the decreasing phase of the profiles. To investigate the periodic feature of the signals, wavelet analysis is performed and the results are demonstrated in panel b. The original data is detrended before the wavelet analysis is performed. The method we perform in the detrending is given by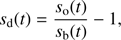 (20)
where sd is the detrended data, so is the original data and sb is the smooth estimate of so. The original data is smoothed with Gaussian filter. We used Morlet wavelet in the analysis and set the wave number to be ω0 = 6. The data before t = 43 s were not taken into account in the wavelet analysis, while the SXR flux in this interval is nearly 0. The results of wavelet analysis show that the signal has a clear single periodicity in the SXR decreasing phase, and the period is about 25 s. The oscillation has a long duration, which is more than five periods. To investigate the nature of the oscillations, we employed running difference analyses. The analyses show that temperature and density near the centre of the apex (i.e. in the turbulent region) also vary with a period of about 25 s. The results of the running difference analysis of temperature are demonstrated in Fig. 5. The total SXR flux is temporally minimal at t = 288.1 s and is located at a peak at t = 301.0 s. This figure clearly shows that the temperature near the centre of the apex decreases with time when the total SXR flux decreases with time (from t = 283.8 s to t = 288.1 s), and the temperature increases with time when the total SXR flux increases with time (from t = 288.1 s to t = 301.0 s). The variation of density is in phase with the variation of temperature as well. This indicates that the oscillations in the total SXR flux are compressional signals.
(20)
where sd is the detrended data, so is the original data and sb is the smooth estimate of so. The original data is smoothed with Gaussian filter. We used Morlet wavelet in the analysis and set the wave number to be ω0 = 6. The data before t = 43 s were not taken into account in the wavelet analysis, while the SXR flux in this interval is nearly 0. The results of wavelet analysis show that the signal has a clear single periodicity in the SXR decreasing phase, and the period is about 25 s. The oscillation has a long duration, which is more than five periods. To investigate the nature of the oscillations, we employed running difference analyses. The analyses show that temperature and density near the centre of the apex (i.e. in the turbulent region) also vary with a period of about 25 s. The results of the running difference analysis of temperature are demonstrated in Fig. 5. The total SXR flux is temporally minimal at t = 288.1 s and is located at a peak at t = 301.0 s. This figure clearly shows that the temperature near the centre of the apex decreases with time when the total SXR flux decreases with time (from t = 283.8 s to t = 288.1 s), and the temperature increases with time when the total SXR flux increases with time (from t = 288.1 s to t = 301.0 s). The variation of density is in phase with the variation of temperature as well. This indicates that the oscillations in the total SXR flux are compressional signals.
 |
Fig. 4. Panel a: temporal evolution of the total flux of SXR emission (solid line) and the smooth estimate of the SXR emission (dashed line). Panel b: wavelet analyses of the SXR emission. The black contour in panel b shows 95% confidence level. The cross-hatched regions represent cone of influence regions, where the edge effect is important. Three dotted lines indicate the times t = 288.1, 292.4 and 301.0 s, respectively. |
 |
Fig. 5. Running difference analysis of temperature. Panel a: T(t = 288.1 s) − T(t = 283.8 s); panel b: T(t = 292.4 s) − T(t = 288.1 s); and panel c: T(t = 301.0 s) − T(t = 296.7 s). The phases of oscillations at the times t = 288.1, 292.4 and 301.0 s refer to Fig. 4. |
Oscillations in flares with periods of ∼1–60 s were interpreted as standing fast sausage modes (Tian et al. 2016). However, the oscillations in our simulation are difficult to interpret by this standard standing fast sausage wave model, which suggests that the phase speed of the waves is given by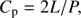 (21) where L is the loop length and P is the period, and the phase speed should be smaller than the external Alfvén speed (Aschwanden 2004). For the oscillations in our simulation, we find 2L/P ≈ 160 Mm/25 s = 6400 km s−1. This value is much larger than the Alfvén speed inner the flare loop (lower than 1000 km s−1) and close to the maximum Alfvén speed outside the flare loop; the outside Alfvén speed ranges from 4000 km s−1 to 8000 km s−1. One probable interpretation is that the oscillations are standing fast sausage modes, where the waves are reflected before they arrive at the opposing footpoints. Instead, the waves are reflected near the apex because of the rapid change in loop radius. As a result, the wavelength is much shorter than 2L. We assume that the wavelength is 2 × 30 Mm = 60 Mm, while the size of the apex is about 20−30 Mm. In this assumption, the phase speed is 2400 km s−1, which is lower than the Alfvén speed outside the apex and is a reasonable value of fast sausage wave phase speed.
(21) where L is the loop length and P is the period, and the phase speed should be smaller than the external Alfvén speed (Aschwanden 2004). For the oscillations in our simulation, we find 2L/P ≈ 160 Mm/25 s = 6400 km s−1. This value is much larger than the Alfvén speed inner the flare loop (lower than 1000 km s−1) and close to the maximum Alfvén speed outside the flare loop; the outside Alfvén speed ranges from 4000 km s−1 to 8000 km s−1. One probable interpretation is that the oscillations are standing fast sausage modes, where the waves are reflected before they arrive at the opposing footpoints. Instead, the waves are reflected near the apex because of the rapid change in loop radius. As a result, the wavelength is much shorter than 2L. We assume that the wavelength is 2 × 30 Mm = 60 Mm, while the size of the apex is about 20−30 Mm. In this assumption, the phase speed is 2400 km s−1, which is lower than the Alfvén speed outside the apex and is a reasonable value of fast sausage wave phase speed.
Besides the 25 s oscillations near the centre of the apex, another type of oscillations is found in the running difference analyses. These oscillations appear near the boundaries of the flare loop. As shown in Fig. 5, negative ΔT propagates from right to left near the upper boundary, while positive ΔT propagates from right to left near the lower boundary. The positive or negative ΔT near the boundary is caused by the variation of the loop boundaries. The oscillation can be seen in animated views of the density variation, where the loop boundaries show a fairly coherent swaying motion. This is reflected in the temperature difference views shown in Fig. 5 where these coherent motions give clear correlated patterns in the temperature at the top and bottom edges of the loop (near its apex). These sideways displacements are characteristic for more kink-type perturbations.
When the density of the plasma and photon density are given, we can compare the role of ICS with that of bremsstrahlung in HXR emission. Equations (5) and (7) in Appendix A of Krucker et al. (2008) are expressions to estimated volume emissivity of ICS and bremsstrahlung, respectively. Here, we estimate the relative contribution of ICS versus bremsstrahlung with these two equations.
For HXR photons of energy ϵ, this ratio is written as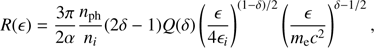 (22)where nph is the number density of mono-energetic photons that have energy ϵi (and are upscattered by ICS), ni is the ambient coronal number density, and δ is the spectral index of energetic electrons. Furthermore, α is the fine-structure constant, and mec2 is the rest energy of an electron. The dimensionless function Q(δ) is given by
(22)where nph is the number density of mono-energetic photons that have energy ϵi (and are upscattered by ICS), ni is the ambient coronal number density, and δ is the spectral index of energetic electrons. Furthermore, α is the fine-structure constant, and mec2 is the rest energy of an electron. The dimensionless function Q(δ) is given by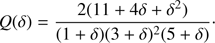 (23)
(23)
The contribution of the inverse Compton process by scattering 2 eV photospheric photons, to 20 keV HXR photons, has been evaluated by Krucker et al. (2008). The authors suggest that the inverse Compton process may play a more important role than bremsstrahlung when the ambient coronal density is lower than 109 cm−3. In our simulations, our plasma density is only 108 cm−3 before the apex is filled with evaporation plasma, therefore their result indicates that this inverse Compton process may determine loop-top HXR emission only before evaporation flows reach the apex. The role of sustained loop-top turbulence, in higher density environments created by KHI interactions in which SXR photons are abundant, was not accounted for, however.
Since Fang et al. (2016) suggested that high energy electrons scatter SXR photons to HXR photons, and thereby contribute to the loop-top HXR source, we investigate this effect here. Firstly, we need to estimate the number density of SXR photons. According to our SXR synthesized results shown in Fig. 3, we can assume that the contribution of a single computational cell of volume 19.5 × 19.5 × 19.5 km3 to the SXR flux measured at a distance of R = 1 AU = 1.5 × 1013 cm is of order fm = 5 × 10−5 photon cm−2s−1. The volume of the loop-top SXR source can clearly be approximated with a sphere of radius 10 Mm, making the total emitting volume Vl = (10 Mm)34π/3 and the area of the loop-top surface Sl = 4π(10 Mm)2. The total SXR flux is then estimated as ft = (Vl/V)fm4πR2 and the SXR photon density is accordingly estimated as nph = ft/(S1c) ≈ 200 cm−3, where c is the light speed. To simplify the calculation, all SXR photons are assumed to have energy of 4 keV. The energetic electrons are assumed to have a hard spectrum δ = 2, and the ion number density is obtained directly from our simulations and is of order ni = 1010 cm−3. According to Eq. (22), the relative contributions of scattering SXR photons to HXR photons and bremsstrahlung for the emission of 20 keV HXR photons is then R (20 keV) ≈ 10−8. This implies that the contribution of the inverse Compton process to scattering SXR photons to HXR photons is very small for the generation of a loop-top HXR source. Still, we emphasize that the formulae used in this work do not account for the extra turbulence we find as an inevitable consequence of KHI. We now address these turbulence properties in what follows.
Turbulence plays an important role in the new scenario presented by Fang et al. (2016), as it is suggested to be an efficient accelerator for electrons and can trap high energy electrons in the loop top. Therefore, turbulence produced by KHI in the apex should be analysed. Figure 6 shows the power spectral density (PSD) of velocity and magnetic field of the turbulence at t = 215 s, and the distribution of magnetic field and the flow field of velocity are also provided. A 2D region (green box in Fig. 6) is selected to perform fast Fourier transform, and then the 2D results are organized to obtain 1D spectra. The 1D spectra are functions of wave number 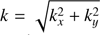 , where kx and ky is the wave number in x and y direction respectively. Island structures and vortices can be found in the plots of magnetic field strength and velocity flow field, respectively. The spectral indexes are close to −5/3 in the spatial scale range of 10−6 < k < 10−5 m−1. The cascade process of energy is clearly illustrated in Fig. 7, which shows their temporal evolution.
, where kx and ky is the wave number in x and y direction respectively. Island structures and vortices can be found in the plots of magnetic field strength and velocity flow field, respectively. The spectral indexes are close to −5/3 in the spatial scale range of 10−6 < k < 10−5 m−1. The cascade process of energy is clearly illustrated in Fig. 7, which shows their temporal evolution.
 |
Fig. 6. Panel a: magnetic field strength at t = 215 s; panel b: spectrum of magnetic field inside the green box; panel c: flow field of velocity at t = 215 s; and panel d: spectrum of velocity inside the green box. White lines in panel a denote magnetic field lines. |
 |
Fig. 7. Panel a: out of plane current component jz at t = 172 s; panel b: temporal evolution of spectra. The region inside the orange box in (panel a) is selected to calculate the spectra. |
To catch the energy cascade process, a larger region is selected to analyse the spectra (orange box in Fig. 7a). Figure 7b provides the PSD of velocity at t = 86, 129 and 172 s. The value of PSD at the maximum wave number k ≈ 2 × 10−4 m−1 are set to one to compare the profiles. We find that the spectra coincide with each other very well in the range k > 10−5 m−1, which indicates that the energy cascade process stops at the scale k ≈ 10−5 m−1. This may explain why the indexes of the spectra departs from −5/3 in the scale k > 10−5 m−1 in Fig. 6. The energy cascades from large scale to small scale, as seen by comparing the three spectra: an enhancement can be found in scale 6 × 10−6 > k > 2 × 10−6 m−1 at t = 129 s, while compared with time t = 86 s; spectra at 172 s show an enhancement in 10−5 > k > 6 × 10−6 m−1 compared with t = 129 s. The plasma states at t = 86, 129, and 172 s are shown on the full domain size in Fig. 2.
We are also interested in the energy transformation and heat-loss evolution of the flare loop. Therefore, the temporal evolutions of total kinetic energy, thermal energy and magnetic energy are calculated. We define the boundaries of the flare loop with the help of plasma temperature. The region where T > 5 MK is assumed to belong to the loop, since the plasma outside the loop has a temperature T < 2 MK and the temperature of plasma inside the loop is higher than 10 MK. The results are demonstrated in panel a of Fig. 8. The ratio of thermal pressure to magnetic pressure β has a wide range in the loop apex. The value of β ranges from 1 to 10 in the dark region in panel e of Fig. 3, while β is as high as several tens in the bright region in this panel. In contrast, β is about 5 × 10−4 in the apex and has an order of 1 in the chromospheric footpoints when energy has not been deposited. Before the evaporation flows collide with each other at t ≈ 75 s, the kinetic energy flow has the same value as the thermal energy flow. After the flows meet each other in the apex, compression causes kinetic energy to transform quickly into thermal energy. The evidence can be found in Fig. 2, where the plasma in the apex is rapidly heated to about 20 MK from about 10 MK when the flows collide with each other. The plasma in the loop remains hot for a long time after most of the energy is deposited in the footpoints, since the radiative cooling is less efficient compared with the heating (Fig. 8) in the hot loop. The temperature of the loop is about 20 MK when the simulation is finished at t = 558 s, and weak turbulence can still be found in the apex. The plasma temperature in our simulation is comparable to that in the flare observations. Nitta et al. (2001) investigated the loop-top temperatures in 36 flare events, and the temperatures in their study are in the range 18−23.5 MK.
 |
Fig. 8. Panel a: temporal evolution of total kinetic energy (black dashed line), thermal energy (red solid line), and magnetic energy (blue dotted line) for hot plasma (T ≥ 5 MK); panel b: evolution of background heating flux (red solid line), and radiative cooling (blue dashed line) for hot plasma. |
4. Parameter surveys
In this section, we investigate what may influence the trigger of KHI and the generation of turbulence. The driving source of the evaporation flows, i.e. the chromospheric energy deposition process, is expected to have great influence on the dynamics of the flare loop. Therefore, we explore parameters of the energy deposition that are considered to be influential: the amount of energy, timescale of deposition, and asymmetry of deposition.
The influence of the energy deposition timescale is investigated with two cases in this paper. Both cases have a resolution of 39 km. Two new cases listed in this work are referred to as case 2 and case 3, respectively, while the case in Sect. 3 is referred to as case 1. Case 2 has the same setting as case 1 except for the resolution. Case 3 has λt = 90 s to let 90% of the energy be deposited in about 6 min, while λt = 60 s in case 2. Hence, the amounts of energy are the same but case 2 has a shorter timescale and stronger instantaneous energy flux than case 3.
The temporal evolution of the velocity of case 2 is shown in Fig. 9a–9c, and that of case 3 is in Fig. 9d–9f. In case 2, turbulence is produced owing to KHI and vortices can be found in Fig. 9c. In contrast, no turbulence is produced and no shear flows can be found in case 3. To study the difference between case 2 and case 3, the parameters of the evaporation flows are analysed. The temporal evolution of density and velocity at the axis of the right loop at a height of h = 10 Mm is shown in Fig. 10. Figure 10 indicates a positive correlation between density or velocity of the flows and the energy flux of footpoint heating. The energy flux is higher in case 2 compared with case 3, since the same amount of energy is deposited in a shorter time. Moreover, the density or velocity of the flow increase faster before a maximum value is achieved in case 2. The flows collide near the apex at t ≈ 70 s in case 2 and at t ≈ 80 s in case 3. The maximum speed of the flows is about 700 km s−1 in case 2 and about 600 km s−1 in case 3 at the measured point.
 |
Fig. 9. Evolution of velocity for case 2 in which λt = 60 s (panel a, b, c) and case 3 in which λt = 90 s (panel d, e, f). |
 |
Fig. 10. Temporal evolution at the centre of the right loop leg at the height of h = 10 Mm of density (black lines) and velocity (red lines) for case 2 with higher energy flux and case 3 (dashed) with lower energy flux. |
As demonstrated in Fig. 2, the flows collide with each other in the apex and two slow shocks are generated before the KHI is triggered. From the Rankine-Hugoniot equations we know that the propagating velocity of a shock is determined by the velocity and density and pressure in the upstream and downstream. For case 2, the shock surface near the axis propagates towards the downstream since the velocity and density in the upstream increase quickly. At the same time, the shock fronts near the loop boundaries propagate upstream to maintain balances of pressure and mass transport because the velocity and density of flows near the boundary are much smaller than those near the axis. As a result, shear flows are generated in the loop apex and KHI can be triggered (Fig. 9b). In contrast, the density and velocity of upstream in case 3 increase slowly, and therefore the shock front near the axis propagates upstream. Because the shock fronts near the boundaries propagate towards upstream as well, no shear flows can be found in the apex and KHI cannot be triggered. In addition, stronger energy flux leads to larger Alfvén Mach numbers. The Alfvén Mach number at the axis of the right loop at a height of h = 10 Mm at t = 151 s is about 1.5 in case 2 and about 0.9 in case 3. This means that KHI is easier triggered in case 2 even if shear flows exist in the apex in both cases. For the same reason, the more energy is deposited the easier KHI is triggered.
A new case (case 4) with a resolution of 39 km is simulated and compared with case 2 to study the influence of the amount of deposited energy. The amount of energy deposited into the footpoints in case 4 is set to 1/3 of that in case 2 with the same timescale of energy deposition. Figure 11a and 11b show the distribution of density at t = 151 s of case 2 and case 4, respectively. In case 2, the density and velocity of the evaporation flows increase quickly, since the energy flux deposited into the footpoints increases quickly. As a result, the flows push both shocks to the middle and high speed flows can go into the loop apex. Therefore, KHI can be triggered and turbulence can be produced. In contrast, evaporation flows fail to go into the apex in case 4, since the density and velocity of the flows increase slowly. Consequently, the flows fail to produce turbulence in this case.
 |
Fig. 11. Panel a: number density at t = 151 s for case 2 with more energy deposited at the footpoints; panel b: density at t = 151 s for case 4 with less energy deposited. The unit of number density is 109 cm−3. |
In the observation of solar flares, the HXR emission often exhibits asymmetric features (Aschwanden et al. 1999). The asymmetry of HXR emission is likely caused by the asymmetric energy deposition at two footpoints. Therefore, it is meaningful to study the influence of asymmetry of energy deposition on the KHI and turbulence. Three new cases (case 5, 6, and 7) are simulated and compared with case 2 to investigate the influence in our work. In these four cases, the amounts of energy deposited in the loop and the timescales of energy deposition are the same, but the ratios of energy deposited at the left footpoint to the right foot-point are different. The ratios in cases 5, 6, and 7 are set to 0, 0.4 and 1.0, respectively, while that in case 2 is 0.8. The corresponding simulation results of the out of plane current component jz at t = 194 s are demonstrated in Fig. 12. The resolution of the cases is 39 km. The vortical structures in each panel provide the information about the location where the KHI is triggered and turbulence is produced. Figure 12 denotes that the location where turbulence is produced is determined by the asymmetry of energy deposition. KHI is always triggered near the location where the interaction of the flows happen. Since the velocity of evaporation flow has a positive correlation with the energy flux deposited in the footpoint, an asymmetry of energy deposition leads to an asymmetry of flow speed. Consequently, KHI tends to be triggered near the apex when the ratio is close to 1 and tends to be triggered away from the apex when the ratio is close to 0, as shown in Fig. 12. We can still observe asymmetric vortex breaking when the heating is symmetric owing to numerical symmetry breaking and inaccuracy as shown in panel (d).
 |
Fig. 12. Out of plane current component jz at t = 194 s for four cases with different energy deposition asymmetries. The asymmetric parameters asym in panels a, b, c, and d are 0, 0.4, 0.8 and 1, respectively. |
When the turbulence is produced away from the apex because of asymmetric footpoint heating, the vortical structures tend to move back and forth near the apex (Fig. 13). The motion of the vertical structures in case 6 seems to have a period of about 300 s. The periodic motion is probably a signal of standing slow-mode wave. The length of the loop is about 80 Mm and the sound speed of 20 MK plasma is about 500 km s−1. The period of a standing slow wave should be about 320 s, which is close to the period of the motion in our simulations. Fang et al. (2015) and Mandal et al. (2016) have demonstrated that footpoint heating can generate slow waves and these reflect back and forth in the loop.
 |
Fig. 13. Temporal evolution of out of plane current component jz for case 6 where asym = 0.4. Turbulence is in the left of apex at t = 215 s, and then appear in the right of apex at t = 366 s. Finally, turbulence can be found in the left of the apex at t = 516 s. |
A case (case 8) in which two evaporation flows shear with each other is also studied. This case has a high resolution of 19.5 km, the same as the resolution of case 1 in Sect. 3. In this new case, energy is deposited at various magnetic field lines to ensure that the evaporation flows shear each other rather than collide with each other. All other cases have the same set of magnetic field lines that are affected at both left and right footpoint, as given by Eq. (12). In Fig. 14, the results of this new case are compared to that of case 1 where the flows collide with each other. Vortical structures can be found in both cases, which denotes that KHI can be triggered in both cases. However, more vortices can be found in the situation that the flows collide with each other. The collision of the evaporation flows leads to an expansion of the flare loop, a decrease of magnetic field strength and a decrease of local Alfvén speed. Therefore, KHI is more easily triggered in the situation in which the flows collide with each other. The interface of two evaporation flows is wider in the shearing case (case 8), which leads to KHI turbulence appearing on a long part of the loop. In contrast, two evaporation flows make contact with each other only in the apex in the collision case (case), which leads to a more local site of KHI and turbulence development.
 |
Fig. 14. Trigger of KHI for two ways the evaporation flows interact with each other. Red denotes the plasma from left footpoint, while blue denotes plasma from the right footpoint. Panels a and c: flows from two footpoints collide with each other; panels b and d: flows shear with each other. |
5. Summary
We numerically study a new scenario proposed by Fang et al. (2016) concerning the origin of the observed turbulence in flare loops and generation of loop-top HXR emission. According to this new scenario, KHI can be triggered when chromospheric evaporation flows from two footpoints that meet and interact with each other in the flare loop apex, and turbulence can be produced by the KHI. The turbulence can act as a trapping region and an efficient accelerator to provide energetic electrons. The accelerated electrons can scatter SXR photons to HXR photons via the inverse Compton process to generate the loop-top HXR source, and add to the HXR bremsstrahlung, although the plasma densities are too high according to parametrized emission models Krucker et al. (2008). We focus on the trigger of KHI and the generation of turbulence. In our numerical study, energy is deposited into the chromospheric footpoints of a coronal loop and evaporation flows are produced owing to the sudden heating. The interaction of the flows, trigger of KHI, and generation of turbulence in the apex are investigated. The temporal evolution of a flare loop, radiative evolution of the flare loop, and energy cascade process of turbulence are studied with a high spatial resolution case. Thereafter, a parameter survey is performed to investigate what may influence the trigger of KHI and the generation of turbulence. The main results are summarized in the following:
-
KHI can be triggered when the evaporation flows interact with each other and turbulence can be produced by the KHI in our simulations.
-
Thermal SXR emission is synthesized and SXR sources are found in the results. The SXR emission appear in the footpoint at first, and then appear in the apex. The footpoint sources disappear when the footpoint heating is finished, but the loop-top source is maintained for several minutes.
-
The spectral indexes of velocity and magnetic field are close to −5/3 in the turbulent region. The energy cascade process in the turbulence is clearly demonstrated in the spectra.
-
When the evaporation flows are produced, the kinetic energy and thermal energy are very close. Kinetic energy is quickly transformed into thermal energy due to compression after the flows collide with each other at t ≈ 75 s and the loop becomes very hot (T > 20 MK).
-
The loop is still very hot (T > 20 MK) when the simulation is finished at t ≈ 10 min owing to inefficient radiative cooling.
-
The KHI is easily triggered when the density and velocity of the evaporation flows increase rapidly. The KHI turbulence is more easily produced when the amount of energy deposited into the footpoints is higher or the timescale of energy deposition is shorter.
-
The location of the turbulence is determined by the ratio of energy deposited at two footpoints. The site of KHI and turbulence development moves away from loop apex when the energy deposited into one footpoint is much more than that deposited into the other footpoint.
-
The conditions in which evaporation flows collide with other and the flows shear with each other are studied, and KHI turbulence can be produced in both conditions.
-
Abundant waves are produced in the flare loops, including compressional modulations in the turbulent zone with a period of about 25 s and standing slow mode wave with a period of about 300 s.
In our simulations, the upward velocity of the flows can reach 700 km s−1 (see Fig. 10). Such a high velocity is not necessary to trigger KHI. Whether or not KHI can be triggered is determined by the Alfvén Mach number, which depends on both velocity and density. In the observations, it does not seem easy for evaporation flows to achieve a velocity of 700 km s−1, but the density of plasma tends to be higher. For example, the electron density of the observed evaporation flows is found to be of the order of 1011 cm−3 in Tian et al. (2014), which is several times what we found in our simulations. Meanwhile, the observed evaporation flows are reported to have a blueshift of ∼260 km s−1. The Alfvén Mach number of the observed evaporation flows is comparable to that in our simulations if the strengths of magnetic field are of the same order. Therefore, we suggest that KHI is not difficult to trigger in solar flares.
Future work is required to study the same scenario in 3D setting to get a clear insight into orientational line of sight effects. A flare loop that contains a reconnection site needs to be adopted to incorporate the KHI effects in a real flare scenario. A more dynamic energy deposit method that distributes flare energy base on the density profile along the loop should be adopted. Test particles need to be added into the simulation to study the effect and physics of particle acceleration and trapping in KHI turbulence. The emission fluxes of HXR generated via ICS and bremsstrahlung can be estimated with the distribution of the test particles. Such calculations can quantify the hardness (δ) of the electron spectrum. The inverse Compton mechanism may contribute to loop-top HXR emission before evaporation flows go into the apex. The contribution is then from scattering photospheric lower energy photons to HXR photons rather than from scattering SXR photons to HXR photons. Bremsstrahlung dominates the HXR emission when the apex is filled with evaporation plasma, according to parametrized models that do not incorporate the turbulence effects. Future work must quantify the roles of the inverse Compton and bremsstrahlung mechanisms in the generation of loop-top HXR sources by comparing the HXR emissions produced via these mechanisms.
Movies
Movie of Fig. 1 Access here
Movie of Fig. 2 Access here
Acknowledgments
This work is supported by the Chinese scholarship council (CSC) and by project GOA/2015-014 (2014-2018 KU Leuven). We would like to thank Tom Van Doorsselaere, Kirit Makwana, Jiansen He, Hui Tian, and Mingzhe Guo for stimulating discussions. The simulations were conducted on the VSC (Flemish Supercomputer Center funded by Hercules foundation and Flemish government).
References
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Gabriel, A. H., Acton, L. W., et al. 1982, Sol. Phys., 78, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2004, Physics of the Solar Corona, an introduction (Chichester, UK: Praxis Publishing Ltd.) [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Sakao, T., Kosugi, T., & Hudson, H. 1999, ApJ, 517, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Bentley, R. D., Doschek, G. A., Simnett, G. M., et al. 1994, ApJ, 421, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Carmichael, H. 1964, NASA Spe. Pub., 50, 451 [Google Scholar]
- Chen, B., & Bastian, T. S. 2012, ApJ, 750, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Colgan, J., Abdallah, J. Jr., Sherrill, M. E., et al. 2008, ApJ, 689, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fang, X., Yuan, D., Van Doorsselaere, T., Keppens, R., & Xia, C. 2015, ApJ, 813, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Yuan, D., Xia, C., Van Doorsselaere, T., & Keppens, R. 2016, ApJ, 833, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Doschek, G. A., Kreplin, R. W., & Mariska, J. T. 1980, ApJ, 241, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, T. 1974, Sol. Phys., 34, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Jakimiec, J., Tomczak, M., Falewicz, R., Phillips, K. J. H., & Fludra, A. 1998, A&A, 334, 1112 [NASA ADS] [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A. J., et al. 2012, J. Comput. Phys., 231, 718 [Google Scholar]
- Kontar, E. P., Bian, N. H., Emslie, A. G., & Vilmer, N. 2014, ApJ, 780, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Perez, J. E., Harra, L. K., et al. 2017, Phys. Rev. Lett., 118, 155101 [NASA ADS] [CrossRef] [Google Scholar]
- Kopp, R. A., & Pneuman, G. W. 1976, Sol. Phys., 50, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Korchak, A. A. 1967, Sov. Astron., 11, 258 [NASA ADS] [Google Scholar]
- Korchak, A. A. 1971, Sol. Phys., 18, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Hannah, I. G., & Lin, R. P. 2007, ApJ, 671, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Battaglia, M., Cargill, P. J., et al. 2008, A&ARv, 16, 155 [Google Scholar]
- Liu, W., Liu, S., Jiang, Y. W., & Petrosian, V. 2006, ApJ, 649, 1124 [Google Scholar]
- Mandal, S., Yuan, D., Fang, X., et al. 2016, ApJ, 828, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., & Ogawara, Y. 1994, Nature, 371, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Milligan, R. O., & Dennis, B. R. 2009, ApJ, 699, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Milligan, R. O., Gallagher, P. T., Mathioudakis, M., et al. 2006, ApJ, 638, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, N. V., Sato, J., & Hudson, H. S. 2001, ApJ, 552, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, S., Imada, S., & Yamamoto, T. T. 2012, Sol. Phys., 276, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, R. F., Vilmer, N., & Brun, A. S. 2015, A&A, 576, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porth, O., Xia, C., Hendrix, T., Moschou, S. P., & Keppens, R. 2014, ApJS, 214, 4 [Google Scholar]
- Shimizu, T., Tsuneta, S., Acton, L. W., et al. 1994, ApJ, 422, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Sturrock, P. A. 1966, Nature, 211, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Su, Y., Veronig, A. M., Holman, G. D., et al. 2013, Nat. Phys., 9, 489 [Google Scholar]
- Tian, H., Li, G., Reeves, K. K., et al. 2014, ApJ, 797, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Young, P. R., Reeves, K. K., et al. 2015, ApJ, 811, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Young, P. R., Reeves, K. K., et al. 2016, ApJ, 823, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, M. 1997, A&A, 317, 223 [NASA ADS] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, C., Teunissen, J., El Mellah, I., Chané, E., & Keppens, R. 2018, ApJS, 234, 30 [Google Scholar]
- Zhitnik, I. A., Kuzin, S. V., Urnov, A. M., et al. 2006, Sol. System Res., 40, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Zhitnik, I. A., Bugaenko, O. I., Ignat’ev, A. P., et al. 2003, MNRAS, 338, 67 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Height profiles of temperature and density before relaxation (dashed lines) and after relaxation (solid lines). |
| In the text | |
 |
Fig. 2. Temporal evolution of number density (left column), velocity |
| In the text | |
 |
Fig. 3. Temporal evolution of synthesized AIA 131 Å emission (DN cm−5 s−1 pix−1) and SXR emission (photon cm−2 s−1). |
| In the text | |
 |
Fig. 4. Panel a: temporal evolution of the total flux of SXR emission (solid line) and the smooth estimate of the SXR emission (dashed line). Panel b: wavelet analyses of the SXR emission. The black contour in panel b shows 95% confidence level. The cross-hatched regions represent cone of influence regions, where the edge effect is important. Three dotted lines indicate the times t = 288.1, 292.4 and 301.0 s, respectively. |
| In the text | |
 |
Fig. 5. Running difference analysis of temperature. Panel a: T(t = 288.1 s) − T(t = 283.8 s); panel b: T(t = 292.4 s) − T(t = 288.1 s); and panel c: T(t = 301.0 s) − T(t = 296.7 s). The phases of oscillations at the times t = 288.1, 292.4 and 301.0 s refer to Fig. 4. |
| In the text | |
 |
Fig. 6. Panel a: magnetic field strength at t = 215 s; panel b: spectrum of magnetic field inside the green box; panel c: flow field of velocity at t = 215 s; and panel d: spectrum of velocity inside the green box. White lines in panel a denote magnetic field lines. |
| In the text | |
 |
Fig. 7. Panel a: out of plane current component jz at t = 172 s; panel b: temporal evolution of spectra. The region inside the orange box in (panel a) is selected to calculate the spectra. |
| In the text | |
 |
Fig. 8. Panel a: temporal evolution of total kinetic energy (black dashed line), thermal energy (red solid line), and magnetic energy (blue dotted line) for hot plasma (T ≥ 5 MK); panel b: evolution of background heating flux (red solid line), and radiative cooling (blue dashed line) for hot plasma. |
| In the text | |
 |
Fig. 9. Evolution of velocity for case 2 in which λt = 60 s (panel a, b, c) and case 3 in which λt = 90 s (panel d, e, f). |
| In the text | |
 |
Fig. 10. Temporal evolution at the centre of the right loop leg at the height of h = 10 Mm of density (black lines) and velocity (red lines) for case 2 with higher energy flux and case 3 (dashed) with lower energy flux. |
| In the text | |
 |
Fig. 11. Panel a: number density at t = 151 s for case 2 with more energy deposited at the footpoints; panel b: density at t = 151 s for case 4 with less energy deposited. The unit of number density is 109 cm−3. |
| In the text | |
 |
Fig. 12. Out of plane current component jz at t = 194 s for four cases with different energy deposition asymmetries. The asymmetric parameters asym in panels a, b, c, and d are 0, 0.4, 0.8 and 1, respectively. |
| In the text | |
 |
Fig. 13. Temporal evolution of out of plane current component jz for case 6 where asym = 0.4. Turbulence is in the left of apex at t = 215 s, and then appear in the right of apex at t = 366 s. Finally, turbulence can be found in the left of the apex at t = 516 s. |
| In the text | |
 |
Fig. 14. Trigger of KHI for two ways the evaporation flows interact with each other. Red denotes the plasma from left footpoint, while blue denotes plasma from the right footpoint. Panels a and c: flows from two footpoints collide with each other; panels b and d: flows shear with each other. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.