| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201833952 | |
| Published online | 18 September 2018 | |
Letter to the Editor
The role of AGN jets in the reionization epoch
Departament de Física Quàntica i Astrofísica, Institut de Ciànces del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB), Martí Franquàs 1, 08028 Barcelona, Spain
e-mail: vbosch@fqa.ub.edu
Received:
25
July
2018
Accepted:
25
August
2018
The reionization of the Universe ends the dark ages that started after the recombination era. In the case of H, reionization finishes around z ~ 6. Faint star-forming galaxies are the best candidate sources of the H-ionizing radiation, although active galactic nuclei may have also contributed. We have explored whether the termination regions of the jets from active galactic nuclei may have contributed significantly to the ionization of H in the late reionization epoch, around z ~ 6−7. We assumed that, as it has been proposed, active galactic nuclei at z ~ 6 may have presented a high jet fraction, accretion rate, and duty cycle, and that non-thermal electrons contribute significantly to the pressure of jet termination regions. Empirical black-hole mass functions were adopted to characterize the population of active galactic nuclei. From all this, estimates were derived for the isotropic H-ionizing radiation produced in the jet termination regions, at z ~ 6, through inverse Compton scattering off CMB photons. We find that the termination regions of the jets of active galactic nuclei may have radiated most of their energy in the form of H-ionizing radiation at z ~ 6. For typical black-hole mass functions at that redshift, under the considered conditions (long-lasting, common, and very active galactic nuclei with jets), the contribution of these jets to maintain (and possibly enhance) the ionization of H may have been non-negligible. We conclude that the termination regions of jets from active galactic nuclei could have had a significant role in the reionization of the Universe at z ≳ 6.
Key words: galaxies: jets / radiation mechanisms: non-thermal / dark ages, reionization, first stars / cosmology: miscellaneous / intergalactic medium
© ESO 2018
1. Introduction
The reionization of the Universe put an end to the dark ages that followed the recombination era, after the big bang. The reionization epoch took place mostly around z ~ 6−8 (e.g. Madau 2017), although the nature of the dominant H-ionizing source(s) is still uncertain. Nowadays the favoured candidates are faint star-forming galaxies, in particular the fainter and less massive ones, so long as the escape fraction of the ionizing radiation is not too low (e.g. Stark 2016)1.
Another possible candidate ionizing source at high redshift is accretion in active galactic nuclei (AGN; e.g. Arons & McCray 1970; Donahue & Shull 1987; Shapiro & Giroux 1987; Meiksin & Madau 1993). Such sources are presently considered to be a minor player in the reionization of H (e.g. Hopkins et al. 2007; Onoue et al. 2017; Parsa et al. 2018; McGreer et al. 2018), although they are still sometimes discussed as potentially important reionization sources (e.g. Giallongo et al. 2015; Grazian et al. 2018), or as indirect factors in the reionization process (e.g. Seiler et al. 2018; Trebitsch et al. 2018; Kakiichi et al. 2018). In addition, a so far undetected, faint AGN population, as for instance accreting intermediate mass black holes in the centre of gas-rich dwarf galaxies, cannot be discarded as significant reionization sources (Silk 2017).
Accretion radiation is not the only form of energy output in AGN. In particular, jets may have actually dominated the energy output of AGN at z ~ 6: (i) the jetted AGN fraction may have been close to one (at least for the most massive black-hole AGN – e.g. Sbarrato et al. 2015, in principle valid as well for less massive black-hole sources); and (ii) the AGN central black holes may have been accreting close to the Eddington limit with a high duty cycle (e.g. Willott et al. 2010; Shankar et al. 2013). Since jets may be as powerful as accretion radiation, or even more (e.g. Ghisellini et al. 2014; Sbarrato et al. 2016), their role in the reionization of the Universe should be considered: if a substantial fraction of the jet energy went to H-ionizing photons, they may have contributed as much as AGN accretion, and perhaps even more.
It is worth mentioning that very energetic cosmic rays may also be efficiently accelerated in AGN jets, and the impact of these cosmic rays on the ionization and heating of the intergalactic medium (IGM) at very high redshift deserves detailed studies (see, in the context of POPIII microquasars, e.g. Tueros et al. 2014; Douna et al. 2018; Romero & Checa 2018). However, cosmic ray production in AGN jets is uncertain. First, only the most energetic cosmic rays can diffuse out of the radio lobes; otherwise, they stay in the lobes and cool through adiabatic losses. Secondly, it is not known which fraction of the jet energy is in the form of very energetic cosmic rays. On the contrary, the termination region of jets are known to be filled by non-thermal electrons that could dominate pressure (e.g. Croston et al. 2018), and these electrons could have efficiently emitted H-ionizing photons via inverse Compton (IC) scattering off CMB photons at high red-shift. As bulk velocities in the lobes are relatively low, this emission would have been rather isotropic. Therefore, in this work we have focussed on the AGN jet termination regions, in particular the lobes inflated by shocked jet material, as sources of H-ionizing photons in the late phase of the reionization epoch. The beamed emission from the (relativistic) jet smaller scales is not considered here, although it could be included if it were very efficient turning jet energy into hard photons. This work is a first step in exploring the role of AGN jets and their termination regions in the late reionization epoch, say at z ~ 6−7; more accurate predictions are left for future studies.
The paper is structured as follows: In Sect. 2, we introduce the prescriptions adopted for the black-hole population at high redshift, together with the assumptions adopted to derive the black-hole jet power. In Sect. 3, we show that the termination regions of the jets of AGN at z ≳ 6 could have been powerful sources of (isotropic) H-ionizing radiation, and estimate how much this radiation may have contributed to (maintain) the reionization of the Universe. Finally, we discuss our results and conclude with a summary in Sects. 4 and 5, respectively.
2. Jet-power function
To assess the importance of AGN jets as H-ionizing sources at z ~ 6−7, that is, the late reionization epoch, first one has to characterize the (total) source jet power function. This is quite difficult at very high redshifts because of the uncertainties concerning: (i) the AGN population at low luminosities (of accretion origin); (ii) the jetted AGN fraction; (iii) the AGN (accretion) luminosity-jet power relation; and (iv) the AGN duty cycle, meaning that the fraction of the time the source was active until z ~ 6. One can otherwise choose to adopt a prescription for the black-hole mass function, which requires assuming, in addition to points similar to (ii), (iii), and (iv) above: (a) the yet uncertain IMBH range of the black-hole mass function (say M ~ 105−107; see, e.g. Mezcua 2017, for a review on IMBH); and (b) the accretion-to-Eddington power ratio. We note that the empirical black-hole mass functions may differ significantly from the real ones due to incompleteness, obscuration, and inactivity (or reduced activity; e.g. Salvador-Solé et al. 2017).
Here, we have adopted empirical black-hole mass functions to estimate the jet power distribution at z ≳ 6 (we simplify the black-hole mass function in the range z ~ 6−7 to that for z = 6). Two cases were adopted: the black-hole empirical mass functions at z = 6 from Shankar et al. (2009) and Willott et al. (2010), which reach with large uncertainties down to a black-hole mass of MBH = 105 M⊙. Our characterization of the black hole population is similar to that of Saxena et al. (2017), although in that work the authors assumed a small jetted black-hole fraction of 1%, whereas here we consider that at z ≳ 6 most of the black holes traced by the mass functions were actively accreting and produced jets.
To estimate the typical AGN duty cycle and accretion rate at z ~ 6, we followed the results by Willott et al. (2010) and Shankar et al. (2013), which point to accretion running close to the Eddington rate with a high duty cycle. In addition, motivated by hints of a dominant jetted AGN population at z ≳ 4 (e.g. Sbarrato et al. 2015), we expected a jetted AGN fraction close to one. Finally, we assumed that the (total) jet power of one source scales with the black-hole Eddington luminosity, that is, Lj ∝ LEdd. In principle, Lj can be higher than the accretion radiation luminosity (see, e.g. Ghisellini et al. 2014; Sbarrato et al. 2016).
3. H-ionizing emission from AGN jet lobes
The jets of AGN propagate through the surrounding medium. At some point, the advance of the jet head is significantly slowed down, and the jet flow is shocked, inflating a hot diluted bubble (the lobe). This bubble pushes a shocked shell of external matter, and the evolution of the whole structure is ruled by the properties of the jet, the medium, and the source age (e.g. Scheuer 1974; Kaiser & Best 2007; Hardcastle 2018). In the recent Universe, two types of source are possible, depending on the morphology of the structures formed by their jets after termination (Fanaroff & Riley 1974): Fanaroff-Riley I (FRI), in which the jets get disrupted closer to the host galaxy and form an irregular termination region of ≲100 kpc; and Fanaroff-Riley II (FRII), in which the jets reach the point at which their ram pressures are in equilibrium with those of the (shocked) IGM, on scales of ~1 Mpc.
3.1. IC cooling and lobe dynamics
Regardless of the AGN type – FRI or FRII – the jet inflated lobes and the lobe-shocked IGM contain together, in the adiabatic phase of the structure growth, all the momentum and energy deposited by the jet. In the radiative phase, the energy is lost through different mechanisms, thermal and non-thermal. Regarding the mass within the lobe, there could be a contribution of entrained external medium.
When the jet-blown structure is old enough, losses due to IC on CMB photons can become relevant for its dynamics. Under equal jet and medium properties, this phase starts earlier at higher redshifts (e.g. Saxena et al. 2017, and references therein). A typical CMB photon at z = 6, of energy ∈0 ≈ 3 k TCMB, z = 6 ≈ 5 × 10−3 eV, is IC scattered up to ∈ = 13.6 eV by electrons of Lorentz factor γion ≈ (3∈/4∈0)1/2 ~ 50. For the CMB energy density at that redshift, uCMB, z = 6 = 4σTCMB, z = 64/c ≈ 10−9 erg cm−3, the IC cooling timescale is tIC ≈ 20(γ/50)−1 Myr (shorter at larger z), which is probably much less than the age of an AGN jet at z ≳ 6 with a high duty cycle (i.e. long-living).
The larger the contribution of non-thermal electrons to the lobe pressure is, the stronger the IC impact on the lobe dynamics will be. Despite the non-thermal electron component of the pressure in these lobes is not well constrained, radio and X-ray observations show that this may easily be a substantial fraction of the total lobe pressure (e.g. Croston et al. 2018). In addition, given the lower adiabatic index of a relativistic gas2 (4/3) with respect to that of a non-relativistic gas (5/3), the relativistic-to-non-relativistic pressure ratio goes as Prel/Pnon-rel ~ V1/3 (V being lobe volume), meaning that even moderate non-thermal pressures can eventually dominate for old enough sources.
One can estimate the distance from the host galaxy at which the lobe isotropic IC radiation can be released. The jet propagation depends only on the medium density as long as the former is supersonic. Thus, the characteristic size of the lobe can be calculated while the jet is active as (e.g. Kaiser & Best 2007; Saxena et al. 2017):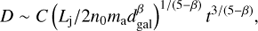 (1)
(1)
where Lj/2 is used because there are two jets per source; C is a constant of O(1) (set to 1 from now on); n0 = 10−25/ma g cm−3 the medium number density at the smallest relevant spatial scale: dgal ≈ 6.2 × 1021 [(1 + z)/3]−1.25 cm for z > 2 (that of the host galaxy); the density profile power-law index (n(r) = n0 (dgal/r)β); and ma ≈ 2 × 10−24 g the average particle mass.
Taking into account that the (proper) average density of the IGM, nIGM ≈ 2 × 10−7(1 + z)3 cm−3, is reached at a (proper) distance from the host galaxy of dIGM ≈ dgal(n0/nIGM)1/β (Saxena et al. 2017), for a typical profile β = 2 one obtains dIGM ~ 20 kpc at z = 6. However, for β = 2 the jet reaches dIGM after a time: (2)
(2)
As tIGM is much less than the age of an AGN jet with high duty cycle, one can set β = 0 for most of the source life, rendering: (3)
(3)
Taking LEdd ~ Lj ~ 1044 erg s−1 translates into a black-hole mass of ~106 M⊙, although we note that the Lj-dependence of tIGM and D is rather weak.
Due to IC losses, a lower limit can be obtained for the jet length simply setting in Eq. (1) t = tIC,bulk, where tIC,bulk is the IC cooling timescale of the energetically dominant non-thermal electrons. This quantity is not well constrained, but unless these electrons have a low-energy cutoff around γmin ≳ 300, it seems likely that tIC,bulk > tIGM. Therefore, it is reasonable to assume that AGN jet lobes at z ~ 6, even those whose dynamics were dominated by IC losses, should have reached D ≳ 10 kpc (see, e.g. Saxena et al. 2017, for similar, more accurate estimates on the lobe sizes). Ionizing photons isotropically produced at those distances from the host galaxy should have easily reached the surrounding IGM, so the escape fraction was one.
It is worth mentioning that even if for some reason IC cooling had been dynamically irrelevant at z ~ 6−7, thermal cooling of the shocked IGM shell could have still released a significant fraction of the jet energy as UV and soft X-rays: ~10% for a long-lasting jet with Lj ~ 1044 erg s−1, under primordial abundances (Sutherland & Dopita 1993), and reaching much farther from the host galaxy (D > 100 kpc).
3.2. Ionizing IC radiation
From the discussion above, it seems likely that AGN jet lobes at z ~ 6−7 were continuously refilled with relativistic electrons, which cooled via IC with CMB photons producing large amounts of ionizing photons. However, the actual fraction of IC scattered photons at the most suitable H-ionizing energies, say far UV, depends on the electron energy distribution.
The electron energy distribution (N, where [N] = energy−1) in jet lobes is expected to be cooled and N ∝ γ−3 or similar, which leads to flat spectral energy distributions (SED) of synchrotron and IC radiation (i.e. vLv ∝ v0 or a spectral index of −1: Lv ∝ v−1). Thus, unless γmin > γion, or N is much steeper than ∝ γ−3 and γmin ~ 1 (meaning less energy at ~ γion), a sub-stantial fraction of the jet energy should have been released in the UV through IC. Even if electrons are injected with γinj > γion, a γmin > γion is not expected under fast IC losses in the Thomson regime, as N below γinj becomes ∝ γ−2 down to the minimum cooled electron energy (i.e. γmin). Such N below γinj implies a moderate hardening of the SED (i.e. vLv ∝ v0.5), but much softer than found, for example, by Wu et al. (2017) at γ ~ 100 for two radio galaxies at z ~ 4. The hard electron distribution of those two objects at γ ~ 100 may be explained, among other factors, by less efficient IC cooling, as z is lower.
We conclude that AGN jet lobes at z ~ 6 may have radiated through IC emission a substantial fraction of the jet energy as H-ionizing photons. The synchrotron (radio) emission from the lobes, produced by electrons with γ ~ 104 ≫ γion (for magnetic fields not very far below equipartition), is expected to be well below the IC emission due to the cooling dominance of IC in Thomson. On the other hand, the synchrotron (radio) emission from the jet termination shocks (the hot spots), may have been as bright as the lobe IC emission because of a higher local magnetic field (Wu et al. 2017).
Taking a cooled population of electrons with N ∝ γ−3, one can approximate the flux for one source in radio (synchrotron radiation from the hot spots), and UV, X- and gamma rays (IC radiation from the lobes), as (4)
(4)
where rc ≈ 8427 Mpc is the comoving radial distance to z = 6. It has been assumed for simplicity that most of the lobe pressure is in the form of non-thermal electrons, and that ~10% of the radiation energy goes to each specific energy band.
3.3. Jet contribution to the reionization
To assess the role of AGN jet lobes to contribute (maintaining and possibly furthering) the reionization of H at z ~ 6−7, we adopted the black-hole mass functions presented in Sect. 2, and fix for each black hole an ionizing luminosity ∝ Lj ∝ LEdd. This yields a H-ionizing luminosity (comoving) density: (5)
(5)
where nBH = φ/MBH ln(10) is the differential (comoving) density of the black-hole mass function (see, e.g. Eq. (6) in Shankar et al. 2009), and the parameter χ includes departures from the optimal scenario, meaning: (i) a jetted AGN fraction of less than one; (ii) an AGN duty cycle <100%; (iii) Lj < LEdd; (iv) a non-dominant lobe non-thermal pressure; and (v) IC radiation mostly below or above UV (in the latter case heating rather than ionizing the medium H, e.g. Shull & van Steenberg 1985; Mirabel et al. 2011). We adopted χ = 0.001 as a conservative case (A), and χ = 0.1 as a very optimistic case (B). Recall that under optimal conditions and Lj > LEdd, χ > 1 is formally possible.
For simplicity, we compare ϵ̇ion at z ~ 6 with the required H-ionizing luminosity (comoving) density of the whole reionization epoch, ϵ̇obs, estimated by Madau (2017) as approximately three ionizing photons per H-atom and Gyr (ϵ̇obs ≈ 1040 erg s−1 Mpc−3 in 13.6 eV photons). We note, however, that a more accurate comparison should properly account for nBH at z > 6, when a strong decline in the empirical nBH is expected with z (e.g. Hopkins et al. 2007; Willott et al. 2010).
The result of the comparison is the following: the computed ϵ̇ion for cases A and B are ≈2 × 1037 erg s−1 Mpc−3 (Willott et al. 2010; ≈1038 erg s−1 Mpc−3 for Shankar et al. 2009) and ϵ̇ion ≈ 2 × 1039 erg s−1 Mpc−3 (Willott et al. 2010; ≈1040 erg s−1 Mpc−3 for Shankar et al. 2009), respectively. Even if very approximate, these results already indicate that jet lobes at z ≳ 6 may have produced ≲1% of the H-ionizing photons in a pessimistic scenario, but their contribution may have been non-negligible (≳20%) under more favorable conditions.
4. Discussion
As mentioned in the previous section, to compare with ϵ̇obs, ϵ̇ion was assumed to be constant for the whole duration of the reionization epoch, but this was likely not the case. For z > 6−7, in addition to the expected decline of the empirical black-hole mass function, the masses of the growing black holes, and thus their Lj, are expected to be lower. On the other hand, the actual number of (jetted) black holes may have been larger than those empirically inferred. For instance, it has been proposed that active IMBH may have been present in all gas-rich dwarf galaxies at z ≳ 6, producing outflows and possibly jets (e.g. Silk 2017; Barai & de Gouveia Dal Pino 2018; see however Latif et al. 2018). In fact, Salvador-Solé et al. (2017) predicts ~100 times more IMBH (M ~ 105 M⊙) at redshift z ~ 6 than the empirical mass functions (Willott et al. 2010). If for instance 10% of those IMBH untraced by empirical studies had produced jets with Lj ~ 0.1 LEdd, their contribution to ϵ̇ion may have been relevant, also at z > 6−7.
In addition to the AGN luminosity function, or the black-hole mass function, the accretion rate (comoving) density (ρ̇acc) at z ~ 6 derived from X-ray background studies can set a limit on the ionizing role of AGN jet lobes assuming ϵ̇ion < ρ̇accc2. Vito et al. (2018) estimates the accretion rate (comoving) density at z ~ 6 as ρ̇acc ~ 10−6 M⊙ yr−1 Mpc−3 (Vito et al. 2018), which yields ϵ̇ion < 6 × 1040 erg s−1 Mpc−3, leaving room for ϵ̇ion to significantly contribute to ϵ̇obs. The estimate for ρ̇acc is model dependent and possibly too conservative, but is not inconsistent with AGN jets being relevant H-ionizing sources at z ≳ 6. The black-hole mass (comoving) densities of the adopted mass functions are ~102−103 M⊙, again consistent with the (model-dependent) limits found in the literature (~103−104 M⊙; e.g. Hopkins et al. 2007; Salvaterra et al. 2012; Comastri et al. 2015; Cappelluti et al. 2017).
It is worth checking, in the jetted AGN scenario studied here, whether ϵ̇ion could represent a non-negligible contribution to the reionization without overcoming the cosmic radiation background (CRB). For the black-hole mass functions adopted here, one can provide an estimate of the broadband flux as: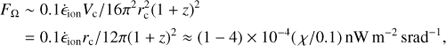 (6)
(6)
where  is the comoving volume of the Universe, z = 6, and a constant source behaviour with z has been assumed. The value of FΩ is an order of magnitude estimate, but can be directly compared with the spectral energy distribution (
is the comoving volume of the Universe, z = 6, and a constant source behaviour with z has been assumed. The value of FΩ is an order of magnitude estimate, but can be directly compared with the spectral energy distribution ( ) shown for example in Fig. 3 in Cooray (2016), which presents values ranging from ~10−3 (radio, gamma rays) to 10−1 nW m−2 srad−1 (X-rays). For instance, for an optimistic χ ~ 0.1, the jetted AGN at z ≳ 6 may have had an important role ionizing the Universe without violating (but somewhat contributing to) the CRB.
) shown for example in Fig. 3 in Cooray (2016), which presents values ranging from ~10−3 (radio, gamma rays) to 10−1 nW m−2 srad−1 (X-rays). For instance, for an optimistic χ ~ 0.1, the jetted AGN at z ≳ 6 may have had an important role ionizing the Universe without violating (but somewhat contributing to) the CRB.
Future, more accurate studies should be devoted to further explore the possibility that AGN jets may have contributed to the reionization of the IGM at z ~ 6 and earlier. In particular, more detailed population prescriptions, including yet untraced IMBH populations, an empirically derived accretion-jet relation for high-z AGN, and a more precise model for the jet lobe dynamics and emission (including the shocked IGM thermal component), would give better constraints on the importance of AGN jets ionizing (and heating) the IGM at z ≳ 6. It would also be valuable to explore the impact of jet lobe relativistic electrons on the CMB spectrum through IC, as arcminute-scale small distortions may be expected (e.g. Yamada et al. 1999; Malu et al. 2017).
5. Summary
In this work, we propose that, at z ≳ 6: (i) accretion was efficient (following, e.g. Willott et al. 2010; Shankar et al. 2013); (ii) jetted AGN were common (following, e.g. Sbarrato et al. 2015); (iii) jets carried a good fraction of the accretion energy (e.g. Ghisellini et al. 2014; Sbarrato et al. 2016); and (iv) AGN jet-inflated lobe pressure has a significant non-thermal electron contribution (e.g. Croston et al. 2018). In addition, we show that a substantial fraction of the jet power could have gone to ionize (and heat) the IGM at z ≳ 6 through CMB IC scattered photons in the lobes. Taking all this into account, and adopting empirical mass functions of black holes at z ~ 6 and extrapolating them to the late reionization epoch (z ~ 6−7) (possibly a conservative characterization of the actual population, e.g. Salvador-Solé et al. 2017; Silk 2017; Barai & de Gouveia Dal Pino 2018), we predict that AGN jet lobes may have contributed non-negligibly to the reionization of the Universe at z ≳ 6.
Nevertheless, it has been proposed that brighter galaxies may have dominated if the reionization duration was relatively short, and their escape fraction high enough (e.g. Sharma et al. 2018).
Acknowledgments
V.B.-R. wants to thank an anonymous referee for constructive and useful comments that helped to improve the manuscript. V.B.-R. wants also to thank Kazushi Iwasawa, Jordi Miralda-Escudé, Massimo Ricotti, and Eduard Salvador for interesting and fruitful discussions on the early Universe. V.B.-R. acknowledges support by the Spanish Ministerio de Economía y Competitividad (MINECO/FEDER, UE) under grant AYA2016-76012-C3-1-P, with partial support by the European Regional Development Fund (ERDF/FEDER), MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”), and the Catalan DEC grant 2014 SGR 86.
References
- Arons, J., & McCray, R. 1970, Astrophys. Lett., 5, 123 [NASA ADS] [Google Scholar]
- Barai, P., & de Gouveia Dal Pino, E. M., 2018, ArXiv e-prints [arXiv:1807.04768] [Google Scholar]
- Cappelluti, N., Li, Y., Ricarte, A., et al. 2017, ApJ, 837, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Gilli, R., Marconi, A., Risaliti, G., & Salvati, M. 2015, A&A, 574, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooray, A. 2016, R. Soc. Open Sci., 3, 150555 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Ineson, J., & Hardcastle, M. J. 2018, MNRAS, 476, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, M., & Shull, J. M. 1987, ApJ, 323, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Douna, V. M., Pellizza, L. J., Laurent, P., & Mirabel, I. F. 2018, MNRAS, 474, 3488 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Ghisellini, G., Tavecchio, F., Maraschi, L., Celotti, A., & Sbarrato, T. 2014, Nature, 515, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Grazian, A., Fiore, F., et al. 2015, A&A, 578, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grazian, A., Giallongo, E., Boutsia, K., et al. 2018, A&A, 613, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardcastle, M. J. 2018, MNRAS, 475, 2768 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R., & Best, P. N. 2007, MNRAS, 381, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Kakiichi, K., Ellis, R. S., Laporte, N., et al. 2018, MNRAS, 479, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Volonteri, M., & Wise, J. H. 2018, MNRAS, 476, 5016 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P. 2017, ApJ, 851, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Malu, S., Datta, A., Colafrancesco, S., et al. 2017, Sci. Rep., 7, 16918 [NASA ADS] [CrossRef] [Google Scholar]
- McGreer, I. D., Fan, X., Jiang, L., & Cai, Z. 2018, AJ, 155, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A., & Madau, P. 1993, ApJ, 412, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Mezcua, M. 2017, Int. J. Mod. Phys. D, 26, 1730021 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., Dijkstra, M., Laurent, P., Loeb, A., & Pritchard, J. R. 2011, A&A, 528, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Onoue, M., Kashikawa, N., Willott, C. J., et al. 2017, ApJ, 847, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Parsa, S., Dunlop, J. S., & McLure, R. J. 2018, MNRAS, 474, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., & Checa, P. S. 2018, Int. J. Mod. Phys. D, 27, 1844019 [NASA ADS] [CrossRef] [Google Scholar]
- Salvador-Solé, E., Manrique, A., Guzman, R., et al. 2017, ApJ, 834, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Haardt, F., Volonteri, M., & Moretti, A. 2012, A&A, 545, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saxena, A., Röttgering, H. J. A., & Rigby, E. E. 2017, MNRAS, 469, 4083 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2015, MNRAS, 446, 2483 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2016, MNRAS, 462, 1542 [NASA ADS] [CrossRef] [Google Scholar]
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Seiler, J., Hutter, A., Sinha, M., & Croton, D. 2018, MNRAS, 480, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Shankar, F., Weinberg, D. H., & Miralda-Escudé, J. 2009, ApJ, 690, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Shankar, F., Weinberg, D. H., & Miralda-Escudé, J. 2013, MNRAS, 428, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, P. R., & Giroux, M. L. 1987, ApJ, 321, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, M., Theuns, T., & Frenk, C. 2018, MNRAS, 477, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., & van Steenberg, M. E. 1985, ApJ, 298, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2017, ApJ, 839, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P. 2016, ARA&A, 54, 761 [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Trebitsch, M., Volonteri, M., Dubois, Y., & Madau, P. 2018, MNRAS, 478, 5620 [Google Scholar]
- Tueros, M., del Valle, M. V., & Romero, G. E. 2014, A&A, 570, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vito, F., Brandt, W. N., Yang, G., et al. 2018, MNRAS, 473, 2378 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Albert, L., Arzoumanian, D., et al. 2010, AJ, 140, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Ghisellini, G., Hodges-Kluck, E., et al. 2017, MNRAS, 468, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, M., Sugiyama, N., & Silk, J. 1999, ApJ, 522, 66 [NASA ADS] [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


