EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 617 (September 2018) A&A, 617 (2018) A36 Full HTML
Free Access
Issue
A&A
Volume 617, September 2018
Article Number A36
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201833112
Published online 17 September 2018

© ESO 2018

1. Introduction

TZ Fornacis (TZ For; HD 20301) is an eclipsing, detached, double-lined binary, which appears in the FK 4 catalogue by Fricke (1963). Andersen & Nordstrom (1983) found both stars to have similar spectral types, classifying them initially as G2 III stars. Eclipses of about 0.15 mag depth were detected photometrically by Olsen (1977), who also confirmed that this Algoltype system consists of two similar early G stars. Andersen et al. (1984) reported preliminary data for TZ For, indicating that both stars have masses close to 2 M⊙, the primary being a G5 giant, and the secondary a slightly evolved post main-sequence star of spectral type F7. At that time TZ For was the second binary after Capella with determined masses, but the first eclipsing one (Olsen 1977), and therefore with much more accurately known masses. The primary was believed, from isochrone matching (at 1.2 Gyr), to be on the first giant branch. The secondary was already known to be fast rotating.

Andersen et al. (1991) updated the observational data with spectroscopic orbit measurements, a spectral analysis for the chemical composition, and a complete ubvy photometric light curve. The resulting masses of 2.05 ± 0.06 M⊙ and 1.95 ± 0.03 M⊙, as well as the radii of 8.32 ± 0.12 R⊙ and 3.96 ± 0.09 R⊙ were, within errors, in agreement with the earlier determinations, but with a factor two improvement in accuracy. The orbital period is 75.7 days and the orbit is circular. The rotation of the primary was found to be synchronized at about 4 ± 1 km s−1, while the secondary rotates at 42 ± 2 km s−1, about 16 times faster than synchronization with the orbital period would require. Effective temperatures were also roughly confirmed at 5000 K and 6300 K. While the secondary was well matched by an evolutionary track at an age of 1.16 × 109 yr, the model for the secondary requires a 10% higher age to match the observed radius and location in the Hertzsprung-Russelldiagram (HRD). However, Andersen et al. (1991) already suspected that models with core overshooting would allow for a satisfying match. In that case, the primary reaches the core helium burning phase and is located in the so-called “clump”. This solution also provides a natural explanation for the synchronization of the primary and leads to an increased system age of 1.75 Gyr. The authors also mention that the primary would not have exceeded its critical Roche radius, not even at its brightest red giant branch (RGB) position. However, using a different set of evolutionary tracks, which also included overshooting, they could not find a satisfactory match.

Since then, TZ For has been used repeatedly as a stringent test for stellar evolution models, always being noted as an exceptional system because of its wide orbit and the advanced evolutionary state of the primary. In particular, with regard to the question of convective overshooting, it has been a favourite object. While Pols et al. (1997) found as best solution a model without overshooting, they remarked that in this case the primary would still be on the RGB and its synchronization would be difficult to explain (see Sect. 2). Consequently, they found a model including overshooting more attractive, which, in agreement with Andersen et al. (1991), puts the primary onto the clump. In contrast, Stancliffe et al. (2015) opt for a RGB solution for this “problematic” object, which they achieve with a larger amount of overshooting than for most of the other 12 detached eclipsing binary systems they investigated.

With the very accurate mass determinations by Gallenne et al. (2016), Valle et al. (2017) conducted an extensive analysis of TZ For with the aim of “calibrating” the amount of overshooting. The parameters of their best solution were used by Higl & Weiss (2017) in their own code and led to an inconsistent result: the primary, now in the core helium burning phase, would have exceeded its Roche volume during the ascent on the RGB, violating the fundamental assumption in all these studies that the system remains detached. This does not imply that the same happened in the models by Valle et al. (2017), where they adopt a different overshooting description without a cutoff function (see the discussion in Sect. 3), but since in this paper there is no comment about the maximum radius reached by the various models in relation to the Roche radius, it is unclear whether the best solutions or any other cases violated this necessary condition1. In any case, the question of Roche-lobe overflow was not addressed in the probability evaluation. We note that in many of the quoted papers the chemical composition was considered as an (within limits) adjustable parameter, while Higl & Weiss (2017) used literature values including errors. In Sect. 3 we will present our own modelling of the two components of TZ For, following mostly the approach of Higl & Weiss (2017). In Table 1 we summarize the default system parameters used in our calculations. Our choice is identical to that of Valle et al. (2017). Deviations will be mentioned explicitly in the text.

Table 1.

Properties of TZ For, taken from Gallenne et al. (2016).

We close this review of previous investigations of the TZ For system by including the work by Eggleton & Yakut (2017), who modelled both components simultaneously including the effects of tidal interaction. Again, the primary was put into the clump phase, but surprisingly their standard mass loss rate had to be reduced by a factor 20 for a successful modelling. A similar investigation will be the content of Sect. 4.

In the next section (Sect. 2) the exceptional properties of the binary system, including the rotation rates of both stars and the implications for the previous history of TZ For will be discussed. In short, the problem in modelling this system lies in the fact that the synchronized rotation of the primary calls for an efficient torquing achieved when the star becomes a red giant. However, the primary must avoid Roche lobe overflow (RLOF) because a post mass transfer system would either exhibit an extreme mass ratio in strong disagreement with the actual one, or even result in a merger. The requirement of a coeval age for both components further restricts the possible solutions and calls for a very specific set of system parameters. After presenting our successful models in Sects. 3 and 4 and discussing the uncertainties, the conclusions will close the paper in Sect. 5.

2. Rotation and mass transfer

2.1. Rotation

The primary’s synchronous rotation is fully accounted for by its evolutionary history and by the effects of tidal interaction, given its envelope structure (convective) and its relatively large radius R1 in units of the orbital separation a, R1/a = 0.069. This, in turn, also implies that we do not have any information about the primary’s rotation when it was on the main sequence.

As to the secondary’s rotation rate, the situation is quite different. Because that star has only just reached the final phases of central hydrogen burning (see Sect. 3), its effective temperature was always high enough for it to keep an essentially radiative envelope. Therefore, given its small relative radius R2/a (current value 0.033, and on the main sequence 0.0070), tidal interaction was never significant. As a consequence, we may assume that its rotational angular momentum has not changed much during its evolution from the early main sequence. This fact allows us now to estimate the secondary’s rotation rate on the main sequence from its current rotational velocity vrot, 2 = 42 km s−1.

If we assume that the star, as a consequence of the weak tidal interaction, kept rotating as a solid body, conservation of angular momentum then yields the following estimate for the secondary’s rotational velocity on the zero age main sequence (ZAMS):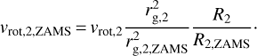(1)

Here, rg,2 and rg,2,ZAMS are the gyration radii, where rg is defined by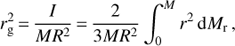(2)

where I is the moment of inertia. R2 and R2, ZAMS are the corresponding radii, and vrot, 2 the observed rotational velocity of the secondary star. From our 1.95 M⊙ stellar model we obtain 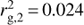and r2g, 2, ZAMS = 0.045. Thus, assuming solid body rotation, we estimate the secondary’s rotational velocity on the ZAMS as vrot, 2, ZAMS ≈ 59 km s−1. This corresponds to a rotation period of Prot, 2, ZAMS ≈ 1.3 d.

If, on the other hand, tidal interaction was completely ineffective in redistributing angular momentum within the star, the specific angular momentum in the radiative layers would be locally conserved. In that case, the surface rotational velocity on the ZAMS is given by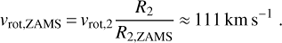(3)

This corresponds to a rotational period on the ZAMS of Prot, 2, ZAMS ≈ 0.69 d.

What these estimates tell us is that the secondary was rotating highly supersynchronously on the main sequence with, assuming solid body rotation, Prot, 2, ZAMS/Porb ≈ 0.017, or Prot, 2, ZAMS/Porb ≈ 0.0091 if the specific angular momentum of the surface layers is conserved. Rapid as this rotation may appear, it is still well below the critical rotation rate. If the critical angular rotation frequency is defined as Ωcrit, 2 = (GM2/R23)1/2, our estimates yield on the main sequence Ωrot, 2/ Ωcrit, 2 ≈ 0.12 in the case of solid body rotation, or Ωrot, 2/ Ωcrit, 2 ≈ 0.22 in the other case. Thus it appears that the rotation rate of the secondary on the main sequence was surprisingly high, but still well below critical rotation. To what extent this is also true for the convective core can of course not be inferred from the available data. However, as we have shown, the secondary may have been rotating pretty fast on the main sequence and therefore, its evolution might well have been affected by rapid core rotation, which, however, we do not model in the present paper.

2.2. Mass transfer

Models for TZ For involving Roche lobe overflow as the primary climbs the RGB are untenable for the following reasons: had the primary of TZ For really undergone even some minor mass loss via Roche lobe overflow, then its initial mass ratio qi = M1, i/M2, 1 would have been larger than its present value, that is, qi > q = 1.057. Now it is well known that binary systems with a mass ratio qi > 1 and with a primary star filling its critical Roche volume during a phase when it has a deep outer convective envelope, as is for example the case while a star is climbing the giant branch on its way to ignition of central helium burning, are highly unstable against runaway mass transfer (see e.g. Ge et al. 2015; Pavlovskii & Ivanova 2015). As a consequence, the mass transfer rate would grow enormously on timescales short compared to the evolutionary timescale of the donor star. Eventually, the mass transfer rate would saturate at a value that is of the order −M1 ≈ M1/τconv ≈ M⊙/yr, where τconv is the convective turnover timescale in the envelope of the mass losing star.

Qualitatively, the outcome of such an evolution, sometimes referred to as convective Case B mass transfer, is well known. Such systems enter a common envelope evolution in which the core of the primary and the companion star spiral-in in a common envelope which, in turn, is formed by the former convective envelope of the donor star. The outcome of such an evolution depends on whether the energy liberated by the spiraling-in process (mainly the gravitational binding energy of the binary and the recombination energy of the envelope) is sufficient to unbind the common envelope (see e.g. Ivanova et al. 2013). If the envelope can be successfully ejected, the result of common envelope evolution is a short-period, detached binary consisting of the core of the former primary and the essentially unchanged secondary star. On the other hand, if envelope ejection fails, the binary merges and eventually forms a single star. Applying standard methods, as for example detailed in Ivanova et al. (2013), to evaluate the outcome of common envelope evolution in our case of interest, we find that the presumed progenitor of TZ For, once it enters RLOF, would merge and end up as a single star. Therefore, mass transfer via RLOF during the RGB-phase of the primary can safely be excluded.

3. Two single stars

3.1. Input physics

We use the Garching Stellar Evolution Code (GARSTEC; Weiss & Schlattl 2008) to evolve two independent single stellar models with the goal of reproducing the measured fundamental parameters listed in Table 1. The GARSTEC computations consider the evolution of the two stars separately, assuming a constant binary orbit. To check the validity of this assumption we ran simulations with BINSTAR (Sect. 4) using the same input physics. Our simulations show that, in the absence of RLOF and wind mass loss, the orbital period remains weakly affected by the effect of tides. The reason is that most of the angular momentum resides in the orbit rather than in the stellar spins. Therefore, the assumption that the system remains detached is justified and the evolution of non-interacting single stars is a valid approach.

All computations start on the pre-main sequence. The mixing-length parameter is αmlt = 1.74, resulting from a standard solar model calibration. The outer boundary condition is an Eddington grey atmosphere. As in Valle et al. (2017), we consider the solar composition of Asplund et al. (2009), but also compare our results to models computed with the solar composition of Grevesse & Noels (1993). The opacity tables were computed for the same relative metal abundances and are a combination of OPAL tables for high temperatures (Iglesias & Rogers 1996), extended at low temperatures by the Wichita State Alexander and Ferguson molecular opacities (Ferguson et al. 2005). The equation of state is also the OPAL one (Rogers & Nayfonov 2002, release 2005). With the exception of the updated 14N(p, γ)15O reaction rate (Marta et al. 2008), we take our reaction rates from the NACRE collaboration (Angulo et al. 1999). For all other details of code and input physics we refer the reader to Weiss & Schlattl (2008).

Our overshooting description is implemented according to Freytag et al. (1996), where overshooting is assumed to be a diffusive process, with the diffusion coefficient D(z) given by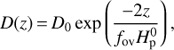(4)

where z is the distance to the Schwarzschild boundary, 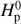the pressure scale height at the convective boundary, and D0=1/3ν. 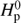the value of the convective diffusion coefficient, with v0 being the velocity of convective mass parcels close to the convective boundary, obtained from mixing length theory. In order to avoid unphysically large overshooting for small convective cores, arising from the diverging pressure scale height near the stellar centre, our implementation is modified by a geometrical cutoff of the overshoot region. We limit the scale length 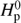in Eq. (4) with respect to the radial extent of the convective zone ΔRCZ by replacing it with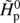 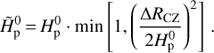(5)

This (artificial) cutoff allows us to model the turnoff morphology of old open clusters and ensures that the convective core during the pre-main sequence evolution of the Sun (and other stars in this mass range) disappears (Schlattl & Weiss 1999). In our simulation, by default we apply this overshooting with the same value of fov at the edge of the convective core and base of the envelope, unless specified otherwise.

The alternative, and more traditional method to implement overshooting, is to simply extend the convectively mixed region by a fixed fraction of the scale height, as 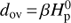, with β being here the overshooting parameter. For small convective cores, dov is sometimes limited as a function of initial stellar mass (e.g. as in Pietrinferni et al. 2004). Since our specific implementation differs from that in the codes used by Valle et al. (2017), it is not surprising that the models do not reproduce the results of that paper. However, in contrast to Valle et al. (2017), who intended to determine the overshooting parameter that leads to a bestfitting model (for two stellar evolution codes), and who investigated in detail the influence of parameter uncertainties, our aim is to define the necessary condition for both a successful system fit and a previous evolution that is consistent with the properties of the binary system. We mention in passing that further physical details, which may influence the ignition of core helium burning and therefore the maximum radius reached on the RGB, may differ between our models and those by Valle et al. (2017). Examples are the conductive opacities and the plasma neutrino emission. The choice of boundary conditions and of αmlt is also known to have an impact on the evolution in the HRD and thus on the RGB tip radius (see e.g. Cassisi 2017).

In all our simulations we ignore mass loss from stellar winds, but take into account the mass defect in the fusion reactions, which are, however, insignificant. The mass ratio being very close to one, both stars are computed with the same values of the mixing length and overshooting parameters.

As in Higl & Weiss (2017), models are considered to reproduce the binary system if they account for the observed radii at the same age. A further indication of the quality of the model is whether positions in the HRD are reproduced at that age. A correspondence in the HRD also implies that the models match the more directly observed temperature and luminosity ratios (see Higl & Weiss 2017, for a discussion). Our intent is not to reproduce the analysis by Valle et al. (2017) and provide another fit to TZ For, but rather to emphasize that beyond the physical parameters of a model, additional sources of uncertainties related for example to the implementation of the overshooting algorithm can have a strong impact on the calibration of observables.

3.2. The influence of overshooting

To start this analysis, we re-computed the models of Valle et al. (2017) with GARSTEC, using the same composition for each model, and equivalent overshooting parameters (Table 2). To transform the overshooting parameter from the overshooting description used in FRANEC (Frascati Raphson Newton Evolutionary Code; F models in Valle et al. 2017) to the diffusive approach implemented in GARSTEC, we approximated fov ≈ β/10 (see e.g. Ventura 2007). The M-models were computed with the Modules for Experiments in Stellar Astrophysics code (MESA; Paxton et al. 2013), where the same overshooting implementation is used as in GARSTEC. Therefore, the value of fov is identical, but nevertheless, the implementation of both the basic mixing-length theory and the overshooting itself differ between codes. This is particularly true for the geometrical cutoff we are using (Eq. (5)).

Valle et al. (2017) determine an overall probability of their models, depending on how well they fit the observables, including the positions in the HRD. The primary may reach the observed radius at two evolutionary phases: on the first giant branch ascent, during hydrogen shell burning, and later, after core helium ignition on the clump. For the five models with the highest probability (F-I, F-II, F-I/II, M-I, M-II) the primary is indeed located in the clump. Repeating these model computations with our code in all cases leads to Roche-lobe overflow while the primary evolves up the RGB (see Col. 7 in Table 2 and Fig. 2), which is untenable as demonstrated in Sect. 2.2. The reason for this discrepancy is clearly due to the use of our cutoff procedure, as can be seen from the characteristics of models G-I and F-II in Table 2 (see also discussion below). The solution could therefore be that the primary is still on the RGB but this results in a significant age discrepancy of about 10% (Col. 5 of Table 2). Furthermore, the positions in the HRD are not reproduced anymore: the primary is cooler than observed, and the secondary is too luminous (see Cols. 9 and 10 in Table 2).

thumbnail Fig. 1.

Evolution in the central temperature-density diagram of the primary star of the TZ For system for various amounts of overshooting as labelled. Models with fov > 0.0175 avoid the off-centre degenerate ignition of helium.
thumbnail Fig. 2.

Evolution of the radii using the parameters given in Valle et al. (2017). The F and M models are shown in red and blue respectively. The F and M models numbered with I, II, and III are represented by solid, dotted, and dashed lines respectively. The F-I/II model is shown with a dashed dotted line. From top to bottom, the panels show the evolution of the primary’s radius relative to its Roche radius, and the primary and secondary radii. The corresponding observed radii including the error ranges are indicated by the horizontal grey long- and short-dashed lines

Table 2.

GARSTEC (Weiss & Schlattl 2008) model parameters.

In models F-III and M-III the overshooting parameter is increased allowing the models to develop a more massive core and consequently to avoid RLOF. In these cases we are able to simultaneously fit the radius of the primary and its HRD position during the clump phase. The HRD position of the secondary, however, is missed for both models. The F-III simulation still shows a significant age discrepancy (Table 2), because the primary reaches its radius already at the very beginning of core helium burning. This is not the case for the M-III primary. Both components are fitted at the same age.

The G-models of Table 2 are variations of the F- and M- models. For G-I we used the parameters of F-II, but removed the cutoff function in our overshooting implementation (Eq. (5)), thereby reducing the difference in the treatment of overshooting with the comparison cases. The primary then avoids the overflow, as in this case the mixed core is larger from the beginning of the main-sequence evolution. The secondary, computed with the same overshooting, experiences a prolonged main sequence, reaching the observed radius and HRD position in the red hook at the end of the main sequence (see Fig. 3). Model G-I therefore yields a good fit to both components of TZ For. Since only the size of the mixed core is decisive to avoid RLOF, the same result can be achieved with the overshooting cutoff being activated, if the overshooting parameter is increased from 0.017 to 0.035 (model G-II).

thumbnail Fig. 3.

HRD of our best fit GARSTEC models. The models for primary and secondary are shown in red and blue, respectively, and the error boxes of their HRD positions are enclosed by lines of the same colour. Solid, dashed, and dotted lines correspond to models G-II, G-I, and G-III, respectively

Since the primary of TZ For is in the transition region between low- and intermediate-mass stars, a change in the core mass induced by overshooting can have a strong impact. In particular low-mass stars that develop degenerate cores reach much larger radii at the RGB tip than their more massive counterparts. Therefore, by increasing the overshooting parameter, the star will develop a more massive core and ignite He at the centre under non-degenerate conditions. In this way the star may remain within its Roche radius at any time. To illustrate the high sensitivity of this model to extra-mixing at the edge of the convective core, we present in Fig. 1 the evolution of the central temperature as a function of central density for various amounts of overshooting. These simulations were computed with the BINSTAR code, using the assumptions of model G-I. As can be seen, a slight increase of fov from 0.0175 to 0.018 has a dramatic effect on the primary. The evolution switches from a degenerate off-centre to a quiet central helium ignition. The increase in the convective core mass induced in this slight increase in fov is very small, of the order of 10−3M⊙, but has a dramatic impact on the radius, which drops from 76 R⊙ to 27 R⊙. As a consequence of this great sensitivity, the marginal RLOF in model M-II can be avoided by either using a higher value of αmlt = 2 or by ignoring overshooting from the bottom of the envelope (Sect. 3.1). Both methods significantly reduce the age difference in the αmlt and the overshooting case to respectively 30 and 70 Myr, but fail to reproduce the HRD positions.

Another crucial parameter is the helium content, which depends on our assumption about the enrichment law, ΔY/ΔZ. Like Valle et al. (2017) we find that a value of two prevents a successful modelling, and a reduced value of one is needed. This is true for both solar composition options, Asplund et al. (2009) or Grevesse & Noels (1993). Model G-III of Table 2 is an example of a successful match with the latter choice for the solar composition using the standard value ΔY/ΔZ = 1. Its higher total metallicity, at the same observed [Fe/H], does not influence the models significantly.

4. The CRAP scenario

4.1. Input physics

The binary calculations were performed with the BINSTAR code using the same input binary physics as described in Siess et al. (2013). The models are computed with the Asplund et al. (2005) solar composition and a mixing length αmlt = 1.75. Core overshooting is modelled by extending mixing beyond the formal Schwarzschild boundary over a distance 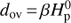as described in Sect. 3.1. In these simulations we assume that the stars are rotating as solid bodies and that the wind carries away the specific orbital angular momentum of the star at its position on the orbit (the so-called Jeans mode).

4.2. Binary models

Before starting our discussion, we would like to stress that in binary evolution calculations, simulations traditionally begin with imposed ZAMS structures. However, in some cases it is very difficult to account for these initial conditions if modelling has started from pre-main sequence initial models. In the case of TZ For however, we are on the safe side because with a period of 75 d, the system always remains detached even though the initial stellar models had a very large radius.

This parenthesis closed, we saw that in order to avoid Roche lobe overflow, the primary has to behave like a more massive star so its RGB tip radius is smaller. One way to do this is to increase the core mass during the main sequence, implying a large core overshooting. The alternative possibility we are exploring here is to start from an initially higher mass primary and enhance the mass loss. Such a wind enhancement was advocated to explain the formation of certain RS CVn binaries where the initially more massive primary (mass M1) is now more evolved and less massive than its companion (mass M2). Unlike Algols, these systems did not evolve through a mass transfer phase implying that wind mass loss had to be substantially increased to explain the reversed mass ratio (q = M1/M2 < 1). To solve the problem, Tout & Eggleton (1988b) came up with the so-called Companion Reinforced Attrition Process (CRAP) whereby tidal friction and dynamo activity would somehow increase the mass loss rate. They devised an expression for the enhancement factor that has the same dependence on the radius as the tidal torque acting onto the star, leading to an effective mass loss rate of the form(6)

where Ṁ is the default mass loss rate, in our case Schröder & Cuntz (2007), R the stellar radius, and RL the Roche radius estimated using the Eggleton (1983) expression. The value of the parameter B has been shown to vary depending on the type of system to be modelled. For example, Tout & Eggleton (1988b) need B ≈ 104 to reproduce the properties of Z Her, an RS CVn binary, while in a different context Siess et al. (2014) advocate a higher value of B ≈ 3.6 × 104 to account for the high eccentricity of the IP Eri system. This parameter thus remains largely unknown as its value likely depends on the structure of the two stars. It should also be noted that the tidally enhanced wind scenario has been advocated to account for the properties of Algols (Tout & Eggleton 1988a), nova-like cataclysmic variable (Qian et al. 2007), to explain the eccentricity of Barium stars (Karakas et al. 2000; Bonačić Marinović et al. 2008), or as a potential second parameter in the shaping of the horizontal branch of globular clusters (Lei et al. 2013).

Since only the primary will suffer this enhanced mass loss, the initial secondary mass is very close to its observed value and, as argued before, a strong overshooting is needed to reproduce its position in the HR diagram. A good fit is obtained for M2 = 1.98 M⊙ and β= 0.22, in very good agreement with the values used by Claret & Gimenez (1995). We stress that the same amount of overshooting is considered for both system components. For the primary the situation is slightly more complicated because the mass at the time the secondary reaches its position on the HR diagram depends on the efficiency of the tidally enhanced wind. The discriminant factor comes from the age constraint. If the primary is initially too massive, even though mass loss is stronger, it will evolve too quickly and it will not be possible to match the properties of both components at the same time. On the other hand, with lower initial primary mass, the CRAP parameter has to be reduced as well as the amount of core overshooting to avoid the age problem just mentioned. Eventually, for B = 0 the model should converge to the previous solution. So there is some degeneracy in the parameters that unfortunately cannot be lifted. To illustrate this binary evolution we consider a system with M1, i ≈ 2.2 M⊙, M2, i ≈ 1.98 M⊙, = 0.22 for both stars, and B ≈ 4000. In this investigation, we did not try to fit exactly the data, which is not intrinsically enlightening, but rather to demonstrate the consistency of this binary scenario.

The evolution of the system is summarized in Fig. 4. During the main sequence, the slow increase in the stellar radius induces a modest spin down of the stars. At the same time, mass loss originating mainly from the more massive component produces a small increase of the orbital period. When the primary leaves the main sequence (at an age of around 995 Myr), the surface velocity drops significantly while the star crosses the Hertzsprung gap. When it reaches the base of the RGB (t ≈ 1.01 Gyr), the primary rotates sub-synchronously and has developed an extended surface convective region. Tidal torques become efficient and angular momentum is transferred from the orbit to the star, producing a shrinkage of the orbital period. As the star climbs the RGB and progressively fills its Roche lobe, mass loss strengthens reaching a value 60 times higher than in the standard evolution without CRAP. During this ascent, the primary loses ≈0.1 M⊙ and owing to efficient tides, it remains synchronized. He ignition occurs around t ≈ 1.0265 Gyr and produces a strong contraction of the star, which is now rotating supersynchronously. Since the primary keeps an extended surface convective zone, angular momentum is now transferred back from the star to the orbit producing an increase in the orbital period. During the subsequent core He burning phase, nothing really happens except for the secondary, which is now evolving off the main sequence and starts to spin down due to expansion. Eventually, at an age of ~1.26 Gyr, both stars reach their observed positions in the HRD (Fig. 5). As pointed out by Claret (2011), given the orbital parameters of TZ For, the primary will always reach synchronization upon arrival on the clump, independent of its initial spin velocity. This is not the case for the secondary where tides are inefficient and one has to consider an initial (ZAMS) surface velocity of ≈70 km s−1, about 15% of the critical rotation rate, to comply with the observations. This value is slightly higher than the estimate provided in Sect. 2.1 because of angular momentum loss from the stellar winds and tides.

thumbnail Fig. 4.

Evolutionary properties of the 2.2+1.98 M⊙, Porb = 69 d system with the enhanced mass loss and for an initial ZAMS surface rotation velocity of 70 km s−1. In the various panels, the solid black and reddotted lines refer to the primary and secondary, respectively. From top to bottom the panels show the Kippenhahn diagram of the primary (a), the evolution of the ratio of the spin to orbital angular velocity (b), of the stellar radii (c), of the surface rotation velocity (d), orbital period (e), and stellar masses (f). The observational constraints are also indicated by the open squares. The estimated age of the system is ~1.26 Gyr.
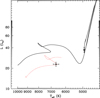thumbnail Fig. 5.

Evolution in the HR diagram of the 2.2+1.98 M⊙, Porb = 69 d system with the enhanced mass loss.

5. Conclusion and discussion

We have presented several options for modelling successfully the detached eclipsing binary system TZ For, which is very interesting because of the quite different evolutionary states of the two components, and the numerous precisely measured system properties. To reach a self-consistent solution, one has to take into account several constraints: the primary is in an advanced stage, either on the RGB or already in the clump phase. Our simulations indicate that a RGB solution faces a big problem associated with the inability of the models to fit at the same age all the system’s properties. If the HRD positions are matched then the stellar radii are reached at different ages, the discrepancy being of the order of 10%. This solution may also pose problems to explain the synchronization of the primary with the orbital motion. From our investigations, we thus conclude that an early RGB solution is not possible mainly because of the age difference. In contrast, being in the core helium burning phase on the clump, the star passed a giant phase with a deep convective envelope where equilibrium tides are very efficient, leading to the observed synchronization irrespective of the initial spin velocity.

During its ascent on the RGB, the primary may, however, overfill its Roche lobe leading to severe mass transfer. Even if the two components did not merge, as we find to be the most likely scenario in Sect. 2.2, the final mass of the primary would be that of the core – a few tenths of a solar mass, which would be in conflict with the measured mass M2. Thus, the RGB evolution has to be terminated at a sufficiently small radius. Since the primary mass (2.05 M⊙) is in the mass range of transition from a degenerate to a non-degenerate ignition of core helium burning, the maximum radius reached on the RGB depends sensitively on the detailed core properties in the earlier phases. The decisive quantity is the extent of the convective core, or, more precisely, of the centrally mixed region on the main sequence.

We have investigated two options to increase the mass of the mixed core: by increasing the initial mass and by invoking convective core overshooting. In the latter case we followed the evolution of both components under the assumption of independent single star evolution. The physical assumptions were, because of the very similar stellar masses, necessarily identical. We showed in Sect. 3.2 that with an increased overshooting parameter of 0.035 (our standard value being 0.017) the system can be fitted both in terms of coeval radius and HRD matching. Alternatively, if we drop the geometrical restriction of the overshooting region (Eq. (5)), a value fov of 0.017 leads to the same result. This is in basic agreement with earlier attempts to model TZ For by Andersen et al. (1991), Valle et al. (2017), and Eggleton & Yakut (2017), however without any of the caveats mentioned in these papers (see Sect. 1). We also showed that employing the same parameters as Valle et al. (2017) in our code, in particular those of their preferred model F-I, would lead to Roche-lobe overflow while the primary climbs the RGB, and thus to an inconsistent model. The main reason is the mentioned geometrical cut for overshooting from small convective cores that is implemented in GARSTEC and not in Valle et al. (2017), but other physical quantities that influence the ignition of helium burning, such as the conductive opacities or the energy loss from neutrino emission, may also influence the maximum radius reached, as well as the detailed implementation of mixing-length theory and the outer boundary conditions provided by the atmosphere model.

The option of unrestricted overshooting (in both stars) is in fact in agreement with the treatment of convective cores in lowmass stars by Pietrinferni et al. (2004), who use a linear, massdependent activation of the overshooting parameter between 1.1 M⊙ and 1.7 M⊙. As such, it would indicate that our own geometrical cutoff approach of Eq. (5) may be too restrictive, and would support the result concerning core overshooting by Higl & Weiss (2017). Alternatively, the need for an extended mixed region might in part be ascribed to an additional mixing effect caused by the fast rotation of the stars on the ZAMS.

The alternative option to limit the radius reached on the RGB is to increase the initial mass of the primary, resulting thus in a larger convective core as well. This, however, has to be done in view of changing the main-sequence lifetime and thus jeopardizing the coeval ages of both components. We tested this option in Sect. 4, where the evolution of the binary system as a whole was modelled with an appropriate code (BINSTAR). Enhanced mass loss according to the CRAP scenario by Tout & Eggleton (1988b) was invoked to reduce the initial primary mass to its present, observed value. Again, a successful fit can be achieved with this approach (Sect. 4.2), at an age of 1.26 Gyr, to be compared to 1.29 Gyr of the fit of Sect. 3.2.

We therefore find that a self-consistent fit of the binary system TZ For is possible by at least two different approaches. Both limit the red giant expansion of the primary star, and both need tuned physical assumptions: either unrestricted core overshooting on the main sequence in spite of its rather low mass, or enhanced mass loss in the post-main sequence phase. We stress the fact that we always used identical physical assumptions for both components. The surprisingly high rotation rate of the secondary remains unexplained, but has no direct influence on our models, except that it may indicate significant rotational mixing on the main sequence.

1

Apparently, the best solution models did not exceed the Roche radius (P. G. Prada Moroni, priv. comm.).

Acknowledgments

We are grateful for helpful and instructive comments by our referee P. G. Prada Moroni. This work was carried out during a visit of LS to the Max Planck institute in Astrophysics in Garching. LS thanks MPA for its kind hospitality. LS is senior FRS-F.N.R.S. research associate.

References

  1. Andersen, J., & Nordstrom, B. 1983, A&AS, 52, 479 [NASA ADS] [Google Scholar]
  2. Andersen, J., Clausen, J. V., Nordstrom, B., & Mayor, M. 1984, in Observational Tests of the Stellar Evolution Theory, eds. A. Maeder, & A. Renzini, IAU Symp., 105, 397 [Google Scholar]
  3. Andersen, J., Clausen, J. V., Nordstrom, B., Tomkin, J., & Mayor, M. 1991, A&A, 246, 99 [NASA ADS] [Google Scholar]
  4. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  5. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
  6. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bonačić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cassisi, S. 2017, Eur. Phys. J. Web Conf., 160, 04002 [Google Scholar]
  9. Claret, A. 2011, A&A, 526, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Claret, A., & Gimenez, A. 1995, A&A, 296, 180 [NASA ADS] [Google Scholar]
  11. Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
  12. Eggleton, P. P., & Yakut, K. 2017, MNRAS, 468, 3533 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
  14. Freytag, B., Ludwig, H.-G., & Steffen, M. 1996, A&A, 313, 497 [Google Scholar]
  15. Fricke, W. 1963, Veröff. Astr. Recheninst. Heidelberg, 11 [Google Scholar]
  16. Gallenne, A., Pietrzyński, G., Graczyk, D., et al. 2016, A&A, 586, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Ge, H., Webbink, R. F., Chen, X., & Han, Z. 2015, ApJ, 812, 40 [NASA ADS] [CrossRef] [Google Scholar]
  18. Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
  19. Higl, J., & Weiss, A. 2017, A&A, 608, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
  22. Karakas, A. I., Tout, C. A., & Lattanzio, J. C. 2000, MNRAS, 316, 689 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lei, Z.-X., Zhang, F.-H., Ge, H.-W., & Han, Z.-W. 2013, A&A, 554, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Marta, M., Formicola, A., Gyürky, G., et al. 2008, Phys. Rev. C, 78, 022802 [NASA ADS] [CrossRef] [Google Scholar]
  25. Olsen, E. H. 1977, A&AS, 29, 313 [NASA ADS] [Google Scholar]
  26. Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [NASA ADS] [CrossRef] [Google Scholar]
  27. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
  28. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  29. Pols, O. R., Tout, C. A., Schroder, K.-P., Eggleton, P. P., & Manners, J. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
  30. Qian, S.-B., Dai, Z.-B., He, J.-J., et al. 2007, A&A, 466, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
  32. Schlattl, H., & Weiss, A. 1999, A&A, 347, 272 [NASA ADS] [Google Scholar]
  33. Schröder, K.-P., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Siess, L., Izzard, R. G., Davis, P. J., & Deschamps, R. 2013, A&A, 550, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Siess, L., Davis, P. J., & Jorissen, A. 2014, A&A, 565, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Stancliffe, R. J., Fossati, L., Passy, J.-C., & Schneider, F. R. N. 2015, A&A, 575, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Tout, C. A., & Eggleton, P. P. 1988a, ApJ, 334, 357 [NASA ADS] [CrossRef] [Google Scholar]
  38. Tout, C. A., & Eggleton, P. P. 1988b, MNRAS, 231, 823 [NASA ADS] [CrossRef] [Google Scholar]
  39. Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2017, A&A, 600, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Ventura, P. 2007, in EAS Pub. Ser., eds. C. W. Straka, Y. Lebreton, & M. J. P. F. G. Monteiro, 26, 79 [CrossRef] [Google Scholar]
  41. Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Properties of TZ For, taken from Gallenne et al. (2016).

In the text
Table 2.

GARSTEC (Weiss & Schlattl 2008) model parameters.

In the text

All Figures

thumbnail Fig. 1.

Evolution in the central temperature-density diagram of the primary star of the TZ For system for various amounts of overshooting as labelled. Models with fov > 0.0175 avoid the off-centre degenerate ignition of helium.
In the text
thumbnail Fig. 2.

Evolution of the radii using the parameters given in Valle et al. (2017). The F and M models are shown in red and blue respectively. The F and M models numbered with I, II, and III are represented by solid, dotted, and dashed lines respectively. The F-I/II model is shown with a dashed dotted line. From top to bottom, the panels show the evolution of the primary’s radius relative to its Roche radius, and the primary and secondary radii. The corresponding observed radii including the error ranges are indicated by the horizontal grey long- and short-dashed lines
In the text
thumbnail Fig. 3.

HRD of our best fit GARSTEC models. The models for primary and secondary are shown in red and blue, respectively, and the error boxes of their HRD positions are enclosed by lines of the same colour. Solid, dashed, and dotted lines correspond to models G-II, G-I, and G-III, respectively
In the text
thumbnail Fig. 4.

Evolutionary properties of the 2.2+1.98 M⊙, Porb = 69 d system with the enhanced mass loss and for an initial ZAMS surface rotation velocity of 70 km s−1. In the various panels, the solid black and reddotted lines refer to the primary and secondary, respectively. From top to bottom the panels show the Kippenhahn diagram of the primary (a), the evolution of the ratio of the spin to orbital angular velocity (b), of the stellar radii (c), of the surface rotation velocity (d), orbital period (e), and stellar masses (f). The observational constraints are also indicated by the open squares. The estimated age of the system is ~1.26 Gyr.
In the text
thumbnail Fig. 5.

Evolution in the HR diagram of the 2.2+1.98 M⊙, Porb = 69 d system with the enhanced mass loss.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.