| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | L17 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201833205 | |
| Published online | 27 August 2018 | |
Letter to the Editor
XMM-Newton detection of the 2.1 ms coherent pulsations from IGR J17379–3747
1
Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu km 0.7, 09042 Monserrato, Italy
e-mail: andrea.sanna@dsf.unica.it
2
ISDC, Department of Astronomy, University of Geneva, Chemin d’Écogia 16, 1290 Versoix, Switzerland
3
INAF, Osservatorio Astronomico di Roma, Via di Frascati 33, 00044 Monteporzio Catone (Roma), Italy
4
Università degli Studi di Palermo, Dipartimento di Fisica e Chimica, via Archirafi 36, 90123 Palermo, Italy
5
INAF, Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047 Selargius (CA), Italy
Received:
10
April
2018
Accepted:
19
July
2018
We report the detection of X-ray pulsations at 2.1 ms from the known X-ray burster IGR J17379–3747 using XMM-Newton. The coherent signal shows a clear Doppler modulation from which we estimate an orbital period of ~1.9 h and a projected semi-major axis of ~8 lt-ms. Taking into account the lack of eclipses (inclination angle of <75°) and assuming a neutron star mass of 1.4 M⊙, we have estimated a minimum companion star of ~0.06 M⊙. Considerations on the probability distribution of the binary inclination angle make the hypothesis of a main-sequence companion star less likely. On the other hand, the close correspondence with the orbital parameters of the accreting millisecond pulsar SAX J1808.4–3658 suggests the presence of a bloated brown dwarf. The energy spectrum of the source is well described by a soft disk black-body component (kT ~ 0.45 keV) plus a Comptonisation spectrum with photon index ~1.9. No sign of emission lines or reflection components are significantly detected. Finally, combining the source ephemerides estimated from the observed outbursts, we obtained a first constraint on the long-term orbital evolution of the order of Ṗorb = (−2.5 ± 2.3) × 10−12 s s−1.
Key words: binaries: general / stars: neutron / X-rays: binaries / accretion, accretion disks
© ESO 2018
1. Introduction
Accreting millisecond X-ray pulsars (AMXPs) are quickly rotating neutron stars (NSs) which accrete mass transferred from a low-mass (≤M⊙) companion star via Roche lobe overflow. The observations of X-ray pulsations at the NS spin period shows that the magnetic field of the NS in these systems is strong enough to channel the mass flow to the magnetic poles. The discovery of AMXPs (Wijnands & van der Klis 1998) demonstrated that a prolonged phase of mass accretion is able to spin up a NS to such a quick rotation. When mass transfer ceases a rotation-powered radio millisecond pulsar (MSP) turns on (Alpar et al. 1982). The discovery of transitional MSPs that are able to switch between accretion and rotation-powered regimes (Archibald et al. 2009; Papitto et al. 2013b) has recently demonstrated the tight evolutionary link shared by neutron stars in low-mass X-ray binaries and radio MSP. Twenty AMXPs have been discovered so far (e.g. Burderi & Di Salvo 2013; Patruno et al. 2017a; Sanna et al. 2018a), a small fraction of the >200 low-mass X-ray binaries known to host a NS. They are all relatively faint X-ray transients which attain a luminosity of 0.01–0.1 Eddington rate at the peak of their outbursts, which are typically a few weeks long. X-ray pulsations at a period ranging between 1.6 ms (Galloway et al. 2005) and 9.5 ms (Sanna et al. 2018a) are observed during the X-ray outburst with a fractional amplitude of the order of ~1−10%. AMXPs have been found in binary systems with an orbital period shorter than a day and as low as ~40 min, indicating companion stars with masses ranging from 0.6 to 0.01 M⊙ (see e.g. Patruno & Watts 2012; Burderi & Di Salvo 2013).
IGR J17379–3747 is a known X-ray burster observed in outburst by the Rossi X-ray Timing Explorer (RXTE) in February 2004 and September 2008 (Markwardt et al. 2008; Shaw et al. 2008; Krimm et al. 2008) and designated XTE J1737–376. The source position was consistent with a faint source reported in the third IBIS/ISGRI soft gamma-ray survey catalogue (Bird et al. 2007), IGR J17379–3747. The peak flux attained during the outbursts ranged between 1.2 and 2.5 × 10−10 erg cm−2 s−1 (2–10 keV), corresponding to a luminosity of 1 − 2 × 1036 erg s−1 assuming a distance d = 8.5 kpc. The spectral energy distribution was described by a power law with Γ ⋍ 1.8–2.2 (see e.g. Strohmayer et al. 2018; Eijnden et al. 2018; Van Den Eijnden et al. 2018). Renewed activity from the source was detected by MAXI/GSC on 2018 March 19 (Negoro et al. 2018), at a 4–10 keV flux of (4 ± 1) × 10−10 erg cm−2 s−1. Very Large Array (VLA) observations performed during the 2018 outburst by Eijnden et al. (2018) detected a flat-spectrum radio counterpart with a flux density of ⋍0.4 mJy at 4.5 and 7.5 GHz at a position consistent with the X-ray source. X-ray coherent pulsation at ~468 Hz has been reported from observations performed by NICER (Strohmayer et al. 2018). In this Letter, we report on the XMM-Newton observation performed on 2018 April 1, almost a week after the beginning of the outburst.
2. Observations and data reduction
2.1. XMM-Newton
XMM-Newton (Jansen et al. 2001) performed a dedicated target of opportunity observation of IGR J17379–3747 (Obs. ID. 0830190301) on 2018 April 1 at 02:12 UTC for an elapsed time of ~45 ks. A few ks after the beginning of the observation a type-I burst was detected with a peak flux of ~1.6 × 10−8 erg cm−2 s−1 (more details on this event will be published elsewhere).
During the observation the Epic-pn (PN) camera was operated in timing mode, Epic-MOS 1–2 in timing mode, while the RGS observed in spectroscopy mode. We filtered the PN and MOS data using the Science Analysis Software (SAS) v.16.1.0 with up-to-date calibration files, and following the standard reduction pipeline EPPROC and EMPROC, respectively. We filtered the source data in the energy range 0.3–10 keV, selecting events with PATTERN ≤ 4 and (FLAG = 0) to retain only events optimally calibrated for spectral analysis. We selected source and background events from the PN regions RAWX [27:47] and [2:8], respectively. The average source spectral properties were analysed by removing the type-I burst detected at the beginning of the observation and integrating the PN and MOS2 spectra during the remaining observational time. Following standard analysis procedure, we generated in all cases the response matrix and the ancillary file using the RMFGEN and ARFGEN tools, respectively. Energy channels have been grouped by a factor of three to take into account the oversampled energy resolution of the instrument, and we also binned the energy spectrum to guarantee at least 25 counts per bin. We discarded both MOS1 (due to the “hot column” issue1) and RGS data because of the poor signal-to-noise ratio (S/N).
For the timing analysis we reported the PN photon arrival times to the solar system barycentre by using the BARYCEN tool (DE-405 solar system ephemeris) adopting the best available source position obtained from the VLA observation of the source (Eijnden et al. 2018), and reported in Table 1.
Spin frequency and orbital ephemeris of IGR J17379–3747 estimated during the three observed outbursts.
2.2. RXTE
IGR J17379–3747 has been observed by RXTE during its enhanced X-ray activity phases in 2004 (Obs. ID. 80138-07-01-00, for a total exposure of ~4 ks) and in 2008 (Obs. IDs. 93044-14-01-00, 93449-01-02-00/01/02/03/04/05, and 93449-01-03-00, for a total exposure of 14 ks). To perform the timing analysis we selected data collected by the PCA (Jahoda et al. 1996) in Event packing mode with time resolution ≤500 μs, which we processed and analysed using the HEASARC FTOOLS v.6.23. To improve the S/N, we selected photon events in the energy range 3–15 keV. We used the FAXBARY tool to apply barycentric corrections.
2.3. INTEGRAL
Following the detection of a new outburst from IGR J17379–3747, a 50 ks INTEGRAL observation was performed from 2018 April 1 at 08:30 to 23:15 (UTC). We analysed all available “science windows” with the OSA 10.2 software distributed by the ISDC (Courvoisier et al. 2003). We used IBIS/ISGRI (Lebrun et al. 2003; Ubertini et al. 2003) and JEM-X (Lund et al. 2003) data. As the observation was carried out during the rapid decay of the source outburst, IGR J17379–3747 was not significantly detected in the IBIS/ISGRI and JEM-X mosaics. We estimated 3σ upper limits on the source flux of 5 × 10−11 erg cm−2 s−1 in the 20–100 keV energy band and 1.0 × 10−10 erg cm−2 s−1 in the 3–20 keV energy band. These are compatible with the flux obtained from the XMM-Newton observation started about 7 h before the INTEGRAL pointings (Sect. 3.2). No evidence of type-I bursts has been found in the JEM-X light curves.
3. Data analysis
3.1. Timing analysis
We searched for coherent signals by generating a power density spectrum (PDS) averaging 225 power spectra produced on 200 s data segments from the XMM-Newton observation (Fig. 1; the type-I burst was removed before performing the timing analysis). A double-peaked feature associated with orbital Doppler shift is significantly detected (>5σ) with a central frequency of ~468.08 Hz and a width of ~6 × 10−2 Hz (see inset in Fig. 1). To investigate binary properties, we created PDS every 1000 s and inspected them for coherent features in the ~6 × 10−2 Hz interval around the mean peak frequency previously mentioned. Assuming a binary Doppler shift, we modelled the time evolution of the spin frequency obtaining the preliminary orbital solution: ν0 = 468.0801(19) Hz, x = 0.064(6) lt-s, Porb = 6699(50) s, TNOD = 58208.965(3) (MJD), where TNOD is the time of passage through the ascending node, Porb is the orbital period, and x is the projected semi-major axis of the NS orbit in light seconds. We note that this timing solution is consistent with the preliminary source ephemeris reported by Strohmayer et al. (2018).
 |
Fig. 1. Leahy normalised (Leahy et al. 1983) PDS, produced by averaging 200 s segments of XMM-Newton data. A statically significant coherent signal is visible at a frequency of ~468 Hz. The inset shows a zoom of the frequency double-peaked profile. |
Starting from these orbital parameters we corrected the photon time of arrivals for the binary motion through the recursive formula valid in the approximation of nearly circular orbits (eccentricity e ≪ 1) [t + x sin M = tarr], where M = 2π(t − TNOD)/Porb, t is the photon emission time and tarr is the photon arrival time to the solar system barycentre. We then iterated the process previously described, searching for coherent signals in PDS created in 500 s data segments. We modelled the residual spin frequency variation in the signal by fitting differential correction to the orbital parameters. We repeated the process until no significant differential corrections were found for the parameters of the model. The most accurate set of orbital parameters obtained with this method are ν0 = 468.08328(2) Hz, x = 0.07694(5) lt-s, Porb = 6765.9(4) s, TNOD = 58208.96642(2) (MJD).
To further investigate the spin frequency and the orbital parameters, we then epoch-folded segments of ~500 s in eight phase bins at the frequency ν0 = 468.08328(2) Hz obtained earlier. We modelled each pulse profile with a sinusoid of unitary period, and we determined the corresponding amplitude and the fractional part of the epoch-folded phase residual. We filtered pulse profiles such that the ratio between their amplitude and the corresponding 1σ uncertainty were equal to or larger than three. To model the temporal evolution of the pulse phase delays we define the function Δø(t) = ø0 + Δν0 (t − T0) + Rorb(t), where T0 represents the reference epoch for the timing solution, Δν0 is the spin frequency correction, and Rorb is the Rømer delay (e.g. Deeter et al. 1981). The described process was iterated until no significant differential corrections were obtained. Best-fit parameters are shown in Table 1. The best pulse profile obtained by epoch-folding the whole XMM-Newton dataset is described well by the superposition of three sinusoids, where the fundamental, second, and third harmonics have fractional amplitudes (background corrected) of ~13%, ~3%, and ~1.3%, respectively.
We searched for coherent X-ray pulsations in the data collected with RXTE during the 2004 and 2008 outbursts of the source. For each outburst, we searched for the best local TNOD (keeping fixed Porb and x to the values reported in Table 1), applying epoch-folding search techniques to the data for each trial TNOD. We detected pulsations in both the 2004 and 2008 outbursts with a statistical significance of 6σ and 5σ (single trial) at a barycentric frequency of 468.08332(25) Hz and 468.0831(2) Hz, and local TNOD = 53056.03926(12) and TNOD = 54721.03253(11) MJD, respectively. The pulse profiles are described well by a sinusoid with background corrected fractional amplitudes of 3.6(5)% and 4.5(4)%, respectively.
Finally, combining the orbital ephemerides measured for the three outbursts of the source, we investigated the orbital period secular evolution by studying the delay accumulated by TNOD as a function the orbital cycles elapsed since its discovery. To make sure of the feasibility of the coherent (orbital) timing analysis we verified the condition
where σTNOD and σPorb are the uncertainties on the time of passage from the ascending node and the orbital period used to create the timing solution, respectively; Ṗorb represents the secular orbital derivative, while N corresponds to the integer number of orbital cycles elapsed by the source during the time interval of interest. To verify Eq. (1) we considered the best available estimate of the orbital period Porb = 6765.90(2) s obtained from the timing analysis of the NICER observations of the latest outburst of the source (Markwardt et al., in prep.). Moreover, to overcome the lack of knowledge on the orbital period derivative (see e.g. Sanna et al. 2018b), we considered the average absolute value of the only two estimates reported for AMXPs (Ṗorb = 3.6(4) × 10−12 s s−1 for SAX J1808.4–3658 and Ṗorb = 1.1(3) × 10−10 s s−1 for SAX J1748.9–2021; see e.g. Di Salvo et al. 2008; Patruno et al. 2017b; Sanna et al. 2017a, 2016), corresponding to Ṗorb ≤ |6| × 10−11 s s−1. With these values for the orbital period and orbital period derivative, we found that Eq. (1) is verified only between the first two outbursts of the source. Phase connecting the orbital solutions of the 2004 and 2008 outbursts of IGR J17379–3747 we obtained an improved estimate of the orbital period Porb,04−08 = 6765.845(4) s. Adopting the more accurate estimate of the orbital period and assuming the same prescription for Ṗorb, we then obtained that Eq. (1) is verified for the 2004–2018 baseline, which includes the three outbursts investigated. To determined the delay accumulated by TNOD we estimated the expected TNOD for constant orbital period, TNOD,PRE(N) = TNOD,04 + N Porb,04−08, where TNOD,04 is the time of passage from the ascending node observed during the 2004 outburst. For each outburst we estimated the quantity TNOD,obs − TNOD,PRE, and we modelled its evolution as a function of the elapsed orbital periods with the quadratic function
where δTNOD,04 represents the correction to the adopted time of passage from the ascending node and δPorb,04−08 is the correction to the orbital period. We obtained an improved estimate of the orbital period Porb = 6765.84521(3) s as well as a first constraint on the orbital period derivative Ṗorb = (−2.5 ± 2.3) × 10−12 s s−1, where the uncertainties are reported at the 1σ confidence level.
3.2. Spectral analysis
We performed a spectral analysis with Xspec 12.10.0 (Arnaud 1996) and fit the average PN and MOS2 spectra in the 0.5–10 keV range (Fig. 2). We assumed Wilms et al. (2000) elemental abundances and Verner et al. (1996) photo-electric cross-sections to model the interstellar medium. We allowed for a normalisation coefficient between instruments to account for cross-instrument calibration offsets.
 |
Fig. 2. Unfolded Epic-pn (red) and MOS2 (black) average spectra of IGR J17379–3747. The residuals from the best fit described in the text are reported in the bottom panel. |
The spectra are described well 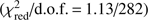 by the typical model used for AMXPs in outburst, comprising an absorbed disk black-body plus a thermally Comptonised continuum with seed photons from the black-body radiation (const×tbabs×[diskbb + nthcomp] in Xspec). We measured an absorption column density of (0.90 ± 0.03) × 1022 cm−2, consistent with that expected in the direction of the source2. We obtained from the fit an inner disk temperature of 0.45 ± 0.03 keV (linked to be the same of the seed photon temperature in the Comptonisation component), and a photon index of 1.88 ± 0.08. The inter-calibration constant of the MOS2 with respect to the PN was found to be 1.08 ± 0.01. The electron temperature of the nthcomp component could not be constrained in the fit and we fixed it to 30 keV, following the results obtained from similar sources (Sanna et al. 2018a). We verified that using reasonably different values of this parameter did not affect the overall fit results. No evidence of spectral lines (e.g. iron K-α) was found by inspecting the residuals from the best fit to the PN and MOS2 data. Considering the iron line properties observed in AMXPs (see e.g. Papitto et al. 2009, 2013a, 2016; Pintore et al. 2016, 2018; Sanna et al. 2017b), for example line energy in the range 6.4–6.97 keV and line width between 0.1 and 0.7 keV, we estimated an upper limit on the equivalent width of any iron line not detected during the source outburst ranging between 50 and 400 eV, still compatible with the lines observed in other AMXPs. The average 0.5–10 keV flux measured from the spectral fit was of (1.16 ± 0.02) × 10−11 erg cm−2 s−1.
by the typical model used for AMXPs in outburst, comprising an absorbed disk black-body plus a thermally Comptonised continuum with seed photons from the black-body radiation (const×tbabs×[diskbb + nthcomp] in Xspec). We measured an absorption column density of (0.90 ± 0.03) × 1022 cm−2, consistent with that expected in the direction of the source2. We obtained from the fit an inner disk temperature of 0.45 ± 0.03 keV (linked to be the same of the seed photon temperature in the Comptonisation component), and a photon index of 1.88 ± 0.08. The inter-calibration constant of the MOS2 with respect to the PN was found to be 1.08 ± 0.01. The electron temperature of the nthcomp component could not be constrained in the fit and we fixed it to 30 keV, following the results obtained from similar sources (Sanna et al. 2018a). We verified that using reasonably different values of this parameter did not affect the overall fit results. No evidence of spectral lines (e.g. iron K-α) was found by inspecting the residuals from the best fit to the PN and MOS2 data. Considering the iron line properties observed in AMXPs (see e.g. Papitto et al. 2009, 2013a, 2016; Pintore et al. 2016, 2018; Sanna et al. 2017b), for example line energy in the range 6.4–6.97 keV and line width between 0.1 and 0.7 keV, we estimated an upper limit on the equivalent width of any iron line not detected during the source outburst ranging between 50 and 400 eV, still compatible with the lines observed in other AMXPs. The average 0.5–10 keV flux measured from the spectral fit was of (1.16 ± 0.02) × 10−11 erg cm−2 s−1.
4. Discussion
We report on the detection of X-ray coherent pulsations at ~468 Hz from the known type-I burster IGR J17379–3747 observed by XMM-Newton during its 2018 outburst. Coherent timing analysis of the ms pulsation allowed to determine properties of the binary system such as its ~1.9 h orbital period and the ~0.08 lt-s NS projected semi-major axis. The orbital ephemerides reported here are consistent with those independently determined with the data collected by the NICER X-ray Timing Instrument between 2018 March 29 and April 1 (Strohmayer et al. 2018).
Combining the binary system mass function f (m2, m1, i) ~ 8 × 10−5M⊙ with the absence of eclipses (inclination angle of i ≲ 75°) in the X-ray light curve, we constrained the mass of the donor star to be m2 ≳ 0.056 M⊙ assuming a NS mass of 1.4 M⊙ (m2 ≳ 0.07 M⊙ for a 2 M⊙ NS). Assuming a Roche-lobe filling donor star and fixing the NS mass, we can compare the companion mass–radius relation with that of theoretical H main-sequence stars (e.g. Tout et al. 1996). We find that for a 1.4 M⊙ NS, main-sequence stars with m2 > 0.16 M⊙ would have a radius equal to or larger than the donor Roche lobe, implying an inclination angle i ≤ 21°. For an isotropic a priori distribution of the binary inclination angles, the probability of observing a system with i ≤ 21° (thus m2 > 0.16 M⊙) is ≤ 7%. In analogy with other AMXPs with very similar orbital parameters, such as SAX J1808.4–3658 and IGR J00291+5934, the companion star could be a hot brown dwarf, likely heated by low-level X-ray radiation during the quiescent phases (e.g. Bildsten & Chakrabarty 2001; Galloway et al. 2005).
The average energy spectrum of IGR J17379–3747 analysed here is described well by a superposition of a soft disk component (kT ~ 0.45 keV) and a hard power law (Γ ~ 1.9), consistent with typical AMXP observed in outburst (e.g. Gierliński & Poutanen 2005; Papitto et al. 2009; Falanga et al. 2013). We found no evidence of emission lines or reflection components in the energy spectrum, in analogy with the AMXPs XTE J1807–294 (Falanga et al. 2005), XTE J1751–305 (Miller et al. 2003), SWIFT J1756.9–2508 (Sanna et al. 2018b), and the recently discovered IGR J16597–3704 (Sanna et al. 2018a). For a source distance of 8.5 kpc, the observed average flux of ~1.2 × 10−11 erg s−1 cm2 (0.5–10 keV) corresponds to a luminosity of L = 4.3 × 1035 erg s−1. Assuming accretion-torque equilibrium, we use this luminosity value to make a rough estimate of the dipolar magnetic field B of the NS
where ζ is a model-dependent dimensionless factor typically between 0.1 and 1 that describes the relation between the magnetospheric radius and the Alfvén radius (see e.g. Ghosh & Lamb 1979; Wang 1996; Bozzo et al. 2009), Pspin is the NS period in units of ms, M is the NS mass, and Ṁ is the mass accretion rate onto the NS surface. Standard NS parameters such as radius R = 10 km and mass M = 1.4 M⊙, we estimate 0.4 × 108 < B < 2.3 × 109G, consistent with the average magnetic field of known AMXPs (see e.g. Mukherjee et al. 2015; Degenaar et al. 2017).
X-ray pulsations was also detected in the RXTE observations of the IGR J17379–3747 corresponding to its 2004 and 2008 outbursts. We note that orbital Doppler shift corrections were required to reveal the coherent pulsation, implying a relatively poor S/N. Combining the barycentric spin frequency values observed for each outburst (see Table 1), we estimated an upper limit (3σ confidence level) of the secular spin derivative −8.3 × 10−13 Hz s−1 < ν̇ < 1.1 × 10−12 Hz s−1. Following Spitkovsky (2006, and references therein) we converted the frequency spin-down upper limit into an upper limit on the magnetic field strength of B < 2.8 × 109G (assuming a NS R = 10 km and an angle α ⋍ 10° between the magnetic hotspot and the rotational pole), consistent with the estimate reported above.
Finally, we investigated the orbital period secular evolution of IGR J17379–3747 by combining the ephemeris of the three observed outbursts of the source, obtaining a more accurate value of the orbital period Porb = 6765.84521(2) s and an orbital period derivative Ṗorb = (−2.5 ± 2.3) × 10−12 s s−1. The large uncertainty on the latter finding does not allow us to unambiguously determine the secular evolution of the system; however, we note that within the uncertainties the value reported for IGR J17379–3747 is still compatible with the fast expansion reported for SAX J1808.4–3658 (Di Salvo et al. 2008; Patruno et al. 2017b; Sanna et al. 2017a). Similar results have been reported for the AMXP Swift J1756.9–2508 (Sanna et al. 2018b). A secular evolution compatible with that observed for the AMXP IGR J00291+5934, which shows evolutionary timescales compatible with conservative mass transfer driven by angular momentum loss via gravitational radiation (GR; Patruno 2017; Sanna et al. 2017c), is however still compatible with our findings. Future outbursts of the source will be of fundamental importance to further constrain the orbital period derivative, hence the secular evolution of the system.
Acknowledgments
We thank the anonymous referee for helpful comments and suggestions that improved the paper. We thank N. Schartel and E. Kuulkers for the possibility to perform the ToO observation in the Director Discretionary Time with XMM-Newton and INTEGRAL, respectively. We also thank the XMM-Newton and INTEGRAL teams for the rapid scheduling of the ToO observations of IGR J17379–3747. A.P. acknowledges funding from the EU Horizon 2020 Framework Programme for Research and Innovation under the Marie Skłodowska-Curie Individual Fellowship grant agreement 660657-TMSP-H2020-MSCA-IF-2014.
References
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bildsten, L., & Chakrabarty, D. 2001, ApJ, 557, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, A. J., Malizia, A., Bazzano, A., et al. 2007, ApJS, 170, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Stella, L., Vietri, M., & Ghosh, P. 2009, A&A, 493, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burderi, L., & Di Salvo, T. 2013, Mem. Soc. Astron. It., 84, 117 [NASA ADS] [Google Scholar]
- Courvoisier, T., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeter, J. E., Boynton, P. E., & Pravdo, S. H. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Pinto, C., Miller, J. M., et al. 2017, MNRAS, 464, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Burderi, L., Riggio, A., Papitto, A., & Menna, M. T. 2008, MNRAS, 389, 1851 [NASA ADS] [CrossRef] [Google Scholar]
- Eijnden, J. V. D., Degenaar, N., Russell, T., et al. 2018, ATel, 11487 [Google Scholar]
- Falanga, M., Bonnet-Bidaud, J. M., Poutanen, J., et al. 2005, A&A, 436, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falanga, M., Kuiper, L., Poutanen, J., et al. 2013, ArXiv e-prints [arXiv:1302.2843] [Google Scholar]
- Galloway, D. K., Markwardt, C. B., Morgan, E. H., Chakrabarty, D., & Strohmayer, T. E. 2005, ApJ, 22, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., & Poutanen, J. 2005, MNRAS, 359, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krimm, H. A., Kennea, J. A., Evans, P. A., & Markwardt, C. B. 2008, ATel, 1714 [Google Scholar]
- Leahy, D. A., Darbro, W., Elsner, R. F., et al. 1983, ApJ, 266, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B., Krimm, H., Wijnands, R., & Swank, J. H. 2008, ATel, 1709 [Google Scholar]
- Miller, J. M., Wijnands, R., Méndez, M., et al. 2003, ApJ, 583, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, D., Bult, P., van der Klis, M., & Bhattacharya, D. 2015, MNRAS, 452, 3994 [NASA ADS] [CrossRef] [Google Scholar]
- Negoro, H., Nakahira, S., Ueno, S., et al. 2018, ATel, 11447 [Google Scholar]
- Papitto, A., Di Salvo, T., D’Aì, A., et al. 2009, A&A, 493, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., D’Aì, A., Di Salvo, T., et al. 2013a, MNRAS, 429, 3411 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Ferrigno, C., Bozzo, E., et al. 2013b, Nature, 501, 517 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Papitto, A., Bozzo, E., Sanchez-Fernandez, C., et al. 2016, A&A, 596, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patruno, A. 2017, ApJ, 839, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., & Watts, A. L. 2012, Astrophys. Space Sci. Lib., [arXiv:1206.2727] [Google Scholar]
- Patruno, A., Haskell, B., & Andersson, N. 2017a, ApJ, 850, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Jaodand, A., Kuiper, L., et al. 2017b, ApJ, 841, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Sanna, A., Di Salvo, T., et al. 2016, MNRAS, 457, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Sanna, A., Riggio, A., et al. 2018, MNRAS, 479, 4084 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Burderi, L., Riggio, A., et al. 2016, MNRAS, 459, 1340 [Google Scholar]
- Sanna, A., Di Salvo, T., Burderi, L., et al. 2017a, MNRAS, 471, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Papitto, A., Burderi, L., et al. 2017b, A&A, 598, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Pintore, F., Bozzo, E., et al. 2017c, MNRAS, 466, 2910 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Bahramian, A., Bozzo, E., et al. 2018a, A&A, 610, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Pintore F., Riggio, A., et al. 2018b, MNRAS, submitted [Google Scholar]
- Shaw, S., Kuulkers, E., Markwardt, C. B., & Galis, R. 2008, ATel, 1711 [Google Scholar]
- Spitkovsky, A. 2006, ApJ, 648, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Ray, P. S., Gendreau, K. C., et al. 2018, ATel, 11507 [Google Scholar]
- Tout, C. A., Pols, O. R., Eggleton, P. P., & Han, Z. 1996, MNRAS, 281, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Den Eijnden, J., Degenaar, N., Russell, T., et al. 2018, ATel, 11520 [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1996, ApJ, 465, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spin frequency and orbital ephemeris of IGR J17379–3747 estimated during the three observed outbursts.
All Figures
 |
Fig. 1. Leahy normalised (Leahy et al. 1983) PDS, produced by averaging 200 s segments of XMM-Newton data. A statically significant coherent signal is visible at a frequency of ~468 Hz. The inset shows a zoom of the frequency double-peaked profile. |
| In the text | |
 |
Fig. 2. Unfolded Epic-pn (red) and MOS2 (black) average spectra of IGR J17379–3747. The residuals from the best fit described in the text are reported in the bottom panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.