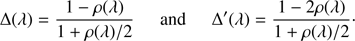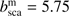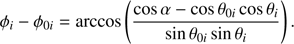| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 15 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201832859 | |
| Published online | 05 September 2018 | |
PYMIEDAP: a Python–Fortran tool for computing fluxes and polarization signals of (exo)planets⋆,⋆⋆
Faculty of Aerospace Engineering, Technical University Delft, Kluyverweg 2, 2629 HS Delft, The Netherlands
e-mail: l.c.g.rossi@tudelft.nl
Received:
20
February
2018
Accepted:
21
April
2018
PYMIEDAP (the Python Mie Doubling-Adding Programme) is a Python-based tool for computing the total linearly and circularly polarized fluxes of incident unpolarized sunlight or starlight that is reflected by solar system planets or moons, respectively, or by exoplanets at a range of wavelengths. The radiative transfer computations are based on an doubling-adding Fortran algorithm and fully include polarization for all orders of scattering. The model (exo)planets are described by a model atmosphere composed of a stack of homogeneous layers containing gas and/or aerosol and/or cloud particles bounded below by an isotropically depolarizing surface (that is optionally black). The reflected light can be computed spatially resolved and/or disk-integrated. Spatially resolved signals are mostly representative for observations of solar system planets (or moons), while disk-integrated signals are mostly representative for exoplanet observations. PYMIEDAP is modular and flexible, and allows users to adapt and optimize the code according to their needs. PYMIEDAP keeps options open for connections with external programs and for future additions and extensions. In this paper, we describe the radiative transfer algorithm that PYMIEDAP is based on and the principal functionalities of the code. We also provide benchmark results of PYMIEDAP that can be used for testing its installation and for comparison with other codes.
Key words: planets and satellites: atmospheres / polarization / radiative transfer
PYMIEDAP is available online under the GNU GPL license at http://gitlab.com/loic.cg.rossi/pymiedap
A copy of the code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/616/A147
© ESO 2018
1. Introduction
Light is usually described only by its total flux, and the total flux is usually also the only parameter that is measured when observing sunlight that is reflected by Earth or other planets in the solar system. A full description of light, however, requires its state of polarization. The state of polarization includes the degree of polarization, P, that is, the ratio of the polarized flux to the total –polarized plus unpolarized– flux, and the direction of polarization, χ. The polarized flux can be subdivided into the linearly polarized flux and the circularly polarized flux. Similarly, the degree of polarization P can be subdivided into the degree of linear polarization Pl and the degree of circular polarization Pc. An excellent description of the polarization of light that is reflected by planetary atmospheres and surfaces can be found in Hansen & Travis (1974). This paper also includes various methods for computing the state of polarization of light that is reflected by a planet such as the so-called doubling-adding method, which is employed by PYMIEDAP, the code that is the topic of this paper.
There are several reasons for measuring the state of polarization of sunlight that is reflected by a planet, or starlight that is reflected by an exoplanet. A first advantage of polarimetry comes from the fact that the light of a solar-type star can be considered to be unpolarized when integrated across the stellar disk. This is known to be true for our Sun (Kemp et al. 1987), and is also supported by other studies of nearby FGK stars: for example, Cotton et al. (2017) showed that while active stars can present polarizations of up to 45 ppm, non-active stars have very limited and practically negligible intrinsic polarization.
Meanwhile, light that is scattered within a planetary atmosphere and/or that is reflected by the planetary surface will usually be (linearly) polarized. For exoplanets, polarimetry could thus allow distinguishing the very faint planetary signal from the much brighter stellar light. In addition, the measurement of a polarized signal would immediately confirm the nature of the object. Seager et al. (2000) presented numerically simulated degrees of (linear) polarization of the combined light of a star and various types of orbiting gaseous planets. When planets are spatially unresolved from their star, the degree of polarization of the system as a whole is the ratio of the polarized planetary flux to the sum of the total planetary flux and the stellar flux. This degree of polarization is obviously very low, on the order of 10−6 (Seager et al. 2000). Stam et al. (2004) presented numerically simulated degrees of (linear) polarization of spatially resolved gaseous planets. For these planets, the degree of polarization can reach several tens of percent, depending on the physical properties of the planet and the planetary phase angle, because they did not include the huge, unpolarized stellar signal. Clearly, the degree of polarization that can be observed for a given exoplanet will depend not only on the intrinsic degree of polarization of the planet, but also on the stellar flux in the background of the planetary signal.
Another interesting use of polarimetry is the characterization of the planetary object. The degree and direction of polarization of light that has been scattered by a planet (locally or diskintegrated) is very sensitive to the properties of the atmospheric scatterers (size, shape, and composition), their spatial distribution, and/or to the reflection properties of the planetary surface (bidirectional reflection and albedo; see e.g. Hansen & Travis 1974; Mishchenko et al. 2002, and references therein), if present. In particular, multiple scattering of light randomizes and hence depolarizes the light, and adds mainly unpolarized light to the reflected signal. The angular dependence of the degree and direction of polarization of the reflected signal thus preserves the angular patterns of the light that is singly scattered by the atmospheric particles or the surface, and that is characteristic for the microphysical properties of the scatterers. A famous application of the use of polarimetry for the characterization of a planetary atmosphere is the retrieval of the composition and size of the cloud particles in Venus’ upper clouds using disk-integrated polarimetry (with Earth-based telescopes) at a range of phase angles and several wavelengths (Hansen & Hovenier 1974). This information could not be derived from total flux measurements because the total flux is less sensitive to the composition and size of the scattering particles. Various types of cloud particles would indeed provide a fit to the total flux measurements.
Even if one were not interested in measurements of polarization and the analysis of polarization data, there are compelling reasons to include polarization in the computation of total fluxes. First, because light is fully described by a vector and scattering processes by matrices, ignoring polarization can induce errors up to several percent in computed total fluxes both locally and disk-integrated (Mishchenko et al. 1994; Stam & Hovenier 2005). In particular, in gaseous absorption bands, where the linear polarization usually differs from the polarization in the continuum (Fauchez et al. 2017; Boesche et al. 2009; Stammes et al. 1994; Aben et al. 1997), such errors will lead to errors in derived gas mixing ratios and cloud top altitudes, for instance (Stam & Hovenier 2005).
Second, many spectrometers are sensitive to the state of polarization of the incoming light because of the optical properties of mirrors and gratings, for example. Knowing the polarization sensitivity of your instrument, for example, through calibration in an optical laboratory, is not sufficient to correct total flux measurements for the state of polarization of the incoming light if the polarization of the light is not known (Stam et al. 2000). However, one could include the computed state of polarization of the observed light, combined with the instrument polarization sensitivity in the retrieval of the total fluxes.
A reason why polarization is usually ignored in radiative transfer computations is probably that codes that fully include polarization for all orders of scattering are more complex than codes that ignore polarization, because the latter treat light as a scalar and scattering processes as described by scalars, while the former have to use vectors and matrices. Polarized radiative transfer codes therefore usually also require more computation time than scalar codes.
In this paper, we present PYMIEDAP, a user-friendly, modular, Python-based tool for computing the total and polarized fluxes of light that is reflected by (exo)planets1. The radiative transfer computations in PYMIEDAP are performed with a doubling-adding algorithm written in Fortran, as described by de Haan et al. (1987), while input and output are handled with Python code. Figure 1 provides a view of the modules composing PYMIEDAP. The blue boxes represent codes written in Fortran, and the red boxes represent Python code. Arrows indicate interfaces using f2py (Peterson 2009). Each PYMIEDAP module is described in more detail in this paper.
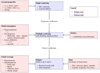 |
Fig. 1. Modules comprising PYMIEDAP. The blue boxes represent Fortran codes, and the red boxes represent Python codes. |
The structure of the paper is as follows. Section 2 provides the definitions of the vector elements that describe the state of polarization of light as used in PYMIEDAP. Section 3 contains the formulae required to calculate the Stokes vectors of sunlight or starlight that is locally reflected by a region on a planet for a range of illumination and viewing geometries. The components of the Fourier-series decomposition of these vectors are stored in files in a database that is accessed to compute reflected light vectors for specific geometries. Section 4 describes the computation of the single-scattering properties of atmospheric gases and aerosols, and the reflection by the surface. Section 5 describes the doubling-adding radiative transfer algorithm used in PYMIEDAP. Section 6 presents the method used to compute the geometries for locally reflected light, and describes how previously stored database files are used to compute the locally reflected light vector as well as how to integrate these locally reflected light vectors across the illuminated and visible part of a planetary disk, in order to obtain the disk-integrated Stokes vector. In Sect. 7 we compare reflected Stokes vectors obtained with PYMIEDAP against previously published results obtained using a similar doubling-adding radiative transfer algorithm without the intermediate step of using precalculated database files, and without the Python shell. Section 8 summarizes the paper and discusses future work. Appendix A provides a detailed description of the format of the database files that is used in the codes. Appendix B provides equations for the computation of some angles used in the code.
2. Defining the flux and polarization of light
The radiance (“intensity”) and state of polarization of a quasimonochromatic beam of light can be described by a Stokes vector I as follows (see, e.g., Hansen & Travis 1974; Hovenier et al. 2004)![$$ I={\left[\begin{array}{c}I\\Q\\U\\V\end{array}\right]}. $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq1.gif) (1)
(1)
Here, the Stokes parameter I is the total radiance, Q and U describe the linearly polarized radiances, and V is the circularly polarized radiance. All four parameters have the dimension W m−2 sr−1 (or W m−3 sr−1 if taken as functions of the wavelength λ). We also use the irradiance or flux vector πF = π[F, Q, U, V], of which all parameters have the dimension W m−2 (or W m−3 if taken as functions of λ). Unless specified otherwise, the equations in this paper also hold for flux vector πF .
Parameters Q and U are defined with respect to a reference plane. We use two types of reference planes:
-
The local meridian plane, which contains the local zenith direction and the direction of propagation of the light. The local meridian plane is used in the computation of Q and U of locally reflected light.
-
The planetary scattering plane, which contains the center of the planet, and the directions to the center of the star and to the observer. This plane is mainly used to define Q and U of light that has been reflected by the planet as a whole, for example, for simulating signals of (spatially unresolved) exoplanets.
Parameters Q and U can be transformed from one reference plane to another using a so-called rotation matrix L (see Hovenier & van der Mee 1983)![$$ L{(\beta)}={\left[\begin{array}{cccc}1&0&0&0\\0&\cos2\beta&\sin2\beta&0\\0&-\sin2\beta&\cos2\beta&0\\0&0&0&1\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq2.gif) (2)
(2)
with β the angle between the two reference planes, measured rotating in the anticlockwise direction from the old to the new reference plane when looking toward the observer (β ≥ 0°).
In PYMIEDAP, the default reference plane for local reflections and disk-integrated reflected light is the planetary scattering plane. For locally reflected light, the vector that is computed with respect to the local meridian plane is rotated to be defined with respect to the planetary scattering plane before being provided as output. As a planet orbits its star, the planetary scattering plane will usually rotate on the sky as seen from the observer, except if the orientation of the orbit is edge-on with respect to the observer (see Fig. 2). By applying additional rotations, Stokes vectors defined with respect to the planetary scattering plane can straightforwardly be redefined to the optical plane of an instrument or the detector, for instance (for a detailed description of these rotations, see Rossi & Stam 2017).
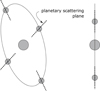 |
Fig. 2. Illustration of the rotation of the planetary scattering plane for an orbit with a random orientation (left) and with edge-on configuration (right). The first case would require further rotations to express the Stokes elements in the reference plane of the observer. |
The degree of polarization of the beam of light described by vector I (Eq. (1)) is defined as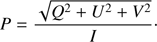 (3)
(3)
The degree of linear polarization is defined as (4)
(4)
and the degree of circular polarization is defined as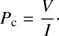 (5)
(5)
While the degree of linear polarization is independent of the choice of reference plane for Stokes parameters Q and U, the direction or angle of linear polarization, χ, is not independent of the choice of reference plane. Angle χ can be derived from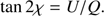 (6)
(6)
The value of χ is chosen in the interval [0°, 180°〉, and such that cos 2χ has the same sign as Q (see Hansen & Travis 1974).
If U = 0, the direction of polarization of the light is either perpendicular (Q < 0,χ = 90°) or parallel (Q > 0,χ = 0°) to the reference plane. In that case, we can use an alternative definition of the degree of linear polarization that captures the information about the direction of polarization, namely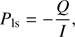 (7)
(7)
where Pls > 0 (Pls < 0) corresponds to light that is polarized perpendicularly (parallel) to the reference plane.
For the circular polarization (Eq. (5)), our convention for the sign is as follows: V and thus Pc is positive when the observer “sees” the electric vector of the light rotating in the anticlockwise direction, and V and thus Pc is negative when the observer “sees” the vector rotating in the clockwise direction.
3. Calculating reflected light
With PYMIEDAP, one can calculate the Stokes vector I (cf. Eq. (1)) of light that is locally reflected by a planet. Here, we refer to locally reflected light if a single combination of illumination and viewing geometries involved in the reflection process applies. With PYMIEDAP, one can also integrate Stokes vectors of locally reflected light across the planet, taking into account variations of the atmospheric properties and/or surface albedo, as well as the variations of the illumination and viewing geometries.
Below, we explain the calculation of the locally reflected light (Sect. 3.1) and the integration of locally reflected light across the illuminated and visible part of a planetary disk (Sect. 3.2). The integration over a smaller part of a planet could straightforwardly be derived from the latter explanation2.
3.1. Calculating locally reflected light
We calculate a locally reflected vector I (see Eq. (1)) according to (see Hansen & Travis 1974)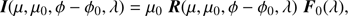 (8)
(8)
with F0 the vector describing the incident light and R the 4 × 4 local planetary reflection matrix. The reference plane for I is the local meridian plane, the plane containing the local zenith direction, and the propagation direction of the reflected light (see Sect. 2).
Furthermore, in Eq. (8), μ = cos θ, with θ the angle between the direction of propagation of the reflected light and the upward vertical (0° ≤ θ < 90°), and μ0 = cos θ0, with θ0 the angle between the upward vertical and the direction to the sun or star (0° ≤ 0 < 90°). The azimuthal difference angle ϕ − ϕ0 is measured between the two vertical planes containing the directions of propagation of the reflected and the incident light, respectively (0° ≤ ϕ − ϕ0 ≤ 180°). To clarify our definition for ϕ − ϕ0 , consider light that is reflected in the vertical plane that contains the local zenith direction, and the direction toward the sun or star. If the reflected light propagates in the half of the vertical plane that contains the sun or star, ϕ − ϕ0 = 180°. If the reflected light propagates in the other half of the plane, ϕ − ϕ0 = 0°.
In PYMIEDAP, it is assumed that the incident sunlight or starlight is unpolarized (Kemp et al. 1987), although this assumption is not inherent to the radiative transfer algorithm (de Haan et al. 1987), and PYMIEDAP could easily be adapted for polarized incident light. Vector F0 of the light that is incident on a model planet thus equals the column vector [F0, 0, 0, 0] or F0[1, 0, 0, 0], where F0 equals the total incident solar/stellar flux measured perpendicular to the direction of incidence divided by π (see Hansen & Travis 1974). For example, if the total incident flux measured perpendicular to the direction of incidence equals S0 W m−2, F0 = S0/π W m−2.
With the assumption of unpolarized incident sunlight or starlight, only the elements of R1, the first column of the 4 × 4 local planetary reflection matrix R are relevant for the calculation of the locally reflected vector I, since Eq. (8) then transforms into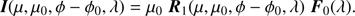 (9)
(9)
The local reflection vector R1 depends on the illumination and viewing geometries and the properties of the local planetary atmosphere and surface. The user can provide PYMIEDAP with a list of illumination and viewing geometries, for example, geometries that pertain to observations from a satellite that orbits a planet. Given the properties of the local atmosphere and surface, the calculation of R1 and subsequently I is performed by PYMIEDAP as described in Sect. 5. We note that the locally reflected light vector I as described by Eq. (9) is defined with respect to the local meridian plane. PYMIEDAP will redefine it with respect to the planetary scattering plane by calculating the local angle β and applying the rotation matrix L as defined in Eq. (2).
When circular polarization is ignored, vector R1 and reflected light vector I each comprise only three elements. When circular and linear polarization are both ignored, R1 and I are scalars, and Eq. (9) could be written as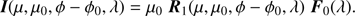 (10)
(10)
In contrast to ignoring linear polarization, ignoring circular polarization usually only leads to very small errors in the computed total and linearly polarized fluxes (Stam & Hovenier 2005). In the following, we assume that polarization (both linear and circular) is taken into account and use vectors and matrices instead of scalars.
3.2. Calculating disk-integrated reflected light
To calculate signals of spatially unresolved planets, such as exoplanets, we integrate the locally reflected starlight as given by Eqs. (9) and (10), over the illuminated and visible part of the planetary disk, according to (see Stam et al. 2006, Eq. 16)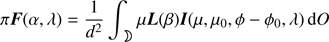 (11)
(11)
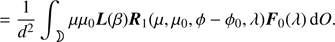 (12)
(12)
Here, πF is the flux vector of the reflected starlight as it arrives at the observer located at a distance d from the planet, with πF the flux measured perpendicularly to the direction of propagation of the light. Furthermore, μ dO/d2 is the solid angle under which surface area dO on the planet is seen by the observer (μ = cos θ). The planet radius r is incorporated in the surface integral (the planet is thus not assumed to be a unit sphere). The reflected light vector πF depends on the planetary phase angle α, that is, the angle between the star and the observer as measured from the center of the planet (0° ≤ α ≤ 180°). The range of observable phase angles for an exoplanet will depend on the orbital inclination and/or on the inner working angle of the instrument.
Furthermore in Eq. (12), each locally reflected vector I, and hence each local reflection matrix R1 , is rotated such that the reference plane is no longer the local meridian plane, but the planetary scattering plane. The local rotation angle β depends on the local viewing angle θ and the location of surface area dO on the planet.
The geometric albedo AG of the planet with radius r at distance d is given by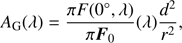 (13)
(13)
where πF0(0°,λ) is the reflected total flux at wavelength λ and phase angle α equal to 0°.
In PYMIEDAP, the integration in Eq. (12) is replaced by a summation over locally reflected Stokes vectors. In order to do so, we divide the planetary disk on the sky in pixels, and compute the locally reflected Stokes vector at the center of each pixel. A pixel contributes to the disk signal when its center is within the disk radius. The integration is then given by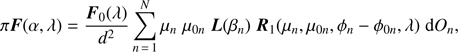 (14)
(14)
with N the number of illuminated and visible pixels on the planetary disk, and with subscript n indicating that μ, μ0, ϕ − ϕ0, and β depend on the location of the pixel on the planet. In addition, μ0, ϕ − ϕ0, and β at a given location of the pixel on the planet depend on the planet phase angle α (Appendix B provides relations that can be used to derive these angles). In the summation, dOn refers to the area of the pixel as measured on the surface of the planet.
Although not explicitly indicated in Eqs. (14) and (12), R1 will usually also depend on the location (of a pixel) on the planet. Typical horizontally inhomogeneities would be the surface coverage and altitude, and the atmospheric composition and structure. The obvious horizontal variations on Earth are of course the oceans and the continents, and in the atmosphere, the clouds. Horizontal inhomogeneities can be taken into account by using different local reflection vectors R1 across the planet (in that case, R1 in Eq. (14) would include a subscript n).
Given a model planet and a planetary phase angle α, the steps to evaluate Eq. (14) are the following:
-
Divide the planet into pixels small enough to be able to assume that the planet properties across each pixel are horizontally homogeneous, and to be able to follow the limb and the terminator of the planet.
-
Calculate for (the center of) each pixel the angles μ (i.e., cos θ), ϕ, and the rotational angle β. These angles are independent of the location of the sun or star with respect to the planet.
-
Calculate for the given phase angle , and for (the center of) each pixel, μ0 (i.e., cos θ0) and ϕ0. These angles depend on the location of the sun or star with respect to the planet.
-
Calculate for (the center of) each pixel the column vector R1 of the locally reflected light using the appropriate database file (see Sect. 5).
-
Perform the summation described by Eq. (14).
The pixels can be defined on the planet, for example, using a latitude and longitude grid, in which case μ dO, the projected area of the pixel (see Eq. (12)), that is, the pixel area as “seen” by the observer (see Fig. 3) will depend on the location of the pixel on the planet. PYMIEDAP uses a grid of equally sized square pixels, similar to detector pixels, and uses the projections of these pixels onto the planet to divide the planet into separate regions. In this case, μ dO is simply the surface area of the square pixel, and there is no need to calculate dO, the surface of the projected pixel on the planet (which can have a complicated shape). The result of the integration will depend on the pixel size and thus on the number of pixels across the planetary disk, in particular at large phase angles, where the pixels should be sufficiently small to resolve the crescent shape of the illuminated part of the planetary disk.
 |
Fig. 3. Sketch of a surface area dO on the planet (side view) and its projection toward the observer. The observer “sees” a pixel area equal to μ dO = cos θ dO, with θ the local viewing zenith angle. |
The computation time increases linearly with N, the number of pixels on the illuminated and visible part of the planetary disk. In order to keep computing times low, it is thus important to find a balance between the number of pixels and the accuracy. The relative error in the total flux of a Lambertian reflecting planet due to the pixel size is shown in Fig. 4. The errors decrease with increasing value of N at any given phase angle α. For a given value of N, the relative error increases with increasing phase angle α, thus with decreasing width of the planetary crescent, but the total disk-integrated flux also decreases with increasing , with πF(180°) = 0.0. Thus while the relative errors at large phase angles can be very large, the absolute errors remain small. For computations across a range of phase angles, PYMIEDAP can automatically increase the number of pixels across the equator Neq (and therefore N) with increasing in order to keep the errors small. The results of this automatic increase of N are also shown in Fig. 4. This “adaptive pixels scheme” can be useful as a trade-off between computational efficiency and the need to resolve the planet at large phase angles, as using a smaller number of pixels for a full planet is usually acceptable, while it might be detrimental to the computed output for thin crescents.
 |
Fig. 4. Difference between the disk-integrated flux F computed using Eq. (14) and computed using the analytical expression for a sphere with a Lambertian reflecting surface and a geometric albedo AG of 1.0 (see Stam et al. 2006, and Eq. (39)) as a function of the planetary phase angle α for various values of Neq, the number of pixels along the planet equator. The difference has been normalized to AG. The dotted line shows that Neq increases with according to Neq(α) = Neq(0°)[1 + sin2(α/2)], with Neq(0°) = 40. |
We note that for horizontally homogeneous planets, the Stokes vector of the hemisphere above the planetary scattering plane equals that of the southern hemisphere, except for the sign of Stokes parameters U and V.
For horizontally homogeneous planets, Stam et al. (2006) described an efficient algorithm that does not require dividing the planet into pixels and that evaluates the disk-integrated Stokes vector πF at arbitrary phase angles α. With this algorithm (which has not been implemented in PYMIEDAP), vectors of horizontally inhomogeneous planets can be approximated using a weighted sum of vectors of horizontally homogeneous planets (see Stam 2008), with the weights depending on the fractions the various inhomogeneities cover on the illuminated and visible part of the planetary disk. With such a weighted sum approximation, one can estimate the range of signals to be expected from an exoplanet. However, because a weighted sum does not account for the actual spatial distribution of the inhomogeneities, and the change therein when a planet rotates about its axis, for example, it cannot be used for interpreting signals of planets that are known to exhibit significant horizontal inhomogeneities. For such applications, the PYMIEDAP pixel approach should be used.
4. Describing the model atmosphere and surface
The PYMIEDAP doubling-adding radiative transfer algorithm assumes a flat model atmosphere that is horizontally homogeneous, but that can be vertically inhomogeneous because different horizontally homogeneous atmospheric layers can be stacked. A model atmosphere is bounded below by a flat, horizontally homogeneous surface. Below, we describe how the scattering by the gaseous molecules, the aerosol particles and the reflection by the surface is implemented in PYMIEDAP.
4.1. The model atmosphere
A model atmosphere consists of a stack of horizontally homogeneous layers. Each atmospheric layer can contain gaseous molecules and/or aerosol particles (including cloud particles). For every layer, the algorithm requires the total optical thickness b, the single-scattering matrix F of the gas and/or aerosol particles in the layer, and their single-scattering albedo a.
The single-scattering of incident light by gas molecules is described by anisotropic Rayleigh scattering (Hansen & Travis 1974), which includes both the inelastic Cabannes scattering and the elastic Raman scattering processes (Young 1981). Although overall energy is thus conserved, narrow spectral features that are due to Raman scattering, such as the filling-in of absorption lines in stellar spectra upon inelastic scattering in the planetary atmosphere (Grainger & Ring 1962; Stam et al. 2002), cannot be reproduced with the PYMIEDAP radiative transfer code.
We use the single-scattering matrix for anisotropic Rayleigh scattering as described by Hansen & Travis (1974):![$$ \boldsymbol F^\mathrm m{(\Theta,\lambda)}={\left[\begin{array}{cccc}A_1^\mathrm m(\Theta,\lambda)&B_1^\mathrm m(\Theta,\lambda)&0&0\\B_1^\mathrm m(\Theta,\lambda)&A_2^\mathrm m(\Theta,\lambda)&0&0\\0&0&A_3^\mathrm m(\Theta,\lambda)&0\\0&0&0&A_4^\mathrm m(\Theta,\lambda)\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq15.gif) (15)
(15)
with the superscript “m” referring to molecules. The single-scattering angle Θ is measured with respect to the direction of propagation of the incoming beam of light: Θ = 0° for forward- and 180° for backward-scattered light.
The single-scattering matrix Fm is normalized at every wave-length λ such that element 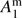 (the “phase function”), averaged over all scattering directions, equals one (see Hansen & Travis 1974). The elements of Fm are the following (Hansen & Travis 1974):
(the “phase function”), averaged over all scattering directions, equals one (see Hansen & Travis 1974). The elements of Fm are the following (Hansen & Travis 1974):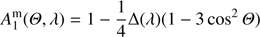 (16)
(16)
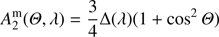 (17)
(17)
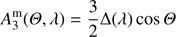 (18)
(18)
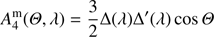 (19)
(19)
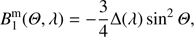 20
20
While the depolarization factor ρ depends on λ (see, e.g., Sneep & Ubachs 2005; Bates 1984), for most gases, the precise spectral dependence is not well known. Typical values for ρ are 0.09 for CO2 (fairly wavelength independent) and 0.0213 for N2 (at 500 nm). The current version of PYMIEDAP assumes a wavelength-independent value for ρ.
Our doubling-adding radiative transfer algorithm (see Sect. 5), does not use the scattering matrix elements themselves, but rather the coefficients of their expansion in generalized spherical functions, as described in detail by de Rooij & van der Stap (1984). The expansion coefficients for anisotropic Rayleigh scattering are given in Stam et al. (2002), for instance, and are, for a given value of ρ, computed by PYMIEDAP.
With PYMIEDAP, the user can directly define bm, the gaseous extinction optical thickness of an atmospheric layer (measured along the vertical direction), or the user can specify the pressure difference across an atmospheric layer and leave PYMIEDAP to compute bm for each given wavelength λ under the assumption of hydrostatic equilibrium, according to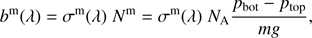 (22)
(22)
with σm the molecular extinction cross-section (in μm2 molecule−1), Nm the column number density of the gas (in molecules μm−2), pbot − ptop the pressure difference (in bars or 10−5 N m−2), NA the constant of Avogadro (i.e., 6.022140857 × 1023), m the mass per mole (in atomic mass units or g mole−1), and g the acceleration of gravity (in m s−2). Besides the pressure levels, the user specifies both m and g. We note that we have left out factors to account for unit conversions in Eq. (22) and in equations below.
The molecular extinction cross-section is the sum of the molecular scattering and absorption cross-sections as follows: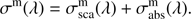 (23)
(23)
Combining this with Eq. (22), it is clear that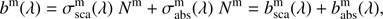 (24)
(24)
with 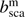 and
and 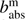 the molecular scattering and absorption optical thicknesses of the layer, respectively. To include gaseous absorption, the user defines the gaseous absorption optical thickness
the molecular scattering and absorption optical thicknesses of the layer, respectively. To include gaseous absorption, the user defines the gaseous absorption optical thickness 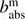 per wavelength.
per wavelength.
PYMIEDAP computes the molecular scattering cross-section 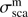 according to
according to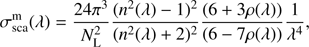 (25)
(25)
with NL Loschmidt’s number, n the refractive index of the gas under standard conditions, and ρ the depolarization factor. The refractive index is usually wavelength dependent, and PYMIEDAP can compute the refractive indices of N2, air, CO2, H2, and He using dispersion formulae that are valid across visible and near-IR wavelengths (Peck & Khanna 1966; Ciddor 1996; Bideau-Mehu et al. 1973; Peck & Huang 1977; Mansfield & Peck 1969). Users can also provide their own values for n.
Aerosol particles are small particles that are suspended in the atmospheric gas. PYMIEDAP considers cloud particles (relatively large particles with relatively high volume number densities) as any other type of aerosol particle. The influence of aerosol particles on the transfer of radiation through an atmospheric layer depends on the layer’s aerosol extinction optical thickness ba, their single-scattering albedo aa , and their single-scattering matrix Fa.
The PYMIEDAP user can specify ba at all required wave-lengths, or provide a value for Na, the layer’s aerosol column number density (in μm−2). In the latter case, PYMIEDAP computes ba from Na and the aerosol extinction cross-section σa, as follows: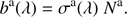 (26)
(26)
Given the microphysical properties of the aerosol particles, PYMIEDAP uses a Mie-algorithm (de Rooij & van der Stap 1984) to compute σa, and through this, ba, for every λ, assuming that the particles are homogeneous and spherical. The microphysical properties to be specified by the user are the particle size-distribution (see de Rooij & van der Stap 1984) and the refractive index. For layered spherical particles, PYMIEDAP uses an adaptation of the algorithm presented by Bohren & Huffman (1983). For these types of particles, the user specifies the refractive indices of the core and the shell, and the core radius as a fraction of the particle radius.
Using the Mie-algorithm or the adapted algorithm for layered spheres, PYMIEDAP also computes the aerosol single-scattering matrix Fa, which has the following form:![$$ \boldsymbol F^\mathrm a{(\Theta,\lambda)}={\left[\begin{array}{cccc}A_1^\mathrm a{(\Theta,\lambda)}&B_1^\mathrm a{(\Theta,\lambda)}&0&0\\B_1^\mathrm a{(\Theta,\lambda)}&A_2^\mathrm a{(\Theta,\lambda)}&0&0\\0&0&A_3^\mathrm a{(\Theta,\lambda)}&B_2^\mathrm a{(\Theta,\lambda)}\\0&0&-B_2^\mathrm a{(\Theta,\lambda)}&A_4^\mathrm a{(\Theta,\lambda)}\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq32.gif) (27)
(27)
and that they are normalized like the scattering matrix Fm (Eq. (15)). This matrix form holds for spherical particles, for particles with a plane of symmetry in random orientation, and for particles that are asymmetric and randomly oriented, while half of the particles are mirror images of the other half (see Hansen & Travis 1974). Rather than the scattering matrix elements themselves, PYMIEDAP uses the coefficients of their expansion into generalized spherical functions (de Rooij & van der Stap 1984).
Obviously, in nature, not all aerosol particles are spherical, and while PYMIEDAP cannot compute the expansion coefficients that describe the scattering of light by non-spherical particles, it can use them when the user provides them. Examples of sources of expansion coefficients of non-spherical particles are those derived from measured matrix elements, such as those in the Amsterdam-Granada Light Scattering Database (Muñoz et al. 2012) For differently shaped particles such as spheroids or ice crystals, various algorithms have been developed to calculate scattering matrix elements, such as the T-matrix method (see Mishchenko et al. 2002) and the ADDA method (Yurkin & Hoekstra 2011). Expansion coefficients derived from those matrix elements could be imported into PYMIEDAP.
Finally, PYMIEDAP computes the atmospheric layer’s total optical thickness b at wavelength λ as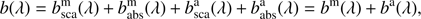 (28)
(28)
the layer’s single-scattering albedo a as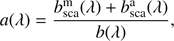 (29)
(29)
and its single-scattering matrix F as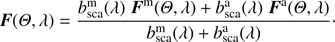 (30)
(30)
We note that if more than one aerosol type (size distribution, shape and refractive index) is used in an atmospheric layer, PYMIEDAP computes the extinction optical thickness, single-scattering albedo and single-scattering matrix of the mixture of aerosol particles using equations similar to Eqs. (28)–(30) before combining the aerosol optical properties with those of the gaseous molecules.
The values for b, a, and F for every atmospheric layer are fed into the adding-doubling radiative transfer algorithm, together with the reflection properties of the surface.
4.2. Model surface
Unless it is pitch black, a planetary surface will reflect incident direct light, that is, the unscattered light from the sun or star, and if there is an atmosphere above the surface, the incident diffuse light, that is, the light from the sun or star that has been scattered and that emerges from the bottom of the atmosphere. The surface albedo as indicates the fraction of all incident light that is reflected back up. This albedo ranges from 0.0 (all incident light is absorbed) to 1.0 (all incident light is reflected).
In PYMIEDAP, the surface reflection is defined through a reflection matrix. In the current version of PYMIEDAP, the surface reflection is Lambertian: it reflects light isotropically and completely depolarized. The (1, 1) element of the reflection matrix of a Lambertian surface equals as and is thus independent of the illumination and viewing geometries, while all other matrix elements equal zero.
5. Radiative transfer algorithm
As described in Eq. (9), to calculate Stokes vector I(μ, μ0, ϕ−ϕ0) of light that is locally reflected by a model planet, we have to compute R1, the first column of the local planetary reflection matrix. The computation of vector R1 includes all orders of scattering in the planetary atmosphere and reflection by the surface (if as > 0.0). PYMIEDAP computes R1, although not directly. Instead, PYMIEDAP produces ASCII files (see Appendix A) that contain the coefficients of the Fourier expansion of R1 for various combinations of μ and μ0. These files, which are stored in a database for repeated use, are accessed to compute R1 for the required combination of (μ, μ0, ϕ − ϕ0). The expansion is described in Sect. 5.1, and the subsequent application for the required geometry is given in Sect. 5.2.
5.1. Fourier expansion of the reflection matrix
Equation (28) in de Haan et al. (1987) shows how a matrix such as the planetary reflection matrix R can be expanded in a Fourier series. Because we only need the first column of this matrix, we can rewrite this expansion as follows: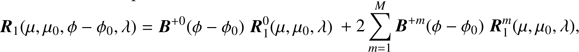 (31)
(31)
where 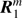 is the first column of the mth Fourier coefficient matrix Rm (0 ≤ m ≤ M). The series is summed until and including coefficient number M, the value of which is determined by the accuracy of the adding-doubling radiative transfer calculations (see de Haan et al. 1987). Matrices B+m and B−m have zeros everywhere except on the diagonal:
is the first column of the mth Fourier coefficient matrix Rm (0 ≤ m ≤ M). The series is summed until and including coefficient number M, the value of which is determined by the accuracy of the adding-doubling radiative transfer calculations (see de Haan et al. 1987). Matrices B+m and B−m have zeros everywhere except on the diagonal: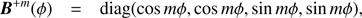 (32)
(32)
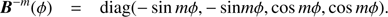 (33)
(33)
An obvious advantage of using the Fourier coefficients vectors  instead of R1 itself is that they are independent of the azimuthal angle difference ϕ − ϕ0. Combining Eqs. (9) and (31)–(33), the elements of vector I describing the light that is locally reflected by a planet are obtained through
instead of R1 itself is that they are independent of the azimuthal angle difference ϕ − ϕ0. Combining Eqs. (9) and (31)–(33), the elements of vector I describing the light that is locally reflected by a planet are obtained through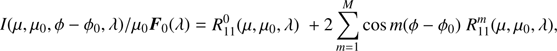 (34)
(34)
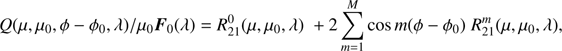 (35)
(35)
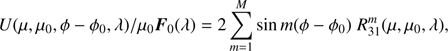 (36)
(36)
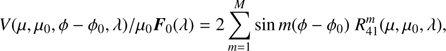 (37)
(37)
with the subscripts 11, 21, 31 and 41 denoting the first, second, third and fourth element of the column vectors 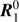 and
and 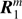 , respectively. For a given model planet, the Fourier file contains
, respectively. For a given model planet, the Fourier file contains 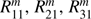 , and
, and 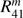 for m = 0 to M for various combinations of μ and μ0 (see Sect. 5.2).
for m = 0 to M for various combinations of μ and μ0 (see Sect. 5.2).
We calculate 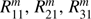 , and
, and 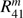 using the accurate and efficient adding-doubling radiative transfer algorithm as described in de Haan et al. (1987). This algorithm includes all orders of scattering, and it fully includes linear and circular polarization for all orders.
using the accurate and efficient adding-doubling radiative transfer algorithm as described in de Haan et al. (1987). This algorithm includes all orders of scattering, and it fully includes linear and circular polarization for all orders.
5.2. Gaussian abscissae
The values of μ and μ0 at which the Fourier coefficients are provided equal the Gaussian abscissae that are used in the adding-doubling algorithm (de Haan et al. 1987) for the Gauss–Legendre integrations over all scattering directions. For example, if 12 abscissae are used for the integrations, we provide the coefficients 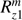 (with z equal to 1, 2, 3, or 4) at these 12 values of μ0 and at the same 12 values of μ, thus at a total of 144 combinations of illumination (μ0) and viewing (μ) geometries.
(with z equal to 1, 2, 3, or 4) at these 12 values of μ0 and at the same 12 values of μ, thus at a total of 144 combinations of illumination (μ0) and viewing (μ) geometries.
The number of Gaussian abscissae that is required to reach a given accuracy with the radiative transfer computations depends strongly on the single-scattering properties of atmospheric aerosol particles. In particular, if the scattered total and polarized fluxes vary strongly with the single-scattering angle (typically when the particles are large with respect to the wavelength λ, see e.g., Hansen & Travis 1974 for sample figures), more abscissae are needed than when they vary smoothly. The required number of abscissae depends also on the illumination and viewing geometries, for example, large solar zenith angles and/or viewing angles usually require more abscissae than small angles. We choose the number of abscissae in the database files such that the coefficients will give accurate results for a wide range of combinations of μ and μ0.
The expansion coefficients provided in a Fourier coefficients file can be used directly to evaluate Eqs. (34)–(37) at one of the available combinations of Gaussian abscissae μ and μ0, and for an arbitrary user-defined value of ϕ − ϕ0. Fourier coefficients at values of μ and/or μ0 that do not coincide with Gaussian abscissae can be obtained by interpolation.
To avoid having to extrapolate to obtain results at the often used values of μ and/or μ0 equal to 1.0 (i.e., θ, θ0 = 0°), which are not part of any set of Gaussian abscissae (which have values higher than 0.0 and lower than 1.0), we have included μ0, μ0 = 1.0 as so-called supplemented μ values (see Sect. 5 of de Haan et al. 1987). The adding-doubling algorithm calculates the Fourier coefficients at these supplemented values as if they were Gaussian abscissae. Thus, if we use M Gaussian abscissae, the Fourier coefficients are provided at M + 1 values of μ and μ0 (thus at (M + 1)2 combinations of μ and μ0).
PYMIEDAP separates the computation and storage of the Fourier coefficients from the computations of the locally reflected light (Eqs. (34)–(37)), and it can indeed skip the Fourier coefficients computation and instead use a previously computed Fourier file to compute the locally reflected light. The advantage of this is that time is saved, because depending on the composition and structure of the model atmosphere, the Fourier computations can take a significant amount of computing time.
6. Horizontally inhomogeneous planets
Because PYMIEDAP is pixel based, it can be applied to horizontally inhomogeneous planets, that is, planets with horizontal variations in their atmosphere and/or surface properties. The user can define such horizontal inhomogeneities using a so-called mask, in which pixels are assigned a value corresponding to a specific atmosphere-surface model combination, for example, “0” for model combination 1, “1” for model combination 2, and so on. When PYMIEDAP computes the locally reflected light for a given pixel, it will do so using the Fourier coefficients file for the model associated with that pixel. A pixel mask can be phase-angle dependent, meaning that a different pattern can be defined for each phase angle, for instance, to simulate a rotating planet.
Common horizontal inhomogeneities on planets are clouds. PYMIEDAP has the following four different types of cloud coverage masks built in (see Fig. 5): sub-solar clouds, polar cusps, latitudinal bands, and patchy clouds.
 |
Fig. 5. Examples of four types of cloud cover: panel a: sub-solar clouds with an angular width σc of 30° at α = 45°; panel b: polar cusps for a threshold latitude Lt of 50° at α = 0°; panel c: latitudinal bands with borders at −90°, −40°, 0°, 25°, and 35°, 90°; and panel d: patchy clouds for a cloud fraction Fc = 0.42 at α = 0°. In all figures, Neq = 80. |
Sub-solar clouds are thought to be relevant for tidally locked planets, such as exoplanets in tight orbits around their parent star (Yang et al. 2013). For these clouds, the pixel grid on the planetary disk is filled such that the region where the local solar zenith angle θ0 is smaller than the user-defined angle σc is assigned one atmosphere-surface model combination, and the other pixels another. This mask can also be used to model a sub-solar ocean (also referred to as “eyeball planet”; Turbet et al. 2016; Pierrehumbert 2011).
Polar cusps are clouds that form where the daily averaged incident solar or stellar flux dips below a certain threshold. For these clouds, the pixels located poleward of the user-defined latitude Lt on the planet are assigned one model combination, and the other pixels another (the planet equator is assumed to be in the middle of the planetary disk). This mask would also be useful to model polar hazes.
Latitudinal bands are bands of clouds covering ranges of latitudes. For these clouds, the user provides an array of latitudes that border the different atmosphere-surface models (the planet equator is assumed to be in the middle of the planetary disk). Such a mask can be useful for planets with belts and zones, or to simulate planets with latitudinal variations.
Patchy clouds are distributed across the planetary disk. They are described by Fc, the fraction of all pixels on the disk that are cloudy, and the spatial distribution of these cloudy pixels. This mask can accept N atmosphere-surface models, each with its own cloud coverage fraction Fc,i, with i = 0, … , N − 1. Patchy cloud patterns are generated by drawing 50 values from a 2D Gaussian distribution centered on a randomly chosen location within the pixel grid. The covariance matrix is given by![$$ \mathrm\Sigma=n_\text{pix}{\left[\begin{array}{cc}x_\text{scale}&0\\0&y_\text{scale}\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq52.gif) (38)
(38)
where xscale and yscale are used to fine-tune the shapes of the cloud patches along the north-south and east-west axes. PYMIEDAP uses xscale = 0.1 and yscale = 0.01 as nominal values in order to generate clouds with a zonal-oriented pattern similar to that observed on Earth. Cloud patches are generated on the planetary disk until the specified value of Fc,i is reached, the overall cover of all types of patches being 1. The cloud fraction Fc is defined at α = 0° because climatologically, the planetary-wide cloud coverage is more relevant than the coverage seen by an observer. The cloud fraction observed at α > 0° can thus differ from the specified value of Fc. An illustration of this cloud distribution is given in Fig. 6, which shows the disk-resolved simulations of flux, linear and circular polarization for 50% cloud cover, as computed by PYMIEDAP.
 |
Fig. 6. Computed disk-resolved locally reflected fluxes I (top), Ps (middle, in percent) and Pc (bottom, in percent) at α = 35° and λ= 0.55 μm, for a patchy cloud cover with Fc = 0.50. The cloud-free pixels have a pure gaseous (CO2) model atmosphere with b = 7.0. The cloudy pixels contain aerosol as described by Stam et al. (2006; we let the model D type aerosol pose as cloud particles). The disk-integrated values are F = 0.32, Ps = 0.10, and Pc = 1.6 × 10−5. For all figures, Neq = 60. |
The disk-integrated signal of a planet covered by patchy clouds will depend on the position of the cloudy pixels on the disk. To capture this variability, the user can choose to draw several patterns randomly at each phase angle. PYMIEDAP will return the average and standard deviations of the values of I, Q, U, and V over all patterns. It can also store the values for each pattern, providing the user insight into the variability.
An example of the variability computed using PYMIEDAP can be found in Rossi & Stam (2017), where it was used to generate the disk-integrated signals of Earth-like exoplanets with varying types and amount of coverage by liquid water clouds. Because we used Fourier coefficients, only a limited number of model computations were necessary: clear sky and cloudy case with different cloud-top altitudes. Furthermore, because the Fourier files allow for computation of the reflected Stokes vector of light for any geometry, it was possible to generate the Stokes vector of each pixel for the clear and cloudy cases, and then apply masks on these grids of pixels to obtain the desired cloud pattern. The variability due to patchy cloud cover could be simulated by simply using 300 patterns that were averaged. Another example of use of patchy cloud masks in PYMIEDAP can be found in Fauchez et al. (2017), where disk-integrated signals of exoplanets with patchy clouds were computed to investigate the effect of such clouds on the spectral signature of the O2 A-absorption band in the flux and polarization of reflected starlight.
7. Benchmark results
Here, we compare results of PYMIEDAP against (published) results obtained with other codes. This comparison allows an assessment of the accuracy of PYMIEDAP’s approach using computed Fourier coefficients files, and our results allow PYMIEDAP users to check their PYMIEDAP installation and understanding of the input and output files.
7.1. Locally reflected light
We compare our results for locally reflected light with those presented in Tables 5, 6, 9 and 10 of de Haan et al. (1987). We use the same adding-doubling algorithm as de Haan et al. (1987), with the same accuracy, that is, 10−6. However, while de Haan et al. (1987) computed the reflected Stokes vectors at precisely the specified values of θ0 and θ, we used a Fourier coefficients file (with θ = θ0 = 0° as supplemented Gaussian abscissae), combined with spline interpolation (with the algorithm from Press et al. 1992) to obtain the reflected Stokes vectors at the same geometries.
Two model atmosphere-surface combinations were considered in de Haan et al. (1987): model 1, with a single-layer atmosphere containing only haze droplets, bounded below by a black surface, and model 2, with an upper atmospheric layer containing only gas and a second, lower layer containing a mixture of gas and haze droplets, bounded below by a Lambertian reflecting surface with albedo As of 0.1. The molecular depolarization factor ρ is 0.0279. The haze particles in both atmospheres are water–haze L particles (Deirmendjian 1969), whose optical properties are calculated at λ = 0.7 μm (for the single-scattering expansion coefficients, see de Rooij & van der Stap 1984). For model 1, 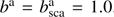 . For model 2,
. For model 2, 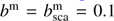 in each layer, and in the lower layer,
in each layer, and in the lower layer, 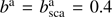 . The incident flux πF0 equals π (F0 is thus 1.0).
. The incident flux πF0 equals π (F0 is thus 1.0).
Table A.1 shows the Stokes vector elements of the locally reflected light for model 1 from de Haan et al. (1987), calculated using PYMIEDAP and 40 Gaussian abscissae (NG = 40). Table A.2 shows the results for model 2. PYMIEDAPpre-calculated Fourier coefficients combined with spline interpolation yield accurate results for both models. We note that when μ = 1.0, that is, the supplemented Gaussian abscissa in our Fourier files (cf. Sect. 5.2), we only have to interpolate between Fourier coefficients for μ0, not for μ.
7.2. Disk-integrated reflected starlight
There are no disk-integrated Stokes parameters in de Haan et al. (1987). We therefore first compare the disk-integrated reflected total flux as computed using PYMIEDAP against the analytical expression for the phase function of a Lambertian reflecting, spherical planet with a surface albedo as, that is (see van de Hulst 1980),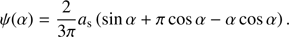 (39)
(39)
Figure 7 shows ψ calculated using PYMIEDAP and as = 1.0. For NG ≥ 20, these results are indistinguishable from those computed by Eq. (39). This comparison also shows the validity of calculating reflected disk-integrated fluxes under the assumption of a locally plane-parallel atmosphere and/or surface.
 |
Fig. 7. Numerical simulations of disk-integrated reflected fluxes (top) and the degree of linear polarization (bottom) as functions of α for different model planets. The flux curves are normalized such that they equal the planetary geometric albedo AG at α = 0°. For all curves, Neq = 20. Dotdashed line (only flux): Lambertian reflecting planet with a surface albedo ass = 1.0. Dashed line: planet with a gaseous atmosphere with |
To test the accuracy of the computed disk-integrated polarization, we compare PYMIEDAP results against results for two Jupiter-like gas planets computed with the same Fourier expansion coefficients, but an integration method that treats the whole planet as a single-scattering particle (Stam et al. 2006; the latter method is only applicable to horizontally homogeneous planets).
The first planet (Sect. 4.1 of Stam et al. 2006) has a purely gaseous atmosphere with 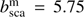 and
and 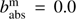 , and ρ = 0.02 (i.e., representative for H2). The surface albedo as = 0.0. Figure 7 shows the disk-integrated reflected total flux and degree of linear polarization as functions of α at λ = 0.55 μm. According to Stam et al. (2006), the geometric albedo AG of this planet is 0.647 and the maximum degree of polarization is 0.37 (this value is reached at α = 93° (note that Stam et al. (2006) used the scattering angle Θ rather than α (Θ = 180.0 − α). Table A.3 shows both the results of Stam et al. (2006) (interpolated linearly to obtain the values at the listed phase angles) and the results from PYMIEDAP. Comparing the results, it is clear that PYMIEDAP is very accurate, even for a relatively small number of Gaussian abscissae (i.e., NG = 20).
, and ρ = 0.02 (i.e., representative for H2). The surface albedo as = 0.0. Figure 7 shows the disk-integrated reflected total flux and degree of linear polarization as functions of α at λ = 0.55 μm. According to Stam et al. (2006), the geometric albedo AG of this planet is 0.647 and the maximum degree of polarization is 0.37 (this value is reached at α = 93° (note that Stam et al. (2006) used the scattering angle Θ rather than α (Θ = 180.0 − α). Table A.3 shows both the results of Stam et al. (2006) (interpolated linearly to obtain the values at the listed phase angles) and the results from PYMIEDAP. Comparing the results, it is clear that PYMIEDAP is very accurate, even for a relatively small number of Gaussian abscissae (i.e., NG = 20).
The second planet (Sect. 4.2 of Stam et al. 2006) has the same gaseous atmosphere and black surface as the first, but with aerosol particles added. The aerosol optical thickness ba = 3.25, yielding a total atmospheric optical thickness b of 9.0 (at λ = 0.55 μm). The aerosol particles are well mixed with the gas molecules, and have the microphysical properties of the model D particles of de Rooij & van der Stap (1984). The disk-integrated reflected flux and degree of linear polarization as functions of computed with PYMIEDAP are shown in Fig. 7. The geometric albedo AG of this second planet is 0.669 according to Stam et al. (2006). Table A.4 is similar to Table A.3, except for the second planet. Because the single-scattering scattering matrix elements of model D aerosol particles show significant angular structures, in particular in the forward- and backward-scattering directions, more Gaussian abscissae are needed (by both disk-integration methods) to achieve accurate results across the whole phase angle range; we used NG = 50.
8. Summary
We presented PYMIEDAP, a modular Python-based tool for computing the total and polarized fluxes of light that is reflected by (exo)planets (or moons) with locally horizontally homogeneous, plane-parallel atmospheres bounded below by a horizontally homogeneous, flat surface. The atmospheres can be vertically inhomogeneous. Horizontally inhomogeneous planets are modeled by assigning different atmosphere-surface combinations to different regions on the planet. The Fortran radiative transfer algorithm is based on the adding-doubling method as described by de Haan et al. (1987), and fully includes linear and circular polarization for all orders of scattering. The single-scattering of light by atmospheric aerosols is computed using Mie-scattering, based on de Rooij & van der Stap (1984).
PYMIEDAP has a two-step approach: first, the adding-doubling radiative transfer computations provide files with Fourier coefficients of the expansion of the local reflection matrix of the model planetary atmosphere and surface, and second, the Fourier coefficients are used to efficiently compute the locally reflected Stokes vectors for every given geometry. The latter Stokes parameters can be summed to provide the disk-integrated Stokes parameters of the reflected starlight. By storing the Fourier-coefficient files for later use, significant amounts of computing time can be saved in the computation of the reflected light vectors.
The modular aspect of PYMIEDAP allows users to define an atmosphere-surface model and to compute spatially resolved and/or disk-integrated signals of a planet at a range of phase angle in a single function call. PYMIEDAP can straightforwardly be used to model signals of horizontally inhomogeneous planets by assigning different atmosphere-surface models to different regions on a planet. Four predefined cloud types or “masks” are included in the code. The modular aspect of the code also allows for step-by-step computations for users who wish to perform more complicated cases.
PYMIEDAP is distributed under the GNU GPL license and we invite interested users to suggest improvements or extensions to broaden the application of the code.
PYMIEDAP is available at http://gitlab.com/loic.cg.rossi/pymiedap
Acknowledgments
L.R. acknowledges the support of the Dutch Scientific Organization (NWO) through the PEPSci network of planetary and exoplanetary science. The authors thank Gourav Mahapatra and Ashwyn Groot, who were so kind as to test the code before its public release.
References
- Aben, I., Helderman, F., Stam, D., & Stammes, P. 1997, in Polarization: Measurement, Analysis, and Remote Sensing, eds. D. Goldstein, & R. Chipman, Proc. SPIE, 3121, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D. R. 1984, Planet. Space Sci., 32, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bideau-Mehu, A., Guern, Y., Abjean, R., & Johannin-Gilles, A. 1973, Opt. Commun., 9, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Boesche, E., Stammes, P., & Bennartz, R. 2009, J. Quant. Spectr. Rad. Transf., 110, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C., & Huffman, D. 1983, Absorption and Scattering of Light by Small Particles (New York: Wiley), 477 [Google Scholar]
- Ciddor, P. E. 1996, Appl. Opt., 35, 1566 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cotton, D. V., Marshall, J. P., Bailey, J., et al. 2017, MNRAS, 467, 873 [NASA ADS] [Google Scholar]
- de Haan, J. F., Bosma, P. B., & Hovenier, J. W. 1987, A&A, 183, 371 [Google Scholar]
- de Rooij, W. A., & van der Stap, C. C. A. H. 1984, A&A, 131, 237 [Google Scholar]
- Deirmendjian, D. 1969, Electromagnetic Scattering on Spherical Polydispersions (New York: Elsevier Scientific Publishing) [Google Scholar]
- Fauchez, T., Rossi, L., & Stam, D. M. 2017, ApJ, 842, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Grainger, J. F., & Ring, J. 1962, Nature, 193, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Hovenier, J. W. 1974, J. Atmos. Sci., 31, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Travis, L. D. 1974, Space Sci. Rev., 16, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hovenier, J. W., & van der Mee, C. V. M. 1983, A&A, 128, 1 [NASA ADS] [Google Scholar]
- Hovenier, J. W., van der Mee, C., & Domke, H. 2004, Transfer of Polarized Light in Planetary Atmospheres; Basic Concepts and Practical Methods (Dordrecht: Kluwer; Berlin: Springer) [Google Scholar]
- Kemp, J. C., Henson, G. D., Steiner, C. T., & Powell, E. R. 1987, Nature, 326, [Google Scholar]
- Mansfield, C. R., & Peck, E. R. 1969, J. Opt. Soc. Am., 59, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., Lacis, A. A., & Travis, L. D. 1994, J. Quant. Spectr. Rad. Transf., 51, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., Travis, L. D., & Lacis, A. A. 2002, Scattering, Absorption, and Emission of Light by Small Particles (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Muñoz, O., Moreno, F., Guirado, D., et al. 2012, J. Quant. Spectr. Rad. Transf., 113, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Peck, E. R., & Huang, S. 1977, J. Opt. Soc. Am., 67, 1550 [NASA ADS] [CrossRef] [Google Scholar]
- Peck, E. R., & Khanna, B. N. 1966, J. Opt. Soc. Am., 56, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, P. 2009, Int. J. Comput. Sci. Eng., 4, 296 [Google Scholar]
- Pierrehumbert, R. T. 2011, Astrophys. J. Lett., 726, L8 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Rossi, L., & Stam, D. 2017, A&A, 607, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., Whitney, B. A., & Sasselov, D. D. 2000, ApJ, 540, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Sneep, M., & Ubachs, W. 2005, J. Quant. Spectr. Rad. Transf., 92, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Stam, D. M. 2008, A&A, 482, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., & Hovenier, J. W. 2005, A&A, 444, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., De Haan, J. F., Hovenier, J. W., & Aben, I. 2000, J. Geophys. Res., 105, 22 [CrossRef] [Google Scholar]
- Stam, D. M., Aben, I., & Helderman, F. 2002, J. Geophys. Res. (Atmos.), 107, 4419 [NASA ADS] [CrossRef] [Google Scholar]
- Stam, D. M., Hovenier, J. W., & Waters, L. B. F. M. 2004, A&A, 428, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stam, D. M., de Rooij, W. A., Cornet, G., & Hovenier, J. W. 2006, A&A, 452, 669 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Stammes, P., Kuik, F., & de Haan, J. 1994, in Proc. PIERS 1994, ed. B. e. a. Arbesser-Rastburg (Dordrecht: Kluwer Acad.), 2255 [Google Scholar]
- Turbet, M., Leconte, J., Selsis, F., et al. 2016, A&A, 596, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van de Hulst, H. C. 1980, Multiple Light Scattering, Tables, Formulas, and Applications, Vols. 1 and 2 (New York: Academic Press) [Google Scholar]
- Yang, J., Cowan, N. B., & Abbot, D. S. 2013, ApJ, 771, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Young, A. T. 1981, Appl. Opt., 20, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Yurkin, M. A., & Hoekstra, A. G. 2011, J. Quant. Spectr. Rad. Transf., 112, 2234 [Google Scholar]
Appendix A: Fourier file formats
Stokes parameters I, Q, U, and V of the locally reflected light for model 1 (see Sect. 7.1; a 1–layer atmosphere with water-haze L-aerosol and a black surface), as listed in Table 5 of de Haan et al. (1987), and as calculated using PYMIEDAP with 40 Gaussian abscissae.
Similar to Table A.1, except for model 2 (see Sect. 7.1; a 2–layer atmosphere with gas and water-haze L-aerosol, and a surface with albedo 0.1), as listed in Table 9 of de Haan et al. (1987) and as calculated using PYMIEDAP with 40 Gaussian abscissae.
Flux and degree of polarization of light that is reflected by a planet with a gaseous atmosphere with b = 5.75, bounded below by a black surface, as a function of α, as computed by Stam et al. (2006) and by using PYMIEDAP. The number of Gaussian abscissae, NG, is 20 and Neq = 100. The fluxes have been normalized such that F(0°) = AG.
Similar to Table A.3, except for a model atmosphere with model D aerosol (de Rooij & van der Stap 1984) added, such that b = 9.0. For these computations, NG = 50.
We describe the format of a Fourier-coefficients file for a given model atmosphere-surface combination below.
The first lines contain comments, including a reference, and they have details on the model atmosphere and surface. The number of these lines depends on the number of layers in the model atmosphere, but they are all preceded by a hash (“#”). In the following, we assume the number of comment lines is N.
Line N + 1 contains a number to describe the size of the reflected light vectors: “1” indicates only I, “3” indicates I, Q, and U, and “4” indicates I, Q, U, and V.
Line N +2 contains the number of Gaussian abscissae G plus the supplemented value 1.0. It thus contains the value G + 1.
Lines N + 3 up to and including N + 4 + NG contain the NG Gaussian abscissae (the cosines of the corresponding illumination and viewing zenith angles) plus the supplemented value 1.0, and the corresponding Gaussian weights. For the supplemented value, this weight is set equal to 1.0.
Starting with line N + NG + 5, the elements of the first column of the local reflection matrix R, that is, 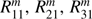 , and
, and 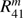 (see Eqs. (34)–(37)) are listed, with m the number of the Fourier term (0 ≤ m ≤ M, with M the number of the last Fourier term). Elements
(see Eqs. (34)–(37)) are listed, with m the number of the Fourier term (0 ≤ m ≤ M, with M the number of the last Fourier term). Elements 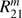 and
and 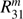 are only listed if the polarized fluxes have been calculated, and element
are only listed if the polarized fluxes have been calculated, and element 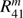 is only listed if the circularly polarized flux has been calculated as well. The matrix elements depend not only on the number of the Fourier term, m, but also on the illumination and viewing zenith angles, that is, on μ and μ0. With NG “true” Gaussian abscissae and 1 supplemented value, we have (NG + 1)2 combinations of μ and μ0.
is only listed if the circularly polarized flux has been calculated as well. The matrix elements depend not only on the number of the Fourier term, m, but also on the illumination and viewing zenith angles, that is, on μ and μ0. With NG “true” Gaussian abscissae and 1 supplemented value, we have (NG + 1)2 combinations of μ and μ0.
Each line has the format m, i, j, 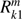 , with k equal to 1, 3, or 4, with i the number of the Gaussian abscissae representing μ (1 ≤ i ≤ NG + 1), and with j the number of the Gaussian abscissae representing μ0 (1 ≤ j ≤ NG + 1). Each file thus has (M + 1)(NG + 1)2 lines with one to four elements of the first column of the local reflection matrix R. For a purely gaseous atmosphere, M = 2, and given NG = 20, the total number of lines with matrix elements is thus 1323. Model atmospheres with aerosol and/or cloud particles will usually require much higher values for M and will thus yield much larger data files.
, with k equal to 1, 3, or 4, with i the number of the Gaussian abscissae representing μ (1 ≤ i ≤ NG + 1), and with j the number of the Gaussian abscissae representing μ0 (1 ≤ j ≤ NG + 1). Each file thus has (M + 1)(NG + 1)2 lines with one to four elements of the first column of the local reflection matrix R. For a purely gaseous atmosphere, M = 2, and given NG = 20, the total number of lines with matrix elements is thus 1323. Model atmospheres with aerosol and/or cloud particles will usually require much higher values for M and will thus yield much larger data files.
Appendix B: Computation of the local angles
We describe here the equations that are used to compute the local illumination and viewing angles θ0i, θi, βi and ϕi − ϕ0i for a pixel i in the pixel grid. First, we define the planetocentric reference frame (ux, uy, uz), where ux and uy lie in the plane of the observer’s sky, while uz points toward the observer.
We assume that the coordinates of pixel i in the plane of the sky are given by (xi, yi). Assuming that the planet is spherical with a radius equal to one, we know that the 3D coordinates of the projected pixel center on the planet are (xi, yi, zi) with 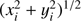 .
.
The local zenith direction for pixel i is given by vector![$$ {\boldsymbol r}_{cp}={\left[\begin{array}{c}x_i\\y_i\\z_i\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq67.gif) (B.1)
(B.1)
and the vector pointing to the star is given by![$$ {\boldsymbol r}_{cs}={\left[\begin{array}{c}\sin\alpha\\0\\\cos\alpha\end{array}\right]}, $$](/articles/aa/full_html/2018/08/aa32859-18/aa32859-18-eq68.gif) (B.2)
(B.2)
where α is the planetary phase angle, that is, the angle between the direction to the observer and the direction to the star as measured from the center of the planet. The local solar/stellar zenith angle is thus given by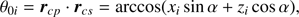 (B.3)
(B.3)
and since the unit vector uz is pointing toward the observer, the local viewing zenith angle is given by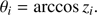 (B.4)
(B.4)
The local azimuthal difference angle ϕi − ϕ0i can be computed using the spherical law of cosines: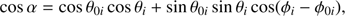 (B.5)
(B.5)
For 0 < α < π, the local rotation angle βi that is used to rotate computed Stokes parameters defined with respect to the local meridian planet to the planetary scattering plane is given by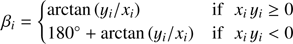 (B.7)
(B.7)
For π < α < 2π, rotation angle βi is given by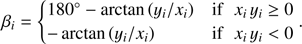 (B.8)
(B.8)
All Tables
Stokes parameters I, Q, U, and V of the locally reflected light for model 1 (see Sect. 7.1; a 1–layer atmosphere with water-haze L-aerosol and a black surface), as listed in Table 5 of de Haan et al. (1987), and as calculated using PYMIEDAP with 40 Gaussian abscissae.
Similar to Table A.1, except for model 2 (see Sect. 7.1; a 2–layer atmosphere with gas and water-haze L-aerosol, and a surface with albedo 0.1), as listed in Table 9 of de Haan et al. (1987) and as calculated using PYMIEDAP with 40 Gaussian abscissae.
Flux and degree of polarization of light that is reflected by a planet with a gaseous atmosphere with b = 5.75, bounded below by a black surface, as a function of α, as computed by Stam et al. (2006) and by using PYMIEDAP. The number of Gaussian abscissae, NG, is 20 and Neq = 100. The fluxes have been normalized such that F(0°) = AG.
Similar to Table A.3, except for a model atmosphere with model D aerosol (de Rooij & van der Stap 1984) added, such that b = 9.0. For these computations, NG = 50.
All Figures
 |
Fig. 1. Modules comprising PYMIEDAP. The blue boxes represent Fortran codes, and the red boxes represent Python codes. |
| In the text | |
 |
Fig. 2. Illustration of the rotation of the planetary scattering plane for an orbit with a random orientation (left) and with edge-on configuration (right). The first case would require further rotations to express the Stokes elements in the reference plane of the observer. |
| In the text | |
 |
Fig. 3. Sketch of a surface area dO on the planet (side view) and its projection toward the observer. The observer “sees” a pixel area equal to μ dO = cos θ dO, with θ the local viewing zenith angle. |
| In the text | |
 |
Fig. 4. Difference between the disk-integrated flux F computed using Eq. (14) and computed using the analytical expression for a sphere with a Lambertian reflecting surface and a geometric albedo AG of 1.0 (see Stam et al. 2006, and Eq. (39)) as a function of the planetary phase angle α for various values of Neq, the number of pixels along the planet equator. The difference has been normalized to AG. The dotted line shows that Neq increases with according to Neq(α) = Neq(0°)[1 + sin2(α/2)], with Neq(0°) = 40. |
| In the text | |
 |
Fig. 5. Examples of four types of cloud cover: panel a: sub-solar clouds with an angular width σc of 30° at α = 45°; panel b: polar cusps for a threshold latitude Lt of 50° at α = 0°; panel c: latitudinal bands with borders at −90°, −40°, 0°, 25°, and 35°, 90°; and panel d: patchy clouds for a cloud fraction Fc = 0.42 at α = 0°. In all figures, Neq = 80. |
| In the text | |
 |
Fig. 6. Computed disk-resolved locally reflected fluxes I (top), Ps (middle, in percent) and Pc (bottom, in percent) at α = 35° and λ= 0.55 μm, for a patchy cloud cover with Fc = 0.50. The cloud-free pixels have a pure gaseous (CO2) model atmosphere with b = 7.0. The cloudy pixels contain aerosol as described by Stam et al. (2006; we let the model D type aerosol pose as cloud particles). The disk-integrated values are F = 0.32, Ps = 0.10, and Pc = 1.6 × 10−5. For all figures, Neq = 60. |
| In the text | |
 |
Fig. 7. Numerical simulations of disk-integrated reflected fluxes (top) and the degree of linear polarization (bottom) as functions of α for different model planets. The flux curves are normalized such that they equal the planetary geometric albedo AG at α = 0°. For all curves, Neq = 20. Dotdashed line (only flux): Lambertian reflecting planet with a surface albedo ass = 1.0. Dashed line: planet with a gaseous atmosphere with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.