| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832824 | |
| Published online | 13 July 2018 | |
Reignited star formation in dwarf galaxies that were quenched during reionization
1
Center for Physical Sciences and Technology,
Saulėtekio al. 3,
Vilnius
10257,
Lithuania
e-mail: eimantas.ledinauskas@ftmc.lt
2
Vilnius University Observatory,
Saulėtekio al. 9, Bldg. III,
Vilnius
03100,
Lithuania
Received:
13
February
2018
Accepted:
21
March
2018
Context. Irregular dwarf galaxies of the Local Group have very varied properties and star formation histories. Some of them formed the majority of their stars very late compared to others. Extreme examples of this are Leo A and Aquarius, which reached the peak of star formation at z < 1 (more than 6 Gyr after the Big Bang). This fact seemingly challenges the ΛCDM cosmological framework because the dark matter halos of these galaxies on average should assemble the majority of their masses before z ~ 2 (<3 Gyr after the Big Bang).
Aims. We investigate whether the delayed star formation histories of some irregular dwarf galaxies might be explained purely by the stochasticity of their mass assembly histories coupled with the effect of cosmic reionization.
Methods. We developed a semi-analytic model to follow the accretion of baryonic matter, star formation, and stellar feedback in dark matter halos with present-day virial masses 109 M⊙ < Mdm,0 < 1011 M⊙ and with different stochastic growth histories obtained using the PINOCCHIO code based on Lagrangian perturbation theory.
Results. We obtain the distributions of observable parameters and the evolution histories for these galaxies. Accretion of baryonic matter is strongly suppressed after the epoch of reionization in some models, but the galaxies continue to accrete dark matter and eventually reach enough mass for accretion of baryonic matter to begin again. These “reborn” model galaxies show delayed star formation histories that are very similar to those of Leo A and Aquarius.
Conclusions. We find that the stochasticity caused by mass assembly histories is enhanced in systems with virial masses ~1010 M⊙ because of their sensitivity to the photoionizing intergalactic radiation field after the epoch of reionization. This results in qualitatively different star formation histories in late- and early-forming galaxies, and it might explain the peculiar star formation histories of irregular dwarf galaxies such as Leo A and Aquarius.
Key words: galaxies: dwarf / galaxies: formation / galaxies: evolution / galaxies: irregular / galaxies: star formation
© ESO 2018
1 Introduction
The Λ cold dark matter (ΛCDM) cosmological framework successfully explains many observational facts about the cosmic microwave background (Planck Collaboration XIII 2016), the large-scale structure of the Universe (Guo et al. 2016), and galaxy formation (Schaye et al. 2015). However, there are some indications that ΛCDM cosmology struggles to explain observations on smaller scales, namely on the scales of dwarf galaxies. Some of the primary disagreements between cosmological structure formation simulations and observations are the following: 1) simulations predict that galaxies like the Milky Way and M31 should have at least an order of magnitude more satellite galaxies than is observed (the missing satellites problem; Klypin et al. 1999); 2) a related and more troubling discrepancy is that simulations predict that galaxies like the Milky Way and Andromeda should host approximately six massive satellite galaxies that should be easily detected but are not observed in reality (the too big to fail problem; Boylan-Kolchin et al. 2011); 3) observations show that density profiles of low-mass galaxies have cores in the centers instead of the cusps that are predicted by cold dark matter simulations (the cusp versus core problem; Oh et al. 2015); 4) star formation histories of some of the Local Group irregular galaxies show a delayed star formation activity that peaks at z ≲ 1. In these galaxies the majority of stars form significantly later than most of the mass is assembled according to dark matter simulations (Cole et al. 2007, 2014). This last problem is the main motivation for this work.
At least some of these problems might be explained by improper comparison between observations and theory, as was shown in the context of the too big to fail (Verbeke et al. 2017) and the cusp versus core (Pineda et al. 2017) issues. Nevertheless, if at least some of these inconsistencies are real, they are very important, because they might argue in favor of some corrections to the standard cosmological model (e.g., warm dark matter: Lovell et al. 2014). However, they could also be a result of various processes related to baryonic matter (Sawala et al. 2016). This might be especially important for dwarf galaxies as they are very sensitive to baryonic physics because of their shallow gravitational potentials. However, simulating complex physics of radiation transfer, star formation, stellar feedback, and active galactic nuclei feedback from first principles requires numerical resources that are currently beyond reach. In order to model these phenomena, simplified subresolution models are used, which have a large number of free parameters and hence have a lower predictive power (Scannapieco et al. 2012). Because of this, it is still unclear whether realistic baryonic matter modeling is enough to bring dwarf galaxy formation models into agreement with observations. Therefore it is important to do more research on dwarf galaxies and check various ideas that could explain their observed peculiarities.
We here concentrate on isolated dwarf irregular galaxies with delayed star formation histories. The most extreme examples of these are the galaxies Leo A and Aquarius. In Aquarius, star formation peaks at z ~ 0.9 (Cole et al. 2014), and in Leo A, it peaks at z ~ 0.2 (Cole et al. 2007). In both of them, star formation has decreased slowly until the present, and both of them are gas rich (Kirby et al. 2017). On average, dwarf galaxies with present-day virial masses ≲ 1010 M⊙ should assemble half of their finalmass at z ≳ 2 (Fakhouri et al. 2010), and their delayed star formation seems to challenge the structure formation models based on Λ CDM cosmology. However, individual mass assembly histories are stochastic and can significantly differ from the averaged history. Because the effect of heating by intergalactic radiation field and stellar feedback strongly depends on the mass of dwarf galaxies, differences in individual mass assembly histories might be amplified and result in even more different observable properties, such as stellar or gas masses and star formation histories for these individual galaxies.
In order to study the star formation histories of isolated dwarf galaxies and investigate whether the observed delayed star formation in some of them might be explained within the standard Λ CDM cosmology, we created a semi-analytic model of dwarf galaxy evolution. We generated dark matter halo merger trees by using the publicly available PINOCCHIO code based on the Lagrangian perturbation theory (Monaco et al. 2013). We then modeled the galaxy evolution by supplementing these merger trees with approximate relations describing the evolution of baryonic matter. This scheme of modeling galaxy evolution in a cosmological context by using precompiled merger trees is not entirely new and dates back to Kauffmann et al. (1993) and Cole et al. (1994). In the context of dwarf galaxies, a similar scheme has been employed in Cloet-Osselaer et al. (2014), where the authors used dark matterhalo merger trees generated by an algorithm based on extended Press-Schecter theory and then used N-body andsmooth particle hydrodynamics code to model the internal evolution of these halos and baryonic matter.
By using our model, we investigated how the stochasticity in mass assembly histories might affect the evolution of isolated dwarf galaxies, and we found that the stochasticity of mass assembly coupled with reionization indeed leads to a wide variety of star formation histories of galaxies with dark matter halos with present-day mass Mdm,0 ~ 109–1010 M⊙ (the characteristic transitional mass below which the accretion of the baryonic matter is strongly suppressed and above which it is suppressed weakly). This results in qualitatively differing star formation histories in the models of late- and early-forming dwarf galaxies. We find that in some late-forming model galaxies, star formation is temporarily suppressed by cosmic reionization, but because they can still accrete dark matter as it is not affected by radiation, they eventually become massive enough to commence accreting baryonic matter and thus begin to form stars once more. Such “reborn” galaxies have been numerically obtained and analyzed in Shen et al. (2014), Benítez-Llambay et al. (2015), Fitts et al. (2017). We show that some of the reborn galaxies in our models have star formation histories that are very similar to those of Leo A and Aquarius, and therefore we conclude that stochasticity of mass assembly might explain their peculiar observed properties.
The model is described in Sect. 2. In Sect. 3 we present the main results. The implications and plausibility of the results are discussed in Sect. 4. The main conclusions are summarized in Sect. 5. We assume a standard Λ CDM cosmology with cosmological parameters H0 = 67.74 km s−1 Mpc−1, Ωb = 0.05, Ωm = 0.31, and ΩΛ = 0.69 from Planck Collaboration XIII (2016).
2 Description of the model
Our model is very similar to other semi-analytic galaxy evolution models (e.g., Lacey et al. 2016; Croton et al. 2016; Cattaneo et al. 2017). The main difference is that we focused on isolated dwarf galaxies and so evaded the necessity of modeling AGN feedback and interactions with more massive galaxies. The main components of each model galaxy were a dark matter halo, a gas disk, and a stellar disk. We modeled their evolution using dark matter halo merger trees and simplified analytical relations that dictate mass changes due to accretion, mergers, star formation, and feedback across the three components.
2.1 Dark matter halo merger trees
To generate dark matter halo merger trees, we used the publicly accessible PINOCCHIO code (Monaco et al. 2013). It is an approximate tool used for dark matter halo catalogs with spatial information at various redshifts based on the Lagrangian perturbation theory. Merger trees obtained from N-body simulation would be more accurate, but the possible inaccuracies of this simplified approach should not be important compared toinaccuracies caused by approximations that we have to make when modeling complex baryonic physics. Therefore we chose this method because it runs orders of magnitude faster than direct N-body simulations, so that the computing power required to obtain the merger treesof sufficient resolution to model low-mass galaxies can be obtained even on a desktop computer. We used a run with box size d ≈ 28 Mpc, sampled with 8003 particles and with periodic boundary conditions. If we assume that the minimal halo comprises ten particles (standard value for PINOCCHIO), then its mass is Mmin ≈ 2 × 107 M⊙, which is enough to resolve merger trees of halos used in this work (Mdm,0 ≥ 109 M⊙).
We here concentrate on isolated dwarf galaxies. Out of all dark matter halos, we therefore only analyzed those that are isolated throughout their whole evolution. We define a halo as isolated if it is farther than 2rvir from all more massive halos, where rvir is the virial radius of the more massive halo. We used a common rvir definition:
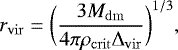 (1)
(1)
where Mdm is dark matter halo mass, ρcrit is the critical density of the Universe and Δvir is the overdensity of the collapsed and virialized spherical top-hat density fluctuation. We used the fitting formula from Bryan & Norman (1998) to derive the value of Δvir, which changes from Δvir ≈ 178 at z > 5 to Δvir≈ 102 at z = 0. Figure 1 shows examples of different mass assembly histories of isolated and non-isolated halos that all have a present-day mass Mdm,0 ≈ 1010 M⊙ to within 10%. Figure 1 shows that isolated halos accumulate their mass on average slightly later than non-isolated halos. The median age of the Universe at which a Mdm,0 ≈ 1010 M⊙ halo accumulates 90% of its final mass is t90 ≈ 6.2 Gyr for isolated halos and t90 ≈ 5 Gyr for non-isolated halos.
 |
Fig. 1 Example dark matter mass assembly histories obtained with PINOCCHIO for isolated (top) and non-isolated (bottom) halos that all have ≈1010 M⊙ (within 10%) mass at z = 0. |
2.2 Dark matter halos
We assumedthat densities of dark matter halos follow the spherically symmetric Navarro-Frenk-White (NFW) profile (Navarro et al. 1996),
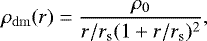 (2)
(2)
where rs is the scale radius. With this profile the total mass of the halo diverges as ln (r∕rs), so we truncated itat the virial radius. The scale radius and virial radius are related via the concentration parameter c ≡ rvir∕rs. The concentration parameter of a particular halo depends on its mass assembly history. To calculate the concentration parameter at a given time t, we used the model of Zhao et al. (2009), which relates c to the time, t0.04, at which the halo assembled 4% of the mass it has at time t:
![\begin{equation*} c(t) = 4 \bigg[ 1 + \bigg( \frac{t}{3.75 t_{0.04}} \bigg)^{8.4} \bigg]^{1/8}.\end{equation*}](/articles/aa/full_html/2018/07/aa32824-18/aa32824-18-eq3.png) (3)
(3)
According to this equation, c approaches 4 when a halo is rapidly growing due to dynamical heating, and it increases when the halo is growing slowly due to relaxation.
To characterize the gravitational potential of the dark matter halo, we used its maximum circular velocity, which for an NFW profile is
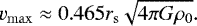 (4)
(4)
2.3 Baryonic matter accretion
The mass ofthe dark matter halo grows in two modes: smooth accretion from the intergalactic medium, and mergers with other halos. We assumed that before the reionization epoch, the smooth baryonic matter accretion rate is always proportional to the smooth dark matter accretion rate,
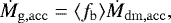 (5)
(5)
where ⟨fb⟩ = Ωb∕Ωdm ≈ 0.19 is the ratio between the average baryonic and dark matter densities in the Universe. During the epoch of reionization, the average temperature of intergalactic gas rapidly increases to ⟨TIGM⟩≈ 2 × 104 K (McQuinn et al. 2009). Therefore low-mass halos are prevented from accreting baryonic matter (Gnedin 2000), and lowest mass halos even lose their gas due to photoevaporation. In order to account for these effects, a simplified algorithm can be used, as shown in Okamoto et al. (2008). We used basically the same algorithm in this work. If the halo virial temperature Tvir < Teq(Δvir∕3), the halo does not accrete any gas. Here Teq(Δvir∕3) is the temperature of intergalacticgas at overdensity Δvir∕3. Virial temperature in this work is defined as
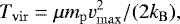 (6)
(6)
where mp is the mass of a proton and μ ≈ 0.63 is the average mass of a gas particle in units of mp. We used vmax instead of the more commonly used virial velocity 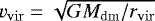 because when rvir is defined by Eq. (1), it increases in time even for a fixed halo mass because of decreasing ρcrit, and this leads to an unphysical decrease in vvir. vmax takes the halo concentration into account and so is less sensitive to this effect. For the lowest mass halos, if Tvir < Teq(Δevp), where Δevp = 106, the gas of the halo is evaporated exponentially at a rate
because when rvir is defined by Eq. (1), it increases in time even for a fixed halo mass because of decreasing ρcrit, and this leads to an unphysical decrease in vvir. vmax takes the halo concentration into account and so is less sensitive to this effect. For the lowest mass halos, if Tvir < Teq(Δevp), where Δevp = 106, the gas of the halo is evaporated exponentially at a rate
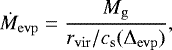 (7)
(7)
where Mg is the mass of the gas disk andcs(Δevp) is the sound speed at temperature Teq(Δevp). We also adopted Teq(Δvir∕3) and Teq (Δevp) dependencies from Okamoto et al. (2008), according to which Teq(Δvir∕3) changes from ≈104 K at z =9 to ≈ 4 ×104 K at z = 0, while Teq (Δevp) ≈ 104 K always.
We treated galaxy mergers very approximately and assumed that the larger halo just accretes all the gas and stars from the smaller haloin one dynamical time. In reality, mergers of galaxies with comparable mass may induce dynamical disk perturbations that might affect the galaxy structure and may lead to starbursts. However, inclusion of these highly complex processes in our phenomenological model would require introducing free parameters, which we tried to avoid. We therefore chose to refrain from treating major mergers in any special way. However, the star formation rate (SFR) during mergers in our model still increases because of the increase in gas mass and therefore gas density (if the accretedhalo had any gas left beforehand). To study how this approximation might affect the results, we calculated models in which mergers with 30% or higher mass ratios induce extreme starbursts during which a fraction f* = 1∕(1 + fej) of all the gas mass is turned into stars and the remaining fraction is ejected, where fej = mej∕m* is the ratio between ejected mass by feedback of a formed stellar population and the mass of that population (see Sect. 2.5 below). We discuss the results of this experiment in Sect. 4.
Numerical simulations and analytic arguments show that for low-mass galaxies, gas accretion should be predominantly in cold mode without formation of a virially shocked hot halo (Dekel & Birnboim 2006; Ocvirk et al. 2008; Birnboim & Dekel 2003). Therefore we assumed that the accreted baryonic mass falls straight to the central rotationally supported gas disk in a dynamical time of the dark matter halo. In order to calculate the size and density of the gas disk, we used the empirical relation by Kravtsov (2013),
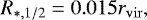 (8)
(8)
where R*,1∕2 is the half-mass radius of the stellar disk. We assumed that the surface density profiles of both gas and stellar disks are exponential,
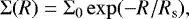 (9)
(9)
where the scale radius is given by Rs = R1∕2∕1.678. Observations show that the scale lengths of gas disks are usually larger than those of stellar disks (e.g., see Table 2 in Read et al. 2017). In absence of any good theoretically motivated relations, we assumed that the scale length of the gas disk Rs,g = 2Rs,*. This is close to the average value in Table 2 of Read et al. (2017). We also experimented with different values of this parameter and discuss the results in Sect. 4.
2.4 Star formation
To calculatethe SFR in the gas disk, we used the physically motivated analytic model by Krumholz (2013), which predicts the star formation law in molecule-poor galaxies and matches observations well. In this model the SFR surface density is calculated by
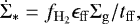 (10)
(10)
where ϵff ≈ 0.01, tff is the free-fall time of the molecular gas and 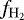 is the mass fraction of gas in molecular form.
is the mass fraction of gas in molecular form. 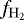 in this model depends on the surface density and metallicity of the gas and also on the volume density of stars and dark matter. This model has a free parameter fc, called clumping factor, which is defined as the ratio of the surface densities that are characteristic of atomic-molecular complexes to the surface density averaged over the resolved scale. As suggested in Krumholz (2013), we used fc = 5 because in our model we only follow the average structure of the gas disk. In this SFR model, it is also assumed that molecules form only on dust grains, so it cannot be used to calculate the SFR in gas with metallicity Z = 0. To compensate for this, we followed Krumholz & Dekel (2012) and assumed that population III stars enrich the surrounding gas to Zprim = 2 × 10−5, as calculated in Wise et al. (2012), and used this as a starting metallicity for primordial gas. We left all the other parameters at their default values as described in Krumholz (2013).
in this model depends on the surface density and metallicity of the gas and also on the volume density of stars and dark matter. This model has a free parameter fc, called clumping factor, which is defined as the ratio of the surface densities that are characteristic of atomic-molecular complexes to the surface density averaged over the resolved scale. As suggested in Krumholz (2013), we used fc = 5 because in our model we only follow the average structure of the gas disk. In this SFR model, it is also assumed that molecules form only on dust grains, so it cannot be used to calculate the SFR in gas with metallicity Z = 0. To compensate for this, we followed Krumholz & Dekel (2012) and assumed that population III stars enrich the surrounding gas to Zprim = 2 × 10−5, as calculated in Wise et al. (2012), and used this as a starting metallicity for primordial gas. We left all the other parameters at their default values as described in Krumholz (2013).
2.5 Stellar feedback
Newly formed stars inject momentum and energy into the surrounding gas via stellar winds, radiation, and supernova explosions. This feedback regulates the star formation efficiency on molecular cloud scales and can create massive gas outflows on galactic scales, which negatively affect the SFR. This effect is especially important for dwarf galaxies, which have low escape velocities, and it is necessary to include feedback into galaxy formation and evolution models in order to match the observed galaxy luminosity function (Baugh 2006). However, stellar feedback is a very complex subject and is far from understood. Different implementations of it give different results (Scannapieco et al. 2012).
We here explicitly modeled only feedback coming from supernova explosions. Small-scale effects of stellar feedback are included implicitly in the empirical star formation efficiency parameter ϵff (see Sect. 2.4). We modeled supernova feedback very approximately by using momentum conservation and assuming that every supernova ejects a gas mass
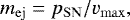 (11)
(11)
from the galaxy. Here pSN is the momentum generated by a supernova (including not only the momentum generated by initial stellar matter ejection, but also by the subsequent adiabatic expansion during the Sedov phase until the energy losses by radiation become non-negligible). We set pSN = 2 × 1043 g cm s−1 according tosimulations of supernovae in a turbulent interstellar medium (e.g., Walch & Naab 2015; Geen et al. 2016). We used momentum instead of energy because a large and uncertain amount of the injected kinetic energy is radiated away while the momentum remains conserved after the Sedov phase. Using energy conservation in a similar fashion would therefore be even more uncertain. Of course Eq. (11) gives approximately the maximum possible ejected mass, and in reality, it is almost certainly lower. However, we did not include any other feedback mechanisms on large scales, therefore we expect that this overly strong supernova feedback somewhat compensates for this.
The supernova rate was calculated as follows. We assumed a Kroupa (2001) initial mass function for the stellar population and further assumed that only stars with 8 M⊙ < Mstar < 25 M⊙ explode as core-collapse supernovae, as more massive stars with a low metallicity typical of dwarf galaxies should experience collapse into black holes without any strong explosion (Heger et al. 2003). This gives about one supernova per 110 M⊙ of stars formed. We further added Type Ia supernovae, which have a rate of ~ 1 per 1000 M⊙ of stars formed (Maoz & Graur 2017), to arrive at a supernovae rate of one per 100 M⊙ of stars formed in the disk.
2.6 Chemical evolution
In order to model the enrichment of the interstellar medium by heavy elements and gas recycling, we used data from the publicly available simple stellar population synthesis code SYGMA (Ritter et al. 2017). Heavy elements were injected directly into the gas disk and then were ejected or converted into stars in proportion to the involved gas mass. We assumed that the ejected heavy elements are rapidly mixed in the interstellar medium and always treated the gas disk as chemically homogeneous, having a uniform average metallicity. We also made the common approximation that heavy elements are ejected in the same time step as their parent stellar population is formed (instantaneous recycling). We used time steps Δ t ≈ 50 Myr, which is longer than the lifetimes of massive stars that explode as supernovae.
3 Results
We calculated models for six samples of dark matter halos, each consisting of about 300 isolated halos with present-day masses Mdm,0 ≈ 109 M⊙, 2.5 × 109 M⊙, 5 × 109 M⊙, 1010 M⊙, 2 × 1010 M⊙, 5 × 1010 M⊙, and 2 × 1011 M⊙ (dispersions of these masses can be seen in Fig. 4, panel a). We chose this mass interval because we expect that both Leo A and Aquarius fall into it based on abundance matching results (Moster et al. 2013; Read et al. 2017). This interval is also interesting because in it, the transition from halos strongly affected by reionization to halos weakly affected occurs, because they have virial temperatures comparable to Teq (Δvir∕3) (see Sect. 2.3) throughout their history.
 |
Fig. 2 Dependence on redshift of the dark matter halo virial mass (a), the virial temperature (b), the gas mass (c), the stellar mass (d), the SFR (e), and the gas metallicity (f) for four halos with different mass assembly histories and nearly the same final halo mass (within 10%). The red dashed line in panel b shows Teq (Δvir∕3), the virial temperature below which smooth accretion of baryons is shut off. |
 |
Fig. 3 Histograms of stellar mass (a), gas mass (b), and gas metallicity (c) at z = 0 for models with present-day dark matter halo masses 2.5 × 109 M⊙ (black), 1010 M⊙ (blue), and 5 × 1010 M⊙ (red). |
 |
Fig. 4 Relations between present-day stellar mass and dark matter halo virial mass (a), gas mass (b), average stellar metallicity (c), and average gas metallicity (d). Black points represent models and red points represent observations. Panel a: Read et al. (2017), panel b: Oh et al. (2015) and Kirby et al. (2017), panel c: Kirby et al. (2013), and panel d: Berg et al. (2012). Blue points in panel a represent the non-isolated galaxies Carina and Leo T, while in panel b, these points represent the galaxies Leo A and Aquarius, which are the focus of this work. Green and blue lines show the M*,0 –Mdm,0 relations from abundance matching (Moster et al. 2013; Read et al. 2017), and dashed lines denote extrapolation. |
3.1 Evolution of parameters in time
The variety of galaxy evolution histories caused by the stochasticity of mass assembly is shown in Fig. 2. This figure showsthe dependence on time of the virial dark matter halo mass (a), the virial temperature (b), the gas mass (c), the stellar mass (d), the total SFR (summed across all the branches of the merger tree) (e), and the average gas metallicity (f) for four Mdm,0 ≈ 1010 M⊙ halos with very different mass assembly histories. We display the mass-weighted average gas metallicity throughout the whole disk Zgas = mmet∕mgas, normalized to solar metallicity from Asplund et al. (2009). The dashed red line in panel b shows the virial temperature below which smooth baryonic matter accretion is turned off Teq(Δvir∕3) (see Sect. 2.3). These four mass assembly histories are chosen because they represent the whole variety quite well. Exceptfor panel e, the plots in Fig. 2 only show the parameters of the main halos in the merger trees.
The black line shows a halo that becomes massive very early and then slowly grows almost solely by smooth accretion. The purple line shows a less extreme example of a halo with a mass assembly history close to the median one. Both of these halos have acquired enough mass by the start of the reionization era to avoid being affected strongly by reionization (the only effect is that less baryonic matter is accreted during mergers with other smaller halos that might be affected). Both of them have peak SFRs at z > 2 and have formed 90% of their stellar mass already at z ≈ 5 and z ≈ 1 respectively.
The blue line shows a halo that acquires its mass later and therefore experiences a period lasting ~ 2 Gyr during and after reionization when there is no smooth accretion of baryonic matter (we subsequently call this the“quenching period”). Because of quenching, the SFR in this galaxy quickly declines after z ≈ 4. However, after z ≈ 2, it starts to increase again and reaches maximum at z ≈ 1 because only at z ≈ 2 has the galaxy acquired enough dark matter mass to start accreting baryonic matter again. This results in a galaxy with a qualitatively different star formation history that is dominated by young stellar populations as ≈ 90% of stellar mass is formed after z = 1.
The cyan line shows an extreme example of a halo that acquires most of its mass at z < 1 and therefore experiences a longer quenching period, lasting ~10 Gyr. As smaller halos that merge with it are also quenched, this halo acquires very small amounts of gas compared to accreted dark matter, and so the SFR remains very low up until z = 0. This results in a galaxy that is dominated by old stellar populations, similarly to the first two example galaxies. Panel c in Fig. 2 shows that the final gas mass depends non-monotonically on halo formation time. Extremely early- and late-forming halos have a present-day gas mass Mgas,0 ≈ 5 × 106 M⊙ and Mgas,0 ≈ 3 × 107 M⊙, respectively (the great jump in gas mass of late-forming halo occurs because it merged with another gas-rich halo immediately before z = 0 and after this experienced rapid accretion), while those with less extreme growth histories have gas masses that are about an order of magnitude higher. The final stellar mass, on the other hand, decreases monotonically with formation time, as is shown in Fig. 2d. The earliest-forming galaxy has M*,0 ≈ 4 × 107 M⊙, while the latest-forming galaxy has M*,0 ≈ 5.5 × 106 M⊙. By combining these two gas and stellar mass dependencies on formation time, it is easy to understand the dependence of gas metallicity, which is shown in panel f of Fig. 2. The earliest-forming galaxy has the highest metallicity because it has the highest final stellar mass but a low final gas mass, so that this results in a higher amount of ejected metals that are contained in a lower amount of gas. This is, of course, only a rough explanation because the model is not a closed box: gas can leave the halo and fall into it.
Of all the models with Mdm,0 ≈ 5 × 109 M⊙, 1010 M⊙, and 2 × 1010 M⊙, baryonic accretion is shut off at least for one time step (50 Myr) in about 70%, 33%, and 21% of the halos, respectively. Additionally, 68%, 17%, and 4% of the halos are quenched for at least 500 Myr, respectively, and 52%, 2%, and 0.3% of the halos are quenched for at least 5 Gyr, respectively. This rapidly changing fraction with increasing mass shows that Mdm,0 ~ 1010 M⊙ is indeed the characteristic transitional mass between halos that are weakly and strongly affected by reionization. These fractions are for the main halos in the merger trees and do not include less massive halos, which are affected more. At this mass range, the stochasticity of the mass assembly is amplified because early-forming halos are weakly affected by reionization, while late-forming halos are strongly affected. As we show in panel e of Fig. 2, this might therefore result in galaxies that have qualitatively different star formation histories even though their dynamical masses at z = 0 are the same.
3.2 Distributions of final parameters
The histograms of the final stellar mass (a), the gas mass (b), and the gas metallicity (c) at z = 0 for samples with Mdm,0 ≈ 2.5 × 109 M⊙, 1010 M⊙, and 5 × 1010 M⊙ are shown in Fig. 3 (the masses are normalized to their corresponding dark matter halo mass). As expected, the stellar mass grows on average super-linearly with the halo mass, so that the ratio of stellar mass to halo mass grows with halo mass. The gas mass increases super-linearly only up to Mdm ~ 1010 M⊙ and then increases sub-linearly. Super-linear growth occurs because up to Mdm,0 ~ 1010 M⊙, the fraction of quenched halos decreases and so on average, they can accrete super-linearly larger amounts of gas. This effect becomes unimportant for halos more massive than Mdm,0 ~ 1010 M⊙. The sub-linear mode occurs because more massive halos have higher star formation densities, which means that they consume and eject higher fractions of their total gas mass. The metallicity between these three masses does not change much. The lower average metallicity of Mdm,0 ≈ 1010 M⊙ models is a result of the higher gas-to-stellar mass ratio in them.
The relations between stellar mass and dark matter halo mass (a), gas mass (b), gas metallicity (c), and stellar metallicity (defined analogously to Zgas) (d) for all the models together with corresponding data from observations (Read et al. 2017; Oh et al. 2015; Kirby et al. 2017, 2013; Berg et al. 2012)are shown in Fig. 4. To facilitate comparison, we converted the dark matter halo virial masses from our model into M200, which is defined similarly as in this work, but Δ = 200 is used instead of Δvir (this definition is used in the cited works). The model data in these plots cluster because the total sample is not continuous in Mdm but consists of seven sub-samples with specific Mdm.
In panel a of Fig. 4, a bimodal distribution of stellar masses can be seen for galaxies with Mdm,0 ≈ 2.5 × 109 M⊙. This bimodality already starts to develop in halos with Mdm,0 ≈ 1010 M⊙ and starts to vanish in halos with Mdm,0 ≈ 109 M⊙. The reason is that this mass interval corresponds to galaxies in transition from weakly affected by reionization to strongly affected by reionization. In this interval, as Fig. 2 shows, late-forming galaxies evolve very differently compared to early-forming galaxies because of reionization and thus create a broadened stellar mass distribution. The bimodality most likely arises only because we assumed a sharp virial temperature cutoff that determines whether a certain galaxy can accrete baryonic matter. We checked this by analyzing the virial temperature dependence on z for the model galaxies. Galaxies corresponding to the lower stellar mass component of the bimodal distribution are strictly those whose virial temperature always remains lower than Teq(Δvir∕3). We therefore conclude that in reality, this distribution should be only broadened but not bimodal, because bimodality should be “washed out” by the smoother transition from the non-accreting to accreting state. This transition also causes a sudden decrease in the ratio between stellar mass and dark matter halo mass at Mdm,0 ~ 109-10 M⊙.
Panel a in Fig. 4 clearly shows that at Mdm,0 > 1011 M⊙, M*,0 in our model grows more slowly with increasing Mdm,0 than in the two relations from abundance matching. This discrepancy might arise because in our model we assumed that stellar feedback ejects gas from the galaxy completely so that it never falls back. In reality, at least some of ejected gas cools down and is eventually reincorporated into the gas disk. So galaxies effectively accrete more gas and can form more stars. This effect increases with mass and thus possibly explains the discrepancy in the higher mass end.
Panel bin Fig. 4 shows a group of outliers with up to 2 orders of magnitude higher Mg,0 in the interval M*,0 = 105-7 M⊙. These outliers are late-forminggalaxies that experienced temporary quenching periods and accreted a significant fraction of their gas very late. They are therefore extremely gas rich at z = 0. It is important to note that the gas mass from Oh et al. (2015) and Kirby et al. (2017) only includes atomic hydrogen. In all of our models the molecular gas fractions are very low (at most ~ 1%), but some fraction of disk gas might be ionized. This fraction probably depends on stellar feedback and cooling rates but is not followed in our model, and there is no simple way to estimate it. The model gas mass shown therefore always needs to be considered as an upper limit of the atomic gas mass.
Panels c and d of Fig. 4 both show that the stellar and gas metallicity in models with M*,0 > 107 M⊙ is too low compared to observed values. These discrepancies also arise because in our model the ejected gas never falls back. This leads to lower retained metal masses than in real galaxies, and this discrepancy grows with increasing galaxy mass. We here mainly considered galaxies with M*,0 ≤ 107 M⊙ (Leo A and Aquarius) where the agreement with observations is good even without the effects of gas fallback, so that we leave a detailed exploration of this effect for future works.
The average gas metallicity decreases with increasing stellar mass at M*,0 ~ 107 M⊙ (panel d in Fig. 4) because many galaxies with lower mass are quenched by cosmic reionization and thus are left with the gas obtained at early times (if these are not evaporated already by z = 0), which have been enriched during initial star formation. More massive galaxies, on the other hand, accrete more of the intergalactic gas at later times, and thus their gas disks are more diluted. In our model infalling intergalactic gas always has primordial metallicity Zprim = 2 × 10−5, while in reality, the average intergalactic metallicity should increase with time as a result of enrichment by gas ejected from galaxies. Including this effect is also explected to decrease the metallicity discrepancy with observations at M*,0 > 107 M⊙ as galaxies would accrete more metals throughout their history.
It is also important to keep in mind that the gas metallicities in Berg et al. (2012) were determined by observing HII regions that correspond to sites of active star formation. Owing to enrichment by forming stars in them, these regions should have higher metallicities than the average metallicity of the disk. This might also at least partly explain the lower metallicity in our models because we only followed an averaged metallicity throughout the whole disk. There is a similar problem when comparing stellar metallicities, as at least some of the stars form from gas that is enriched by massive stars that formed earlier in the same region. Kirby et al. (2013) also used only red giant stars, which on average are older than the whole stellar population and therefore probably represent the chemical composition of a galaxy at earlier times. However, these effects are not expected to produce very great changes, and modeling them in detail is beyond the scope of this work.
3.3 Comparison to the galaxies Leo A and Aquarius
The star formation history of the blue model in panel e of Fig. 2 has similar features to the measured star formation histories of Leo A and Aquarius. In order to analyze whether these observed star formation histories can be explained by this model in more detail, we calculated models for all isolated dark matter halos in our PINOCCHIO run with masses in the interval from 6 × 109 M⊙ < Mdm,0 < 1.3 × 1010 M⊙. This samplecontains 1927 different galaxies. Outside of this interval, similar star formation histories are extremely rare. To estimate the occurrence frequency of models similar to Leo A and Aquarius, we counted the number of them that form a fraction flate of their stars only at z < 1 (later than ≈ 6 Gyr after the Big Bang). We also counted only those galaxies that have 106 < M*,0 < 5 × 106 (similar to the values observed in Leo A and Aquarius, see Table 1). Out of all galaxies in this sample, 16 (0.8%) models have flate ≥ 0.7 (similar to Leo A) and 53 (2.8%) models haveflate ≥ 0.5 (similar to or more extreme than Aquarius). We also checked and visually confirmed that the star formation histories of these models resemble the observed ones.
In Fig. 5 we show example models with star formation histories similar to those of Leo A and Aquarius together with those derived from observations (Cole et al. 2007, 2014). The black solid lines show model star formation histories averaged in the same time bins as those from observations to facilitate comparison. The agreement between observations of Leo A and the model is very good: in all time bins except for the earliest one, the two agree to within 30%, and the difference in the earliest bin is only a factor 5. For Aquarius, the differences between the model and observations are larger, but in all time bins, they do not exceed a factor ~ 3. This clearly shows that the qualitative form of the star formation histories in these models is very similar to the observed ones. Furthermore, it would almost certainly be possible to find models that match better if we were to increase the sample of mass assembly histories. We did not do that, however, because this qualitative agreement shows sufficiently well that such star formation histories could be explained, and it would be naive to expect that a semi-analytic model could reconstruct star formation histories of individual real galaxies in high detail. We stress that we did not need to fine-tune the parameters of the model in order to reproduce the qualitative features of the star formation histories of the dwarfs Leo A and Aquarius. Rather, the setup of the model already provides such star formation histories as a consequence of including the effects of reionization on the baryon accretion into galaxies.
The final dark matter halo, gas, and stellar masses and the average stellar metallicity of the same models as in Fig. 5 are shown in Table 1 together with the corresponding parameters of Leo A and Aquarius determined from observations (Kirby et al. 2017). The stellar masses of the model galaxies are similar to the observed ones, but the gas mass in the models is about 21 and 36 times higher than in Leo A and Aquarius, respectively. We discuss the possible causes of this large discrepancy in Sect. 4. The mass of metals in Aquarius is about 3 times higher than in the model. This discrepancy probably arises because the gas mass is too high, which dilutes the enrichment.
Stellar masses, gas masses, and average stellar metallicities of the galaxies Leo A and Aquarius from Kirby et al. (2017; metallicity is in [Fe/H]) and corresponding parameters at z = 0 of the models shown in Fig. 5.
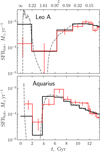 |
Fig. 5 Example model star formation histories similar to those of the dwarf galaxies Leo A (top) and Aquarius (bottom). Gray dashed lines show the star formation histories of the models, red lines show the star formation histories determined from observations (Cole et al. 2007, 2014), and black solid lines show the star formation histories of the models averaged in same time intervals as those from observations to facilitate comparison. |
4 Discussion
The results presented in the previous section show that for dark matter halos with present-day virial masses Mdm,0 ~ 109-10 M⊙, the stochasticity from mass assembly histories is amplified by the reionization epoch in a sense that the late-forminghalos are temporarily quenched, while the early-forming halos are not quenched. This can result in qualitatively different star formation histories. Early-forming dark matter halos have the highest SFR at z ≈ 4-10, after which time it monotonically declines. On the other hand, for most of the late-forming halos, the SFR declines rapidly after the reionization epoch and then begins to rise again when the halos become massive enough for smooth baryon accretion to become possible again. In the latter scenario, galaxies have minor old stellar populations and are dominated by stars that formed at z< 2. These features are qualitatively similar to those of some irregular dwarf galaxies, such as Leo A and Aquarius, and Fig. 5 shows that this scenario might indeed explain their star formation histories. However, as shown in Table 1, our model predicts that galaxies with these star formation histories should have ~ 20-30 times more gas mass at z = 0 than is observed in Leo A or Aquarius. This discrepancy is interesting because on average, our models agree quite well with observations (Fig. 4), at least for galaxies with M* < 107 M⊙. This might mean that in galaxies with delayed star formation histories such as Leo A and Aquarius, there are some additional, maybe external, processes that are not accounted for in our model. One possible solution would be to include modelling the ionized gas fraction in the galaxy, because now we compare the total gas mass in our models with only the observationally constrained atomic gas mass. Other more exotic solution would be to include the effects of AGNs. Recently, evidence for active intermediate-mass black holes has been found in ever smaller dwarf galaxies (Pardo et al. 2016), and there are no known reasons why it would be impossible for them to exist in even smaller galaxies such as Leo A or Aquarius. This is of course speculative, but worth considering, as feedback from AGNs could at least partially solve many known problems with dwarf galaxies (Silk 2017). In our case, AGN winds or jets could increase the SFR by generating turbulence and compressing gas (Kalfountzou et al. 2017; Gaibler et al. 2012) and might also easily eject significant amounts of gas from low-mass galaxies such as Leo A and Aquarius. Interestingly, these galaxies both show large holes in their HI maps1 (Hunter et al. 2012). Such gas ejection might result in galaxies with similar star formation histories but significantly lower gas masses at z = 0, thus solving the discrepancy. We plan to investigate this possibility in the future.
Other formation scenarios, where these “late-blooming” galaxies form early and then do not form stars for a very long time because of the absence of any perturbations, or where they assemble their mass extremely late, seem less likely because such growth histories are extremely rare according to structure formation simulations based on Λ CDM cosmology (we did not find any examples of these in our whole sample of merger trees). It therefore seems that the effect of reionization as described in this work is a more natural explanation. Of course, even though we find models with star formation histories similar to those of Leo A and Aquarius, the fraction of these models is quite small (see Sect. 3.3) and these models are clearly outliers. However, Leo A and Aquarius might also be outliers in reality. To fully answer the question whether our model can successfully explain their evolution, a statistical abundance investigation and comparison is therefore needed. The gas mass discrepancy that we find could also be thought of as evidence that the standard Λ CDM cosmology fails at small scales (for a review of more evidence for this, see Bullock & Boylan-Kolchin 2017). This claim is very strong, however, and more conventional solutions should first be explored.
Other works have also found that dwarf galaxies with strongly delayed star formation histories tend to reside in late-forming 109-10M⊙ halos (Shen et al. 2014; Benítez-Llambay et al. 2015; Fitts et al. 2017). These works also all found that reionization probably plays a very important role in explaining how dwarf galaxies with two-component stellar populations (old and young) could be formed. Another work, published while our paper was in review, shows that a similar reignition of star formation in dwarf galaxies could occur when they collide with cosmic web or tidal gas streams left over from galaxy mergers (Wright et al. 2018). These galaxies also form in late-forming dark matter halos with similar masses as in this work and also tend to have significantly higher gas masses as opposed to other similar-mass dwarfs. There might apparently be several mechanisms at play in the formation of galaxies such as Leo A and Aquarius, and similar resulting observational properties mean that they could be hard to separate.
We also find that some Mdm,0 ≲ 1010M⊙ models are quenched for so long that their SFR begins to increase only at z ~ 0 (see the cyan model in Fig. 2). In these cases, galaxies end up with stellar masses M*,0 ~ 105-6 M⊙ and their baryonic mass is completely dominated by the gas with Mgas,0 ~ 107-8 M⊙. This might explain some observed extremely gas-dominated dwarf galaxies (e.g., Begum et al. 2005). In addition, our model predicts a steepening decrease in the number of galaxies with M*,0 < 106 M⊙ (panel a in Fig. 4) because of the effect of reionization on low-mass halos. This might help solve the missing satellites problem.
Of course, the model we presented is highly simplified. Like in other semi-analytic galaxy formation models, a major weakness is the modeling of stellar feedback as it involves a complex interplay between many different processes on different scales. However, to our knowledge, there are currently no more realistic and practical ways to model it analytically, and we must wait for progress in this area. Another major simplification is that we did not take into account the instabilities in the gas disk that can occur during major mergers. In the model, during mergers with non-empty dark matter halos, the SFR increases only because of the rapid increase in the gas mass. In reality, these merger-induced instabilities could lead to starbursts, which might even drive the gas out of the dark matter halo and leave the remaining galaxy quenched. As mentioned in Sect. 2.3, to study how these starbursts might affect our results, we calculated models in which extreme starbursts occur during major mergers (mergers with mass ratios of 30% or higher). We assumed that during these starbursts, a fraction of the gas is turned into stars and the remaining gas is ejected proportionally to the formed stellar mass, so that in total, all of the gas would be used up. This treatment is certainly too extreme, but it is well suited to studying how our results would change by including more realistic major merger physics because the changes then should only be smaller than with this extreme adjustment. We find that including extreme starbursts does not stronglychange the final parameter distributions. In most of the models, major mergers occur very early (at z ≳ 2), so that the effect is washed out by the later evolution. In some models with late major mergers, the star formation is of course quenched and so their star formation history is altered strongly, but these models only constitute a minority. In addition, we find that most temporarily quenched models preserve their star formation histories, similar to Leo A and Aquarius. From these results, we conclude that including merger-induced starbursts probably does not change our main results and conclusions.
We also calculated models with a different gas disk scale length compared to the stellar disk (Sect. 2.3), namely with Rs,g = Rs,*, 1.5Rs,*, and 3Rs,*. Shorter scale lengths lead to more concentrated gas disks and thus to higher SFRs. On average, this does not affect the final parameter distributions significantly, so that letting it vary would only increase their dispersion. It does change the star formation histories of individual galaxies, however. With shorter scale lengths, galaxies tend to form their stars earlier, and with greater scale lengths, they form stars later. By varying this scale length ratio, it would be possible to find better-matching models to Leo A and Aquarius. We also find that models with Rs,g = Rs,* that have similar star formation histories to Leo A and Aquarius have ~ 10–20 times more gas mass than is observed, thus reducing the discrepancy by a factor of about 2, but they still cannot solve it completely. It is important to keep in mind that to our knowledge, there is no reason for the ratio between scale lengths of gas and stellar disks to be constant throughout the whole evolution of a galaxy. This might also have important effects on the resulting star formation histories, but we leave this question for future research.
Nevertheless, with all these shortcomings, the model still predicts galaxy parameters similar to the observed ones (Fig. 4). This is achieved, contrary to other semi-analytic galaxy formation models, without optimizing any free parameters. All the coefficients and parameters (e.g., star formation efficiency, clumping parameter, and momentum generated by supernovae) are taken from observations or numerical simulations and are held fixed. The agreement between this model and observations may be easily improved by finding best-fit values for these parameters, but we chose not to do this because it would decrease the predictive power of the model. Our simple model works because we here studied probably the simplest type of galaxies: isolated and low-mass galaxies. As galaxy formation and evolution is a very complex process incorporating many different processes on very different space- and timescales, it might be very useful to first understand the simplest systems and only then proceed to more complex large galaxies.
5 Conclusions
We used a semi-analytic model to study the effect of mass assembly stochasticity on the evolution of isolated dwarf galaxies with present-day virial masses Mdm,0 ~ 109-11 M⊙. The main conclusions of this work are listed below:
- 1)
The interval of dark matter halo virial masses at z = 0 that is studied in this work (109-11 M⊙) includes the characteristic transitional mass below which halos are strongly affected by cosmic reionization and above which they are affected weakly;
- 2)
Because of the different possible mass assembly histories, a fraction of galaxies at this mass are strongly affected by reionization, while the remaining ones are affected weakly. This can result in qualitatively differing star formation histories of different galaxies with the same dynamical mass at z = 0;
- 3)
The models in which dark matter halos assemble their mass later than with an average mass assembly history have star formation histories that are at least qualitatively similar to those of the dwarf galaxies Leo A and Aquarius;
- 4)
However, these models tend to have 20–30 times more gas mass than is observed, thus indicating that some additional processes need to be included to completely reconstruct these galaxies.
The results also show that isolated dwarf galaxies can be modeled quite successfully using semi-analytic models without optimizing any free parameters. This might be very useful in studying large parameter volumes as semi-analytic models require far fewer computational resources than 3D hydrodynamical models. The model we presented has some major approximations, but it is possible to relax or soften at least some of them and make the model even more realistic in the future.
Acknowledgements
We thank the anonymous referee for helpful comments and thought-provoking questions. We also thank V. Vansevičius, D. Narbutis, and P. Monaco, the creator of PINOCCHIO, for helpful discussions and comments. This research was funded by a grant (No. LAT-09/2016) from the Research Council of Lithuania.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M. 2006, Rep. Prog. Phys., 69, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Begum, A., Chengalur, J. N., & Karachentsev, I. D. 2005, A&A, 433, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benítez-Llambay, A., Navarro, J. F., Abadi, M. G., et al. 2015, MNRAS, 450, 4207 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Skillman, E. D., Marble, A. R., et al. 2012, ApJ, 754, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Blaizot, J., Devriendt, J. E. G., et al. 2017, MNRAS, 471, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Cloet-Osselaer, A., De Rijcke, S., Vandenbroucke, B., et al. 2014, MNRAS, 442, 2909 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Aragon-Salamanca, A., Frenk, C. S., Navarro, J. F., & Zepf, S. E. 1994, MNRAS, 271, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., Skillman, E. D., Tolstoy, E., et al. 2007, ApJ, 659, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., Weisz, D. R., Dolphin, A. E., et al. 2014, ApJ, 795, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Stevens, A. R. H., Tonini, C., et al. 2016, ApJS, 222, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Fitts, A., Boylan-Kolchin, M., Elbert, O. D., et al. 2017, MNRAS, 471, 3547 [NASA ADS] [CrossRef] [Google Scholar]
- Gaibler, V., Khochfar, S., Krause, M., & Silk, J. 2012, MNRAS, 425, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Hennebelle, P., Tremblin, P., & Rosdahl, J. 2016, MNRAS, 463, 3129 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y. 2000, ApJ, 542, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, H., Zheng, Z., Behroozi, P. S., et al. 2016, MNRAS, 459, 3040 [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Ficut-Vicas, D., Ashley, T., et al. 2012, AJ, 144, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Kalfountzou, E., Stevens, J. A., Jarvis, M. J., et al. 2017, MNRAS, 471, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., & Guiderdoni, B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Cohen, J. G., Guhathakurta, P., et al. 2013, ApJ, 779, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Rizzi, L., Held, E. V., et al. 2017, ApJ, 834, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2013, MNRAS, 436, 2747 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Dekel, A. 2012, ApJ, 753, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Lovell, M. R., Frenk, C. S., Eke, V. R., et al. 2014, MNRAS, 439, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Graur, O. 2017, ApJ, 848, 25 [Google Scholar]
- McQuinn, M., Lidz, A., Zaldarriaga, M., et al. 2009, ApJ, 694, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, P., Sefusatti, E., Borgani, S., et al. 2013, MNRAS, 433, 2389 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., & Teyssier, R. 2008, MNRAS, 390, 1326 [NASA ADS] [Google Scholar]
- Oh, S.-H., Hunter, D. A., Brinks, E., et al. 2015, ApJ, 149, 180 [Google Scholar]
- Okamoto, T., Gao, L., & Theuns, T. 2008, MNRAS, 390, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Pardo, K., Goulding, A. D., Greene, J. E., et al. 2016, ApJ, 831, 203 [CrossRef] [Google Scholar]
- Pineda, J. C. B., Hayward, C. C., Springel, V., & Mendes de Oliveira, C. 2017, MNRAS, 466, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, J. I., Iorio, G., Agertz, O., & Fraternali, F. 2017, MNRAS, 467, 2019 [NASA ADS] [Google Scholar]
- Ritter, C., Côté, B., Herwig, F., Navarro, J. F., & Fryer, C. 2017, ApJS, submitted [arXiv:1711.09172] [Google Scholar]
- Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 457, 1931 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., Wadepuhl, M., Parry, O. H., et al. 2012, MNRAS, 423, 1726 [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Shen, S., Madau, P., Conroy, C., Governato, F., & Mayer, L. 2014, ApJ, 792, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2017, ApJ, 839, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Verbeke, R., Papastergis, E., Ponomareva, A. A., Rathi, S., & De Rijcke S. 2017, A&A, 607, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walch, S., & Naab, T. 2015, MNRAS, 451, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Turk, M. J., Norman, M. L., & Abel, T. 2012, ApJ, 745, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. C., Brooks, A. M., Weisz, D. R., & Christensen, C. R. 2018, MNRAS, submitted [arXiv:1802.03019] [Google Scholar]
- Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2009, ApJ, 707, 354 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Stellar masses, gas masses, and average stellar metallicities of the galaxies Leo A and Aquarius from Kirby et al. (2017; metallicity is in [Fe/H]) and corresponding parameters at z = 0 of the models shown in Fig. 5.
All Figures
 |
Fig. 1 Example dark matter mass assembly histories obtained with PINOCCHIO for isolated (top) and non-isolated (bottom) halos that all have ≈1010 M⊙ (within 10%) mass at z = 0. |
| In the text | |
 |
Fig. 2 Dependence on redshift of the dark matter halo virial mass (a), the virial temperature (b), the gas mass (c), the stellar mass (d), the SFR (e), and the gas metallicity (f) for four halos with different mass assembly histories and nearly the same final halo mass (within 10%). The red dashed line in panel b shows Teq (Δvir∕3), the virial temperature below which smooth accretion of baryons is shut off. |
| In the text | |
 |
Fig. 3 Histograms of stellar mass (a), gas mass (b), and gas metallicity (c) at z = 0 for models with present-day dark matter halo masses 2.5 × 109 M⊙ (black), 1010 M⊙ (blue), and 5 × 1010 M⊙ (red). |
| In the text | |
 |
Fig. 4 Relations between present-day stellar mass and dark matter halo virial mass (a), gas mass (b), average stellar metallicity (c), and average gas metallicity (d). Black points represent models and red points represent observations. Panel a: Read et al. (2017), panel b: Oh et al. (2015) and Kirby et al. (2017), panel c: Kirby et al. (2013), and panel d: Berg et al. (2012). Blue points in panel a represent the non-isolated galaxies Carina and Leo T, while in panel b, these points represent the galaxies Leo A and Aquarius, which are the focus of this work. Green and blue lines show the M*,0 –Mdm,0 relations from abundance matching (Moster et al. 2013; Read et al. 2017), and dashed lines denote extrapolation. |
| In the text | |
 |
Fig. 5 Example model star formation histories similar to those of the dwarf galaxies Leo A (top) and Aquarius (bottom). Gray dashed lines show the star formation histories of the models, red lines show the star formation histories determined from observations (Cole et al. 2007, 2014), and black solid lines show the star formation histories of the models averaged in same time intervals as those from observations to facilitate comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


