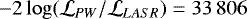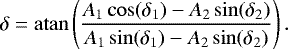| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201732446 | |
| Published online | 26 July 2018 | |
LASR-guided stellar photometric variability subtraction
The Linear Algorithm for Significance Reduction
Department of Physics, University of Idaho,
875 Perimeter Drive MS 0903,
Moscow,
ID
83844, USA
e-mail: ahle6481@vandals.uidaho.edu
Received:
11
December
2017
Accepted:
9
April
2018
We develop a technique for removing stellar variability in the light curves of δ-Scuti and similar stars. Our technique, which we name the Linear Algorithm for Significance Reduction (LASR), subtracts oscillations from a time series by minimizing their statistical significance in frequency space. We demonstrate that LASR can subtract variable signals of near-arbitrary complexity and can robustly handle close frequency pairs and overtone frequencies. We demonstrate that our algorithm performs an equivalent fit as prewhitening to the straightforward variable signal of KIC 9700322. We also show that LASR provides a better fit to seismic activity than prewhitening in the case of the complex δ-Scuti KOI-976.
Key words: asteroseismology / stars: variables: delta Scuti / methods: numerical / methods: data analysis / techniques: polarimetric
© ESO 2018
1 Introduction
Recent observing programs such as the Kepler mission have demonstrated that stellar variability in high mass stars often renders transit light curves unusable (Basri et al. 2010). Additionally, high-mass stars often rotate rapidly, inducing an oblate shape and a pole-to-equator luminosity gradient across the stellar surface (Barnes 2009; Barnes et al. 2011; Ahlers et al. 2015; Ahlers 2016). These two effects add challenges to traditional light curve analysis, radial velocity measurements, Doppler tomography, and Rossiter McLaughlin measurements (Gimenez 2006; Udry et al. 2007).
Approximately 60% of stars in the Kepler field of view display more stellar variability than the Sun (McQuillan 2013). Such variability produces effects in transit light curves that make traditional fitting challenging or impossible. Many of these targets are low-mass stars with variability caused by non-sinusoidal effects such as sunspots in their convective exteriors. Techniques for analyzing non-sinusoidal or non-periodic signals in the light curves such as the autocorrelation function (McQuillan et al. 2014) and Gaussian processes (Aigrain et al. 2016) produce strong results when applied to such stars. However, high-mass stars behave quite differently. At ~6250 K and hotter, stars invert to become radiative rather than convective at their surface (Winn et al. 2010). These stars have weak or nonexistent sunspots, and commonly rotate rapidly as a mostly-rigid body throughout their lifetimes. High-mass stars in the classical instability strip pulsate with radial and nonradial modes at high amplitudes. Therefore, analysis of stellar variability in the light curves of high-mass stars comes with a unique set of challenges and must be handled differently than variability in low-mass stars.
For classical pulsators such as Delta Scuti (δ-Scuti) and Gamma Doradus stars, the technique of “prewhitening” serves as the traditional method of asteroseismic analysis of transit light curves (e.g., Hernández et al. 2009; Poretti et al. 2009). Prewhitening fits sinusoids to photometry in an iterative process. This algorithm performs least-squares fits of several of the highest-amplitude oscillations in the time domain, determining approximate frequency, amplitude, and phase values for those oscillations. Prewhitening then fits several next-highest amplitude oscillations as a running total with the original fit, repeating this process until stellar variability has been resolved.
Prewhitening often serves as an adequate method for removing stellar variability and determining the frequencies of oscillation in classical pulsators. However, we explore an alternate route out of necessity: we found that prewhitening provided an inadequate fit of the complex signal of Kepler Object of Interest (KOI) 976. KOI-976 is a high-amplitude, rapidly rotating δ-Scuti star with a complex variable signal. We tried to remove stellar variability from the transit light curve of KOI-976 by applying prewhitening, but we found that the complex signal contained too many oscillations for an accurate least-squares fit in the time domain. This roadblock led us to explore removing stellar variability in frequency-space instead through a new process that we call the Linear Algorithm for Significance Reduction (LASR).
In this paper we develop a frequency-domain method for removing the asteroseismic signal of high-mass pulsators. In Sect. 2 we detail the LASR technique. In Sect. 3 we apply LASR to a synthetic dataset and to δ-Scutis KIC 9700322 and KOI-976 to compare our technique against prewhitening. In Sect. 4 we discuss how LASR compares with existing techniques for analyzing variability in photometric data.
2 Methods
The Linear Algorithm for Significance Reduction (LASR) serves as an alternate method to prewhitening for signal reduction. It resolves a linear combination of oscillations in a time series by minimizing each oscillation’s significance in the frequency domain. The algorithm operates linearly: it reduces the highest-amplitude frequency, subtracts it from the time series, and then reduces the new highest-amplitude frequency.
The LASR technique has two primary advantages over traditional prewhitening. First, because it operates in frequency space, LASR’s fitting process treats every oscillation as independent and avoids the degeneracies and complex parameter space that prewhitening encounters for datasets containing many oscillation modes. Second, the computer code behind LASR is extremely simple to run and requires very little knowledge of signal processing, making it an accessible technique for inexperienced researchers. In Sect. 2.1, we detail the algorithm for significance reduction. In Sect. 2.2, we discuss handling interdependent frequencies including close frequency pairs and integer-multiple frequencies. In Sect. 2.3, we detail our best-fit error analysis. In Appendix B we mathematically derive that LASR’s straight-forward approach to subtracting stellar oscillations is robust for sinusoidal variability.
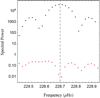 |
Fig. 1 A periodogram window for the highest-amplitude peak in the synthetic time series discussed in Sect. 3.1. We set LASR to sample the spectral power of this peak 25 times. The black and red points show the Pi (ω) before and after LASR minimized the peak’s significance. The unreduced oscillation shows a clear peak with aliasing on either side. The dashed line marks the true frequency of this oscillation. LASR successfully reduces this oscillation and yields correct measurements of its (w, A, δ) values (see Table 2). |
2.1 LASR algorithm
LASR combines two well-known tools for signal processing: the Lomb-Scargle normalized periodogram, and the downhill simplex routine. To remove a single oscillation from a time series, LASR creates a window of the power spectrum of the time series around the peak of that oscillation (Fig. 1). It then applies the downhill simplex routine to minimize that peak’s significance.
We use the traditional Lomb-Scargle normalized periodogram (Press 2007) for spectral analysis. The variations in brightness in high-amplitude δ-Scuti stars correspond to ~5% variations inuncertainty. We test whether these variations in uncertainty affect LASR by comparing the traditional Lomb-Scargle normalized periodogram with the generalized periodogram (e.g., Zechmeister & Kürster 2009; Vio et al. 2010), which applies weights to each time bin according to its photometric uncertainty. We find no noticeable differences between the two methods for δ-Scuti stars KOI-976 and KIC 9700322. In the case of different noise properties and instrument systematics, more computationally expensive techniques that better handle time bin uncertainty may provide better results in the significance reduction process. Such systematics do not appear in this analysis; we therefore favor the traditional Lomb–Scargle periodogram:
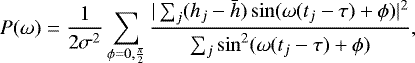 (1)
(1)
where hj is the photometric flux value at time tj, σ is the standard deviation in the dataset, ϕ is a phase offset that includes the values 0 and π∕2, and ω = 2πf is the angular frequency being sampled. The offset τ is defined as
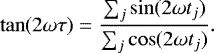 (2)
(2)
Several works exist to explain the statistical significance of frequency peaks in a periodogram (e.g., Press 2007; Baluev 2008). We represent the statistical significance of an oscillation in our dataset by sampling a window of frequencies around the peak. LASR evenly samples frequencies in a window approximately three times the full width of the peak.
LASR’s adjustable window width depends on the width of frequency peaks; in general, a longer time series means narrower peaks in a periodogram. For KOI-976’s short cadence photometry discussed in Sect. 3, we sample P(ω) 40 times in a window width of 0.7 μHz. We sum P(ω) values and use the resulting value to represent the significance Si(ω, A, δ) of the ith oscillation in our dataset as a function of frequency ω, amplitude A, and phase δ.
The goal of LASR is to find the (w, A, δ) values that minimize S(ω, A, δ). To do this, LASR uses a downhill simplex routine (Nelder & Mead 1965; Press 2007) to find the minimum of S(ω, A, δ). We choose this minimization routine over more robust routines such as Powell’s Method (Brent 2013) because of the well-behaved parameter space that results from minimizing oscillations in the frequency domain (see Appendix B). In Appendix A.1 we list the necessary inputs to operate LASR and discuss computation times for running the algorithm and in Appendix A.2 we provide pseudocode for writing this routine in any computer programming language.
2.2 LASR and interdependent frequencies
In general, LASR removes oscillations from a dataset one at a time because they are linearly independent from one another. However, two scenarios arise where this assumption fails: close frequency pairs and overtone frequencies.
We define close frequency pairs as oscillations close enough together in frequency space that spectral analysis cannot resolve them individually (Fig. 2), which can cause problems for prewhitening. If two frequencies exist close enough together that their periodogram windows (described in Sect. 2.1) overlap, then Si (ω, A, δ) cannot be properly minimized. Close frequency pairs are common both for complex datasets with many independent oscillations and for short time series that yield wide frequency peaks in their periodograms. LASR’s solution, however, is simple: just remove both peaks at once. LASR can remove any number of peaks simultaneously by minimizing a combined Si (ω, A, δ) function that samples P(ω) values for all relevant peaks, and then minimizing that function within a single large simplex.
Overtone frequencies can be more challenging because they are not mathematically independent. The power spectrum of an oscillation can be changed dramatically by integer multiple frequencies. Therefore, minimizing Si (ω, A, δ) for a single frequency in this scenario will result in a poor determination of its (w, A, δ) values.
The solution is again to simply remove both peaks simultaneously. The underlying challenge stems from recognizing that this behavior is occurring in the first place. In our analysis of KOI-976, we identify all relevant frequencies through spectral analysis before applying the LASR technique to search for such resonances. We find scant evidence of this scenario arising in KOI-976, but we test simultaneous subtraction in an idealized dataset in Sect. 3.1 and show its successful determination of (w, A, δ) for overtone frequencies (Table 2).
 |
Fig. 2 Log-scale plot of the power spectrum of two close frequencies (f2 and f3 in Table 2). The two oscillations appear in frequency space as a single asymmetric peak (black). LASR minimizes the significance of both peaks simultaneously (red) and accurately determines the (w, A, δ) of both oscillations. LASR samples frequencies of a periodogram window for each frequency; for close frequency pairs these two windows overlap. |
2.3 Error analysis
We find the uncertainty in our best-fit parameters by calculating the covariance matrix of our dataset. Following Andrae (2010), we estimate that the likelihood function 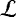 of our model is nearly Gaussian at its maximum, allowing us to calculate the model’s covariance matrix using the Fisher information matrix
of our model is nearly Gaussian at its maximum, allowing us to calculate the model’s covariance matrix using the Fisher information matrix 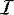 :
:
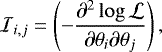 (3)
(3)
where θi is the ith model parameter and 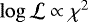 . We numerically approximate these second derivatives in each element of the Fisher matrix as
. We numerically approximate these second derivatives in each element of the Fisher matrix as
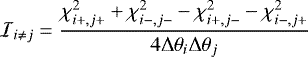 (4)
(4)
where 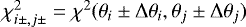 and Δθi is a very small step away from that parameter’s best-fit value. In our calculations we use a frequency step size of Δf = 10−10Hz, a normalized amplitude step size of ΔA = 10−6, and a phase step size of Δp = 10−4.
and Δθi is a very small step away from that parameter’s best-fit value. In our calculations we use a frequency step size of Δf = 10−10Hz, a normalized amplitude step size of ΔA = 10−6, and a phase step size of Δp = 10−4.
We calculate the covariance matrix 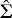 of our best-fit model by taking the inverse of the Fisher matrix
of our best-fit model by taking the inverse of the Fisher matrix  . We test whether
. We test whether 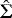 is positive definite by checking that all of its eigenvalues are positive. We take the diagonal elements of the covariance matrix to be the 1σ variance of our model parameters.
is positive definite by checking that all of its eigenvalues are positive. We take the diagonal elements of the covariance matrix to be the 1σ variance of our model parameters.
Global parameters of the synthetic data we generate to test LASR.
3 Results
We demonstrate the LASR technique by applying it to a synthetic time series and by applying it to δ-Scuti KOI-976’s short-cadence Kepler photometry. We establish LASR’s ability to measure the frequency, amplitude, and phase (w, A, δ) of oscillations in a time series containing Gaussian noise, time gaps, overtone frequencies, and close frequency pairs in Sect. 3.1. We demonstrate that LASR provides a much better fit to KOI-976’s complex variable signal than traditional time-domain prewhitening in Sect. 3.3.
3.1 LASR subtraction of synthetic oscillations
We create a synthetic time series containing seven oscillation modes commonly seen in a δ-Scuti variable star. We list the global parameters of the synthetic data in Table 1. We create a 90-day time series with a 1-min cadence and add Gaussian noise and data gaps that would commonly occur in Kepler photometry. We include five data gaps: four periodic gaps that represent masked-out transits, and one large gap representing the gaps commonly seen in short-cadence Kepler photometry. The synthetic time series includes correlated noise commonly seen in Kepler data. We generate Gaussian noise using a Box–Muller transform (Box & Muller 1958; Press et al. 1992) and weight each uncertainty with a lag-1 autocorrelation between successive time samples (Haykin 2006).
We include a small periodic transit in our synthetic time series to test its effects on our output code. The transit represents an Earth-radius planet orbiting a δ-Scuti star with a transit depth smaller than Kepler’s detection limit. We list the transit parameters in Table 1. When testing its effects on our fitting process, we find this injected transit causes no significant influence on our results. In general, we find that transits do not influence the LASR algorithm until their transit depths grow larger than its photometric 1-σ uncertainty. At that limit, transits are readily visible in the time series and should be removed. We include this transit to show that low-amplitude transits at or below the detection limit do not noticeably affect out fitting results. In our algorithm, we treat removing time bins affected by transits as a standalone prerequisite before applying our significance reduction routine.
We add seven oscillation modes to the synthetic data to test LASR’s capabilities. We include a single high-amplitude oscillation at 228.7 μHz as an example of a stand-alone mode in the dataset. We add a close frequency pair at 252.5 μHz and 252.6 μHz to test LASR’s ability to reduce oscillations that cannot be individually subtracted through spectral analysis. Additionally, we include three frequencies at integer multiples of one another to test LASR’s ability to remove resonant, interdependent frequencies. We also add one oscillation whose photometric amplitude matches the synthetic data’s 1σ uncertainty value to test our algorithm’s ability to remove frequencies near the limit of statistical significance.
We subtract oscillations in order of highest-significance peak to lowest-significance (see Table 2 and Fig. 3). LASR subtracts the single large peak (f1 ) quickly and without difficulty. For the close frequency pair f2 and f3, we imitate a real time series by falsely identifying it as a single peak (see Fig. 2). We tried a single starting frequency value of 252.53 μHz and could not reduce the window’s significance below 67.4%. We then set LASR to remove two close frequencies and immediately found the values listed in Table 2. LASR also yielded accurate (w, A, δ) values for the resonant f4, f5 , and f6 frequencies in a simultaneous fit.
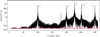 |
Fig. 3 Total power spectrum of the synthetic time series before (black) and after (red) LASR reduction of its seven oscillations. As we show in Table 2, LASR reduces all oscillations by over 99.9% of their original significance and yields accurate (w, A, δ) values. The injected transit causes no noticeable effect on the power spectrum. |
Oscillations added to a synthetic dataset to test LASR’s ability to subtract variability.
3.2 LASR comparison to prewhitening: KIC 9700322
We subtract variability from the δ-Scuti star KIC 9700322 and compare our results to Breger et al. (2011), who fit stellar variability using the statistical package period04. Following Breger et al. (2011), we use incorporate Kepler’s third quarter short cadence photometry in our fit and measure 76 frequencies. We show our best-fit of the stellar variability in Fig. 4 and compare the five highest-amplitude and five lowest-amplitude oscillations to Breger et al. (2011) in Table 3.
Our best-fit using LASR agrees almost completely with the frequencies and amplitudes found in Breger et al. (2011). We successfully model KIC 9700322’s stellar variability throughout Kepler’s Q3 short cadence time series. We obtain a reduced χ2 value of 1.13 for our fit; KIC 9700322’s slightly reddened noise and its photometric outliers were the main causes for this value’s deviation from unity. In the case of relatively straightforward variability, LASR and prewhitening are equivalently reliable, with the added bonus for LASR of only ever fitting a small parameter space at any time.
Stellar frequencies and amplitudes of δ-Scuti KIC 9700322 measured using our algorithm and using the prewhitening program period04 (Breger et al. 2011).
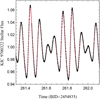 |
Fig. 4 Sample of KIC 9700322’s stellar variability (black) and our best-fit of the variable signal (red) using LASR. Our fit yeilds a reduced χ2 value of 1.13. |
3.3 LASR subtraction of KOI-976
We perform the same variability subtraction process as that described in Sect. 3.1 on Kepler Object of Interest (KOI) 976, a rapidly rotating δ-Scuti star that hosts an eclipsing binary companion. KOI-976 displays typical seismic activity for a δ-Scuti variable, possessing a few dominant nonradial modes between ~100 μHz − 300 μHz, as well as many low-amplitude oscillations spanning ~0 μHz − 500 μHz. In this analysis, we treat the star as a rigid rotator whose variable signal is well-modelled as a linear combination of sinusoids, which typically serves as an adequate assumption for δ-Scuti stars.
We perform this analysis on KOI-976’s two available quarters of 1-min Kepler photometry available on the Mikulski Archive for Space Telescopes. We use KOI-976’s presearch data conditioning data (PDC) available through the Kepler analysis pipeline (Smith et al. 2012) and find no relevant differences between the PDC and raw-data versions of the photometry. KOI-976’s time series contains a single transit by its stellar companion, as well as several significant data gaps. We mask out the transit and treat it as another gap in the time series. These gaps produce significant aliasing in periodograms. As we show in Fig. 1, LASR subtraction of an oscillation removes both a peak and its aliases, so even very large data gaps are surmountable through this technique.
We follow the process detailed in Sect. 2 and remove KOI-976’s oscillations from the time series one at a time, exceptin the cases of close frequency pairs and overtone frequencies. We start with the highest-significance peak and work our way down to the significance detection limit based on KOI-976’s photometric uncertainty of ~ 10−4. In total, we subtract off 319 frequencies. Figure 5 shows the original and reduced frequency power spectrum of this dataset.
LASR successfully minimizes all significant frequencies present in KOI-976’s short-cadence photometry. Figure 6 contrasts LASR with prewhitening and shows that LASR provides a better fit of KOI-976’s oscillations than prewhitening through linear regression. We obtain a log-likelihood ratio between the two methods of 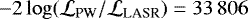 , indicating a superior resolution of KOI-976’s variability using our technique. We perform error analysis following Sect. 2.3.
, indicating a superior resolution of KOI-976’s variability using our technique. We perform error analysis following Sect. 2.3.
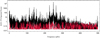 |
Fig. 5 Lomb–Scargle periodogram of KOI-976’s short-cadence photometry before (black) and after (red) subtracting stellar variability. LASR reduced the spectral power of all oscillations from ~ 104 at the max to ~1.0. We reduce the representative significance of all subtracted oscillations by at least 98% and find that all significant oscillations are well-modelled as sinusoids. |
 |
Fig. 6 A comparison of variability subtraction using LASR (red) and traditional prewhitening (blue). We fit all KOI-976 short-cadence photometry and display a ~ 1 day sample of KOI-976’s short-cadence photometry with best-fit (top panel) and its best-fit residuals (bottom panel). LASR produces a superior fit of KOI-976’s seismic activity with a log-likelihood ratio of
|
4 Discussion and conclusion
Our results show that LASR successfully removes stellar variability commonly seen in classical pulsators. Our technique can remove oscillations from photometry of arbitrary complexity so long as they are well-modelled as sinusoids. We find that for the rapidly-rotating δ-Scuti KOI-976, LASR serves as a superior method for variability subtraction over the traditional prewhitening approach of linear regression in the time domain. In particular, we find that LASR more accurately fits the frequencies of individual oscillations. It also better-resolves close frequency pairs that can be very difficult to identify when fitting in the time domain. Combined with LASR’s reliability, relatively low computation cost, and ease-of-use, we consider our technique to be a useful tool for spectral analysis in asteroseismology.
We develop LASR out of necessity: we originally attempted to subtract variability from KOI-976 following traditional prewhitening methodology that has successfully resolved the oscillations of other δ-Scuti stars (Breger et al. 2011, 2012). We found, however, that for KOI-976, we could not obtain accurate frequencies using this technique. We observed several undesired aliasing effects occurring in the low-frequency range of our dataset due to these imperfect fits. We demonstrate that for thisdataset, LASR successfully minimizes significant frequencies without producing aliasing effects (Fig. 5) and provides a better fit of KOI-976’s variable signal than prewhitening (Fig. 6).
We put forth LASR as one of many tools available for analyzing photometry. Existing tools such as Period04 (Lenz & Breger 2004) and others (Akritas & Bershady 1996; Vio & Wamsteker 2002; Rohlfs & Wilson 2013) provide robust and well-established techniques for signal processing of photometry. Additional techniques exist for analyzing stellar variability that contains non-sinusoidal or pseudo-periodic signals. These methods include modelling signals as multivariate random variables through Gaussian processes (MacKay 1998; Rasmussen & Williams 2006; Aigrain et al. 2016), detecting signals through autocorrelation functions (Edelson & Krolik 1988; McQuillan et al. 2014), and analyzing time-variable signals through wavelet analysis. These techniques are important tools for transit detection, denoising signals, and removing pseudo-periodic stellar signals or oscillations that vary with time. They are particularly useful for analysis of dwarf stars, where solar flares, sunspots, and non-rigid stellar rotation produce complex variable signals in photometry that must be modelled as random events. These techniques produce strong results in subtracting stellar variability, but often come with the complications of being computationally expensive or from treating stellar variability as a random. The LASR routine serves as an inexpensive and straightforward tool for analyzing high-mass stars, which typically do not possess sunspots or flares (Didelon 1984), whose surfaces behave as rigid rotators (Suarez et al. 2005), and whose oscillations commonly remain constant over long timescales when on the main sequence (Breger & Pamyatnykh 1998).
LASR currently subtracts stellar variability that is well-modelled as a linear combination of sinusoids. Future works can expand this technique to combine LASR’s significance reduction with Gaussian processes or wavelet analysis to analyze other forms of stellar variability. Such an approach could resolve a stellar signal without sacrificing information by treating seismic activity as a random process. Additionally, wavelet analysis could expand LASR’s purview to the variable signal of heartbeat stars (Hambleton et al. 2013; Smullen & Kobulnicky 2015) in the future.
Appendix A LASR algorithm
A.1 Inputs and usage
LASR uses inputs to control its downhill simplex routine that customize its behavior to the target time series. We list the global parameters that typically remain constant throughout the subtraction process:
-
Frequency scale factor to set initial downhill step sizes. When working with KOI-976’s high-precision photometry, we use a scale factor of 10−3 μHz.
-
Amplitude scale factor. Within an order of magnitude of the highest-significance oscillation’s amplitude is typically adequate. This value can be set smaller as LASR subtracts smaller oscillations in the dataset.
-
Phase scale, typically set to 1.0.
-
Number of downhill steps for LASR to take. Convergence typically occurs within 50–100 steps for an independent oscillation, but requires about twice as many steps for close frequency pairs or overtone frequencies.
-
The half-width of the peak of the highest-significance frequency in the dataset. This value determines the width of the periodogram window for LASR to sample during each subtraction. For KOI-976 we used a halfwidth of 0.35 μHz.
-
The number of frequencies to sample in the periodogram window. We find that 10 points provide an adequate sampling of the periodogram window in our analysis, but because of LASR’s relatively low computational cost we use 25 points.
LASR requires the following inputs to subtract an oscillation:
-
Starting guess for frequency. Easily obtained via periodogram with sufficient accuracy.
-
Starting guess for amplitude. Order-of-magnitude values serve an adequate guess, as shown in Table 2.
-
Starting guess for phase. Any value between 0 and 2π typically suffices.
A.2 LASR pseudocode
We write this algorithm in c++ using established techniques for periodograms and downhill simplex routines following (Press 2007). Our program includes proprietary optimization code and personalized libraries that make direct sharing of this program impractical. However, the LASR routine is straightforward to create. We provide an outline below that uses a periodogram window as a black-box function in a downhill simplex routine to minimize significance and determine an oscillation’s (w, A, δ) values. We also make an open-source version of our code available online 1.
A.3 Benchmark results
We list benchmark performance results of the LASR routine in Table A.1 using the KOI-976 short-cadence data set. The computation time scales with the size of the time series and the desired precision, driven mainly by the cost of calculating periodogram significance values. To speed up our computation time, we compute trigonometric recurrences of the periodogram (Press 2007) using two processors in parallel. In general, we find that N = 100 downhill steps is typically enough to determine the best-fit (w, A, δ) values of an oscillation to six significant figures and that 25 periodogram window samples robustly represents a frequency’s significance.
Quantities describing the LASR’s computation time using KOI-976’s short cadence photometry.
The computation time is primarily dedicated to calculating periodograms. Press (2007) shows how, depending on the choice of algorithm, Lomb-Scargle periodograms scale as N log(N), where N is the number of points in the time series. The fitting precision is controlled by the LASR’s downhill simplex algorithm. The rate of convergence can vary largely between datasets, but we find that when fitting one oscillation (three parameters) in KOI-976’s short cadence photometry, we typically achieve four significance figures after ~ 50 downhill steps and six significant figures after ~100 downhill steps.
Appendix B Derivation: one minimum per parameter
The oscillation significance S(ω, A, δ) is a black box function that represents the significance of the residuals of a subtracted oscillation. In this section we provide a derivation showing that S(ω, A, δ) has only one minimum per parameter (i.e. that S(ω, A, δ) is U-shaped in each dimension over all values) so long as the actual frequency and subtracted frequency are relatively close (|(ω1 − ω2)∕(ω1 + ω2)|≲ 0.1).
We startwith two sine waves ψ1 = A1 sin(ω1t + δ1) and ψ2 = A2 sin(ω2t + δ2), where Ai, ωi , and δi represent the amplitude, frequency, and phase of each function. A standard oscillation subtraction is therefore represented by
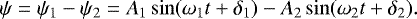 (B.1)
(B.1)
Assuming ω1 ≈ ω2, Eq. (B.1) can be expanded as
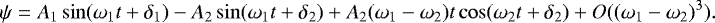 (B.2)
(B.2)
Utilizing the Harmonic Addition theorem (e.g., Nahin 2001), the zeroth-order terms (A1 sin(ω1t + δ1) − A2 sin(ω1t + δ2)) can be expressed as a single sine wave Asin(ω2t + δ), where
 (B.3)
(B.3)
Therefore, this subtraction can be represented as
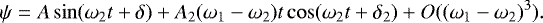 (B.5)
(B.5)
Because S(ω, A, δ) is roughly proportional to the square of the amplitude of ψ, minimizing Eq. (B.5) minimizes S(ω, A, δ). The oscillation residual ψ is minimized via minimizing A and ω1 − ω2. A is minimized via minimizing A1 − A2 and δ1 − δ2. These are the only minima that appear in ψ; therefore, only one global minimum per parameter exists.
References
- Ahlers, J. P. 2016, AJ, 832, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ahlers, J. P., Barnes, J. W., & Barnes, R. 2015, AJ, 814, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Parviainen, H., & Pope, B. 2016, MNRAS, 459, 2408 [NASA ADS] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R. 2010, ArXiv e-prints [arXiv:1009.2755] [Google Scholar]
- Baluev, R. V. 2008, MNRAS, 385, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W. 2009, AJ, 705, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W., Linscott, E., & Shporer, A. 2011, Astrophys. J. Supp. Ser., 197, 10 [Google Scholar]
- Basri, G., Walkowicz, L. M., Batalha, N., et al. 2010, AJ, 141, 20 [Google Scholar]
- Box, G., & Muller, M. 1958, Ann. Math. Stat., 29, 610 [CrossRef] [Google Scholar]
- Breger, M., & Pamyatnykh, A. 1998, A&A, 332, 958 [Google Scholar]
- Breger, M., Balona, L., Lenz, P., et al. 2011, MNRAS, 414, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Fossati, L., Balona, L., et al. 2012, AJ, 759, 62 [Google Scholar]
- Brent, R. P. 2013, Algorithms for Minimization Without Derivatives (Englewood Cliffs: Courier Corporation) [Google Scholar]
- Didelon, P. 1984, Astron. Astrophys. Supp. Ser., 55, 69 [NASA ADS] [Google Scholar]
- Edelson, R., & Krolik, J. 1988, AJ, 333, 646 [Google Scholar]
- Gimenez, A. 2006, AJ, 650, 408 [Google Scholar]
- Hambleton, K., Degroote, P., Conroy, K., et al. 2013, EAS Pub. Ser., 64, 285 [CrossRef] [Google Scholar]
- Haykin, S. 2006, Nonlinear Methods of Spectral Analysis (New York: ), 34 [Google Scholar]
- Hernández, A. G., Moya, A., Michel, E., et al. 2009, A&A, 506, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2004, Proc. Int. Astron. Union, 2004, 786 [Google Scholar]
- MacKay, D. J. 1998, NATO ASI Series F Computer and Systems Sciences, 168, 133 [Google Scholar]
- McQuillan, A. 2013, PhD Thesis (Oxford: University of Oxford) [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, Astrophys. J. Supp. Ser., 211, 24 [Google Scholar]
- Nahin, P. J. 2001, The Science of Radio (New York: Springer Science + Business Media) [CrossRef] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comp. J., 7, 308 [Google Scholar]
- Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H. 2007, Numerical Recipes 3rd Edition: The Art of Scientific Computing (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C: The Art of Scientific Computing, 274 [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. 2006, Gaussian Processes for Machine Learning, 1 (Cambridge, UK: MIT Press) [Google Scholar]
- Rohlfs, K., & Wilson, T. L. 2013, Tools of Radio Astronomy (New York: ) [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Smullen, R. A., & Kobulnicky, H. A. 2015, AJ, 808, 166 [Google Scholar]
- Suarez, J. C., Bruntt, H., & Buzasi, D. 2005, A&A, 438, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Fischer, D., & Queloz, D. 2007, Protostars and Planets V, 951, 685 [NASA ADS] [Google Scholar]
- Vio, R., & Wamsteker, W. 2002, A&A, 388, 1124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vio, R., Andreani, P., & Biggs, A. 2010, A&A, 519, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Oscillations added to a synthetic dataset to test LASR’s ability to subtract variability.
Stellar frequencies and amplitudes of δ-Scuti KIC 9700322 measured using our algorithm and using the prewhitening program period04 (Breger et al. 2011).
Quantities describing the LASR’s computation time using KOI-976’s short cadence photometry.
All Figures
 |
Fig. 1 A periodogram window for the highest-amplitude peak in the synthetic time series discussed in Sect. 3.1. We set LASR to sample the spectral power of this peak 25 times. The black and red points show the Pi (ω) before and after LASR minimized the peak’s significance. The unreduced oscillation shows a clear peak with aliasing on either side. The dashed line marks the true frequency of this oscillation. LASR successfully reduces this oscillation and yields correct measurements of its (w, A, δ) values (see Table 2). |
| In the text | |
 |
Fig. 2 Log-scale plot of the power spectrum of two close frequencies (f2 and f3 in Table 2). The two oscillations appear in frequency space as a single asymmetric peak (black). LASR minimizes the significance of both peaks simultaneously (red) and accurately determines the (w, A, δ) of both oscillations. LASR samples frequencies of a periodogram window for each frequency; for close frequency pairs these two windows overlap. |
| In the text | |
 |
Fig. 3 Total power spectrum of the synthetic time series before (black) and after (red) LASR reduction of its seven oscillations. As we show in Table 2, LASR reduces all oscillations by over 99.9% of their original significance and yields accurate (w, A, δ) values. The injected transit causes no noticeable effect on the power spectrum. |
| In the text | |
 |
Fig. 4 Sample of KIC 9700322’s stellar variability (black) and our best-fit of the variable signal (red) using LASR. Our fit yeilds a reduced χ2 value of 1.13. |
| In the text | |
 |
Fig. 5 Lomb–Scargle periodogram of KOI-976’s short-cadence photometry before (black) and after (red) subtracting stellar variability. LASR reduced the spectral power of all oscillations from ~ 104 at the max to ~1.0. We reduce the representative significance of all subtracted oscillations by at least 98% and find that all significant oscillations are well-modelled as sinusoids. |
| In the text | |
 |
Fig. 6 A comparison of variability subtraction using LASR (red) and traditional prewhitening (blue). We fit all KOI-976 short-cadence photometry and display a ~ 1 day sample of KOI-976’s short-cadence photometry with best-fit (top panel) and its best-fit residuals (bottom panel). LASR produces a superior fit of KOI-976’s seismic activity with a log-likelihood ratio of
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.