| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 5 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201732490 | |
| Published online | 12 June 2018 | |
The emergence of the galactic stellar mass function from a non-universal IMF in clusters
1
Niels Bohr International Academy, Niels Bohr Institute,
Blegdamsvej 17,
2100
Copenhagen, Denmark
e-mail: sami.dib@gmail.com
2
Department of Physics and Astronomy, University of Western Ontario,
London,
Ontario
N6A 3K7, Canada
Received:
18
December
2017
Accepted:
9
February
2018
We investigate the dependence of a single-generation galactic mass function (SGMF) on variations in the initial stellar mass functions (IMF) of stellar clusters. We show that cluster-to-cluster variations of the IMF lead to a multi-component SGMF where each component in a given mass range can be described by a distinct power-law function. We also show that a dispersion of ≈0.3 M⊙ in the characteristic mass of the IMF, as observed for young Galactic clusters, leads to a low-mass slope of the SGMF that matches the observed Galactic stellar mass function even when the IMFs in the low-mass end of individual clusters are much steeper.
Key words: stars: luminosity function, mass function / galaxies: clusters: general / galaxies: stellar content / open clusters and associations: general
© ESO 2018
1 Introduction
The initial mass function (IMF) of stars (i.e. the mass distribution of stars at their birth) is of fundamental importance in astrophysics. The IMF controls the efficiency of star formation in molecular clouds (Nakamura & Li 2007; Dib 2011; Dib et al. 2013; Hony et al. 2015), the radiative and mechanical feedback from stars into the interstellar medium (e.g. Dib et al. 2006, 2011; Padoan et al. 2016; Martizzi et al. 2016), and the dynamical and chemical evolution of galaxies (Bekki & Tsujimoto 2014). Thus, the characterisation of the correct shape of the mass function of stars both on cluster and galactic scales is of vital importance. For the nearby Galactic field stars in the mass range 0.4 ≲ M⋆∕M⊙≲ 10, Salpeter (1955) found that the stellar mass function is well described by a power law 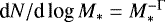 (with Γ ≈ 1.35), where dN is the number of stars between log M* and log M* + d log M*. Since then, there has been a persistent effort to refine the description of the shape of the IMF in individual stellar clusters and of the stellar mass function in the Milky Way and other galaxies. Various surveys suggest that the mass function of stars in the Galactic field, which is not corrected for the effects of the binary population, rises from the brown dwarf and low stellar mass regime until it peaks at ≈0.25–0.4 M⊙, after which it declines steeply in the intermediate-to-high mass regime (Scalo 1986; Bochanski et al. 2010; Rybizki & Just 2015). Several distribution functions are used to describe its shape, such as a multi-component power law (Kroupa 2001; Kroupa et al. 2013), a lognormal coupled to a power law (Chabrier 2005), a tapered power law (Parravano et al. 2011), or a modified lognormal (Basu et al. 2015).
(with Γ ≈ 1.35), where dN is the number of stars between log M* and log M* + d log M*. Since then, there has been a persistent effort to refine the description of the shape of the IMF in individual stellar clusters and of the stellar mass function in the Milky Way and other galaxies. Various surveys suggest that the mass function of stars in the Galactic field, which is not corrected for the effects of the binary population, rises from the brown dwarf and low stellar mass regime until it peaks at ≈0.25–0.4 M⊙, after which it declines steeply in the intermediate-to-high mass regime (Scalo 1986; Bochanski et al. 2010; Rybizki & Just 2015). Several distribution functions are used to describe its shape, such as a multi-component power law (Kroupa 2001; Kroupa et al. 2013), a lognormal coupled to a power law (Chabrier 2005), a tapered power law (Parravano et al. 2011), or a modified lognormal (Basu et al. 2015).
Many studies have also attempted to derive the shape of the IMF1 of stars in individual stellar clusters. Stars in young clusters (i.e. with ages ≲10–12 Myr) that have not undergone an extensive dynamical evolution have roughly the same age and metallicity, and are located at the same distance, thus one can presume that their observed present-day mass functions are nearly identical to their IMFs. Some of the most recent studies have suggested that there are non-negligible, intrinsic cluster-to-cluster variations in the set of parameters that characterise the shape of the IMF among the population of young stellar clusters in the Milky Way (Dib 2014; Dib et al. 2017; Mallick et al. 2014), but also in globular clusters (Zaritsky et al. 2014). Using a Bayesian approach, Dib (2014) showed that the IMF parameters for eight young Galactic stellar clusters do not overlap at the 1σ confidence limit interval. Using a different method, Dib et al. (2017) showed that the fraction of isolated O stars measured in a sample of 341 clusters from the Milky Way Stellar Clusters Survey (MWSC; Kharchenko et al. 2013; Schmeja et al. 2014) can only be reproduced by populations of Galactic clusters that have a substantial intrinsic scatter in the set of parameters that characterise their IMF.
When connecting the IMF in clusters to the mass function of stars in a galaxy by integrating over an initial cluster mass function (ICMF), all previous studies have assumed that the IMF of each individual cluster is indistinguishable from that of the mass function of the Galactic field, setting aside its normalisation, which is determined by the available stellar mass in each cluster (e.g. Weidner & Kroupa 2005; Haas & Anders 2010; Weidner et al. 2013). In this work, we explore the effect of cluster-to-cluster variations in the IMF on the resulting galactic stellar mass function for a single generation of stars (i.e. the SGMF) and compare the results to the observationally derived Galactic mass function.
2 The IMF of individual clusters
We use a description of the IMF in clusters that is given by the tapered power-law function (TPL, De Marchi et al. 2010; Parravano et al. 2011; Dib et al. 2017). This is a convenient form because the TPL can be described with only three free parameters, and also because Dib et al. (2017) inferred the appropriate distribution functions of the IMF parameters of young Galactic clusters using a TPL description of the IMF. The TPL function is given by
![\begin{equation*} \phi\left(\textrm{log} M_{*}\right)=\frac{{\textrm{d}}N_{*}} {{\textrm{d}}\textrm{log}M_{*}}=A_{*}\times M_{*}^{-{\rm{\Gamma}}}\left\{1-\exp\left[-\left(\frac{M_{*}}{M_{\textrm{ch}}}\right)^{\gamma+{\rm{\Gamma}}}\right] \right\},\end{equation*}](/articles/aa/full_html/2018/06/aa32490-17/aa32490-17-eq2.png) (1)
(1)
where Γ is the slope in the intermediate- to high-massregime, γ is the slope in the low-mass regime, Mch is the characteristic mass, and A* is the normalisation coefficient, which is set by the cluster mass Mcl (i.e. 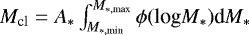 , with M*,min and M*,max being the minimum and maximum stellar masses). Dib (2014) showed that the mean values of Γ, γ, and Mch for the star system IMFs (i.e. not corrected for binarity) for a sample of eight young Galactic clusters is Γobs = 1.37, γobs = 0.91, and Mch,obs = 0.41 M⊙, with standard deviations of
, with M*,min and M*,max being the minimum and maximum stellar masses). Dib (2014) showed that the mean values of Γ, γ, and Mch for the star system IMFs (i.e. not corrected for binarity) for a sample of eight young Galactic clusters is Γobs = 1.37, γobs = 0.91, and Mch,obs = 0.41 M⊙, with standard deviations of 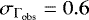 ,
,  , and
, and 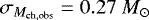 , respectively. Dib et al. (2017) showed that this level of intrinsic scatter for each of these parameters is necessary in order to reproduce the fraction of isolated O stars that is measured in young Galactic clusters in the Milky Way. They showed that when the IMF is described by a TPL function, the fraction of isolated O stars measured in a large sample of Galactic young clusters (341 clusters in the MWSC survey) can be reproduced by models in which the parameters of the IMF are drawn from Gaussian functions with mean values of
, respectively. Dib et al. (2017) showed that this level of intrinsic scatter for each of these parameters is necessary in order to reproduce the fraction of isolated O stars that is measured in young Galactic clusters in the Milky Way. They showed that when the IMF is described by a TPL function, the fraction of isolated O stars measured in a large sample of Galactic young clusters (341 clusters in the MWSC survey) can be reproduced by models in which the parameters of the IMF are drawn from Gaussian functions with mean values of 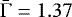 ,
, 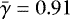 , and
, and 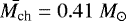 and standard deviations of σΓ = 0.6, σγ = 0.25, and
and standard deviations of σΓ = 0.6, σγ = 0.25, and 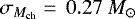 , thus matching the direct parameter inference of Dib (2014). Interestingly, three-dimensional star-cluster simulations show that this level of dispersion in the characteristic mass is plausible and can be attributed to variations in the level of turbulent support in star-forming molecular clouds (Haugbølle et al. 2018). Other authors have suggested that variations in all of the IMF parameters can be caused by cloud-to-cloud variations in the mean level of accretion rates onto protostellar cores (e.g. Basu & Jones 2004; Myers 2009; Dib et al. 2010), or by the coalescence of protostars in high-density environments (Shadmehri 2004; Dib et al. 2007, 2008).
, thus matching the direct parameter inference of Dib (2014). Interestingly, three-dimensional star-cluster simulations show that this level of dispersion in the characteristic mass is plausible and can be attributed to variations in the level of turbulent support in star-forming molecular clouds (Haugbølle et al. 2018). Other authors have suggested that variations in all of the IMF parameters can be caused by cloud-to-cloud variations in the mean level of accretion rates onto protostellar cores (e.g. Basu & Jones 2004; Myers 2009; Dib et al. 2010), or by the coalescence of protostars in high-density environments (Shadmehri 2004; Dib et al. 2007, 2008).
3 The single-generation galactic mass function
For a fixed shape of the IMF, the mass function of a single generation (SGMF) of young stars (i.e. stars in the embedded phase of clusters or over a given time span in cluster ages τcl of the order of 10–12 Myr) in a galaxy would be given by
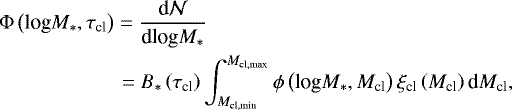 (2)
(2)
where ξcl represents the ICMF (the mass function of clusters at their birth within the time span τcl), Mcl,min and Mcl,max are the upper and lower mass cut-offs in cluster mass, and B* is a normalisation coefficient. The function 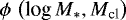 is a representation of the IMF (i.e., Eq. (1)) that allows for a potential dependence of the IMF on cluster mass2, Mcl. One common representation of the ICMF is a power-law function with an exponential truncation at the high-mass end,
is a representation of the IMF (i.e., Eq. (1)) that allows for a potential dependence of the IMF on cluster mass2, Mcl. One common representation of the ICMF is a power-law function with an exponential truncation at the high-mass end,
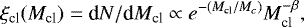 (3)
(3)
where Mc is the mass that marks the turnover from the power law to the exponential regime. For spiral galaxies Mc is found to be ≈2 × 105 M⊙ (Jordán et al. 2007; Larsen 2009). Eq. (2) represents the general form of an SGMF with a universal IMF. There could be potential dependencies between the mass of the cluster, Mcl, and the shape of the IMF and/or between Mcl and the maximum stellar mass M*,max that can be found in the cluster, as has been suggested by Weidner & Kroupa (2004). In our case, we do not assume any relationship between Mcl and the shape of the IMF, nor between Mcl and M*,max, and the analytical description of Eq. (2) can be further simplified by taking ϕ (log M*) out of the integral such that
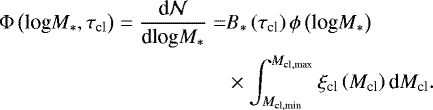 (4)
(4)
Thus, the term that contains the integration over Mcl acts as a simple normalisation term, and the shape of the SGMF would be indistinguishable from that of the IMF of individual clusters. If the set of parameters that describe the shape of the IMF (i.e. θi) for the population of young galactic clusters (or clusters that form within a timespan τcl) each have an intrinsic scatter as suggested by Dib (2014) and Dib et al. (2017), then Eq. (2) should be replaced by
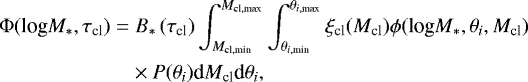 (5)
(5)
where P(θi) is the probability distribution function of each parameter θi. When the IMF is described by the TPL (Eq. (1)), Eq. (5) becomes
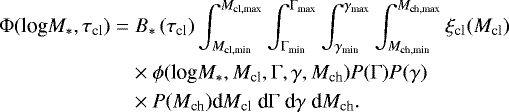 (6)
(6)
The normalisation coefficient B* is given by the total mass available in all clusters for a given ICMF, Σcl, with
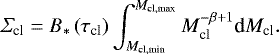 (7)
(7)
For a given galactic star formation rate (SFR) and a timescale of interest (τcl), the value of Σcl is given by Σcl = SFR × τcl under the assumption that the SFR is constant within the timescale τcl. In a similar fashion to Eq. (2), if no correlation between Mcl and the shape of the IMF is assumed, as in our case, then Eq. (6) can be further simplified by performing the integration over Mcl separately, and the integration is reduced to
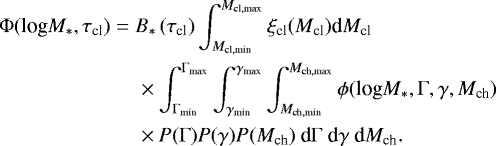 (8)
(8)
We explore the dependence of the SGMF shape on the level of scatter in the parameters that characterise the IMF of individual clusters. We describe the distributions of Γ, γ, and Mch with Gaussian functions:

with mean values 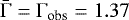 ,
, 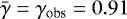 , and
, and 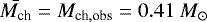 , which are the values measured for the Milky Way stellar clusters (Dib 2014). The standard deviations of the three parameters are parametrised as
, which are the values measured for the Milky Way stellar clusters (Dib 2014). The standard deviations of the three parameters are parametrised as 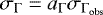 , σγ = aγσγ,obs, and
, σγ = aγσγ,obs, and 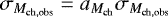 , where
, where 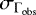 , σγ,obs, and
, σγ,obs, and 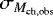 are the observed values by Dib (2014) quoted in Sect. 2, and where aΓ, aγ, and
are the observed values by Dib (2014) quoted in Sect. 2, and where aΓ, aγ, and 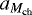 are free parameters. The work of Dib et al. (2017) suggests that a value of
are free parameters. The work of Dib et al. (2017) suggests that a value of  is related to intrinsic cluster-to-cluster variations in the Milky Way clusters, at least for the sample of 341 clusters they have tested, and that stochastic effects due to random sampling around a universal IMF that can affect low-mass clusters are not enough to reproduce the statistics of isolated O stars in Galactic clusters. However, the model presented in this work is independent of whether the standard deviation of each of the parameters is due to intrinsic cluster-to-cluster variations or if stochastic sampling effects contribute. Therefore we consider cases where aΓ, aγ, and
is related to intrinsic cluster-to-cluster variations in the Milky Way clusters, at least for the sample of 341 clusters they have tested, and that stochastic effects due to random sampling around a universal IMF that can affect low-mass clusters are not enough to reproduce the statistics of isolated O stars in Galactic clusters. However, the model presented in this work is independent of whether the standard deviation of each of the parameters is due to intrinsic cluster-to-cluster variations or if stochastic sampling effects contribute. Therefore we consider cases where aΓ, aγ, and 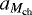 are varied in a wide range between 0.25 and 1.5.
are varied in a wide range between 0.25 and 1.5.
The information on the lower and upper limits of these parameters for Galactic clusters is limited. We adopt the same limits found by Dib (2014) and used in Dib et al. (2017), namely 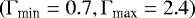 ,
, 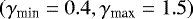 , and
, and 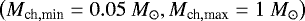 . We also assume that β = 2, Mc = 2 × 105 M⊙, and use a value of τcl = 12.3 Myr, and a galactic SFR of 1 M⊙ yr−1 (Robitaille & Whitney 2010). Stellar masses were considered in the range [0.004–120] M⊙, and we do not impose any relationship between the cluster mass and maximum stellar mass in the cluster because we have found little evidence for the existence of such a relation (Dib et al. 2017).
. We also assume that β = 2, Mc = 2 × 105 M⊙, and use a value of τcl = 12.3 Myr, and a galactic SFR of 1 M⊙ yr−1 (Robitaille & Whitney 2010). Stellar masses were considered in the range [0.004–120] M⊙, and we do not impose any relationship between the cluster mass and maximum stellar mass in the cluster because we have found little evidence for the existence of such a relation (Dib et al. 2017).
Using the distributions in Eqs. (9)–(11), the integral in Eq. (8) is solved numerically. We first consider the effects on the SGMF of a dispersion in each of the parameters separately. The three stacked plots in the top left panel of Fig. 1 display the effects on the SGMF of the distribution of Γ, with P(Γ) being described by a Gaussian function centred at 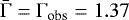 and a standard deviation σΓ = aΓσΓ,obs, with aΓ that is varied between 0.25 and 1.5. The distributions of γ and Mch (P(γ) and P(Mch)) are taken to be delta functions located at the positions of their observed values by Dib (2014), namely γobs = 0.91, and Mch,obs = 0.41 M⊙. A larger cluster-to-cluster scatter in Γ results in an increased deviation from a pure power-law function at the high-mass end and in a shallower slope of the SGMF. The same effect has been observed by Cerviño & Luridiana (2006), who explored the existence of scatter in the high-mass slope on a single power-law function. The three sub-panels compare our results to the stellar mass function inferred for the nearby Galactic field by Kroupa (2001), Chabrier (2005), and Parravano et al. (2011). Ideally, the results of our models should be compared to a single generation of stars in a galaxy. In the Milky Way, the best comparison could be performed with the young stellar populations (i.e. stars with ages ≲ 10–12 Myr). However, the mass function of young stars that are present both in clusters and in the field of the Milky Way is not well established. It should be noted that the slope of the Galactic field stellar mass function adopted by Chabrier (2005) and Parravano et al. (2011) is the one derived by Salpeter (i.e. Γ = 1.35), while the value adopted by Kroupa (also Γ = 1.35) is a mean value derived for Galactic clusters in the Milky Way. These values are not corrected for the effects of stellar evolution. Our results yield a shallower slope than the Galactic field in the high stellar mass regime (because of contributions from the wings in P(Γ)), and also do not take into account corrections for the effects of stellar evolution. While this is beyond the scope of the present work, we anticipate that taking into account such corrections in our models would steepen the slope of the SGMF in this mass range and improve the fit to the Galactic field stellar mass function.
and a standard deviation σΓ = aΓσΓ,obs, with aΓ that is varied between 0.25 and 1.5. The distributions of γ and Mch (P(γ) and P(Mch)) are taken to be delta functions located at the positions of their observed values by Dib (2014), namely γobs = 0.91, and Mch,obs = 0.41 M⊙. A larger cluster-to-cluster scatter in Γ results in an increased deviation from a pure power-law function at the high-mass end and in a shallower slope of the SGMF. The same effect has been observed by Cerviño & Luridiana (2006), who explored the existence of scatter in the high-mass slope on a single power-law function. The three sub-panels compare our results to the stellar mass function inferred for the nearby Galactic field by Kroupa (2001), Chabrier (2005), and Parravano et al. (2011). Ideally, the results of our models should be compared to a single generation of stars in a galaxy. In the Milky Way, the best comparison could be performed with the young stellar populations (i.e. stars with ages ≲ 10–12 Myr). However, the mass function of young stars that are present both in clusters and in the field of the Milky Way is not well established. It should be noted that the slope of the Galactic field stellar mass function adopted by Chabrier (2005) and Parravano et al. (2011) is the one derived by Salpeter (i.e. Γ = 1.35), while the value adopted by Kroupa (also Γ = 1.35) is a mean value derived for Galactic clusters in the Milky Way. These values are not corrected for the effects of stellar evolution. Our results yield a shallower slope than the Galactic field in the high stellar mass regime (because of contributions from the wings in P(Γ)), and also do not take into account corrections for the effects of stellar evolution. While this is beyond the scope of the present work, we anticipate that taking into account such corrections in our models would steepen the slope of the SGMF in this mass range and improve the fit to the Galactic field stellar mass function.
Similarly, the top right panel and the bottom left panels in Fig. 1 display the effects on the SGMF of scatter in γ and in Mch. The dispersion in theses case is described by Gaussian functions centred at their observed values, and the standard deviations are varied such that aγ and 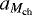 are varied between 0.25 and 1.5. The distributions of the parameters that are not varied are described by delta functions located at their observed positions. As for the case with Γ, a larger dispersion in the parameter γ leads to more flattening of the SGMF slope in this mass range. However, the effects of even the largest dispersion considered for this parameter (i.e. aγ = 1.5) do not leadto a substantial flattening of the low-mass slope of the SGMF. A 1σ dispersion in Mch of the order of the one measured byDib (2014; i.e., ≈0.3 M⊙) leads to two interesting features in the SGMF. Firstly, cluster-to-cluster variations of Mch lead to the formation of a “plateau” in the SGMF, similar to the one suggested in the Kroupa Galactic mass function. Secondly, this level of dispersion in Mch leads to a flattening of the SGMF in the low-mass end, even if the mean value of γ for the ensemble of clusters is much steeper (
are varied between 0.25 and 1.5. The distributions of the parameters that are not varied are described by delta functions located at their observed positions. As for the case with Γ, a larger dispersion in the parameter γ leads to more flattening of the SGMF slope in this mass range. However, the effects of even the largest dispersion considered for this parameter (i.e. aγ = 1.5) do not leadto a substantial flattening of the low-mass slope of the SGMF. A 1σ dispersion in Mch of the order of the one measured byDib (2014; i.e., ≈0.3 M⊙) leads to two interesting features in the SGMF. Firstly, cluster-to-cluster variations of Mch lead to the formation of a “plateau” in the SGMF, similar to the one suggested in the Kroupa Galactic mass function. Secondly, this level of dispersion in Mch leads to a flattening of the SGMF in the low-mass end, even if the mean value of γ for the ensemble of clusters is much steeper (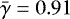 ).
).
The bottom right panel in Fig. 1 displays cases where all the three parameters have a scatter and their distributions functions are described by Gaussian functions whose mean values are fixed at the observed values, and standard deviations are varied between 0.25 and 1.5 times the observed values. When all three parameters have cluster-to-cluster variations, all the features in which they influence the SGMF individually are preserved, namely a shallower slope and a deviation from a pure power-law function in the intermediate to high stellar mass regime, a shallower slope than that of individual clusters in the low stellar mass regime, and the formation of a plateau inthe low to intermediate stellar mass regime. The slope of the SGMF in the low-mass regime (i.e. M* < 0.03 M⊙) is 0.89, 0.85, 0.81, 0.78, and 0.75 for the cases were  , and 1.5, respectively, which are shallower than the mean value of 0.91 for observed clusters. It is interesting to note that a model with
, and 1.5, respectively, which are shallower than the mean value of 0.91 for observed clusters. It is interesting to note that a model with 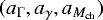 = (0.75, 0.75, 0.5) provides an excellent fit to the Kroupa Galactic field mass function and is also compatible with the Parravano et al. (2011) Galactic field mass function. Further work is needed to investigate the effect of more complex parameter distributions of the IMF parameters when more constraints from observations become available. The sample of clusters from the MWSC survey used by Dib et al. (2017) to constrain the distributions of the IMF parameters did not distinguish between bound clusters and more loose stellar associations. Recently, Chandar et al. (2017) argued that the fraction of young stars in compact clusters in nearby galaxies is ≈ 25% of the total young stellar population. It would be interesting to explore whether the IMF parameters for hierarchical structures have distributions of the IMF parameters distinct from those of more compact bound clusters. If this were the case, it would be necessary to adopt more complex distributions (e.g. bi-modal distributions) of the IMF parameters in order to construct the SGMF. With the current observational constraints, the main result of this paper is that an SGMF that resembles the Galactic field mass function can result from the summation of a large population of stellar clusters whose IMFs vary significantly, and which can individually be very different from the SGMF.
= (0.75, 0.75, 0.5) provides an excellent fit to the Kroupa Galactic field mass function and is also compatible with the Parravano et al. (2011) Galactic field mass function. Further work is needed to investigate the effect of more complex parameter distributions of the IMF parameters when more constraints from observations become available. The sample of clusters from the MWSC survey used by Dib et al. (2017) to constrain the distributions of the IMF parameters did not distinguish between bound clusters and more loose stellar associations. Recently, Chandar et al. (2017) argued that the fraction of young stars in compact clusters in nearby galaxies is ≈ 25% of the total young stellar population. It would be interesting to explore whether the IMF parameters for hierarchical structures have distributions of the IMF parameters distinct from those of more compact bound clusters. If this were the case, it would be necessary to adopt more complex distributions (e.g. bi-modal distributions) of the IMF parameters in order to construct the SGMF. With the current observational constraints, the main result of this paper is that an SGMF that resembles the Galactic field mass function can result from the summation of a large population of stellar clusters whose IMFs vary significantly, and which can individually be very different from the SGMF.
 |
Fig. 1 Single-generation Galactic stellar mass for various choices of the dispersion in the three parameters of the stellar clusters IMFs: Γ, γ, and Mch. The three stacked images in the top left panel show cases with cluster-to-cluster variations only in Γ, the top right panel displays cases with variations only in γ, and the lower left panel displays cases that include variations only in Mch. The ensemble of black curves in each of the stacked images are similar. The models in each of the stacked images are compared to the Kroupa (2001), Chabrier (2005), and Parravano et al. (2011) Galactic field stellar mass function (red line) with their associated uncertainties (hatched regions in red). |
Aknowledgements
We thank the anonymous referee for useful comments and suggestions. SD acknowledges the hospitality of the University of Western Ontario, where part of this work has been completed. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. SB was supported by a Discovery grant from NSERC.
References
- Basu, S., & Jones, C. E. 2004, MNRAS, 347, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., Gil, M., & Auddy, S. 2015, MNRAS, 449, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Tsujimoto, T. 2014, MNRAS, 444, 3879 [NASA ADS] [CrossRef] [Google Scholar]
- Bochanski, J. J., Hawley, S. L., Covey, K. R., et al. 2010, AJ, 139, 2679 [NASA ADS] [CrossRef] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Chandar, R., Fall, S. M., Whitmore, B. C., & Mulia, A. J. 2017, ApJ, 849, 128 [NASA ADS] [CrossRef] [Google Scholar]
- De Marchi, G., Paresce, F., & Portegies Zwart, S. 2010, ApJ, 718, 23 [Google Scholar]
- Dib, S. 2011, ApJ, 737, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S. 2014, MNRAS, 444, 1957 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dib, S., Bell, E., & Burkert, A. 2006, ApJ, 638, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Kim, J., & Shadmehri, M. 2007, MNRAS, 381, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Shadmehri, M., Gopinathan, M., Kim, J., & Henning, T. 2008, in Massive Star Formation: Observations Confront Theory, eds. H., Beuther, H., Linz, & T., Henning, ASP, Conf. Ser., 387 [Google Scholar]
- Dib, S., Shadmehri, M., Padoan, P., et al. 2010, MNRAS, 405, 401 [NASA ADS] [Google Scholar]
- Dib, S., Piau, L., Mohanty, S., & Braine, J. 2011, MNRAS, 415, 3439 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Gutkin, J., Brandner, W., & Basu, S. 2013, MNRAS, 436, 3727 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Schmeja, S., & Hony, S. 2017, MNRAS, 464, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Haas, M. R., & Anders, P. 2010, A&A, 512, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haugbølle, T., Padoan, P., & Nordlund, Å 2018, ApJ, 854, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Hony, S., Gouliermis, D. A., Galliano, F., et al. 2015, MNRAS, 448, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., McLaughlin, D. E., Côté, P., et al. 2007, ApJS, 171, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in Planets, Stars and Stellar Systems, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science+Business Media), 5 [Google Scholar]
- Larsen, S. S. 2009, A&A, 494, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallick, K. K., Ojha, D. K., Tamura, M., et al. 2014, MNRAS, 443, 3218 [NASA ADS] [CrossRef] [Google Scholar]
- Martizzi, D., Fielding, D., Faucher-Giguère, C.-A., & Quataert, E. 2016, MNRAS, 459, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, ApJ, 706, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F.,& Li, Z.-Y. 2007, ApJ, 662, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Pan, L., Haugbølle, T., & Nordlund, Å. 2016, ApJ, 822, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Parravano, A., McKee, C. F., & Hollenbach, D. J. 2011, ApJ, 726, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, 11 [Google Scholar]
- Rybizki, J., & Just, A. 2015, MNRAS, 447, 3880 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scalo, J. M. 1986, Fundam. Cosm. Phys., 11, 1 [Google Scholar]
- Schmeja, S., Kharchenko, N. V., Piskunov, A. E., et al. 2014, A&A, 568, A51 [CrossRef] [EDP Sciences] [Google Scholar]
- Shadmehri, M. 2004, MNRAS, 354, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2005, ApJ, 625, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., Pfamm-Altenburg, J., & Vazdekis, A. 2013, MNRAS, 436, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Colucci, J. E., Pessev, P. M., Bernstein, R. A., & Chandar, R. 2014, ApJ, 796, 71 [NASA ADS] [CrossRef] [Google Scholar]
Throughout the paper, we strive to keep the terminology as clear as possible. The term IMF is reserved for individual clusters, the term SGMF is the cumulative IMF for a population of clusters, and the term galactic/Galactic mass function refers to the stellar mass function of a galaxy/the Milky Way.
The dependence of the IMF on the cluster mass under the assumption of a universal IMF could stem from the existence of a cluster mass-maximum stellar mass relation (Weidner & Kroupa 2004).
All Figures
 |
Fig. 1 Single-generation Galactic stellar mass for various choices of the dispersion in the three parameters of the stellar clusters IMFs: Γ, γ, and Mch. The three stacked images in the top left panel show cases with cluster-to-cluster variations only in Γ, the top right panel displays cases with variations only in γ, and the lower left panel displays cases that include variations only in Mch. The ensemble of black curves in each of the stacked images are similar. The models in each of the stacked images are compared to the Kroupa (2001), Chabrier (2005), and Parravano et al. (2011) Galactic field stellar mass function (red line) with their associated uncertainties (hatched regions in red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


