| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732253 | |
| Published online | 25 May 2018 | |
Knotty protostellar jets as a signature of episodic protostellar accretion?
1
Institute of Fluid Mechanics and Heat Transfer,
TU Wien,
Vienna
1060, Austria
e-mail: eduard.vorobiev@univie.ac.at
2
Research Institute of Physics, Southern Federal University,
Rostov-on-Don
344090, Russia
3
University of Vienna, Department of Astrophysics,
Vienna
1180, Austria
4
European Southern Observatory,
Av. Alonso de Cordova,
3107
Vitacura, Santiago de Chile, Chile
5
Department of Physics, State University of New York at Fredonia,
280 Central Ave.,
Fredonia,
NY
14063, USA
6
Department of Astronomy, University of Geneva,
Ch. d’Ecogia 16,
1290 Versoix, Switzerland
Received:
7
November
2017
Accepted:
17
January
2018
Aims. We aim to study the causal link between the knotty jet structure in CARMA 7, a young Class 0 protostar in the Serpens South cluster, and episodic accretion in young protostellar disks.
Methods. We used numerical hydrodynamics simulations to derive the protostellar accretion history in gravitationally unstable disks around solar-mass protostars. We compared the time spacing between luminosity bursts Δτmod, caused by dense clumps spiralling on the protostar, with the differences of dynamical timescales between the knots Δτobs in CARMA 7.
Results. We found that the time spacing between the bursts have a bi-modal distribution caused by isolated and clustered luminosity bursts. The former are characterized by long quiescent periods between the bursts with Δτmod = a few × (103–104) yr, whereas the latter occur in small groups with time spacing between the bursts Δτmod = a few × (10–102) yr. For the clustered bursts, the distribution of Δτmod in our models can be fit reasonably well to the distribution of Δτobs in the protostellar jet of CARMA 7, if a certain correction for the (yet unknown) inclination angle with respect to the line of sight is applied. The Kolmogorov–Smirnov test on the model and observational data sets suggests the best-fit values for the inclination angles of 55–80°, which become narrower (75–80°) if only strong luminosity bursts are considered. The dynamical timescales of the knots in the jet of CARMA 7 are too short for a meaningful comparison with the long time spacings between isolated bursts in our models. Moreover, the exact sequences of time spacings between the luminosity bursts in our models and knots in the jet of CARMA 7 were found difficult to match.
Conclusions. Given the short time that has passed since the presumed luminosity bursts (tens to hundreds years), a possible overabundance of the gas-phase CO in the envelope of CARMA 7 compared to what could be expected from the current luminosity may be used to confirm the burst nature of this object. More sophisticated numerical models and observational data on jets with longer dynamical timescales are needed to further explore the possible causal link between luminosity bursts and knotty jets.
Key words: stars: formation / stars: protostars / stars: jets / stars: variables: general
© ESO 2018
1 Introduction
Low-mass stars are generally understood to form due to the gravitational collapse of dense gas and dust clouds known as prestellar cores. The bulk of the final stellar mass is accumulated in the early evolutionary phase known as the embedded phase of star formation when the nascent star is still surrounded by the infalling parental core. However, the manner in which the stellar mass is accumulated, via steady or time-varying accretion, is poorly understood. A wide range of protostellar accretion rates inferred in the embedded phase (e.g., Enoch et al. 2009) suggests that accretion is time-variable, but other explanations are also possible.
In the simplest model of low-mass star formation, an isothermal sphere collapses, starting from the center of the core with the mass infall rate 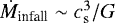 (Larson 1969; Shu 1977), which tapers off with time due to a depleting mass reservoir in the parental core (Vorobyov & Basu 2005). Variations in the initial positive density perturbations and infall rates declining with time can, in principle, explain a wide range of accretion rates inferred for young embedded stars without the need to invoke strong time variability.
(Larson 1969; Shu 1977), which tapers off with time due to a depleting mass reservoir in the parental core (Vorobyov & Basu 2005). Variations in the initial positive density perturbations and infall rates declining with time can, in principle, explain a wide range of accretion rates inferred for young embedded stars without the need to invoke strong time variability.
There is one caveat to this simple picture: the instantaneous infall rate Ṁinfall is not identical to the accretion rate on the star Ṁ, because most of the cloud core material lands on a circumstellar disk before reaching the star. Various physical processes that take place in the disk, such as the magnetorotational, thermal and gravitational instabilities, can trigger strong bursts when the matter is transported through the disk toward the star (e.g., Bell & Lin 1994; Armitage et al. 2001; Zhu et al. 2009; Vorobyov & Basu 2005, 2015; D’Angelo & Spruit 2012; Armitage 2016; Meyer et al. 2017). The prototypical examples of these bursts are known as FU-Orionis-type (FUor) and EX Lupi-type (EXors) luminosity outbursts featuring an increase in luminosity of three to five magnitudes compared to the pre-burst state (Audard et al. 2014), though the driving force of these two types of outburst can be distinct. About half of the known FUors are young embedded objects as indicated by silicate features in absorption (Quanz et al. 2007). The youngest known FUor, HOPS 383, belongs to the Class 0 phase (Safron et al. 2015).
Observational manifestations of accretion variability are not limited to energetic FUor and EXor bursts. Recent variability monitoring campaigns (e.g., Pena et al. 2017; Herczeg et al. 2017) indicate that young embedded stars demonstrate intrinsic (not extinction related) variability of different strengths and periods, ranging from days to years and showing both rises and dips in the light curves. Numerical models featuring gravitationally unstable disks demonstrate accretion variability that can explain the observed range of mass accretion rates in embedded star-forming regions (Vorobyov 2009), although these somewhat underestimate the amplitude of short-term variability on the order of months and years (Elbakyan et al. 2016). Models with gravitationally unstable disks are also successful in resolving the luminosity problem (Dunham & Vorobyov 2012), according to which the mean luminosity of embedded protostars isabout an order of magnitude lower than that predicted by the simple spherical collapse models (Kenyon et al. 1990).
Clearly, observations of FUors and variability monitoring campaigns can provide information on accretion variability on human-life timescales. But what about indicators of past variability? Bursts are short-lived phenomena and may be simply missed. Accretion variability in general may be a transient phenomenon, having periods of strong activity, alternated with longer quiescent phases. Fortunately, certain chemical species in the collapsing envelopes, such as CO, can retain signatures of past accretion bursts (Lee 2007; Visser & Bergin 2012; Vorobyov et al. 2013a; Frimann et al. 2017; Rab et al. 2017). Because typical freeze-out times of these species onto dust grains in the envelope (a few kyr) are much longer than the burst duration (a few tens to hundred years), they can linger in the gas phase in the envelope long after the system has returned into a quiescent stage, and their abnormally high abundance can be used to infer the past accretion bursts.
In this paper, we focus on another phenomenon – protostellar jets – that may be used to trace back the history of protostellar accretion. Jets were first observed as a sequence of shock fronts, or knots, seen at optical wavelengths and known as Herbig-Haro (HH) objects (e.g., Reipurth & Cernicharo 1995). Shocked gas from the jets can survive for thousands of years and often propagate for a few pc from their driving source powered by disk accretion (Reipurth & Aspin 1997). The origin of the knots can be attributed to a launching mechanism at the jet base that is variable in time (e.g., Bonito et al. 2010). Arce et al. (2007) summarized evidence in favor that episodic variation in the mass-loss rate can produce a chain of knotty shocks and bow shocks along the jet axis. Here, we test a hypothesis that the presence of a sequence of knots in protostellar jets is related to a time-variable driving force caused by episodic accretion of matter from accretion disk onto the central protostar (e.g., Plunkett et al. 2015). The knots can track many episodes of accretion bursts, and not just the most recent/strongest, as it may be the case for the chemical tracers. We analyze the characteristics of luminosity bursts of different strengths obtained in hydrodynamical models of gravitationally unstable disks and compare them with available observational data on the time spacing of the knots in protostellar jets. Complemented with predictions from disk chemical models, jets may provide invaluable constraints on models of episodic accretion, holding records on the number and time of intense accretion bursts during protostellar evolution (Hsieh et al. 2016).
The paper is organized as follows. In Sect. 2 we provide a brief description of the numerical model. In Sects. 3 and 4, we analyze the characteristics of the model accretion and luminosity bursts, respectively. The comparison of time spacings between the bursts and differences in dynamical timescales of the knots is performed in Sect. 5. Our main conclusions and the model limitations are summarized in Sect. 6.
2 Description of the model
In this section, we provide a brief description of the hydrodynamical model used in this paper to derive the protostellar accretion rates. A detailed description of the model can be found in Vorobyov & Basu (2015). We started our numerical simulations from the gravitational collapse of a prestellar core and continued into the embedded phase of stellar evolution, during which the protostar and protostellar disk were formed. Simulations were terminated at the end of the embedded phase when most of the core had accreted onto the star plus disk system. The age of the protostar at this instance was 0.3 Myr.
To save computational time and avoid too small time-steps, we introduced a sink cell at rs.c. = 6 AU. We imposed free outflow boundary conditions so that the matter is allowed to flow out of the computational domain but is prevented from flowing in. The sink cell is dynamically inactive; it contributes only to the total gravitational potential and secures a smooth behavior of the gravity force down to the stellar surface. To accelerate the computations, the equations of mass, momentum, and energy transport were solved in the thin-disk limit, justification for which is provided in Vorobyov & Basu (2010). The following physical processes in the disk were considered: disk self-gravity, cooling due to dust radiation from the disk surface, heating via stellar and background irradiation, and turbulent viscosity using the α-parameterization. The α-parameter is set to a constant value of 5 × 10−3. The hydrodynamics equations are solved in polar coordinates on a numerical grid with 512 × 512 grid zones. The solution procedure is similar to the ZEUS code (Stone & Norman 1992) and is described in detail in Vorobyov & Basu (2010).
Our numerical simulations start from a prestellar core with the radial profiles of column density Σ and angular velocity Ω described asfollows:
![\begin{eqnarray*} {\mathrm{\Sigma}}(r) & = & {r_0 {\mathrm{\Sigma}}_0 \over \sqrt{r^2+r_0^2}}\:, \\ {\mathrm{\Omega}}(r) & = &2 {\mathrm{\Omega}}_0 \left( {r_0\over r}\right)^2 \left[\sqrt{1+\left({r\over r_0}\right)^2 } -1\right],\end{eqnarray*}](/articles/aa/full_html/2018/05/aa32253-17/aa32253-17-eq2.png) (1) (2)
(1) (2)
where Σ0 and Ω0 are the gas surface density and angular velocity at the center of the core. These profiles have a small near-uniform central region of size r0 and then transition to an r−1 profile; they are representative of a wide class of observations and theoretical models (André et al. 1993; Dapp & Basu 2009). The core is truncated at rout, which is also the outer boundary of the active computational domain (the inner boundary is at rs.c. = 6 AU). Different values of rout are chosen to generate cores of different mass Mcore. The central angular velocity Ω0 is chosen so as to generate cores with ratios of rotational to gravitational energy β that is consistent with the values inferred for prestellar cores by Caselli et al. (2002). The initial gas temperature is set to 10 K throughout the core, which is also the background temperature of external irradiation.
Model parameters.
 |
Fig. 1 Mass accretion rates on the central protostar (the blue solid lines) and the disk infall rates (the red dashed lines) as a function of time in models 1 and 2. The bottom panel shows the corresponding rates in model 2, but with disk self-gravity artificially turned off. |
3 Analysis of accretion and infall rates
In this section, we analyze the mass transport rates, defined as − 2πrΣvr, where Σ is the gas surface density and vr is the radial gas velocity. We calculated the mass transport rates through the sink cell at r = 6.0 AU and at a distance of r = 2000 AU from the central star. The former quantity serves as a proxy for the mass accretion rate onto the star Ṁ* and the latter quantity represents the mass infall rate onto the disk Ṁinfall. We note that the disk radius in our models is smaller than 1000 AU, but gravitational multibody scattering of gaseous clumps from the disk may produce perturbations in the gas flow in the vicinity of the disk, so that we calculated Ṁinfall at a distance of 2000 AU where the gas inward flow is unperturbed. We also note that Ṁ* may be modified by physical processes in the inner disk, such as the magnetorotational instability, not taken into account in our simulations. This may introduce additional variability to the protostellar accretion rates obtained in our models and may explain why our models somewhat underestimate the variability amplitudes at timescales on the order of a few years and even months when compared to observations.
We consider two models, the parameters of which are presented in Table 1. The parameters of these models are similar to models 1 and 2 in Vorobyov & Basu (2015). Figure 1 presents Ṁ* (blue solid lines) and Ṁinfall (red dashed lines) vs. time for our models. The evolutionary time presented in this work is counted from the instanceof the central protostar formation rather than from the onset of the gravitational collapse of prestellarcores because the duration of the collapse phase may vary from model to model. Clearly, Ṁ* demonstrates a time-variable behavior in both models, whereas Ṁinfall is steady and gradually declines with time because of gas depletion in the envelope. The mass infall on the disk is one of the key parameters that triggers and sustains gravitational instability and fragmentation in the disk (e.g., Vorobyov & Basu 2005; Kratter et al. 2008) by replenishing the disk mass reservoir lost via accretion on the star. A decline of Ṁinfall results in weakening of both gravitational instability and accompanying accretion variability.
As shown in Vorobyov & Basu (2010, 2015), accretion variability is caused by a combination of two effects: the nonlinear interaction between different spiral modes in the gravitationally unstable disk and infall of gaseous clumps formed in the disk via gravitational fragmentation. In particular, the spiral arms produce regular, long-term variability and the inspiralling clumps produce strong accretion bursts when destroyed and accreted by the star. To demonstrate the influence of disk gravitational instability on the character of the protostellar accretion rate, we show in the bottom panel of Fig. 1 the accretion and infall rates obtained in model 2 but with disk self-gravity artificially turned off. Clearly, the variability in Ṁ* greatly reduced, whereas Ṁinfall remained essentially similar to the case with disk self-gravity. It may appear as though the mean accretion rate is similar in the cases with and without self-gravity. We checked the stellar masses M* at the same time instances and found that the model with disk self-gravity has a systematically higher M*. For instance, M* = 0.146 M⊙ in the model without disk self-gravity, whereas M* = 0.315 M⊙ in the model with self-gravity. The mismatch becomes more pronounced with time. This means that the model with disk self-gravity is in fact characterized by a systematically higher mean accretion rate, which is consistent with disk self-gravity being the dominant mass transport mechanism in the early embedded phase of disk evolution (Vorobyov & Basu 2009).
To drive accretion variability on timescales of hundreds of thousands of years requires that large disk masses (or high disk-to-star mass ratios) be sustained for this length of time. This can be achieved by continuing mass replenishment from the infalling envelope in the embedded phase of star formation, lasting for about 0.1–0.5 Myr (e.g., Evans et al. 2009; Vorobyov 2011). High optical extinction and silicate features in absorption toward about half of the known FUors imply that these objects are still embedded in their parental cores (Quanz et al. 2007; Audard et al. 2014) and, hence, may have massive disks. Indeed, the recent estimates of disk masses in three FUors (Cieza et al. 2018) seem to confirm that they possess massive disks (Mdisk≳0.1M⊙), sufficient to trigger gravitational instability and fragmentation (see Fig. 1 in Vorobyov 2013).
4 Analysis of protostellar luminosities
In this section, we analyze the protostellar luminosities obtained in our models. The total protostellar luminosity Ltot is calculated as the sum of the photospheric luminosity Lph, arising fromthe gravitational compression of the star and deuterium burning in its core, and the accretion luminosity Lacc = GM*Ṁ*∕(2R*), arising due to the gravitational energy of the accreting matter. Here, M* and R* are the mass and radius of the protostar. The former is calculated using Ṁ and the latter (and also Lph) is computed using the Lyon stellar evolution code coupled to the main hydrodynamics code in real time as described in Vorobyov & Basu (2015).
The red lines in Fig. 2 represent the total luminosities as a function of time for the same two models as in Fig. 1. Clearly, Ltot demonstrates high variability with luminosity bursts of different strength, which is a direct consequence of variable protostellar accretion rates. To investigate the possible causal link between episodic accretion and knotty jet structure, we needed to distinguish short-lived luminosity bursts caused by infalling gaseous clumps from regular long-term variability caused by perturbations from large-scale spiral arms. To do this, we first introduced the background luminosity, in which strong luminosity bursts were artificially filtered out as follows:
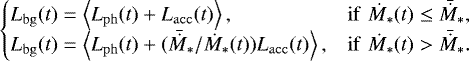 (3)
(3)
Here, Ṁ*(t) is the instantaneous protostellar accretion rate and 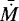 the accretion rate averaged over the age of the star in our simulations (which is 0.3 Myr). During the bursts, Ṁ* (t) is much greater than
the accretion rate averaged over the age of the star in our simulations (which is 0.3 Myr). During the bursts, Ṁ* (t) is much greater than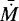 . Multiplying Lacc(t) by
. Multiplying Lacc(t) by 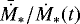 means that the instantaneous accretion rate Ṁ* in the formula for Lacc is substituted with a time-averaged accretion rate
means that the instantaneous accretion rate Ṁ* in the formula for Lacc is substituted with a time-averaged accretion rate 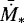 , which effectively removes accretion bursts. In Eq. (3), the angle brackets indicate time-averaging over a period of 104 yr with the LOcally WEighted Scatterplot Smoothing (LOWESS) method using weighted linear least squares and a second-order polynomial model (Cleveland & Devlin 1998). The smooth background luminosities for each model are shown with Fig. 2 by the black solid lines.
, which effectively removes accretion bursts. In Eq. (3), the angle brackets indicate time-averaging over a period of 104 yr with the LOcally WEighted Scatterplot Smoothing (LOWESS) method using weighted linear least squares and a second-order polynomial model (Cleveland & Devlin 1998). The smooth background luminosities for each model are shown with Fig. 2 by the black solid lines.
As a second step to distinguishing luminosity bursts from regular variability, we make an assumption that Ltot must be at least two and a half times higher (one magnitude in brightness) than Lbg during the burst. The duration of each burst must be less than 500 yr to filter out slow rises and drops in luminosity. The bursts that are 2.5, 6.25, 15.6, and 39 times (1, 2, 3, and 4 magnitudes) higher than Lbg are hence called 1-, 2-, 3-, and 4-mag bursts, respectively. In addition, we required that Ltot on both sides of the peak value drop at least by a factor of 2.5 to filter out small kinks in a smoothly increasing or decreasing luminosity curve.
The resulting luminosity bursts in model 1 are marked in Fig. 3 with the filled triangles. Clearly, model 1 shows a number of bursts of various magnitude. Some bursts are isolated while others are closely packed. The insets in Fig. 3 magnify short time periods of evolution featuring an isolated luminosity burst (left) and a series of closely packed bursts (right). The former are caused by compact and dense clumps that withstand the tidal torques when approaching the star until they are accreted through the sink cell, while the latter are caused by extended fragments that were stretched by tidal torques in a series of smaller clumps when approaching the star, with each of the smaller clumps causing one burst (see Fig. 13 in Vorobyov & Basu 2015). V1057 Cyg is a prototype of isolated luminosity bursts, showing a steep rise followed by a slow decline over timescales of several tens of years, while V346 Ori may present an observational example of the clustered burst, the light curve of which shows an intermittent pattern with a deep drop between the previous and the current burst (Kraus et al. 2016; Kóspál et al. 2017).
For each of two models listed in Table 1, we calculated the number of 1-, 2-, 3-, and 4-mag bursts Nbst. In particular, by the 1-mag burst we mean all bursts with luminosity greater than two and a half times the background luminosity (1-mag cutoff), but is lower than 2.52 times the background luminosity (2-mag cutoff). The 2-, 3-, and 4-mag bursts are defined accordingly, with an exception of the 4-mag bursts having no upper limit. The results are presented in the second column of Table 2. Clearly, the number of bursts rapidly decreases from 1- to 4-mag ones. This can be understood as a consequence of tidal stretching and disruption of massive extended fragments into smaller clumps when approaching the star, making strong bursts a less likely outcome. The mass function of forming clumps is also skewed toward objects of smaller mass, from a few Jupiter masses to a few tens of Jupiter masses (Vorobyov et al. 2013b).
The peak values of stellar luminosity and mass accretion rate during the bursts are presented in the third and forth column of Table 2. In particular, the third column shows the maximum luminosity Lmax, minimum luminosity Lmin and arithmetic mean luminosity Lmean for all bursts in each model. The fourth column shows the corresponding values for accretion rates: Ṁmax, Ṁmin, and Ṁmean. As can be expected, the luminosities and mass accretion rates increase with increasing magnitude of the burst.
To calculate the burst duration, we analyzed the shape of each burst as illustrated in Fig. 4. More specifically, we calculated the duration of each burst with respect to the prominence of the burst. The prominence of the burst measures how much the burst stands out due to its intrinsic height and its location relative to other peaks. To calculate the prominence, we extend a horizontal line from the peak to the left and right until the line does one of the following: a) crosses the mass accretion curve (the blue line) because there is a higher peak, b) reaches the left or right end of the mass accretion curve. We then find the minimum of the mass accretion curve in each of the two intervals defined in the previous step. The higher of the two minima specifies the reference level. The height of the peak above this reference level is its prominence. We assumed the duration of the burst equal to the distance between the points where the descending total luminosity (on both sides from the peak) intercepts the green horizontal burst duration line beneath the peak at a vertical distance equal to one third of the burst prominence. Clearly, there is some freedom in choosing the position of the horizontal lines, but our resulting values of the burst durations are in reasonable agreement with what is known about durations of FUor luminosity outbursts (Audard et al. 2014). The maximal duration (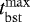 ), minimal duration (
), minimal duration (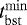 ) and arithmetic mean of burst durations (
) and arithmetic mean of burst durations (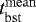 ) are presented in the fifth column of Table 2. Strong 3- and 4-mag luminosity bursts that are most relevant to FUor luminosity outbursts, have burst durations ranging from several to tens of years, with the longest duration of 191 yr. These values are consistent with durations of FUor outbursts (Audard et al. 2014), especially if we take into account that the longest outburst, that of FU Orionis itself, has been in the active state for more than 80 yr already and so far shows no sign of fading. The durations of weaker 1- and 2-mag bursts are a factor of several longer (because they are caused by accretion of tidally stretched clumps), though remaining within reasonable limits. We note that such bursts may be more difficult to observe, especially in the deeply embedded phases of stellar evolutions. We also calculated the total duration of bursts (
) are presented in the fifth column of Table 2. Strong 3- and 4-mag luminosity bursts that are most relevant to FUor luminosity outbursts, have burst durations ranging from several to tens of years, with the longest duration of 191 yr. These values are consistent with durations of FUor outbursts (Audard et al. 2014), especially if we take into account that the longest outburst, that of FU Orionis itself, has been in the active state for more than 80 yr already and so far shows no sign of fading. The durations of weaker 1- and 2-mag bursts are a factor of several longer (because they are caused by accretion of tidally stretched clumps), though remaining within reasonable limits. We note that such bursts may be more difficult to observe, especially in the deeply embedded phases of stellar evolutions. We also calculated the total duration of bursts (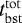 ) for each model. The resulting values are presented in the sixth column of Table 2. Total burst duration is much shorter than the considered evolution time of a few hundred thousand years. This explains why luminosity bursts are rarely observed, but must be numerous during the early evolution of young protostars.
) for each model. The resulting values are presented in the sixth column of Table 2. Total burst duration is much shorter than the considered evolution time of a few hundred thousand years. This explains why luminosity bursts are rarely observed, but must be numerous during the early evolution of young protostars.
In our models, the mass accretion rate Ṁ* is calculated at the position of the inner sink cell, rs.c. = 6 AU. The question that arises is how much Ṁ* can be sensitive to the choice of rs.c.. We varied the value of rs.c. in other studies from 10 AU (Vorobyov & Basu 2005, 2015) to 2.0 AU (Elbakyan et al. 2016) and found little difference in the qualitative behavior of the mass accretion rate. On the other hand, as fragments formed in the outer disk approach the star, they must be inevitably stretched out due to tidal torques. How much of the fragment material finally reaches the star and how much is retained by the inner disk is an open question (e.g., Nayakshin & Lodato 2012). An additional complication is that the very inner disk regions (≲a few AU) may trigger accretion bursts on their own. The effect of a sudden mass deposition onto the inner disk, as if by infall of a fragment migrating through the disk onto the star, has been investigated by Ohtani et al. (2014). These authors find that such an event can lead to the FU-Orionis-like eruption due to triggering of the magneto-rotational instability at sub-AU scales. The effect of the inner disk on the mass accretion rate history requires focused high-resolution studies, which are planned for the near future.
 |
Fig. 2 Total (accretion plus photospheric) luminosity versus time in models 1 and 2 shown by the red lines. The black solid line presents the background luminosity (see text for more detail). |
 |
Fig. 3 Total luminosity (red lines) and background luminosity (thick black lines) vs. time in model 1. The blue line shows the one-magnitude cutoff above the background luminosity and the black triangles mark the luminosity bursts. The right and left insets present examples of the isolated and clustered luminosity bursts. See text for more detail. |
Summary of burst characteristics.
5 Knotty jets and episodic bursts
Jets from young stellar objects have been known for over three decades. Despite the fact that the mechanisms responsible for launching the protostellar jets are not fully understood, it is generally accepted that there exists a causal link between the jet launching process and dynamical interaction of accreted matter with the stellar and/or disk magnetic field (Frank et al. 2014). Jets were first observed in the mid 20th century as a sequence of knots seen at optical wavelengths and known as “Herbig-Haro (HH) objects”, and now many HH objects are known (e.g., Reipurth & Cernicharo 1995). The swept up molecular gas is known as the molecular outflow, and thought to be another manifestation of the same mass loss process from the forming starplus disk system. Molecular jets can also show knot morphology. The origin of these knots can be attributed to a launching mechanism at the jet base that is variable in time (e.g., Bonito et al. 2010). For instance, Dopita (1978) and Reipurth & Aspin (1997) suggested that short period intense accretion events caused by instabilities in the FU Orionis-type accretion disks could be responsible for the HH flows with multiple working surfaces. Arce et al. (2007) summarized evidence in favor that episodic variation in the mass-loss rate can produce a chain of knotty shocks and bow shocks along the jet axis. Observations of jets on spatial scales of hundreds to thousands of AU makeit possible to investigate mass accretion variability on dynamical timescales up to a few thousand years, much longer than what is possible with a series of direct observations of the accretion process (Ellerbroek et al. 2014).
Observations of knots at different epochs can reveal how the outflow varies with time. This can help to reconstruct the time periods when the knots were formed and reveal their pattern of occurrence. In most cases, however, observationsof the line-of-sight velocities from one epoch are only available. In this paper, we made use of the data on CARMA 7, a Class 0 object in the Serpens South cluster observed by Plunkett et al. (2015) using the Atacama Large Millimeter/submillimeter Array (ALMA). The outflow ejecta revealed 22 knots (11 in each direction), the most recent having the highest line-of-sight velocity. The dynamic timescale for each knot was estimated as τobs= D∕Vflow(cos i∕sin i), where D is the distance (projected on the plane of the sky) between the knot and protostar, Vflow is the line-of-sight velocity of the knots, and i is the (unknown) inclination of the outflow with respect to the line of sight. The authors found dynamic timescales for each of the identified knots ranging from 100 yr to 6 000 yr (uncorrected for the inclination angle, discussed later in this section), assuming that the knots travel with constant velocity from the time of their launch. They suggested that knots might be related to an episodic ejection mechanism, such as accretion bursts caused by disk instabilities. In this case, the difference between the dynamic timescales of the knots Δτobs can provide the durations of quiescent phases between episodic ejections.
We were then able to calculate the time spacings Δτmod between the subsequent bursts in our models and compare them with the differences in dynamic timescales between the knots Δτobs in the jet of CARMA 7. More specifically, we calculated Δτmod as the time spacing between two consequent luminosity peaks comprising a range of magnitudes. For instance, Δτmod for luminosity bursts of 1-4-mag signifies a time spacing between two consequent luminosity peaks of all magnitudes, whereas Δτmod for luminosity bursts of 4-mag denotes a time spacing between two luminosity peaks of 4-mag (skipping all bursts of lesser magnitude). The normalized distribution of Δτmod in model 1 is presented in Fig. 5 with the filled histograms. More specifically, the upper-left panel presents the normalized distribution of Δτmod for bursts of all four magnitudes, while the other three panels show the normalised distributions for the bursts of increasingly higher magnitudes as indicated in the legends. Interestingly, Δτmod is characterized by a bi-modal distribution with one maximum at ≈ 100 yr and the other maximum at a few × (103–104) yr. The bi-modality is a direct consequence of the isolated and clustered burst modes (Vorobyov & Basu 2015). In the former, quiescent periods between luminosity bursts are long (on the order of thousands to tens of thousand years), whereas in the latter, bursts occur one after another on timescales of tens to hundred years. We note that the bi-modality diminishes for strong 4-mag bursts because they rarely occur in the clustered mode. A similar bi-modal distribution of Δτmod was also found in model 2.
The solid lines in Fig. 5 present the distribution of Δτobs (uncorrected for inclination) for the jet of CARMA 7. We calculated the distribution of Δτobs taking the corresponding data for both the northern and southern parts of the jet, rather than constructing separate distributions, to increase statistics and decrease the noise of the distribution. In contrast to the model Δτmod distribution, the observed distribution of Δτobs does not show bi-modality and has a maximum at ≈300–400 yr, falling almost in-between the two peaks in the model distribution. The lack of bi-modality can be attributed to relatively short dynamic timescales of the knots (more distant knots might have dissipated due to interaction with the ambient medium), while the mismatch in the maxima of the model and observed distributions might be less severe if we applied a correction for inclination.
The inclination angle of the jet with respect to the line of sight in CARMA 7 is poorly constrained. Therefore, we performed the K-S test using the unbinned observational and theoretical data sets of Δτmod and Δτobs to find the inclination angle at which both distributions agree best. For the observational data, we applied an inclination angle correction from i = 5° to i = 85° with a step of 5°. For the model data, we retained values of Δτmod that are equal to or shorter than the maximum observed difference in dynamical timescales of the knots 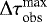 , the latter also corrected for the corresponding inclination. Here and in the following text, we have used the truncated set of model data, because the jet structure in CARMA 7 was analyzed only for a narrow field of view. This means that more distant knots with longer Δτobs may exist in CARMA 7, for which we have at present no information. Counting in the model data with
, the latter also corrected for the corresponding inclination. Here and in the following text, we have used the truncated set of model data, because the jet structure in CARMA 7 was analyzed only for a narrow field of view. This means that more distant knots with longer Δτobs may exist in CARMA 7, for which we have at present no information. Counting in the model data with 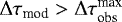 could lead to potentially wrong conclusions.
could lead to potentially wrong conclusions.
Figure 6 presents the results of the K–S test (P-values) for both considered models as a function of the inclination angle. We considered bursts of various magnitudes, but excluded the model data for which the statistics were too poor to make firm conclusions (model 1, 4-mag). In all cases, the K–S test has a clear peak value (higher than the minimum value of 0.05 required to formally pass the test) at a certain inclination angle. The resulting P-values and best-fit inclination angles i for both models are summarized in Table 3. The best-fit inclination angle increases with the increasing amplitude of the bursts, but is constrained within a range of 55–80°. In fact, if we exclude the 1-mag bursts, the window of best-fit inclination angles becomes even narrower, 75–80°. The wider the spread of the inferred inclination angles for the models that include 1-mag bursts may indicate that these bursts are too weak to create a significant response in the jet and produce notable knots. The inclusion of these weak bursts in the statistical analysis might have created some sort of “noise”, which spreads inferred inclination angles. We note that these inclination angles are only rough estimates based on an assumption of a causal link between accretion bursts and jet knots, and need to be confirmed by independent measurements.
Figures 7 and 8 show the model and observational distributions of Δτmod and Δτobs after correction for the best-fit inclination angle for models 1 and 2, respectively. The model data sets were cut, so that 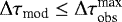 , where
, where 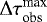 was also corrected for the corresponding inclination. Clearly, the observational distribution of Δτobs now fits better to our theoretical predictions. We note that remained model data correspond to the clustered burst mode with a peak of Δτmod at a few × 102 yr. We concludethat strong luminosity bursts (>1-mag) can match the observed distribution of Δτobs in the knotsof CARMA 7 for inclination angles that are constrained within a rather narrow range, i = 70–80°. The range of inferred inclination angles becomes somewhat wider (i = 55–80°), if weaker luminosity bursts (1-mag) are also considered. The independent knowledge of the inclination angle in CARMA 7 is needed to further constrain the luminosity burst strengths that can reproduce the observed time spacings between the knots.
was also corrected for the corresponding inclination. Clearly, the observational distribution of Δτobs now fits better to our theoretical predictions. We note that remained model data correspond to the clustered burst mode with a peak of Δτmod at a few × 102 yr. We concludethat strong luminosity bursts (>1-mag) can match the observed distribution of Δτobs in the knotsof CARMA 7 for inclination angles that are constrained within a rather narrow range, i = 70–80°. The range of inferred inclination angles becomes somewhat wider (i = 55–80°), if weaker luminosity bursts (1-mag) are also considered. The independent knowledge of the inclination angle in CARMA 7 is needed to further constrain the luminosity burst strengths that can reproduce the observed time spacings between the knots.
Given our constrains on the inclination angle, we can estimate the time passed since the last burst. The shortest dynamical time (uncorrected for the inclination) for the nearest knot is 100 yr. For the inclination angles in the i = 55–80° range, the resulting times passed since the last burst are ≈17–70 yr. The magnitude of the last burst is difficult to constrain from our analysis. However, if we assume that the last burst was sufficiently strong (≥3-mag or more than afactor of 15 in luminosity), then it might have heated notably the surrounding envelope (CARMA 7 is a class 0 object), thus evaporating certain chemical species, such as CO, from dust grains. The freeze-out time of the gas-phase CO back on dust grains is much longer, on the order of hundreds to thousand years (Visser & Bergin 2012; Vorobyov et al. 2013a; Frimann et al. 2017). Therefore, the possible overabundance of the gas-phase CO in the envelope of CARMA-7, as compared to what can be expected from the current luminosity, can be used to confirm the recent luminosity burst in this object. Even if the latest burst was not sufficiently strong to produce a notable heating in the envelope, more distant bursts that occurred no longer than a few hundred years ago may still be stronger and therefore may leave chemical signatures in the envelope.
A good agreement between the model and observed distributions of Δτ (for certain inclination angles) tells us that the time spacings between the bursts in our models are similar in magnitude to the differences in dynamical timescales of the observed knots. However, at this point in the analysis we still did not know if we were able to reproduce the exact sequence of Δτobs for 11 northern and 11 southern knots in CARMA 7. To check this, we first calculated the sum
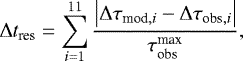 (4)
(4)
which is the residual time left after subtracting the observed sequences of Δτobs from the model sequence of Δτmod and then normalized to the maximum dynamical timescale of the knots 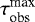 . Because there are more luminosity bursts in our models than knots in CARMA 7, we shifted the observed sequence of Δτobs along the line of increasing time in our models to find the time instance when the residual Δ tres is minimal, indicating the time instance when the best match between the model and observed sequences of Δτ is achieved. We performed this analysis for both models, but show here only the results for model 1, for which the best agreement was found. For the model data, we used luminosity bursts of all magnitudes (1–4-mag) and for the observational data we used 11 northern and southern knots. The observational data were corrected for the best-fit inclination found from the K-S test (see Table 3). The corresponding values of Δ tres as a function of time (elapsed from the instance of protostar formation) are shown in the top panel of Fig. 9 and the minimum of Δ tres is indicated on the figure. There are no data for t > 0.2 Myr because there are less than 11 bursts in model 1 left at advanced evolutionary times.
. Because there are more luminosity bursts in our models than knots in CARMA 7, we shifted the observed sequence of Δτobs along the line of increasing time in our models to find the time instance when the residual Δ tres is minimal, indicating the time instance when the best match between the model and observed sequences of Δτ is achieved. We performed this analysis for both models, but show here only the results for model 1, for which the best agreement was found. For the model data, we used luminosity bursts of all magnitudes (1–4-mag) and for the observational data we used 11 northern and southern knots. The observational data were corrected for the best-fit inclination found from the K-S test (see Table 3). The corresponding values of Δ tres as a function of time (elapsed from the instance of protostar formation) are shown in the top panel of Fig. 9 and the minimum of Δ tres is indicated on the figure. There are no data for t > 0.2 Myr because there are less than 11 bursts in model 1 left at advanced evolutionary times.
The middle and bottom panels in Fig. 9 show Δτobs and Δτmod as a function of the knot serial number at the time instance when the best fit between the observed and model data was found (marked with the red circles in the top panel). All 11 knots in the northern (middle panel) and southern (bottom panel) jet were used for comparison with the model data, but only ten are shown because we calculated the difference in dynamical timescales between the adjacent knots (i.e., 2–1, 3–2, etc.). Clearly, for some knots, the time spacings between the bursts Δτmod differ substantially from the differences in dynamical timescales between the knots Δτobs. For the northern jet, the mismatch shown by the arrows is greater than Δτobs itself for knot 2 and it is comparable to Δτobs for knots 4, 8, and 11, while other knots show good agreement (e.g., 3, 6, 7, and 9). For the southern jet, the agreement is particularly worse for knots 6, 8, and 9. The northern-jet knots close to the protostar show a more linear Δτobs vs. τobs correlation (see Fig. 2e in Plunkett et al. 2015), which matches better the modeling results. The difference in the time spacings between the northern and southern jets could be due to different inclinations of the two branches due to precession. Similarly, the other model revealed good correlation only for part of the knots in CARMA 7. Nevertheless, we emphasize that finding a perfect match on the basis of only two models is probably a very unlikely event. The stochastic nature of accretion bursts in gravitationally unstable disks and the effect of environment on the jet and outflow propagation can complicate the comparison. We intend to continue searching for a better match once more models become available.
 |
Fig. 4 Total luminosity vs. time plot (blue line) illustrating our procedure for calculating the characteristics of the bursts including their prominence (vertical red lines) and duration (horizontal green lines). |
 |
Fig. 5 Normalized distribution of time spacings between the luminosity bursts (Δτmod) of various magnitudes (1–4, 2–4, 3–4, and 4 mag) in model 1 shown with the filled histogram. The solid linehistogram shows the distribution of differences in dynamical timescales between the knots (Δτobs) in CARMA 7 without correction for an inclination angle. |
 |
Fig. 6 P-values of the K–S test using the unbinned observational and theoretical data sets of Δτmod and Δτobs as a function of (unknown) inclination angle in CARMA-7. The results for different models are distinguished by lines with different color as indicated in the legend. Luminosity bursts comprising various magnitude ranges (1–4, 2–4, 3–4, and 4 mag) are considered. |
 |
Fig. 7 Similar to Fig. 5, but with the observational data Δτobs corrected for the best-fit inclination angles as indicated in Table 3. |
K–S test results for the entire jet (the sum of the northern and southern parts).
 |
Fig. 9 Top panel: residual times left after subtracting the observed sequences of Δτobs from the model sequence of Δτmod in model 1 and then normalized to the maximum dynamical timescale of the knots in CARMA 7. The blue and red curves correspond to the northern and southern knots, respectively. The red circles mark the minimum values which correspond to the best fit between the observational and model data. Middle and bottom panels: Δτobs and Δτmod as a function of the knot serial number at the time instance when the best fit between the observed and model data was found. The middle panel provides the comparison for the northern knots, while the bottom panel – for the southern knots. The arrows show the mismatch between the individual data pairs. |
6 Conclusions
In this paper, we studied numerically the mass accretion history of (sub)solar mass protostars during the embedded phase of evolution using numerical hydrodynamics simulations of gravitationally unstable protostellar disks in the thin-disk limit. The accretion variability resulting from gravitational instability and fragmentation of protostellar disks was analyzed to obtain the characteristics of accretion and luminosity bursts that occurred during the embedded phase. In particular, we identified luminosity bursts with different magnitudes (from 1-mag to >4-mag corresponding to an increase in luminosity from a factor of 2.5 to >39) and calculated time spacings between the bursts Δτmod. We further compared Δτmod with the differences in dynamical timescales of knots Δτobs recently detected in the jet of CARMA 7, a young protostar in the Serpens South cluster (Plunkett et al. 2015). More specifically, we compared the model and observed distribution functions and also the exact sequences of Δτmod and Δτobs. We aimed to investigate apossible causal link between the episodic mass accretion onto the protostar and the knotty jet structure. Our results can be summarized as follows:
-
Gravitationally unstable protostellar disks are characterized by time-varying protostellar accretion with episodic bursts. Accretion variability is strong in the early evolution, but subsides with time as the gravitational instability weakens because of diminishing mass infall from the envelope. Artificially turning off disk self-gravity (and hence gravitational instability) results in significant reduction of accretion variability.
-
The timespacings between the luminosity bursts Δτmod in gravitationally unstable disks show a bi-modal distribution, with the first peak at ≈100 yr and the second peak at a few × (103–104) yr, depending on the strength of the bursts. The bimodality is caused by two modes of luminosity bursts: isolated and clustered ones (see Vorobyov & Basu 2015, for detail). In particular, the isolated bursts are characterized by long quiescent periods, whereas clustered bursts occur one after another on timescales of a few × (10–102) yr.
-
The distribution of Δτmod in our models can be fit reasonably well to the distribution of differences in dynamical timescales of the knots Δτobs in the protostellar jet of CARMA-7, if a correction for the (yet unknown) inclination angle is applied to the observational data set and the model data are truncated to retain only clustered bursts. The K-S test on the unbinned model and observational data sets suggests a narrow range of the best-fit inclination angles (i = 75–80°), if strong luminosity bursts (>1-mag) are considered. The range of inferred inclination angles becomes somewhat wider (i = 55–80°), if weaker luminosity bursts (1-mag) are also considered. This may indicate that 1-mag bursts introduce some sort of a ‘noise’ and are in fact too weak to produce notable knots.
-
Notwithstanding a good agreement between the model and observed distributions of Δτmod and Δτobs, the exact sequences of time spacings between the luminosity bursts in our models and knots in the jet of CARMA 7 were found difficult to match. More models and observational data are needed to further explore this issue.
Given our constrains on the inclination angle, we estimated the times passed since the last luminosity burst to be ≈17–70 yr. This is much shorter than the typical freeze-out time of CO in the envelope, on the order of hundreds to thousands years (Visser & Bergin 2012; Vorobyov et al. 2013a; Rab et al. 2017). Recent surveys of deeply embedded protostars (e.g., Jørgensen et al. 2015; Frimann et al. 2017) indicate that a notable fraction of sources show extended CO emission that is inconsistent with their current luminosity, implying a recent luminosity burst that heated the envelope and evaporated CO, which is currently in the process of re-freezing. This means that we may expect the overabundance of the gas-phase CO in the envelope of CARMA 7 (recall that this is a Class 0 object) if the most recent bursts are strong enough to evaporate this species in the envelope. The search for an extended CO emission in CARMA 7 can therefore confirm the recent luminosity burst in this object.
Finally, we note that we have not taken into account some important effects. For instance, the luminosity bursts in our models are triggered by disk gravitational fragmentation with subsequent infall of gaseous clumps on the star. Other luminosity bursts mechanisms can operate concurrently (and also in disks stable to fragmentation) and increase the number of luminosity bursts. In addition, varying velocity of the blobs ejected at different epochs together with the inhomogeneous ambient medium, may lead to complex mutual interactions of the blobs, which were not taken into account. Therefore, deceleration of the knots and also interactions of knots with each other (collisions) should be considered in later works. In Plunkett et al. (2015), only a small region near CARMA-7 was analyzed. Beyond that area, the outflows are confused with other surrounding outflows from nearbyprotostars. There may be outflow knots with longer time intervals than those studied in Plunkett et al. (2015).
Acknowledgments
The authors are thankful to the anonymous referee for constructive comments that helped to improve the manuscript. This work was supported by the Austrian Science Fund (FWF) under research grant I2549-N27 and the Swiss National Science Foundation (SNSF) (project number 200021L_163172). OD acknowledges support from the Austrian Research Promotion Agency in the framework of the Austrian Space Application Program (FFG-854025). V. Elbakyan acknowledges support from the Russian Ministry of Education and Science Grant 3.5602.2017. The simulations were performed on the Vienna Scientific Cluster (VSC-3) and on the Shared Hierarchical Academic Research Computing Network (SHARCNET).
References
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., Shepherd, D., Gueth, F., et al. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 951, 245 [NASA ADS] [Google Scholar]
- Armitage, P. J. 2016, ApJ, 833, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., Livio, M., & Pringle, J. E. 2001, MNRAS, 324, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Audard, M., Brahm, P., Dunham, M. M., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 387 [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bonito, R., Orlando, S., Peres, G., et al. 2010, A&A, 511, 42 [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Ruíz-Rodríguez, D., Perez, S., et al. 2018, MNRAS, 474, 4347 [NASA ADS] [CrossRef] [Google Scholar]
- Cleveland, W. S., & Devlin, S. J. 1998, J. Am. Stat. Assoc., 83, 596 [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2012, MNRAS, 420, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Dapp, W. B., & Basu, S. 2009, MNRAS, 395, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A. 1978, A&A, 63, 237 [NASA ADS] [Google Scholar]
- Dunham, M. M., & Vorobyov, E. I. 2012, ApJ, 747, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Elbakyan, V. G., Vorobyov, E. I., & Glebova, G. M. 2016, Astron. Rep., 60, 679 [Google Scholar]
- Ellerbroek, L. E., Podio, L., Dougados, C., et al. 2014, A&A, 563, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoch, M. L., Evans, N. J., II, Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Frimann, S, Jorgensen, J. K., Dunham, M. M., et al. 2017, A&A 602, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 914, 451 [NASA ADS] [Google Scholar]
- Herczeg, G. J., Johnstone, D. I., Mairs, S. et al. 2017, ApJ, submitted [Google Scholar]
- Hsieh, T.-H., Lai, S.-P., Belloche, A., & Wyrowski, F. 2016, ApJ 826, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Visser, R., Williams, J. P., & Bergin, E. A. 2015, A&A, 579, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., Hartmann, L. W., Strom, K. M., & Strom, S. E. 1990, ApJ, 99, 869 [Google Scholar]
- Kóspál, A., Abrahám, P., Csengeri, T., et al. 2017, ApJ, 843, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Kratter, K. M., Matzner, C. D., & Krumholz, M. R. 2008, ApJ, 681, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, S., Caratti o Garatti, A., Garcia-Lopez, R., et al. 2016, MNRAS, 462, 61 [Google Scholar]
- Larson, R. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E. 2007, J. Kor. Astron. Soc., 40, 83 [Google Scholar]
- Meyer, D. M.-A., Vorobyov, E. I., Kuiper, R., & Kley, W. 2017, MNRAS, 464, 90 [Google Scholar]
- Nayakshin, S.,& Lodato, G. 2012, MNRAS, 426, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ohtani, T., Kimura, S. S., Tsuribe, T., & Vorobyov, E. I. 2014, PASJ, 66, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Pena, C. C., Lucas, P. W., Minniti, D. et al. 2017, MNRAS, 465, 3011 [NASA ADS] [CrossRef] [Google Scholar]
- Plunkett, A. L., Arce, H. G., Mardones, D., et al. 2015, Nature, 527, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Henning, T., Bouwman, J., et al. 2007, ApJ, 668, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Rab, Ch., Elbakyan, V., Vorobyov, E., et al. 2017, A&A, 604, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B., & Aspin, C. 1997, AJ, 114, 2700 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., & Cernicharo, J. 1995, RMxAA, 1, 43 [Google Scholar]
- Safron, E. J., Fischer, W. J., Megeath, S. et al. 2015, ApJ, 800, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Visser, R., & Bergin, E. A. 2012, ApJ, 754, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2009, ApJ, 704, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2011, ApJ, 729, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2013, A&A, 552, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, MNRAS, 360, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2009, MNRAS, 393, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2010, ApJ, 719, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2015, ApJ, 805, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Baraffe, I., Harries, T., & Chabrier, G. 2013a, A&A, 557, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., Zakhozhay, O. V., & Dunham, M. M. 2013b, MNRAS, 433, 3256 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., & Gammie, C. 2009, ApJ, 694, 1045 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
K–S test results for the entire jet (the sum of the northern and southern parts).
All Figures
 |
Fig. 1 Mass accretion rates on the central protostar (the blue solid lines) and the disk infall rates (the red dashed lines) as a function of time in models 1 and 2. The bottom panel shows the corresponding rates in model 2, but with disk self-gravity artificially turned off. |
| In the text | |
 |
Fig. 2 Total (accretion plus photospheric) luminosity versus time in models 1 and 2 shown by the red lines. The black solid line presents the background luminosity (see text for more detail). |
| In the text | |
 |
Fig. 3 Total luminosity (red lines) and background luminosity (thick black lines) vs. time in model 1. The blue line shows the one-magnitude cutoff above the background luminosity and the black triangles mark the luminosity bursts. The right and left insets present examples of the isolated and clustered luminosity bursts. See text for more detail. |
| In the text | |
 |
Fig. 4 Total luminosity vs. time plot (blue line) illustrating our procedure for calculating the characteristics of the bursts including their prominence (vertical red lines) and duration (horizontal green lines). |
| In the text | |
 |
Fig. 5 Normalized distribution of time spacings between the luminosity bursts (Δτmod) of various magnitudes (1–4, 2–4, 3–4, and 4 mag) in model 1 shown with the filled histogram. The solid linehistogram shows the distribution of differences in dynamical timescales between the knots (Δτobs) in CARMA 7 without correction for an inclination angle. |
| In the text | |
 |
Fig. 6 P-values of the K–S test using the unbinned observational and theoretical data sets of Δτmod and Δτobs as a function of (unknown) inclination angle in CARMA-7. The results for different models are distinguished by lines with different color as indicated in the legend. Luminosity bursts comprising various magnitude ranges (1–4, 2–4, 3–4, and 4 mag) are considered. |
| In the text | |
 |
Fig. 7 Similar to Fig. 5, but with the observational data Δτobs corrected for the best-fit inclination angles as indicated in Table 3. |
| In the text | |
 |
Fig. 8 Similar to Fig. 7, but for model 2. |
| In the text | |
 |
Fig. 9 Top panel: residual times left after subtracting the observed sequences of Δτobs from the model sequence of Δτmod in model 1 and then normalized to the maximum dynamical timescale of the knots in CARMA 7. The blue and red curves correspond to the northern and southern knots, respectively. The red circles mark the minimum values which correspond to the best fit between the observational and model data. Middle and bottom panels: Δτobs and Δτmod as a function of the knot serial number at the time instance when the best fit between the observed and model data was found. The middle panel provides the comparison for the northern knots, while the bottom panel – for the southern knots. The arrows show the mismatch between the individual data pairs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


