| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731545 | |
| Published online | 17 May 2018 | |
Three-dimensional simulations of the interaction between the nova ejecta, accretion disk, and companion star★
1
Departament de Física, EEBE, Universitat Politècnica de Catalunya,
c/ Eduard Maristany 10,
08930
Barcelona, Spain
e-mail: jordi.jose@upc.edu
2
Institut d’Estudis Espacials de Catalunya,
c/ Gran Capità 2-4, Ed. Nexus-201,
08034
Barcelona, Spain
3
Departament de Física, Universitat Politècnica de Catalunya,
c/ Esteve Terrades 5,
08860
Castelldefels, Spain
4
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Strasse 1,
85748
Garching bei München, Germany
5
School of Physics and Astronomy, Monash University,
Clayton 3800,
Victoria, Australia
6
Monash Centre for Astrophysics (MoCA), Monash University,
Clayton 3800,
Victoria, Australia
7
South African Astronomical Observatory,
PO Box 9, Observatory Rd.,
7935
Cape Town, South Africa
8
Astronomy Department, University of Cape Town,
7701
Rodenbosch, South Africa
9
South Africa National Institute for Theoretical Physics,
Private Bag X1, Matieland,
7602
Stellenbosch, South Africa
Received:
11
July
2017
Accepted:
20
December
2017
Context. Classical novae are thermonuclear explosions hosted by accreting white dwarfs in stellar binary systems. Material piles up on top of the white dwarf star under mildly degenerate conditions, driving a thermonuclear runaway. The energy released by the suite of nuclear processes operating at the envelope, mostly proton-capture reactions and β+-decays, heats the material up to peak temperatures ranging from 100 to 400 MK. In these events, about 10−3–10−7 M⊙, enriched in CNO and, sometimes, other intermediate-mass elements (e.g., Ne, Na, Mg, and Al) are ejected into the interstellar medium.
Aims. To date, most of the efforts undertaken in the modeling of classical nova outbursts have focused on the early stages of the explosion and ejection, ignoring the interaction of the ejecta, first with the accretion disk orbiting the white dwarf and ultimately with the secondary star.
Methods. A suite of 3D, smoothed-particle hydrodynamics (SPH) simulations of the interaction between the nova ejecta, accretion disk, and stellar companion were performed to fill this gap; these simulations were aimed at testing the influence of the model parameters—that is, the mass and velocity of the ejecta, mass and the geometry of the accretion disk—on the dynamical and chemical properties of the system.
Results. We discuss the conditions that lead to the disruption of the accretion disk and to mass loss from the binary system. In addition, we discuss the likelihood of chemical contamination of the stellar secondary induced by the impact with the nova ejecta and its potential effect on the next nova cycle.
Key words: novae, cataclysmic variables / nuclear reactions, nucleosynthesis, abundances / hydrodynamics
Movies showing the full evolution of several models are available online at https://www.aanda.org and at http://www.fen.upc.edu/users/jjose/Downloads.html
© ESO 2018
1 Introduction
The coupling of spectroscopic determinations of chemical abundances, photometric studies of light curves, and hydrodynamic simulations of the accretion, expansion, and ejection stages has been instrumental in our understanding of the nova phenomenon. The scenario envisaged assumes a white dwarf star hosting the explosion in a close binary system (see, e.g., Sanford 1949; Joy 1954; Kraft 1964, for some of the first systematic observations that revealed the binary nature of novae). The low-mass, main sequence stellar companion overfills its Roche lobe and matter flows through the inner Lagrangian point of the system; this companion is frequently a K-M dwarf, although observations increasingly support the presence of more evolved companions in some systems. A fraction of this hydrogen-rich matter lost by the secondary spirals via an accretion disk and ultimately piles up on top of the white dwarf (typically, at a rate ~10−8–10−10 M⊙ yr−1). The accreted envelope layers get gradually compressed by the continuous matter infall under mildly degenerate conditions. Compressional heating initiates nuclear reactions and a thermonuclear runaway ensues. The thermonuclear origin of nova explosions was first theorized by Schatzman (1949, 1951). This was followed by a number of significant contributions in the 1950s and 1960s (see, e.g., Cameron 1959; Gurevitch & Lebedinsky 1957), including pioneering attempts to mimic the explosion through the coupling of radiative transfer in an optically thick expanding shell with hydrodynamics (Giannone & Weigert 1967; Rose 1968; Sparks 1969).
To date, most of the efforts undertaken in the modeling of nova outbursts have focused on the early stages of the explosion and ejection (see Starrfield et al. 2008, 2016; José & Shore 2008; José 2016, for recent reviews). Therefore, key aspects of the evolution of these systems, associated with the interaction of the ejecta, first with the accretion disk orbiting the white dwarf, and ultimately with the secondary star, have been largely unexplored1. Shortly after the outer layers of the white dwarf expand and achieve escape velocity, a fraction of the ejected material is expected to collide with the secondary star. As a result, part of the nova ejecta mixes with the outermost layers of the secondary. The resulting chemical contamination may have potential implications for the next nova cycle, once mass transfer from the secondary resumes.
Novae are also prolific dust producers. Infrared (Evans & Rawlings 2008; Gehrz et al. 1998; Gehrz 2008) and ultraviolet observations (Shore et al. 1994) have unambiguously revealed dust forming episodes in the ejected shells accompanying some nova outbursts ~100 days after the explosion. In fact, it has been suggested that novae may have contributed to the inventory of presolar grains isolated from meteorites. A major breakthrough in the identification of nova candidate grains was achieved by Amari et al. (2001); Amari (2002); these authors reported several SiC and graphite grains, which were isolated from the Murchison and Acfer 094 meteorites and had abundance patterns qualitatively similar to those predicted by models of nova outbursts: that is, low 12 C/13C and 14 N/15N ratios, high 30 Si/28Si and close-to-solar 29 Si/28Si ratios, and high 26 Al/27Al and 22 Ne/20Ne ratios. However, to quantitatively match the grain data, mixing between material synthesized in the explosion and more than ten times as much unprocessed, isotopically close-to-solar material was required. The collision of the ejecta, either with the accretion disk or withthe secondary star, may naturally provide the required chemical dilution to explain the reported grain data.
Moreover, the unexpected discovery of very high-energy emission (>100 MeV), first observed in the symbiotic binary V407 Cygni (Abdo et al. 2010), and subsequently detected in a number of novae (e.g., V407 Cyg, V1324 Sco, V959 Mon, V339 Del, V1369 Cen), by the Large Area Telescope on board the Fermi γ-ray space observatory (Fermi LAT), has also been linked to shock acceleration in the ejected shells after interaction with a wind from the secondary2. This has confirmed novae as a distinct class of γ-ray sources (Ackermann et al. 2014).
All the above-mentioned aspects stress the need for a thorough description of the dynamics of the system after the nova explosion, following the collision of the ejecta with the accretion disk, and subsequently, with the secondary star. The present paper aims at filling this gap. The manuscript is organized as follows. The method of computation, input physics, and initial conditions adopted are described in Sect. 2. A full account of the 3D simulations of the interaction of the ejecta with the accretion disk, and ultimately with the main sequence companion, is presented in Sect. 3. The effect of the different parameters on the stability of the accretion disk and on the amount of mass lost from the system is also analyzed in Sect. 3. The expected level of chemical contamination of the outer layers of the secondary star is discussed in Sect. 4. A summary of the most relevant conclusions of this paper is presented in Sect. 5.
2 Model and input physics
2.1 Initial configuration
The 3D computational domain3 of the simulations discussed in this paper includes the white dwarf that hosts the nova explosion, the expanding nova ejecta, the accretion disk, and the main sequence companion.
2.1.1 White dwarf star
The white dwarf is modeled as a 0.6 M⊙ point-like mass, which is enough to account for its gravitational pull on the system. The expanding ejecta, which at the beginning of the 3D simulations is located between 0.65 R⊙ (inner edge) and 0.72 R⊙ (outer edge) from the underlying white dwarf, has a mean metallicity of Z = 0.54, and a mass, density, and velocity profiles corresponding to the values computed with the 1D code SHIVA (see Sect. 2.2, for details).
2.1.2 Main sequence star
A 1 M⊙, solar metallicity, main sequence companion is adopted as the secondary. The star has spherical symmetry and is built in hydrostatic equilibrium conditions. A polytropic equation of state with γ = 5∕3 was considered. The corresponding density and internal energy profiles were subsequently mapped onto a 3D particle distribution. To avoid a substantial computational load, only the outer layers of the main sequence star were considered, since during the collision between thenova ejecta and the secondary, particles are not expected to penetrate deep inside the star. Even though preliminary simulations performed in this work suggest that the ejecta may penetrate, at most, through the outer ~0.1 R⊙ of the secondary, the outermost ~0.2 R⊙ (0.15 M⊙) of the star wastaken into account. The rest of the star was replaced by a point-like mass located at its center. To generate theinitial 3D particle distribution of the outer main sequence layers, the initial 1D density profile is sliced into several shells of equal radius. For each shell, a glass technique was implemented (White 1996). In essence, a cube is filled with a random number of particles until a uniform distribution is achieved, from which a shell with constant density is extracted. The same procedure is used for each shell at various densities and is also adopted for the accretion disk and ejecta (assuming in this case axial symmetry). The initial density profile for the outer main sequence layers is shown in Fig. 1. For convenience, and to guarantee good accuracy in the interpolated functions, all smoothed-particle hydrodynamics (SPH) particles used in this work have the same mass, ~ 10−8 M⊙. One can easily infer the number of SPH particles within each mass shell from its total mass. About 3.8 million SPH particles were used to model the outer ~0.2 R⊙ (0.15 M⊙) of the secondary. To guarantee that the resulting 3D structure is in hydrostatic equilibrium, the stellar secondary is relaxed for a total time on the order of 20 orbital periods.
 |
Fig. 1 Initialdensity profiles for the outer main sequence layers (after relaxation) and the accretion disk. |
2.1.3 Mass-accretion disk
We modeled the accretion disk that orbits the point-like white dwarf in Keplerian rotation according to the Shakura–Sunyaev, V-shaped disk solution (Shakura & Sunyaev 1973; Frank et al. 2002). In our fiducial model (hereafter, Model A; see Table 1) we assumed a solar-composition disk with a mass of 2 × 10−5 M⊙ and a geometry given by a ratio of height to radius of H∕R = 0.03, (see Sects. 3.4 and 3.5, for the effect of these parameters on the simulations). Other models of accretion disks (e.g., flared disks) and inclusion of alternative assumptions (smaller extended disks; see Warner 2003) will be addressed in a future paper; see Puebla et al. (2007) for a comparison between current disk models and observational data. In this work, the accretion disk contains only a few thousand SPH particles, which is the truly limiting factor of the simulations; the nova ejecta contains up to 19 000 SPH particles. The sound-crossing time throughout the disk is ~4 h, while the time required for the ejecta to reach and hit the disk is ~6 min. Therefore, no relaxation of the disk, also built by means of the cubic glass technique, is needed. The initial density profile for the mass-accretion disk is shown in Fig. 1.
Models computed.
2.2 Model
The first stages of the evolution of the nova outbursts, through accretion, expansion, and ejection, were modeled by means of the 1D, spherically symmetric, Lagrangian, hydrodynamic code SHIVA (see José & Hernanz 1998; José 2016, for details). When the inner edge of the ejecta reached a size of 0.65 R⊙, the structure was mapped onto a 3D domain, which also included the white dwarf that hosts the nova explosion, the accretion disk, and the main sequence companion. The evolution of the system was subsequently followed with the 3D smoothed-particle hydrodynamics (SPH) code GADGET-2 (Springel et al. 2001; Springel & Hernquist 2002; Springel 2005). This parallelized, explicit, Lagrangian, mesh-free code describes fluids in terms of a set of discrete elements (hereafter, particles). Their continuous properties (e.g., density, temperature, and velocity) are obtained through kernel interpolation and summation over all neighboring particles. In the simulations presented in this paper, a cubic spline kernel was adopted. To handle shocks, GADGET-2 uses the artificial viscosity prescription developed by Monaghan (1997), together with a viscosity limiter for pure shear flows (Balsara et al. 1995). In addition, the code computes gravitational interactions using a hierarchical oct-tree algorithm (Barnes & Hut 1986). Time steps are controlled by means of a Courant factor taken as 0.15. The gravitational softening of the SPH particles was approximated by their smoothing lengths. It is worth noting that GADGET-2 enables density contrasts since it offers adaptive smoothing lengths (Springel & Hernquist 2002).
The characteristic size of the overall binary system, for a given set of values of the masses of the primary and secondary stars, is determined by the orbital period. In the simulations reported in this work, a value of Porb= 8.9 h was adopted. This is a representative value of long-period classical nova systems, Porb> 7 h, which may represent about 20% of all novae (Tappert et al. 2013). We did not consider the rotation of the binary system since the overall duration of the interaction between the ejecta, the disk, and the secondary is very small. In fact, the orbital period adopted is ~12 times longerthan the time it takes for the ejecta to reach and hit the main sequence companion. We did not consider the effect of the Coriolis and centrifugal forces either. These effects introduce angular momentum and viscous-shear dissipation, which may affect the trajectories of some of the ejecta particles as they travel toward the secondary. Such effects will be addressed in a future manuscript.
3 Results: disk stability and mass loss
Observations suggest that the accretion disk does not always get disrupted by a nova outburst4. Indeed, in some systems, the presence of a disk has been confirmed only a few months/years after the explosion (see, e.g., Leibowitz et al. 1995; Retter et al. 1997, 1998; Skillman et al. 1997; Hernanz & Sala 2002), which is clearly at odds with the typical timescales required for a disk to assemble (on the order of decades). It has been suggested that the accretion disk is only disrupted if the system is an intermediate polar (Retter 2003). In those systems, the magnetic field could truncate the inner regions of the disk, which would be less massive than in nonmagnetic systems, and therefore, prone to be disrupted by a nova explosion. However, it is worth noting that the mass and mean density of such disks are also poorly constrained quantities from an observational viewpoint.
To elucidate the possible effect of the nova outburst on the accretion disk, we considered a suite of models aimed at testing the influence of the different parameters of the system (i.e., mass and velocity of the ejecta, mass, and geometry of the accretion disk; see Table 1).
3.1 Evolution of Model A
Model A describes the interaction between Mejecta = 5.1 × 10−4 M⊙, ejected froma 0.6 M⊙ white dwarf during a nova outburst (with a maximum velocity of the ejecta of 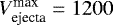 km s−1), and a 2 × 10−5 M⊙ accretion disk (with H∕R = 0.03), subsequently followed by the collision with a 1 M⊙ main sequence companion (see Table 1). Snapshots of the evolution of this model, in terms of density, are shown in Fig. 2. Movies showing the full evolution of this model are available online.
km s−1), and a 2 × 10−5 M⊙ accretion disk (with H∕R = 0.03), subsequently followed by the collision with a 1 M⊙ main sequence companion (see Table 1). Snapshots of the evolution of this model, in terms of density, are shown in Fig. 2. Movies showing the full evolution of this model are available online.
The ejecta hits the disk a few seconds after the beginning of the simulation (Fig. 2, upper panels). The energy released during the collision heats the disk, which achieves a maximum temperature of 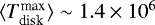 K; only a handful of SPH particles (~20) reach Tmax ~ 1.2 × 107 K. This suggests that nuclear reactions do not play a relevant role in the interaction5. Only a small fraction of the nova ejecta hit the disk (
K; only a handful of SPH particles (~20) reach Tmax ~ 1.2 × 107 K. This suggests that nuclear reactions do not play a relevant role in the interaction5. Only a small fraction of the nova ejecta hit the disk (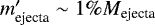 ); the mean kinetic energy,
); the mean kinetic energy, 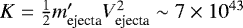 ergs. A crude estimate of the gravitational binding energy of the disk can be obtained from U ~ GMWDMdisk∕rmean, where G is the gravitational constant, MWD is the mass of the underlying white dwarf, and Mdisk and rmean are the mass of the disk and the mean distance between the white dwarf and the disk. Estimates for Model A yield U ~ 6 × 1043 ergs, which are similar to the kinetic energy of the impinging ejecta. In Model A, simulations reveal the total disruption of the disk (middle left panel), which gets totally swept up and mixed with the ejecta. However, other models with different choices for the geometry (H∕R), mass, and velocity of the disk, and mass of the ejecta, may yield different outcomes (see below).
ergs. A crude estimate of the gravitational binding energy of the disk can be obtained from U ~ GMWDMdisk∕rmean, where G is the gravitational constant, MWD is the mass of the underlying white dwarf, and Mdisk and rmean are the mass of the disk and the mean distance between the white dwarf and the disk. Estimates for Model A yield U ~ 6 × 1043 ergs, which are similar to the kinetic energy of the impinging ejecta. In Model A, simulations reveal the total disruption of the disk (middle left panel), which gets totally swept up and mixed with the ejecta. However, other models with different choices for the geometry (H∕R), mass, and velocity of the disk, and mass of the ejecta, may yield different outcomes (see below).
At about t ~ 17 min (middle panels), a mixture of ejecta and disk material impinges on the main sequence companion. The temperature increases slightly in the outermost layers of the secondary, but not enough to spark nuclear reactions. In the collision, a subset of the ejecta/disk particles penetrate through the outer layers of the secondary, reaching a maximum depth of ~ 1.1 × 10−5 M⊙ from the surface. The energy released in the collision drives a moderate expansion of the outer layers of the star (lower panels). Since the secondary overfills its Roche lobe, part of the material incorporated into the main sequence star is later re-accreted by the white dwarf, as soon as mass-transfer resumes and the accretion disk is re-established.
About ~ 4.7 × 10−4 M⊙ (i.e., 88% of the mixture of disk and nova ejecta) leave the binary system in Model A. In contrast, only ~ 2 × 10−5 M⊙ (3.7%; mostly nova ejecta) remain gravitationally bound to the main sequence companion, while ~ 4.6 × 10−5 M⊙ (8.7%) are bound to the white dwarf (see Table 2). A small amount of mass, 2 × 10−7 M⊙, involving only a handful of SPH particles, is expelled from the outer main sequence layers in the interaction with the nova ejecta. Figure 3 shows the time evolution of the mass leaving the binary system in Model A and for all models reported in this paper. The early and sharp increase in mass loss (t ≤ 10 min) results from the interaction between the nova ejecta and the disk, when the latter gets totally swept up and mixed with the former. Most of the ejecta and disk mixture leaves the binary system. The longer-term evolution of the mass loss plot (t > 10 min) reveals that little is expelled from the outer main sequence layers as a result of the impact with the nova ejecta.
To test the feasibility of these results, a higher resolution run with twice the number of particles as Model A (hereafter, Model A hres) was also performed. As shown in Table 2 (see also Fig. 3), both models A and A hres yield similar results, which suggests that the overall number of particles adopted in this paper was appropriate. Movies showing the full evolution of Model Ahres are also available online.
 |
Fig. 2 Cross-sectional slice in the binary orbital plane (XY) showing the density of Model A at various stages of the interaction between the nova ejecta and the accretion disk, subsequently followed by a collision with the main sequence companion. A movie showing the full evolution of this model, modelA-XY.avi, is available online. See also modelA-YZ.avi, for a movie depicting the evolution of the system from a side view (YZ plane). Snapshots and movies were generated by means of the visualization software SPLASH (Price 2007). |
Mass (ejecta plus disk) gravitationally bound to the secondary star, ΔMMS, and to the white dwarf, ΔMWD, and total mass leaving the binary system, ΔMesc, together with their fractions (in %) over the total ejecta plus disk masses, after collision with the nova ejecta. The parameter Δ MMS,lost is the mass lost by the main sequence star in the interaction with the nova ejecta.
 |
Fig. 3 Time evolution of the mass leaving the binary system for the models reported in this paper. |
3.2 Effect of the mass of the nova ejecta
We considered two values for the mass of the nova ejecta, Mejecta, to analyze the effect of this parameter. As shown in Table 2, a comparison between our fiducial Model A (characterized by Mejecta = 5.1 × 10−4 M⊙) and Model E (with Mejecta = 1.6 × 10−3 M⊙) reveals that,as expected, increasing the mass of the ejecta translates into larger masses gravitationally bound to the white dwarf (Δ MWD) and to the main sequence companion (ΔMMS), at the end of the simulations. In turn, the total amount of mass lost from the system, Δ Mesc, also increases. We found an identical pattern when comparing Models B and F (for which a maximum velocity of the nova ejecta of 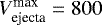 km s−1 was assumed) and Models G and H (for which
km s−1 was assumed) and Models G and H (for which 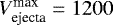 km s−1, but is twice the mass of the disk compared to Model A). There is one exception to this: whereas the accretion disk gets fully disrupted in Models A, B, E, F, and H, the disk survives the collision with the ejecta in Model G (Fig. 4). This can be understood from the ratios Mejecta/Mdisk adopted in the various models; the lowest value, Mejecta/Mdisk ~ 13, corresponds to Model G, which suggests that only disks with masses much lower than the ejecta undergo total disruption. The fact that the disk gets disrupted in Model H but not in Model G affects the dynamics of the system and results in a moderately larger amount of mass that remains bound to the white dwarf in the former. Except for this peculiar case, the fraction of the overall massavailable (i.e., ejecta plus disk) that escapes the binary system (or remains bound to the main sequence or to the white dwarf) does not depend much on the choice of the mass of the nova ejecta (see Table 2). We note, indeed, that the fraction of mass leaving the system increases from 59% to 89%, while the fraction that remains bound to the white dwarf drops from 31% to 8%, when comparing Models G and H. As reported for Model A, small amounts of mass, up to 1.4 × 10−6 M⊙, involving only a few SPH particles, are expelled (if any) from the outer main sequence layers in the interaction with the nova ejecta, and values increase for larger nova ejected masses.
km s−1, but is twice the mass of the disk compared to Model A). There is one exception to this: whereas the accretion disk gets fully disrupted in Models A, B, E, F, and H, the disk survives the collision with the ejecta in Model G (Fig. 4). This can be understood from the ratios Mejecta/Mdisk adopted in the various models; the lowest value, Mejecta/Mdisk ~ 13, corresponds to Model G, which suggests that only disks with masses much lower than the ejecta undergo total disruption. The fact that the disk gets disrupted in Model H but not in Model G affects the dynamics of the system and results in a moderately larger amount of mass that remains bound to the white dwarf in the former. Except for this peculiar case, the fraction of the overall massavailable (i.e., ejecta plus disk) that escapes the binary system (or remains bound to the main sequence or to the white dwarf) does not depend much on the choice of the mass of the nova ejecta (see Table 2). We note, indeed, that the fraction of mass leaving the system increases from 59% to 89%, while the fraction that remains bound to the white dwarf drops from 31% to 8%, when comparing Models G and H. As reported for Model A, small amounts of mass, up to 1.4 × 10−6 M⊙, involving only a few SPH particles, are expelled (if any) from the outer main sequence layers in the interaction with the nova ejecta, and values increase for larger nova ejected masses.
 |
Fig. 4 Same as Fig. 2, but for density plots corresponding to Model G at different times. In this model the accretion disk does not get totally swept up in the impact with the nova ejecta. Snapshots and movies were generated by means of the visualization software SPLASH (Price 2007). |
3.3 Effect of the velocity of the ejecta
Three values for the maximum velocity of the ejecta, 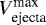 , representative of classical nova systems (Gehrz et al. 1998), were adopted to analyze the influence of this parameter as follows: 800 km s−1, 1200 km s−1, and 3000 km s−1. Comparison between Models A and B reveals that an increase in the velocity of the ejecta yields larger ejected masses from the binary system, while reducing the amount of mass that remains gravitationally bound, either to the white dwarf or to the main sequence companion.
, representative of classical nova systems (Gehrz et al. 1998), were adopted to analyze the influence of this parameter as follows: 800 km s−1, 1200 km s−1, and 3000 km s−1. Comparison between Models A and B reveals that an increase in the velocity of the ejecta yields larger ejected masses from the binary system, while reducing the amount of mass that remains gravitationally bound, either to the white dwarf or to the main sequence companion.
The fraction of nova ejecta plus disk mass that escapes the binary system (or remains bound to the main sequence or to the white dwarf) follows exactly the same trend. However, in sharp contrast to the results reported in Sect. 3.2, the specific fractions depend significantly on the values adopted for the velocity of the ejecta (Table 2). For instance, the fraction of mass leaving the system increases from 60% to 89%, while the fractions that remain bound to the white dwarf or to the main sequence drop from 30% to 8%, and from 10% to 4%, respectively, when comparing Models D and I. Similar patterns are observed regardless of whether the disk gets disrupted or not (see, e.g., Models C, D and I, Models E and F, and Models G and J, for which different combinations of masses of the ejecta and disk have been adopted). Higher velocities for the nova ejecta drive, as expected,larger (but always tiny) amounts of mass lost by the main sequence companion; a maximum value of 2.4 × 10−6 M⊙ is achieved in Model I.
It is worth mentioning that while the accretion disk is disrupted in Models A, B, E, and F, it survives the impact with the ejecta in all models characterized by moderately low Mejecta/Mdisk ratios (e.g., Models C, D, I, and G, with Mejecta∕Mdisk ranging between 5.5 and 13). We note, however, that Model J, characterized by Mejecta∕Mdisk = 13, results in disk disruption too. This is caused by the large kinetic energy and momentum carried by the impinging ejecta, which in this particular model expands with a maximum velocity of 3000 km s−1.
3.4 Effect of the mass of the accretion disk
The mass of the accretion disk that orbits around the white dwarf is a poorly constrained quantity. Accordingly, we considered a series of disks with different masses, constructed in the framework of the Shakura & Sunyaev model. A comparison between Models A and C, for which two different values of the mass of the disk, Mdisk, were adopted (2 × 10−5 and 10−4 M⊙, respectively) reveals, as mentioned before, that the lower the mass of the disk, the larger the probability of disruption. Hence, while the disk in Model A gets disrupted by the nova blast, it survives the impact in Model C. The same pattern is found for Models B and D, which are characterized by a lower expansion velocity of the nova ejecta (800 km s−1), and Models K and G, for which a different geometry of the disk, with a larger H∕R ratio, was assumed. Increasing the mass of the accretion disk reduces in turn the amount of mass lost by the binary system, and conversely increases the amount of mass that remains gravitationally bound to the white dwarf and main sequence companion6.
The fraction of nova ejecta plus disk mass that escapes the binary system (or remains bound to the main sequence or to the white dwarf) follows the same pattern, and values show a clear dependence on the accretion disk mass.
3.5 Effect of H/R
So far, we analyzed the interaction of the nova ejecta with accretion disks characterized by a height to radius ratio of H∕R = 0.03. However, observations increasingly support a dispersion in the value of H∕R, within the range 0.03–0.1 (see Maccarone 2014; Shafter & Misselt 2006; Knigge et al. 2000). The influence of this parameter on the dynamical properties of the system was analyzed by means of Model K, in which a ratio of H∕R = 0.06 was adopted for the accretion disk. Comparison between Model K and our fiducial Model A suggests that an increase in H∕R has a similar effect as a reduction in the velocity of the expanding nova ejecta: here, a larger H∕R results in an increase of the effective impact cross-section between disk and ejecta. This decelerates a larger portion of the ejecta, and as a result, the amount of mass gravitationally bound to the white dwarf and main sequence companion increases, while the overall masslost from the binary system decreases. The fraction of nova ejecta plus disk mass that escapes the binary system (or remains bound to the main sequence or to the white dwarf) follows exactly the same trend. A thorough comparison between Models A and K reveals that the specific fractions depend significantly on the adopted H∕R ratio (Table 2).
4 Chemical pollution of the secondary star
One of the possible outcomes of the dynamical interaction between the nova ejecta and main sequence companion is the pollution of the secondary, enhancing the metal content of its outer layers. The degree of contamination induced by the impact with the nova ejecta can be estimated from the overall number of particles gravitationally bound to the main sequence star (see, e.g., Lombardi et al. 2006). But this is by no means straightforward. On the one hand, the models presented in this work follow the evolution of the binary system for about 3000 s, which corresponds to ~ 0.1 Porb. At this stage, a large number of particles gravitationally bound to the secondary are still orbiting around in a corona that surrounds the star. Even though such particles eventually fall into the star, it is difficult to anticipate how deep these particles penetrate into its envelope.Self-consistent calculations of these advanced stages would require a prohibitively intense computational effort for many orbital periods to compute the corresponding infalling trajectories. And even if such numerical simulations were feasible, a detailed account of the chemical profiles of the outer layers of the secondary would require the use of more realistic initial models for the main sequence star (see, e.g., Sills & Lombardi 1997) and the inclusion of important physical mechanisms that would be operating simultaneously (e.g., chemical diffusion and convection). This is clearly out of the scope of thepresent paper. However, to illustrate the expected levels of chemical pollution, we provide some crude estimates of the compositional changes in the outer layers of the secondary at different mass depths, for Model A. Assuming that all the gravitationally bound particles still in orbit are incorporated and mixed with the outer 10−6 M⊙ of the main sequence companion, a mean metallicity of Z ~ 0.18 is expected at those layers, in the hemisphere hit by the nova ejecta. The expected level of contamination obviously decreases when considering deeper layers (i.e., Z ~ 0.036 for 10−5 M⊙, and Z ~ 0.019 for 10−4 M⊙).
A final issue involves the relevance of these results in the framework of systems with low-mass secondaries (M ≤ 2 M⊙), in which the presence of a convective envelope may wash out any trace of chemical pollution induced by the impact with the nova ejecta. This aspect was addressed by Marks & Sarna (1998) and Marks et al. (1997), who analyzed the effect of re-accretion of material ejected during nova outbursts on the chemical evolution of the secondary, for binary systems with similar orbital periods and masses to those reported in this manuscript. The low-mass main sequence stars were evolved taking into account all major processes that may affect their surface composition as follows: nuclear reactions, mass loss, convection, thermohaline mixing, and contamination with the nova ejecta. Using a control model, where no nova ejecta was incorporated into the secondary, they reported elemental (e.g., C and N) and isotopic differences (12 C/13C, 14 N/15N, 16 O/17O) on the surface layers of the secondary stars induced by the impact with the ejecta. Therefore, one may expect some effect on the next nova cycle, once mass transfer onto the white dwarf component resumes, even in binaries with low-mass secondaries. This aspect, however, deserves in-depth analysis.
5 Conclusions
We computed 11 3D SPH simulations of the interaction between the nova ejecta, the accretion disk, and the stellar companion aimed at testing the influence of the different parameters (i.e., mass and velocity of the ejecta and the mass and geometry of the accretion disk) on the dynamical and chemical properties of the binary system. The main conclusions reached in this work are summarized as follows:
-
we investigated the conditions leading to the disruption of the accretion disk that orbits the white dwarf star. In 7 out of the 11models computed, the disk gets fully disrupted and swept up. In all these models, the disks are characterized by masses much smaller than that of the ejecta. Our simulations show that in models with V-shaped disks with height-to-radius ratios of H∕R = 0.03 and Mejecta/Mdisk ≤ 5.5 (Mejecta/Mdisk ≤ 13, for H∕R = 0.06) the disk survives the impact with the nova blast;
-
small amounts of mass, up to 1.4 × 10−6 M⊙ are expelled from the outer main sequence layers in the interaction with the nova ejecta. No ejection is reported from 2 out of the 11 models computed;
-
an increase of the mass of the nova ejecta yields, in general, larger amounts of mass lost by the binary system, and larger masses gravitationally bound to the white dwarf and to the main sequence companion. The fraction of the overall mass available (i.e., ejecta plus disk) that escapes the binary system (or remains bound to the main sequence or to thewhite dwarf) does not depend much on the choice of the mass of the nova ejecta. However, the dynamics of the system is influenced by disk disruption when the increase of the mass of the nova ejecta modifies the stability of the disk, thereby moderately affecting the distribution of masses that remain gravitationally bound to the white dwarf or to the main sequence along with the amount of mass lost from the system. For instance, when comparing Models G (disk partially disrupted) and H (disk fully disrupted and swept up by the ejecta), the fraction of mass that leaves the binary system increases from 59% to 89%, while the fraction that remains bound to the white dwarf drops from 31% to 8%;
-
an increase in the velocity of the ejecta results in larger ejected masses from the binary system, while reducing the amount of mass that remains gravitationally bound, either to the white dwarf or to the main sequence, regardless of whether the disk gets disrupted or not. This results from the larger kinetic energy and momentum carried by the impinging ejecta when its velocity is increased. The fraction of nova ejecta plus disk mass that escapes the binary system (or remains bound to the main sequence or to the white dwarf) follows exactly the same trend. The specific fractions depend much on the values adopted for the velocity of the ejecta. The large kinetic energy and momentum carried by the ejecta in models with
 km s−1
can lead to disk disruption even for models characterized by relatively low Mejecta∕Mdisk
ratios, as in Model J;
km s−1
can lead to disk disruption even for models characterized by relatively low Mejecta∕Mdisk
ratios, as in Model J; -
an increase of the mass of the accretion disk reduces the amount of mass lost by the binary system, and conversely, increases the amount of mass gravitationally bound to the white dwarf and to the main sequence companion. For instance, when comparing Models A (Mdisk = 2.04 × 10−5 M⊙) and C (Mdisk = 9.28 × 10−5 M⊙), the fraction of mass that leaves the binary system decreases from 88% to 67%, while the fractions that remain bound to the white dwarf and main sequence star increase from 9% to 25% and 4% to 8%, respectively. This results from the smaller kinetic energy and momentum transferred to the disk particles per unit mass when the mass of the disk is increased, which in turn reduces the probability of disk disruption by the nova blast;
-
an increase in the height-to-radius ratio of the disk has similar effects to a reduction of the velocity of the expanding ejecta: the larger effective impact cross-section between disk and ejecta slows down a larger fraction of the nova ejecta, which in turn increases the mass gravitationally bound to the white dwarf and main sequence star, while reducing the overall mass lost by the binary system;
-
a certain level of chemical contamination of the stellar secondary is induced by the impact with the nova ejecta; a mean metallicity of Z ~ 0.18 is estimated at the outer 10−6 M⊙ layers in the hemisphere hit by the ejecta, for Model A. This may have potential effects on the next nova cycle.
Since the problem is intrinsically 3D we cannot rely on 2D or axisymmetric approximations. A possible way to increase the resolution is to use a conical 3D computational domain, in which the point-like white dwarf is located at the vertex of the cone, so that only a fraction of the ejecta and disk, together with the full stellar secondary, are taken into account. The expected gain in resolution could reach a factor of ~2, having ~10 more particles in the conical computational domain, with respect to the simulations reported in this paper.
Movies
modelA_hres-YZ Access here
modelA_hres-XY Access here
Movies of Fig. 2: modelA-YZ Access here
Movies of Fig. 2: modelA-XY Access here
Movies of Fig. 4: modelG-YZ Access here
Movies of Fig. 4: modelG-XY Access here
Acknowledgements
The authors would like to thank Ruben M. Cabezón, for many fruitful discussions and exchanges. This work has been partially supported by the Spanish MINECO grant AYA2014-59084-P, and by the AGAUR/Generalitat de Catalunya grant SGR0038/2014. SM is grateful to the South African National Research Foundation (NRF) for a research grant. This paper is dedicated to Enrique García-Berro, who passed away in a tragic accident during the revision of the manuscript.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, Science, 329, 817 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2014, Science, 345, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Amari, S., 2002, NewAR, 46, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Amari, S., Gao, X., Nittler, L. R., et al. 2001, ApJ, 551, 1065 [Google Scholar]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., 1995, J. Comput. Phys., 121, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W. 1959, ApJ, 130, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., & Orlando, S. 2010, ApJ, 720, L195 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A., & Rawlings, M. C. 2008, in Classical Novae, 2nd edn., eds. M. F. Bode, & A. Evans (Cambridge, UK: Cambridge Univ. Press), 308 [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 2002, Accretion Power in Astrophysics, 3rd edn. (Cambridge, UK: Cambridge Univ. Press) [Google Scholar]
- García-Senz, D., Badenes, C., & Serichol, N. 2012, ApJ, 745, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrz, R. 2008, in Classical Novae, 2nd edn., eds. M. F. Bode, & A. Evans (Cambridge, UK: Cambridge Univ. Press), 167 [CrossRef] [Google Scholar]
- Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Giannone, P., & Weigert, A. 1967, Z. Astrophys., 67, 41 [NASA ADS] [Google Scholar]
- Gurevitch, L. E., & Lebedinsky, A. I., 1957, in Non-Stable Stars, eds. G. H. Herbig (Cambridge, UK: Cambridge Univ. Press), 77 [Google Scholar]
- Hernanz, M., & Sala, G. 2002, Science, 298, 393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- José, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton, FL: CRC/Taylor and Francis) [CrossRef] [Google Scholar]
- José, J., & Hernanz, M. 1998, ApJ, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
- José, J., & Shore, S. 2008, in Classical Novae, 2nd edn., eds. M. F. Bode, & A. Evans (Cambridge, UK: Cambridge Univ. Press), 121 [CrossRef] [Google Scholar]
- Joy, A. H. 1954, ApJ, 120, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Long, K. S., Hoard, D. W., Szkody, P., & Dhillon, V. S., 2000, ApJ, 539, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., 1964, ApJ, 139, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Leibowitz, E. M., Mendelson, H., Mashal, E., Prialnik, D., & Seitter, W. C. 1992, ApJ, 385, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, Jr., J. C., Proulx, Z. F., Dooley, K. L., et al. 2006, ApJ, 640, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Maccarone, T. J. 2014, Space Sci. Rev., 183, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, P. B., & Sarna, M. J. 1998, MNRAS, 301, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, P. B., Sarna, M. J., & Prialnik, D. 1997, MNRAS, 290, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J. 1997, J. Comput. Phys., 136, 298 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Price, D. J. 2007, Publ. Astron. Soc. Aust., 24, 159 [Google Scholar]
- Puebla, R. E., Diaz, M. P., & Hubeny, I. 2007, AJ, 134, 1923 [Google Scholar]
- Retter, A. 2003, in Symbiotic Stars Probing Stellar Evolution, ASP Conf. Proc., 303. eds. R. L. M. Corradi, R. Mikolajewska, & T. J. Mahoney, (San Francisco: ASP), 232 [Google Scholar]
- Retter, A., Leibowitz, E. M., & Kovo-Kariti, O. 1998, MNRAS, 293, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., Leibowitz, E. M., & Ofek, E. O. 1997, MNRAS, 286, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, W. K. 1968, ApJ, 152, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Sanford, R. F. 1949, ApJ, 109, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Schatzman, E. 1949, Ann. Astrophys., 12, 281 [NASA ADS] [Google Scholar]
- Schatzman, E. 1951, Ann. Astrophys., 14, 294 [NASA ADS] [Google Scholar]
- Shafter, A. W., & Misselt, K. A. 2006, ApJ, 644, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N., & Sunyaev, R. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shore, S. N., De Gennaro Aquino, I., Schwarz, G. J., et al. 2013, A&A, 553, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shore, S. N., Starrfield, S., Gonzalez-Riestra, R., Hauschildt, P. H., & Sonneborn, G. 1994, Nature, 369, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Sills, A., & Lombardi, J. C. 1997, ApJ, 484, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, D. R., Harvey, D., Patterson, J., & Vanmunster, T. 1997, PASP, 109, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. M. 1969, ApJ, 156, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, W. R. 2008, in Classical Novae, 2nd edn., eds. M. F. Bode, & A. Evans (Cambridge, UK: Cambridge Univ. Press), 77 [CrossRef] [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, W. R. 2016, PASP, 128, 051001 [NASA ADS] [CrossRef] [Google Scholar]
- Tappert, C., Schmidtobreick, L., Vogt, N., & Ederoclite, A. 2013, MNRAS, 436, 2412 [NASA ADS] [CrossRef] [Google Scholar]
- Tatischeff, V., & Hernanz, M. 2007, ApJ, 663, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 2003, Cataclysmic variable Stars (Cambridge, UK: Cambridge Univ. Press) [Google Scholar]
- White S. D. M. 1996, in Cosmology and Large-Scale Structure, eds. R. Schaefer, J. Silk, M. Spiro, & J. Zinn-Justin (Amsterdam: Elsevier), 349 [Google Scholar]
We note, however, that a similar scenario, the interaction between the material ejected in a type Ia supernova and the companion star, has been addressed in a number of papers (see, e.g., Marietta et al. 2000; García-Senz et al. 2012).
Diffusive shock acceleration of electrons and protons, with a maximum energy of a few TeV, was predicted by Tatischeff & Hernanz (2007) in the framework of the 2006 outburst of the recurrent nova RS Ophiuchi. See also Shore et al. (2013) for an explanation of the origin of X-ray emission in Nova Mon 2012 based on internal shocks driven by the collision of filaments that freeze out during expansion.
The presence of a disk, and its key role in the simulations reported in this paper, does not allow us to rely on SPH axisymmetric codes to increase the resolution of the models, in contrast to other astrophysical scenarios such as type Ia supernovae (see, e.g., García-Senz et al. 2012).
See, however, Drake & Orlando (2010), for simulations of recurrent nova systems leading always to full disruption of the accretion disks.
All Tables
Mass (ejecta plus disk) gravitationally bound to the secondary star, ΔMMS, and to the white dwarf, ΔMWD, and total mass leaving the binary system, ΔMesc, together with their fractions (in %) over the total ejecta plus disk masses, after collision with the nova ejecta. The parameter Δ MMS,lost is the mass lost by the main sequence star in the interaction with the nova ejecta.
All Figures
 |
Fig. 1 Initialdensity profiles for the outer main sequence layers (after relaxation) and the accretion disk. |
| In the text | |
 |
Fig. 2 Cross-sectional slice in the binary orbital plane (XY) showing the density of Model A at various stages of the interaction between the nova ejecta and the accretion disk, subsequently followed by a collision with the main sequence companion. A movie showing the full evolution of this model, modelA-XY.avi, is available online. See also modelA-YZ.avi, for a movie depicting the evolution of the system from a side view (YZ plane). Snapshots and movies were generated by means of the visualization software SPLASH (Price 2007). |
| In the text | |
 |
Fig. 3 Time evolution of the mass leaving the binary system for the models reported in this paper. |
| In the text | |
 |
Fig. 4 Same as Fig. 2, but for density plots corresponding to Model G at different times. In this model the accretion disk does not get totally swept up in the impact with the nova ejecta. Snapshots and movies were generated by means of the visualization software SPLASH (Price 2007). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


