| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732109 | |
| Published online | 27 April 2018 | |
NELIOTA: First temperature measurement of lunar impact flashes
1
IAASARS, National Observatory of Athens,
15236
Penteli, Greece
e-mail: bonanos@astro.noa.gr
2
Scientific Support Office, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC),
2201 AZ
Noordwijk, The Netherlands
3
Chair of Astronautics, Technical University of Munich,
85748
Garching, Germany
4
Department of Physics, University of Crete,
71003
Heraklion, Greece
Received:
16
October
2017
Accepted:
2
January
2018
We report the first scientific results from the NELIOTA (NEO Lunar Impacts and Optical TrAnsients) project, which has recently begun lunar monitoring observations with the 1.2-m Kryoneri telescope. NELIOTA aims to detect faint impact flashes produced by near-Earth meteoroids and asteroids and thereby help constrain the size-frequency distribution of near-Earth objects in the decimeter to meter range. The NELIOTA setup, consisting of two fast-frame cameras observing simultaneously in the R and I bands, enables – for the first time – direct analytical calculation of the flash temperatures. We present the first ten flashes detected, for which we find temperatures in the range ~1600 to 3100 K, in agreement with theoretical values. Two of these flashes were detected on multiple frames in both filters and therefore yield the first measurements of the temperature drop for lunar flashes. In addition, we compute the impactor masses, which range between ~100 g and ~50 kg.
Key words: Moon / meteorites, meteors, meteoroids / surveys
© ESO 2018
1 Introduction
The estimation of the impact flux of near-Earth objects (NEOs) is important not only for the protection of human civilization, but also for the protection of space assets, which could be damaged or at least perturbed even by small, mm- to cm-size impactors. A recent example that reveals this necessity was the Chelyabinsk event in 2013, which was caused by a 20-m impactor and member of the NEO population. This collision was responsible for 1500 injured civilians and a few thousand damaged human assets in the area (Popova et al. 2013). The precise flux density of objects in this size range is not yet well known. A promising method for constraining NEO flux densities in this size range is via the detection of impact flashes on the Moon.
A plethora of laboratory impact experiments have been conducted over the last 40 years initiated primarily to study spacecraft shielding, using mainly metallic materials (Holsapple et al. 2002, and references therein). Apart from these technical experiments, hypervelocity impacts (impact speeds v > 1 km s−1) are also studied at small scales. One important goal is to extrapolate the results to larger size and velocity scales, towards the understanding of the collisions on planetary surfaces by asteroids and comets or even among the small bodies, for example the inter-asteroid collisions in the Main Belt. It has been clearly shown that several impactor parameters, such as the impactor’s size, density, velocity and impact angle affect the collision outcome, for example, the crater formation and the size and speed of the ejecta plume (Ryan & Melosh 1998; Housen et al. 1999; Housen & Holsapple 2003, 2011; Avdellidou et al. 2016, 2017). Observations have shown that, for example, highly porous objects tend to be destroyed tens of km above the surface of the Earth, as was the case with 2008 TC3 (Jenniskens et al. 2009; Bischoff et al. 2010) and the Benesov bolide (Borovicka et al. 1998).
Telescopic surveys, such as the Catalina Sky Survey (Drake et al. 2009) and Pan-STARRS (Chambers et al. 2016), are continuously discovering new objects, which are verified by follow-up observations from observers all around the world. Space missions such as WISE and the Spitzer Space Telescope, along with spectroscopic observations, provide valuable data to start characterizing the physical properties of NEOs, such as their diameters, albedos, and spectral types. Over 16 300 NEOs have been identified (HORIZONS System 2016, as of August 2017) of which only 1142 have known diameters d (Delbo’ et al. 2017), with the smallest ones being less than ten meters. The NEO population consists of small bodies delivered from the source regions of the Main Belt via mean motion and secular resonances with the planets (Bottke et al. 2000, 2002). Currently, the completeness of the observed sample is at d ~ 1 km, as surveys are not able to massively detect NEOs that are smaller than a few tens of meters in diameter. In fact, the very small bodies are usually detected when their position on their orbit comes at close proximity to Earth. For example, the 4-m near-Earth asteroid 2008 TC3 was discovered only 19 h prior to its impact on Earth and immediate radar observations provided its size (Jenniskens et al. 2009).
During the last decades, advances have been made by several groups leading to a better estimation of the sizes of small impactors and their flux on the Moon, correcting for the Earth as a target. This was done by calculating the luminous efficiency η of the detected flashes, which is defined as the fraction of the impactor’s kinetic energy (KE) that is emitted as light at visible wavelengths (L), that is, L= η × KE. Great uncertainties occur during these calculations when the events originate from sporadic NEOs (those not associated to meteor streams), since the collisional velocity of the meteoroids on the Moon is unknown. Several authors adopt average impact speeds for the lunar surface spanning a wide range between 16 and 24 km s−1 (Ortiz et al. 2000, 2002; Suggs et al. 2014). Uncertainties in the speed estimation lead to uncertainties of the luminous efficiency value η. The current estimations of the luminous efficiency of the lunar impactors range over an order of magnitude resulting in weakly constrained masses. However, when the impact events are linked to a known meteoroid stream, this unknown parameter can be constrained (e.g., Bellot Rubio et al. 2000) yielding masses that can be appended to the current known impactors’ size distribution (Harris et al. 2015) and can also be used for further studies.
Apart from the NEO flux and size distribution, the lunar surface serves as a large-scale impact laboratory to study the impact events. The term “large-scale” refers both to the impactor sizes and speeds when comparing them to laboratory-based hypervelocity experiments, where the sizes of impactors are typically a few mm and the speeds below 8 km s−1 (e.g., Burchell et al. 1999). The collisions of NEOs on the Moon give rise to several phenomena that can be detected and further studied, such as impact cratering (Speyerer et al. 2016), seismic waves (Oberst & Nakamura 1991) and the enhancement of the lunar atmosphere with sodium (Verani et al. 1998; Smith et al. 1999).
The light flash produced by an impact depends on several parameters, including the mass and speed of the impactor. Even when the mass and speed are known, the different combinations of mineralogical compositions of both the target and impactor will affect the result. Pioneering laboratory experiments were conducted more than 40 years ago, using dust accelerators and photomultipliers with filters at several wavelengths, allowing the estimation of the plasma temperature (Eichhorn 1975, 1976; Burchell et al. 1996a,b). Therefore the study of impact flashes could provide insight to the complex problem of energy partitioning during an impact event, when the majority of physical parameters are constrained or measured (e.g., mass and speed of the impactor, crater size, ejecta speed).
The NELIOTA project1 (Xilouris et al., in prep.) provides the first lunar impact flash observations performed simultaneously in more than one wavelength band. In Sect. 2 we present the instrumentation, observation strategy and the first ten lunar impact flashes from NELIOTA, providing their durations and magnitudes. In Sect. 3, we focus on the first ever measurement of impact flash temperatures using our two-colour observation technique, while in Sect. 4 we present a new approach to estimate the impactors’ masses. The discussion and conclusions are given in Sect. 5.
2 Observations
NELIOTA has upgraded the 1.2-m Kryoneri telescope2 and converted it to a prime-focus instrument with a focal ratio of f/2.8 for lunar monitoring observations. The telescope has been equipped with two identical Andor Zyla scientific CMOS cameras, which are installed at the prime focus and are thermoelectrically cooled to 0°. A dichroic beam-splitter with a cut-off at 730 nm directs the light onto the two cameras (2560 × 2160 pixels2, 6.48 μm per pixel), which observe in visible and near-infrared wavelengths using R and I Cousin filters, respectively. The maximum transmittance of each filter is at λR = 641 nm and λI = 798 nm, corresponding to a maximum quantum efficiency of ~50% and ~40%, respectively. The field-of-view of this setup is 16.0′× 14.4′. We use the 2 × 2 binning mode, which yields a pixel-scale of 0.8″, as it best matches the 1.2–1.5″ average seeing and results in a lower volume of data. Currently, the NELIOTA system has the largest telescope with the most evolved configuration that performs dedicated monitoring of the Moon, in search of faint lunar impact flashes.
Observations are conducted on the dark side of the Moon, between lunar phases ~0.1 and 0.4. The maximum lunar phase during which observations can be obtained is set by the strength of the glare coming from the sun-lit side of the Moon. The observations begin/end ~20 min after/beforethe sunset/sunrise and last for as long as the Moon is above an altitude of 20°. The altitude limit is set due to limitations from the dome slit. The cameras simultaneously record at a frame rate of 30 frames-per-second or every 33 ms, in 2 × 2 binning mode. The exposure time of each frame is 23 ms, followed by a read-out time of 10 ms. The observations are split into “chunks” that are 15 min in duration. At the end of each chunk, a standard star is observed for calibration purposes. The standard stars have been carefully selected (a) to be as close as possible to the altitude of the Moon and (b) to have similar color indices to the expected colors of the flashes (i.e., 0.3 < R − I < 1.5 mag). Flat-field images are taken on the sky before or after the lunar observations, while dark frames are obtained directly after the end of the observations. The duration of the observations varies between ~25 min and ~4.5 h, depending on the lunar phase and the time of year.
The novelty of the NELIOTA instrumentation setup is that it simultaneously acquires data from two detectors and at two different wavelengths. This setup enables the validation of a flash from a single telescope and site, since a real event that is bright enough will be detected by both cameras at the same position and at the same time, whereas cosmic ray artefacts will only be detected by one camera at any given position and time. Although satellites are also common artefacts, they are typically recorded as streaks. Satellites moving at low enough speeds so as not to show up as streaks in our 23-ms exposure time have to be far away – assuming, in the worst case, an object with a perigee of 300 km, the apogee has to be at least at 17 500 km to result in an apparent movement of less than 1 pixel per 23 ms. At this distance, an object with a reflectivity of 0.5 would need to be at least 2 m in size to be detected as a magnitude-11 flash. Geosynchronous satellites could also produce artefacts due to reflection of sunlight off their solar panels. However, since their positions are well known and clustered around a declination of approximately zero, they pose no major concern as artefacts, as they can be ruled out by using available catalogs of geosynchronous satellite positions.
This paper presents and analyzes the first ten flashes that were validated during the testing phase and the first months of the NELIOTA campaign, from February to July 2017. These flashes originate from sporadic NEOs. We checked various orbital catalogs of satellites and could not find any objects in front of the Moon at the times of the detected flashes. We note that the synchronization of the cameras during the frame acquisition for these flashes is better than 6 ms. All validated flashes are made available on the NELIOTA website within 24 h of the observations.
Photometry
The data reduction is performed automatically by the NELIOTA pipeline (described in Xilouris et al., in prep.) using the median images of the respective calibration files (flat and dark images). These master-images are used to calibrate the data of the Moon as well as those of the standard stars. The pipeline searches for flashes on the images, after computing and subtracting a running, weighted average image, which removes the lunar background.
Due to the nonuniform background around a flash, which is caused by surface features of the Moon (e.g., craters, maria) and earthshine, we performed photometry of the flashes on background-subtracted images. We created these images by subtracting a median lunar image based on the five frames before and five frames after the event. Aperture photometry with the AIP4WIN software (Berry & Burnell 2000) was then performed for both the flashes and standard stars observed nearest in time for each flash. Optimal apertures corresponding to the maximum in the signal-to-noise ratio (S/N) of the flux measurement were used for the flashes to avoid adding noise from the subtracted background, while large apertures were used for the standards. Since the standard stars are observed at approximately the same airmass as the lunar surface, we can compute the flash magnitudes in each filter as:
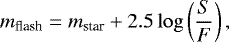 (1)
(1)
where mstar and mflash are the calibrated magnitude of the standard star and the magnitude of the flash, respectively, and S and F are the fluxes of the star and flash for the same integration time. All photometric measurements and error determinations were independently computed using the IRAF3 apphot package and were found to agree within errors with the results from AIP4WIN.
Table 1 presents the date and universal time at the start of the observation for each impact flash detection, its R and I-band magnitude and error, the durationrecorded in I, as well as the temperature and mass measurements are described in the following sections. The flash durations are estimated by multiplying the 33-ms frame rate by the number of frames the flash was detected on and are thus upper limitsto the real flash duration. The durations range between 33 and 165 ms, in agreement with previously reported values (e.g., Yanagisawa & Kisaichi 2002). We note that Flashes 2, 6, 7, and 10 were detected over multiple, consecutive frames. Flashes 2 and 10 are the brightest flashes in the current dataset and had simultaneous detections in both bands in consecutive frames. They are used below to measure the temperature evolution of the flashes.
3 Temperature estimation of the impact flashes
The NELIOTA observations provide the first observational evidence for the temperature of impact flashes. Since we measure the emitted flux density in two different filters (R and I), we can determine the flash temperature by comparing the intensities in the two wavelength bands. Assuming black-body emission (Eichhorn 1975; Burchell et al. 1996b; Ernst & Schultz 2004; Suggs et al. 2014), a given temperature will result in a specific ratio between the measured intensities in the R and I-bands.
The ratio of the energies E1∕E2 released in two different wavelengths depends only on the temperature T. Here we present an analytical method for calculating the temperatures of the NELIOTA flashes. The Planck formula is given by:
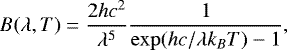 (2)
(2)
where h = 6.62 × 10−34 kg m2 s−1 is the Planck constant, c = 3 × 108 m s−1 the speed of light, kB = 1.38 × 10−23 kg m2 s−2 K−1 the Boltzmann constant, T and λ the temperature of the flash and the wavelength of the photons, respectively. Dividing the Planck formula with the energy E = hc∕λ per photon, we obtain the photon radiance per wavelength LP(λ, T):
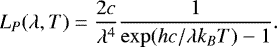 (3)
(3)
Equation (3) is now linked to the absolute flux, fλ, of the flash as:
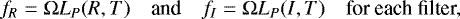 (4)
(4)
where Ω is a constant. Since the observations are performed simultaneously at two different wavelengths, R and I, we measure the two instrumental fluxes for the flash (FR and FI) and for the standard star (SR and SI ). These measured fluxes are linked to theabsolute ones (fR, fI and sR, sI) with the factors ξR and ξI, which depend on the instrument and atmospheric transmission. Therefore, for each λ we get:
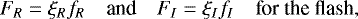 (5)
(5)
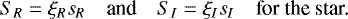 (6)
(6)
Using the color of the standard star (R − I), which is known from the literature, and the ratio of Eq. (6) we obtain the value of the ratio of ξI ∕ξR,
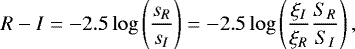 (7)
(7)
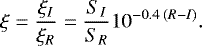 (8)
(8)
The ξ value is now used to find the ratio of the flash flux in both filters fR∕fI using Eq. (5). From the ratio of Eq. (4), substituting the LP (R, T)/LP(I, T) expressions from Eq. (3) and the fR∕fI using Eq. (5), we have:
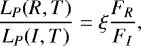 (9)
(9)
and thus thetemperature T becomes theonly unknown parameter, which is calculated numerically using Eq. (9).
For eachevent, we performed 105 Monte Carlo simulations in order to compute the standard deviation of each temperature measurement. At each iteration, random numbers were obtained from the observed flux distribution. The values of fR and fI were extracted from a Gaussian distribution centered at the nominal value of each flux, while adopting the standard deviation that resulted from the photometry. All temperatures and their uncertainties are presented in Table 1.
The multi-frame Flashes 2 and 10 enable us to calculate the drop of the temperature for the first time, as they have simultaneous detections in both bands in consecutive frames. We find a temperature decrease of 1325 ± 104 K for Flash 2 and 20 ± 73 K for Flash 10, that is, between the first detection and the subsequent one 33 ms later. The temperature evolution appears very different for each case and indicates a large difference in the impactor size, as a larger and heavier object will take longer to cool. A larger sample of multi-frame flashes from NELIOTA will allow us to determine the cooling behavior of the flashes and its relation to the impactor mass. Figure 1 illustrates the light curve evolution for the four multi-frame flashes and temperature evolution for Flashes 2 and 10. The data are plotted at the end of the frame read-out of the corresponding measurement. All I-band light curves have a similar slope. Flash 2 presents a steeper decrease in the R-band than in the I-band.
Dates, universal times (UT), magnitudes in each filter, duration recorded in the I-band and listed forthe first entry of each flash, temperatures and impactor masses of the first ten NELIOTA flashes.
4 Mass estimation of the impactors
The first step for the mass estimation is to derive the luminosity L of the impact event. Given that observations up to now were mostly carried out using a single R-band filter, the value of L was not well constrained (Bellot Rubio et al. 2000; Bouley et al. 2012; Ortiz et al. 2015; Madiedo et al. 2015; Suggs et al. 2014, 2017). In this paper, we are able to estimate T for the first time from the two wavelength bands provided by NELIOTA, and therefore can directly derive the luminous energy. Assuming black-body radiation from a spherical area, the bolometric energy is expressed in Joules as:
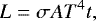 (10)
(10)
where σ =5.67 × 10−8 W m−2 K−4 is the Stefan-Boltzmann constant, A = 2πr2 the emitting area of radius r for a flash near the lunar surface, T the flash temperaturederived above, and t the exposure time of the frame when the photons were integrated. However, this calculation is not straightforward since we do not know the size of the radiating plume. A reasonable assumption is that the flashes are not resolved and thus the area is smaller than the pixel-scale (0.8″), which corresponds to a linear distance of ~1500 m at the center of the Moon’s disk.
The flux of the event at a specific wavelength, fλ, is related to Planck’s law expressed in photon radiance per wavelength (as described in Eqs. (3) and (4)):
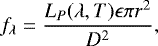 (11)
(11)
where r is the radius of the radiative area, D the Earth–Moon distance at the time of the observation and ϵ the emissivity, which we assume to be 1. The monochromatic flux of the flash fλ can be calculated from:
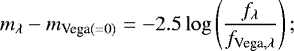 (12)
(12)
therefore Eq. (11) can be solved for the unknown area of radius r. For the error estimation in r, we followed the approach described for the T error estimation. We performed Monte Carlo simulations for the absolute flux estimation using Eq. (12), by randomly selecting flash magnitudes (mλ) from their Gaussian distribution, with centers and standard deviations from the values of Table 1. This procedure was repeated for each filter and returned the absolute fluxes with their 1σ values. In turn, these values were used as input for new Monte Carlo simulations, the calculation of r, and the final value comes from the average of the A-value that was found for each filter. We use a simple average of the two derived areas (one for each filter) for a single event since the differences were small. The luminosity of the flash L, which now can be easily derived from Eq. (10), is just a fraction η (luminous efficiency) of the impactor’s initial kinetic energy KE:
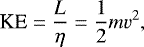 (13)
(13)
where m in kg is the mass of the impactor and v in m s−1 the impact speed. In this work we use the formula derived by Swift et al. (2011) and also used by Suggs et al. (2014):
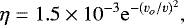 (14)
(14)
where vo = 9.3 km s−1, in order to estimate the luminous efficiencies η1 and η2 for two extreme impact velocities, 16 km s−1 and 24 km s−1 (Steel 1996; McNamara et al. 2004), respectively. Table 1 presents the resulting masses, which range between 0.3 and 55 kg for η1 = 1.07 × 10−3 and 0.1−20 kg for η2 = 1.29 × 10−3.
 |
Fig. 1 Upper panel: light curves of the four multi-frame events in the I (filled circles; solid line) and R (open circles; dotted line) bands. Lower panel: temperature evolution for Flashes 2 and 10. |
5 Discussion and conclusions
NELIOTA is the first lunar monitoring system that enables the direct temperature measurement of observed lunar impact flashes, thanks to its unique twin camera and two-filter observation setup. Until now, the temperature could only be estimated, as it was based on modeling or experimental work. For example, Suggs et al. (2014) used T = 2800 K from Nemtchinov et al. (1998). Cintala (1992) suggested that the flash temperatures, which depend on the type of material on the lunar surface, should range between 1700 K and 3800 K. The agreement of the values we obtain for the first NELIOTA flashes ( ~1600 to 3100 K) with the theoretical range is of great importance for estimating the luminosity of an impact flash and therefore its mass and size.
The estimation of the masses of the impactors is a challenging procedure because many factors contribute to the mass uncertainty. The uncertainties of the observed fluxes contribute to the temperature estimation, which propagates to the calculation of the radiating area A and then to the calculation of the bolometric luminosity L. However, the parameter that has the most important effect for the mass estimation is the luminous efficiency. Luminous efficiencies derived from laboratory experiments (Ernst & Schultz 2005) tend to be smaller by a few orders of magnitude compared tothe ones derived from observations. Previous studies have proposed various values for the luminous efficiency, for example, η ~ 2 × 10−3 from observations of lunar Leonids (Bellot Rubio et al. 2000). While we compute η from Eq. (14) to be ~ 1.1–1.3 × 10−3, other extreme values have been used for the sporadic impactor population. Specifically, when values in the range 10−3 < η < 10−4 are used, the mass of the same impactor can differ by an order of magnitude, even larger than the one we calculate here. Since large uncertainties exist in the calculation of the mass due to the unknown impact velocity, any estimation of the size will also be uncertain. Despite these uncertainies, our mass estimates (100 g to 55 kg) are at least an order of magnitude higher than the values (0.4 g to 3.5 kg) reported by Suggs et al. (2014).
The impactors can be either asteroidal or cometary in origin, implying a difference in the density. Even if we consider the scenario that the bodies are near-earth asteroids, their densities can span a large range. Bulk densities of asteroids differ according to their mineralogy and macroporosity (Britt et al. 2002; Carry 2012). However, there now exists a large collection of meteorites, pieces of asteroids, and an advanced knowledge of their densities. Average bulk densities of meteorites are between 1600 and 7370 kg m−3, where these extremes correspond to carbonaceous and iron meteorites, respectively (Consolmagno & Britt 1998; Britt & Consolmagno 2003; Consolmagno et al. 2008; Macke et al. 2010, 2011a,b). For all these reasons, new laboratory experiments using several types of materials will be very important for understanding impacts and the flash-generation mechanism, as they will provide a database of the impact parameters and their correlations (mass, impact speed, composition, flash duration, etc.).
In summary, we report the first ten lunar impact flashes detected by the NELIOTA project, using the 1.2 m Kryoneri telescope. The multi-band capability of the NELIOTA cameras enables us to directly measure the temperatures of the impact flashes for the first time and to estimate the impactor masses. We find the measured temperature values ( ~1600 to 3100 K) to agree with previously published theoretical estimates, as discussed above. Furthermore, our sample contains four multi-frame flashes, two of which offer the opportunity for the estimation of the temperature evolution of the flash. We find a decrease of 1325 ± 104 K for Flash 2 in 33 ms, while the decrease in the same time interval for Flash 10 (20 ± 73 K) is consistent with zero. This difference is likely related to the fact that the impactor producing Flash 10 has a mass that is an order of magnitude larger than that of the impactor producing Flash 2. We also note that Flash 10 does not appear as a point source. We expect future detections of multi-frame and multi-band flashes with NELIOTA to provide a large enough sample for it to help determine the temperature evolution properties of impact flashes. Furthermore, our mass estimations rely on direct measurement of the luminous energy, given the directly measured temperature. The mass estimates that we report (100 g to 55 kg) are higher than previous estimations, despite the range of values assumed for the impact velocities and the resulting values of η.
Obtaining NEO flux densities requires increasing the number of measurements of lunar impact flashes made during meteor showers. These will be important for estimating the impactor sizes, since their impact velocity will be constrained. NELIOTA is expected to contribute to detections of stream impact flashes, which will also constrain the critical, yet uncertain, value of η. The multi-band capability of NELIOTA will generate valuable statistics on the temperatures of impact flashes and their evolution. The comparison of these measurements with the laboratory results will provide insight to the physics of impact flashes.
Acknowledgements
AL, EMX, AD, IBV, PB, AF and AM acknowledge financial support by the European Space Agency under the NELIOTA program, contract No. 4000112943. This work has made use of data from the European Space Agency NELIOTA project, obtained with the 1.2-m Kryoneri telescope, which is operated by the Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, National Observatory of Athens, Greece. Thanks to Danielle Moser, Robert Suggs and Steven Ehlert (NASA Marshall Space Flight Center) for discussions and comments on the manuscript. CA would like to thank Regina Rudawska and Elliot Sefton-Nash (ESTEC/ESA) for input.
References
- Avdellidou, C., Price, M. C., Delbo, M., et al. 2016, MNRAS, 456, 2957 [NASA ADS] [CrossRef] [Google Scholar]
- Avdellidou, C., Price, M. C., Delbo, M., et al. 2017, MNRAS, 464, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R., Ortiz, J. L., & Sada, P. V. 2000, ApJ, 542, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Berry, R., & Burnell, J. 2000, The Handbook of Astronomical Image Processing (Richmond, VA: Willmann-Bell), xxviii, 624 [Google Scholar]
- Bischoff, A., Horstmann, M., Pack, A., et al. 2010, Meteor. Planet. Sci., 45, 1638 [CrossRef] [Google Scholar]
- Borovicka, J., Popova, O. P., Nemtchinov, I. V., et al. 1998, A&A, 334, 713 [NASA ADS] [Google Scholar]
- Bottke, W. F., Jedicke, R., Morbidelli, A., et al. 2000, Science, 288, 2190 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bouley, S., Baratoux, D., Vaubaillon, J., et al. 2012, Icarus, 218, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Britt, D. T., & Consolmagno, G. J. 2003, Meteor. Planet. Sci., 38, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Britt, D. T., Yeomans, D., Housen, K., et al. 2002, Asteroids III, eds. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 485 [Google Scholar]
- Burchell, M. J., Cole, M. J., & Ratcliff, P. R. 1996a, Icarus, 122, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Burchell, M. J., Kay, L., & Ratcliff, P. R. 1996b, Adv. Space Res., 17, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Burchell, M. J., Cole, M. J., McDonnell, J. A. M., & Zarnecki, J. C. 1999, Meas. Sci. Technol., 10, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Cintala, M. J. 1992, J. Geophys. Res., 97, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Consolmagno, G. J., & Britt, D. T. 1998, Meteor. Planet. Sci., 33, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Consolmagno, G., Britt, D., & Macke, R. 2008, Chemie der Erde/Geochemistry, 68, 1 [Google Scholar]
- Delbo’, M., Walsh, K., Bolin, B., et al. 2017, Science, 357, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2009, ApJ, 696, 870 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eichhorn, G. 1975, Planet. Space Sci., 23, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Eichhorn, G. 1976, Planet. Space Sci., 24, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Ernst, C. M., & Schultz, P. H. 2004, in Lunar and Planetary Sci. Conf., eds. S. Mackwell, & E. Stansbery, 35 [Google Scholar]
- Ernst, C. M., & Schultz, P. H. 2005, in Lunar and Planetary Sci. Conf., eds. S. Mackwell, & E. Stansbery, 36 [Google Scholar]
- Harris, A. W., Boslough, M., Chapman, C. R., et al. 2015, in Asteroid Impacts and Modern Civilisation: Can We Prevent a Catastrophe? eds. P. Michel, F. E. DeMeo, & W. F. Bottke, Asteroids IV (Tucson: University of Arizona Press), 835 [Google Scholar]
- Holsapple, K., Giblin, I., Housen, K., et al. 2002, Asteroids III, eds. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 443 [Google Scholar]
- Housen, K. R., & Holsapple, K. A. 2003, Icarus, 163, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Housen, K. R., & Holsapple, K. A. 2011, Icarus, 211, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Housen, K. R., Holsapple, K. A., & Voss, M. E. 1999, Nature, 402, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Shaddad, M. H., Numan, D., et al. 2009, Nature, 458, 485 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Macke, R. J., Consolmagno, G. J., Britt, D. T., & Hutson, M. L. 2010, Meteor. Planet. Sci., 45, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Macke, R. J., Britt, D. T., & Consolmagno, G. J. 2011a, Meteor. Planet. Sci., 46, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Macke, R. J., Consolmagno, G. J., & Britt, D. T. 2011b, Meteor. Planet. Sci., 46, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Organero, F., et al. 2015, A&A, 577, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McNamara, H., Jones, J., Kauffman, B., et al. 2004, Earth, Moon, and Planets, 95, 123 [Google Scholar]
- Nemtchinov, I. V., Shuvalov, V. V., Artemieva, N. A., et al. 1998, in Lunar Planet. Sci. Conf., 29 [Google Scholar]
- Oberst, J., & Nakamura, Y. 1991, Icarus, 91, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Sada, P. V., Bellot Rubio, L. R., et al. 2000, Nature, 405, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Quesada, J. A., Aceituno, J., et al. 2002, ApJ, 576, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Madiedo, J. M., Morales, N., et al. 2015, MNRAS, 454, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, O. P., Jenniskens, P., Emel’yanenko, V., et al. 2013, Science, 342, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, E. V., & Melosh, H. J. 1998, Icarus, 133, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, S. M., Wilson, J. K., Baumgardner, J., & Mendillo, M. 1999, Geophys. Res. Lett., 26, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Speyerer, E. J., Povilaitis, R. Z., Robinson, M. S., et al. 2016, Nature, 538, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Steel, D. 1996, Space Sci. Rev., 78, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Suggs, R. M., Moser, D. E., Cooke, W. J., et al. 2014, Icarus, 238, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Suggs, R. M., Ehlert, S. R., & Moser, D. E. 2017, Planet. Space Sci., 143, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Swift, W. R., Moser, D. E., Suggs, R. M., et al. 2011, in Meteoroids: The Smallest Solar System Bodies, eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, Proc. Meteroids Conf., Breckenridge, CO, USA, May 24–28, 2010, 125 [Google Scholar]
- Verani, S., Barbieri, C., Benn, C., et al. 1998, Planet. Space Sci., 46, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Yanagisawa, M., & Kisaichi, N. 2002, Icarus, 159, 31 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Dates, universal times (UT), magnitudes in each filter, duration recorded in the I-band and listed forthe first entry of each flash, temperatures and impactor masses of the first ten NELIOTA flashes.
All Figures
 |
Fig. 1 Upper panel: light curves of the four multi-frame events in the I (filled circles; solid line) and R (open circles; dotted line) bands. Lower panel: temperature evolution for Flashes 2 and 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


