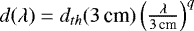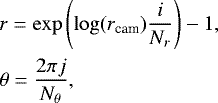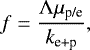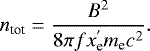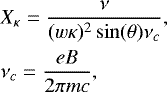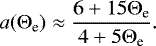| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201732025 | |
| Published online | 16 April 2018 | |
General relativistic magnetohydrodynamical κ-jet models for Sagittarius A*
1
Department of Astrophysics/IMAPP, Radboud University Nijmegen,
PO Box 9010,
6500 GL
Nijmegen, The Netherlands
e-mail: j.davelaar@astro.ru.nl
2
ASTRON,
Dwingeloo, The Netherlands
Received:
2
October
2017
Accepted:
29
November
2017
Context. The observed spectral energy distribution of an accreting supermassive black hole typically forms a power-law spectrum in the near infrared (NIR) and optical wavelengths, that may be interpreted as a signature of accelerated electrons along the jet. However, the details of acceleration remain uncertain.
Aim. In this paper, we study the radiative properties of jets produced in axisymmetric general relativistic magnetohydrodynamics (GRMHD) simulations of hot accretion flows onto underluminous supermassive black holes both numerically and semi-analytically, with the aim of investigating the differences between models with and without accelerated electrons inside the jet.
Methods. We assume that electrons are accelerated in the jet regions of our GRMHD simulation. To model them, we modify the electrons’ distribution function in the jet regions from a purely relativistic thermal distribution to a combination of a relativistic thermal distribution and the κ-distribution function (the κ-distribution function is itself a combination of a relativistic thermal and a non-thermal power-law distribution, and thus it describes accelerated electrons). Inside the disk, we assume a thermal distribution for the electrons. In order to resolve the particle acceleration regions in the GRMHD simulations, we use a coordinate grid that is optimized for modeling jets. We calculate jet spectra and synchrotron maps by using the ray tracing code RAPTOR, and compare the synthetic observations to observations of Sgr A*. Finally, we compare numerical models of jets to semi-analytical ones.
Results. We find that in the κ-jet models, the radio-emitting region size, radio flux, and spectral index in NIR/optical bands increase for decreasing values of the κ parameter, which corresponds to a larger amount of accelerated electrons. This is in agreement with analytical predictions. In our models, the size of the emission region depends roughly linearly on the observed wavelength λ, independently of the assumed distribution function. The model with κ = 3.5, ηacc = 5–10% (the percentage of electrons that are accelerated), and observing angle i = 30° fits the observed Sgr A* emission in the flaring state from the radio to the NIR/optical regimes, while κ = 3.5, ηacc < 1%, and observing angle i = 30° fit the upper limits in quiescence. At this point, our models (including the purely thermal ones) cannot reproduce the observed source sizes accurately, which is probably due to the assumption of axisymmetry in our GRMHD simulations. The κ-jet models naturally recover the observed nearly-flat radio spectrum of Sgr A* without invoking the somewhat artificial isothermal jet model that was suggested earlier.
Conclusions. From our model fits we conclude that between 5% and 10% of the electrons inside the jet of Sgr A* are accelerated into a κ distribution function when Sgr A* is flaring. In quiescence, we match the NIR upper limits when this percentage is <1%.
Key words: black hole physics / accretion, accretion disks / acceleration of particles / radiation mechanisms: non-thermal / radiative transfer
© ESO 2018
1 Introduction
In general relativistic magnetohydrodynamics (GRMHD) global simulations of weakly radiating accretion flows onto a black hole, the electron energy distribution function is not explicitly modeled. In these simulations, the accreting plasma is collisionless (i.e., the Coulomb mean free path for electrons is much larger than GM/c2), which means that the electrons are decoupled from the dynamically important, more massive protons. The processes that control the electron distribution function, such as magnetic reconnection, dissipation of turbulent energy, shocks, and/or other plasma effects that particle-in-cell simulations show, cannot be resolved with the current computational grids used in global simulations of the accretion flows. To predict the radiative properties of GRMHD accretion flows, and to improve the predictive power of the theory of accretion with respect to observations, sub-grid models for electron heating and acceleration have to be invoked.
Sagittarius A* (Sgr A*) is a supermassive black hole system that allows one to observationally test the aforementioned GRMHD models of accretion flows (Goddi et al. 2017). Millimeter-Very Long Baseline Interferometry (mm-VLBI) is capable of resolving the shadow of the event horizon (Falcke et al. 2000), making this an ideal laboratory not only to tests Einstein’s General Theory of Relativity (GR) but also to investigate electron acceleration in the vicinity of a black hole. Most of the radiative models for Sgr A*, which are based on post-processing GRMHD simulations, assume that electrons have a thermal, relativistic (Maxwell–Jüttner) distribution function, and that the proton-to-electron temperature ratio is constant across the simulation domain (Goldston et al. 2005; Noble et al. 2007; Mościbrodzka et al. 2009; Dexter et al. 2010, 2012a; Shcherbakov et al. 2012). When the proton-to-electron temperature is constant, the disk dominates the images and spectra since most of the matter resides there. We have recently extended these radiative models by making the temperature ratios a function of the plasma β parameter, where 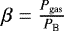 is the ratio of gas to magnetic pressures. In these extended models, the electrons are hotter in the more magnetized plasma, which is usually outflowing from the system. The reason for this is that the previously mentioned models do not recover the flat radio spectra. The β parameterization enforces that the disk emission is suppressed by significantly decreasing the temperature of the electrons in those regions. As a consequence of this, the jet will be the dominant source of emission. These modifications to the electron temperature model allowed us to recover some basic observational characteristics of Sgr A* (a roughly flat radio spectral slope and a size vs. wavelength relationship that is in agreement with observations) (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014; Chan et al. 2015b,a; Gold et al. 2017). Our model for the electron temperatures as a function of the β plasma parameter is now roughly confirmed with extended-GRMHD simulations that self-consistently take into account the evolution of the electron temperatures (Ressler et al. 2015, 2017). Moreover, GRMHD simulations with the new electron temperatures can naturally explain the symbiosis of disks and jets observed in many accreting black hole systems (Falcke & Biermann 1995; Mościbrodzka et al. 2016a).
is the ratio of gas to magnetic pressures. In these extended models, the electrons are hotter in the more magnetized plasma, which is usually outflowing from the system. The reason for this is that the previously mentioned models do not recover the flat radio spectra. The β parameterization enforces that the disk emission is suppressed by significantly decreasing the temperature of the electrons in those regions. As a consequence of this, the jet will be the dominant source of emission. These modifications to the electron temperature model allowed us to recover some basic observational characteristics of Sgr A* (a roughly flat radio spectral slope and a size vs. wavelength relationship that is in agreement with observations) (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014; Chan et al. 2015b,a; Gold et al. 2017). Our model for the electron temperatures as a function of the β plasma parameter is now roughly confirmed with extended-GRMHD simulations that self-consistently take into account the evolution of the electron temperatures (Ressler et al. 2015, 2017). Moreover, GRMHD simulations with the new electron temperatures can naturally explain the symbiosis of disks and jets observed in many accreting black hole systems (Falcke & Biermann 1995; Mościbrodzka et al. 2016a).
Observations of Sgr A* show flares in the near infrared (NIR)/optical wavelengths with a spectral index of α ≈ −0.7 ± 0.3 (Bremer et al. 2011). These flares are indicators of accelerated non-thermal electrons in the accretion flow, which is not accounted for in our previous models of Sgr A*.
Due to computational constraints, it is challenging to make a first-principles model for particle acceleration in GRMHD simulations (but see Chael et al. 2017). A simpler approach can be adopted in which the non-thermal particles are included in a phenomenological prescription. The accelerated electrons can be described by a hybrid distribution function that is constructed by “stitching” a power-law tail onto a thermal distribution function. The hybrid distribution function is then described by a few free parameters: the power law index (p), the acceleration efficiency (η, which is the amount of energy in the accelerated electrons compared to the total energy budget), and the maximum Lorentz factor (γmax) or the Lorentz factor at which radiative cooling starts to dominate (γc). The minimum Lorentz factor (γmin) is then calculated at the “stitching” point. With an underlying model for the accreting plasma, these free parameters can be then constrained by comparing the model emission to the observational data.
One of the first attempts to model electrons around Sgr A* with the hybrid distribution function is presented in Özel et al. (2000). Their underlying model for the accreting plasma is a semi-analytical radiatively inefficient accretion flow (RIAF; Narayan & Yi 1994, 1995a,b; Chen et al. 1995). Özel et al. (2000) found that the observed low-frequency shoulder of the Sgr A* spectrum is well described by emission from RIAF electrons described by a hybrid distribution function with η ≈ 0.01 and p = 3–3.5. Similar conclusions were later reached by, e.g., Yuan et al. (2003) and Broderick et al. (2016).
Recently, Mao et al. (2017) studied the effects of accelerated electrons in GRMHD simulations on the mock spectra and millimeter images of Sgr A* using either a hybrid distribution function (with p = 3.5 and various values of η) or a multi-Maxwellian distribution function. They found that the accelerated, high energy electrons not only alter the observed spectral energy distribution (SED) shape but also lead to more extended and diffuse resolved millimeter images of the source in the case of the hybrid distribution function. This has a few interesting implications for interpreting the VLBI observations of Sgr A* (Bower et al. 2004, 2014; Shen et al. 2005; Doeleman et al. 2008; Brinkerink et al. 2016). Similarly to early semi-analytical model by Özel et al. (2000), Mao et al. (2017) assumed constant acceleration parameters in the entire simulation domain, which is reasonable but does not have to be the case. For example, Ball et al. (2016) insert accelerated electrons in low-β regions where particle acceleration is expected to occur via magnetic reconnection of GRMHD simulations of Sgr A*, and study the impact of accelerated electrons on the emitted SED with the goal to explain NIR and X-ray flares observed in Sgr A*. Their best fit model assumes the electron acceleration efficiency η = 0.1 and a power-law index p = 3.5. A similar approach (with p = 3–3.5 and acceleration efficiency proportional to magnetic energy) was earlier adopted by Dexter et al. (2012b) to model the size of the near-horizon emission in M87 radio core (hereafter M87*).
In this paper, we study the effects of particle acceleration on spectra and images of axisymmetric GRMHD models of accretion flows with jets. The goal is to extend our current models with electron acceleration to see if it is possible to obtain the nearly flat SED of Sgr A* and set constraints on the amount of electron acceleration during NIR/optical flares. Our underlying accretion model assumes that the proton-to-electron temperature ratio is a function of the plasma β parameter and that electrons are hotter in low-β regions of the simulations that are associated with the jet outflow. We model emission from radio to NIR/optical frequencies. The main source of photons in the magnetized, relativistically hot plasma studied here is the synchrotron process. We ignore inverse-Compton scatterings, hence do not model the X-ray emission.
The accelerated electrons investigated in this paper are described by the κ distribution function (Vasyliunas 1968) instead of the hybrid distribution function. The κ distribution function smoothly connects the thermal core to the power-law tail (which is not the case in the hybrid model), and better describes processes such as first-order Fermi acceleration (Livadiotis & McComas 2013). The derivation of the function can be found in Livadiotis & McComas (2009). The κ distribution function is related to the thermal distribution function as a limit
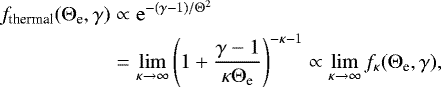 (1)
(1)
where κ is a free parameter of the distribution function, and Θe is the dimensionless temperature of the electrons involved. In the power-law part of the distribution function, the parameter κ is related to the power-law index p by κ = p + 1, such that in the limit of γ ≫ 1 the κ distribution function asymptotically approaches fκ(Θ, γ) ∝ γ−p. The κ distribution function has been used to describe plasma in the solar wind (Decker & Krimigis 2003) and plasmas in, e.g., coronal flares on the Sun (Livadiotis & McComas 2013). Theoretically Kunz et al. (2016) found that the distribution function of accelerated particles in accreting systems follows a κ distribution.
The paper is organized as follows. In Sects. 2.1 and 2.2, we explain how the GRMHD simulations are set up. In Sect. 2.3, we describe radiative transfer parameters and the acceleration of electrons. We present and discuss the results in Sects. 3 and 4, respectively.
2 Methods
2.1 GRMHD simulation
Our accreting plasma model is based on GRMHD simulations of magnetized gas around a supermassive, spinning black hole. The simulation begins with a torus in hydrostatic equilibrium in a Keplerian orbit around a Kerr black hole (Fishbone & Moncrief 1976). The size of the initial torus is set by two parameters: the inner edge of the torus rin = 6 GM/c2, and the radius rmax = 12 GM/c2 of the pressure maximum of the torus, where GM/c2 is the simulation length unit. We evolve the flow with the GRMHD code HARM2D, where we used the standard setup for reconstruction schemes and constrained transport as described in Gammie et al. (2003).
The initial torus is seeded with a weak poloidal magnetic field where the topology follows the isodensity contours of the torus. The strength of the magnetic field is set via the dimensionless plasma β parameter defined as:
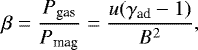 (2)
(2)
where γad is the adiabatic index, u is the internal energy density, and B is the magnetic field strength. The initial torus has a minimum β = 100; in other words, initially, the magnetic fields are relatively weak.
We are interested in modeling ν = 109–1015 Hz emission originating from the inner accretion flow (high-energy end of the spectrum) and the extended jet (low-energy end of the spectrum). Models of low-frequency emission from the jet require the simulation to be radially extended to an outer radius of rout = 1000 GM/c2. We evolve the simulation until the final time tf = 4000 GM/c3, where GM/c3 is the simulation time unit. This tf allows the jet to reach the outer boundary of the computational domain. The simulation duration corresponds to 15 orbital periods of the torus.
2.2 Numerical grid for simulating disks and jets
The dynamical simulation is carried out in mixed modified Kerr–Schild (MMKS) coordinates (Noble et al. 2007) (X0 , X1, X2, X3), which are related to standard Kerr–Schild coordinates (t, r, θ, ϕ) by:
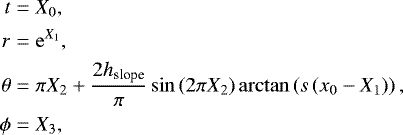 (3)(4)(5)(6)
(3)(4)(5)(6)
where hslope, s, and x0 are free parameters of the coordinates system that can be used to refine the coordinate grid near the equatorial plane, where the most dense region of the disk resides, and in the polar regions where a jet is expected to form. The parameter hslope controls the grid spacing near the equatorial plane in the innermost region of the simulation. The parameter x0 is defined as x0 ≡ log(rtr), where rtr is a transition radius at which the grid transitions from a parabolic to a conical shape along the jet axis, and s defines how rapidly this transition occurs.
The simulation is performed in two dimensions, with a grid resolution of NX1 × NX2 = 512 × 528 and grid parameters hslope = 0.35, s = 2, and rtr = 50 GM/c2. A visualization of the MMKS coordinate system is presented in Fig. 1.
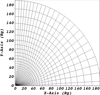 |
Fig. 1 Upper half of an MMKS coordinate system that focuses the grid resolution in the polar regions. For clarity, a lower resolution grid is displayed. |
2.3 Radiative transfer model and electron distribution functions
The SEDs and images of the GRMHD accretion flow models are computed using general-relativistic, ray-tracing radiative transport scheme RAPTOR (Bronzwaer et al., in prep.).
The GRMHD simulations are scale-free, this means that the quantities obtained are unitless. Calculation of mock observations of these models requires scaling them to c.g.s. units. The scaling depends on observational constraints such as distance, the mass of the black hole, and the matter content of the accretion disk. The simulation length unit is  , the time unit is
, the time unit is 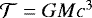 , and the mass unit is
, and the mass unit is 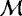 . While a good estimate of the black hole mass, M, exists for Sgr A* (hence the length unit [cm] and time unit [s] are reasonably well-known), the accretion mass unit,
. While a good estimate of the black hole mass, M, exists for Sgr A* (hence the length unit [cm] and time unit [s] are reasonably well-known), the accretion mass unit, 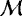 is a free parameter of the system, which has to be constrained by fitting our model spectrum to observations. The parameter
is a free parameter of the system, which has to be constrained by fitting our model spectrum to observations. The parameter 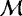 determines the density of the accretion flow, and thus the mass accretion rate onto the black hole. The dimensionless accretion rate Ṁ sim can be converted to the accretion rate in c.g.s. units by
determines the density of the accretion flow, and thus the mass accretion rate onto the black hole. The dimensionless accretion rate Ṁ sim can be converted to the accretion rate in c.g.s. units by 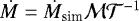 . To convert the plasma density, specific internal energy, and magnetic field strength from code units to c.g.s. units we use the following scaling factors:
. To convert the plasma density, specific internal energy, and magnetic field strength from code units to c.g.s. units we use the following scaling factors: 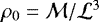 , u0 = ρ0c2, and
, u0 = ρ0c2, and 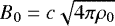 .
.
In the GRMHD simulation, we only evolve protons. We, therefore, need assumptions for the electron distribution functions and how the density and temperature of the electrons depend on the computed plasma variables.
We divide the simulation volume into three regions: the disk; the jet-sheath; and the jet-spine. In each region, we assume different electron distribution functions. In the disk region, we assume that electrons have a thermal (Maxwell–Jüttner) distribution function. We accelerate electrons in the jet-sheath region, defined using the Bernoulli parameter Be = −hut > 1.02 (Mościbrodzka & Falcke 2013) with h the gas enthalpy and ut the time component of the four-velocity. We neglect any emission from the jet-spine region, defined using the magnetization parameter 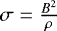 . The matter content and energy content of jet-spine is set by numerical floor values. These numerical floor values can result in unphysical large fluctuations in temperature that must be excluded from the synthetic images. This is caused by the conservative nature of the scheme that HARM2D uses; the magnetic energy is large while the internal energy is low, therefore, tiny fluctuations of the magnetic energy can result in large fluctuations of the internal energy because the codes will enforce conservation of energy. This behavior in the jet spine can be found in the regions close to θ = 0 and π where σ > 1.0, any radiation from these regions is ignored.
. The matter content and energy content of jet-spine is set by numerical floor values. These numerical floor values can result in unphysical large fluctuations in temperature that must be excluded from the synthetic images. This is caused by the conservative nature of the scheme that HARM2D uses; the magnetic energy is large while the internal energy is low, therefore, tiny fluctuations of the magnetic energy can result in large fluctuations of the internal energy because the codes will enforce conservation of energy. This behavior in the jet spine can be found in the regions close to θ = 0 and π where σ > 1.0, any radiation from these regions is ignored.
The electron temperature, Te, is computed assuming that the proton-to-electron coupling depends on plasma magnetization (Mościbrodzka et al. 2016b, 2017). We use the following law for the coupling of the electron and proton temperatures:
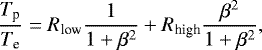 (7)
(7)
where 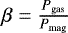 is the ratio of the gas pressure to the magnetic field pressure Pmag = B2∕2. Rlow and Rhigh are free parameters. In a strongly magnetized plasma, β ≪ 1 and TpTe → Rlow. In a weakly magnetized plasma, β ≫ 1 and so TpTe → Rhigh. We set Rlow = 1 and Rhigh = 25 so that the electrons are cooler in the disk and hotter toward the jet.
is the ratio of the gas pressure to the magnetic field pressure Pmag = B2∕2. Rlow and Rhigh are free parameters. In a strongly magnetized plasma, β ≪ 1 and TpTe → Rlow. In a weakly magnetized plasma, β ≫ 1 and so TpTe → Rhigh. We set Rlow = 1 and Rhigh = 25 so that the electrons are cooler in the disk and hotter toward the jet.
The energy distribution function of accelerated electrons in the jet-sheath is described by a combination of a thermal distribution and the relativistic κ distribution function (Livadiotis & McComas 2009):
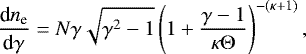 (8)
(8)
where κ is a free parameter, Θ is the dimensionless temperature defined as Θe ≡ kbTe∕mec2, and N is a normalization (that depends on Θe and κ) such that 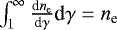 . The κ distribution function consists of a non-thermal power-law tail that smoothly connects to a thermal-like core. In the limit of κ →∞, the κ function asymptotically approaches the thermal distribution function with temperature Θ e. Figure 2 shows the κ distribution function for a few values of the κ parameter.
. The κ distribution function consists of a non-thermal power-law tail that smoothly connects to a thermal-like core. In the limit of κ →∞, the κ function asymptotically approaches the thermal distribution function with temperature Θ e. Figure 2 shows the κ distribution function for a few values of the κ parameter.
For large γ, the distribution function asymptotically approaches a power-law with index p that is related to κ by κ ≡ p + 1. Hence, the spectral index α of the optically thin part of the observed spectrum (where the observed flux density is Fν ∝ να) is associated with the κ parameter via 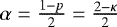 (Rybicki & Lightman 1979).
(Rybicki & Lightman 1979).
Fit formulas for the synchrotron emissivities and absorptivities for thermal and κ distribution functions, which are used in the radiative transfer models, were taken from Pandya et al. (2016).
To capture all of the emission at low and high frequencies, we need a field of view for our camera of 2000 GM/c2 (the extent of the GRMHD simulation domain). The code calculates the total flux density at every frequency by calculating null geodesics and simultaneously performing radiative transport calculations (Bronzwaer et al., in prep.). Therefore it has the same field of view at every frequency. In the case of a uniform camera grid, one needs a very high resolution to resolve the source at both low and high frequencies simultaneously. This is because the high-frequency emission originates mainly from near the event horizon, a region that is much smaller than the extended jet structures seen at lower frequencies. In order to resolve the horizon with a uniform camera at this large field of view, one needs resolutions of around 10.0002 pixels, increasing the runtime of the code significantly. To overcome this runtime issue, and to obtain converged SEDs, we implemented a polar logarithmic camera grid into RAPTOR. We describe the camera grid in Appendix A and show that our SEDs are converging if we use 512 pixels in log(r) and 256 pixels in θ.
 |
Fig. 2 κ distribution function for different values of the κ parameter (dashed lines). In the limit of large κ (black dashed line) the relativistic thermal distribution function is recovered (green solid line). |
3 Results
3.1 GRMHD jet structure
In Fig. 3, we show the density, magnetic field strength, and electron temperature of a time slice of the GRMHD simulation. In each panel, the color maps are overplotted with contours of σ =1 and Be = 1.02, which define the jet-sheath region where electrons experience acceleration. The rightmost panel in Fig. 3 shows that a thin sheath of high-temperature gas coincides with the unbound, outflowing matter.
Figure 4 displays time- and shell-averaged radial profiles of ne , B, and Te in the simulation. The radial profiles are calculated using the following definition:
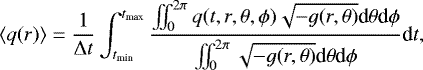 (9)
where tmin = 3000 GM/c3 and tmax = 4000 GM/c3 and Δt = tmax − tmin. The averaging uses 100 time slices of the GRMHD model, which corresponds to 5.47 h.
(9)
where tmin = 3000 GM/c3 and tmax = 4000 GM/c3 and Δt = tmax − tmin. The averaging uses 100 time slices of the GRMHD model, which corresponds to 5.47 h.
Figure 4 shows that the radial profiles of the quantities of interest follow power-laws. We compare the radial dependencies of these quantities to the Blandford–Königl jet model (Blandford & Königl 1979, hereafter BK79, see also Falcke & Biermann 1995), which is often invoked to explain the flat-spectrum radio cores observed in the centers of active galactic nuclei. In the BK79 model, the jet density decreases with radius as ne ∝ r−2, the magnetic field strength as B ∝ r−1, and the electron temperature Te is constant.
We find that in our GRMHD simulations, the electron temperatures are roughly constant up to 100 GM/c2 in the jet-sheath. A possible explanation for the temperature deviation from isothermality at larger radii is that the initial torus is relatively small compared to the size of the computational domain, and thus cannot collimate the jet at large radii; without the pressure support of a large disk, the outflowing plasma in the jet decompresses adiabatically, which results in the observed temperature decrease. In the accretion disk, the electron temperature follows a virial temperature profile, T ∝ r−1, as expected. In our simulation, the radial profile of the magnetic field strength does not resemble B ∝ r−1, but it is slightly steeper. It is likely that the radial profile of the B field strength along the jet in our numerical model is an artifact associated with the axisymmetric character of the simulation and the corresponding numerical difficulties. This difficulty arises because the turbulence in the magnetic field weakens due to the azimuthal symmetry of the 2D simulation. The radial structures of the inflows and outflows in the axisymmetric GRMHD simulation carried out here are consistent with those presented in similar axisymmetric models presented in Noble et al. (2007) and in Mościbrodzka & Falcke (2013).
 |
Fig. 3 Color maps of the plasma density (left panel), the magnetic field strength (middle panel), and the dimensionless electron temperature at t = 4000 GM/c3 of the simulation. We show the inner regions of the upper half of the simulation domain. The gas density and magnetic field strength are given in the simulation code units. The electron temperature is computed using Eq. (7) with Rlow = 1 and Rhigh = 25 (right panel). Each panel also shows contours of constant σ = 1 (dashed contour) and Be = 1.02 (solid contour). Regions where Be > 1.02 are outflowing. |
 |
Fig. 4 Radial profiles of the dimensionless number density (left panel), the magnetic field strength (middle panel), and the dimensionless electron temperature (right panel) shown in Fig. 3. Here, the simulation data is additionally time- and shell-averaged. Green and red lines correspond to plasma in the jet-sheath and accretion disk, respectively. Left and middle panels: blue lines represent the analytical model from BK79. Right panel: blue line represents the virial temperature profile. |
3.2 SEDs and synchrotron maps of κ-jet models
In this section, we present SEDs and radio, millimeter, and NIR images of models where all electrons in the jet-sheath are described by the κ distribution function. The adopted free parameters of the model are listed in Table 1. We investigate how the model SEDs and images of the source change with the κ parameter and with the observing angle. We measure the source sizes at various wavelengths using image moments (Hu 1962). Aside from model-to-model comparison, we qualitatively compare the synthetic SEDs and source sizes to Sgr A* observational data collected from the literature.
Figure 5 (upper panels) shows model SEDs at three observing angles. Since the observational data are collected non-simultaneously, the model SEDs are time-averaged over Δt = 500 GM/c3 = 2.74 h. The best-fit model SED is for κ = 5 and i = 30°. With these parameters, the model shows similar flux levels to the observed fluxes at radio frequencies (Melia & Falcke 2001 and references therein), and is consistent with observational constraints at NIR frequencies (upper limits of NIR fluxes and flares). Unless the fact that we recover the correct flux values the spectral index of the best fit model is inconsistent with observational constraints (α ≈ −0.7 ± 0.3; Bremer et al. 2011). Therefore a model where the electrons are distributed into a single κ distribution function is, in the case of Sgr A*, ruled out, but can still be of interest for other sources, e.g., M87*.
To decrease the spectral index, lower κ values are needed. One could decrease the amount of NIR emission by decreasing the number of accelerated electrons at the jet launching point by having a mix of electrons in the κ distribution function and a thermal distribution function. This idea is explored in Sect. 3.3.
Figure 5 (lower panels) displays the spectral slopes as a function of observing frequency. Between ν = 10 and 230 GHz, the spectra for models with accelerated electrons have flatter spectral slopes in comparison to the spectral slopes of the thermal model. At the NIR/optical frequencies, we observe a relation between the spectral index α and κ given by 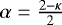 . This is expected behavior of optically-thin synchrotron emission because κ = p + 1 (Rybicki & Lightman 1979).
. This is expected behavior of optically-thin synchrotron emission because κ = p + 1 (Rybicki & Lightman 1979).
Our models demonstrate a strong dependence between the radio flux and the observer’s viewing angle as predicted, e.g., by Falcke & Biermann (1995). At lower inclinations, the jet points more towards the observer, the relativistic velocities inside the jet (γβ ≈ 5), boost the emission to higher flux values. In the thermal model, we see lower flux values at radio frequencies (ν < 1010 Hz) compared to fluxes obtained by Mościbrodzka & Falcke (2013). This is because the authors of that paper assumed an isothermal jet up to 1000 GM/c2, by setting the Te,jet = constant inside the outflowing region of the simulation. When adding accelerated electrons in the jet, we observe an increase in flux at the low and high-frequency sides of the synchrotron bump. This is in agreement with results obtained by Özel et al. (2000) and Yuan et al. (2003). As already mentioned in the introduction, these previous works used RIAF models, where the electrons are accelerated in the accretion disk. Our calculations show that it is also possible to recover the low-frequency “shoulder” and high-frequency “tail” by inserting the accelerated electrons in the jet outflow.
Figures 6–8 show time-averaged radio, millimeter, and NIR synthetic images of Sgr A* for κ = 4 (left panel) and for a relativistic thermal electron distribution function (right panel) at three observing angles. The choice for κ = 4.0 is arbitrary, and serves as an illustration of the difference between the κ and thermal models. The synchrotron maps are overplotted with ellipses that represent the FWHM of the major and minor axes of the source, as well as its orientation on the sky. In models with accelerated electrons, the jet is more elongated compared to the models without electron accelerations. The difference in size is most noticeable in the NIR band. The extra emission produced by electrons in the high-energy tail is evident when subtracting the thermal model from the κ = 4 model, as in the rightmost panels in Figs. 6–8.
Finally, Fig. 9 compares the synthetic and observed (intrinsic, i.e., after subtraction of the scattering screen that is detected towards the Sgr A*) sizes of the emitting region for different κ models at three observing angles in the optically thick part of the spectrum. We plot both the major and minor axes of the source. Observationally, the source size follows a power-law relationship as a function of λ: size ~ λq, where q = 1 (Bower et al. 2006). We find that the major and minor size of the source model increase with increasing observing wavelength λ, which is consistent with observations. At each wavelength, the model size increases with decreasing κ and decreases with increasing observing angle. Which κ parameter recovers the observed size-λ relationship best? The size of the minor axes is marginally consistent with the 1.3 mm observations in the case of the thermal and κ-jet models at i = 60° and i = 90° (see, two right top panels in Fig. 9). All models produce jets with sizes consistent with the error margins of the observations, but only down to λ= 7 mm. At λ < 7 mm, all models overestimate the size of Sgr A*. There are two possible explanations for this:
- (i)
The axisymmetry of our simulations causes the appearance of ring-like structures in the flow which are also visible in the synthetic images. These ring-like structures are not present in 3D simulations, which may decrease the source size of the models;
- (ii)
Time-averaging the synthetic images results in concentrated emission that is smeared out over a larger volume as it propagates outwards, thereby increasing the measured model source sizes.
High-resolution, fully three-dimensional, radially extended GRMHD model of an accreting black hole with phenomenological prescriptions for the shape of non-thermal electron distribution function along the jet will be explored in a subsequent publication.
Parameters that are used in the radiative transfer simulations of Sgr A*.
 |
Fig. 5 SED overplotted with observational data (top) and spectral index (down) for thermal and κ models for Sgr A* at three different observing angles. Observational data from Melia & Falcke (2001), NIR flares from Genzel et al. (2003) and Dodds-Eden et al. (2009). |
 |
Fig. 6 Synthetic images for κ models (left panels) and thermal models (middle panels) for Sgr A* at three different frequencies for an observing angle i = 30° (with respect to the black hole spin axis). The spatial resolution and field of view of our camera is 0.2 GM/c2 and 100 GM/c2 respectively. Overplotted in white are the source sizes estimates, major and minor axis, and orientation of the ellipse, which are calculated by using image moments. Right panels: the additional emission for Sgr A* in the κ = 4 model at three different frequencies. This emission is localized by subtracting the thermal synthetic images from the κ = 4 images. |
 |
Fig. 9 First and third row: major (first row) and minor (third row) axis sizes
of the jet model as a function of observing wavelength for both thermal and
κ
electrons together with measured intrinsic sizes of Sgr A*
reported by Bower et al. (2006) and Doeleman et al. (2008). Dotted lines are
|
3.3 Fitting the particle distribution function of Sgr A*
From observations of NIR flares, the spectral index of Sgr A* is α ≈ −0.7 ± 0.3 (Bremer et al. 2011). This would result in a κ value of 3.5. The κ = 3.5 models, however, overproduce the amount of flux in the NIR band. This is caused by injecting too many accelerated electrons in the jet sheath. In order to control the number of accelerated electrons, we use a superposition of a relativistic thermal and a κ distribution in the jet sheath. The percentage of κ distributed electrons is given by the free parameter ηacc. The result of these fits for various values of ηacc can be seen in Fig. 10. The model where ηacc = 1% fits the quiescence NIR observations, while a value of ηacc = 5−10% fits the NIR flares. In both, the quiescence and flaring states, we recover the observed spectral index of α ≈ −0.7 ± 0.3 (Bremer et al. 2011).
 |
Fig. 10 SED overplotted with observational data (top) and spectral index (down) for various ratios of thermal and κ models for Sgr A* at an observing angle of i = 30°. Observational data from Melia & Falcke (2001), NIR flares from Genzel et al. (2003) and Dodds-Eden et al. (2009). |
4 Discussion
4.1 SEDs of the jet launching zone as a function of electron distribution functions
Various electron temperature models were used in the past to explain the flat-to-inverted SEDs of radio jets. In Mościbrodzka & Falcke (2013) and Mościbrodzka et al. (2014), an isothermal jet model was introduced, the electron temperature was set to a constant value inside outflowing regions of the accretion flow, and in the disk, the temperature ratio was set to a constant value. In Mościbrodzka et al. (2016b), the temperature ratio between the protons and electrons was described as a function of the plasma β parameter. More recent work by Ressler et al. (2015) showed that there is indeed a relation between temperature and plasma β.
In this work, we present a new set of models. We use the plasma β prescription for the proton-to-electron temperature ratio in the disk, and we add accelerated electrons along the jet. The accelerated electrons are described by the κ distribution function for electrons. With these κ-jet models, we recover the flat-to-inverted SEDs reported by observers, while we relax the assumption of an isothermal jet. The best fit pure κ model fits the radio and NIR flux when κ = 5.0 and i = 30, but does not recover the spectral index of α = −0.7 in the NIR. Therefore a mixed model of κ distributed electrons and thermal electrons is favored.
If we use a mixed distribution (a superposition of a thermal and a κ distribution) to describe the electrons inside the jet, instead of κ only, we obtain a better fit to the observed SEDs. For NIR upper limits in quiescence, we obtain a fit with κ = 3.5, ηacc < 1%, and an observing angle i = 30°, while for flaring states we obtain κ = 3.5, ηacc = 5–10%, and an observing angle i = 30°. With these values we also recover the observed spectral index of α = −0.7 ± 0.3. By considering ηacc as a free parameter, we add an extra degree of freedom to our models. We think that it is justified to assume that only a subsection of the electrons will encounter the shock structures. All of our 100% κ jet models do not fit the spectral index of Sgr A*; these models could, on the other hand, be valuable for different sources where the percentage of electrons that are accelerated could be large, e.g., M87*. Current GRMHD simulation cannot resolve shocks and are unable to capture the micro-physics of electron heating, future particle-in-cell simulations are necessary to fully understand the micro-physics involved.
In the case of our best fit model where the percentage of electrons in the κ distribution is ηacc = 5–10%, we can calculate the electrons acceleration efficiency as explained in Appendix C. Our electrons acceleration efficiency η for the mixed model results in η = 0.06–0.12, which is also similar to Mao et al. (2017) and Ball et al. (2016), unless the fact that Mao et al. (2017) and Ball et al. (2016) insert the accelerated electrons in different regions.
The best fit viewing angle is inconsistent with earlier papers like Markoff et al. (2007), where an inclination of i > 75° is favored, and Broderick et al. (2009) and Dexter et al. (2010), who report an inclination of i = 50°. The inconsistency arises because lower viewing angles are necessary to fit the radio frequencies. This is a consequence of the relaxation of an isothermal jet since Mościbrodzka & Falcke (2013) obtained fits with higher viewing angles. In our κ-jet models, inclinations higher than ≈60° are excluded.
BK79 introduced an analytical model of a jet to describe nearly-flat spectra radio cores of galaxies. Similar work was done by Falcke & Biermann (1995), who showed a strong connection between the disk and the jet to explain radiative properties of accreting black holes, such as radio luminosity and source size. It was assumed that the emitting electrons were in a power-law distribution; we repeated these calculations in Appendix B, but using the κ distribution function instead. We find a strong correlation between the source radio-flux as a function of the κ parameter, which decreases with increasing κ values as can be seen in Fig. B.2. We recover a radio flux that is independent of ν, which is in agreement with both the BK79 model and Falcke & Biermann (1995).
The difference between the κ and thermal models are relatively large at low- (radio) and high-frequency (optical/NIR) emission compared to the mm-wavelengths. The mm-emission is produced close to the disk, and the relatively small difference in flux density between the κ and thermal models shows that the mm-emission is produced by the thermal electrons.
4.2 Intrinsic size of the κ-jet model as a function of λ
The synthetic radio images clearly show a more extended jet structure for Sgr A* when emission from accelerated electrons is included in the outflows. By adding accelerated electrons, the energy in the population increases. In this circumstance, the more energetic electrons emit photons at higher frequencies compared to their thermal counterparts. In general, for a given radiation frequency, the electrons radiate in different regions of the jet; the further away from the black hole one looks, the lower amount of emission is (since the magnetic field strength and the number density decay with increasing radius). When we accelerate the electrons in the jet, the energy available for emitting radiation increases. This results in a larger contribution to the total emission at larger radii compared to the thermal case, and hence in a more extended source. The observed and modeled core size follow a size-wavelength dependency FWHM ∝ λq. In all κ-jet models, q ≲ 1 for λ > 3 cm. Our results can be understood in terms of a simple model presented in Appendix B, where we derive an analytical expression that explains the source size as a function of κ.
5 Conclusion
We analyzed the radial structure of jets produced in two-dimensional GRMHD simulations of an accreting black hole. Our simulations show a clear, thin jet-sheath region that follows the BK79 jet model in the inner 100 GM/c2, consistent with previous findings. The effects of various initial and boundary conditions on the thermal structure of the radially extended jets should be investigated in fully 3D models, because in 2D, the turbulence weakens due to azimuthal symmetry, and the accretion rate, and hence the outflow rate, decrease over time.
We analyzed the impact of the particle acceleration in the jet-sheath on the observed radio flux and the jet emission region size. Our numerical results are confirmed by a simple semi-analytic jet model. We show that both, the radio flux and the size of the emitting region in the jet, increase with decreasing κ parameter. At this time, all our models are too large compared to observational constraints from Sgr A* system, which is again likely an artifact of axisymmetry. However, our model easily recovers a nearly-flat radio SED of Sgr A* while relaxing the assumption of a fully isothermal jet. Our κ-jet model with κ = 3.5, ηacc = 1% and observing angle i = 30° fits the Sgr A* emission in quiescence. Additionally, our κ-jet model with κ = 3.5, ηacc = 5–10%, and observing angle i = 30°, fits the observed fluxes of Sgr A* when the source is in flaring state.
Acknowledgements
This work was funded by the ERC Synergy Grant “BlackHoleCam-Imaging the Event Horizon of Black Holes” (Grant 610058). We thank Jason Dexter for useful comments on the manuscript. This research has made use of NASA’s Astrophysics Data System.
Appendix A Polar logarithmic camera
In order to resolve the emission profile at all frequencies, we adapted the camera of RAPTOR to a logarithmic polar camera. In the case of a uniform camera grid, one needs a very high resolution to resolve both the low and high frequency in one SED. We therefore distribute our impact parameters (see Bronzwaer et al., in prep.) as follows:
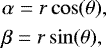 (A.1)(A.2)
(A.1)(A.2)
where i, j are the pixel indices and Nr, Nθ are the number of pixels in r and θ respectively.
After the radiative transfer calculations, each intensity must be scaled by the size of the corresponding pixel; in polar coordinates, this surface element is given by dA = rdrdθ, where
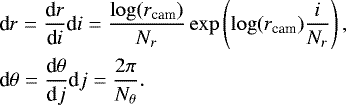 (A.3)(A.4)
(A.3)(A.4)
We calculated the convergence rate of this image grid by first calculating the square of the relative difference between the resolution under consideration and a high resolution polar grid of 1024 × 1024. We then sum this result over all frequencies, and divide this by the number of frequencies to calculate the reduced squared deviation. The deviation with respect to the high resolution run rapidly decreases several orders of magnitude with increasing resolution, as can be seen in Fig. A.1.
 |
Fig. A.1 Relative difference between SEDs at different resolutions with respect to an SED at a resolution of 1024 × 1024. |
We show in Fig. A.2 that the difference between our polar grid resolution of 512 × 256 is converged up to 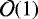 percent at all frequencies. It is evident from this image that, especially in order to resolve the high frequency emission, one needs a high resolution image grid.
percent at all frequencies. It is evident from this image that, especially in order to resolve the high frequency emission, one needs a high resolution image grid.
 |
Fig. A.2 Relative difference between SEDs at different resolutions with respect to an SED at a resolution of 1024 × 1024. |
Appendix B The size of a synchrotron photosphere as a function of κ and λ
Here we calculate the source size and source radio luminosity of a relativistic magnetized jet as a function of the κ parameter. We follow the same approach as Falcke & Biermann (1995, hereafter FB95), the only difference being that our distribution function is not a power-law distribution function but the κ distribution function. The jet in FB95 is assumed to be conically shaped, the opening angle of the jet being given by
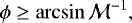 (B.1)
(B.1)
where 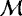 is the relativistic Mach number.
is the relativistic Mach number.
Our particle distribution function is given by:
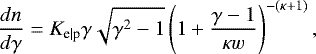 (B.2)
(B.2)
where γ is the Lorentz factor, w is a parameter that is equal to the dimensionless temperature of the particles in the GRMHD simulation, κ is a free parameter that in the optically thin regime is related to the power-law index p by κ = p + 1, and Ke∣p is a normalization constant that determines the total amount of particles.
For simplicity, we assume that w and κ are the same for both the electrons and protons. Similarly to FB95, we assume that there is an equipartition between the magnetic energy UB and the energy of the particles Ue+p within a factor ke+p, such that
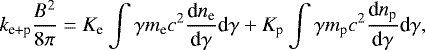 (B.3)
(B.3)
where B is the magnetic field strength, me is the electron mass, c is the speed of light, and mp is the mass of the proton.
Integrating Eq. (B.3) results in
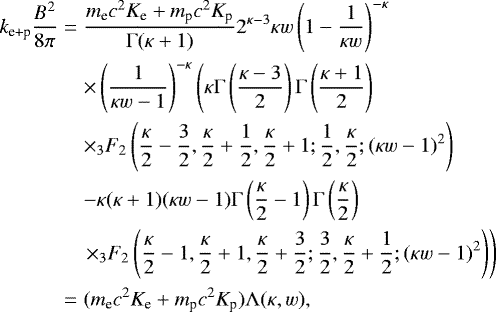 (B.4)
(B.4)
where Γ(x) is the Gamma function, 3F2 is the third hypergeometrical function of the second kind, and the function Λ(κ, w) contains all dependencies on κ and w.
We can then use this result to obtain an expression for the normalization factor Ke to find
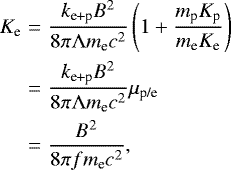 (B.5)
(B.5)
and μp/e is the proton to electron ratio:
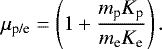 (B.7)
(B.7)
With the normalization factors known, we can now calculate the number density of the electrons by integrating Eq. (B.2):
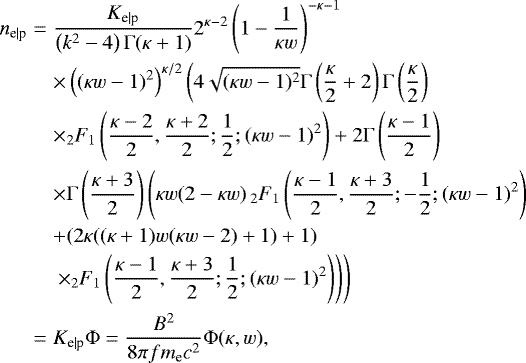 (B.8)
(B.8)
where 2F1 is the second hypergeometrical function of the first kind, and Φ(κ, w) again contains all dependencies on κ and w.
Similarly to FB95, we can define a ratio between the total number density and the electron number density as
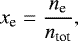 (B.9)
(B.9)
and a modified ratio as
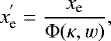 (B.10)
(B.10)
The mass supply of the jet is in FB95 given as a fraction of the mass supply of the disk, which results in
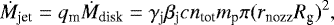 (B.12)
(B.12)
where qm is the matter fraction of the outflowing matter, γj is the Lorentz factor of the bulk of the jet, βj is the bulk velocity of the jet, and rnozz is the width of the jet nozzle.
We can use this expression to calculate ntot, which is given by
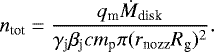 (B.13)
(B.13)
We now use the result of Eq. (B.11) to find, for Bnozz,
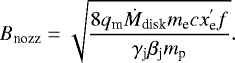 (B.14)
(B.14)
We have now obtained all initial conditions for the jet at the nozzle.
We use the same function for rjet(zjet) as FB95, which is given by
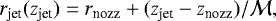 (B.15)
(B.15)
where rnozz is the size of the nozzle of the jet, and 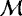 is the Mach number. This relation asymptotically approaches
is the Mach number. This relation asymptotically approaches
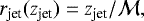 (B.16)
(B.16)
if zjet ≫ znozz.
Conservation of mass and magnetic energy results in expressions for B and ne as a function of radius given by
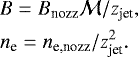
The internal energy also follows 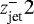 , resulting in an isothermal jet.
, resulting in an isothermal jet.
According to FB95, the Mach number is given by
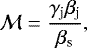 (B.19)
(B.19)
which is the ratio between the proper flow speed and the sound speed of the jet. The sound speed is given by
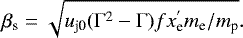 (B.20)
(B.20)
The optical depth of a conical jet is given by
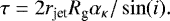 (B.21)
(B.21)
The location at which τ = 1 is the point where the jet becomes Synchrotron self-absorbed; this is a measure of the size of the jet. To find this distance Zssa, we use the absorptivity based on the κ distribution function, where we assume that we are in the low frequency limit;
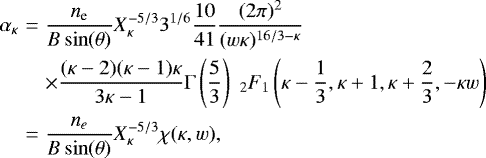 (B.22)
(B.22)
and χ(κ, w) again contains only dependencies on κ and w.
Inserting B(zjet), ne (zjet) and solving for Zssa results in
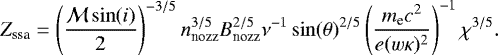 (B.25)
(B.25)
We find a relation for the size as a function of frequency given by 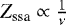 . As a function of wavelength this results in Zssa ∝ λ which is in agreement with recent observations of Sgr A* (Doeleman et al. 2008; Bower et al. 2006). Inserting
. As a function of wavelength this results in Zssa ∝ λ which is in agreement with recent observations of Sgr A* (Doeleman et al. 2008; Bower et al. 2006). Inserting 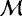 , Bnozz and nnozz results in a relation between the source size and the κ parameter given by
, Bnozz and nnozz results in a relation between the source size and the κ parameter given by
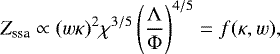 (B.26)
(B.26)
where the function f(κ, w) is plotted in Fig. B.1.
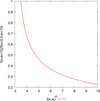 |
Fig. B.1 Source size at a given frequency as a function of κ, where the size is defined as the radius at which the source transitions from optically thick to thin. |
We can now also calculate the total radio luminosity by integrating
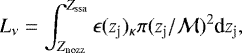 (B.27)
(B.27)
where we use that the emissivity is given by
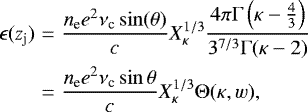 (B.28)
(B.28)
and Θ(κ, w) again only depends on κ and w.
If we assume that we can neglect the lower boundary of the integral (where τ ≫ 1), we obtain
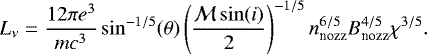 (B.29)
(B.29)
The total radio flux is independent of frequency, as one would expect. Inserting 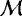 , Bnozz and nnozz results in a relation between Lν and κ given by
, Bnozz and nnozz results in a relation between Lν and κ given by
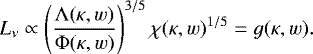 (B.30)
(B.30)
The resulting function g(κ, w) is plotted inFig. B.2.
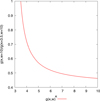 |
Fig. B.2 Radio flux in the optically thick part of the SED as a function of κ. |
Appendix C Particle acceleration efficiency
What is the electron acceleration efficiency in our pure κ-jet models as a function of κ parameter? The κ distribution function smoothly connects a power-law to a thermal core; it is, therefore, difficult to define the electron acceleration efficiency as was done in previous works. To compute the efficiency, we introduce our modified acceleration efficiency ηmod, which is defined as the ratio of the electrons that got shifted to higher γ values (the power-law part), compared to a purely thermal distribution, and the electrons that experience only a small shift (the thermal core). The thermal core and power-law part of the κ distribution function are defined in Fig. C.1 (left panel). If we compare a purely thermal distribution with a κ distribution we can distinguish three different regions; S1, S2 , and S3. S1 is the region where the thermal distribution is larger than the κ distribution, S2 is the region where they overlap, and S3 is the region where the κ distribution is larger. Since both distribution function are normalized to the same value, we know that S1 and S3 have to be equal in surface, and therefore, contribute an equal amount of electrons to the total amount of electrons. The consequence of this is that, when comparing a κ model to the thermal case, the number of electrons in S1 in the thermal models is shifted towards higher energies in the region S3 in the case of the κ-jet models. The region S2 is the number of electrons that are in the thermal core of the κ distribution function. This enables us to quantify the number of electrons that shift to higher energies by integrating the difference between the thermal and κ distribution up to the point γmax where the two distribution functions are equal (nthermal(γmax, Θe) = nκ(γmax, Θe)).
Figure C.1 (middle panel) shows the ratio between the electrons that get shifted to the power-law tail and the total number density of electrons along the jet as a function of the distance from the core for adopted values of the κ parameter. Note that the particle number densities in the S1 and S3 regions in Fig. C.1 (left panel) are equal, hence the fractional number density of electrons in the power-law tail can be defined as:
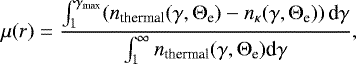 (C.1)
where integration in the numerator is carried out between 1 and γmax and where the electron temperature Θe(r) is a function of radius as displayed in the rightmost panel in Fig. 4. The fractional number density in the jet region increases with decreasing κ values, and is nearly constant as a function of radius.
(C.1)
where integration in the numerator is carried out between 1 and γmax and where the electron temperature Θe(r) is a function of radius as displayed in the rightmost panel in Fig. 4. The fractional number density in the jet region increases with decreasing κ values, and is nearly constant as a function of radius.
 |
Fig. C.1 Left panel: an illustration of the calculation of μ (Eq. (C.1)) for one value of κ. Middle panel: ratio of particle number densities between the power law tail and the thermal core of the κ distribution function along the jet. Right panel: number density, in code units, of electrons in the power-law part of the κ distribution function. |
Figure C.1 (right panel) displays the number density of electrons in the κ distribution function that occupy the power-law part of the distribution function. Note that the particle number density is given here in code units. To convert these values to [particles/cm3], one has to multiply with n0, which is given for Sgr A* in Table 1.
Finally, we define the modified acceleration efficiency ηmod as the ratio of the total energy of the electrons in the S3 region to those in the S2 region, i.e., the ratio of energy in the power-law tail to the energy in the quasi-thermal core:
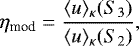 (C.2)
(C.2)
where 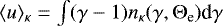 is the kinetic energy of electrons integrated over the energy distribution function. Figure C.2 (left panel) shows the modified particle acceleration efficiency for various values of κ.
is the kinetic energy of electrons integrated over the energy distribution function. Figure C.2 (left panel) shows the modified particle acceleration efficiency for various values of κ.
In Fig. C.2 (middle panel), we compare the total energy in the κ distribution to the total energy in a purely relativistic thermal distribution function. The ratio of κ and thermal kinetic energies is given by
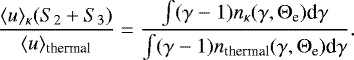 (C.3)
We find that for the smallest κ parameter, the energy within a radius of 100 GM/c2 is about 20 times higher compared to a purely relativistic thermal distribution, and this increases to 70 times higher at larger radii, where the temperature in the jet decreases, and can, therefore, explain the increase in energy ratio. The Maxwell–Jüttner distribution function narrows for small values of Θe , hence adding a power-law has a larger relative effect on the energy content while the absolute difference is smaller.
(C.3)
We find that for the smallest κ parameter, the energy within a radius of 100 GM/c2 is about 20 times higher compared to a purely relativistic thermal distribution, and this increases to 70 times higher at larger radii, where the temperature in the jet decreases, and can, therefore, explain the increase in energy ratio. The Maxwell–Jüttner distribution function narrows for small values of Θe , hence adding a power-law has a larger relative effect on the energy content while the absolute difference is smaller.
 |
Fig. C.2 Left panel: our modified energy efficiency ηmod. Middle panel: ratio of kinetic energy in κ to a purely relativistic Maxwell–Jüttner distribution function along the jet. The electron temperatures along the jet are shown in Fig. 4 (right panel). Right panel: ratio between the energy in the thermal distribution to the simulation energy. |
How much energy is in thermal electrons (and the κ distribution function) compared to the energy available in the simulation? The total energy in thermal electrons is analytically given by (Gammie & Popham 1998)
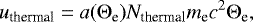 (C.4)
(C.4)
Figure C.2 (right panel) shows the ratio uthermal∕usim, the energy in a thermal distribution to the energy available in the simulations:
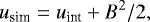 (C.6)
(C.6)
where uint is the internal energy density, and B the magnetic field strength. The value of this ratio is around 0.1–0.3. We can therefore only use radiative transfer models that are self consistent, i.e., 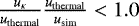 , which is the case for κ > 3.
, which is the case for κ > 3.
In the case of mixed κ models we can calculate the particle acceleration efficiency as follows
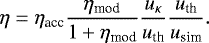 (C.7)
(C.7)
References
- Ball, D., Özel, F., Psaltis, D., & Chan, C.-k. 2016, ApJ, 826, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, S., Harris, W. E., Blakeslee, J. P., & Flynn, C. 2010, A&A, 524, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biretta, J. A., Stern, C. P., & Harris, D. E. 1991, AJ, 101, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Herrnstein, R. M., et al. 2004, Science, 304, 704 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bower, G. C., Goss, W. M., Falcke, H., Backer, D. C., & Lithwick, Y. 2006, ApJ, 648, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Markoff, S., Brunthaler, A., et al. 2014, ApJ, 790, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bremer, M., Witzel, G., Eckart, A., et al. 2011, A&A, 532, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkerink, C. D., Müller, C., Falcke, H., et al. 2016, MNRAS, 462, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Fish, V. L., Doeleman, S. S., & Loeb, A. 2009, ApJ, 697, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Fish, V. L., Johnson, M. D., et al. 2016, ApJ, 820, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Narayan, R., & Saḑowski, A. 2017, MNRAS, 470, 2367 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C.-k., Psaltis, D., Özel, F., et al. 2015a, ApJ, 812, 103 [Google Scholar]
- Chan, C.-K., Psaltis, D., Özel, F., Narayan, R., & Saḑowski, A. 2015b, ApJ, 799, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Abramowicz, M. A., Lasota, J.-P., Narayan, R., & Yi, I. 1995, ApJ, 443, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., & Krimigis, S. M. 2003, Adv. Space Res., 32, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Agol, E., Fragile, P. C., & McKinney, J. C. 2010, ApJ, 717, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Agol, E., Fragile, P. C., & McKinney, J. C. 2012a, J. Phys. Conf. Ser., 372, 012023 [CrossRef] [Google Scholar]
- Dexter, J., McKinney, J. C., & Agol, E. 2012b, MNRAS, 421, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Dodds-Eden, K., Porquet, D., Trap, G., et al. 2009, ApJ, 698, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Weintroub, J., Rogers, A. E. E., et al. 2008, Nature, 455, 78 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Schenck, D. E., et al. 2012, Science, 338, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Falcke, H., & Biermann, P. L. 1995, A&A, 293, 665 [NASA ADS] [Google Scholar]
- Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS] [Google Scholar]
- Falcke, H., Melia, F., & Agol, E. 2000, ApJ, 528, L13 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., & Popham, R. 1998, ApJ, 498, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444 [Google Scholar]
- Gammie, C. F., Shapiro, S. L., & McKinney, J. C. 2004, ApJ, 602, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934 [CrossRef] [PubMed] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Fritz, T. K., et al. 2009, ApJ, 707, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Goddi, C., Falcke, H., Kramer, M., et al. 2017, Int. J. Mod. Phys. D, 26, 1730001 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, R., McKinney, J. C., Johnson, M. D., & Doeleman, S. S. 2017, ApJ, 837, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Goldston, J. E., Quataert, E., & Igumenshchev, I. V. 2005, ApJ, 621, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., Li, H., Daughton, W., & Liu, Y.-H. 2014, Phys. Rev. Lett., 113, 155005 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2013, ApJ, 775, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hilburn, G., & Liang, E. P. 2012, ApJ, 746, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, M. 1962, IRE Trans. Inf. Theory, 8, 179 [Google Scholar]
- Kunz, M. W., Stone, J. M., & Quataert, E. 2016, Phys. Rev. Lett., 117, 235101 [NASA ADS] [CrossRef] [Google Scholar]
- Livadiotis, G., & McComas, D. J. 2009, J. Geophys. Res., 114, A11105 [NASA ADS] [CrossRef] [Google Scholar]
- Livadiotis, G., & McComas, D. J. 2013, Space Sci. Rev., 175, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Walker, R. C., & Junor, W. 2007, ApJ, 660, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Mahadevan, R., & Quataert, E. 1997, ApJ, 490, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Dexter, J., & Quataert, E. 2017, MNRAS, 466, 4307 [Google Scholar]
- Markoff, S., Bower, G. C., & Falcke, H. 2007, MNRAS, 379, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F., & Falcke, H. 2001, ARA&A, 39, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., & Falcke, H. 2013, A&A, 559, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H., & Leung, P. K. 2009, ApJ, 706, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Falcke, H., Shiokawa, H., & Gammie, C. F. 2014, A&A, 570, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Noble, S. 2016a, A&A, 596, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016b, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Dexter, J., Davelaar, J., & Falcke, H. 2017, MNRAS, 468, 2214 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995a, ApJ, 444, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995b, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Krolik, J. H., & Hawley, J. F. 2009, ApJ, 692, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Leung, P. K., Gammie, C. F., & Book, L. G. 2007, Class. Quant. Grav., 24, S259 [Google Scholar]
- Özel, F., Psaltis, D., & Narayan, R. 2000, ApJ, 541, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Pandya, A., Zhang, Z., Chandra, M., & Gammie, C. F. 2016, ApJ, 822, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, M. A., Fernández-Ontiveros, J. A., Markoff, S., Espada, D., & González-Martín, O. 2016, MNRAS, 457, 3801 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Tchekhovskoy, A., Quataert, E., Chandra, M., & Gammie, C. F. 2015, MNRAS, 454, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Tchekhovskoy, A., Quataert, E., & Gammie, C. F. 2017, MNRAS, 467, 3604 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (Wiley) [Google Scholar]
- Shcherbakov, R. V., Penna, R. F., & McKinney, J. C. 2012, ApJ, 755, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Z.-Q., Lo, K. Y., Liang, M.-C., Ho, P. T. P., & Zhao, J.-H. 2005, Nature, 438, 62 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. L., Barth, A. J., Ho, L. C., & Sarzi, M. 2013, ApJ, 770, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper half of an MMKS coordinate system that focuses the grid resolution in the polar regions. For clarity, a lower resolution grid is displayed. |
| In the text | |
 |
Fig. 2 κ distribution function for different values of the κ parameter (dashed lines). In the limit of large κ (black dashed line) the relativistic thermal distribution function is recovered (green solid line). |
| In the text | |
 |
Fig. 3 Color maps of the plasma density (left panel), the magnetic field strength (middle panel), and the dimensionless electron temperature at t = 4000 GM/c3 of the simulation. We show the inner regions of the upper half of the simulation domain. The gas density and magnetic field strength are given in the simulation code units. The electron temperature is computed using Eq. (7) with Rlow = 1 and Rhigh = 25 (right panel). Each panel also shows contours of constant σ = 1 (dashed contour) and Be = 1.02 (solid contour). Regions where Be > 1.02 are outflowing. |
| In the text | |
 |
Fig. 4 Radial profiles of the dimensionless number density (left panel), the magnetic field strength (middle panel), and the dimensionless electron temperature (right panel) shown in Fig. 3. Here, the simulation data is additionally time- and shell-averaged. Green and red lines correspond to plasma in the jet-sheath and accretion disk, respectively. Left and middle panels: blue lines represent the analytical model from BK79. Right panel: blue line represents the virial temperature profile. |
| In the text | |
 |
Fig. 5 SED overplotted with observational data (top) and spectral index (down) for thermal and κ models for Sgr A* at three different observing angles. Observational data from Melia & Falcke (2001), NIR flares from Genzel et al. (2003) and Dodds-Eden et al. (2009). |
| In the text | |
 |
Fig. 6 Synthetic images for κ models (left panels) and thermal models (middle panels) for Sgr A* at three different frequencies for an observing angle i = 30° (with respect to the black hole spin axis). The spatial resolution and field of view of our camera is 0.2 GM/c2 and 100 GM/c2 respectively. Overplotted in white are the source sizes estimates, major and minor axis, and orientation of the ellipse, which are calculated by using image moments. Right panels: the additional emission for Sgr A* in the κ = 4 model at three different frequencies. This emission is localized by subtracting the thermal synthetic images from the κ = 4 images. |
| In the text | |
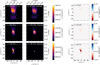 |
Fig. 7 As Fig. 6, but for an observing angle of i = 60°. |
| In the text | |
 |
Fig. 8 As Fig. 6, but for an observing angle of i = 90°. |
| In the text | |
 |
Fig. 9 First and third row: major (first row) and minor (third row) axis sizes
of the jet model as a function of observing wavelength for both thermal and
κ
electrons together with measured intrinsic sizes of Sgr A*
reported by Bower et al. (2006) and Doeleman et al. (2008). Dotted lines are
|
| In the text | |
 |
Fig. 10 SED overplotted with observational data (top) and spectral index (down) for various ratios of thermal and κ models for Sgr A* at an observing angle of i = 30°. Observational data from Melia & Falcke (2001), NIR flares from Genzel et al. (2003) and Dodds-Eden et al. (2009). |
| In the text | |
 |
Fig. A.1 Relative difference between SEDs at different resolutions with respect to an SED at a resolution of 1024 × 1024. |
| In the text | |
 |
Fig. A.2 Relative difference between SEDs at different resolutions with respect to an SED at a resolution of 1024 × 1024. |
| In the text | |
 |
Fig. B.1 Source size at a given frequency as a function of κ, where the size is defined as the radius at which the source transitions from optically thick to thin. |
| In the text | |
 |
Fig. B.2 Radio flux in the optically thick part of the SED as a function of κ. |
| In the text | |
 |
Fig. C.1 Left panel: an illustration of the calculation of μ (Eq. (C.1)) for one value of κ. Middle panel: ratio of particle number densities between the power law tail and the thermal core of the κ distribution function along the jet. Right panel: number density, in code units, of electrons in the power-law part of the κ distribution function. |
| In the text | |
 |
Fig. C.2 Left panel: our modified energy efficiency ηmod. Middle panel: ratio of kinetic energy in κ to a purely relativistic Maxwell–Jüttner distribution function along the jet. The electron temperatures along the jet are shown in Fig. 4 (right panel). Right panel: ratio between the energy in the thermal distribution to the simulation energy. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.