| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731716 | |
| Published online | 07 May 2018 | |
Energy distribution of relativistic electrons in the kiloparsec scale jet of M 87 with Chandra
1
Max-Planck-Institut für Kernphysik,
P.O. Box 103980,
69029
Heidelberg, Germany
e-mail: sun@mpi-hd.mpg.de
2
ZAH, Institut für Theoretische Astrophysik, Heidelberg University,
Philosophenweg 12,
69120
Heidelberg, Germany
3
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place,
Dublin 2, Ireland
4
Gran Sasso Science Institute,
7 viale Francesco Crispi,
67100
L’Aquila (AQ), Italy
5
MEPHI,
Kashirskoe shosse 31,
115409
Moscow, Russia
Received:
4
August
2017
Accepted:
24
January
2018
The X-ray emission from the jets in active galactic nuclei (AGN) carries important information on the distributions of relativistic electrons and magnetic fields on large scales. We reanalysed archival Chandra observations on the jet of M 87 from 2000 to 2016 with a total exposure of 1460 kiloseconds to explore the X-ray emission characteristics along the jet. We investigated the variability behaviours of the nucleus and the inner jet component HST-1, and confirm indications for day-scale X-ray variability in the nucleus contemporaneous to the 2010 high TeV γ-ray state. HST-1 shows a general decline in X-ray flux over the last few years consistent with its synchrotron interpretation. We extracted the X-ray spectra for the nucleus and all knots in the jet, showing that they are compatible with a single power law within the X-ray band. There are indications that the resultant X-ray photon index exhibit a trend, with slight but significant index variations ranging from ≃ 2.2 (e.g. in knot D) to ≃ 2.4−2.6 (in the outer knots F, A, and B). When viewed in a multiwavelength context, a more complex situation can be seen. Fitting the radio to X-ray spectral energy distributions (SEDs) assuming a synchrotron origin, we show that a broken power-law electron spectrum with break energy Eb around 1 (300 μG/B)1/2 TeV allows a satisfactory description of the multiband SEDs for most of the knots. However, in the case of knots B, C, and D we find indications that an additional high-energy component is needed to adequately reproduce the broad-band SEDs. We discuss the implications and suggest that a stratified jet model may account for the differences.
Key words: X-rays: galaxies / galaxies: individual: M 87 / radiation mechanisms: non-thermal
© ESO 2018
1 Introduction
M 87 (Virgo A, NGC 4486, 3C 274), the giant elliptical galaxy located in the Virgo cluster at a distance of 16.7 ± 0.6 Mpc (1′′ = 78 pc), is one of the closest radio galaxies (Blakeslee et al. 2009; Jordán et al. 2005). It is known to host a central black hole with a mass of ≃(3–6) × 109 M⊙ (Macchetto et al. 1997; Gebhardt et al. 2011; Walsh et al. 2013) and a one-sided ~30′′ scale jet (Marshall et al. 2002; Harris et al. 2003). The jet is characterised by a viewing angle between 10°–25° and reveals superluminal motion of optical components of (4–6)c within 6′′ of the nucleus based on HST observations (Biretta et al. 1999). Its jet power Pj is somewhat uncertain with estimates ranging from a few times 1043 erg s−1 up to 1045 erg s−1 (e.g. Reynolds et al. 1996; de Gasperin et al. 2012; Mościbrodzka et al. 2016; Levinson & Globus 2017). Owing to its proximity and high surface brightness at radio wavelengths and above, M 87 has become a key laboratory to investigate the property of relativistic jets (e.g. Doeleman et al. 2012; Hada et al. 2016; Mertens et al. 2016; Britzen et al. 2017).
Both the nucleus and several bright jet knots have been detected at radio, optical, and X-ray wavelengths. Their broad-band spectral energy distributions (SEDs) have been extensively studied (e.g. Biretta et al. 1991; Sparks et al. 1996; Perlman et al. 2001; Zhang et al. 2010). The high-resolution observations performed by Chandra in the X-ray band make it possible to investigate the spectral energy distributions of the jet substructures in or close to the spectral cut-off regions, imposing important constraints on radiation models (e.g. Marshall et al. 2002; Wilson & Yang 2002; Perlman & Wilson 2005; Waters & Zepf 2005; Zhang et al. 2010).
Owing to the accumulative exposure and the recently enhanced software tools of Chandra, an improved analysis can now be performed to derive more accurate spectrometric information and to further investigate radiation mechanisms in this region. In this paper we present the results of a detailed analysis of the Chandra data on the M 87 nucleus and knots observed from 2000 to 2016. The paper is structured as follows. In Sect. 2 we describe details of the Chandra data reduction process, light curve analysis, and spectral analysis. In Sect. 3 we construct the radio to X-ray SEDs of the substructures (knots) in M87 and provide model fits to infer the spectral distributions of the parent particles. We discuss the consequences in Sect. 4.
2 Chandra data analysis
The Chandra X-ray Observatory (CXO), launched in 1999, provides unprecedented angular resolution ≤ 0.5′′ X-ray imaging andspectroscopy over the energy band 0.1–10 keV (15–0.12 nm) (Weisskopf et al. 2000, 2002). Its Science Instrument Module (SIM) holds the two focal plane instruments, the Advanced CCD Imaging Spectrometer (ACIS) and the High Resolution Camera (HRC). The ACIS is used for spectroscopic studies in the energy range 0.2–10 keV. The HRC accurately records the position, number, and energy of X-rays, and images over the range of 0.1–10 keV1. In this paper, the Chandra data reduction and spectra extraction are performed using CIAO (v4.8) tool and the Chandra Calibration Database (CALDB, v4.7.2). We perform the spectral analysis with Sherpa2.
2.1 Data preparation
We collected the Chandra ACIS timed exposure (TE) mode observations from April 15, 2000 (ObsID 517), to June 12, 2016 (ObsID 18856), to perform a detailed analysis of the M 87 jet and nucleus. In Table 1 we list all the observations, including 99observations with a 0.4 s frame time and 13 observations with a 3.2/3.1 s frame time. The total exposure time is over 1460 kiloseconds. Figure 1 provides an exemplary case, showing the ObsID 1808 X-ray image binned into 0. ′′ 123 per pixel and smoothed with a Gaussian of FWHM = 0. ′′3.
To avoid pile-up (i.e. two or more photons arriving at the same pixel during a single frame time, thus mimicking a single event with the sum of the energies; see e.g. Davis 2001), we generally selected the observations with frame time of 0.4 s for all substructures analyses. However, because knots E, F, I, B, and C, as shown in Fig. 1, are much fainter than the nucleus, HST-1, knot D, and knot A, we also included the observations with frame time of 3.2/3.1 s in the analysis of these knots.
To reduce uncertainties caused by the position offsets of different observations, we performed the astrometric corrections as follows. In order to obtain more reliable source localisation during the process of astrometric correction, the effect of broad-band energy on the exposure map needs to be avoided. Thus, we first produced the exposure-corrected image, the weighted exposure map, and the weighted PSF map. Finally, we performed wcs_match and wcs_update to match all selected Chandra observations with a reference observation ObsID 1808 separately. We defined the source region of each knot based on the X-ray positions in Table 1 of Perlman & Wilson (2005). The source and background regions are shown in Fig. 1.
 |
Fig. 1 Image from the observation on July 30, 2000 (ObsID 1808), in the 0.2–10 keV, binned in 0. ′′ 123 per pixel and smoothed with a Gaussian of FWHM = 0. ′′3. The source and background regions are indicated by green shapes. Units of right ascension are hours:minutes:seconds, and units of declination are degrees:arcminutes:arcseconds. |
2.2 Time variability
To study the time variabilities, we extracted the flux for each observation in the 0.3–7 keV energy band and built the light curves for each region.
2.2.1 Nucleus
The nucleus reveals significant variabilities as shown in the top panel of Fig. 2. We defined five flaring periods, labelled 1–5, and present zoomed-in light curves in Fig. 2. To investigate the characteristic timescales of these flares in more detail, we fitted the light curves with an exponential function of the form
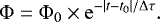 (1)
(1)
Here Δτ = τd∕ln(2), τd is the characteristic timescales of each flare. We froze t0 to the time of the highest data point for each flare, and Φ0 and τd are free parameters. In principle, the rising and decay timescale can be different. The current data set, however, prevents us from deriving the differences of the two timescales due to the limited time coverage, especially in the rising stage. Thus, for flares 1, 2, and 4 we performed fits assuming that both the rising and decaying stage have the same τd. For flares 3 and 5 we only fit the decaying stage. The corresponding values of Φ0, τd, and t0 are listed in Table 1. The characteristic timescale for flare 5 is shortest with τd = 3.9 ± 1.7 days. This flare is contemporaneous to the rapid TeV γ-ray flare seen on April 910, 2010 (MJD 55296; see e.g. Abramowski et al. 2012; Harris et al. 2011). The day-scale activity seen at X-ray and TeV energies in this context favours a common physical origin of this emission (Abramowski et al. 2012; Aliu et al. 2012).
 |
Fig. 2 Top: Chandra 0.3–7 keV light curve for the nucleus from July 29, 2000 (MJD 51754), to March 17, 2016 (MJD 57464). Five flares (red data points, labelled 1–5) are selected for further analysis in the following. Bottom: zoomed-in light curves of the five flares. The solid lines show the fitting results by using Eq. (1). |
Fitting parameters for the selected flares of the nucleus using a symmetric exponential function.
2.2.2 HST-1
HST-1 shows significant variability over time, revealing flux variations much larger than those of the nucleus. During the period from 2002 to 2010 the total X-ray energy flux varied by one order of magnitude, reaching an extreme high state in 2005 (see Fig. 3).
The 2005 X-ray high state of HTS-1 seemingly correlates with a high state of M 87 at TeV energies exhibiting rapid day-scale activity (Aharonian et al. 2006). Early models thus assumed a common physical origin, while the apparent absence of such a correlation for the subsequent TeV high state in 2010 has been taken as disfavouring it. We note that there are several reasons why day-scale TeV activity related to HST-1 now appears disfavoured (see Rieger & Aharonian 2012, for review and discussion). The presence or absence of a possible X-ray -TeV correlation, however, seems rather less conclusive in this regard as changes in the magnetic field and radiating particle number in a synchrotron (X-ray) and inverse Compton (IC; TeV) approach could fully accommodate both of them.
The X-ray flux of HST-1 seems to be continuously decreasing since 2007 with a characteristic decay timescale of ~ (0.5–1) yr. This supports previous indications (Harris et al. 2009), and while dominant IC cooling is not excluded (e.g. Perlman et al. 2011), seems compatible with the synchrotron cooling timescale of electrons producing ~ 1 keV photons in a ~milligauss magnetic field, 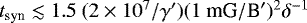 yr. This could be taken as providing some additional evidence for a synchrotron origin of the X-ray emission.
yr. This could be taken as providing some additional evidence for a synchrotron origin of the X-ray emission.
For the analysis of the spectral variations of HST-1 presented in Sect. 2.3, we divide the high-activity period from January 16, 2002 (MJD 52290), until May 14, 2010 (MJD 55330), into five sections denoted by H1, H2, H3 H4, and H5. The observation on July 30, 2000 (ObsID 1808), and the observations after May 13, 2009 (ObsID 10286), are treated as low state (L). The observations from April 01, 2009 to May 14, 2010, on the other hand, belong to a transition period between the high and the low state, and have thus been included in the following in both, L and H5 spectral calculations. For a bright source, pile-up could lead to distortions in the energy spectrum (e.g. Harris et al. 2006). Using the pileup_map tool, we estimated the pile-up fraction and found that for H2, H3, and H4 the fraction is larger than 10%, even though we have only selected observations with a frame time of 0.4 s to avoid pile-up. Thus, for the following spectral analysis we only include H1, H5, and L for HST-1.
 |
Fig. 3 Chandra 0.3–7 keV light curve for HST-1 during the same time interval as in Fig. 2. The black points are considered to belong to the low state (L). The dashed lines, on the other hand, separate the high state from January 16, 2002 (MJD 52290), to May 14, 2010 (MJD 55330), into five subsections, that are labelled H1, H2, H3, H4, and H5. The data from April 01, 2009 to May 14, 2010, belong to a transition period between high and low state, and have thus been included in both L and H5 calculations. |
2.2.3 Other knots
Knot D and knot A show no significant variability. The flux variations lie within the statistical errors of the flux determination, which is 15% for knot D and 5% for knot A. The fluxes derived for knots E, F, I, B, and C have significant uncertainties due to the limited statistics of the observations. We do not find any evidence of variability even after re-binning the observations. With the exception of HST-1, we thus combined all observations for the following spectral analysis of the knots.
2.3 Spectral analysis
For the spectral analysis we performed an aperture photometry using specextract on the nucleus and each knot. The source and background regions are as defined in Fig. 1.
2.3.1 Nucleus and HST-1 during low states and in early 2010
The nucleus is highly variable and suffers from pile-up even for observations with frame times of 0.4 s during the flare peak period H2, H3, andH4, which could affect the inherent spectral energy distribution (e.g. lead to spectral hardening). Thus, we only use the observations during the period of H1, H5, and L for temporal spectral analyses of nucleus and knot HST-1. To improve the statistics, we combine the observations on time ranges of a few months up to one and a half years. We simultaneously fit the spectra in each time range using a single power law plus Galactic absorption model. To suitably deal with the pile-up we add an additional pile-up model jdpileup to the spectral fit. The time bins and the fitted indices are listed in Table 2. No obvious spectral variability seems apparent. In addition, wealso provide a detailed analysis of those observations contemporaneous to the 2010 TeV flare. In 2010 HST-1 was back to a state comparable with the pre-2004 time, during which pile-up was found to be fairly mild (Harris et al. 2006; Russell et al. 2015). The fitted indices for the nucleus in April/May 2010 are shown in Table 3 along with those for HST-1. The photon indices for the nucleus are on average close to Γ ~ 2.1 − 2.2, which seems compatible with earlier (non-flaring) results reported in Wilson & Yang (2002) and Perlman & Wilson (2005), see also the results in Table 2. A hint for spectral variations during 2010 might be seen in the nucleus, while the HST-1 spectrum appears stable, though the short exposures limit inferences. Combing observations for HST-1 (in a set of three) to improve statistics, however, yields results that are compatible with no spectral change. Our values for the nucleus are similar to those in Harris et al. (2011). Our results for HST-1, however, are harder than those reported in Harris et al. (2011), yet still compatible within the 1σ error bars. We note that in our analysis the error bars are much larger due to the additional free parameters in the pile-up model that has been included in our analysis. For sources closer than one arcsec, such as the nucleus and HST-1 (which are separated by 0.86′′), an “eat-thy-neighbour” effect may in principle occur (Harris et al. 2006, 2009), where photons arriving within the same frame time and 3 × 3 pixel grid are registered as a single event at the location of the pixel with the larger energy. As suggested by Harris et al. (2009) this effect is not expected to cause serious problems below a detector-based intensity limit of 4 keV s−1 (e.g. for the pre-2004 and post-2006 time for HST-1).
The X-ray photon indices for the nucleus are in principle in the range of those achievable by Comptonisation in a hot accretion flow. Early models in fact assumed that the quiescent nuclear X-ray emission in M 87 is produced by an ADAF (e.g. Reynolds et al. 1996; Di Matteo et al. 2003). The similarities of the nuclear spectrum to that of the jet and its knots, and the strong brightness increase towards the nucleus (see Fig. 5), however, suggest that this “nuclear” emission is instead dominated by the jet (Wilson & Yang 2002). This is supported by the fact that the luminosity of a hot accretion flow at low accretion rates Ṁ roughly scales with Ṁ2, i.e. LADAF ∝Ṁ2, while that of the jet with Lj ∝Ṁ, so that for low Ṁ the jet starts to dominate (Yuan & Narayan 2014; Feng & Wu 2017). The evidence for strong nuclear activity over time fits well into this.
X-ray photon indices for the nucleus and HST-1 during the period of H1, H5, and L.
X-ray photon indices for the nucleus and HST-1 during the 2010 TeV flare.
 |
Fig. 4 Chandra 0.3–7 keV light curves for knots D, E, F, I, A, B, and C during the same time interval as in Fig. 2. |
 |
Fig. 5 Flux density (top panel) and power-law photon index (bottom panel) in the X-ray 0.3–7 keV band along the jet. The source regions are separated by the dashed lines. For this representation all observations with frame time 0.4 s are used for the nucleus, while for HST-1 only “HST-1 L” data are employed. |
2.3.2 Combined X-ray spectra of the knots
For all knots, except HST-1, we fit multiple observations simultaneously. For HST-1 we exclude observations during H2, H3, and H4 in the spectral analysis due to significant pile-up.
In the X-ray band all knots can in principle be well fitted with a single power law plus Galactic absorption model, none seems to require an obvious break or additional component within the X-ray band itself (but see below). Table 4 lists the best-fit parameter values and the reduced χ2 value. The reduced χ2 values reveal that all fits are acceptable at a 90% confidence level. Leaving the absorption column density NH free in the fit yields valuesdeviating significantly from the Galactic one (Perlman & Wilson 2005). Harris et al. (2006) have reported a mutual dependence between NH and α in the fitting process, leading to some uncertainty. For comparison, we thus also provide results with NH frozen to the Galactic value. We note that we do not find evidence for a significant deviation (Osone 2017) from a pure power law in the X-ray band for knot A if NH is kept frozen.
The derived photon indices for different knots are significantly different, ranging from ≃ 1.89 (knot C) to ≃ 2.61 (knot F). The results roughly match those obtained by Wilson & Yang (2002, 2004) and Perlman & Wilson (2005). In Fig. 5 we plot the profiles of the flux density and photon index αx along the jet. For the regions of the nucleus, knots HST-1, D, and A, we define the size of the stripes of 0.45′′ and 2.0′′ along and perpendicular to the jet. For the other regions, we use 0.45′′× 1.5′′ rectangular regions correspondingly. If the signals are too weak, we combine several strips together. We again used the single power law plus Galactic absorption model to fit each region. Finally, we used the best-fit model to simulate the energy flux of the de-convolved non-thermal emission. In this process we divided the X-ray energy interval between 0.3 keV and 7 keV into four bins in logarithmic space. The derived X-ray data points are listed in Table 5. With the exemption of the outermost knot C, the X-ray photon index along the jet exhibits a trend similar to that reported in Perlman & Wilson (2005), with slight but significant index variations ranging from ≃ 2.2 (e.g. in knot D) to ≃ 2.4 − 2.6 (in knots F, A, and B). There is little evidence that the inter-knot regions have significantly steeper spectra than the adjacent knots, reinforcing the need for a distributed acceleration mechanism.
According to Fig. 5 the X-ray flux density along the jet exhibits significant changes on comparably small scales around the knot D and knot A regions. Radio and optical observations indicate that the knot D region is in fact composed of several subregions (e.g. Perlman & Wilson 2005; Avachat et al. 2016, see also below). Our modelling of the broad-band SED of the knots in Sect. 3, on the other hand, suggests that for knot regions B and C, and to some (weaker) extent also for knot region D, an additional X-ray emitting component is needed to achieve a satisfactory SED fit. It seems conceivable that these X-ray features are related to a blending of unresolved longitudinal or radial substructures (i.e. related to lateral jet stratification).
Results for the X-ray spectral fitting of the knots.
Deconvolved X-ray flux densities of the knots for different energy bands.
3 SED modelling
In order to gain further insights, we constructed the radio to X-ray SEDs of the knots and provided model fits to infer the characteristics of the parent particle distribution. We selected contemporaneous multiwavelength data to ensure an adequate reconstruction. The optical to X-ray spectra of the H1, H5, and L state of knot HST-1 are taken from the 2002 December, 2003 February, and 2003 April HST observationsin Perlman et al. (2003), respectively. The radio data are from Giroletti et al. (2012) based on observations between 2006 and 2010 with the Very Long Baseline Array (VLBA) at 1.7 GHz for H1, and between 2009 and 2011 with the European VLBI Network (EVN) at 5 GHz for the statuses H5 and L. We also used the published optical–near-infrared data from Perlman et al. (2001), and the ultraviolet data from Waters & Zepf (2005) for knots D, E, F, I, A, B, and C. The black points in the radio energy band are from Perlman et al. (2001). We did not include the radio data points of Biretta et al. (1991) in the spectral fitting, yet regarded them as a reference for the radio spectral indices because of the uncertainties with regard to these measurements (see e.g. Perlman & Wilson 2005). It should also be noted that although our region C could be further divided into the subregions C1 and C2, we only include the ultraviolet fluxes for C1. This simplification appears justified considering the much lower ultraviolet flux from C2. For comparison, we also plot the X-ray flux density from Marshall et al. (2002) with grey symbols in Fig. 6.
There are in principle several possible non-thermal scenarios for the origin of large-scale X-ray emission, such as inverse Compton (IC) upscattering of either synchrotron (synchrotron self-Compton; IC-SSC) or cosmic microwave background (IC-CMB) photons, or direct synchrotron emission of relativistic electrons or protons (e.g. Aharonian 2002; Harris & Krawczynski 2002; Zhang et al. 2009, 2010; Georganopoulos et al. 2016). As discussed in Wilson & Yang (2002), to account for the keV X-ray flux by means of leptonic IC-SSC processes, the magnetic field has to be substantially lower than equipartition. In the case of IC-CMB it is possible to boost the X-ray flux by relativistic bulk motion, but this requires high Doppler factors δ ≃ (10–40) and very small angles θ ≃ (1.2°–4.7°) between the jet and the line of sight (Harris & Krawczynski 2002). Though HST observations indicate that moderate superluminal motion in M 87 could persist out to knot C (Meyer et al. 2013), such values remain highly unlikely. Moreover, IC radiation by a power-law electron distribution in the Thomson regime is expected to exhibit a spectral index similar to that for synchrotron radiation, yet the observed X-ray spectra of the knots are all significantly steeper than the radio spectra (exhibiting spectral indices αrr ~ 0.5, e.g. Biretta et al. 1991). An IC origin of the X-ray emission in M 87 thus appears disfavoured (see also Biretta et al. 1991; Meisenheimer et al. 1996; Wilson & Yang 2002; Perlman & Wilson 2005; Zhang et al. 2010), and we therefore only consider an electron synchrotron origin in the following.
We use Naima (Zabalza 2015) to explore the characteristics of the radiating particle distribution. Naima is a numerical package that includes a set of non-thermal radiative models and a spectral fitting procedure. The best-fit and uncertainty distributions of spectral model parameters are derived through Markov chain Monte Carlo (MCMC; Foreman-Mackey et al. 2013) sampling of their likelihood distributions. The code allows us to implement different functions and includes tools to perform MCMC fitting of non-thermal radiative processes to the data. Given the radio to X-ray data of the knots in M 87, the simplest functional form to take into account is a broken power law,
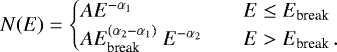 (2)
(2)
For the fitting process, the parameters A, α1, Ebreak, and α2 are left as free parameters and we assume non-relativistic motion for the entire jet. Our results (Table 6) show that the SEDs of knots E, F, I, and A could in principle be satisfactorily described by synchrotron emission of a broken power-law electron distribution with an index α1 ≃ 2.3 resembling that of particle acceleration at highly relativistic shocks (e.g. Achterberg et al. 2001). The second index α2 for these knots deviates from that of a classical cooling break. This is interesting, but could possibly be accounted for by deviations from a homogeneous one-zone approach and/or some additional re-acceleration (e.g. Liu & Shen 2007; Sahayanathan 2008; Liu et al. 2017). Diffusive synchrotron radiation from random small-scale magnetic fields could offer an alternative explanation (Fleishman 2006), although the observed high radio and optical polarisation (e.g. Avachat et al. 2016) may complicate this interpretation. As an alternative a log-parabola model (cf. Massaro et al. 2004; Tramacere et al. 2007),
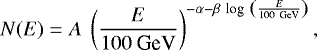 (3)
(3)
has also been employed to fit the SEDs, and the corresponding results are presented in Table 6. A comparison of the MLL values for a broken power-law and a log-parabola model, using the Bayesian information criterion (BIC), shows that the first is preferred over the second.
The SEDs of knots D, B, and C, on the other hand, cannot be well-fitted assuming a homogeneous source region and the broken power-law from Eq. (2). In principle, this should not come as a surprise given the morphological complexity of the knots and the evidence of internal jet stratification (e.g. Perlman & Wilson 2005; Avachat et al. 2016). The findings are nevertheless quite interesting and provide a first indication that the X-ray emission of large-scale AGN jets might reveal some excess above a simple power-law extension from the optical fluxes, and in fact consist of multiple contributions. To explore this in more detail, we added an additional electron component to fit the X-ray data. For simplicity we chose a two exponential cut-off power-laws model,
![\begin{align*}N(E) &= A_{1}~E^{-\alpha_{1}}~\textrm{exp}\left[-\left(\frac{E}{E_{\textrm{cutoff}1}}\right)^{\beta}\right]\nonumber\\ &+A_{2}~E^{-\alpha_{2}}~\textrm{exp}\left[-\left(\frac{E}{E_{\textrm{cutoff}2}}\right)^{\beta}\right] ,\end{align*}](/articles/aa/full_html/2018/04/aa31716-17/aa31716-17-eq6.png) (4)
(4)
treating again A1, α1, Ecutoff1, A2, α2, and Ecutoff2 as free parameters for the fit. We note that alternative descriptions (e.g. two broken power laws with exponential cut-off) are in principle possible, yetrequire that some additional parameters be fixed. In our phenomenological fit the two components are treated as independent. We note, though, that the correlation between the X-ray flux maxima and the synchrotron break frequencies (e.g. Perlman & Wilson 2005) suggest that the X-ray emitting particles are not completely independent from those at lower energies. The results should thus be treated only as a first guide. To reduce the free parameters in our fit (Eq. (4)), we fixed the parameter β to 1 and 2, corresponding to the escaping and cooling-dominated regime, respectively. We assume a magnetic field strength of B = 300 μG (Heinz & Begelman 1997; Marshall et al. 2002) as a reference value in all our calculations. This is certainly a simplification as the magnetic field strength is expected to be different for different regions, for example it can vary by a factor of ~ 2 when different knots are compared (e.g. Biretta et al. 1991; Meisenheimer et al. 1996). We note however, that in the fitting procedure B scales as 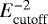 and A−0.5, so that a different B only affects the best-fit value of the break or cut-off energy, and the absolute normalisation.
and A−0.5, so that a different B only affects the best-fit value of the break or cut-off energy, and the absolute normalisation.
The derived model parameters as well as the total energy in non-thermal electrons, We, with 1σ errors are listed in Table 6. Figure 6 shows the corresponding synchrotron model fits for the observed SEDs of the knots. The curves represent the SED models with the maximum likelihood. For knots D, B, and C, the dashed curves and the dot-dashed curves are derived from two exponential cut-off power-law components, respectively, as noted above. The derived values for the required energy in non-thermal electrons range up to We ≃ 1053 erg (knot A) and imply a jet kinetic power Pj ≳ 1043 erg s−1, compatible with other estimates for the general jet power (see Introduction). The energy density in electrons, ue, is typically comparable to (or somewhat less than) that in magnetic fields, uB = B2∕(8π), ensuring efficient confinement.
Our findings provide indications that for knot regions D, B, and C an additional X-ray emitting component is needed to achieve a satisfactory SED description. The indications are strongest in the case of knot C where the X-ray emission seems particularly hard, and less strong in the case of knot D. It is worth noting that radio and optical observations show that the knot D region, located approximately between 2 and 5 arcsec, reveals extended structures and can be further divided into subregions D-East, D-Middle, and D-West, each with additional subcomponents (e.g. Perlman & Wilson 2005; Avachat et al. 2016). Similarly, knot B, located approximately between 13 and 16 arcsec, can be divided into the subcomponents B1 (broader and brighter) and B2, while the knot C region, located approximately between 17 and 19 arcsec, can be divided into the subregions C1 and C2 (Perlman & Wilson 2005; Avachat et al. 2016). It seems thus conceivable that the inferred two-component electron distribution can in principle be accounted for by a superposition of electrons from different subregions. Moreover, the features seen in the optical tend to be slightly narrower than those seen in radio, suggesting that the radiating particles, although co-located, may not necessarily have to be truly co-spatial. We note that we have incorporated only the simplest broken power-law function to fit the SED of the knots (except for B, C, and D) and formally cannot rule out the possibility that the SEDs ofthese knots are produced by more than one electron component as well. Noting these caveats, the respective parent electrons distributions are shown in Fig. 7. As can be seen, for the considered normalisation of the magnetic field strength the electron distribution tends to show a break at energies around one TeV (γb ~ 2 × 106) and needs to extend up to multi-TeV energies (γ ~ 108). These high-energy electrons cannot travel more than a few parsecs before exhausting their energies due to synchrotron cooling. A synchrotron origin thus requires an efficient and continuous in situ acceleration of electrons along the jet.
Inverse Compton (IC) up-scattering of cosmic microwave background (CMB) photons (hνCMB) by these relativistic electrons will result in γ-ray emission extending up to 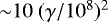 TeV. The characteristic energy flux levels νFν at TeV energies are, however, a factor of ~ uCMB∕uB ~ 10−3 lower than those seen at X-ray energies (νFν ≲ 10−12 erg cm−1 s−1). This TeV emission would thus be below the flux sensitivity limit of current γ-ray instruments.
TeV. The characteristic energy flux levels νFν at TeV energies are, however, a factor of ~ uCMB∕uB ~ 10−3 lower than those seen at X-ray energies (νFν ≲ 10−12 erg cm−1 s−1). This TeV emission would thus be below the flux sensitivity limit of current γ-ray instruments.
SEDs fit results of the knots of M 87.
 |
Fig. 6 SEDsfitting results assuming a synchrotron origin of the X-ray emission. The curves represent the best-fit models. Forknots D, B, and C both a broken power-law fit and a fit based on two exponential cut-off power-law components (dashed and dot-dashed curves, with superposition corresponding to the solid curve) assuming β = 1 are shown. The X-ray flux densities from Marshall et al. (2002) are also plotted for comparison (grey symbols). |
 |
Fig. 6 continued. |
 |
Fig. 7 Parent electron distributions derived from the fitting in Fig. 6. For knots D, B, and C, only the results of the two exponential cut-off power laws are shown. The grey shadow areas correspond to a 2σ confidence level. |
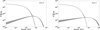 |
Fig. 7 continued. |
4 Conclusions
We have collected Chandra ACIS data for M 87 between 2000 and 2016 with a total exposure of about 1.5 Ms to perform a temporal and spectral analysis of its nucleus and knots. The extracted X-ray light curves of the nucleus and HST-1 reveal significant variability. We confirm indications for day-scale nuclear X-ray variability contemporaneous to the TeV flare in April 2010. HST-1 shows a decline in X-ray flux since 2007 compatible with its synchrotron origin.
The X-ray spectra of the nucleus and jet knots are all formally compatible with a single power law. The resultant X-ray photon index reveals a trend, with index variations ranging from ≃ 2.2 (e.g. in knot D) to ≃ 2.4–2.6 (in the outer knots F, A, and B). When placed in a multiband context, a more complex situation is seen. Modelling the radio to X-ray SEDs with a synchrotron model, a single broken power-law electron distribution with a break at around Eb ~ 1 TeV (assuming B ~ 300 μG) seemingly allows a satisfactorily SED description for most knots. However, for knots B, C, and D an additional high-energy component is needed to account for the broad-band SEDs. This may be partly due to a blending of different (non-resolved) components and/or the occurrence of additional acceleration and emission processes.
The most favourable interpretation for the origin of the X-ray emission is synchrotron radiation of relativistic electrons. This requires that electrons should be able to reach and sustain energies of 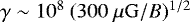 in the presence of losses, i.e. an in situ acceleration of electrons in the jet and its knots. The necessary acceleration efficiency η, defined by tacc = γmec∕(ηeB) (Aharonian et al. 2002), would be of the order of η ≳ 3 × 10−4 (B∕300μG), and likely to be in the reach of stochastic acceleration scenarios (e.g. Rieger et al. 2007). Localised (first-order Fermi) shock acceleration alone, however, would not be sufficient given that here is little evidence for the inter-knot regions to have significantly steeper spectra than the adjacent knots.
in the presence of losses, i.e. an in situ acceleration of electrons in the jet and its knots. The necessary acceleration efficiency η, defined by tacc = γmec∕(ηeB) (Aharonian et al. 2002), would be of the order of η ≳ 3 × 10−4 (B∕300μG), and likely to be in the reach of stochastic acceleration scenarios (e.g. Rieger et al. 2007). Localised (first-order Fermi) shock acceleration alone, however, would not be sufficient given that here is little evidence for the inter-knot regions to have significantly steeper spectra than the adjacent knots.
The homogeneous broken power-law model exhibits a change in indices exceeding that induced by simple cooling effects. Assuming a continuous power-law injection, Perlman & Wilson (2005) have suggested that an energy-dependent filling factor facc(γ) ∝ γ−ξ of the acceleration regions (with ξ ~ 0.3, i.e. occupying a smaller fraction at higher energies), might account for these breaks. Alternative explanations could be a spatial varied propagation of the relativistic electrons or a different particle injection spectrum in a different energy band. However, to some extent all of these assumptions are ad hoc, and detailed modelling as well as an advanced morphological analysis in different energy bands would be required to further qualify them.
There are clear indications that in the case of knots B, C, and D an additional electron contribution is needed to account for the X-ray emission in a multiband context. We formally cannot rule out the possibility that the SEDs of other knots are also produced by a two-component (or more) electron distribution, though the smoothness of the fits might seem to argue for the opposite, i.e. there is no evidence that the X-ray emission in these knots consists of separate spectral components.
The additional electron component indicated in the case of knots B, C, and D is consistent with a bump or a spike-like feature at high energy. This appears compatible with a scenario where electron acceleration occurs in a shear layer and radiative loss is effective (Ostrowski 2000). The short cooling time of the relativistic electrons generally requires that in addition to a possible localised shock-type scenario there must be some distributed in situ acceleration occurring along the jet. Stochastic or shear acceleration could present a natural explanation for this (e.g. Liu et al. 2017). There is circumstantial evidence for a decreased thermal gas emissivity along the jet that appears consistent with the dynamical effects of a cocoon dominated by cosmic rays (CR) accelerated at the shearing jet side boundary (Dainotti et al. 2012). The hint of a CR cocoon and the spectral shape of therelativistic electrons in these knots could indicate that efficient shear acceleration indeed is taking place along the jet in M 87, which seems to link well into the broader evidence for a stratified or spine-sheath flow (e.g. Perlman et al. 1999).
Acknowledgements
We thank the referee Eric Perlman for the very useful comments and suggestions that helped to improve the paper. X.N. Sun thanks Jin Zhang for helpful discussions, and acknowledges the financial support of the China Scholar Council. F.M.R. kindly acknowledges support by a DFG Heisenberg Fellowship (RI 1187/4-1). This research hasmade use of data obtained from the Chandra Data Archive and the Chandra Source Catalog, and software provided by the Chandra X-ray Center (CXC) in the application packages CIAO, ChIPS, and Sherpa.
Appendix
Chandra observations of M 87.
References
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, ApJ, 746, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2002, MNRAS, 332, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Belyanin, A. A., Derishev, E. V., Kocharovsky, V. V., & Kocharovsky, V. V. 2002, Phys. Rev. D, 66, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Science, 314, 1424 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aliu, E., Arlen, T., Aune, T., et al. 2012, ApJ, 746, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Avachat, S. S., Perlman, E. S., Adams, S. C., et al. 2016, ApJ, 832, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Biretta, J. A., Stern, C. P., & Harris, D. E. 1991, AJ, 101, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Biretta, J. A., Sparks, W. B., & Macchetto, F. 1999, ApJ, 520, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, ApJ, 694, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Fendt, C., Eckart, A., & Karas, V. 2017, A&A, 601, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dainotti, M. G., Ostrowski, M., Harris, D., Siemiginowska, A., & Siejkowski, H. 2012, MNRAS, 426, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, J. E. 2001, ApJ, 562, 575 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Orrú, E., Murgia, M., et al. 2012, A&A, 547, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, T., Allen, S. W., Fabian, A. C., Wilson, A. S., & Young, A. J. 2003, ApJ, 582, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Schenck, D. E., et al. 2012, Science, 338, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feng, J., & Wu, Q. 2017, MNRAS, 470, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D. 2006, MNRAS, 365, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gebhardt, K., Adams, J., Richstone, D., et al. 2011, ApJ, 729, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., Meyer, E., & Perlman, E. 2016, Galaxies, 4, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Giroletti, M., Hada, K., Giovannini, G., et al. 2012, A&A, 538, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., & Krawczynski, H. 2002, ApJ, 565, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Biretta, J. A., Junor, W., et al. 2003, ApJ, 586, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Cheung, C. C., Biretta, J. A., et al. 2006, ApJ, 640, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Cheung, C. C., Stawarz, Ł., Biretta, J. A., & Perlman, E. S. 2009, ApJ, 699, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Massaro, F., Cheung, C. C., et al. 2011, ApJ, 743, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Heinz, S., & Begelman, M. C. 1997, ApJ, 490, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Côté, P., Blakeslee, J. P., et al. 2005, ApJ, 634, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Levinson, A., & Globus, N. 2017, MNRAS, 465, 1608 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W.-P., & Shen, Z.-Q. 2007, ApJ, 668, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R.-Y., Rieger, F. M., & Aharonian, F. A. 2017, ApJ, 842, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Macchetto, F., Marconi, A., Axon, D. J., et al. 1997, ApJ, 489, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L., Miller, B. P., Davis, D. S., et al. 2002, ApJ, 564, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meisenheimer,K., Roeser, H.-J., & Schloetelburg, M. 1996, A&A, 307, 61 [NASA ADS] [Google Scholar]
- Mertens, F., Lobanov, A. P., Walker, R. C., & Hardee, P. E. 2016, A&A, 595, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, E. T., Sparks, W. B., Biretta, J. A., et al. 2013, ApJ, 774, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osone, S. 2017, ArXiv e-prints [arXiv:1706.00683] [Google Scholar]
- Ostrowski, M. 2000, MNRAS, 312, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., & Wilson, A. S. 2005, ApJ, 627, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Biretta, J. A., Zhou, F., Sparks, W. B., & Macchetto, F. D. 1999, AJ, 117, 2185 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Biretta, J. A., Sparks, W. B., Macchetto, F. D., & Leahy, J. P. 2001, ApJ, 551, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Harris, D. E., Biretta, J. A., Sparks, W. B., & Macchetto, F. D. 2003, ApJ, 599, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Adams, S. C., Cara, M., et al. 2011, ApJ, 743, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., Di Matteo, T., Fabian, A. C., Hwang, U., & Canizares, C. R. 1996, MNRAS, 283, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, F. M.,& Aharonian, F. 2012, Mod. Phys. Lett. A, 27, 1230030 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, F. M., Bosch-Ramon, V., & Duffy, P. 2007, Ap&SS, 309, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, H. R., Fabian, A. C., McNamara, B. R., & Broderick, A. E. 2015, MNRAS, 451, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Sahayanathan, S. 2008, MNRAS, 388, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., Biretta, J. A., & Macchetto, F. 1996, ApJ, 473, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Tramacere, A., Massaro, F., & Cavaliere, A. 2007, A&A, 466, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, J. L., Barth, A. J., Ho, L. C., & Sarzi, M. 2013, ApJ, 770, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, C. Z., & Zepf, S. E. 2005, ApJ, 624, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Tananbaum, H. D., Van Speybroeck, L. P., & O’Dell, S. L. 2000, in X-Ray Optics, Instruments, and Missions III, eds. J. E. Truemper, & B. Aschenbach, Proc. SPIE, 4012, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S.,& Yang, Y. 2002, ApJ, 568, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S.,& Yang, Y. 2004, ApJ, 610, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V. 2015, in 34th International Cosmic Ray Conference (ICRC2015), Int. Cosmic Ray Conf., 34, 922 [Google Scholar]
- Zhang, J., Bai, J.-M., Chen, L., & Yang, X. 2009, ApJ, 701, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Bai, J. M., Chen, L., & Liang, E. 2010, ApJ, 710, 1017 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fitting parameters for the selected flares of the nucleus using a symmetric exponential function.
X-ray photon indices for the nucleus and HST-1 during the period of H1, H5, and L.
All Figures
 |
Fig. 1 Image from the observation on July 30, 2000 (ObsID 1808), in the 0.2–10 keV, binned in 0. ′′ 123 per pixel and smoothed with a Gaussian of FWHM = 0. ′′3. The source and background regions are indicated by green shapes. Units of right ascension are hours:minutes:seconds, and units of declination are degrees:arcminutes:arcseconds. |
| In the text | |
 |
Fig. 2 Top: Chandra 0.3–7 keV light curve for the nucleus from July 29, 2000 (MJD 51754), to March 17, 2016 (MJD 57464). Five flares (red data points, labelled 1–5) are selected for further analysis in the following. Bottom: zoomed-in light curves of the five flares. The solid lines show the fitting results by using Eq. (1). |
| In the text | |
 |
Fig. 3 Chandra 0.3–7 keV light curve for HST-1 during the same time interval as in Fig. 2. The black points are considered to belong to the low state (L). The dashed lines, on the other hand, separate the high state from January 16, 2002 (MJD 52290), to May 14, 2010 (MJD 55330), into five subsections, that are labelled H1, H2, H3, H4, and H5. The data from April 01, 2009 to May 14, 2010, belong to a transition period between high and low state, and have thus been included in both L and H5 calculations. |
| In the text | |
 |
Fig. 4 Chandra 0.3–7 keV light curves for knots D, E, F, I, A, B, and C during the same time interval as in Fig. 2. |
| In the text | |
 |
Fig. 5 Flux density (top panel) and power-law photon index (bottom panel) in the X-ray 0.3–7 keV band along the jet. The source regions are separated by the dashed lines. For this representation all observations with frame time 0.4 s are used for the nucleus, while for HST-1 only “HST-1 L” data are employed. |
| In the text | |
 |
Fig. 6 SEDsfitting results assuming a synchrotron origin of the X-ray emission. The curves represent the best-fit models. Forknots D, B, and C both a broken power-law fit and a fit based on two exponential cut-off power-law components (dashed and dot-dashed curves, with superposition corresponding to the solid curve) assuming β = 1 are shown. The X-ray flux densities from Marshall et al. (2002) are also plotted for comparison (grey symbols). |
| In the text | |
 |
Fig. 6 continued. |
| In the text | |
 |
Fig. 7 Parent electron distributions derived from the fitting in Fig. 6. For knots D, B, and C, only the results of the two exponential cut-off power laws are shown. The grey shadow areas correspond to a 2σ confidence level. |
| In the text | |
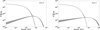 |
Fig. 7 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


