| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201731277 | |
| Published online | 27 April 2018 | |
Collisionless Boltzmann equation approach for the study of stellar discs within barred galaxies
Observatoire astronomique de Strasbourg, Université de Strasbourg, CNRS,
11 rue de l’Université,
67000
Strasbourg, France
Received:
30
May
2017
Accepted:
18
November
2017
We have studied the kinematics of stellar disc populations within the solar neighbourhood in order to find the imprints of the Galactic bar. We carried out the analysis by developing a numerical resolution of the 2D2V (two-dimensional in the physical space, 2D, and two-dimensional in the velocity motion, 2V) collisionless Boltzmann equation and modelling the stellar motions within the plane of the Galaxy within the solar neighbourhood. We recover similar results to those obtained by other authors using N-body simulations, but we are also able to numerically identify faint structures thanks to the cancelling of the Poisson noise. We find that the ratio of the bar pattern speed to the local circular frequency is in the range ΩB∕Ω = 1.77 to 1.91. If the Galactic bar angle orientation is within the range from 24 to 45 degrees, the bar pattern speed is between 46 and 49 km s−1 kpc−1.
Key words: methods: numerical / galaxies: kinematics and dynamics / solar neighborhood
© ESO 2018
1 Introduction
Since the analysis of the hipparcos observations, it has been known that the velocity field of stars within the solar neighbourhood is highly structured. The wavelet analysis of the velocity distribution of stars has shown that structures are present at all scales (Chereul et al. 1998, 1999) with the smallest scales being of the order of 3 km s−1. Many of these structures correspond to identified moving groups or streams. At the largest scale, the Hercules stream is a distinct structure clearly recognisable with hipparcos observations (Dehnen 1998). Later, these results were confirmed and improved with the availability of radial velocities in complement to hipparcos proper motions and parallaxes (Famaey et al. 2005; Antoja et al. 2008). It is now generally admitted that most of the moving groups does not result from the dissolution of stellar clusters. The reason being that stars from a moving group are generally not coeval and have different chemical abundances (see Famaey et al. 2008; Pompéia et al. 2011; Bensby et al. 2014; but see Tabernero et al. 2017). It is now accepted that most moving groups must result from a dynamical process. The most popular explanation concerning the Hercules streams is the proximity of the Sun to the outer Lindblad resonance (OLR) produced by the rotating Galactic bar. Other dynamical explanations were also proposed as streams induced by chaotic motion (Fux 2001; Raboud et al. 1998) or by the ILR of spiral arms (Sellwood 2010). These explanations hold for the two main structures within the (V R, V θ) velocity field. It is suspected that non stationarity, combined to the effects of the bar and spiral arms, leads to the substructures seen at the smallest velocity scales. The recent surveys RAVE (Kunder et al. 2017), SEGUE (Yanny et al. 2009), LAMOST (Xiang et al. 2017), and now Gaia DR1 (Gaia Collaboration 2016) have allowed us to probe larger distances from the immediate solar neighbourhood and to compare the structures of the velocity field at different positions within the Galaxy (Antoja et al. 2015; Monari et al. 2016a,b), and above the Galactic mid-plane (Monari et al. 2014).
The existing models of dynamical processes that explain the observed moving groups are based on different approaches: firstly, analytical study of local resonances (Monari et al. 2016a), secondly, particle-test in a time evolving gravitational potential (Minchev et al. 2007, 2010, 2011) or finally, live N-body simulations (Quillen et al. 2011). Realistic simulations based on N-body (particle test or live) are still limited by the number of particles and they poorly model the faintest structures that remain dominated by the Poisson noise. On the other hand, analytical models of resonances allow to consider more precisely the presence of dynamical substructures within the velocity field, but this implies specific development for each resonance.
Here, to circumvent these limitations, we have considered the resolution of the collisionless Boltzmann equation (CBE) that can be seen as an ideal N-body simulation in the limit of N tends to the infinity. This drastically different approach can be compared with other models. A significant advantage is the easiest identification of the smallest substructures, not dimmed and confused with the Poisson noise fluctuations. However some specific limitations related to the numerical resolution of the CBE exists and will be discussed. Here, we have limited our study to a model that is two-dimensional in space and in velocities (2D2V) of a galactic stellar disc within a rotating barred potential.
The numerical resolution of the CBE had not been frequently envisaged in the context of galactic dynamics. It does not allow to easily follow individual stars and orbits, and it also requires large numerical resources of CPU and memory. Only recently have full 3D3V galactic evolution models been achieved (Yoshikawa et al. 2013; Sousbie & Colombi 2016). We mention some previous works based however on smaller dimensionality by Colombi et al. (2015) with a detailed bibliography, Alard & Colombi (2005) and also pioneering works to study the stability of galactic discs by Nishida et al. (1981) and Watanabe et al. (1981). We also refer the reader to the 1D2V Vlasov-Poisson resolution by Valentini et al. (2005; see also Mangeney et al. 2002). Our numerical resolution of the CBE is based on their numerical analysis.
To close this introduction, we note that the Boltzmann collisionless equation (so named on the recommendation of Hénon), is frequently named the Vlasov equation although this is not historically justified (see Hénon 1982, for a discussion) while other designations exist.
The paper proceeds as follows. Section 2 describes the numerical scheme to solve the CBE and Sect. 3 the galactic modelling (potential and initial distribution function of stars) with the results of some tests. Section 4 describes the results of Galactic modelling of stellar streams and gives the comparison with previous numerical studies of stellar streams followed by a conclusion (Sect. 5).
2 Numerical integration of the CBE
The numerical integration used to solve the CBE is based on the splitting method, coupled with a finite difference upwind scheme. The algorithm is borrowed from the works of Mangeney et al. (2002) and Valentini et al. (2005) that solve the CBE in a 1D2V case (cartesian in coordinate and cylindrical in velocities). Their scheme provides a second order accuracy in space and time and they give the detail of the equations that they have developed. They are succinctly reproduced here and adapted to the 2D2V case.
With f(x, y, xx, vy, t) the distribution function and Fx, Fy the forces, our CBE resolution is performed in Cartesian coordinates:
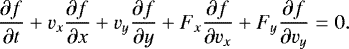
The two main steps are, first, the time discretisation and, second, the space and velocity discretisation. The splitting scheme allows us to split the evolution of the distribution function into two steps, one in the physical space, the other in the velocity space (Cheng & Knorr 1976).
The numerical scheme to solve the 2D2V Boltzmann equation can be written with the operators Λ and Θ, following a similar evolution operator notation used by Mangeney et al. (2002):

with the forces calculated just after the first half-time step.
Thus, the multidimensional CBE equation is splitted into four different one-dimensional equations of the general form
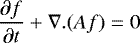 (1)
(1)
that are solved by the van Leer’s upwind scheme (van Leer 1976; Harten 1982) described in Valentini et al. (2005). This scheme is second order in space and time and is stable under the Courant condition.
Test
Detailed tests are given in Valentini et al. (2005) in a 1D2V case. Here, we want to model distribution functions that are stationary solutions of the BCE and we check that these solutions are not modified by numerical diffusion or oscillations. Since we want to model the stellar kinematics during a few dozen of rotation of a Galactic bar, we only need to check the stationarity over a few hundred dynamical times. We determine the smallest size of Gaussian structures in the phase space that are not altered by the numerical diffusion during that period of time. For the resolution of Eq. (1), we have also tested otsher schemes that are described and accuracy are detailed in Toro (2009): a basic Godunov scheme, another scheme of Godunov with a central difference scheme that is second-order, a Lax-Wendroff scheme, a Warming-Beam scheme (a second-order upwind method), and a Fromm scheme.
We have examined the impact of strong gradients and the numerical diffusion in 1D, 2D, and 3D cases, looking at the evolution of a distribution function Gaussian in space and velocities. We have checked the conservation of the initial distribution function with time and through space using two types of models: the first have no forces but do have periodic boundaries in order to examine a uniform advection (with 1, 2 or 3D). A second series of test models have harmonic potential (2D), or using the following equation as a 3D case
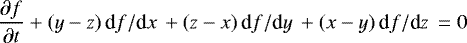
For this second series of models, the distribution function (DF) f rotates around the origin (2D case) or around the axis of direction (1,1,1) (3D case). All these simulations show conditions under which the shape ofthe DF remains unmodified.
From the different tested schemes, we have selected the van Leer scheme that is the most conservative, the other ones being more diffusive. In this case, a Gaussian DF (in space and in velocity) remains unaffected as long as its width is larger or equal to four pixels of the grid. It does not vary by more than a few percent in amplitude for at least 300 dynamical times.
More accurate algorithms exist as for instance the positive flux conservation (PFC) scheme of Filbet et al. (2001) used by (Yoshikawa et al. 2013). With this algorithm, steeper gradients can be accurately modelled. However, we implement the Mangeney algorithm owing to its relative simplicity to code up and since the ~1% precision reached is sufficient for our purposes.
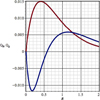 |
Fig. 1 Ratio of the tangential force, Qθ (red), and radial force, Qr (blue), of thebar to the radial force of the disc, with ϵ = 0.1 and Rb = 0.408, depending on the Galactic radius. |
3 Galactic modelling
We are interested in modelling the velocity field of stars and in examining the impact of the galactic bar rotation within the solar neighbourhood. For that purpose, we model the gravitational potential of the galaxy with an analytic axisymmetric disc that has a circular velocity curve rising from the Galactic centre and becoming flat at large distances. The circular velocity curve is given by:

We set v∞ = 1 and a = 0.3. The analytic bar potential is modelled by including a bisymmetric perturbation to the axisymmetric potential given by:
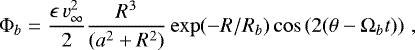
where ϵ gives the strength of the bar, and Rb its radial extension. We set Rb = 0.408. Then the ratio of the maximal tangential force Fbar,θ to the radial force of the disc is:

Figure 1 shows QR and Qθ for ϵ = 0.1, the ratios of the maximal radial and tangential bar forces to the radial force of the axisymmetric disc component. This can be compared with similar figures of bar forces used for the determination of stellar galactic orbits (Athanassoula et al. 1983). We fixed the angular velocity of the bar Ω p = 1.6652, so the outer Linblad resonance (OLR) is exactly Rolr = 1, the corotation radius Rcor = 0.52 and there is no ILR. In the case ϵ = 0.1, the ratio of bar to axysimmetric forces is QR = 0.0084 at Rolr The mass of the bar is increased linearly with time from a null mass at time T = 0 to its maximum value at T = 30 (approximately eight rotations of the bar) and then its mass is set constant.
The integration grid is cartesian. Its lower and upper bounds in x and y are equal to ± 1.5, and are ± 1.3 in vx and vy velocity coordinates. The 4D grid size is 2884 pixel size, corresponding to steps of 0.01 for position and 0.009 for velocity (scaling for a galaxy with Rolr = 8.5 kpc and V c = 220 km s−1, gives steps of 85 pc and 2 km s−1). Since the effective resolution is four pixels to avoid numerical diffusion or numerical oscillations, the effective resolutions are 0.05 in x − y and 0.036 in vx − vy. (respectively 340 pc and 8 km s−1).
We chose at T = 0 an initial Shu-type distribution function (Shu 1969). This distribution function depends only on E and Lz and the corresponding stellar density is nearly radially exponential (Bienaymé 1999) with a scale length Rρ = 0.29 (assuming Rolr = 8.5 kpc gives Rρ = 2.5 kpc).
![\begin{equation*} f(x,y,v_x,v_y)= \frac{2 {\mathrm{\Omega}}}{\kappa} \frac{\Sigma}{2 \pi \sigma^2} \exp \left[- \frac{E-E_c(L_z)}{\sigma^2} \right] \vspace*{-5pt} \end{equation*}](/articles/aa/full_html/2018/04/aa31277-17/aa31277-17-eq8.png)
The initial radial velocity dispersion σR is set constant. Here, we only present results for the two cases σR = 0.1 and 0.2 corresponding to 22 km s−1 and 44 km s−1 if V c = 220 km s−1.
Test with axisymmetric potentials
We have tested and verified the reliability of our numerical integrations in the 2D2V case. First, we have considered simple axisymmetric potentials (ϵ = 0) for which Shu distribution functions are exact stationary solutions of the Boltzmann equation. Using such DFs as initial conditions, we look at the numerical constancy of the DF during 32 rotations of the bar (t = 120).
With a 2884 grid size and a sufficiently high initial velocity dispersions (σR ≥ 0.1) and for radii not too close from the centre, R > 0.15, and away from the outer boundary, R < 1.35, we find that the initial Shu DF is nearly invariant over a long period of time. The density distribution remains exponential and conserves the same scale length (Rρ = 0.29 from T = 0 to 120), while the density decreases by less than 0.1 % for each ΔT = 20 step, at the exception of outer region, R > 1.35, where the density decreases due to the lost flow moving outside of the grid and not compensated by an equivalent inflow. The velocity distribution f(V R, V θ) also stays nearly unchanged, with the velocity dispersion (σR ~ 0.1 and σθ ~ 0.07) changing by less than 0.1 % for each ΔT = 20 step. With this grid size, the initial velocity dispersion cannot be much smaller values without introducing diffusion.
Close to the centre of the grid and for V θ values close to zero, the vθ component of the initial Shu DF has a very strong gradient. There, large numerical diffusion and oscillations appear. Within these inner parts of the simulation R < 0.15 and after a relatively short time (t ~ 20 or 5 bar rotation) the DF reaches a stationary state.
Our (lack of) boundary conditions (BCs) at the physical border of the grid implies that any flow moving outside of the 4D grid is lost. It results that the areas in the corners of the x− y square domain (R >1.5) are rapidly emptied. On a longer timescale, the density at R > 1.35 slowly decreases. To avoid the sweeping of the grid in the outer x− y corners, we have tried another BC by fixingthe DF along the x−y border to the initial Shu DF. Comparing both BCs does not show visible differences for the velocity distribution when R ≤ 1.4.
For the simulations with barred potentials studied in the next paragraph, both BCs lead to identical numerical results for the stellar distribution function when R is smaller than 1.4. As the bar is progressively introduced, the DF widens within the bar and quickly evolves towards a stationary state. After T = 32, the mass ofthe bar is set constant and the DF quickly stops to evolve. Thus, from T = 32 to T = 113 and within the frame rotating with the bar, the relative change of the density is of the order of one percent.
4 Stellar steams
The purpose of this work is the study of orbital resonances and stellar streams within the Galactic disc. The identification of streams in the solar neighbourhood necessitates the statistical identification of overdensities in the velocity space. It implies the use of adapted statistical tools to minimize the number of false detections due the Poisson noise resulting from star counts (Chereul et al. 1999). Within the solar neighbourhood two main large streams, including the Hercules stream, are identified. Smaller streams are also well identified. However, due to the limited number of hipparcos stars within 150 pc distances and with accurate 3D velocities, the faintest visible structures may be statistical noise. This difficulty is reduced by the recent advent of the Gaia DR1/TGAS survey (Gaia Collaboration 2016) and will be drastically minimized thanks to the forthcoming Gaia surveys that will have order of magnitudes larger samples of stars. Now the same difficulty arises analysing N-body simulations, especially analysing a small space volume. Conversely, the CBE resolution allows us to cancel the Poisson noise and to reach very high contrasts between the different streams. This is a significant advantage over N-body simulations. CBE resolution also allows us to compare entirely different methods to study the same physics.
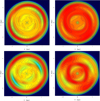 |
Fig. 2 Contrast of the stellar density distribution. (upper left) model A: σR = 0.1, ϵ = 0.1 (upper right) model B: σR = 0.2, ϵ = 0.1 (lower left) model C: σR = 0.1, ϵ = 0.3 (lower right)model D: σR = 0.2, ϵ = 0.3. The major bar axis orientated at 34 degrees from the horizontal axis. Corotation at R = 0.52 and OLR at R = 1. Range of colours is given with an arbitrary scale, different for each image to maximise the contrast (red is positive and blue negative). |
Main characteristics of models.
4.1 Models
Here, we have followed the evolution of the stellar disc distribution function within a barred potential. We have considered the impact of the two following parameters: the force of the bar, the velocity dispersion of the stellar component. In each case, we visually examined the distribution function. A wider variety of models have been considered to explore other model parameters, but we only present these that mimic what we know of our Galaxy and of the stellar kinematics.
We present four models (A to D, Fig. 2 and Table 1) with two different strengths of the bar (ϵ = 0.1 and 0.2) and two different values of the initial radial velocity dispersion (σR = 0.1 and 0.2). The initial velocity dispersion is set constant with radius and it corresponds to the values of 20 and 40 km s−1, if V c = 220 km s−1, corresponding to the dispersions of the young and old thin discs at the solar position, for instance see Wojno et al. (2016).
For these models, Fig. 2 shows the contrast of the density ρ(x, y, t) − ρ(x, y, t = 0): the initial exponential disc density is subtracted, making discernible the structures within the stellar disc. We note the two rings of overdensity at radius R = 0.4 and R = 1, close to the corotation and to the OLR. At time T = 95 or 25 bar rotation, the orientation of the bar, rotating counterclockwise, is 34 degrees from the x-axis. In the case of the strongest bar, we also note an enhancement of the density within the rings. The enhancement is located at the extremities of the bar in the case of the corotation ring, and perpendicularly to the bar orientation in the case of the OLR ring. Close to the solar position, R ~ 1 and at time T = 95, a nearly stationary state is reached. This corresponds to ~25 bar rotations or 15 Galactic rotations of stars (i.e. ~3.6 Gy in Galactic timescale). Faint spiral-like structures are also visible. Not surprisingly, structures seen within the disc are stronger in the case of the strongest bar, and fatter in the case of the highest initial velocity dispersions.
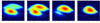 |
Fig. 3 (VR, V θ) velocity distributions for model D at R = 0.94, 1.0, 1.1, 1.2 and θ = 30 degrees at T = 94.8. |
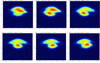 |
Fig. 4 (VR, V θ) velocity distributions for model A at R = 1.0 and θ = 0, 30, 60, 90, 120, 150 degrees at T = 94.8. |
4.2 Resonnances
In the vicinity of resonances, the computed DFs split in two or more components associated to the resonant orbits. Close to the OLR, the velocity distribution (VR, Vθ) is bimodal. The backbone of these two streams are two (1:2) resonant orbits aligned and anti-aligned to the bar. Figure 3 shows the variations of the velocity distribution (VR, Vθ) at different positions. It shows the relative position of the two maxima and their relative amplitude that change along a Galactic radius orientated at a 30 degree angle with respect to the bar main axis (approximately the observed angle between the Galatic centre – Sun axis and the bar main axis). Figure 4 shows the changes of the same two streams at the OLR (R = 1) by varying the position angle with respect to the bar (0 or 180 degrees is the alignment along the main bar axis, and +30 to 45 degrees is the approximate position of the Sun, backwards of the direction of the rotation of the bar (Antoja et al. 2009, 2012, 2014; Dehnen 1998, 1999, 2000; Bovy 2010; Minchev et al. 2007, 2010; Monari et al. 2014, 2015, 2017a). At larger radii, we also identify another important kinematic signature, the (1:1) resonance (Fig. 5), obtained with a simulation of model-type D but with a larger grid and x− y steps (xmax = ymax = 2.5). We note that the two velocity maxima are separated by about Δ Vθ = 44 km s−1 and this structure should be located at ~3 kpc from the Sun towards the Galactic anticentre. It could be detectable with existing proper motion surveys.
4.3 Stationarity
From the CBE in a stationary frame with a constant angular velocity (Binney & Tremaine 2008, Eq. 4.284) and a potential with two axis of symmetry, we can deduce the following symmetry relation for the distribution functions: f(x, y, u, v) = f(x, −y, u, −v) = f(−x, y, −u, v), if the x and y axis are the axis of symmetry of the potential. It implies that along the two axis of the bar θ sym = 0 and π∕2, then f(R, Φsym, vR, vt) = f(R, Φsym, −vR, vt). Along these axis, the DF f is even with respect to vR. For the same reasons, the final stationary density distribution must have the same x and y axis of symmetry. As noted by Fux (2001) and Mühlbauer & Dehnen (2003), this property can be used to estimate the degree of stationarity achieved within the simulations.
Figure 2 shows the density distribution of A to D models at T = 95 where the symmetries are immediately recognizable. It is at the corotation radius that the departure from symmetry is the largest. However, in these regions and also towards the centre, the velocity distributions are very symmetric and smooth. They do not present any visible structure or separated streams.
Initially, we were expecting to see different stellar streams close to the corotation, streams associated to the periodic orbits identified byAthanassoula et al. (1983). This is not the case and looking at the exact shape of periodic orbits in our potentials at the corotation, we realise that the orbital shapes are significantly different from these in Athanassoula et al. (1983). The fact that we use a simple quadrupole for the bar potential appears insufficient to correctly model the inner part of the galaxy. For this reason, we postpone the analysis of the kinematics in the inner part of the galactic models to a future work.
At OLR, R = 1; we note that symmetry is achieved in the density profile along the major bar axis, but not along the minor bar axis. This is also visible in the velocity distribution: only at Φ = 0 the mean radial velocity 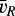 is nearly null.
is nearly null.
The (VR, Vθ) distribution at the OLR (R = 1, Φ = 90) (Fig. 6, left), shows two streams or orbital families. The orbital family with the largest Vθ has a symmetric distribution,while the other one has a slight inclination. Looking more precisely at this second family, we see that the orbits close to the periodic orbit (VR = 0, Vθ = 0.85) are tilted in this diagram and thus are not yet phase-mixed. However for this family, the orbits distant from the periodic orbit show a symmetry with respect to the VR = 0 axis and are phase-mixed. In Fig. 6 right, the asymmetry on the positive VR side is related to this same orbital family.
Finally, if we examine the same distributions shown in Fig. 6 at very different steps T = 32, 64, or 94, (respectively 9, 17 and 25 bar rotation) we do not see visible evolution of the streams. This signifies that the phase space mixing is much slower than the dynamical time of the galaxy and that the phase mixing will not be achieved over the duration of the run performed here.
Figure 7 shows an extreme case of lack of symmetry (at R = 0.94 and θ = 0). In that narrow region of the Galaxy, these asymmetric structures are likely related to the initial conditions. There, the observed streams should give poor constraints on the galactic gravitational potential.
In Fig. 5, R = 1.5, θ = + 30 degrees, with a (1:1) orbit, the departure from symmetry (seen by comparison of the same plot at R = 1.5, θ = − 30 degrees) is the “plume” located at (VR = 0.2, Vθ = 1). This reveals the difficulties that will arise when models will be compared with Gaia observations in order to identify the nature of observed streams within the disc.
 |
Fig. 5 (VR, Vθ) velocity distribution at R = 1.5 and T = 94.8. The main orbits is the nearly circular orbit and the secondary one is a (1, 1) resonant orbit. |
 |
Fig. 6 (VR, Vθ) velocity distribution for model C, with a strong bar and a small velocity dispersion, at two positions. Left: R = 1, θ = 90 degrees, right: R = 1.1, θ = 0 degree. One orbital family has the Vr = 0 axis symmetry, the other one, not yet fully phase mixed has not. |
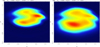 |
Fig. 7 Close to the main axis of the bar, four streams in the case of the strong bar at T = 95, R = 0.94, and θ = 0 with (left) σR = 0.1 (right) σR = 0.2. |
4.4 OLR streams
Our results obtained close to the OLR can be directly compared with other studies that model the Hercules stream in the solar neighbourhood (Famaey et al. 2005, 2008), a stream usually explained by the proximity of the bar OLR with the solar position, see Dehnen (1998, 1999, 2000); Antoja et al. (2009, 2012, 2014); Minchev et al. (2007, 2010); Bovy (2010); Monari et al. (2014, 2015, 2017a), other interpretations have been proposed: Sellwood (2010); Pérez-Villegas et al. (2017) but see also Monari et al. (2017a).
The CBE modelling allows us to obtain a smoother representation of the velocity field, by contrast with N-body or test-particle simulations limited by the Poisson noise. The CBE resolution gives us a fine quantification of the stream properties and models accurately the faintest structures. We find many similarities between our results from the CBE resolution and from published N-body approaches, and we confirm conclusions previously published about the possible location of the Sun with respect to the Galactic bar.
Our results are qualitatively similar to the (VR, Vθ) distribution at various positions as shown for instance by Dehnen (2000, Fig. 2), Minchev et al. (2010, Fig. 1), and Bovy (2010, Fig. 2). This is the reason we do not reproduce the corresponding plots from our own simulations. The relative position and amplitude of the two (1:2) streams vary rapidly depending on the Galactic position angle and radius. From the comparison of models with the observations of (U, V) velocities from hipparcos measurements, we can deduce the position of the Sun and also the pattern speed of the bar.
4.5 Comparison with solar neighbourhood observations
Based on the analysis of stellar proper motions and distances from hipparcos observations, Dehnen (2000) identified the Hercules stream, distinctly separated from the main stellar stream. Based on 3D velocity data, Famaey et al. (2005) also identified a clear-cut separation. Later based on RAVE data, Antoja et al. (2014) studied the evolution of the Hercules stream with Galactic radii. Recently using Gaia DR1/TGAS data complemented with LAMOST data, Monari et al. (2017a) identified the separation between these two streams over an extended range of Galactic radii towards the Galactic anticentre
The characteristics of the stellar streams seem to depend on the different observed stellar populations. We also note that the presence of substructures makes a precise quantitative comparison difficult. The model-observation comparison is also limited by our poor knowledge of the distance to the Galactic centre, of the circular velocity at the solar position, and of the solar velocity with respect to the local standard of rest (LSR; if it were possible to define unambiguously these two last quantities for a barred galaxy). For all these reasons, we will not discuss these points further.
All these elements limit the possibility of building an accurate quantitative model for comparison of the separation between the observed streams, their relative orientation and their relative amplitude. This will be certainly improved thanks to the future Gaia data by increasing the stellar sample size and also the space volume probed. Here we will consider only a rough model calibrated to recover the position and velocity of the Sun, we set Vc = 220 km s−1, R = 8.5 kpc, and assume unknown the LSR velocity. In doing so, we reach the same conclusion as Antoja et al. (2014): it relates the Galactic angular velocities (of the bar and of the circular orbit at the Sun Galactic radius) to the position angle of the Sun with respect to the major bar axis (positive in the bar counter rotating direction). If θ ranges from 24 to 45 degrees, they obtain a range for Ωb∕Ω from 1.80 to 1.90.
Close to the OLR and from the perspective of our models, we notice that the relative amplitude the two streams, their respective position, and their orientation in the (VR, Vθ) plane, quickly vary with the Galactic position (radius R and bar angle θ). For a given position, increasing ϵ, the strength of the bar, results in an increase of the number of stars within the Hercules stream. It also increases the separation between the two streams. Finally, we note that our numerical simulations show that increasing the velocity dispersion changes the ratio number of stars between the two streams. It also significantly increases the separation between the streams, this is expected from the separation of periodic orbits that depends on the bar strength, see figure 2 in Athanassoula et al. (1983).
We find, as Antoja et al. (2014) does, that the relative aspect of the two streams remains approximately identical over a large domain. The hipparcos double stream aspect (Hercules plus main stream) is seen in our models with the correct orientation if R is within the range 1 to 1.4 (varying the θ position). If we restrict the possible angles in the range of accepted values between 24 to 45 degrees, we obtain for the ratio Ω b ∕Ω a range from 1.77 to 1.91 with R varying respectively from 1.02 to 1.10, so just beyond the OLR. This gives us a “high” angular velocity for the bar. If R = 8.5 kpc and Vc = 220 km s−1, then Ω b is between 46 and 49 km s−1 kpc−1.
Other effects have not been considered in the present analysis, such as the exact shape of the circular velocity curve, a more realistic bar potential, or the modification of scale lengths of the Galactic disc for the density Rρ and for the kinematics Rσ. However, an important effect not considered is the non-stationarity. We have used quasi stationary models for comparison with data. Their density is effectively nearly constant after T = 30 (8 bar rotation), and then the relative aspect of the two streams close to the OLR varies very slowly. But, if the Galactic bar is quickly evolving, a direct comparison with our models would be partly questionable. This would introduce a supplementary uncertainty for the determination of the solar neighbourhood position within the models.
This preliminary work allows us to verify the reliability of the BCE numerical resolution to analyse stellar streams, and it shows an improvement to model faint structures in the phase space by comparison with N-body simulations. Future works are planned andwe will replace the quadruple galactic bar with more realistic gravitational potentials. This is necessary to analyse the behaviour of streams close to the corotation. More realistic potentials will be also necessary for a comparison to Gaia observations. We will implement the algorithm of Filbet et al. (2001) that minimizes numerical diffusion and oscillations in the neighbourhood of strong density and velocity gradients. Such an algorithm will improve the resolution.
From symmetry arguments, we have noticed that we did not achieved exact stationary solutions for the DFs. We suppose that this could be achieved by forcing symmetry of the distribution functions during the numerical evolution. We expect it will shorten the numerical time to reach a stationary state. This will allow a direct comparison with the stationary solutions obtained by analytical means by Monari et al. (2017b) and with theoretical predictions.
After having considered the effect of bar resonances, we will examine the impact of resonances of spiral arms. We intend to study the combined effects of bar and spiral arms and the related non stationarity of the potential. This is frequently advocated as an explanation of the split of stellar streams in smaller ones as they are seen with hipparcos and Gaia data. Since these structures are faint in current N-body simulations, and are at the limit of the Poisson noise fluctuations, it will be fruitful to reexamine this question by solving the Boltzmann equation.
5 Conclusion
The code presented in this paper solves the collisionless Boltzmann equation (CBE) in a four-dimensional phase space, two-dimensional in the physical space (2D) and two-dimensional in the velocity motion (2V). It is applied to the study of the stellar kinematics within the disc of a barred galaxy.
We have shown that a numerical resolution of the CBE can be used to model the stellar kinematics of a spiral galaxy. We numerically recovered the (1:2) resonnance of the OLR created by a rotating bar that is usually advocated to explain the main stellar streams observed within the solar neighbourhood. We recovered similar results to these obtained by different authors using N-body simulations (Dehnen 2000; Minchev et al. 2010; Antoja et al. 2014). The CBE code cancels the statistical noise allowing us to follow faint structures and densities within the phase space. We confirm the probable position of the Sun with respect to the Galactic centre and the Galactic bar orientation as well as the bar pattern speed found by Dehnen (2000) and Minchev et al. (2010). Recent analyses of the disc stellar kinematics on larger scales in the solar neighbourhood (Antoja et al. 2014; Monari et al. 2017a) corroborate the interpretation of the Sun position as being close to the bar OLR. Our simulations confirms these findings.
Gaia data will provide more accurate informations about the two (1:2) resonant orbits, and also on the Galactic bar orientation. The bar pattern speed and the position of other important resonances as the corotation will be also constrained more tightly. The partial phase mixing of stellar orbits will probably make this task laborious. We expect that the kinematic signatures seen in our simulation, like the (1:1) resonant orbit at R = 1.5 (i.e. 12 kpc), should be detected. All such features will help to constrain the disc kinematics and the Galactic gravitational potential.
Acknowledgement
We would like to thank Ivan Minchev for a very opportune question while we recently met at the Gaia meeting in Nice, and Benoit Famaey and Christian Boily for pertinent remarks.
References
- Alard, C., & Colombi, S. 2005, MNRAS, 359, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Figueras, F., Fernández, D., & Torra, J. 2008, A&A, 490, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoja, T., Valenzuela, O., Pichardo, B., et al. 2009, ApJ, 700, L78 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Helmi, A., Bienaymé, O., et al. 2012, MNRAS, 426, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Helmi, A., Dehnen, W., et al. 2014, A&A, 563, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoja, T., Monari, G., Helmi, A., et al. 2015, ApJ, 800, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Bienaymé, O., Martinet, L., & Pfenniger, D. 1983, A&A, 127, 349 [NASA ADS] [Google Scholar]
- Bienaymé, O. 1999, A&A, 341, 86 [NASA ADS] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Princeton, NJ, (Princeton University Press), 1987 [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J. 2010, ApJ, 725, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Chereul, E., Crézé, M., & Bienaymé, O. 1998, A&A, 340, 384 [NASA ADS] [Google Scholar]
- Chereul, E., Crézé, M., & Bienaymé, O. 1999, A&AS, 135, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheng, C. Z., & Knorr, G. 1976, J. Comput. Phys., 22, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., Sousbie, T., Peirani, S., Plum, G., & Suto, Y. 2015, MNRAS, 450, 3724 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1998, AJ, 115, 2384 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1999, ApJ, 524, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2000, AJ, 119, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Famaey, B., Siebert, A., & Jorissen, A. 2008, A&A, 483, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filbet, F., & Sonnendrücker, E. 2003, Comput. Phys. Commun., 150, 247 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Filbet, F., Sonnendrücker, E., & Bertrand, P. 2001, J. Comput. Phys., 172, 166 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fux, R. 2001, A&A, 373, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration, (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harten, A. 1982, J. Comput. Phys., 135, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Hénon, M. 1982, A&A, 114, 211 [NASA ADS] [Google Scholar]
- Kunder, A., Kordopatis, G., Steinmetz, M., et al. 2017, AJ, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Mangeney, A., Califano, F., Cavazzoni, C., & Travnicek, P. 2002, J. Comput. Phys., 179, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Nordhaus, J., & Quillen, A. C. 2007, ApJ, 664, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Boily, C., Siebert, A., & Bienaymé, O. 2010, MNRAS, 407, 2122 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monari, G., Helmi, A., Antoja, T., & Steinmetz, M. 2014, A&A, 569, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monari, G., Famaey, B., & Siebert, A. 2015, MNRAS, 452, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Famaey, B., & Siebert, A. 2016a, MNRAS, 457, 2569 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Famaey, B., Siebert, A., et al. 2016b, MNRAS, 461, 3835 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Kawata, D., Hunt, J. A. S., & Famaey, B. 2017a, MNRAS, 466, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Famaey, B., Fouvry, J.-B., & Binney, J. 2017b, MNRAS, 471, 4314 [NASA ADS] [CrossRef] [Google Scholar]
- Mühlbauer, G., & Dehnen, W. 2003, A&A, 401, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nishida, M. T., Yoshizawa, M., Watanabe, Y., Inagaki, S., & Kato, S. 1981, PASJ, 33, 567 [NASA ADS] [Google Scholar]
- Pérez-Villegas, A., Portail, M., Wegg, C., & Gerhard, O. 2017, ApJ, 840, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Pompéia, L., Masseron, T., Famaey, B., et al. 2011, MNRAS, 415, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Raboud, D., Grenon, M., Martinet, L., Fux, R., & Udry, S. 1998, A&A, 335, L61 [NASA ADS] [Google Scholar]
- Sellwood, J. A. 2010, MNRAS, 409, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1969, ApJ, 158, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., & Colombi, S. 2016, J. Comput. Phys., 321, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Tabernero, H. M., Montes, D., González Hernández, J. I., & Ammler-von Eiff, M. 2017, A&A, 597, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toro, E.F. 2009, Rieman Solvers and Numerical Methods for Fluid Dynamics (Springer) [CrossRef] [Google Scholar]
- Valentini, F., Veltri, P., & Mangeney, A. 2005, J. Comput. Phys., 210, 730 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1976, J. Comput. Phys., 23, 263 [Google Scholar]
- Watanabe, Y., Inagaki, S., Nishida, M. T., Tanaka, Y. D., & Kato, S. 1981, PASJ, 33, 541 [NASA ADS] [Google Scholar]
- Wojno, J., Kordopatis, G., Steinmetz, M., et al. 2016, MNRAS, 461, 4246 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, M.-S., Liu, X.-W., Yuan, H.-B., et al. 2017, MNRAS, 467, 1890 [NASA ADS] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377–99 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, K., Yoshida, N., & Umemura, M. 2013, ApJ, 762, 116 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Ratio of the tangential force, Qθ (red), and radial force, Qr (blue), of thebar to the radial force of the disc, with ϵ = 0.1 and Rb = 0.408, depending on the Galactic radius. |
| In the text | |
 |
Fig. 2 Contrast of the stellar density distribution. (upper left) model A: σR = 0.1, ϵ = 0.1 (upper right) model B: σR = 0.2, ϵ = 0.1 (lower left) model C: σR = 0.1, ϵ = 0.3 (lower right)model D: σR = 0.2, ϵ = 0.3. The major bar axis orientated at 34 degrees from the horizontal axis. Corotation at R = 0.52 and OLR at R = 1. Range of colours is given with an arbitrary scale, different for each image to maximise the contrast (red is positive and blue negative). |
| In the text | |
 |
Fig. 3 (VR, V θ) velocity distributions for model D at R = 0.94, 1.0, 1.1, 1.2 and θ = 30 degrees at T = 94.8. |
| In the text | |
 |
Fig. 4 (VR, V θ) velocity distributions for model A at R = 1.0 and θ = 0, 30, 60, 90, 120, 150 degrees at T = 94.8. |
| In the text | |
 |
Fig. 5 (VR, Vθ) velocity distribution at R = 1.5 and T = 94.8. The main orbits is the nearly circular orbit and the secondary one is a (1, 1) resonant orbit. |
| In the text | |
 |
Fig. 6 (VR, Vθ) velocity distribution for model C, with a strong bar and a small velocity dispersion, at two positions. Left: R = 1, θ = 90 degrees, right: R = 1.1, θ = 0 degree. One orbital family has the Vr = 0 axis symmetry, the other one, not yet fully phase mixed has not. |
| In the text | |
 |
Fig. 7 Close to the main axis of the bar, four streams in the case of the strong bar at T = 95, R = 0.94, and θ = 0 with (left) σR = 0.1 (right) σR = 0.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation*} \mathrm{\Sigma}= \mathrm{\Sigma}_0 \exp [ -R_c(L_z)/R_{\rho}] \vspace*{-5pt} \end{equation*}](/articles/aa/full_html/2018/04/aa31277-17/aa31277-17-eq9.png)