| Issue |
A&A
Volume 612, April 2018
H.E.S.S. phase-I observations of the plane of the Milky Way
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201730824 | |
| Published online | 09 April 2018 | |
Characterising the VHE diffuse emission in the central 200 parsecs of our Galaxy with H.E.S.S.
1
Centre for Space Research, North-West University,
2520 Potchefstroom,
South Africa
2
Universität Hamburg,
Institut für Experimentalphysik,
Luruper Chaussee 149,
22761 Hamburg,
Germany
3
Max-Planck-Institut für Kernphysik,
PO Box 103980,
69029 Heidelberg,
Germany
4
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place,
Dublin 2,
Ireland
5
National Academy of Sciences of the Republic of Armenia,
Marshall Baghramian Avenue,
24, 0019 Yerevan,
Armenia
6
Yerevan Physics Institute,
2 Alikhanian Brothers St.,
375036 Yerevan,
Armenia
7
Institut für Physik,
Humboldt-Universität zu Berlin,
Newtonstr. 15,
12489 Berlin,
Germany
8
University of Namibia, Department of Physics,
Private Bag 13301,
Windhoek,
Namibia
9
GRAPPA, Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
10
Department of Physics and Electrical Engineering, Linnaeus University,
351 95 Växjö,
Sweden
11
Institut für Theoretische Physik,
Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum,
Germany
12
GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of High-Energy Physics, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
13
Institut für Astro- und Teilchenphysik,
Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck,
Austria
14
School of Physical Sciences, University of Adelaide,
5005 Adelaide,
Australia
15
LUTH, Observatoire de Paris, PSL Research University, CNRS, Université Paris Diderot,
5 place Jules Janssen,
92190 Meudon,
France
16
Sorbonne Universités,
UPMC Université Paris 06,
Université Paris Diderot,
Sorbonne Paris Cité, CNRS, Laboratoire de Physique Nucléaire et de Hautes Énergies (LPNHE),
4 place Jussieu,
75252 Paris Cedex 5,
France
17
Laboratoire Univers et Particules de Montpellier,
Université Montpellier,
CNRS/IN2P3,
CC 72, Place Eugène Bataillon,
34095 Montpellier Cedex 5,
France
18
DSM/Irfu,
CEA Saclay,
91191 Gif-Sur-Yvette Cedex,
France
19
Astronomical Observatory, The University of Warsaw,
Al. Ujazdowskie 4,
00-478 Warsaw,
Poland
20
Aix-Marseille Université,
CNRS/IN2P3, CPPM UMR 7346,
13288 Marseille,
France
21
Instytut Fizyki Ja̧drowej PAN,
ul. Radzikowskiego 152,
31-342 Kraków,
Poland
22
Funded by EU FP7 Marie Curie, grant agreement No. PIEF-GA-2012-332350
23
School of Physics, University of the Witwatersrand,
1 Jan Smuts Avenue,
Braamfontein, 2050 Johannesburg,
South Africa
24
Laboratoire d’Annecy-le-Vieux de Physiquedes Particules,
Université Savoie Mont-Blanc, CNRS/IN2P3,
74941 Annecy-le-Vieux,
France
25
Landessternwarte,
Universität Heidelberg, Königstuhl,
69117 Heidelberg,
Germany
26
Université Bordeaux,
CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan,
33175 Gradignan,
France
27
Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center,
10691 Stockholm,
Sweden
28
Wallenberg Academy Fellow
29
Institut für Astronomie und Astrophysik,
Universität Tübingen,
Sand 1,
72076 Tübingen,
Germany
30
Laboratoire Leprince-Ringuet,
École Polytechnique, CNRS/IN2P3,
91128 Palaiseau,
France
31
APC,
AstroParticule et Cosmologie,
Université Paris Diderot, CNRS/IN2P3, CEA/Irfu,
Observatoire de Paris,
Sorbonne Paris Cité,
10,
rue Alice Domon et Léonie Duquet,
75205 Paris Cedex 13,
France
32
Univ. Grenoble Alpes,
IPAG; CNRS, IPAG,
38000 Grenoble,
France
33
Department of Physics and Astronomy, The University of Leicester, University Road,
Leicester, LE1 7RH,
UK
34
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences,
ul. Bartycka 18,
00-716 Warsaw,
Poland
35
Institut für Physik und Astronomie,
Universität Potsdam,
Karl-Liebknecht-Strasse 24/25,
14476 Potsdam,
Germany
36
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Erlangen Centre for Astroparticle Physics,
Erwin-Rommel-Str. 1,
91058 Erlangen,
Germany
37
DESY,
15738 Zeuthen,
Germany
38
Obserwatorium Astronomiczne,
Uniwersytet Jagielloński,
ul. Orla 171,
30-244 Kraków,
Poland
39
Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University,
Grudziadzka 5,
87-100 Torun, Poland
40
Department of Physics, University of the Free State,
PO Box 339,
9300 Bloemfontein,
South Africa
41
Heisenberg Fellow (DFG),
ITAUniversität Heidelberg,
69120 Heidelberg,
Germany
42
GRAPPA, Institute of High-Energy Physics, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
43
Department of Physics, Rikkyo University,
3-34-1 Nishi-Ikebukuro,
Toshima-ku,
171-8501 Tokyo,
Japan
44
Japan Aerospace Exploration Agency (JAXA), Institute of Space and Astronautical Science (ISAS),
3-1-1 Yoshinodai,
Chuo-ku, Sagamihara,
229-8510 Kanagawa,
Japan
45
Now at The School of Physics, The University of New South Wales,
2052 Sydney,
Australia
★ Corresponding author: H.E.S.S. Collaboration,
e-mail: contact.hess@hess-experiment.eu
Received:
20
March
2017
Accepted:
7
June
2017
The diffuse very high-energy (VHE; >100 GeV) γ-ray emission observed in the central 200 pc of the Milky Way by H.E.S.S. was found to follow dense matter distribution in the central molecular zone (CMZ) up to a longitudinal distance of about 130 pc to the Galactic centre (GC), where the flux rapidly decreases. This was initially interpreted as the result of a burst-like injection of energetic particles 104 yr ago, but a recent more sensitive H.E.S.S. analysis revealed that the cosmic-ray (CR) density profile drops with the distance to the centre, making data compatible with a steady cosmic PeVatron at the GC. In this paper, we extend this analysis to obtain, for the first time, a detailed characterisation of the correlation with matter and to search for additional features and individual γ-ray sources in the inner 200 pc. Taking advantage of 250 h of H.E.S.S. data and improved analysis techniques, we perform a detailed morphology study of the diffuse VHE emission observed from the GC ridge and reconstruct its total spectrum. To test the various contributions to the total γ-ray emission, we used an iterative 2D maximum-likelihood approach that allows us to build a phenomenological model of the emission by summing a number of different spatial components. We show that the emission correlated with dense matter covers the full CMZ and that its flux is about half the total diffuse emission flux. We also detect some emission at higher latitude that is likely produced by hadronic collisions of CRs in less dense regions of the GC interstellar medium. We detect an additional emission component centred on the GC and extending over about 15 pc that is consistent with the existence of a strong CR density gradient and confirms the presence of a CR accelerator at the very centre of our Galaxy. We show that the spectrum of full ridge diffuse emission is compatible with that previously derived from the central regions, suggesting that a single population of particles fills the entire CMZ. Finally, we report the discovery of a VHE γ-ray source near the GC radio arc and argue that it is produced by the pulsar wind nebula candidate G0.13−0.11.
Key words: gamma rays: general / gamma rays: ISM / Galaxy: center / cosmic rays
© ESO 2018
1 Introduction
There is growing evidence that the Galactic centre (GC) plays a key role in particle acceleration in the Galaxy. The most prominent evidence is the presence of the huge Fermi bubbles extending 10 kpc above and below the Galactic disk (Bland-Hawthorn & Cohen 2003; Su et al. 2010; Ackermann et al. 2014). Even if their physical origin is still unknown, the object or processes powering them has to be within the central hundreds of parsecs around the GC.
The H.E.S.S. discovery of diffuse very high-energy (VHE; >100 GeV) γ-ray emission in the GC region extending over 1° in longitude and spatially correlating with the dense gas of the central molecular zone (CMZ) has revealed that the region (the so-called GC ridge) is pervaded by VHE cosmic-rays (CRs) with a density up to a factor nine times larger than the value measured locally at Earth (Aharonian et al. 2006a, Paper I). The observation of this diffuse emission has also been reported above the TeV by the VERITAS and MAGIC collaborations (Archer et al. 2016; Ahnen et al. 2017). As the diffuse γ-ray emission does not follow the gas distribution beyond 1.0−1.3°, or 140–180 pc at 8 kpc distance, it was first interpreted as the result of a massive impulsive injection of CRs by a source close to the GC. This picture has now dramatically changed with the recent observation of a pronounced gradient in the CR density profile deduced from the diffuse VHE γ-ray emission in the central 200 pc (H.E.S.S. Collaboration 2016, Paper II). This profile, peaking in the inner tens of parsecs, is found to be consistent with the propagation of particles injected by a steady source located at the GC itself. Furthermore, no cut-off is found in the γ-ray spectrum of the diffuse emission extracted from a region at 0.15−0.45° (20−63 pc) distance to the GC, making this source the first Galactic PeVatron, which accelerates charged particles to energies of at least 1 PeV (1015 eV).
In this work, we extend the analysis presented in Paper II to further the morphology and energy spectrum studies of the VHE γ-ray emission in the central 200 pc and look for additional components and sources. To do so, we take advantage of the large data set accumulated by H.E.S.S. from 2004 to 2012 and of improved analysis methods now available (Becherini et al. 2011; Khelifi et al. 2015)to perform a 2D iterative maximum-likelihood analysis and extract the various spatial components required to model the total emission from the GC ridge, which is an approach similar to that used for the H.E.S.S. Galactic plane survey (HGPS; H.E.S.S. Collaboration 2018a). Since there is no reliable 3D model of the gas distribution in the CMZ, we do not model the ridge emission with a physically motivated CR density, but resort to an empirical model made of several components and study the residual emission to search for new individual sources or a diffuse excess of γ-rays.
After a presentation of the data set and the data reduction technique employed, we detail the 2D maximum-likelihood fitting technique. We then present the result of the iterative procedure. We describe the various components required to reproduce the 2D morphology of the GC ridge diffuse emission and extract the total spectrum. We show that the emission fills the entire CMZ, correlates with dense matter, extends at larger latitude, and exhibits a spectrum compatible with that previously derived in the very central part of the CMZ, revealing that PeV CRs prevade an even wider area in the CMZ than previously published. We also detect an extended central component around Sgr A⋆ and show that it most likely originates from an enhancement of CRs in the inner tens of pc around the GC, thereby confirming the results obtained in Paper II. Finally, we report the detection of a new point-like γ-ray source HESS J1746−285 in the vicinity of the GC radio arc (Yusef-Zadeh et al. 1984). After presenting the physical characteristics of this source, we compare it to known objects in the region and show that its position is consistent with the pulsar wind nebula (PWN) candidate G0.13−0.11 (Wang et al. 2002).
2 Analysis
2.1 H.E.S.S. observations and data analysis
The High Energy Stereoscopic System (H.E.S.S.) is an array of imaging atmospheric Cherenkov telescopes located at 1835 m altitude in the Khomas highlands of Namibia. The H.E.S.S. array is designed to detect and image the brief optical Cherenkov flash emitted from air showers, induced by the interaction of VHE γ-rays with the Earth’s atmosphere. In the first phase of H.E.S.S., during which the data used here were recorded, the array consisted of four 13 m telescopes placed on a square of 120 m side length. γ-ray events were recorded when at least two telescopes in the array were triggered in coincidence (Funk et al. 2004), allowing for a stereoscopic reconstruction of γ-ray events (for further details see Aharonian et al. 2006b).
In 2012, H.E.S.S. entered its second phase with the addition of a fifth large 28 m telescope at the centre of the array. The addition of this telescope, which is able to trigger both independently and in concert with the rest of the array, increases the energy coverage of the array to lower energies. The work presented in the following sections does not use data recorded with the large telescope.
The data set selected for the analysis includes observations within 5° of the GC position, conducted between 2004 and 2012. Applying standard data quality selection criteria and keeping only four-telescope observations we used a total live time of 259 h with a mean zenith angle of 22°. The data were analysed with an advanced multivariate analysis procedure developed to improve the sensitivity to weak signals and optimised for morphological studies of very extended sources (Becherini et al. 2011; Khelifi et al. 2015). This analysis provides a good angular resolution of 0.077° (68% containment radius of the point spread function; PSF), crucial for the study shown here, and an average energy threshold of ~350 GeV. The γ-ray measurements by ground-based Cherenkov telescopes suffer from irreducible backgrounds from air showers induced by charged CRs, electrons, protons, and heavier nuclei, which can mimic γ-ray air showers. Modelling and subtraction techniques are needed for these CR backgrounds. To generate such 2D background maps for the production of γ-ray excess images, we used an adaptive ring background method that is suitable for crowded regions, excluding known regions of γ-ray emission from the background ring (Berge et al. 2007; H.E.S.S. Collaboration 2018a). All the results shown here were cross-checked with an alternative H.E.S.S. calibration and analysis chain that was used for the HGPS production (H.E.S.S. Collaboration 2018a). The instrument response functions, PSF, and γ-ray exposure were produced following the approach described in H.E.S.S. Collaboration (2018a). To compare the molecular matter and the γ-ray emission in the central 200 pc of the Galaxy to each other, we produced a map over a region that covers the full CMZ extension from 358.5° to 1.8° in longitude and ± 1.5° in latitude. A 0.5° ×0.5° region centred on HESS J1745−303 (Aharonian et al. 2008) was excluded from the maps in order not to bias the fit with unrelated emission. For the spectral analysis, the background was estimated using the reflected region method (Berge et al. 2007), where the background was derived from circular off-source regions with the same angular size and γ-ray detection efficiency as the on-source region. The differential VHE γ-ray spectrum was then fitted with a spectral model by forward folding it with the instrument response functions (Piron et al. 2001; Jouvin et al. 2015).
2.2 General morphology of the GC ridge emission
Figure 1 (top) shows the γ-ray significance map of the GC region smoothed with the H.E.S.S. PSF. Beyond the two bright sources, HESS J1745−290 and G0.9+0.1, the fainter diffuse emission is visible along with the extended source HESS J1745−303. Using the fluxes derived from the model fit (see Sect. 2.4 below), we can produce a significance map of the ridge emission with the point sources subtracted. Figure 1 (bottom) shows this map with cyan contours overlaid, which indicate the molecular gas density distribution as traced by the line of the 1−0 transition in the CS molecule (Tsuboi et al. 1999). The GC ridge emission is detected up to ℓ = 1.5° along the Galactic plane, following the full CMZ extension, but with a fading brightness in its tail regions confirming the result of Paper I. Additionally, some faint emission at high latitude (|b| > 0.2°) beyond the CS emission region is now visible. The γ-ray map also shows more details and features regarding the massive molecular complexes Sgr B2, Sgr C, and Sgr D at ℓ = 1.2°, which are clearly resolved.
The longitude profile of the GC ridge diffuse emission is shown in Fig. 2. We compare the data with the model proposed in Paper I to account for an impulsive injection of CRs based on the CS map multiplied by a Gaussian of 0.8° width and centred at the GC. This model fails to reproduce the central excess of emission that we clearly see in the γ-ray profile. This requires the presence of a strong gradient in the CR distribution peaking around the GC. Conversely, this measured central excess of emission is well reproduced by a model in which the Gaussian is replaced by the integrated density profile of a steady CR source (Paper II). The position of the γ-ray data peak appears slightly shifted from the CR model, mainly because the emission in the central 30 pc is not correlated with the 2D CS distribution. Therefore, in the following, we do not try to reproduce the diffuse γ-ray emission by such a physically motivated model that would in any case be based on the simplistic hypothesis of a homogeneous gas density along the line of sight. We would be forced to use such an assumption because we lack a full 3D gas distribution (see discussion in Sect. 2.3). Since this approach does not reproduce the data well, we resorted to building an empirical model made of multiple components that individually have no immediate physical meaning but taken together reproduce the data.
 |
Fig. 1 VHE γ-ray images of the GC region in Galactic coordinates and smoothed with the H.E.S.S. PSF. Top: γ-ray significance map is shown. Bottom: residual significance map after subtraction of the two point sources G0.9+0.1 and HESS J1745−290 is shown. The cyan contours indicate the density of molecular gas as traced by the CS brightness temperature integrated over the local standard of rest (LSR) velocity from −200 to 200 km s−1 (Tsuboi et al. 1999) and smoothed with the H.E.S.S. PSF (0.077°). The outer contour level is 36 K km s−1, which is about six times the noise level (Tsuboi et al. 1999). The position of the new H.E.S.S. source HESS J1746−285, which is coincident with the GC radio arc (Yusef-Zadeh et al. 1984), is indicated with a black cross. |
 |
Fig. 2 Longitude profile of the VHE γ-ray GC ridge emission in units of excess counts∕arcmin2. The CR background and the two point sources HESS J1745−290 and G0.9+0.1 were subtracted from the counts map. The profile has been integrated over − 0.3° < b < +0.3°. The green line shows the model based on the VHE emission profile used in Paper I, which includes a central 0.8° width Gaussian multiplied by the CS map. This does not account for the clear excess at the GC position. As shown in Paper II the latter is rather well reproduced by a profile obtained with a 1∕r CR density integrated over a homogeneous gas density in the line of sight and multiplied by the integrated CS map (blue line). |
2.3 Emission model fit
To derive the various contributions to the total γ-ray emission, we used a 2D maximum-likelihood approach similar to that used for the construction of the HGPS catalogue (H.E.S.S. Collaboration 2018a). A 2D model of the expected event counts was fitted to the data assuming the events obey Poisson statistics. The model takes into account the estimated CR backgrounds and a physical γ-ray model weighted by the γ-ray exposure and convolved with the H.E.S.S. PSF. The different model components are:
-
The estimated charged particle background event map (the normalised OFF map; see H.E.S.S. Collaboration 2018a) left constant during the fit procedure.
-
A 2D model of the Galactic large-scale unresolved emission (Abramowski et al. 2014) left constant during the fit procedure. In order to estimate this contribution, we excluded regions with significant emission from the map and fit this Galactic component over a large box of 10° × 8°, assuming a simple emission profile with a flat distribution in Galactic longitude and a Gaussian distribution in Galactic latitude, weighted by the γ-ray exposure (see the details of the approach in H.E.S.S. Collaboration 2018a).
-
The point sources HESS J1745−290, which is coincident with Sgr A⋆, and HESS J1747−281, which is coincident with the composite supernova remnant (SNR) G0.9+0.1. After a first fit, the positions of these point sources are fixed but their amplitude is left free and fitted in each step of the procedure.
-
The CR induced γ-ray emission in the GC ridge. This component is assumed to be the product of a gas map and a 2D symmetrical Gaussian following the procedure used in Paper I and referred as Dense Gas Component (DGC) thereafter. The normalisation and Gaussian extension of this component are fitted.
-
Other ad hoc Gaussian components are added to the model, depending on the residual map, at each step of the process.
The choice of the gas tracer to model the main GC ridge diffuse emission component might affect the fit result. The main constituent of the interstellar gas in the central 200 pc is the molecular matter distributed into a set of very dense clouds, whereas no more than 10 percent is present in the form of atomic gas (Ferrière et al. 2007). A full 3D model of the CMZ molecular clouds would be well suited to determine the exact distribution of γ-ray emission over the ridge, but so far no satisfactory model is available. Indeed, our poor knowledge of the true gas kinematics near the GC renders the methods based on kinetics conversions between velocities and distance unreliable. Several 2D matter templates derived from millimeter molecular tracers of the interstellar gas distribution in the CMZ are available. The lines of HCN(1−0) and CS(1−0) are optically thin tracers of dense gas and are bright enough to be detected over most of the CMZ, whereas other molecules are detected only in the densest cores (Jones et al. 2012). Here, we used the CS (1−0) line emission (Tsuboi et al. 1999). To test the impact of the actual gas tracer used, we tested the HCN (1−0) transition from Jones et al. (2012) and obtained consistent results confirming that CS is a robust tracer. We therefore only show results obtained with CS in the following. We note that all these surveys are only sensitive to dense gas (n > 104 cm−3 ). We therefore expect our main ridge component based on CS to miss regions of more diffuse gas. Furthermore, most tracers suffer from self-absorption in extremely dense regions such as the core of Sgr B2. The model must be poor in this specific region. The recent high-angular resolution column density map of the central part of the CMZ derived from thermal images of cold dust (Molinari et al. 2011) does not suffer from this problem but its sensitivity to the high ionisation rate in the core of Sgr B2 can also affect the derived density.
The iterative fitting process was performed using the Sherpa software package (CIAO v4.5; Refsdal et al. 2009). The model parameter values and associated confidence intervals are given for the best fit model in Table 1 and each step is detailed in Table A.1. The model was tested against H.E.S.S. data during the fitting procedure and two criteria – a good statistical fit and the distribution of residuals – guided the search for the best model. The significance of different components was measured by the likelihood ratio test statistic (TS), TS = 2log(Ln+1∕Ln), comparing the likelihood between model n and model n + 1. At each step, a significance map of the residual and a TS map was created, allowing us to search for features that should be included in the model. This comparison of TS values remains an important tool for selecting models that provide gradual improvements when fitting the data. In the limit of a large number of counts per bin the TS for the null hypothesis is asymptotically distributed as a χ2 ∕d.o.f., where d.o.f.,the degrees of freedom, is the number of free parameters that describe the different model components. The detection threshold is set to TS > 30, following the prescription used for the HGPS (see Sect. 4.8 of H.E.S.S. Collaboration 2018a).
In order to quantify the fit quality, we used the Sherpa implementation of the Cash statistic (Cash 1979), CSTAT1 , divided by the number of degrees of freedom, which is of the order of 1 for good fits. Since this criterion may only be used if the number of counts in each bin is high, we rebinned the maps to ensure this condition is fulfilled. We also checked that the statistical significances of the residuals at each position are consistent with those expected from a large number of Monte Carlo simulations assuming the final model.
Parameters describing the components for the final model.
2.4 Results of the emission model
In this section we present our main results from the template-based likelihood fit analysis. The individual components that contribute to the final model are added step by step as illustrated in Fig. 3. The final fitresult is summarised in Table 1, and the results of the individual components are detailed in Table A.1. The contribution of the model components to the total γ-ray emission is shown in the form of longitude and latitude profiles in Fig. 4.
The dominant DGC is modelled by the dense matter template multiplied by a Gaussian centred on |ℓ| = 0°, |b| = 0° with extension σ. The latter is not physically motivated but is required by the data. It provides the characteristic scale of the extension of CRs in the GC ridge region. With a fitted value of σ = 1.1° the extension is found to be slightly larger than previously estimated in Paper I, where σ = 0.8° was found to yield the best fit to the data. The DGC represents a large flux fraction of ~ 50% of the total GC ridge emission, confirming that the latter is dominantly from CRs interacting with dense matter.
An additional large-scale component (LSC), modelled as a 2D Gaussian with position fixed on SgrA⋆ and normalisation and extension (σX, σY ) fitted as free parameters, is required to reproduce the γ-ray emission especially at large latitudes. This component extends ± 30 pc in latitude and ± 150 pc in longitude, and represents a non-negligible flux fraction of 30% of the total GC ridge emission. We discuss the possible origin of this component in Sect. 3.
An additional extended γ-ray emission excess is also detected in the very central 30 pc region, as illustrated by the residuals in Fig. 3. This central component (CC), which is modelled by a 2D symmetric Gaussian centred on SgrA⋆ , is detected at 8.7σ significance level. It has an intrinsic extension of 0.1° and its flux represents ~ 15% of that of the ridge. Representing a fraction of ~30% of the GC source HESS J1745−290 and an intrinsic extension of almost twice the H.E.S.S. PSF, we can rule out the conclusion that this component arises from a contamination from the central point source due to systematic uncertainties of the PSF (see H.E.S.S. Collaboration 2018a). As we discuss in the next section, this additional component is in good agreement with the physical interpretation developed in Paper II.
After the subtraction of the CC, a significant but localised excess is still visible in the residuals (see fourth row of Fig. 3). Adding a Gaussian component at this position results in an increase of ΔTS = 48 or a significance of about 5.9σ. Changing the dense gas tracer as a model basis in the CMZ does not strongly change this significance, confirming the detection of a new source in this region. Called HESS J1746−285, this new source is located at Galactic position ℓ = 0.14° ± 0.01°, b = −0.11° ± 0.02° and has no significant extension within uncertainties. For further discussions of this new γ-ray source, see Sect. 4 below. After this final step in the fitting procedure, no further component is found to be significant in the residuals and the iteration is stopped.
The major source of systematic uncertainties of our measurement is the imperfect estimate of the charged CR-induced background of the H.E.S.S. image. In order to study how robust the inferred model components and parameter values are against systematic variations of this background, we artificially change the background normalisation by ± 2%, which is the typical systematic background uncertainty (Berge et al. 2007), and reapply the full iterative procedure to rederive the model components. This allows us to estimate typical systematic intervals for each parameter and test of the robustness of a component detection. The LSC is most sensitive to background uncertainties with a resulting variation of ± 50% in amplitude, around ± 15% in longitude and ± 25% in latitude extensions. The uncertainty on the DGC component amplitude is also large at ± 30%. The associated spatial extension is relatively stable (within 10%). The other more localised components remain stable. The systematic errors given in Table 1 also include a global flux normalisation uncertainty of about 30% added in quadrature.
 |
Fig. 3 Successive stages of the iterative fitting process shown here. The model count map of each individual component (correlated with the H.E.S.S. PSF) added in each step of the analysis is shown in the left-hand column (in units of counts per pixel) and the corresponding residual significance map (in units of significance level) is shown in the right-hand column, both in Galactic coordinates. From top to bottom we show background plus G0.9+0.1 plus HESS J1745−290 plus Galactic large-scale unresolved, the dense gas component (DGC), the central component (CC), the large-scale component (LSC), and the new source HESS J1746−285. The residualLi & Ma significance maps are computed using the data counts map as signal and the model map (correlated with the H.E.S.S. PSF) as background. |
 |
Fig. 4 New longitude (left) and latitude (right) profiles of the VHE γ-ray GC ridge emission in unit of excess counts∕arcmin2. The normalised background map and the two point sources HESS J1745−290 and G0.9+0.1 were subtracted from the γ-ray counts map using the fitted model parameters. The longitude profile was integrated over − 0.3° < b < +0.3° and the latitude profile over 359.5° < l < +0.5°. Coloured lines show how the different components of the model reproduce the data. In particular, the LSC accounts for the high latitude residual emission, and the CC accounts for the central residual excess. The Galactic large-scale emission (Abramowski et al. 2014) does not contribute signficantly in this region. |
3 Galactic centre ridge diffuse emission
3.1 Morphology
The results given above confirm that most of the diffuse GC ridge γ-ray emission is distributed like the dense gas in this region. About 50% of the emission is found to closely follow the CS template up to a projected longitudinal distance of ~1.0° or 140 pc from the GC. The dip in γ-ray emission beyond 100−150 pc is likely from a combination of decreasing CR density with distance to the GC and a more diffuse matter distribution along the line of sight. This notion is supported by the face-on view of the CMZ provided by Sawada et al. (2004), which shows that the region around 1.3° is much more spread out along the line of sight than the central part of the CMZ.
We find that an additional large-scale emission, i.e. the LSC above, is required to reproduce the observed morphology. Even if part of this diffuse emission is sensitive to systematic uncertainties of charged CR backgrounds, its detection is clearly significant beyond statistical and systematic uncertainties. This component does not correlate with dense gas tracers; in particular its latitude extension is larger. This is because CS does not fully trace both the densest CMZ structures and the more diffuse gas. It has in fact been estimated that about 30% of the molecular gas in the region is found in a diffuse H2 phase of density ~100 cm−3 (Dahmen et al. 1998). This is in good agreement with the relative contribution of the LSC to the total GC ridge emission. A natural explanation for this is therefore that most of the LSC flux is from CRs pervading the central 200 pc and interacting with this diffuse phase of molecular hydrogen. The atomic gas could also be invoked as it has been established as an important ISM component for some TeV sources. However the atomic gas represents no more than 10 percent of the gas in the CMZ (Ferrière et al. 2007), which is not enough to explain the entire LSC. Further studies could however be carried out using recent high-resolution HI images (McClure-Griffiths et al. 2012).
Inverse Compton (IC) emission from VHE electrons in the region cannot be formally excluded, but requires a broad distribution of sources in the inner 200 pc. The radiative losses are large enough to prevent propagation on such scales. The spectral shape of this component should then be significantly different from the DGC. Unresolved sources could also contribute to the emission. Finally, some contribution from the densest structures in the CMZ is also likely, as suggested by the presence of a hotspot at the position of the core of Sgr B2, which is however not significant enough to be detected as an individual source component.
Finally, the most interesting feature we find is the central component, which is centred on the GC and has a radius of about 15 pc. It further proves the presence of a gradient of CRs peaking around the GC as shown in Paper II. To quantify this, we estimate the ratio of the energy density of CRs, wCR (in eV cm−3 ), confined in the central 30 pc, to the average density in the whole CMZ, considering the extensions and luminosities of the CC and DGC components, respectively. We assume that the gas density nH is uniform in the region. The volume V CMZ containing 50% of the GC ridge flux is a cylinder of 170 pc radius and 30 pc thickness. The average CR density in this region is wCMZ ∝ LCMZ∕V CMZ, where LCMZ is total VHE luminosity. Similarly, the 50% flux equivalent volume of the CC is a sphere of 23 pc radius. Therefore the ratio of CR density in the central 20 pc over the density in the whole CMZ is ∝LCC∕LCMZ × V CMZ∕V CC ~ 10. If we estimate this ratio for CRs following a 1∕r profile, as expected for a steady source (Paper II), we indeed confirm that the energy densities between the central region and the entire CMZ differ by a factor of the order of 10. This shows that the empirical model used to reproduce the GC ridge morphology is fully compatible with the stationary source hypothesis; a large portion, if not all, of the CRs pervading the CMZ are accelerated at the GC or its direct vicinity.
Unresolved sources might also contribute to this central excess, in particular SNRs, given the high supernova rate in the CMZ. On the other hand, the soft thermal X-ray emission that traces SNRs in the CMZ is much more extended (up to 0.2°−0.3° around the GC; Ponti et al. 2015) and fails to reproduce the morphology of the VHE γ-ray emission measured with H.E.S.S. Similarly, the electrons injected by the population of PWNe detected with Chandra in the inner 30 pc (Muno et al. 2008; Johnson et al. 2009) could potentially provide a large γ-ray luminosity. But given the large infrared (IR) and optical photon field energy densities in the GC region, the measured energy spectra should show pronounced Klein-Nishina suppression effects in the TeV γ-ray range, which is inconsistent with the hard spectrum without any cut-off reported in Paper II in the central 0.45°. The PWNe scenario is therefore highly disfavoured. The CC is very likely due to a peak of the CR density caused by an accelerator at or very near the GC. The overall diffuse γ-ray emission measured from the central 200 pc of the Milky Way is consistent with CRs injected by this central accelerator, diffusing away and interacting along the GC ridge.
3.2 Total spectrum
The total GC ridge spectrum is evaluated over the large area |ℓ| < 1°, |b| < 0.3° by dividing it into smaller regions, performing the spectral analysis in each region and summing up the energy spectra to perform a global fit over all regions together. Eleven rectangular regions of similar area (2.7 × 10−5 sr) are defined over the GC ridge. These regions cover most of the diffuse emission and are chosen to have a surface brightness as similar as possible. Two regions of 0.2° radius around G0.9+0.1 and Sgr A⋆ are excluded from the analysis ensuring negligible contamination (<2%) from the bright point sources. A region of 0.1° around the new source HESS J1746−285 is also excluded from the analysis.
Under the hypothesis that the spectral characteristics do not vary across the ridge, all individual regions have been analysed independently, stacked up, and fitted to obtain the average energy spectrum shown in Fig. 5. This method ensures a small dispersion of observation conditions and instrument response functions per region when building the individual spectra. The same method also permits us to choose, for each individual rectangular region, a sufficient number of background regions, following the reflected region method (Berge et al. 2007); this would not be possible for spectral analysis of one single very large region (i.e. the whole GC ridge). Following this procedure, some of the background regions overlap with each other leading to double counting of background events; the resulting statistical uncertainties are thus too small by 25% and the uncertainties of the resulting total spectrum shown in Fig. 5 are corrected for this.
The derived spectrum of the entire GC ridge can be described by a power law with a hard photon index of 2.28± 0.03stat ± 0.2syst. This result is compatible with the previous spectrum obtained in Paper I considering the larger analysis region used here. The spectrum is fitted in an energy range that extends up to 45 TeV, a maximum energy beyond which our systematic uncertainty for such a faint signal does not allow us to constrain the spectral shape robustly. No significant spectral cut-off is found. We compare the γ-ray spectrum with a simple power-law model of the parent proton population with high-energy cut-off at 1 PeV in Fig. 5. As seen in this figure, the flux points are in good agreement with a proton cut-off energy at or above 1 PeV and with the flux points from the inner 0.45° (or 63 pc) obtained in Paper II.
The total ridge γ-ray flux in the box |ℓ| < 1°, |b| < 0.3° is estimated at Φ(>1 TeV ) = 1.5 × 10−11 TeV cm−2 s−1, which corresponds to a total γ-ray luminosity of Lγ (>1 TeV ) = 2 × 1035 erg s−1 at the GC distance. This is slightly smaller than the value derived from the 2D analysis but considered consistent with this value in view of the limited extension considered here. Since the γ-ray emission is entirely due to the decay of neutral pions produced by proton-proton interactions, we can express the total energy of CR protons as WCR = Lγ × tpp, with Lγ the γ-ray luminosity and 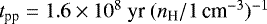 , where nH is the gas density. This implies a total CR energy of Wpp(>10 TeV ) ~ 1 × 1049 erg confined in the CMZ for a typical value of nH ~ 100 cm−3.
, where nH is the gas density. This implies a total CR energy of Wpp(>10 TeV ) ~ 1 × 1049 erg confined in the CMZ for a typical value of nH ~ 100 cm−3.
 |
Fig. 5 Very high-energy γ-ray flux per unit solid angle in the Galactic centre region (black data points). The spectrum of the GC ridge region, |ℓ| < 1°, |b| < 0.3°, is shown. Allerror bars show the 1σ standard deviation and are corrected to account for some background double counting due to the stacking procedure. The spectrum is fitted over an energy range up to 45 TeV. It can be described by a power law with a photon index of 2.28 ± 0.03stat ± 0.2syst and a differential flux at 1 TeV of 1.2 ± 0.04stat ± 0.2syst × 10−8 TeV −1 cm−2 s−1 sr−1. For comparison, the blue line is the γ-ray spectrum resulting from a power-law proton spectrum with a cut-off at 1 PeV. |
4 A new VHE source in the vicinity of the GC radio arc: HESS J1746−285
4.1 Position and spectrum
HESS J1746−285 is detected at Galactic position ℓ = 0.14° ± 0.01°, b = −0.11° ± 0.02°. The systematic uncertainties on the knowledge of the exact morphologies used for the various components to model the GC ridge diffuse emission can be large. To estimate these, we evaluate the impact of using HCN rather than CS as a tracer for dense gas and also the impact of changing the normalisation of the CR background. We find the systematic error on the source position to be 0.02°. No significant extension is found and we place an upper limit on the extension at 0.05°.
Because of the relatively large intensity of the GC ridge emission, extracting the intrinsic spectrum of HESS J1746−285 requires special care. The spectrum of the diffuse emission in the source extraction region must be estimated and included in the modelling of the total observed spectrum.
The spectral extraction is therefore performed in two circular regions with radii of 0.09°. One is centred on the best fit position of HESS J1746−285 and the other onthe symmetric position with respect to the GC. The diffuse emission spectral contribution can then be evaluated on the second region and included in the modelling of the observed counts of the source region after renormalising the flux according to the ridge emission morphology obtained with the 2D analysis. The implicit assumption made here is that its spectral shape does not vary significantly over the central 50 pc.
After applying the flux correction factor, found to be ~0.9, the parameters are fixed and used to model to spectrum of the source region, which consists of the charged CR background, the ridge emission, and the intrinsic spectrum of HESS J1746−285 described by a power law. The intrinsic spectrum of HESS J1746−285 has a flux normalisation of F(1 TeV) = (1.8 ± 0.5) × 10−13 cm−2 s−1 TeV−1 and an index of 2.2 ± 0.2 for the energy range above 0.350 TeV (see Fig. 6). The errors include the uncertainty of the ridge emission, which are obtained by varying the ridge component parameters by their statistical errors. This gives a luminosity in the range 0.35−10 TeV of about 7 × 1033 erg s−1 at 8 kpc distance.
Both MAGIC and VERITAS collaborations have recently found significant excesses in the vicinity of HESS J1746−285 (Archer et al. 2016; Ahnen et al. 2017), but their studies are based on much lower observation times and do not take into account the contribution of underlying diffuse emission. The existence of an excess of diffuse emission around this position is clearly visible from the early images of the GC ridge emission in Paper I and is due to the presence of the massive molecular complex Sgr A. The existence of a faint source (below the percent Crab flux) on top of this diffuse emission requires a detailed modelling of the latter as described above. We therefore consider VER J1746−289 and MAGIC J1746−285 to be a mix of the ridge emission, which is very intense around the Sgr A molecular complex, and HESS J1746−285 emission.
 |
Fig. 6 Very high-energy γ-ray spectrum of the region centred on the position of HESS J1746−285, fitted with the sum of two power laws. The GC ridge contribution is fixed and the intrinsic source spectrum of HESS J1746−285 is fitted to the data. In red, we show the fixed ridge power-law contribution to the total spectrum. The intrinsic spectrum of HESS J1746−285 was estimated to have a flux normalisation of F(1TeV) = (1.8 ± 0.5) × 10−13 cm−2 s−1 TeV−1 and an indexof 2.2 ± 0.2 for the energy range above 0.350 TeV. The errors include the uncertainty of the GC ridge emission, which are obtained by varying the ridge component parameters by their statistical errors. |
4.2 Nature of the source
HESS J1746−285 is positionally coincident with the confused Fermi-LAT source 3FGL J1746.3−2851c at ℓ = 0.149°, b = −0.103° (Acero et al. 2015). The spectrum of the latter is found to be significantly curved with a log-parabola shape with index 2.42 ± 0.07 and β =0.34 ± 0.06. This spectrum is also present in the 1FHL catalogue as 1FHL J1746.3−2851 (Ackermann et al. 2013), with a large flux above 1 GeV of 6.6 × 10−9 ph cm−2 s−1 and a very soft index of 3.2 ± 0.3. It is not listed in the catalogue of sources above 50 GeV (Ackermann et al. 2016).
HESS J1746−285 lies on the edge of the so-called GC radio arc (Yusef-Zadeh et al. 1984) at the centre of the radio arc bubble, which is a large (9 pc diameter) open circular structure visible in mid-IR images (Levine et al. 1999; Rodríguez-Fernández et al. 2001), as shown in the left panel of Fig. 7. This radio arc bubble is apparently connected to the Quintuplet cluster, which is one of the three young massive stellar clusters in the GC region. The estimated age of this cluster is ~4 Myr and its luminosity is 1.2 × 1041 erg/s (Figer et al. 1999). This cluster is the dominant source of optical/UV radiation in the region and is responsible for most of the ionisation in the bubble (Simpson et al. 2007). The radio arc bubble is filled with soft thermal X-rays, which are likely produced by supernova explosions and massive stellar winds from the Quintuplet cluster (Ponti et al. 2015).
Figure 7 (right panel) shows the confidence-level contours on the best fit position of HESS J1746−285 superimposed on a 2−10 keV exposure-corrected Chandra image. The source is coincident with an X-ray non-thermal filamentary structure called G0.13−0.11, which has been proposed to be a PWN candidate (Wang et al. 2002). The luminosity derived from Chandra observations for G0.13−0.11 in the 2−10 keV range is L = 3 × 1033 erg∕s with a spectral photon index between 1.4 and 2.5. Wang et al. (2002) estimated the spin-down power of the putative pulsar, Ė , to be of the order of 1035 erg/s. Given the good positional coincidence and point-like nature of the VHE γ-ray source, we consider G0.13−0.11 to be the most likely origin of HESS J1746−285. We explore this scenario further below.
The X-ray PWN is a filament of 2″ × 40″. The cooling time of electrons along the filament imposes an upper limit on the magnetic field of 300 μG. The thickness of the filament also constrains the magnetic field to be larger than 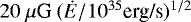 (Wang et al. 2002). No significant cooling is visible along the filament (Johnson et al. 2009).
(Wang et al. 2002). No significant cooling is visible along the filament (Johnson et al. 2009).
We can estimate the optical radiation field energy density produced by the nearby Quintuplet cluster at the position of the PWN candidate, assuming it lies at the projected distance (9 pc at 8 kpc), to be 250 eV/cm3. Given the abundance of early-type stars in the cluster, the effective temperature of the radiation field is ~35 000 K (Rodríguez-Fernández et al. 2001; Contini 2009).
The infrared energy density is likely dominated by the emission from G0.18−0.04, the so-called “sickle”. Its luminosity is ~3.5 × 1040 erg/s with a temperature TFIR (FIR: far infrared) of about 50 K (Pohl 1997). At the projected distance of the PWN candidate this implies an energy density of 50 eV/cm3. This is to be considered a lower limit of the actual density at the PWN position since the rest of the bubble should contribute to the FIR emission as well. In the following, we consider an FIR radiation density of 100 eV/cm3 that is consistent with values estimated for the CMZ at large (Crocker 2012). With such large radiation densities, the evolution of the nebula is likely driven by inverse Compton losses, which can explain the hard X-ray spectrum observed by Chandra (Hinton & Aharonian 2007).
We compute the spectrum radiated by electrons injected by the putative pulsar as a function of time taking into account pulsar braking (seee.g. H.E.S.S. Collaboration 2018b) and energy dependent losses (Hinton & Aharonian 2007). We use the GAMERA package to compute the time evolution of the electron population (Hahn 2015). The spectrum at injection is chosen to be an E−2 power law extending up to 100 TeV and the injected power is assumed to be equal to the pulsar spin-down power at any time. The magnetic field in the nebula is assumed to be constant and we used the two radiation fields discussed above along with the cosmic microwave background. We first consider the case of a steady injection and find that a spin-down power of Ė = 2 × 1035 erg/s and an ambient magnetic field of B = 45 μG reproduce the X-ray and VHE data (see Fig. 8). If the pulsar has experienced significant spin-down, we might expect a strong flux below 100 GeV because of the accumulation of cooled electrons, which might explain at least part of the flux of the Fermi-LAT source. Assuming dipolar evolution of the pulsar Ė (H.E.S.S. Collaboration 2018b), we find that a large initial spin-down power of Ė0 = 7 × 1038 erg/s with a spin-down time of τ0 = 500 yr and a pulsar age of 30 kyr can account for the slope above 10 GeV while preserving an Ė ~ 1035 erg/s required to explain the X-ray and VHE γ-ray luminosities (see Fig. 8). Accounting for most of the GeV flux is more complex and requires extremely high Ė0.
There are probably several other possible origins for 3FGL J1746.3−2851c, for example GCridge emission, emission from the radio arc, or pulsed GeV emission from the putative pulsar. The latter explanation would require a γ-ray efficiency of the pulsar close to 100%, if its current Ė is of the order of a few 1035 erg/s. This is possible if the actual spin-down power is larger and the fraction of power transferred to the relativistic wind is not very large. Finally, Heard & Warwick (2013) have found an enhancement of soft thermal X-rays around G0.13−0.11, which they attribute to the remnant of the progenitor supernova. This SNR could also contribute to the γ-ray flux. The point-like nature of HESS J1746−285 is difficult to reconcile with that scenario, however.
 |
Fig. 7 Left: three colour MSX (Price et al. 2001) IR image of the radio arc bubble (bands C, D, and E). Red contours overlaid show the confidence-level contours at 68%, 95%, and 99% on the best fit position of the new detected source HESS J1746−285 derived from the TS map of the fitted position; white contours show the radio arc emission at 90 cm. TheQuintuplet cluster is the bright source on the top left part of the bubble. Right: Chandra 2−10 keV mosaic image of the field surrounding G0.13−0.11 using all available public data. The image is exposure-corrected and smoothed with a Gaussian with a width of σ = 2.5″ to highlight the filamentary emission. Green contours show the HCN emission of the molecular cloud G0.11−0.11 integrated inthe range 10−30 km s−1 (following Tsuboi et al. 2011). |
 |
Fig. 8 Spectral energy distribution of the PWN G0.13−0.11. The butterflies show the spectral confidence regions of G0.13−0.11 measured with Chandra (Wang et al. 2002), of 1FHL J1746.3−2851 (Ackermann et al. 2013) and of HESS J1746−285. The upper limit is obtained from the 90 cm map of LaRosa et al. (2000). The lines show two models of PWN emission for G0.13−0.11, assuming an IC dominated evolution of the particles (see Sect. 4.2 for details). The X-ray and VHE γ-ray spectra are well accounted for by an electron population injected at a few 1035 erg/s (steady-state model, blue). Part of the flux observed above 10 GeV could be explained assuming a significant decay of the pulsar spin-down power (relic model, red). |
5 Conclusions
The complete H.E.S.S. I data set of the GC region provides a very detailed view of the VHE γ-ray emission in the central 200 pc of the Galaxy. After subtraction of the two main point sources, HESS J1745−290 and G0.9+0.1, the GC ridge emission appears very clearly distributed in the manner of dense gas as traced by the CS molecule over a projected distance of 140 pc and fades beyond that. Emission from the main molecular complexes Sgr A, B, and C is clearly visible and fainter emission from the Sgr D region are clearly visible. Moreover, the longitude profile now clearly exhibits a peak at the GC position that is not visible in the gas distribution. The γ-ray emission is a clear sign of a source of CRs at or near the GC.
We have built an empirical model of the GC ridge diffuse VHE γ-ray emission morphology based on an iterative 2D maximum-likelihood method. Starting from a minimal model consisting of the two main point sources and a diffuse component constructed from a map of dense gas (traced by the CS molecule) and multiplied by a Gaussian to account for the lower brightness beyond longitudes of 1°, we added Gaussian components until further components were not found to yield a significant improvement of the model fit to the data.
Beyond the main diffuse component, which represents 50% of the total flux, we find that a large-scale emission extending to high latitudes, which does not correlate with dense gas tracers, is required to reproduce the observed morphology. This component, which accounts for about 30% of the total flux, is likely the result of CR interactions with gas in a diffuse phase that dense molecular clouds tracers are not able to map. Additional contributions from unresolved sources and IC emission from VHE electrons in the region cannot be excluded. An additional component is found for the central 30 pc. Its flux is 15% of the total ridge emission.
These three components provide a good model of the diffuse emission in the central 200 pc and are consistent with the radial 1∕r gradient of CRs in the CMZ, which are possibly accelerated at the supermassive black hole itself, as concluded in Paper II. The spectrum extracted in the whole region is well fitted by a power law of photon index 2.3 with no significant evidence of a cut-off. This γ-ray spectrum proves the presence of a PeV-scale proton population not only in the central 40 pc, but over the entire CMZ including its external more diffuse phase.
Finally, we detect the new point-like source HESS J1746−285 that is spatially coincident with the Fermi-LAT arc source 3FGL J1746.3−2851c and the X-ray PWN candidate G0.13−0.11 at the centre of the radio arc IR bubble; this feature is possibly linked to the young and massive Quintuplet cluster. The intrinsic spectral index of HESS J1746−285 is found to be ~2.2 and its luminosity is 7 × 1033 erg/s at the GC distance, which is twice as large as that of the X-ray nebula. This supports a physical association with the PWN. We have shown that, taking the radiation energy densities in the vicinity of the Quintuplet cluster into account, the X-ray and VHE γ-ray spectra can be well reproduced by a steady injection of electrons by a pulsar with a spin-down power of a few times 1035 erg/s. It is difficult to explain the GeV emission in this scenario. The Fermi-LAT source might be connected to another possibly related phenomenon, for example the pulsar itself or the underlying SNR. Chandra has resolved more than a dozen such PWN candidates in the GC. Albeit fainter than G0.13−0.11 they might have detectable emission in the VHE domain and may be resolved in the future.
The approach presented here does not allow us to separate the spectra of the various components extracted in the morphological analysis, which limits our understanding of their origin. Owing to its enhanced sensitivity and superior angular resolution, the Cherenkov Telescope Array (CTA; Acharya et al. 2013) will be crucial for understanding the properties of the ridge diffuse emission because it will resolve the substructures in much more detail and will be able to perform combined spectral and morphological analysis in a 3D fit to characterise CR acceleration and propagation in the GC region.
Acknowledgements
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the Innsbruck University, the Austrian Science Fund (FWF), and the Austrian Federal Ministry for Science, Research and Economy, and by the University of Adelaide and the Australian Research Council. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. This work benefited from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation.
Appendix A
Results of the iterative fit
References
- Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2014, Phys. Rev. D, 90, 122007 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Acharya, B. S., Actis, M., Aghajani, T., et al. 2013, Astropart. Phys., 43, 3 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, ApJS, 209, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Albert, A., Atwood, W. B., et al. 2014, ApJ, 793, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, Nature, 439, 695 (Paper I) [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, A&A, 483, 509 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017, A&A, 601, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Archer, A., Benbow, W., Bird, R., et al. 2016, ApJ, 821, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Becherini, Y., Djannati-Ataï, A., Marandon, V., Punch, M., & Pita, S. 2011, Astropart. Phys., 34, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bland-Hawthorn, J., & Cohen, M. 2003, ApJ, 582, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, M. 2009, MNRAS, 399, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, R. M. 2012, MNRAS, 423, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Dahmen, G., Huttemeister, S., Wilson, T. L., & Mauersberger, R. 1998, A&A, 331, 959 [NASA ADS] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figer, D. F., McLean, I. S., & Morris, M. 1999, ApJ, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Funk, S., Hermann, G., Hinton, J., et al. 2004, Astropart. Phys., 22, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, J. 2015, in Proc. 34th International Cosmic Ray Conference (ICRC 2015) [Google Scholar]
- Heard, V., & Warwick, R. S. 2013, MNRAS, 434, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., Aharonian, F., et al.) 2016, Nature, 531, 476 (Paper II) [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018a, A&A 612, A1 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018b, A&A 612, A2 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinton, J. A., & Aharonian, F. A. 2007, ApJ, 657, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, S. P., Dong, H., & Wang, Q. D. 2009, MNRAS, 399, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, P. A., Burton, M. G., Cunningham, M. R., et al. 2012, MNRAS, 419, 2961 [NASA ADS] [CrossRef] [Google Scholar]
- Jouvin, L., Lemière, A., Terrier, R., et al. 2015, in Proc. 34th International Cosmic Ray Conference (ICRC 2015) [Google Scholar]
- Khelifi, B., Djannati-Ataï, A., Jouvin, L., et al. 2015, in Proc. 34th International Cosmic Ray Conference (ICRC 2015) [Google Scholar]
- LaRosa, T. N., Kassim, N. E., Lazio, T. J. W., & Hyman, S. D. 2000, AJ, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, D., Morris, M., & Figer, D. 1999, in The Universe as Seen by ISO, eds. P. Cox, & M. Kessler, ESA SP, 427, 699 [NASA ADS] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2012, ApJS, 199, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Bally, J., Noriega-Crespo, A., et al. 2011, ApJ, 735, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Baganoff, F. K., Brandt, W. N., Morris, M. R., & Starck, J.-L. 2008, ApJ, 673, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M. 1997, A&A, 317, 441 [NASA ADS] [Google Scholar]
- Ponti, G., Morris, M. R., Terrier, R., et al. 2015, MNRAS, 453, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. D., Egan, M. P., Carey, S. J., Mizuno, D. R., & Kuchar, T. A. 2001, AJ, 121, 2819 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, B. L., Doe, S. M., Nguyen, D. T., et al. 2009, in Proc. 8th Python in Science Conference, Pasadena, CA, eds. G. Varoquaux, S. van der Walt, & J. Millman [Google Scholar]
- Rodríguez-Fernández, N. J., Martín-Pintado, J., & de Vicente P. 2001, A&A, 377, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sawada, T., Hasegawa, T., Handa, T., & Cohen, R. J. 2004, MNRAS, 349, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. P., Colgan, S. W. J., Cotera, A. S., et al. 2007, ApJ, 670, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuboi, M., Handa, T., & Ukita, N. 1999, ApJS, 120, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuboi, M., Tadaki, K.-I., Miyazaki, A., & Handa, T. 2011, PASJ, 63, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Q. D., Lu, F., & Lang, C. C. 2002, ApJ, 581, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Morris, M., & Chance, D. 1984, Nature, 310, 557 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 VHE γ-ray images of the GC region in Galactic coordinates and smoothed with the H.E.S.S. PSF. Top: γ-ray significance map is shown. Bottom: residual significance map after subtraction of the two point sources G0.9+0.1 and HESS J1745−290 is shown. The cyan contours indicate the density of molecular gas as traced by the CS brightness temperature integrated over the local standard of rest (LSR) velocity from −200 to 200 km s−1 (Tsuboi et al. 1999) and smoothed with the H.E.S.S. PSF (0.077°). The outer contour level is 36 K km s−1, which is about six times the noise level (Tsuboi et al. 1999). The position of the new H.E.S.S. source HESS J1746−285, which is coincident with the GC radio arc (Yusef-Zadeh et al. 1984), is indicated with a black cross. |
| In the text | |
 |
Fig. 2 Longitude profile of the VHE γ-ray GC ridge emission in units of excess counts∕arcmin2. The CR background and the two point sources HESS J1745−290 and G0.9+0.1 were subtracted from the counts map. The profile has been integrated over − 0.3° < b < +0.3°. The green line shows the model based on the VHE emission profile used in Paper I, which includes a central 0.8° width Gaussian multiplied by the CS map. This does not account for the clear excess at the GC position. As shown in Paper II the latter is rather well reproduced by a profile obtained with a 1∕r CR density integrated over a homogeneous gas density in the line of sight and multiplied by the integrated CS map (blue line). |
| In the text | |
 |
Fig. 3 Successive stages of the iterative fitting process shown here. The model count map of each individual component (correlated with the H.E.S.S. PSF) added in each step of the analysis is shown in the left-hand column (in units of counts per pixel) and the corresponding residual significance map (in units of significance level) is shown in the right-hand column, both in Galactic coordinates. From top to bottom we show background plus G0.9+0.1 plus HESS J1745−290 plus Galactic large-scale unresolved, the dense gas component (DGC), the central component (CC), the large-scale component (LSC), and the new source HESS J1746−285. The residualLi & Ma significance maps are computed using the data counts map as signal and the model map (correlated with the H.E.S.S. PSF) as background. |
| In the text | |
 |
Fig. 4 New longitude (left) and latitude (right) profiles of the VHE γ-ray GC ridge emission in unit of excess counts∕arcmin2. The normalised background map and the two point sources HESS J1745−290 and G0.9+0.1 were subtracted from the γ-ray counts map using the fitted model parameters. The longitude profile was integrated over − 0.3° < b < +0.3° and the latitude profile over 359.5° < l < +0.5°. Coloured lines show how the different components of the model reproduce the data. In particular, the LSC accounts for the high latitude residual emission, and the CC accounts for the central residual excess. The Galactic large-scale emission (Abramowski et al. 2014) does not contribute signficantly in this region. |
| In the text | |
 |
Fig. 5 Very high-energy γ-ray flux per unit solid angle in the Galactic centre region (black data points). The spectrum of the GC ridge region, |ℓ| < 1°, |b| < 0.3°, is shown. Allerror bars show the 1σ standard deviation and are corrected to account for some background double counting due to the stacking procedure. The spectrum is fitted over an energy range up to 45 TeV. It can be described by a power law with a photon index of 2.28 ± 0.03stat ± 0.2syst and a differential flux at 1 TeV of 1.2 ± 0.04stat ± 0.2syst × 10−8 TeV −1 cm−2 s−1 sr−1. For comparison, the blue line is the γ-ray spectrum resulting from a power-law proton spectrum with a cut-off at 1 PeV. |
| In the text | |
 |
Fig. 6 Very high-energy γ-ray spectrum of the region centred on the position of HESS J1746−285, fitted with the sum of two power laws. The GC ridge contribution is fixed and the intrinsic source spectrum of HESS J1746−285 is fitted to the data. In red, we show the fixed ridge power-law contribution to the total spectrum. The intrinsic spectrum of HESS J1746−285 was estimated to have a flux normalisation of F(1TeV) = (1.8 ± 0.5) × 10−13 cm−2 s−1 TeV−1 and an indexof 2.2 ± 0.2 for the energy range above 0.350 TeV. The errors include the uncertainty of the GC ridge emission, which are obtained by varying the ridge component parameters by their statistical errors. |
| In the text | |
 |
Fig. 7 Left: three colour MSX (Price et al. 2001) IR image of the radio arc bubble (bands C, D, and E). Red contours overlaid show the confidence-level contours at 68%, 95%, and 99% on the best fit position of the new detected source HESS J1746−285 derived from the TS map of the fitted position; white contours show the radio arc emission at 90 cm. TheQuintuplet cluster is the bright source on the top left part of the bubble. Right: Chandra 2−10 keV mosaic image of the field surrounding G0.13−0.11 using all available public data. The image is exposure-corrected and smoothed with a Gaussian with a width of σ = 2.5″ to highlight the filamentary emission. Green contours show the HCN emission of the molecular cloud G0.11−0.11 integrated inthe range 10−30 km s−1 (following Tsuboi et al. 2011). |
| In the text | |
 |
Fig. 8 Spectral energy distribution of the PWN G0.13−0.11. The butterflies show the spectral confidence regions of G0.13−0.11 measured with Chandra (Wang et al. 2002), of 1FHL J1746.3−2851 (Ackermann et al. 2013) and of HESS J1746−285. The upper limit is obtained from the 90 cm map of LaRosa et al. (2000). The lines show two models of PWN emission for G0.13−0.11, assuming an IC dominated evolution of the particles (see Sect. 4.2 for details). The X-ray and VHE γ-ray spectra are well accounted for by an electron population injected at a few 1035 erg/s (steady-state model, blue). Part of the flux observed above 10 GeV could be explained assuming a significant decay of the pulsar spin-down power (relic model, red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


