| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201630358 | |
| Published online | 04 May 2018 | |
Well-defined EUV wave associated with a CME-driven shock
1
Universidade do Vale do Paraíba – UNIVAP, Av. Shishima Hifumi, 2911 Urbanova,
São José dos Campos,
SP,
Brazil
e-mail: rfldoug@gmail.com
2
NAT – Núcleo de Astrofísica Teórica, Universidade Cruzeiro do Sul, Rua Galvão Bueno,
868 Liberdade,
São Paulo,
SP,
Brazil
e-mail: caiuslucius@gmail.com
Received:
26
December
2016
Accepted:
9
January
2018
Aims. We report on a well-defined EUV wave observed by the Extreme Ultraviolet Imager (EUVI) on board the Solar Terrestrial Relations Observatory (STEREO) and the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO). The event was accompanied by a shock wave driven by a halo CME observed by the Large Angle and Spectrometric Coronagraph (LASCO-C2/C3) on board the Solar and Heliospheric Observatory (SOHO), as evidenced by the occurrence of type II bursts in the metric and dekameter-hectometric wavelength ranges. We investigated the kinematics of the EUV wave front and the radio source with the purpose of verifying the association between the EUV wave and the shock wave.
Methods. The EUV wave fronts were determined from the SDO/AIA images by means of two appropriate directions (slices). The heights (radial propagation) of the EUV wave observed by STEREO/EUVI and of the radio source associated with the shock wave were compared considering the whole bandwidth of the harmonic lane of the radio emission, whereas the speed of the shock was estimated using the lowest frequencies of the harmonic lane associated with the undisturbed corona, using an appropriate multiple of the Newkirk (1961, ApJ, 133, 983) density model and taking into account the H/F frequency ratio fH∕fF = 2. The speed of the radio source associated with the interplanetary shock was determined using the Mann et al. (1999, A&A, 348, 614) density model.
Results. The EUV wave fronts determined from the SDO/AIA images revealed the coexistence of two types of EUV waves, a fast one with a speed of ~560 km s−1, and a slower one with a speed of ~250 km s−1, which corresponds approximately to one-third of the average speed of the radio source (~680 km s−1). The radio signature of the interplanetary shock revealed an almost constant speed of ~930 km s−1, consistent with the linear speed of the halo CME (950 km s−1) and with the values found for the accelerating coronal shock (~535–823 km s−1), taking into account the gap between the radio emissions.
Key words: Sun: coronal mass ejections (CMEs) / Sun: UV radiation / Sun: corona / Sun: radio radiation
© ESO 2018
1 Introduction
Among the large-scale wave phenomena that take place on the Sun, shock waves play an important role in the dynamics of the solar corona. The main eruptive phenomena responsible for these shocks are solar flares and coronal mass ejections (CMEs). In shocks driven by flares, shock formation involves the local expansion of the hot flare plasma, whereas a CME-driven shock is produced by the eruption of a large-scale structure that evolves into a CME, in which the shock wave is perennially supplied by the energy from the CME (Vršnak & Cliver 2008).
The longest known signatures of shocks in the solar corona are the type II bursts (Payne-Scott et al. 1947), which are narrow-band slow-drift emissions observed in radio dynamic spectra, produced by plasma oscillations caused by the propagation of a fast-mode magnetohydrodynamic (MHD) shock through the solar corona (Nelson & Melrose 1985). The radio emission is observed at multiples of the electron plasma frequency, given by 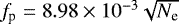 [MHz], in which Ne [cm−3] is the electron number density, primarily at the fundamental and second harmonic emissions, and sometimes at the third harmonic emission (see, e.g., Zlotnik et al. 1998; Cunha-Silva et al. 2014).
[MHz], in which Ne [cm−3] is the electron number density, primarily at the fundamental and second harmonic emissions, and sometimes at the third harmonic emission (see, e.g., Zlotnik et al. 1998; Cunha-Silva et al. 2014).
The causal relationship between a type II burst and MHD shock was proposed by Uchida (1960) and Wild (1962). Such an association became evident from the interpretation of the Moreton waves (Moreton 1960), which are global wave signatures in the chromosphere, observed in Hα, whose high speeds (~1000 km s−1) led to the Uchida (1968) theory of the fast-mode MHD shock wave. Although the shock wave propagates into the corona from the flare site, part of its energy is refracted back down into the chromosphere. There is a direct correlation between Moreton waves and some metric type II bursts and the interpretation of the Moreton wave as a chromospheric counterpart of a true coronal wave became consistent with the observations (see, e.g., Hudson 2011).
Although there is a consensus that all type II bursts at dekameter and longer wavelengths are signatures of CME-drivenshocks (see, e.g., Cane et al. 1987; Gopalswamy et al. 2000; Vršnak & Cliver 2008) and most of the metric type II bursts can be attributed to CMEs (see, e.g., Cliver et al. 2004; Gopalswamy et al. 2013), type II emissions without CMEs are sometimes observed, particularly at frequencies considerably higher (~300–900 MHz) than the typical frequency range (~100–200 MHz) of these radio emissions (see, e.g., Magdalenić et al. 2012).
Anotherinteresting global wave-like disturbance observed on the Sun is the “EUV wave” or “EIT wave”, characterized by propagating brightness fronts in the extreme ultraviolet (EUV), whose first well-defined observations were carried out by the Extreme-ultraviolet Imaging Telescope (EIT), on board the Solar and Heliospheric Observatory (SOHO) (see, e.g., Moses et al. 1997; Thompson et al. 1998), after the primary observations of the phenomenon reported by Neupert (1989), who interpreted it as an EUV counterpart of the Moreton wave.
The controversy over the wave nature of the EUV waves arises from the difficulties regarding the physical interpretation of their complex behavior, which cannot be satisfactorily explained by either the wave or the pseudo-wave theory (see, e.g., Gallagher & Long 2011; Patsourakos & Vourlidas 2012; Warmuth 2015). Although the wave-like behavior of the EUV wave is clearly evident in regions of intense variation in the plasma conditions, especially in active regions, where the source of the EUV wave lies, the interpretation of the EUV wave as a fast-mode wave seems to be insufficient, since some events show speeds considerably below any feasible coronal Alfvén speed (see, e.g., Delannée 2000; Hudson 2011).
However, observations from STEREO/EUVI and SDO/AIA have revealed higher initial speeds (~600–2000 km s−1) for some EUV waves (see, e.g., Long et al. 2008; Veronig et al. 2008; Lemen et al. 2012) and some case studies show a good correlation between the speeds of the EUV wave and the source of the associated metric type II burst (see, e.g., Cunha-Silva et al. 2015a,b). These observations may be explained by some studies that show the coexistence of two types of EUV waves, a fast-mode wave and a slower pseudo-wave, as was revealed by the high-cadence observations of SDO/AIA (see, e.g., Chen & Wu 2011; Schrijver et al. 2011; Asai et al. 2012; Shen & Liu 2012) and as was predicted by Chen et al. (2002, 2005).
In this article, we present an interesting case study of an EUV wave observed by STEREO/EUVI-A and SDO/AIA, associated with a shock wave driven by a halo CME observed by SOHO/LASCO-C2/C3, in which the propagation of the shock wave through both the corona and the interplanetary medium was evidenced by the observations of type II bursts.
2 Observations and analysis
The halo CME responsible for the EUV wave formation was observed on 9 March 2012 at 04:26:09 UT by SOHO/LASCO-C2/C3, with onset at ~03:41:00 UT, according to the 12-second cadence SDO/AIA images, and at 03:43:49 UT, determined by linear backward-extrapolation of the heights, according to the LASCO CME Catalog. The identification of the EUV wave is revealed to be more efficient in the 193 Å (Fe XII) channel, which corresponds to the coronal plasma at temperatures of ~1.26 MK.
Figure 1 shows the temporal evolution of the EUV wave, observed by STEREO/EUVI-A 195 Å as bright fronts ahead of an EUV bubble and by SDO/AIA 193 Å as bright fronts projected on the solar disk.
The temporal evolutions of the EUV wave fronts recorded by SDO/AIA 193 Å along the directions indicated in Fig. 1g are presented in Fig. 2.
The halo CME associated with the EUV wave was a disk event (N17° W12°) which took place in NOAA active region 11 429 and was accompanied by an M6.3 soft X-ray (SXR) flare observed by the Geostationary Operational Environmental Satellites (GOES).
The expansion of the CME was also responsible for driving a shock wave whose propagation was evidenced by coronal and interplanetary radio signatures. Figure 3 shows the type II emission recorded in the frequency range of 45–441 MHz by CALLISTO-SSRT (Russia), a spectrometer from the extended-Compound Astronomical Low-cost Low-frequency Instrument for Spectroscopy and Transportable Observatories (e-CALLISTO) (see, e.g., Benz et al. 2009). The type II burst started at ~03:41:20 UT (harmonic emission), approximately together with the onset of the EUV wave, and intensified from ~03:43:30 UT, approximately simultaneously with the onset of the fast accelerating phase of the CME, according to the EUV images.
The short duration (~1 min) of the intensified type II emission during the onset of the fast acceleration phase of the CME can be explained by the presence of a subsequent moving self-contained magnetic structure or plasmoid (see, e.g., Dulk 1985) produced by fast electrons (~100 keV) during the impulsive phase of the M6.3 SXR flare, as evidenced by the occurrence of a moving type IV burst with onset approximately simultaneously with the intensification of the type II emission, as shown in Fig. 4.
Simões et al. (2013) studied the M6.3 SXR flare that accompanied the halo CME and found a clear implosion of coronal loops during the impulsive phase of the flare.
The causal relationship between the CME and the shock wave was corroborated by the occurrence of a well-defined interplanetary type II burst observed by the Radio and Plasma Wave Investigation (WAVES) RAD2 instrument on board the Wind satellite, as shown in Fig. 5. The comparison between the heights of the type-II-emitting shock segments in the solar corona and interplanetary medium, obtained using empirical density models (presented in the next section), is shown in Fig. 6.
 |
Fig. 1 Running-difference images of STEREO/EUVI-A 195 Å and SDO/AIA 193 Å showing the EUV wave formation (accompanied by EUV bubble) for (a) 03:40:30 UT; (b) 03:45:30 UT; (c) 03:50:30 UT; (d) 03:55:30 UT; (e) 04:00:30 UT; (f) 03:42:12 UT; (g) 03:45:36 UT; (h) 03:47:48 UT; (i) 03:50:24 UT; and (j) 03:52:48 UT. The slices A and B, shown in (g), represent the directions along which the speed of the EUV wave was determined. |
 |
Fig. 2 Temporal evolutions of the EUV wave fronts along slice A (top), where only a slow EUV wave with an initial speed of ~150 km s−1 is visible andalong slice B (bottom), where both a fast EUV wave (~560 km s−1) and a slower one (~250 km s−1) are visible. |
 |
Fig. 3 Dynamic spectrum of the type II burst recorded by CALLISTO-SSRT on 9 March 2012, with onset at ~03:41:20 UT, associated with the formation of an EUV wave and a shock wave driven by a halo CME during its fast acceleration phase. |
 |
Fig. 4 Dynamic spectrum of the type II burst succeeded by a moving type IV burst recorded by CALLISTO-SSRT on 9 March 2012, representing a CME-driven shock wave accompanied by a moving self-contained magnetic structure produced by fast electrons accelerated during the impulsive phase of the associated flare. |
 |
Fig. 5 Interplanetary type II burst with fundamental and harmonic emissions observed in the frequency range of 1–14 MHz by the Wind WAVES RAD2 instrument on 9 March 2012, with onset at ~04:10 UT, around 10 min after the diffusion of the associated EUV wave. |
 |
Fig. 6 Comparison between the heights of the type-II-emitting shock segments in the corona and interplanetary medium, obtained using the one-fold and the four-fold Newkirk (1961) density model (solar corona) and the Mann et al. (1999) density model (interplanetary medium). |
3 Methods, models, and equations
The kinematics of the EUV wave was investigated with reference to the bright fronts observed by SDO/AIA 193 Å, considering their temporal evolutions (distance-time diagrams) along two appropriate directions (Figs. 1 and 2).
The heights of the source of the metric type II burst associated with the coronal shock wave were estimated with reference to the whole bandwidth of the harmonic emission, taking into account the H/F frequency ratio fH ∕fF = 2 and using an appropriate multiple of the Newkirk (1961) density model
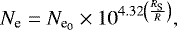 (1)
(1)
where 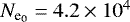 cm−3, R is the heliocentric distance and RS is the solar radius.
cm−3, R is the heliocentric distance and RS is the solar radius.
For the interplanetary medium, the heights of the source of the dekameter-hectometric type II burst were determined using the Mann et al. (1999) density model
![\begin{equation*} N(R)=N_{\textrm{S}}\times \mathrm{exp}\left[\frac{A}{{R_{\mathrm{S}}}} \left(\frac{{R_{\mathrm{S}}}}{R}-1 \right) \right],\end{equation*}](/articles/aa/full_html/2018/04/aa30358-16/aa30358-16-eq4.png) (2)
(2)
where NS = 5.14 × 109 cm−3 and 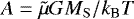 , in which G is the gravitational constant, MS the mass of the Sun, kB the Boltzmann constant, the mean molecular weight
, in which G is the gravitational constant, MS the mass of the Sun, kB the Boltzmann constant, the mean molecular weight 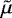 has a value of 0.6, and T = 1.0 × 106 K.
has a value of 0.6, and T = 1.0 × 106 K.
The radial speed [dR∕dt] of the type-II-emitting shock segment in the corona, estimated using an appropriate multiple [n] of the Newkirk (1961) density model applied to the lowest frequencies of the harmonic emission, which are associated with the undisturbed corona, is given by (Cunha-Silva et al. 2014):
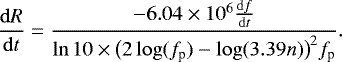 (3)
(3)
For the interplanetary medium, the radial speed of the type-II-emitting shock segment can be determined using the Mann et al. (1999) density model applied to the lowest frequencies of the harmonic emission:
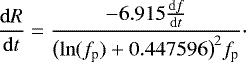 (4)
(4)
Since the band-splitting in the event is not clear, the relative band-split, defined as BDW = (fU − fL)∕fL, where fU and fL are the frequencies at the upper and lower frequency branches, respectively, is determined based on the statistical results found by Vršnak et al. (2002).
The density jump at the shock front [X] is determined from BDW (Vršnak et al. 2002):
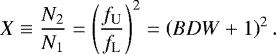 (5)
(5)
Assuming a shock perpendicular to the magnetic field and β → 0, the Alfvén Mach number [MA] can be obtained using (Vršnak et al. 2002):
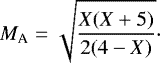 (6)
(6)
The Alfvén speed [vA] is obtained from the shock speed [vsh] and MA:
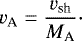 (7)
(7)
The magnetic field [B] at the shock passage can be estimated either by the band-splitting width (Vršnak et al. 2002) or the standoff distance of the shock (Gopalswamy & Yashiro 2011). Since neither of them is very clear in the event, we adopted the statistical approximation of the band-splitting width found by Vršnak et al. (2002). As we can see from Fig. 2 of Vršnak et al. (2002), for fF ≈ 70 MHz, the band-splitting width is ~0.1–0.3, which corresponds to an Alfvén Mach number of 1.1–1.5 in the case of a perpendicular shock (see Fig. 9 of Vršnak et al. (2002)). With this approximation, based on the method proposed by Vršnak et al. (2002), we can estimate the magnetic field:
![\begin{equation*} B=5.0\times10^{-7}v_{\textrm{A}}\sqrt{N_{\textrm{e}}} \ \ [\mathrm{G}].\end{equation*}](/articles/aa/full_html/2018/04/aa30358-16/aa30358-16-eq12.png) (8)
(8)
The results obtained for the magnetic field were compared with those obtained by means of linear potential extrapolations of the magnetic field from line-of-sight (LOS) photospheric magnetograms (see, e.g., Selhorst et al. 2008) provided by the Magnetic Imager (HMI) on board SDO, adopting the magnetic field solution proposed by Nakagawa & Raadu (2008) and the boundary conditions revised by Seehafer (1978).
4 Results and discussion
The comparison between the heliocentric distances of the radial propagation of the EUV wave, observed by the STEREO/EUVI-A instrument, and the heliocentric distances of the radio source associated with the shock formation, obtained using the one-fold and the four-fold Newkirk (1961) density model is presented in Fig. 7. The results obtained using the one-fold Newkirk (1961) model are compatible with the heliocentric distances of the radial propagation of the EUV wave, taking into account the uncertainties of 8–11% in the EUV measurements.
The results shown in Fig. 7 support the correspondence between the shock wave and the fast-mode EUV wave. However, the coexistence of a fast EUV wave and a slower one, as shown in the SDO/AIA 193 Å images, corroborates the occurrence of two different physical mechanisms for the coronal wave phenomena produced by a CME since the speed range of the slow EUV wave (~150–250 km s−1) is very different from that of a fast-mode wave (see, e.g., Long et al. 2008; Veronig et al. 2008; Lemen et al. 2012; Nitta et al. 2013)and can be interpreted as being of a pseudo-wave (see, e.g., Chen et al. 2002, 2005; Attrill et al. 2007; Delannée et al. 2008; Chen & Wu 2011).
Table 1 presents the physical parameters obtained for the shock wave associated with the fast EUV wave and its regions of propagation, determined in relation to the lowest frequencies of the harmonic lane of the associated type II emission.
Given that the four-fold Newkirk (1961) density model is suitable for estimating the magnetic field in active regions and the estimation of the magnetic field based on the method proposed by Vršnak et al. (2002) is model dependent, the values of B (Table 1) were determined using this model. For comparison, the results obtained for the magnetic field in the upstream regions of the shock using Eq. (8) and those obtained using linear potential extrapolation from SDO/HMI magnetograms are shown in Fig. 8. Aside from the initial heliocentric distances of the event, the results are compatible.
 |
Fig. 7 Heliocentric distances of the radial propagation of the EUV wave observed by STEREO/EUVI-A 195 Å, together with the heliocentric distances of the type II emission (in gray) obtained using the one-fold and the four-fold Newkirk (1961) density model and considering the whole bandwidth of the harmonic emission. |
Shock speed [νsh], Alfvén speed [νA], and magnetic field strength [B] in the upstream regions of the shock.
 |
Fig. 8 Magnetic field strength in the upstream regions of the shock, obtained from the type II emission, using the four-fold Newkirk (1961) density model, together with the results obtained by means of linear potential extrapolation (continuous line) from SDO/HMI magnetograms. |
5 Conclusions
We investigated a well-defined EUV wave observed by STEREO/EUVI-A and SDO/AIA, clearly associated with a shock wave driven by a halo CME observed by the SOHO/LASCO-C2/C3, as evidenced by the observations of metric and dekameter-hectometric type II bursts.
From the SDO/AIA images, we found a weak fast EUV wave, together with a more intense and slower one, which supports the coexistence of two types of EUV waves (a fast-mode wave and a slower pseudo-wave), as was predicted by Chen et al. (2002) and Chen et al. (2005) and reported by Chen & Wu (2011), Schrijver et al. (2011), Asai et al. (2012), and Shen & Liu (2012).
In addition, the observations of the EUV wave by STEREO/EUVI-A support the occurrence of EUV waves as a dome in the shape of a quasi-circular shell (see, e.g., Warmuth 2015), as revealed by both data analysis (Veronig et al. 2010; Grechnev et al. 2011)and numerical simulations (see, e.g., Uchida 1968; Wang et al. 2009, 2015; Afanasyev & Uralov 2011; Selwa et al. 2012; Downs et al. 2012). However, the EUVI data are not clear enough to see two types of EUV waves. The difference in the intensities of the two types of EUV waves found in the time-distance diagram may account for the discrepancy between the solar limb and the disk observations.
Acknowledgements
R.D.C.S. acknowledges the scholarship from CAPES, the Brazilian Federal Agency for Support and Evaluation of Graduate Education within the Ministry of Education of Brazil. C.L.S. acknowledges financial support from the São Paulo Research Foundation (FAPESP), grant number 2014/10489-0. F.C.R.F. thanks CNPq, the National Counsel of Technological and Scientific Development for the scholarship granted under process 308755/2012-0. A.J.O.S. thanks CAPES for the scholarship grant. The authors are grateful to the e-CALLISTO and Wind/WAVES science teams for the solar radio data. The EUV images were courtesy of the NASA/STEREO/EUVI and NASA/SDO/AIA consortia. The authors are grateful to the anonymous referee for the helpful remarks on this article which have significantly improved its quality and presentation.
References
- Afanasyev, A. N., & Uralov, A. M. 2011, Sol. Phys., 273, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Asai, A., Ishii, T. T., Isobe, H., Kitai, R., et al. 2012, ApJ, 745, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Attrill, G. D. R., Harra, L. K., van Driel-Gesztelyi, L., & Démoulin, P. 2007, ApJ, 656, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O., Monstein, C., Meyer, H., et al. 2009, Earth Moon Planets, 104, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Sheeley, N. R. J., & Howard, R. A. 1987, J. Geophys. Res., 92, 9869 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., & Wu, Y. 2011, ApJ, 732, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Wu, S. T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Fang, C., & Shibata, K. 2005, ApJ, 622, 1202 [Google Scholar]
- Cliver, E. W., Nitta, N. V., Thompson, B. J., & Zhang, J. 2004, Sol. Phys., 225, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha-Silva, R. D., Fernandes, F. C. R., & Selhorst, C. L. 2014, Sol. Phys., 289, 4607 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha-Silva, R. D., Fernandes, F. C. R., & Selhorst, C. L. 2015a, A&A, 578, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha-Silva, R. D., Fernandes, F. C. R., & Selhorst, C. L. 2015b, Adv. Space Res., 56, 2804 [NASA ADS] [CrossRef] [Google Scholar]
- Delannée, C. 2000, ApJ, 545, 512 [Google Scholar]
- Delannée, C., Török, T., Aulanier, G., & Hochedez, J. F. 2008, Sol. Phys., 247, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N., & Sokolov, I. V. 2012, ApJ, 750, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Dulk, G. A. 1985, ARA&A, 23, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, P. T., & Long, D. M. 2011, Space Sci. Rev., 158, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N., & Yashiro, S. 2011, ApJ, 736, L17 [Google Scholar]
- Gopalswamy, N., Kaiser, M. L., Thompson, B. J., et al. 2000, Geophys. Res. Lett., 27, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N., Thompson, W. T., Davila, J. M., et al. 2009, Sol. Phys., 259, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N., Xie, H., Mäkelä, P., et al. 2013, Adv. Space Res., 51, 1981 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Afanasyev, A. N., Uralov, A. M., et al. 2011, Sol. Phys., 273, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S. 2011, Space Sci. Rev., 158, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Klassen, A., Aurass, H., Mann, G., & Thompson, B. J. 2000, A&AS, 141, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., Boerner, P. F., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Long, D. M., Gallagher, P. T., McAteer, R. T. J., & Bloomfield, D. S. 2008, ApJ, 680, L81 [Google Scholar]
- Magdalenić, J., Marqué, C., Zhukov, A. N., Vršnak, B., & Veronig, A. 2012, ApJ, 746, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, G., Classen, H. T., & Aurass, H. 1995, A&A, 295, 775 [NASA ADS] [Google Scholar]
- Mann, G., Jansen, F., MacDowall, R. J., et al. 1999 A&A, 348, 614 [NASA ADS] [Google Scholar]
- Mann, G., Klassen, A., Aurass, H., & Classen, H. T. 2003, A&A, 400, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreton, G. E. 1960, AJ, 65, 494 [Google Scholar]
- Moses, D., Clette, F., Delaboudinière, J.-P., et al. 1997, Sol. Phys., 175, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y.,& Raadu, M. A. 1972, Sol. Phys., 25, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, G. J., & Melrose, D. B. 1985, in Solar Radiophysics, eds. D. J. McLean, & N. R. Labrum (Cambridge: Cambridge Univ. Press), 333 [Google Scholar]
- Neupert, W. M. 1989, ApJ, 344, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Newkirk, G. J. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, N. V., Schrijver, C. J., Title, A. M., & Liu, W. 2013, ApJ, 776, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., & Vourlidas, A. 2012, Sol. Phys., 281, 187 [NASA ADS] [Google Scholar]
- Payne-Scott, R., Yabsley, D. E., & Bolton, J. G. 1947, Nature, 160, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Aulanier, G., Title, A. M., Pariat, E., et al. 2011, ApJ, 738, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Seehafer, N. 1978, Sol. Phys., 58, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Selhorst, C. L., Silva-Válio, A., & Costa, J. E. R. 2008, A&A, 488, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Poedts, S., & DeVore, C. R. 2012, ApJ, 747, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Liu, Y. 2012, ApJ, 752, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Simões, P. J. A., Fletcher, L., Hudson, H. S., & Russell, A. J. B. 2013, ApJ, 777, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res. Lett., 25, 2465 [Google Scholar]
- Uchida, Y. 1960, PASJ, 12, 376 [NASA ADS] [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Veronig, A. M., Temmer, M., & Vršnak, B. 2008, ApJ, 681, L113 [Google Scholar]
- Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M., & Vršnak, B. 2010, ApJ, 716, L57 [Google Scholar]
- Vršnak, B., & Cliver, E. W. 2008, Sol. Phys., 253, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., Magdalenić, J., Aurass, H., & Mann, G. 2002, A&A, 396, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, H., Shen, C., & Lin, J. 2009, ApJ, 700, 1716 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Liu, S., Gong, J., Wu, N., & Lin, J. 2015, ApJ, 805, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Warmuth, A. 2015, Liv. Rev. Sol. Phys., 12, 3 [Google Scholar]
- Wild, J. P. 1962, J. Phys. Soc. Japan, 17, 249 [Google Scholar]
- Zlotnik, E. Y., Klassen, A., Klein, K. L., Aurass, H., & Mann, G. 1998, A&A, 331, 1087 [NASA ADS] [Google Scholar]
All Tables
Shock speed [νsh], Alfvén speed [νA], and magnetic field strength [B] in the upstream regions of the shock.
All Figures
 |
Fig. 1 Running-difference images of STEREO/EUVI-A 195 Å and SDO/AIA 193 Å showing the EUV wave formation (accompanied by EUV bubble) for (a) 03:40:30 UT; (b) 03:45:30 UT; (c) 03:50:30 UT; (d) 03:55:30 UT; (e) 04:00:30 UT; (f) 03:42:12 UT; (g) 03:45:36 UT; (h) 03:47:48 UT; (i) 03:50:24 UT; and (j) 03:52:48 UT. The slices A and B, shown in (g), represent the directions along which the speed of the EUV wave was determined. |
| In the text | |
 |
Fig. 2 Temporal evolutions of the EUV wave fronts along slice A (top), where only a slow EUV wave with an initial speed of ~150 km s−1 is visible andalong slice B (bottom), where both a fast EUV wave (~560 km s−1) and a slower one (~250 km s−1) are visible. |
| In the text | |
 |
Fig. 3 Dynamic spectrum of the type II burst recorded by CALLISTO-SSRT on 9 March 2012, with onset at ~03:41:20 UT, associated with the formation of an EUV wave and a shock wave driven by a halo CME during its fast acceleration phase. |
| In the text | |
 |
Fig. 4 Dynamic spectrum of the type II burst succeeded by a moving type IV burst recorded by CALLISTO-SSRT on 9 March 2012, representing a CME-driven shock wave accompanied by a moving self-contained magnetic structure produced by fast electrons accelerated during the impulsive phase of the associated flare. |
| In the text | |
 |
Fig. 5 Interplanetary type II burst with fundamental and harmonic emissions observed in the frequency range of 1–14 MHz by the Wind WAVES RAD2 instrument on 9 March 2012, with onset at ~04:10 UT, around 10 min after the diffusion of the associated EUV wave. |
| In the text | |
 |
Fig. 6 Comparison between the heights of the type-II-emitting shock segments in the corona and interplanetary medium, obtained using the one-fold and the four-fold Newkirk (1961) density model (solar corona) and the Mann et al. (1999) density model (interplanetary medium). |
| In the text | |
 |
Fig. 7 Heliocentric distances of the radial propagation of the EUV wave observed by STEREO/EUVI-A 195 Å, together with the heliocentric distances of the type II emission (in gray) obtained using the one-fold and the four-fold Newkirk (1961) density model and considering the whole bandwidth of the harmonic emission. |
| In the text | |
 |
Fig. 8 Magnetic field strength in the upstream regions of the shock, obtained from the type II emission, using the four-fold Newkirk (1961) density model, together with the results obtained by means of linear potential extrapolation (continuous line) from SDO/HMI magnetograms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


