[https://doi.org/10.1051/0004-6361/201525895]
[https://doi.org/10.1051/0004-6361/201525922]
| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | C2 | |
| Number of page(s) | 3 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201525895e | |
| Published online | 08 May 2018 | |
Corrigendum
Bayesian peak bagging analysis of 19 low-mass low-luminosity red giants observed with Kepler (Corrigendum)
1
INAF – Osservatorio Astrofisico di Catania,
via S. Sofia 78,
95123
Catania, Italy
e-mail: enrico.corsaro@oact.inaf.it
2
Instituut voor Sterrenkunde, KU Leuven,
Celestijnenlaan 200D,
3001
Leuven, Belgium
3
IRFU, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
4
Université Paris Diderot, AIM, Sorbonne Paris Cité, CEA, CNRS,
91191
Gif-sur-Yvette,
France
Received:
23
January
2018
Accepted:
23
January
2018
Key words: stars: oscillations / stars: evolution / stars: late-type / methods: statistical / methods: numerical / methods: data analysis / errata, addenda
1 Improved ellipsoidal sampling
In Corsaro et al. (2015a), we used the Bayesian estimation code DIAMONDS for a peak-bagging analysis of 19 oscillating red giants. DIAMONDS uses the nested sampling method in which the prior is sampled under the hard constraint that the likelihood of each new point must be better than the one of the worst point, after which the latter is discarded from the “live” sample. To avoid a high rejection rate by sampling low-likelihood regions, the algorithm only samples inside ellipsoids around the most interesting regions of the parameter space. These ellipsoids are constructed using the covariance matrix of live points, but since they do not exactly coincide with the true iso-likelihood contours, they are enlarged by a factor f to avoid missing relevant parts of the sampling space. To boost the performance, this enlargement is then gradually phased out as the live sample concentrates on the high-likelihood regions and the ellipsoids are becoming a progressively better approximation of the iso-likelihood contours.
It turns out that in the configuration of DIAMONDS used in Corsaro et al. (2015a), the law adopted to estimate the initial enlargement factor as a function of the number of free parameters (see Corsaro 2018) was leading to ellipsoidal sampling regions that were too small in the final stages of the computation. Although none of the estimates of the peak bagging parameters are affected, their Bayesian credible intervals (i.e. the errors on the model parameters estimated from the marginal probability distributions) are affected by roughly a factor of two. We therefore recalibrated the relation between the initial enlargement fraction f0, and the number of free fit parameters k that define the inference problem. The new relations are:

for Nlive = 500 and 1000, respectively. Both laws are defined for an optimal number of clusters, Nclust in the range 3–4, assume a shrinking rate α = 0, a maximum number of drawing attempts from the prior distribution of Mattempts = 5 × 104, and a value of δfinal = 1 for the termination condition (see Corsaro & De Ridder 2014 for more details on the configuring parameters of the code).
2 Assessing the new calibration
To prove that the new calibration provides trustworthy results, we compare the newly estimated credible intervals of the mode frequencies with the theoretical errors on the frequencies of isolated ℓ = 0 modes as derived by Libbrecht (1992); Ballot et al. (2008):
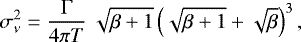 (3)
(3)
where T is the total observing time of the original time-series, Γ the linewidth of the ℓ = 0 mode considered, and β is the ratio between the background level evaluated for the frequency ν0 and the corresponding height of the peak (or equivalently the inverse of the signal-to-noise ratio of the oscillation peak).
To show how well the Bayesian credible intervals estimated by DIAMONDS agree with the theoretical errors as a function of the dimension of the parameter space, we use KIC 12008916 as a test case. The solid lines in Fig. 1 show the new calibration of f0 as a function of the number of fit parameters, for live sample sizes 500 and 1000 (see Eqs. (1) and (2)). On top of these curves we show the f0 values used by DIAMONDS for 37 independent peak-bagging computations, each one using a different number of peaks (and thus different values of k) in the Fourier spectrum of KIC 12008916. The ratio between the theoretical frequency error and the one computed by the newly calibrated DIAMONDS is near perfect for parameter spaces with up to k = 40 dimensions1. The derived frequency credible intervals (not the frequencies themselves!) only start to deviate somewhat from the theoretical ones for a parameter space with k > 40, but still giving acceptable results up to k ~ 60. We have also tested the relation with Nlive = 500 on a different star, the red clump KIC 5112373, by fitting up to k = 54 free parameters, and we found that the Bayesian credible intervals are in good agreement with expected errors from theory (on average within 10 %).
 |
Fig. 1 Initial enlargement fraction f0 used in DIAMONDS, as a function of the number of dimensions involved in the inference problem, k. The 37 independent computations shown in the plot (one for each symbol) are performed using a peak-bagging analysis on the test star KIC 12008916 and a number of live points of Nlive = 500 (squares) and Nlive = 1000 (circles). The color of the symbols indicates the ratio ϵcorr between the theoretical (Eq. 3) and computed error (the latter obtained from the Bayesian inference performed with DIAMONDS) on the ℓ = 0 mode frequencies involved in the fit. For ϵcorr = 1 we have perfect agreement between predicted and computed errors. The dashed vertical line delimits a transition to a high-dimensional regime in which the calibration of f0 becomes more critical and the computed errors can be underestimated with respect to the prediction by more than 30%. |
3 Correction factors
As mentioned before, the frequencies, amplitudes, and linewidths published by Corsaro et al. (2015a) are unaffected by the new calibration, but their Bayesian credible intervals were underestimated. To overcome this issue, one has to multiply the published Bayesian credible intervals of each oscillation mode parameter (i.e. frequency, amplitude, linewidth, and independently of the angular degree) by an average correction factor ⟨ϵcorr ⟩, which we computed for each of the 19 stars of the sample by considering all its significant ℓ = 0 modes, and by comparing the published intervals with the theoretical errors from Eq. (3). In Table 1 we list the average correction factors for all the 19 stars analyzed by Corsaro et al. (2015a). After the correction is applied, the Bayesian credible intervals appear in line with the errors predicted from theory, as shown in Fig. 2.
The new calibration also affects the credible intervals of the parameters that define the acoustic glitch model derived from the second frequency differences by Corsaro et al. (2015b). In this case we repeated the fits of the acoustic glitch model with DIAMONDS, adopting the new calibration law for Nlive= 1000, α = 0, δfinal = 1, Mattempts = 5 × 104. By comparing the published values of the credible intervals with the new ones, we derived an averaged correction factor ⟨ϵcorr,2⟩ for each star (see Table 1), which has to be applied to the Bayesian credible intervals of all the glitch model fit parameters published by Corsaro et al. (2015b). We find that in general the previous Bayesian credible intervals were underestimated with respect to the corrected ones, by a factor ranging from about 1.1 to 3.5, except for the stars KIC 9882316 and KIC 10257278 for which we have an overestimation by about a factor of two. We also found that the stars KIC 3744043, KIC 9882316, KIC 10257278, KIC 11913545 have a published acoustic depth that is incorrect due to a wrong choice of the uniform prior boundary on the parameter and of the presence of a multi-modal solution for the acoustic depth. We have thus estimated the new acoustic depths for these targets and reported their corrected values in Table 1. These corrected acoustic depths are now well in agreement with the predicted values from modeling obtained by Pérez Hernández et al. (2016; see their Fig. 13). The new Bayesian credible intervals, as corrected in this work, yield an average precision of ~ 5 % in the acoustic depth, so about two times that previously published by Corsaro et al. (2015b).
We emphasize that all these correction factors are only to be applied to the Bayesian credible intervals of the fit parameters published by Corsaro et al. (2015a) and Corsaro et al. (2015b), and not to any future peak-bagging analysis done with DIAMONDS. As mentioned in the previous section, the new calibration of the current version of DIAMONDS already mitigates the problem.
Average correction factors per star ⟨ϵcorr⟩ (for the parameters of the peak bagging analysis) and ⟨ϵcorr,2⟩ (for the parameters of the acoustic glitch analysis) indicating the factors for which the Bayesian credible intervals published by Corsaroet al. (2015a) and by Corsaro et al. (2015b), respectively, have to be multiplied.
 |
Fig. 2 Effect of the correction on the Bayesian credible intervals of the ℓ = 0 mode frequencies published by Corsaro et al. (2015a). The credible intervals rescaled by the corresponding linewidth Γ of each peak are shown as a function of their signal-to-noise ratio, β−1. The red squares show the values before the correction, the blue circles show the values after the correction. The thick red line is the theoretical prediction using Eq. (3). |
Acknowledgements
E. C. is funded by the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No. 664931. We thank G. R. Davies for useful discussions.
References
- Ballot, J., Appourchaux, T., & Toutain, T. 2008, Astron. Nachr., 329, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Corsaro, E. 2018, in Asteroseismology and Exoplanets: Listening to the Stars and Searching for New Worlds, eds. T. Campante, N. Santos, & M. Monteiro, ASSP, 49, 137 [NASA ADS] [Google Scholar]
- Corsaro, E. & De Ridder J. 2014, A&A, 571, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corsaro, E., De Ridder, J., & García, R. A. 2015a, A&A, 579, A83 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Corsaro, E., De Ridder, J., & García, R. A. 2015b, A&A, 578, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G. 1992, ApJ, 387, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez Hernández, F., García, R. A., Corsaro, E., Triana, S. A., & De Ridder J. 2016, A&A, 591, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
More details on the derivation of the new calibration are also available in the latest release of the user guide manual of the code, which can be downloaded from the public GitHub repository of DIAMONDS https://github.com/EnricoCorsaro/DIAMONDS.
© ESO 2018
All Tables
Average correction factors per star ⟨ϵcorr⟩ (for the parameters of the peak bagging analysis) and ⟨ϵcorr,2⟩ (for the parameters of the acoustic glitch analysis) indicating the factors for which the Bayesian credible intervals published by Corsaroet al. (2015a) and by Corsaro et al. (2015b), respectively, have to be multiplied.
All Figures
 |
Fig. 1 Initial enlargement fraction f0 used in DIAMONDS, as a function of the number of dimensions involved in the inference problem, k. The 37 independent computations shown in the plot (one for each symbol) are performed using a peak-bagging analysis on the test star KIC 12008916 and a number of live points of Nlive = 500 (squares) and Nlive = 1000 (circles). The color of the symbols indicates the ratio ϵcorr between the theoretical (Eq. 3) and computed error (the latter obtained from the Bayesian inference performed with DIAMONDS) on the ℓ = 0 mode frequencies involved in the fit. For ϵcorr = 1 we have perfect agreement between predicted and computed errors. The dashed vertical line delimits a transition to a high-dimensional regime in which the calibration of f0 becomes more critical and the computed errors can be underestimated with respect to the prediction by more than 30%. |
| In the text | |
 |
Fig. 2 Effect of the correction on the Bayesian credible intervals of the ℓ = 0 mode frequencies published by Corsaro et al. (2015a). The credible intervals rescaled by the corresponding linewidth Γ of each peak are shown as a function of their signal-to-noise ratio, β−1. The red squares show the values before the correction, the blue circles show the values after the correction. The thick red line is the theoretical prediction using Eq. (3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


