| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732155 | |
| Published online | 19 March 2018 | |
Tensile strength of 67P/Churyumov–Gerasimenko nucleus material from overhangs
1
Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille,
Marseille, France
e-mail: Nicholas.Attree@lam.fr
2
Physikalisches Institut, Sidlerstr. 5, University of Bern,
3012
Bern, Switzerland
3
Institute of Planetary Research, DLR,
Rutherfordstrasse 2,
12489,
Berlin, Germany
4
Max-Planck-Institut für Sonnensystemforschung,
37077
Göttingen, Germany
5
Department of Physics and Astronomy, Padova University,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
6
Centro de Astrobiologia (INTA-CSIC),
Villanueva de la Canada,
28691
Madrid, Spain
7
International Space Science Institute,
Hallerstrasse 6,
3012
Bern, Switzerland
8
Scientific Support Office, European Space Agency,
2201
Noordwijk, The Netherlands
9
Department of Physics and Astronomy, Uppsala University,
Box 516,
75120
Uppsala, Sweden
10
PAS Space Research Center,
Bartycka 18A,
00716
Warszawa, Poland
11
Institute for Geophysics and Extraterrestrial Physics, TU Braunschweig,
38106
Braunschweig, Germany
12
Department of Astronomy, University of Maryland,
College Park,
MD
20742-2421, USA
13
LESIA, Obs. de Paris, CNRS, Univ Paris 06, Univ. Paris-Diderot,
5 place J. Janssen,
92195
Meudon, France
14
LATMOS, CNRS/UVSQ/IPSL,
11 boulevard d’Alembert,
78280
Guyancourt, France
15
Centro di Ateneo di Studi ed Attività Spaziali, “Giuseppe Colombo” (CISAS), University of Padova,
via Venezia 15,
35131
Padova, Italy
16
Department of Industrial Engineering, University of Padova,
35131
Padova, Italy
17
CNR-IFN UOS Padova LUXOR,
via Trasea 7,
35131
Padova, Italy
18
UNITN, Universit di Trento,
via Mesiano, 77,
38100
Trento, Italy
19
INAF - Osservatorio Astronomico,
Via Tiepolo 11,
34143
Trieste, Italy
20
Instituto de Astrofisica de Andalucía (CSIC),
Glorieta de la Astronomía s/n,
18008
Granada, Spain
21
Institute for Space Science, Nat. Central Univ.,
300 Chung Da Rd.,
32054
Chung-Li, Taiwan
22
Operations Department, European Space Astronomy Centre/ESA,
PO Box 78, Villanueva de la Canada,
28691
Madrid, Spain
23
Centre for Astrophysics and Planetary Science, School of Physical Sciences (SEPnet), The University of Kent,
Canterbury
CT2 7NH, UK
24
Southwest Research Institute,
1050 Walnut St., Boulder,
CO
80302, USA
25
NASA Ames Research Center,
Moffett Field,
CA
94035, USA
26
MTA CSFK Konkoly Observatory,
Konkoly Thege M. ut 15-17,
1121
Budapest, Hungary
Received:
23
October
2017
Accepted:
20
December
2017
We directly measured twenty overhanging cliffs on the surface of comet 67P/Churyumov–Gerasimenko extracted from the latest shape model and estimated the minimum tensile strengths needed to support them against collapse under the comet’s gravity. We find extremely low strengths of around 1 Pa or less (1 to 5 Pa, when scaled to a metre length). The presence of eroded material at the base of most overhangs, as well as the observed collapse of two features andthe implied previous collapse of another, suggests that they are prone to failure and that the true material strengths are close to these lower limits (although we only consider static stresses and not dynamic stress from, for example, cometary activity). Thus, a tensile strength of a few pascals is a good approximation for the tensile strength of the 67P nucleus material, which is in agreement with previous work. We find no particular trends in overhang properties either with size over the ~10–100 m range studied here or location on the nucleus. There are no obvious differences, in terms of strength, height or evidence of collapse, between the populations of overhangs on the two cometary lobes, suggesting that 67P is relatively homogenous in terms of tensile strength. Low material strengths are supportive of cometary formation as a primordial rubble pile or by collisional fragmentation of a small body (tens of km).
Key words: comets: general / comets: individual: Churyumov–Gerasimenko / Methods: observational
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0;), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0;), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Material strength is an important parameter in constraining the formation and evolution of comets and in explaining their morphological diversity. Low strengths support the conclusion that comets are primordial rubble piles, accreted gently (collision velocities from ~1 m s−1 to tens of m s−1) in the early solar system, as opposed to remnants from higher velocity collisions (from hundreds of m s−1 to km s−1 ) which would undergo impact compaction and would leave them with higher strengths (Davidsson et al. 2016). The strength of cliffs and overhangs against collapse also directly relates to cometary activity as cliff collapses are an important source of jets and outbursts (Vincent et al. 2016; Pajola et al. 2017).
The tensile strength of cometary nucleus material has been estimated for a number of comets and using a number of different methods: observations of comet break-ups from rotation (see e.g. Davidsson 2001), or close encounters with the Sun (Klinger et al. 1989; Steckloff et al. 2015) or Jupiter (Asphaug & Benz 1996); laboratory experiments (Blum et al. 2006, 2014; Bar-Nun et al. 2007); computer modelling (Greenberg et al. 1995; Biele et al. 2009); and, in the case of 67P/Churyumov–Gerasimenko (hereafter 67P), observations of cliffs, overhangs, and boulders. As summarised by Groussin et al. (2015), strength estimates vary over several orders of magnitude for cometary material, but are generally low: in the range of pascals to tens of pascals for tensile strength (σT )at the metre scale, and larger for shear and compressive strengths. The discussion of scale is important because consolidated material generally shows decreasing strength at larger scales, following a power law proportional to d−q, with length scale d and an exponent of q ~ 0.6 for water ice (Petrovic 2003).
For 67P, the high quality of the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS) allowed the examination of a variety of features at the metre and decametre scale and, from this, Groussin et al. (2015) measured the tensile strength of an overhang and a collapsed feature, estimating σT = 1–3 Pa and <150 Pa at the 5–30 m scale. When scaled to 1 m, this gives σT = 8–39 Pa and <1150 Pa for these features, which are located in the Imhotep and Maftet regions, on the head and body of the comet, respectively (see Thomas et al. 2015 and El-Maarry et al. 2015 for a detailed description of the 67P regions). Vincent et al. (2017) also measured the heights of cliffs and derived 1–2 Pa strengths at the decametre scale across the surface of 67P in order for the cliffs not to collapse.
The goal of this work is to perform a more comprehensive survey of the overhanging cliffs across the surface of comet 67P in order to quantify material strengths and to determine its homogeneity or heterogeneity. In Section 2 we describe the method developed to identify and measure overhanging cliffs. The results are presented in Section 3 and discussed in Section 4, and conclusions are drawn in Section 5.
2 Method
We measured the overhang properties using a digital terrain model (DTM) or shape model of comet 67P, constructed using the Stereo Photogrammetry (SPG) technique from the Rosetta/OSIRIS images. Groussin et al. (2015) showed that the alternative Stereo Photoclinometry (SPC) technique can underestimate the number of high-slope facets compared to SPG, making SPG a more appropriate technique for studying sharp topography. We used the latest shape model (SPG-SHAP7; Preusker et al. 2017) with 22 million vertices, with a typical spacing of 1–2 m and orientation uncertainty of 2–5∘ . For computational reasons, we used a decimated version (2 million facets, ~7 m lateral vertex spacing) of the full shape model. Gravitational vectors were calculated for each facet following the method of Jorda et al. (2012), which includes centrifugal forces, and were then compared to the facet normal vectors to produce a map of gravitational slope. Locally flat regions have a gravitational slope of 0∘ , while vertical cliffs are at 90∘ and anything larger is an overhang. There are 15 358 facets (0.77% of the total number) with slopes greater than 90∘ and approximately 5000 greater than 100∘ . A number of these are artefacts of the reconstruction, but many are real overhanging features visible in the OSIRIS images.
Due to the complicated shape of the nucleus, and the presence of artefacts in the reconstructed shape model, it was deemed impossible to automatically detect and characterise every overhanging feature. Instead we identified, by eye, a number of features and investigated them in detail. The features were selected by picking the most obvious large groupings of overhanging facets on the shape model from all over the nucleus. Selecting the largest (actually deepest) overhangs places the strongest constraints on strength. We examined the spatial distribution of selected features to ensure good coverage in Section 3.
For each selected feature, a local DTM is extracted from the full model, and a vertical profile of the overhang is computed in the following way. First, the negatives of the gravitational vectors are plotted on each high-slope facet. These point “up”, i.e. away from the centre of gravity, and in an overhang region will penetrate inside the shape model before exiting it again at the top of the overhang (see Fig. 1). The two facets where the gravitational vector enters and exits the nucleus define the coordinates of the “base” and “top” of the overhang. Selecting a third point as a facet on the “face” of the overhang, perpendicular to the gravity vector, defines a plane, whose intersection with the shape model can be calculated. The final step is to project the coordinates of the intersection points onto the plane itself and then rotate the data to align them with the local gravity vector. This vector will vary across the overhang, but the differences over such short distances ( ~100 m) are negligible, and the “base” gravity vector is used for the whole profile here. A profile of the shape model along the chosen vector is then recovered.
From this profile, an estimate of the strength of the overhang can be calculated using the equations of a cantilevered beam. Following Tokashiki & Aydan (2010) and using the coordinate frame centred on the overhang base (as shown in Fig. 1), the maximum stress from bending is found at x = 0 and decreases along the length. The material tensile strength must be at least as large as this maximum stress to prevent immediate failure and collapse. For a beam of unit thickness and length L and height h, this can be expressed as
 (1)
where
(1)
where 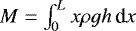 is the total bending moment acting on the cantilever from its own unit weight: unit density, ρ = 537.8 kg m−3 (Preusker et al. 2017), times the magnitude of the local gravity, g. For simple beam shapes, this can be integrated directly. In a rectangular beam, for example, h is constant and the bending moment evaluates to M = hρgL2∕2, while stress becomes
is the total bending moment acting on the cantilever from its own unit weight: unit density, ρ = 537.8 kg m−3 (Preusker et al. 2017), times the magnitude of the local gravity, g. For simple beam shapes, this can be integrated directly. In a rectangular beam, for example, h is constant and the bending moment evaluates to M = hρgL2∕2, while stress becomes
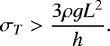 (2)
(2)
For a trapezium shaped beam, as shown in Fig. 1, h varies along the length, but the integral can still be evaluated, so that this time the stress becomes
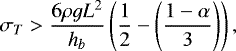 (3)
(3)
where α = hs∕hb is the ratio of the height at the far-end to the base height. These two equations are useful approximations for many overhangs and were used in the previous works (Groussin et al. 2015; Tokashiki & Aydan 2010). In our case, however, we have the full overhang profile from the shape model and can therefore integrate this directly, without having to use one of these approximations. We do this numerically by first interpolating the profile shape to a regularly spaced series of x positions (separated by dx); then measuring h at each of these; and finally making the sum  , where N = L∕dx.
, where N = L∕dx.
As can be seen from Eqs. (2) and (3), the overhang length is the most important parameter for constraining the material strength, and this remains true for the numerical integration. Therefore, for each of our overhangs we select the intersection plane to compute the profile along the deepest part of the overhang, by choosing the base facet with a gravity vector penetrating most deeply into the shape model (maximum L). In most cases, this is obvious from visual inspection and in cases with several similar facets, similar strength estimates will be derived.
There is an uncertainty in the position of all coordinates measured on the shape mode, which can be conservatively estimated as the average radius of a facet. For our two million facet model this is ~1.6 m. In addition, the uncertainty in the orientation of each facet has been estimated as Δθ ≈±5∘ (Jorda et al. 2012) and in practice this can dominate over the positional uncertainty. We therefore estimate the uncertainties in overhang proportions by rotating each profile by ±Δθ, computing the integral and measuring h, and then combining this uncertainty with the position error. Uncertainties in tensile strength are then derived using the standard error propagation formulae.
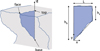 |
Fig. 1 Overhang measurement method using the coordinates of three facets of the overhang, at the base, top, and face, to define a plane and to find its intersection with the shape model. Aligning the profile with the local gravity vector, g, then allows the various overhang parameters to be measured, as in Tokashiki & Aydan (2010). |
3 Results
Table 1 shows the results for the 20 overhanging features analysed. Overhang heights are between ~10 and 100 m and depths are generally only ~10 m (Fig. 2), with a single feature (number 2) having a greater depth of almost 40 m. This feature, part of a cliff in the Babi region facing Hapi, is visually the largest overhang on the shape model, but is otherwise unremarkable.
The calculated overhang strengths are very low, with a mean of 0.3 Pa and an average uncertainty of ± 0.22 Pa. Figure 3 shows the distribution in measured strengths and those scaled from the feature length-scale, h, to 1 m, using the power law for ice (the scaling law for ice is used, despite the large dust content, as a first estimate and for easeof comparison with previous studies). The scaled strengths all lie between 0 and 5 Pa, apart from the single large outlier of feature 2. Nonetheless, the uncertainty in sigma for this feature could easily bring its value in linewith the others. We detect no particular relation between strength, scaled or raw, and overhang height, suggesting a uniform strength over the range of ~ 10–100 m.
Figures 4–6 show the locations of each measured feature on the comet’s surface, along with all the high-slope facets. High-slopes are typically clustered into curvilinear chains of cliffs. The only large area lacking high-slopes (other than artefacts) is the smooth, dusty terrain of Hapi. Our selected overhangs are well distributed across the surface, with features seen in both hemispheres, both cometary lobes and in a variety of cometary regions. No particular trends are noted between overhang properties and location, and there are no significant differences between theaverage strengths on each lobe, suggesting a uniformity in the capacity of the 67P material to support overhangs.
The features have a variety of morphologies, as can be seen in their profiles and accompanying OSIRIS images in Figs. 7–10. They range from large, shallow cliffs to protruding blocks and the lips of pit walls. Most have a shallow trapezium or triangular shape; a number have curving top surfaces and are not obvious caves, but rather are steep cliffs which lean slightly outwards towards their tops, producing an overhanging region. Several features are actually double or triple overhangs (features 1, 4, 16, and19 in Figs. 7–10), and for these we split the integration region before calculating the momentof each area and manually summing them together. Nearly all the overhangs examined here show some evidence of collapse or erosion, such as boulders and debris fields at their bases. The exceptions are features 1, 4, and 17, where the possible debris is some distance away due to the overhangs’ positions at the top of tall cliffs, and 3 and 20, where its presence is slightly ambiguous.
Of particular interest are features 5, 12, and 15. Feature 12 is the same as the failed section already measured in Groussin et al. (2015). The overhang in Ash near feature 5 was seen to undergo a collapse between May and December 2015 (El-Maarry et al. 2017a, supplementary Fig. 2). We examined a local high-resolution DTM of thearea (F. Preusker, priv. comm.), but unfortunately we were unable to produce a profile of the collapsed region, due to technical issues. Measuring directly from the DTM in a 3D model viewer, however, weestimate the overhanging segment to have L ≈ 12 m and h ≈ 31 m, giving σT ≈ 0.4 Pa with the rectangular approximation of Eq. (2), in line with the other overhangs measured here. Similarly, feature 15, located in Seth and named Aswan, was seen to collapse in July 2015 (triggering an outburst, Pajola et al. 2017). They measured the overhanging section as 65 × 12 m, again consistent with the 63 × 11 m, σ = 0.33 Pa found here.
Locations (in the Cheops frame) and properties of each measured overhang.
 |
Fig. 2 Maximum height and depth of each of the measured overhangs. |
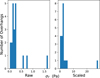 |
Fig. 3 Lower limit of tensile strengths for the measuredoverhangs. On the right the data have been scaled from the feature length scale (h) to the equivalent strength at the metre scale. |
 |
Fig. 4 Location of the measured overhangs (orange diamonds). Also shown are high-slope facets on the shape model with the colour scheme: green ≥ 100∘ , 100∘ > blue ≥ 90∘, and 90∘ > red ≥ 85∘. |
 |
Fig. 6 Location of the measured overhangs on the shape model. |
 |
Fig. 5 Location of the measured overhangs. The colour scheme shows the tensile strength (unscaled) on a log scale. |
 |
Fig. 7 Overhangs 1–5. On the left: representative, contrast enhanced, OSIRIS images: NAC_2014-12-01T21.02.45, NAC_2016-05-13T06.42.54, NAC_2016-07-16T06.46.11, NAC_2014-10-01T06.49.53, and NAC_2014-10-01T04.36.23, respectively. A visualisation of the overhang on the shape model is shown in the middle; the facets are colour-coded by slope as above (green ≥ 100∘, 100∘ > blue ≥ 90∘, and 90∘ > red ≥ 85∘). On the right: shape model profile along an intersection through the overhang is shown in blue and our interpolated area for integration in black. |
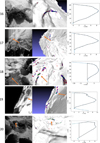 |
Fig. 10 Overhangs 16–20. Same as Fig. 7 with images NAC_2016-03-19T23.04.57, NAC_2015-01-16T01.44.08, NAC_2014-10-02T00.26.22, NAC_2016-04-29T15.55.45, and NAC_2016-03-19T16.38.38, respectively. |
 |
Fig. 8 Overhangs 6–10. Same as Fig. 7 with images NAC_2016-07-09T03.28.54, NAC_2014-10-05T16.55.16, NAC_2016-06-07T21.07.00, NAC_2016-05-20T08.01.06, and NAC_2016-03-13T16.53.39, respectively. |
 |
Fig. 9 Overhangs 11–15. Same as Fig. 7 with images NAC_2014-09-22T01.37.07, NAC_2016-07-09T21.44.48, NAC_2014-09-23T09.42.48, NAC_2016-04-23T18.12.52, and NAC_2014-10-02T00.26.22, respectively. |
4 Discussion
4.1 Are overhangs representative of bulk nucleus strength?
The strengths estimated above are lower limits; the material must have at least this tensile strength in order not to immediatelycollapse under its own weight, but could be much stronger. The presence of collapses, however, implies thatoverhangs may be close to failure and that these estimates may indeed be close to the actual material strength.
Conversely, Vincent et al. (2017) and Pajola et al. (2017) argue that cliff heights are not controlled by intrinsic material strength but by external erosion, in which case observed features would not be limited by gravity and tensile strengths could be greater. Many of the features examined here have clearly fractured cliff walls (e.g. 2, 6, 9, 10, 13, 15, 16, and 18), some reminiscent of thermal contraction crack polygons (Auger et al. 2015, 2018), which may imply additional processes such as thermal stresses and sublimation that can weaken them until failure occurs. Additionally, material strength can vary on a local scale. For example, results from the MUPUS and SESAME experiments on the Philae lander (Spohn et al. 2015; Knapmeyer et al. 2017), as well as theoretical (Kossacki et al. 2015) and laboratory work (Gruen et al. 1993; Kochan et al. 1989), suggest a hard, ice bonded layer with much greater strength within a few metres of the surface. The SESAME results, in particular, suggest a layer at depths of 10–50 cm with a tensile strength of the order of MPa (Knapmeyer et al. 2017).
In order to consider these possibilities, we compared the dimensions of the measured overhangs with the depths of a hard layer, and with those of temperatures relevant for thermal processing, using a comet thermal model described in Attree et al. (2018). Our model takes into account a spherical nucleus (orientated according to its pole with RA = 69.57∘ , DEC = 64.01∘ (J2000) and with a rotational period of P = 12.40 hr; Jorda et al. 2016), solar insulation, and heat conductivity (Groussin & Lamy 2003). We computed the temperature on the surface and inside the nucleus over one complete revolution, taking into account the diurnal and seasonal changes in insolation with heliocentric distance. To ensure convergence, we used a time step of 12.4 s and ran the thermal model over five complete revolutions. We then computed the maximum temperature over an orbital period, experienced at each depth interval (for 2000 depth intervals of a thickness of one-fifth of a diurnal skin depth each) for three different values of thermal inertia: I = 10, 50, and 250 J m−2 K−1 s−1∕2.
Figure 11 shows the resulting thermal profiles at the equator. The horizontal lines show conservative estimates for the temperatures where sublimation is negligible compared to the erosion rate at perihelion (one thousandth of its value) for water ice (160 K) and CO2 (85 K). Depths of 2.8 m for water ice, and 8.4 m for CO2 ,therefore define the limits to which we would expect sublimation to affect material properties. Our overhangs are typically ~10 m deep and, with one exception (feature 9), all have L > 5 m. Assuming H2O is the dominant volatile component, we therefore expect our strength measurements to be probing material which has not been thermally processed. Furthermore, since pressure inside the comet is of the order of tens to hundreds of Pa (Groussin et al. 2015), thermal or compressional processing should not affect material below these depths and we expect the measured tensile strength to be a good approximation of that of the bulk nucleus.
A hard, ice bonded layer will increase the average strength of near surface material. The fact that we measure such low strengths, however, implies that the hard layer is localised and does not contribute significantly to the average strength of cometary material at depth. This is consistent with an estimated hard layer thickness of 0.1–0.5 m, compared to the ~5–10 m deep overhangs. Therefore, we conclude this section by reinforcing the idea that the tensile strengths measured above ( ~0–5 Pa when scaled to metre lengths) are indeed representative of bulk cometary tensile strengths at the decametre scale.
 |
Fig. 11 Maximum temperature reached with depth at the equator of 67P for three different values of thermal inertia. Horizontal lines indicate conservative estimates for the temperaturewhere sublimation is negligible (compared to the erosion rate at perihelion) for water ice (160 K) and CO2 (85 K). |
4.2 Dynamic stresses
Thus far our analysis has only focused on the strength of overhangs that resist the static stress of their own weight; however, dynamic stresses should also be present on the comet. These mightinclude stresses induced by rotational changes (Hviid et al. 2016; Hirabayashi et al. 2016), as well as seismic events, such as cometary activity/outbursts and impacts (e.g. Thomas & Robinson 2005).
Impact features are rare on the 67P surface; only a few, small craters ( ~10 s of metres) were detected during the Rosetta mission (El-Maarry et al. 2017b), and it seems unlikely that they provide a comet-wide mechanism for overhang collapse. Activity related stresses, on the other hand, are very likely to have occurred during the comet’s approach to the Sun, but quantifying them remains difficult due to the still poorly understood activity mechanisms. Seismic energy, released from a particular source of cometary activity, should fall off with the square of the distance times some attenuation factor (Thomas & Robinson 2005), which may be large due to the comet’s fractured and porous nature. As a first-order estimate, the stress in a weak elastic wave is σ = Usi79vρ (Melosh 1989) which, with a wave velocity of U > 80 m s−1 (as measured by experiments on Philae; Knapmeyer et al. 2017) and assuming a particle velocity of v = 1 cm s−1, will be at least 430 Pa, greater than the strength estimates here. Continuous activity is not localised to particular regions, however, and even transient outburst features are found all over the nucleus, suggesting that it will be hard to correlate the locations of activity with collapsed overhangs (the exception being where collapses trigger outbursts, as in the case of Aswan above).
Due to the reaction force on the nucleus, activity can alter cometary orbit and rotation, and several studies have investigated the stresses induced by such changes in rotation pattern on 67P’s complex shape. Both Hviid et al. (2016) and Hirabayashi et al. (2016) found large stresses of up to several hundred Pa centred on the neck region. These dynamic stresses indeed exceed static stress and would lead to failure if the material had the strengths measured here. Our measured overhangs (both those with and without collapse features) have no apparent correlation with the neck, however. Additionally, the presence of collapses in features 5 and 12 (located on the big lobe, far from the neck) argues for static-stress induced failure. A full analysis of the correlation between activity- and rotation-driven stress patterns and the location of overhangs could put further constraints on the material strength, but is beyond the scope of this paper. Here we must limit our conclusion to the following: that static stress analysis provides lower limits to cometary material strength, but which may indeed be close to the real values due to the presence of overhangs which appear to have collapsed under their own weight.
5 Conclusion
We examined 20 overhanging cliffs, measuring their vertical profiles using the up-to-date SPG SHAP7 shape model (Preusker et al. 2017) of comet 67P. From this we derive lower limits for the material’s tensile strength in order to support such overhangs against gravity. Overhangs are generally shallow (most have depths ~10 m) and so the resulting tensile strengths are very small: σT ~ 1 Pa or less at the decametre scale and ~0–5 Pa when scaled to metre lengths (except for one outlier at ~28 Pa, but with relatively large uncertainties). Nevertheless, the presence of eroded material at the base of most overhangs, the observed collapse of two features, and the implied previous collapse of another suggests that they are near to failure. Thus, a σT value of a few pascals is a good estimate for the tensile strength of the 67P nucleus material, although further analysis of dynamic stresses, such as those caused by cometary activity and rotation changes, is warranted. Thermal modelling shows little material alteration at relevant depths in the subsurface, suggesting that this value is a reasonable approximation for bulk strengths at depth. This is in good agreement with previous estimates (as can be seen in the summary Table in Groussin et al. 2015) from modelling (Greenberg et al. 1995; Biele et al. 2009), laboratory experiments (Bar-Nun et al. 2007; Blum et al. 2014), and some observations (Asphaug & Benz 1996; Steckloff et al. 2015), including cliff heights (Vincent et al. 2017). Other observations, such as those of the break-up of sungrazing and rotating comets (Klinger et al. 1989; Davidsson 2001), suggest somewhat higher values of tens of Pa to ~100 Pa. The Groussin et al. (2015) overhang results are slightly higher than those presented here because their overhang shapes were approximated as rectangular and are different from the shape model profiles used here.
We find no particular trends in overhang properties with size over the ~10–100 m range studied here, or with location on the nucleus. There are no obvious differences, in terms of strength, height, or evidence of collapse, between the populations of overhangs on the two cometary lobes, suggesting that 67P is relatively homogenous in terms of tensile strength.
Such a low and homogeneous strength has implications for the formation and evolution of 67P. In terms of evolution, low strengths mean that material is easily eroded by sublimation, gas pressure, and thermal fracturing, and is vulnerable to collapse under its own gravity. Collapses naturally explain the retreating cliffs, with debris fields and fallen boulders at their feet, seen across the comet (see e.g. Pajola et al. 2015, 2017; El-Maarry et al. 2017a), as well as the presence of the overhangs themselves. These may form from the partial collapse of sections of cliff following preexisting weaknesses or may be further weakened by thermal fracturing (see the model of erosion in Attree et al. 2018). Cometary outgassing activity has been linked to such collapses (Pajola et al. 2017) and to active cliff faces in general (Vincent et al. 2016), demonstrating that cliffs and overhangs are important areas of erosion on cometary surfaces.
Low bulk strengths support the conclusions of Davidsson et al. (2016) that 67P represents a primordial rubble pile, directly accreted from the proto-solar nebular by hierarchical aggregation or streaming instabilities, or is a collisional fragment from a small body (tens of km). A fragment, or rubble pile of fragments, from the disruption of a larger body ( ~1000 km) would inherit some of that body’s properties, such as higher density and higher strength material from impact compaction and/or thermal processing and differentiation. Low strength is more consistent with early formation at low collision velocities (Skorov & Blum 2012) in a dynamically cold disk, whilst a homogeneity between the two lobes of 67P could imply a similar formation mechanism for both.
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 686709. This work was supported by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number 16.0008-2. The opinions expressed and arguments employed herein do not necessarily reflect the official view of the Swiss Government. OSIRIS was built by a consortium of the Max-Planck-Institut für Sonnensystemforschung, Göttingen, Germany; the CISAS University of Padova, Italy; the Laboratoire d’Astrophysique de Marseille, France; the Instituto de Astrofisica de Andalucia, CSIC, Granada, Spain; the Research and Scientific Support Department of the ESA, Noordwijk, Netherlands; the Instituto Nacional de Técnica Aeroespacial, Madrid, Spain; the Universidad Politéchnica de Madrid, Spain; the Department of Physics and Astronomy of Uppsala University, Sweden; and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), France (CNES), Italy (ASI), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged. We thank the Rosetta Science Operations Centre and the Rosetta Mission Operations Centre for the successful rendezvous with comet 67P/Churyumov–Gerasimenko.
References
- Asphaug, E., & Benz, W. 1996, Icarus, 121, 225 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Attree, N., Groussin, O., Jorda, L., et al. 2018, A&A, 610, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auger, A.-T., El-Maarry, M. R., Groussin, O., et al. 2015, in European Planetary Science Congress 2015 (EPSC2015), 27 September to 2 October, 2015, Nantes, France, id.EPSC2015-516, 10 [Google Scholar]
- Auger, A.-T., Groussin, O., Jorda, L., et al. 2018, Icarus, 301, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Bar-Nun, A., Pat-El, I., & Laufer, D. 2007, Icarus, 187, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Biele, J., Ulamec, S., Richter, L., et al. 2009, Acta Astronaut., 65, 1168 [Google Scholar]
- Blum, J., Schräpler, R., Davidsson, B. J. R., & Trigo-Rodríguez, J. M. 2006, ApJ, 652, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., Gundlach, B., Mühle, S., & Trigo-Rodriguez, J. M. 2014, Icarus, 235, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R. 2001, Icarus, 149, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., Sierks, H., Güttler, C., et al. 2016, A&A, 592, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Maarry, M. R., Thomas, N., Giacomini, L., et al. 2015, A&A, 583, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Maarry, M. R., Groussin, O., Thomas, N., et al. 2017a, Science, 355, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- El-Maarry, M. R., Groussin, O., Thomas, N., et al. 2017b, in European Planetary Science Congress, EPSC2017, 11 [Google Scholar]
- Greenberg, J. M., Mizutani, H., & Yamamoto, T. 1995, A&A, 295, L35 [NASA ADS] [Google Scholar]
- Groussin, O., & Lamy, P. 2003, A&A, 412, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groussin, O., Jorda, L., Auger, A.-T., et al. 2015, A&A, 583, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruen, E., Gebhard, J., Bar-Nun, A., et al. 1993, J. Geophys. Res., 98, 15 [Google Scholar]
- Hirabayashi, M., Scheeres, D. J., Chesley, S. R., et al. 2016, Nature, 534, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Hviid, S., Hüttig, C., Groussin, O., et al. 2016, in AAS/Division for Planetary Sciences Meeting Abstracts, 48, 211.05 [Google Scholar]
- Jorda, L., Lamy, P., Gaskell, R., et al. 2012, Icarus, 221, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Jorda, L., Gaskell, R., Capanna, C., et al. 2016, Icarus, 277, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Klinger, J., Espinasse, S., & Schmidt, B. 1989, in Physics and Mechanics of Cometary Materials, eds. J. J. Hunt, & T. D. Guyenne (ESA Special Publication), 302 [Google Scholar]
- Knapmeyer, M., Fischer, H.-H., & Knollenberg, J. 2017, Icarus, submitted [Google Scholar]
- Kochan, H., Roessler, K., Ratke, L., et al. 1989, in Physics and Mechanics of Cometary Materials, eds. J. J. Hunt, & T. D. Guyenne (ESA Special Publication), 302 [Google Scholar]
- Kossacki, K. J., Spohn, T., Hagermann, A., Kaufmann, E., & Kührt, E. 2015, Icarus, 260, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Melosh, H. J. 1989, Impact Cratering: A Geologic Process (New York: Oxford University Press), Vol. 11 [Google Scholar]
- Pajola, M., Vincent, J.-B., Güttler, C., et al. 2015, A&A, 583, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pajola, M., Höfner, S., Vincent, J. B., et al. 2017, Nat. Astron., 1, 0092 [CrossRef] [Google Scholar]
- Petrovic, J. J. 2003, J. Mater. Sci., 38, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2017, A&A, submitted [Google Scholar]
- Skorov, Y. & Blum, J. 2012, Icarus, 221, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spohn, T., Knollenberg, J., Ball, A. J., et al. 2015, Science, 349, 6247 [CrossRef] [Google Scholar]
- Steckloff, J. K., Johnson, B. C., Bowling, T., et al. 2015, Icarus, 258, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, P. C., & Robinson, M. S. 2005, Nature, 436, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015, Science, 347, aaa0440 [CrossRef] [Google Scholar]
- Tokashiki, N., & Aydan, O. 2010, Dokobu Gakkai Ronbunshuu, 66, 397 [CrossRef] [Google Scholar]
- Vincent, J.-B., Oklay, N., Pajola, M., et al. 2016, A&A, 587, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, J.-B., Hviid, S. F., Mottola, S., et al. 2017, MNRAS, 469, S329 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overhang measurement method using the coordinates of three facets of the overhang, at the base, top, and face, to define a plane and to find its intersection with the shape model. Aligning the profile with the local gravity vector, g, then allows the various overhang parameters to be measured, as in Tokashiki & Aydan (2010). |
| In the text | |
 |
Fig. 2 Maximum height and depth of each of the measured overhangs. |
| In the text | |
 |
Fig. 3 Lower limit of tensile strengths for the measuredoverhangs. On the right the data have been scaled from the feature length scale (h) to the equivalent strength at the metre scale. |
| In the text | |
 |
Fig. 4 Location of the measured overhangs (orange diamonds). Also shown are high-slope facets on the shape model with the colour scheme: green ≥ 100∘ , 100∘ > blue ≥ 90∘, and 90∘ > red ≥ 85∘. |
| In the text | |
 |
Fig. 6 Location of the measured overhangs on the shape model. |
| In the text | |
 |
Fig. 5 Location of the measured overhangs. The colour scheme shows the tensile strength (unscaled) on a log scale. |
| In the text | |
 |
Fig. 7 Overhangs 1–5. On the left: representative, contrast enhanced, OSIRIS images: NAC_2014-12-01T21.02.45, NAC_2016-05-13T06.42.54, NAC_2016-07-16T06.46.11, NAC_2014-10-01T06.49.53, and NAC_2014-10-01T04.36.23, respectively. A visualisation of the overhang on the shape model is shown in the middle; the facets are colour-coded by slope as above (green ≥ 100∘, 100∘ > blue ≥ 90∘, and 90∘ > red ≥ 85∘). On the right: shape model profile along an intersection through the overhang is shown in blue and our interpolated area for integration in black. |
| In the text | |
 |
Fig. 10 Overhangs 16–20. Same as Fig. 7 with images NAC_2016-03-19T23.04.57, NAC_2015-01-16T01.44.08, NAC_2014-10-02T00.26.22, NAC_2016-04-29T15.55.45, and NAC_2016-03-19T16.38.38, respectively. |
| In the text | |
 |
Fig. 8 Overhangs 6–10. Same as Fig. 7 with images NAC_2016-07-09T03.28.54, NAC_2014-10-05T16.55.16, NAC_2016-06-07T21.07.00, NAC_2016-05-20T08.01.06, and NAC_2016-03-13T16.53.39, respectively. |
| In the text | |
 |
Fig. 9 Overhangs 11–15. Same as Fig. 7 with images NAC_2014-09-22T01.37.07, NAC_2016-07-09T21.44.48, NAC_2014-09-23T09.42.48, NAC_2016-04-23T18.12.52, and NAC_2014-10-02T00.26.22, respectively. |
| In the text | |
 |
Fig. 11 Maximum temperature reached with depth at the equator of 67P for three different values of thermal inertia. Horizontal lines indicate conservative estimates for the temperaturewhere sublimation is negligible (compared to the erosion rate at perihelion) for water ice (160 K) and CO2 (85 K). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


