EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 611 (March 2018) A&A, 611 (2018) A57 Full HTML
Free Access
Issue
A&A
Volume 611, March 2018
Article Number A57
Number of page(s) 9
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201629017
Published online 27 March 2018

© ESO 2018

1 Introduction

The Sun is an intense source of radio waves. Its nonthermal radio radiation is strongly related to flares, which are caused by the release of energy during reconfigurations of the Sun’smagnetic field. Thus, flares represent a manifestation of magnetic reconnection in the solar corona (Priest 1981). They are essentially defined as a localized sudden enhancement of the Sun’s electromagnetic radiation over a broad spectrum, from radio waves up to γ-rays (Svestka 1981). They are also accompanied by the generation of energetic particles (Heyvaerts 1981). Evidence for electron acceleration is seen in so-called solar type-III radio bursts (Wild 1950), which are a common phenomenon of the solar radio radiation. Examples of such bursts are presented in Figs. 1 and 2. Type-III bursts appear as short-lived broadband events and a rapid drift from high to low frequencies in dynamic radio spectra (Wild 1950).

The Sun’s nonthermal radio radiation in the megahertz range is considered to be plasma emission (Melrose 1985). It can be generated in the corona by energetic electrons that excite electrostatic plasma oscillations, for example Langmuir waves, which are then converted into radio waves via nonlinear plasma processes (Melrose 1985). Consequently, the radio emission occurs near the local electron plasma frequency fpe and/or its harmonics (Melrose 1985). Since the electron plasma frequency depends on the electron number density Ne , that is, 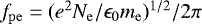(e, elementary charge; ϵ0 , permittivity of free space; me, electron mass), and because of the gravitational density stratification of the corona, higher and lower frequencies are emitted in the lower and higher corona, respectively. If a radio source propagates through the corona, its motion causes a frequency drift in the associated dynamic radio spectrum. Because of this relation, the rapid drift of type-III bursts is interpreted as radio signatures of rapidly propagating beams of energetic electrons (Wild 1950). If these electrons penetrate into interplanetary space, they can generate interplanetary type-III bursts from the megahertz down to the kilohertz range. The instruments onboard the ISEE-3 (International Sun Earth Explorer) spacecraft observed interplanetary type-III bursts and the arrival of the associated electrons at the spacecraft. Both measurements confirmed that type-III bursts are in fact generated by energetic electrons (Lin et al. 1981).

The electron beam associated with a type-III burst excites Langmuir waves. Their feedback to the beam should lead to its destruction on time scales of the inverse electron plasma frequency ( ≈10−8 s at 100 MHz), that is, much faster than a type-III bust lifetime (Wild 1950) that can reach hours for interplanetary type-III bursts. This is referred to as Sturrock’s dilemma (Sturrock 1964). However, this rapid destruction is avoided by the formation of “beam-plasma-structures” (Zheleznyakov & Zaitsev 1970; Kontar et al. 1998; Mel’Nik et al. 1999; Reid & Ratcliffe 2014).

Radio images of solar type-III radio bursts localizing the radio source in the corona were already obtained with early interferometers at Culgoora (Wild 1970), Nancay (Bougeret et al. 1970) and Clark Lake (Kundu et al. 1983) at megahertz frequencies corresponding to a distance of a few solar radii. With the Nancay radio heliograph (Bougeret et al. 1970) the sources of a few type-III bursts were localized in open coronal magnetic flux tubes (Klein et al. 2008). Radio imaging observations of type-III bursts in the lower corona at 1 to 1.5 GHz were done with the Jansky Very Large Array by (Chen et al. 2013). Although the radio sources could not be resolved, their centroid positions could be determined and their trajectories could be reconstructed over a distance of 2 arcmin.

The LOw Frequency ARray (LOFAR) is a novel radio interferometer (van Haarlem et al. 2013) that can operate as a dynamic spectroscopic radio imager of the Sun in the frequency ranges from 10−90 MHz (low band: LBA) and 110−250 MHz (high band: HBA) with high sensitivity and resolution. Therefore solar observations with LOFAR have the potential to reveal new aspects of solar radio bursts. One of them concerns the path of the type-III burst source with respect to the solar magnetic field. It is assumed that the electron beams of solar type-III bursts, and consequently the emission regions, follow coronal magnetic-field lines (Gopalswamy et al. 1987). However, up to now, there is no direct observational evidence for this assumption in the high corona due to the lack of radio imaging of this part of the corona, that is, in the low frequency range.

Here, we present results of high-resolution imaging and spectroscopic LOFAR observations of the Sun. The corresponding data analysis is described in Sect. 2. With LOFAR we can now measure the spatio-temporal evolution of type-III burst sources with high accuracy (see Sect. 3). The structure of the magnetic field in the corona can be derived by extrapolation of photospheric magnetic-field data, which is provided daily by the Solar Dynamics Observatory (SDO) space mission. These extrapolations allow us to study the path of the sources of solar type-III radio bursts with respect to the coronal magnetic field (see Sect. 4). Additionally, the radial density profile can be derived in the high corona by means of these measurements (see Sect. 4). The results are summarized in Sect. 5.

thumbnail Fig. 1

Dynamic radio spectrum (bottom) of the LOFAR observation of the Sun on June 23, 2012, showing the normalized flux density in arbitrary units. Time and frequency resolution are given by Δt and Δf. Typical signatures of three type-III bursts are found at 11:00:05, 11:00:11 and 11:01:54 UTC. The vertical features between the second and third burst are broadband radio frequency interference (RFI). The simultaneous X-ray flux from the GOES 15 satellite (top) does not indicate any flare activity.
thumbnail Fig. 2

Dynamic radio spectrum of the type-III burst at 11:00:05 UT on June 23, 2012. It starts at 55 MHz and drifts to lower frequencies.

2 Solar LOFAR data analysis

The LOFAR radio interferometer (van Haarlem et al. 2013) currently consists of 50 antenna stations, most of them located in the Netherlands, and twelve of them in neighboring European countries. LOFAR operates in the frequency ranges from 10 to 90 and 110 to 250 MHz, in full polarization, and with high sensitivity and resolution for imaging spectroscopy. Its so calleddigital sub-arrays allow the simultaneous observationsof different radio sources (target and calibrator sources) with the same antenna stations. This is important for the calibration of dynamic sources like the Sun.

During the commissioning phase of LOFAR, the Sun was observed from 11:00 to 11:10 UT on June 23, 2012, with 22 core and 9 remote stations in LBA outer configuration in the frequency range from 30 to 80 MHz at 11 equidistant frequencies. Each of these 11 frequency sub-bands had a bandwidth of 195 kHz and a subdivision into 64 channels. Two sub-array pointings were formed and directed to the Sun and to Virgo A. The latter was used as a calibrator. For each sub-array pointing, the data from the individual LOFAR stations were correlated for 496 baselines and integrated to time steps of 0.94 s at the computing centre in Groningen, and stored as CASA (McMullin et al. 2007) “Measurement Sets” for further post processing. Simultaneously, the flux density of the sub-array pointing to the Sun was recorded as dynamic spectrum (Stappers et al. 2011) at the same frequencies but with an increased time resolution of 9.8 ms and stored in LOFAR’s HDF5 format for dynamic spectra.

Post-processing was done with LOFAR’s Solar Imaging Pipeline (Breitling et al. 2015); it was developed for the KSP “Solar Physics and Space Weather with LOFAR” (Mann et al. 2011)at the Leibniz-Institut für Astrophysik Potsdam, and represents an extension of LOFAR’s Standard Imaging Pipeline (Heald et al. 2011) for imaging spectroscopy of the Sun. The first step was the pre-processing with LOFAR’s Default Pre-processing Pipeline. This included flagging the channels of the calibrator data for RFI with the AOFlagger (Offringa et al. 2013). The Sun data was not flagged in order to preserve all variable radio features. Subsequently, the channels (excluding channel numbers 1, 2, 63 and 64) of all sub-bands were averaged to one channel per sub-band to reduce the amount of data by a factor of 60. Furthermore the uv-range was limited to 0–1000 wavelength to exclude data exceeding the sub-arcminute resolution limit of the corona that is caused by turbulence. This data does not contribute useful imaging information and excluding it simplifies calibration and further reduces the amount of data. The second step was calibration with LOFAR’s BlackBoard Selfcal system. Here, amplitude and phase corrections were determined for every second of calibrator data using a corresponding sky model for Virgo A. The solutions were then transferred to the data of the Sun. The third step was imaging the corrected data by applying the multi-scale CLEAN algorithm provided by CASA and transforming from equatorial to solar coordinates. This was done for every time step and frequency. For the images discussed here, an additional phase-only self-calibration was applied using the CLEAN components as a model. Then imaging was repeated as before, resulting in a more compact source with reduced noise with unchanged position. Further self-calibration cycles did not change the images significantly and hence were not applied. The position of the Sun was used to verify the astrometric consistency of the images; it remained unchanged over time and frequency also when no burst was visible.

The dynamic spectrum was produced with the Spectrummaker of the Solar Imaging Pipeline. This identifies and excludes channels with a high standard deviation caused by RFI. The spectrum averages the remaining channels of each sub-band and scales them to values between 0 and 1. To make the scaling more robust against RFI, the highest 1% of the recorded values are ignored for the scaling and truncated to 1. To emphasize the burst signatures, the values are gamma corrected. For the same reason, the data of Fig. 1 are additionally scaled from −0.2 to 1.3. Intermediate values between the 11 frequency sub-bands are interpolated.

3 LOFAR observation of solar type-III radio bursts

During LOFAR’s observations of the Sun on June 23, 2012, three type-III bursts were observed as presented in Fig. 1 which shows the dynamic radio spectrum from LOFAR (bottom) and the simultaneous X-ray flux (top) measured by the GOES 15 satellite. The X-ray flux shows no strong enhancement or variation. However, the radio spectrum shows type-III radio bursts, at 11:00:05, 11:00:11 and 11:01:54 UTC, typical of radio noise storm activity, which is not accompanied by any X-ray activity. Figure 2 also shows the first burst in higher time resolution of 0.01 s. The burst starts at 55 MHz and drifts to 30 MHz in the time range from 11:00:05 to 11:00:10 UTC, resulting in a frequency drift of − 5 MHz s−1. Such a drift rate is typical for type-III bursts in this frequency range (Mann & Klassen 2002). Shortly after its onset, the burst also appears at 60 MHz indicating a reverse burst propagating in the opposite direction. The second and third bursts behave similarly.

Dynamic imaging was performed simultaneously to the dynamic spectra at the 11 observing frequencies with a time resolution of 1 s. Figures 3 to 5   show four of these images for each burst at theonset time of the bursts. The white solid and dashed semicircles mark the distances of 1 and 2 R⊙. The radio bursts appear as compact bright radio source at a distance between 2 and 2.5 R⊙. Their brightness exceeds that of the thermal radio emission from the Sun, thus explaining why the region of the Sun is dark. The source size is represented by the yellow contour line at a flux density level of 50% of the image peak flux density. It exceeds the size of the point spread function (PSF) which is shown by the top-right, dashed blue ellipse. This ellipse represents the full width at half maximum (FWHM) major and minor axis of a Gaussian fit to the PSF. The PSF is determined by the actual array configuration that provided data to an image and is calculated for each image individually. The blue, green, and yellow markers show the centroid positions of the radio source of the three burstsand their observed propagation path. The centroid coordinates were determined within the 80% flux density contour, by weighting each position by its flux density.The corresponding helioprojective-Cartesian X and Y coordinates and radial distance robs from the center of the Sun are given in Table 1. The statistical error of these coordinates was estimated from a Gaussian fit to the 80% flux density contour according to Condon (1997) with CASA; it is about 10 arcsec or 0.01 R⊙. The robs increases to lower frequencies. The white lines represent the Sun’s coronal magnetic field, which was extrapolated from the photospheric magnetic field using the potential-field source-surface (PFSS) method provided by the SolarSoft software package (Schrijver & De Rosa 2003). The photospheric magnetic field was measured by the Helioseismic and Magnetic Imager (HMI; Lemen et al. 2012) aboard the SDO satellite. Only field lines originating within a spherical sector with longitude of ±15 degrees from the western limb are shown. The last images at 30 MHz in Figs. 3 to 5 show all centroids of a burst together with an extreme ultraviolet (174 Å) image of the structure of the lower corona by the SWAP instrument (Halain et al. 2013) of the PROBA2 satellite. The covered region by this image is as dark as at the other frequencies.

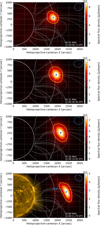thumbnail Fig. 3

LOFAR images at four frequencies of the first type-III burst starting at 11:00:05 UTC (Fig. 2). The yellow line shows the size of the radio source at a contour level of 50% of its peak flux density. Its high flux density makes the thermal emission from the Sun invisible on this color scale. The markers show the burst’s centroid position (Table 1) at each frequency. They reveal the burst’s propagation path when shown all together as in the last image at 30 MHz. It also shows an extreme ultraviolet (174 Å) image of the Sun from the PROBA2 satellite. The coronal magnetic field is shown by the white lines. The white solid and dashed circles indicate the distances of 1 and 2 R⊙, respectively. The blue, dashed ellipse (top right) represents the FWHM of the Gaussian fit of the PSF.
thumbnail Fig. 4

As in Fig. 3 but for the second type-III burst starting at 11:00:11 UTC.
thumbnail Fig. 5

As in Fig. 3 but for the third type-III burst starting at 11:01:54 UTC.
Table 1

Astrometric parameters of the type-III burst sources.

4 Refraction of radio radiation in the corona

The LOFAR data of radio bursts above the solar limb provide a new opportunity to study the radial propagation of type-III bursts in the upper corona with high spatial and temporal resolution. However, to fully exploit the spatial information provided by LOFAR, refraction of radio radiation in the corona has to be taken into account. The refraction is determined from ray tracing simulations that will be explained in detail in a forthcoming publication by Vocks et al. (2018). They are based on Snell’s law, n1 sinθ1 = n2 sinθ2, where n is the index of refraction and θ is the angle to the gradient of n in two different media. In a plasma, n < 1 and can be expressed by the plasma frequency fpe as 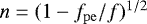. A radio ray path is obtained by integration over the differential changes of θ along its path for a given coronal density profile. Since n < 1, radio waves in a spherically symmetric corona of decreasing density are refracted in radial direction as shown by Fig. 6. This model is based on the assumption that the type-III-emitting electrons are propagating in the plane of sky, which is supported by the radio source propagation along magnetic field lines extrapolated from the solar limb in Figs. 3–5. Since n drops to zero as f approaches fpe , refraction of fundamental and harmonic emission is so strong that emission in the plane of sky is not directly observable at Earth because of the large angle from the radial direction. But scatteringof radio emission on coronal density inhomogeneities from turbulence can explain indirect observations of radio bursts in the plane of sky (Riddle 1974). Figure 6 shows the apparent and actual location of a refracted radio signal in the plane of sky with radial distance robs and rref , respectively. The actual source position can be considered as the scattering location of fundamental or harmonic emission. However it cannot be the place of fundamental or harmonic plasma emission, because the density is lower than a density corresponding to fpe. Therefore the emission happens at a distance closer to the Sun of rf and rh . The value of rref depends on the coronal density profile, and for a given density profile there is a smallest possible rref where a radio source in the plane of sky can be observed at Earth (Fig. 6). Since the scattering inhomogeneities drop with distance from the Sun, most scattering can be expected from the closest possible rref . So in our calculations we determine the smallest rref for a given density profile and scale the density profile until the corresponding robs agrees with observations. We have used the barometric density profile by Newkirk (1961) with the scaling factor α. Once α is determined, rf and rh can be calculated by inverting f = fpe(Ne(r)). The results for the LOFAR type-III burst observations are given in Table 1. The source locations for fundamental and harmonic emission are shown in Fig. 7. The difference between rf and rh to robs are about −10% and 15% to 30%, respectively.

thumbnail Fig. 6

Refraction in the corona of four radio ray paths (solid lines) with different viewing angles to an observer on Earth as determined from ray tracing simulations for a frequency of 55 MHz and a barometric density profile (Newkirk 1961) with α = 3.3. Fundamental radio emission generated in the plane of sky at a radial distance from the Sun rf is scattered at the distance rref and refracted to Earth where its observed at a radial distance robs . The distance robs is given by the intersection of the plane of sky with the nonrefracted path indicated by the dashed line.
thumbnail Fig. 7

Positions where fundamental (red bordered markers) and harmonic emission (plain markers) from a radio burst is generated according to ray-tracing simulations (Table 1). The observed centroid positions of the radio bursts lie in between.

5 Propagation of type-III bursts

The radio sources appear first at 55.5 MHz and then at lower but also higher frequencies in the dynamic radio spectrum and in the images. This indicates a burst and its reverse burst, propagating in opposite directions.

The elongated source structure can be explained as emission from a spherical sector in the plane of sky. Projection along the line of sight leads to a reduced source diameter in width while the length remains invariant and a measure for the true source diameter. Figure 8 shows the length of the 50% flux density contour versus robs ; it was determined at an angle of 110 degrees to the helioprojective-Cartesian X direction. This is the average orientation of the maximum source diameter of all images. The statistical error of 3% in length was also determined from a Gaussian fit with CASA. The source size is growing with distance from the Sun. A similar result was found by Saint-Hilaire et al. (2013). It could be interpreted as a widening of the electron beams associated with the bursts.

The magnetic field lines mainly extend in a radial direction and coincide with the path of the type-III burst sources. This supports a propagation in the plane of sky. As they drift to lower frequencies, we find that the burst sources follow the field lines. In this particular case, some magnetic field lines are closed and could confine the electrons to the corona. This could be an explanation for why this burst is not detected at lower frequencies, that is, in the interplanetary space, with the radio spectrometer aboard the WIND satellite. This also agrees with the current picture of type-III bursts as signatures of beams of energetic electronspropagating along magnetic field lines in the corona.

The radio images also lead to the path-time diagram for a radio sourcein the plane of sky. The propagation distance Δs and time t are the distance and time between neighboring centroids. Their cumulated propagation distance s is the sum of all Δs starting from 55.5 MHz. The propagation velocity v = Δs∕Δt. Table 2 shows these parameters as observed and for the emission region of fundamental and harmonic radiation as determined from ray-tracing simulations. Figure 9 shows the corresponding path-time diagrams for the observed, fundamental, and harmonic emission regions. The error bars reflect the uncertainties of the bursts’ onset times and of the centroid coordinates. In any case, the movement of the type-III radio sources is nonuniform in the plane of sky (Fig. 9) that is, the source velocities are continuously increasing. According to the general picture of type-III radio bursts (Zheleznyakov & Zaitsev 1970; Kontar et al. 1998; Mel’Nik et al. 1999; Reid & Ratcliffe 2014), energetic electrons propagating along magnetic field lines are the source of type-III radio bursts. They excite Langmuir waves which are converted into radio waves seen as type-III radio bursts. In the case of a beam of monoenergetic electrons, that is, electrons with a constant velocity, thecorresponding type-III radio burst source would move with a constant velocity. Since this is not the case here (Fig. 9), the type-III radio bursts are not generated by a simple monoenergetic beam of electrons, but by an ensemble of energetic electrons with a spread velocity distribution. An explanation is beyond the scope of this work but it could be the result of propagation effects of an electron ensemble with different velocities.

If the electron propagation is not perfectly aligned with the plane of sky, then the analysis in Fig. 9 can be affected by propagation effects. Any path component perpendicular to the plane of sky increases the actual path length. But this would mean that the speed of an electron beam would have to be even higher than the one derived based on the plane-of-sky assumption. The apparent acceleration of the radio bursts in Fig. 9 would require a very special geometry, as an monoenergetic electron beam would have to start out of the plane of sky in the lower corona and then continuously align better with it.

thumbnail Fig. 8

Length l of the radio source versus projected radial distance r from the center of Sun in the plane of sky for the three type-III radio bursts at frequencies from 55.5 to 30.1 MHz.
Table 2

Parameters of propagation of the type-III bursts according to observations (obs) and ray tracing simulations for fundamental (f) and harmonic (h) emission locations.

thumbnail Fig. 9

Path-time diagrams of the three type-III radio bursts as obtained from the observed (sobs ), fundamental (sf) and harmonic (sh) emission regions in the plane of sky according to Table 2. The sources propagate with increasing speed. The error in time is either one or two time steps of 0.94 s depending on how clearly the image of the burst’s onset could be distinguished. The statistical error of s is about 0.01 R⊙ and hidden by the marker.

6 Coronal density measurements

The observation of plasma emission along the propagation path of a solar radio burst provides information about the coronal density profile. The density profile is obtained from the plasma frequency’s corresponding electron number densities 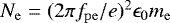and the radial distance of the radio source.

The density profile for rf and Ne from Table 1 is shown in Fig. 10 for the three observed type-III radio bursts. We note that rh and Ne∕4 would result in the same density profile. For comparison, the density models by Newkirk (1961) and Mann et al. (1999) are also shown. The Newkirk (1961) model results from white-light scattering measurements in the corona. The radial profile of the electron number density is described by 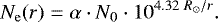(1)

White-light scattering measurements by Koutchmy (1994) showed that the Newkirk model represents a good approximation for the electron number density profile above quiet equatorial regions, in dense loops, and in extremely dense loops for α = 1, 4, and 10, respectively. This corresponds to a barometric density behavior with a coronal temperature of 1.4 × 106 K. A three-fold Newkirk model (α = 3) fits the LOFAR data well. This is already indicated by the α(rf) values listed in the right column of Table 1, which scatter around a value of 3 for all observed radio bursts and frequencies.

The density model by Mann et al. (1999) results from a special solution of Parker’s wind equation (Parker 1958). The model describes the density behavior from the bottom of the corona out to 1 AU, and its three-fold version is in good agreement with observations. For the inner corona, it behaves like a barometric density model with a temperature of 1.0 × 106 K and hence a steeper density gradient. A three-fold Mann model also fits the LOFAR data well.

thumbnail Fig. 10

Radial electron number density profile of the corona as derived from the three type III radio bursts observations and ray tracing simulations (Table 1). The three-fold coronal density models by Newkirk (1961) and Mann et al. (1999) are shown for comparison.

7 Summary

These measurements of type-III radio bursts were enabled by high-resolution dynamic imaging spectroscopy using LOFAR in the frequency range 30–80 MHz. For the first time we see images of a burst and its reverse burst. We find the source sizes increasing with propagation distance and that the propagation paths agree with a propagation along the coronal magnetic field lines in projection to the plane of sky. This is consistent with the current understanding of solar type-III radio bursts as radio signatures of beams of energetic electrons (Wild 1950). Since the propagation of the type-III radio burst sources shows a nonuniform movement, the type-III burst radio radiation is not generated by monoenergetic electron beams, but by ensembles of electrons with a broad distribution of velocities (and energies). Furthermore, we directly determined the electron number density profile in the corona from the LOFAR measurements of the source positions of the type-III radio bursts. The profile agrees well with three-fold coronal density models by Newkirk (1961) and Mann et al. (1999). Independently assuming fundamental or harmonic emission, the density profile corresponds to a barometric density behavior with a coronal temperature of 1.4 × 106 K.

Acknowledgements

Financial support was provided by the German Federal Ministry of Education and Research (BMBF in the framework of the Verbundforschung, D-LOFAR 05A11BAA). The authors would like to thank Mark DeRosa’s help for extending the magnetic field calculations beyond the default distance, NASA’s SDO and ESA’s PROBA2 teams as well as the DAM and ARTEMIS observatories for providing open access to their data, and J. Anderson, A. Warmuth, J. Hessel, and G. Heald for their careful reading of the manuscript. LOFAR, designed and constructed by ASTRON, has facilities in several countries that are owned by various parties (each with their own funding sources) and are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy. C. F. acknowledges financial support from the “Agence Nationale de la Recherche” through grant ANR-09-JCJC-0001-01.

References

  1. Bougeret, J.-L., Caroubalos, C., Mercier, C., & Pick, M. 1970, A&A, 6, 406 [NASA ADS] [Google Scholar]
  2. Breitling, F., Mann, G., Vocks, C., Steinmetz, M., & Strassmeier, K. G. 2015, Astron. Comput., 13, 99 [NASA ADS] [CrossRef] [Google Scholar]
  3. Chen, B., Bastian, T. S., White, S. M., et al. 2013, ApJ, 763, L21 [NASA ADS] [CrossRef] [Google Scholar]
  4. Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
  5. Gopalswamy, N., Kundu, M. R., & Szabo, A. 1987, Sol. Phys., 108, 333 [NASA ADS] [CrossRef] [Google Scholar]
  6. Halain, J.-P., Berghmans, D., Seaton, D. B., et al. 2013, Sol. Phys., 286, 67 [NASA ADS] [CrossRef] [Google Scholar]
  7. Heald, G., Bell, M. R., Horneffer, A., et al. 2011, J. Astrophys. Astron., 32, 589 [NASA ADS] [CrossRef] [Google Scholar]
  8. Heyvaerts, J. 1981, Recent developments in solar flare models, Tech. rep., Paris VII Univ., France [Google Scholar]
  9. Klein, K.-L., Krucker, S., Lointier, G., & Kerdraon, A. 2008, A&A, 486, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Kontar, E. P., Lapshin, V. I., & Mel’Nik, V. N. 1998, Plasma Phys. Rep., 24, 772 [NASA ADS] [Google Scholar]
  11. Koutchmy, S. 1994, Adv. Space Res., 14, 29 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Kundu, M. R., Gergely, T. E., Turner, P. J., & Howard, R. A. 1983, ApJ, 269, L67 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
  14. Lin, R. P., Potter, D. W., Gurnett, D. A., & Scarf, F. L. 1981, ApJ, 251, 364 [NASA ADS] [CrossRef] [Google Scholar]
  15. Mann, G., & Klassen, A. 2002, in Solar Variability: From Core to Outer Frontiers, ed. A. Wilson, ESA SP, 506, 245 [NASA ADS] [Google Scholar]
  16. Mann, G., Jansen, F., MacDowall, R. J., Kaiser, M. L., & Stone, R. G. 1999, A&A, 348, 614 [NASA ADS] [Google Scholar]
  17. Mann, G., Vocks, C., & Breitling, F. 2011, Planetary, Solar and Heliospheric Radio Emissions (PRE VII), 507 [Google Scholar]
  18. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
  19. Mel’Nik, V. N., Lapshin, V., & Kontar, E. 1999, Sol. Phys., 184, 353 [NASA ADS] [CrossRef] [Google Scholar]
  20. Melrose, D. B. 1985, in Solar Radiophysics: Studies of Emission from the Sun at Metre Wavelengths, eds. D. J. McLean & N. R. Labrum (Cambridge: Cambridge University Press), 177 [Google Scholar]
  21. Newkirk, Jr., G. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
  22. Offringa, A. R., de Bruyn, A. G., Zaroubi, S., et al. 2013, A&A, 549, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
  24. Priest, E. R. 1981, in Solar Flare Magnetohydrodynamics, ed. E. R. Priest (NewYork: Gordon and Breach Science Publishers), 1 [Google Scholar]
  25. Reid, H. A. S., & Ratcliffe, H. 2014, Res. Astron. Astrophys., 14, 773 [NASA ADS] [CrossRef] [Google Scholar]
  26. Riddle, A. C. 1974, Sol. Phys., 35, 153 [NASA ADS] [CrossRef] [Google Scholar]
  27. Saint-Hilaire, P., Vilmer, N., & Kerdraon, A. 2013, ApJ, 762, 60 [NASA ADS] [CrossRef] [Google Scholar]
  28. Schrijver, C. J., & De Rosa, M. L. 2003, Sol. Phys., 212, 165 [Google Scholar]
  29. Stappers, B. W., Hessels, J. W. T., Alexov, A., et al. 2011, A&A, 530, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Sturrock, P. A. 1964, NASA SP, 50, 357 [NASA ADS] [Google Scholar]
  31. Svestka, Z. 1981, in Solar Flare Magnetohydrodynamics, ed. E. R. Priest (New York: Gordon and Breach Science Publishers), 47 [Google Scholar]
  32. van, Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Vocks, C., Mann, B., Breitling, F., et al. 2018, A&A, submitted [Google Scholar]
  34. Wild, J. P. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 541 [Google Scholar]
  35. Wild, J. P. 1970, Proc. Astron. Soc. Aust., 1, 365 [NASA ADS] [CrossRef] [Google Scholar]
  36. Zheleznyakov, V. V., & Zaitsev, V. V. 1970, Sov. Astron., 14, 47 [NASA ADS] [Google Scholar]

All Tables

Table 1

Astrometric parameters of the type-III burst sources.

In the text
Table 2

Parameters of propagation of the type-III bursts according to observations (obs) and ray tracing simulations for fundamental (f) and harmonic (h) emission locations.

In the text

All Figures

thumbnail Fig. 1

Dynamic radio spectrum (bottom) of the LOFAR observation of the Sun on June 23, 2012, showing the normalized flux density in arbitrary units. Time and frequency resolution are given by Δt and Δf. Typical signatures of three type-III bursts are found at 11:00:05, 11:00:11 and 11:01:54 UTC. The vertical features between the second and third burst are broadband radio frequency interference (RFI). The simultaneous X-ray flux from the GOES 15 satellite (top) does not indicate any flare activity.
In the text
thumbnail Fig. 2

Dynamic radio spectrum of the type-III burst at 11:00:05 UT on June 23, 2012. It starts at 55 MHz and drifts to lower frequencies.
In the text
thumbnail Fig. 3

LOFAR images at four frequencies of the first type-III burst starting at 11:00:05 UTC (Fig. 2). The yellow line shows the size of the radio source at a contour level of 50% of its peak flux density. Its high flux density makes the thermal emission from the Sun invisible on this color scale. The markers show the burst’s centroid position (Table 1) at each frequency. They reveal the burst’s propagation path when shown all together as in the last image at 30 MHz. It also shows an extreme ultraviolet (174 Å) image of the Sun from the PROBA2 satellite. The coronal magnetic field is shown by the white lines. The white solid and dashed circles indicate the distances of 1 and 2 R⊙, respectively. The blue, dashed ellipse (top right) represents the FWHM of the Gaussian fit of the PSF.
In the text
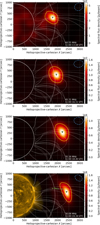thumbnail Fig. 4

As in Fig. 3 but for the second type-III burst starting at 11:00:11 UTC.
In the text
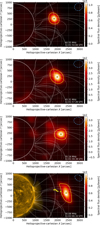thumbnail Fig. 5

As in Fig. 3 but for the third type-III burst starting at 11:01:54 UTC.
In the text
thumbnail Fig. 6

Refraction in the corona of four radio ray paths (solid lines) with different viewing angles to an observer on Earth as determined from ray tracing simulations for a frequency of 55 MHz and a barometric density profile (Newkirk 1961) with α = 3.3. Fundamental radio emission generated in the plane of sky at a radial distance from the Sun rf is scattered at the distance rref and refracted to Earth where its observed at a radial distance robs . The distance robs is given by the intersection of the plane of sky with the nonrefracted path indicated by the dashed line.
In the text
thumbnail Fig. 7

Positions where fundamental (red bordered markers) and harmonic emission (plain markers) from a radio burst is generated according to ray-tracing simulations (Table 1). The observed centroid positions of the radio bursts lie in between.
In the text
thumbnail Fig. 8

Length l of the radio source versus projected radial distance r from the center of Sun in the plane of sky for the three type-III radio bursts at frequencies from 55.5 to 30.1 MHz.
In the text
thumbnail Fig. 9

Path-time diagrams of the three type-III radio bursts as obtained from the observed (sobs ), fundamental (sf) and harmonic (sh) emission regions in the plane of sky according to Table 2. The sources propagate with increasing speed. The error in time is either one or two time steps of 0.94 s depending on how clearly the image of the burst’s onset could be distinguished. The statistical error of s is about 0.01 R⊙ and hidden by the marker.
In the text
thumbnail Fig. 10

Radial electron number density profile of the corona as derived from the three type III radio bursts observations and ray tracing simulations (Table 1). The three-fold coronal density models by Newkirk (1961) and Mann et al. (1999) are shown for comparison.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.