EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 610 (February 2018) A&A, 610 (2018) A53 Full HTML
Free Access
Issue
A&A
Volume 610, February 2018
Article Number A53
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201731751
Published online 28 February 2018

© ESO 2018

1 Introduction

Modern scenarios of the coevolution between supermassive black holes (BHs) and their host galaxies envisage star formation and BH accretion to be in situ time-coordinated processes (e.g., Lapi et al. 2006, 2011, 2014; Lilly et al. 2013; Aversa et al. 2015; Mancuso et al. 2016) that are triggered by the early collapse of the host dark matter halos, but are subsequently controlled by self-regulated baryonic physics and in particular by energy or momentum feedbacks from supernovae or stellar winds and AGNs. This results in a distinctive evolutionary pattern for the emission that is associated with the stellar and the nuclear component.

In a nutshell, during the early stages of a massive galaxy evolution, huge gas reservoirs can sustain violent, almost constant star formation rates (SFRs) M˙⋆ ≳ 102 M⊙ yr−1, while the ambient medium is quickly enriched with metals and dust; in these conditions, the galaxy behaves as a bright submillimeter (submm)/far-IR source. After a time of about several times 108 yr, the SFR is abruptly quenched by the energy/momentum feedback from the central supermassive BH, and the environment is cleaned out; thereafter, the stellar populations evolve passively and the galaxy becomes a red and dead (early-type) spheroid.

From the point of view of the central BH, gas is abundantly available from the surroundings in the early stages, so that considerable accretion rates can sustain mildly super-Eddington emission. However, during these early stages, the BH bolometric luminosity is substantially lower than that of the host galaxy, so that the dust-enshrouded AGN may be observable only as a faint X-ray nucleus. The nuclear power in self-regulated conditions increases exponentially, however, and after some 108 yr progressively attains or even exceeds the nuclear power from star formation in the host; interstellar gas and dust are removed and star formation is appreciably reduced or quenched, so that the overall system behaves as an optical quasar. Residual gas present in the central regions of the galaxy can be accreted onto the BH at progressively lower sub-Eddington accretion rates, as observed on average in unobscured AGNs.

The coevolution scenario sketched above has been extensively tested (see Lapi et al. 2014; Mancuso et al. 2016, 2017 and references therein) on a wealth of data including SFR/stellar mass functions of galaxies and AGN luminosity/BH mass functions; IR/submm/radio counts and redshift distributions; main sequences of star-forming galaxies (SFR vs. stellar mass correlation) and AGNs (nuclear X-ray power vs. SFR or stellar mass); and redshift evolution of the cosmic SFR and BH mass density. However, the picture requires further validation especially in the early stages of the coevolution. These stages are plainly difficult to pinpoint given the sensitivity and resolution limits of current X-ray and far-IR facilities.

Fortunately, strong gravitational lensing by foreground objects offers an extraordinary potential to advance our understanding of these elusive early stages. It not only yields flux boosting that can reach factors μ ≥ 10, allowing us to explore regions of the luminosity/redshift space that would otherwise be unaccessible, but also stretches the images by factors ≃μ1∕2, allowing thestudy of fine spatial details.

Observations have shown that almost all high-redshift (z > 1) dust-obscured star-forming galaxies selected in the submm with a flux density above ~ 100 mJy at 500 μm are gravitationally lensed by a foreground galaxy or a group/cluster of galaxies (see Negrello et al. 2010, 2014, 2017; Wardlow et al. 2013; Nayyeri et al. 2016). These submm bright sources are rare (< 0.3 deg−2 at S500 μm > 100 mJy, Negrello et al. 2007) and therefore only detectable in wide-area submm surveys, like those conducted by the Herschel Astrophysical Terahertz Large Area Survey (H-ATLAS; Eales et al. 2010). The detected z > 1 objects are generally dusty galaxies with SFRs >102 M⊙ yr−1, occurring in a strongly dust-enshrouded environment and thus corresponding to far-IR luminosity LFIR > 1012 L⊙.

Some of them show excess emission in the mid-IR (Negrello et al. 2014) if compared to the commonly used spectral energy distributions (SEDs) of galaxies with intense star formation. This excess may be accounted for by nuclear activity (Fritz et al. 2006), but the mid-IR data alone are not sufficient to draw firm conclusions about the presence of an AGN, let alone characterize it, because the data indicate that AGNs, if present, are weak. Furthermore, the SED fitting requires photometric information over a broad spectral range without which the solutions might strongly depend on the fitting templates.

On the one hand, high-resolution and high-sensitivity X-ray data might unambiguously confirm the presence or absence of a significant AGN emission. On the other hand, high-resolution and high-sensitivity mm-wavelength data are valuable for identifying the dust and gas properties associated with both the star formation process and for tracing the nuclear feeding and feedback process dynamics. By combining them, we can estimate the physical properties of the galaxy components and the relative roles of star formation and nuclear activity in shaping the galaxy SEDs and in contributing to the energy budget of the galaxies.

Observations established beyond any reasonable doubt that the growth of galaxies and super-massive BHs is intimately connected. This was shown by examining the nuclear activity in X-rays in galaxies with high SFRs that were mainly selected at FIR or submm wavelengths (e.g., Mullaney et al. 2012; Wang et al. 2013; Delvecchio et al. 2015) or by studying the star formation in AGN host galaxies. Follow-up at FIR and (sub)mm wavelengths of X-ray selected AGNs and of optically selected QSOs further corroborated the results (e.g., Mullaney et al. 2012; Page et al. 2012; Santini et al. 2012).

With a similar approach, we confirm the properties of the nuclear activity in two lensed galaxies that were detected in the Herschel-ATLAS catalogs. The galaxies are characterized by high SFRs. We study them by means of X-ray Chandra ACIS-S observations and exploit high-resolution mm data that are available in the ALMA Science Archive. With these new data, we improve previously established models of our targets and attempt to estimate the star formation and BH properties.

The outline of this paper is the following: in Sect. 2 we present the two targets, in Sect. 3 we present the X-ray Chandra observations, and in Sect. 4 we presented the ALMA archival data. In Sect. 5 we discuss our estimates of the properties for the two targets together with what the properties imply for coevolutionary models. Our conclusions are finally summarized in Sect. 6.

We adopt the standard flat cosmology (Planck Collaboration XIII 2016) with rounded parameter values: matter density ΩM = 0.32, baryon density Ωb = 0.05, Hubble constant H0 = 100 h km s−1 Mpc−1 with h = 0.67, and mass variance σ8 = 0.83 on a scale of 8 h−1 Mpc. Stellar masses and SFRs (or luminosities) of galaxies are evaluated assuming the Chabrier (2003) IMF.

2 Targets: SDP.9 and SDP.11

The galaxies SDP.9 (HATLAS J090740.0-004200) and SDP.11 (HATLAS J091043.1-000322) were first detected in the HATLAS first observations of a field 4 × 4 sq deg, taken during the Science Demonstration Phase (SDP; Maddox et al. 2010). These observations reached a 5σ noise level of 33.5 mJy beam−1 at 250 μm (Negrello et al. 2010). The galaxies have a flux density above 100 mJy at 500 μm and are detected in the SPIRE and PACS bands (i.e., between 100 to 500 μm, Eales et al. 2010; Poglitsch et al. 2010).

The Z-Spec spectrometer observed the lens candidates and detected CO lines at redshifts of z = 1.577 ± 0.008 and z = 1.786 ± 0.005 for SDP.9 and SDP.11, respectively (Lupu et al. 2012). Optical images of the foreground lens with the Keck telescope at g and i bands confirmed that the optical profiles are consistent with elliptical galaxies (Negrello et al. 2010). Follow-up observations with the SMA at 880 μm (Bussmann et al. 2013) and with the Hubble Space Telescope (HST) at 1.1 and 1.6 μm (Negrello et al. 2014) confirmed them to be lensed galaxies.

Dye et al. (2014) modeled the lensed systems as being lensed by elliptical galaxies at redshifts of 0.6129 ± 0.00005 and 0.7932 ± 0.0012. The magnification factors μ were estimated to be 6.29 and 7.89 (8.8 and 10.9 according to Bussmann et al. 2013) for the two galaxies (see Table 2 of Negrello et al. 2014 for a comprehensive summary of all the measures flux densities and modeled properties).

The selected objects have 12 and 22 μm flux densities, measured by the Wide-field Infrared Explorer (WISE; Wright et al. 2010) survey, in “excess” by up to an order of magnitude to what is expected from purely star-forming SED templates; this therefore suggests a dust-obscured AGN. However, mid-IR excesses indicate that an AGN, if present, is weak. From the spectral decomposition made possible by combining the available data over a wide frequency range, Negrello et al. (2014, see their Fig. 6) evaluated AGN bolometric luminosities LAGN ~ 5.1 × 1045 erg s−1 for SDP.9 and LAGN ~ 4.3 × 1046 erg s−1 for SDP.11, although these values may be overestimated because they were evaluated in a poorly sampled spectral region where contamination might enhance the signal in an unpredictable way. For these reasons, we consider these values as an indication only for the presence of an AGN and as loose upper limits of its luminosity.

In the near-IR, SDP.9 consists of a dominant emitting region of ~ 1 kpc and a smaller and fainter region separated by a few kpc that is responsible for the fainter structure observed in the Einstein ring, which has a radius of ~ 0.71 arcsec (Dye et al. 2014). Based on the SED fitting, Negrello et al. (2014) estimated that the background source has a mass in stars M⋆ ~ 7.1 × 1010 M⊙. Lupu et al. (2012) estimated a comparable mass in molecular gas, Mgas ~ 3.4 × 1010 M⊙ on the basis of the CO emission. The gas fraction is fgas = 0.32, and the galaxy forms stars at a rate of 366 M⊙ yr−1.

The galaxy SDP.11 is reconstructed in the near-IR in a complex combination of several knots that are distributed within a region of a few kpc. These knots are responsible for the small-scale structure observed in the Einstein ring, which has a radius of ~ 0.84 arcsec (Dye et al. 2014). According to the SED fitting, the source has a higher SFR than SDP.9, SFR = 650 M⊙ yr−1, and a higher mass in stars M⋆ ~ 1.9 × 1011M⊙. The CO observations of Lupu et al. (2012) indicate a comparable gas mass Mgas ~ 3.0 × 1010 M⊙ and hence a lower gas fraction, fgas = 0.14.

We note that Lupu et al. (2012) adopted a linear relation (Mgas = αCOLCO) to convert the CO luminosity into gas mass with a slope αCO = 0.8, which is comparable with typical values observed in local ultraluminous IR galaxies (ULIRGs). Recent observations in the radio and mm bands of starburst galaxies at z > 1.5 (Aravena et al. 2016; Béthermin et al. 2016; Popping et al. 2017) indicate that 0.8 < αCO < 1.5 for populations of galaxies that are similar to our targets. This indicates that our mass estimates are most likely a lower limit of the actual gas mass content of the galaxies.

We also note that the SED fitting procedure implies uncertainties as high as ~50% of the stellar mass. These systematic errors can be due to the uncertain separation between lens and source and can provide up to an additional factor ~ 2, but they are not crucial to our findings.

Emission from the region of the two targets is present in the FIRST2 maps at 1.4 GHz at levels of 1.21 ± 0.14 and 0.72 ± 0.12 mJy for SDP.9 and SDP.11, respectively. Emission from stronger sources located within a few arcmin of the two galaxies does not allow us to fully discard the possibility of a small spurious contamination, at least for SDP.9. The conversion of the SFR, as estimated form the Herschel maps, into radio signal at this frequency using the Bonzini et al. (2015) relation after scaling for the magnification factor does not discard the possibility that an AGN contribution might be responsible for the remaining emission.

3 Chandra X-ray observations

The galaxies SDP.9 and SDP.11 were observed by Chandra in Cycle 16, with the ACIS-S3 CCD at the aimpoint, for a total exposure time of 55.3 ks (on January 10, 2015) and 19.8 ks (on February 28 and March 23, 2015), respectively. Very faint mode was used for the event telemetry format, and ASCA grade 0, 2, 3, 4, and 6 events were used in the analysis, which has been carried out using the ciao v4.7 software. Both sources are clearly detected, with 14 counts each in the 0.5–7 keV band within a circular region of 2′′ radius centered on the positions reported in Sect. 2, and 8 counts in the observed 2–7 keV band. The 0.5–7 keV Chandra images of SDP.9 and SDP.11, centered on these positions, are shown in Fig. 1. Remarkably, the 0.5 arcsec Chandra on axis resolution is able to resolve the X-ray emission from the lensed components. The X-ray emission better matches in position the SMA data than the HST images.

The lownumber of detected photons significantly limits the spectral constraints that can be obtained from the X-ray analysis. To provide basic information for both sources, however, we fit the spectra extracted from the Chandra data using simplemodels (within xspec v.12.9, Arnaud 1996) and the Cash statistics (Cash 1979), which is appropriate for low-count spectra.

Fitting the spectrum of SDP.9 with a power law provides Γ = 1.1 ± 1.0, which is suggestive of obscuration. When we fixed Γ to 1.8, as is typically observed in AGN and quasars (e.g., Piconcelli et al. 2005), we obtained a column density of ≈ 5.2 × 1022 cm−2 at the source redshift (3σ upper limit of ≈ 3.3 × 1023 cm−2). The observed 2–10 keV flux is ≈ 3.6 × 10−15 erg cm−2 s−1, and the derived apparent rest-frame 2–10 keV luminosity (corrected for absorption but not for magnification) is ≈ 3.7 × 1043 erg s−1. The faint flux of SDP.9 explains the non-detection of the source (with an upper limit of ≈ 10−14 erg cm−2 s−1 in the 0.5–8 keV band) in the XMM-ATLAS survey (Ranalli et al. 2015). This survey covers a 6 deg2 area with an average exposure of 3 ks. The non-detection of the AGN in XMM-Newton suggests that it is obscured, with an estimated column density of at least 1023 cm−2, as observed in other bright submm galaxies (Johnson et al. 2013).

For SDP.11, we combined the photons of the two observations into a single spectrum. As for SDP.9, a power-law model provides an apparently flat spectrum, with Γ = 1.0 ± 0.9. If we assume Γ = 1.8, the column density would be 3.2 × 1022 cm−2 (3σ upper limit of ≈ 2.4 × 1023 cm−2). The observed 2–10 keV flux is ≈1.2 × 10−14 erg cm−2 s−1, and the apparent rest-frame 2–10 keV luminosity (again corrected for absorption but not for magnification) is ≈1.2 × 1044 erg s−1.

After we corrected them for the magnification factors, the intrinsic X-ray luminosities are ≈ 5.9 × 1042 erg s−1 and ≈ 1.5 × 1043 erg s−1 for SDP.9 and SDP.11, respectively. We can estimate the contributionfrom star formation processes to the 2–10 keV luminosities assuming the relation reported in Ranalli et al. (2003) and the SFRs obtained from SED fitting (Sect. 2). The derived values are ≈ 1.9 × 1042 erg s−1 (SDP.9) and ≈ 3.3 × 1042 erg s−1 (SDP.11), meaning that the X-ray intrinsic luminosities are a factor ≈3–4.5 higher than those that might be associated with stellar processes. Based on the analysis of the 6Ms CDFS data, Lehmer et al. (2016) have recently derived more refined scaling relations between the X-ray luminosity of galaxies and their SFR, stellar mass, and redshift of the form L2−10 keV = αM⋆ + βSFR, where α and β increase with redshift. By applying the scaling relations of Lehmer et al. (2016; see their Table 4), the 2–10 keV luminosities that can be ascribed to stellar processes would be ~ 30% higher than those estimated with the Ranalli et al. relation. We note that because of the large uncertainties of ≈ 30–40% in the measured X-ray luminosities, which are dominated by the low photon statistics, the measured values would still be compatible within ~ 2.0–2.5σ with being produced by star formation. However, the systematically higher measured values again point toward an AGN-related nature.

We finally note that any X-ray emission associated with star formation should occur primarily at low energies. This would produce an apparently lower value for the measured nuclear obscuration in low-counting statistics spectra as those of SDP.9 and SDP.11, which would mean that the intrinsic X-ray luminosities quoted for the two objects are likely lower limits.

thumbnail Fig. 1

HST/WFC3 lens-subtracted F160W images (brightness scale in μJy arcsec−2, left panel) and Chandra 0.5/7 keV images (right panel) of SDP.9 and SDP.11, overlaid with signal-to-noise ratio (S/N) contours at 880 μm from the SMA (in steps of 3, 6, and 9, Bussmann et al. 2013; Negrello et al. 2014).

4 ALMA millimeter observations

The two targets were included in a low-resolution observation with ALMA in Cycle 1 (2012.1.00915, PI: Lupu). On the basis of these data, Oteo et al. (2017) investigated dense circumnuclear region emissions through HCN(3-2), HCO+ (3-2), HNC(3-2), and CO(3-2) transitions properties. HCN(3-2), HCO+ (3-2), and CO(3-2) lines have been detected with ALMA for both the targets, while HNC(3-2) was detected only in SDP.9. These spectral line intensity ratios and their relation with the continuum emission suggest that the intense star formation could be associated with massive dense molecular gas reservoirs and high dense molecular gas fractions.

High-resolution (< 0.1 arcsec) observations have been carried out for both our targets. The observations are still ongoing for SDP.11 (2015.1.01362.S, PI: Gordon). In the following, we report our reduction, imaging, and analysis of the available data for SDP.9 in the ALMA Science archive of the Cycle 4 project. This project was performed with a different approach than has recently been presented by Wong et al. (2017). Presenting our detailed image analysis is necessary as this analysis is the input to the modeling of SDP.9 that we discuss in the next section.

4.1 SDP.9 high-resolution observations

ALMA Cycle 3 observations for SDP.9 were obtained in the framework of a project aiming at detecting traces of the emission from the foreground lens with subarcsec resolution (ID: 2015.1.00415, PI: Wong). A 1.875 GHz wide spectral window was centered on 268.34 GHz to include the CO(6-5) emission that is redshifted according to the 1.577 ± 0.008 value estimated in Bussmann et al. (2013). Three additional spectral windows centered on 266.21, 254.01, and 251.51 GHz were used to estimate the continuum. The native spectral resolution of the data is 31.250 MHz (corresponding to ~35 km s−1 after Hanning smoothing).

Baselines as long as 16.196 km were used to reach a resolution of 0.02 arcsec. A total of 4.3 h, split into two execution blocks, was enough to reach 0.1 μJy sensitivity over the ~7.3 GHz band used for the continuum (after flagging the channels including the CO(6-5) line).

Calibration was made manually, and no major problem was found. Imaging was performed in an interactive way to apply a mask, with standard Briggs weighting scheme (robustness parameter set to 0.5) and no tapering. The final maps have a resolution of 0.02 × 0.02 arcsec (corresponding to ~65 pc on the lensed galaxy plane).

The continuum peak was detected to >20σ (see Fig. 2). The CO(6-5) image cube was generated with a 70 km s−1 spectral resolution (see Fig. 3) to increase sensitivity on the line tail. The peak of the spectrum was offset with respect to the expected position, and has an asymmetrical tail toward higher frequencies. The peak estimated over a region that includes the whole galaxy corresponds to a redshift 1.5753 ± 0.0003, assuming the FWHM of the tail on the higher redshift, which has a Gaussian profile as an estimation of the error, consistent with past estimates (1.577 ± 0.008), but evaluated now to a better accuracy. The value of 1.5747 ± 0.0002 reported by Wong et al. (2017) is well within the line size, but we caution that our as well as their quoted accuracy values do not take the asymmetric tail of the line into consideration. This tail extends more than 250 MHz (half-width at half-maximum), corresponding to a Δ z ~ 0.0024, which improves the accuracy quoted by Bussmann et al. (2013).

While the overall distributions of continuum and CO brightness overlap along the ring (see Fig. 4), the velocity distribution pattern (see the second panel in Fig. 5) shows a clear geometrical offset in the velocity components that could be associated with two separated emitting components. In some of the knots, a bimodal distribution of the line is clearly visible: in these cases, the difference in velocity among the two components is ~300 km s−1.

thumbnail Fig. 2

ALMA high-resolution continuum 1.3 mm observationsof SDP.9.
thumbnail Fig. 3

SDP.9 CO(6-5) channel maps and spectrum of the whole galaxy. A velocity of 0 km s−1 was assumed corresponding to the expected position for CO(6-5), assuming it is redshifted according to the past estimates by Bussmann et al. (2013).
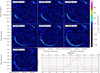thumbnail Fig. 4

SDP.9 CO(6-5) brightness distribution overlaid with the continuum contours (6, 12, and 18σ) for the NW and the SE images of the lensed galaxy.
thumbnail Fig. 5

SDP.9 CO(6-5) 0, 1, and 2 momenta of the line distribution, corresponding to the integrated brightness, velocity distribution and velocity dispersion.

5 Modeling the emission of SDP.9

We performed lens modeling in order to obtain the lens parameters, reconstruct the source emission, and retrieve other useful information such as the total magnification μ. There are mainly two different approaches to lens modeling. The so-called parametric methods describe both the lens and the source profile with analytical models (such as the singular isothermal ellipsoid or the Sersic profile), and they explore the parameter space to obtain the set that minimizes a χ2 statistics between the observed and modeled surface brightness count distribution on the lens plane. When the source morphology is complex or clumpy (such as in the case of dusty star-forming galaxies), the results tend to be an oversimplification of the real physical situation. Non-parametric or semi-parametric methods aim to reconstruct the original source morphology by assuming a pixellated distribution for the surface brightness of the background galaxy. They exploit a simple matrix formalism with the introduction of a regularization term that ensures a certain degree of smoothness in the reconstructed source (Warren & Dye 2003; Suyu et al. 2006).

We hereadopt the regularized semilinear inversion method of Warren & Dye (2003), improved by adopting an adaptive source planepixelization scheme (Nightingale & Dye 2015), and extended to include interferometric data (Dye et al. 2017; Enia et al., in prep.; we refer to these references for more details).

In order to reduce computational time, not every pixel enters the modeling algorithm, only the pixels inside a mask containing the lensed image, with minimum background sky. The lens is a singular isothermal ellipsoid (SIE; Kormann et al. 1994) that is described by five parameters: the Einstein radius rE, the position angle ϕ defined as the orientation of the semi-major axis measured counterclockwise from the west, the ellipticity defined as the ratio between the minor and major axis of the ellipsoid, and the displacement of the lens centroid Δ xL and Δ yL with respect to the HST image center. The lens parameter space is explored using multinest (Feroz et al. 2009).

Lens modeling results are reported in Table 1. Both data sets lead to the same set of parameters, which are similar to other results shown in literature (Bussmann et al. 2013; Dye et al. 2014). This proves the strength and suitability of our model.

The results are shown in Fig. 6. Properties such as magnification and sizes are computed by perturbing the lens model parameters 1000 times around their best-fit values; the reported final values and errors are the median and the 16th and 84th percentile of the distribution. For each iteration, magnifications are evaluated as 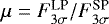μ=F3σLP∕F3σSP$\mu=F^{\rm LP}_{3\sigma}/F^{\rm SP}_{3\sigma}$, where 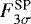F3σSP$F^{\rm SP}_{3\sigma}$ is the total flux inside the source plane (SP) pixels with S∕N ≥ 3 and 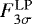F3σLP$F^{\rm LP}_{3\sigma}$ is the total flux inside the corresponding lensed pixels. 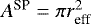Similarly, reff is measured from the reconstructed source area, and we recall that ASP=πreff2$A^{\rm SP} = \pi r_{\rm eff}^2$.

The retrieved magnifications are 7.80 and 17.39 for the HST/WFC3 and ALMA observations, respectively. The first value is higher than (but consistent within 2.5σ with) the value μtot ~ 6.3 reported in Dye et al. (2014, but the lens was modeled with a singular power-law ellipsoid and was reported to be more spherical than what we find), the second is almost twice the value of μ880 reported in Bussmann et al. (2013), even though it is worth noting that in this case, the lens modeling method was fully parametric, with the reconstructed source modeled with a Sersic profile. The high value of μ1.3 is expected since the reconstructed source is compact and peaks close to the lens caustic. The source properties are reported in Table 2.

The observed lens planes and reconstructed source planes are superimposed in Fig. 7. The visual inspection of the lensing morphology clearly shows a displacement between the two data sets. This is frequently observed in this type of source (Dye et al. 2015; Fu et al. 2012) and reflects the intrinsic nature of the observations. The near-IR emission traces the direct light of stars that are partially or not at all obscured by dust, while the submm emission directly traces the dust-reprocessed photons from the UV radiation field of newborn stars, which is completely or almost completely obscured. This displacement is then reproduced on the reconstructed source plane, with a distance between the two emission peaks of ~0.9 kpc.

A first-order lens modeling with the previously found HST parameter set was also performed on available Chandra X-ray data in order to constrain the position of the peak signal, since any further analysis needs data at higher resolution. The peak is cospatial with the submm signal, and along with the mid-IR excess observed in the source SED, this suggests an obscured AGN in the galaxy.

Table 1

Lens modeling results for the HST 1.6 μm and ALMA 1.3 mm data for SDP.9.

thumbnail Fig. 6

Lens modeling results on the HST/WFC3 (top) and ALMA data (bottom). Left panels: original lens plane. The tiny white ellipse in the bottom left corner of the ALMA original lens plane is the final image-restored beam. The best-fit lens plane is shown in the central panel of the left column; the panel on its right shows the residuals. Right panels: reconstructed source plane on Voronoi tassels. Contours are from 3σ level to the maximum S/N with steps of 3 (ALMA) and 5 (HST). White and red curves are the lens caustics and critics, respectively, on the lens plane and on the source plane; the angular and physical scales are reported in white in the bottom right corner of every panel.
thumbnail Fig. 7

Left panel: observed original lens plane. Right panel: reconstructed source plane. Grey scale is the HST/WFC3 1.6 μm data, rainbow colorscale the 1.3 mm ALMA data. The green circle marks the position of the reconstructed Chandra peak within 5σ.

6 Discussion

Our Chandra-ACIS observations confirmed that by observing strongly lensed submm-bright galaxies, we can access earlier stages of the coevolutionary scenario than previously possible. So far, available X-ray data allowed testing the in situ coevolution scenario only at relatively old galactic ages of ≲109 yr, when the BH has grown enough for its X-ray luminosity to be detectable at substantial redshift (z > 1). This study constitutes a successful pilot study of the coevolution between BHand galaxy growth at high redshifts, in a low X-ray luminosity regime associated with the early stages of galaxy evolution.

The two strongly lensed galaxies analyzed in this workfeature (intrinsic) SFRs of several 102 M⊙ yr−1 corresponding to far-IR luminosities LFIR≳1046 erg s−1 ; the stellar masses M⋆ are ~1011 M⊙, implying (for nearly constant SFR, see Papovich et al. 2011; Smit et al. 2012; Citro et al. 2016) rather young ages τage ≈ M⋆∕SFR of a few 108 yr. In the SFR vs. M⋆ diagram at z ~ 2, these galaxies are therefore slightly offset with respect to the main-sequence locus (Rodighiero et al. 2011, 2014; Speagle et al. 2014; see Fig. 8) because the main-sequence locus is classically defined for mass-selected samples, while the galaxies considered here are far-IR selected. Mass selection tends to pick up star-forming galaxies at the end of their main star formation period, when their age is τage≲1 Gyr and their mass is fully accumulated, while far-IR selection tends to pick them up unbiased with respect to age and stellar mass (see Mancuso et al. 2016). Hence, our targets are intrinsically richer in gas because they are typically younger than main-sequence galaxies with the same SFR. However, in the selection process, we picked up objects with specificSFRs lower than other selected FIR samples in order to have higher chance of observing the X-ray nuclear emission.

The galaxies SDP.9 and SDP.11 still retain appreciable amounts of gas Mgas≳ a few 1010 M⊙, implying depletion timescales τdepl ≈ Mgas∕SFR ≳ of several 107 yr. Provided that further gas infall may well occur from a hot atmosphere, this is a lower limit for the depletion time; the star formation will likely proceed for a more realistic τdepl≳ a few 108 yr, when the objects will move to a position on the main sequence. Furthermore, a higher value for the αCO conversion factor could enhance the gas mass by a factor of ≲2, and as a consequence, allow higher values of the depletion time by similar factors.

The intrinsic (demagnified and obscuration-corrected) X-ray luminosities amount to LX≲1043 erg s−1; we note that these values are appreciably higher (by a factor 3–4.5) than the expected X-ray emission from star formation LX,SFR≳1042 erg s−1. The nuclear bolometric luminosities (using the Hopkins et al. 2007 corrections) are on the order of LAGN≳1044 erg s−1, a factor 102 lower than LFIR and corresponding to a BH mass MBH ≈ 106 M⊙ for an Eddington ratio around unity (as expected in these early stages when a wealth of material is available for accretion, Alexander et al. 2008). The two galaxies are therefore located slightly below the main sequence of AGNs (Mullaney et al. 2012; Rodighiero et al. 2015; see Fig. 2). Adopting the standard ratio MBH∕M⋆ ≈ a few 10−3 between the final BH and stellar masses would imply a relic BH mass of MBH ≈ 10−3 × 1011M⊙108 M⊙. The corresponding bolometric luminosities will be around LAGN ≈ 1046 erg s−1, comparable to the far-IR luminosity from star formation; at that time, the energetic feedback from the AGN will probably quench the star formation process and terminate further accretion onto the BH.

In order to increase its mass by a factor 102 from the observed to the expected final value over τdepl ≈ a few 108 yr, the BH must grow in a self-regulated exponential fashion; the related accretion e-folding timescale τef ln 102 ≈ 5 τef ≈ a few 108 yr is indeed found to be consistent with τdepl. This implies that (i) star formation and BH accretion are not always proportional to each other during galaxy evolution, and (ii) the most likely mechanism to build up the final BH-to-stellar-mass ratio should allow low-angular momentum gas to be stored in a massive circumnuclear reservoir at a rate proportional to the SFR. For the two galaxies discussed here, a reservoir mass on the order of 108 M⊙ is implied; the size Rres of the reservoir are required to correspond to several times the BH influence radius GMBH∕σ2 ≈ ReMBH∕M⋆, and therefore need to amount to Rres ≈ 10–100 pc for an effective radius Re ≈ 10 kpc.

A crucial probe of the above interpretation will be provided by observationsof the reservoir in strongly lensed dust enshrouded galaxies. Strong gravitational lensing with amplification factors ≈ 10 may produce an apparent size of a reservoir with physical size Rres ≈ 10–100 pc to ≈ 0.02–0.07 arcsec, which is well within the resolution achievable with ALMA (see Kawakatu et al. 2007; Maiolino 2008; Spaans & Meijerink 2008; Lapi et al. 2014). Our modeling of SDP.9 strongly indicates that dust and X-ray emission coexist in an unresolved region smaller than 375 pc (see Table 2 and Fig. 7).

thumbnail Fig. 8

Positions (red stars) of SDP.9 and SDP.11 in the main sequences of AGNs (LX or LAGN vs. M⋆, left panel) and star-forming galaxies (SFR vs. M⋆, right panel). Data based on a mass-selected sample are from Rodighiero et al. (2015; black circles), with the cyan shaded area illustrates the typical scatter around the mean relationship.
Table 2

Source properties for SDP.9: magnification factors μ, brightness area of the reconstructed source, and source radii within 3 and 5σ.

7 Conclusions

We presented Chandra and ALMA observations of two strongly lensed galaxies, SDP.9 (HATLAS J090740.0-004200) and SDP.11 (HATLAS J091043.1-000322), which we selected in the Herschel-ATLAS catalogs for their excess emission in the mid-IR regime and for their relatively low specific SFR with respect to common FIR selected samples at redshift ≳1.5. These parameters indicate the possible presence of nuclear activity in the early stages of the galaxy formation. Both targets were detected in the X-ray, which strongly indicates highly obscured nuclear activity.

ALMA observations for SDP.9 for the continuum and CO(6-5) spectral line with high resolution (0.02 arcsec, corresponding to ~ 65 pc at the distance of the galaxy) allowed us to estimate the lensed galaxy redshift to a better accuracy than pre-ALMA estimates (1.5753 ± 0.0003) and to model the emission of the optical, millimetric, and X-ray band emission for this galaxy. We demonstrated that the millimeric and X-ray emission are both generated in the nuclear environment, which strongly supports the scenario that this object has nuclear activity. Despite its low resolution (~ 0.5 arcsec), the X-ray model clearly peaks in the nuclear region, in strong concordance with the mm peaks. This confirms that the X-ray emission has a nuclear origin, and the peak might be considered as the result of nuclear activity. This complements a set of low-resolution observations (Oteo et al. 2017) in the mm bands for both SDP.9 and SDP.11 that suggested that intense star formation might be associated with massive dense molecular gas reservoirs and high dense molecular gas fractions.

On the basis of the X-ray data, we attempted an estimate of star formation and BH properties for both our targets. By taking advantage of the lensing magnification, we identified weak nuclear activity associated with high-z galaxies with high SFRs. This was useful to extend the investigation of the relationship between star formation and nuclear activity to two intrinsically less luminous high-z star-forming galaxies than was possible so far. Because our results are only based on two objects, they cannot constrain the evolutionary models. They provide interesting hints, however, and set an observational path for addressing the role of star formation and nuclear activity in forming galaxies.

Acknowledgments

The scientific results reported in this article are based on observations made by the Chandra X-ray Observatory. This paper makes use of the following ALMA data: 2015.1.00415.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. M.M., M.N., and A.L. acknowledge partial financial support by PRIN-INAF 2012 project “Looking into the dust-obscured phase of galaxy formation through cosmic zoom lenses in the H-ATLAS”. M.M. and C.M. acknowledge partial financial support by the Italian Ministero dell’Istruzione, Università e Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001). A.L., C.M., and L.D. acknowledge partial support by PRIN INAF 2014 “Probing the AGN/galaxy co-evolution through ultra-deep and ultra-high-resolution radio surveys”. A.L. acknowledges partial support from the PRIN MIUR 2015 “Cosmology and Fundamental Physics: Illuminating the Dark Universe with Euclid” and from the RADIOFOREGROUNDS grant (COMPET-05-2015, agreement number 687312) of the European Union Horizon 2020 research and innovation program. M.N. has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 707601. G.D.Z. acknowledges partial financial support by ASI/INAF agreement 2014-024-R.0 for the Planck LFI activity of Phase E2. We acknowledge J. Gonzales-Nuevo, M. Baes, A. Cooray, I. Oteo, D.A. Riechers, A. Omont, P. Ranalli, I. Georgantoupoulos, L. Fan, S. Serjeant, and F. Carrera for useful comments to some sections of the paper and to the proposal. We acknowledge the work and coordination activity of the core team for the Herschel-ATLAS collaboration, in the framework of which the targets were observed. We acknowledge the referee, G. Rodighiero, for the useful comments.

References

  1. Alexander, D. M, Brandt, W. N., Smail, I., et al. 2008, AJ, 135, 1968 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aravena, M, Spilker, J. S., Bethermin, M., et al. 2016, MNRAS, 457, 4406 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H.Jacoby, & J. Barnes, The First Ten Years, 101, 17, ISBN: 1080-7926, eISBN: 978-1-58381-437-6 [Google Scholar]
  4. Béthermin, M, De Breuck, C., Gullberg, B., et al. 2016, A&A, 586, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bonzini, M, Mainieri, V., Padovani, P., et al. 2015, MNRAS, 453, 1079 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bussmann, R. S, Pérez-Fournon, I., Amber, S., et al. 2013, ApJ, 779, 25 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
  9. Citro, A., Pozzetti, L., Moresco, M, & Cimatti, A. 2016, A&A, 592, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dannerbauer, H., Kurk, J. D., De Breuck, C., et al. 2014, A&A, 570, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Delvecchio, I, Lutz, D., Berta, S., et al. 2015, MNRAS, 449, 373 [Google Scholar]
  12. Dye, S., Negrello, M., Hopwood, R., et al. 2014, MNRAS, 440, 2013 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dye, S, Furlanetto, C., Swinbank, A. M., et al. 2015, MNRAS, 452, 2258 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dye, S, Furlanetto, C, Dunne, L, et al. 2017, ArXiv e-prints [arXiv:1705.05413] [Google Scholar]
  15. Eales, S, Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
  16. Feroz, F, Gair, J. R, Hobson, M. P, & Porter, E. K. 2009, Class. Quant. Grav., 26, 215003 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fritz, J, Franceschini, A, & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
  18. Fu, H, Jullo, E., Cooray, A., et al. 2012, ApJ, 753, 134 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hopkins, P. F, Lidz, A., Hernquist, L., et al. 2007, ApJ, 662, 110 [NASA ADS] [CrossRef] [Google Scholar]
  20. Imanishi, M, Nakanishi, K, & Izumi, T. 2016, AJ, 152, 218 [NASA ADS] [CrossRef] [Google Scholar]
  21. Johnson, S. P, Wilson, G. W., Wang, Q. D., et al. 2013, MNRAS, 431, 662 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kawakatu, N, Andreani, P, Granato, G. L, & Danese, L. 2007, ApJ, 663, 924 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kormann, R, Schneider, P, & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
  24. Lapi, A, Shankar, F., Mao, J., et al. 2006, ApJ, 650, 42 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lapi, A, González-Nuevo, J., Fan, L., et al. 2011, ApJ, 742, 24 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lapi, A, Raimundo, S., Aversa, R., et al. 2014, ApJ, 782, 69 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lehmer, B. D, Basu-Zych, A. R, Mineo, S, et al. 2016, ApJ, 825, 7 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lilly, S. J, Carollo, C. M, Pipino, A, Renzini, A, & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lupu, R. E, Scott, K. S., Aguirre, J. E., et al. 2012, ApJ, 757, 135 [NASA ADS] [CrossRef] [Google Scholar]
  30. Maddox, S. J, Dunne, L, Rigby, E, et al. 2010, A&A, 518, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Maiolino, R. 2008, New Astron. Rev., 52, 339 [NASA ADS] [CrossRef] [Google Scholar]
  32. Mancuso, C, Lapi, A., Shi, J., et al. 2016, ApJ, 833, 152 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mancuso, C, Lapi, A., Prandoni, I., et al. 2017, ApJ, 842, 95 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mullaney, J. R, Daddi, E., Béthermin, M., et al. 2012, ApJ, 753, L30 [NASA ADS] [CrossRef] [Google Scholar]
  35. Nayyeri, H, Keele, M., Cooray, A., et al. 2016, ApJ, 823, 17 [NASA ADS] [CrossRef] [Google Scholar]
  36. Nightingale, J. W, & Dye, S. 2015, MNRAS, 452, 2940 [NASA ADS] [CrossRef] [Google Scholar]
  37. Negrello, M, Perrotta, F., González-Nuevo, J., et al. 2007, MNRAS, 377, 1557 [NASA ADS] [CrossRef] [Google Scholar]
  38. Negrello, M, Hopwood, R., De Zotti, G., et al. 2010, Science, 330, 800 [NASA ADS] [CrossRef] [Google Scholar]
  39. Negrello, M, Hopwood, R., Dye, S., et al. 2014, MNRAS, 440, 1999 [NASA ADS] [CrossRef] [Google Scholar]
  40. Negrello, M, Amber, S., Amvrosiadis, A., et al. 2017, MNRAS, 465, 3558 [NASA ADS] [CrossRef] [Google Scholar]
  41. Page, M. J, Symeonidis, M., Vieira, J. D., et al. 2012, Nature, 485, 213 [NASA ADS] [CrossRef] [Google Scholar]
  42. Papovich, C, Finkelstein, S. L, Ferguson, H. C, Lotz, J. M, & Giavalisco, M. 2011, MNRAS, 412, 1123 [NASA ADS] [Google Scholar]
  43. Piconcelli, E, Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Planck Collaboration XIII 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Poglitsch, A, Waelkens, C, Geis, N, et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Popping, G, Decarli, R., Man, A. W. S., et al. 2017, A&A, 602, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ranalli, P, Comastri, A, & Setti, G. 2003, A&A, 399, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Ranalli, P, Georgantopoulos, I., Corral, A., et al. 2015, A&A, 577, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Rodighiero, G, Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
  50. Rodighiero, G, Renzini, A., Daddi, E., et al. 2014, MNRAS, 443, 19 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rodighiero, G, Brusa, M., Daddi, E., et al. 2015, ApJ, 800, L10 [NASA ADS] [CrossRef] [Google Scholar]
  52. Santini, P, Rosario, D. J, Shao, L, et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Smit, R, Bouwens, R. J., Franx, M., et al. 2012, ApJ, 756, 14 [NASA ADS] [CrossRef] [Google Scholar]
  54. Spaans, M, & Meijerink, R. 2008, ApJ, 678, L5 [NASA ADS] [CrossRef] [Google Scholar]
  55. Speagle, J. S, Steinhardt, C. L, Capak, P. L, & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
  56. Suyu, S. H, Marshall, P. J, Hobson, M. P, & Blandford, R. D. 2006, MNRAS, 371, 983 [NASA ADS] [CrossRef] [Google Scholar]
  57. Wang, R, Wagg, J., Carilli, C. L., et al. 2013, ApJ, 773, 44 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wardlow, J. L, Cooray, A., De Bernardis, F., et al. 2013, ApJ, 762, 59 [NASA ADS] [CrossRef] [Google Scholar]
  59. Warren, S. J, & Dye, S. 2003, ApJ, 590, 673 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wong, K. C, Ishida, T., Tamura, Y., et al. 2017, ApJ, 843, L35 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wright, E. L, Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Lens modeling results for the HST 1.6 μm and ALMA 1.3 mm data for SDP.9.

In the text
Table 2

Source properties for SDP.9: magnification factors μ, brightness area of the reconstructed source, and source radii within 3 and 5σ.

In the text

All Figures

thumbnail Fig. 1

HST/WFC3 lens-subtracted F160W images (brightness scale in μJy arcsec−2, left panel) and Chandra 0.5/7 keV images (right panel) of SDP.9 and SDP.11, overlaid with signal-to-noise ratio (S/N) contours at 880 μm from the SMA (in steps of 3, 6, and 9, Bussmann et al. 2013; Negrello et al. 2014).
In the text
thumbnail Fig. 2

ALMA high-resolution continuum 1.3 mm observationsof SDP.9.
In the text
thumbnail Fig. 3

SDP.9 CO(6-5) channel maps and spectrum of the whole galaxy. A velocity of 0 km s−1 was assumed corresponding to the expected position for CO(6-5), assuming it is redshifted according to the past estimates by Bussmann et al. (2013).
In the text
thumbnail Fig. 4

SDP.9 CO(6-5) brightness distribution overlaid with the continuum contours (6, 12, and 18σ) for the NW and the SE images of the lensed galaxy.
In the text
thumbnail Fig. 5

SDP.9 CO(6-5) 0, 1, and 2 momenta of the line distribution, corresponding to the integrated brightness, velocity distribution and velocity dispersion.
In the text
thumbnail Fig. 6

Lens modeling results on the HST/WFC3 (top) and ALMA data (bottom). Left panels: original lens plane. The tiny white ellipse in the bottom left corner of the ALMA original lens plane is the final image-restored beam. The best-fit lens plane is shown in the central panel of the left column; the panel on its right shows the residuals. Right panels: reconstructed source plane on Voronoi tassels. Contours are from 3σ level to the maximum S/N with steps of 3 (ALMA) and 5 (HST). White and red curves are the lens caustics and critics, respectively, on the lens plane and on the source plane; the angular and physical scales are reported in white in the bottom right corner of every panel.
In the text
thumbnail Fig. 7

Left panel: observed original lens plane. Right panel: reconstructed source plane. Grey scale is the HST/WFC3 1.6 μm data, rainbow colorscale the 1.3 mm ALMA data. The green circle marks the position of the reconstructed Chandra peak within 5σ.
In the text
thumbnail Fig. 8

Positions (red stars) of SDP.9 and SDP.11 in the main sequences of AGNs (LX or LAGN vs. M⋆, left panel) and star-forming galaxies (SFR vs. M⋆, right panel). Data based on a mass-selected sample are from Rodighiero et al. (2015; black circles), with the cyan shaded area illustrates the typical scatter around the mean relationship.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.