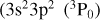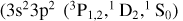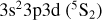| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201731243 | |
| Published online | 23 February 2018 | |
Dielectronic recombination data for dynamic finite-density plasmas
XV. The silicon isoelectronic sequence
1
Department of Physics, Western Michigan University,
Kalamazoo,
MI
49008, USA
2
Department of Physics, University of Strathclyde,
Glasgow
G4 0NG, UK
e-mail: gorczyca@wmich.edu
Received:
24
May
2017
Accepted:
26
November
2017
Context. We aim to present a comprehensive theoretical investigation of dielectronic recombination (DR) of the silicon-like isoelectronic sequence and provide DR and radiative recombination (RR) data that can be used within a generalized collisional-radiative modelling framework.
Aims. Total and final-state level-resolved DR and RR rate coefficients for the ground and metastable initial levels of 16 ions between P+ and Zn16+ are determined.
Methods. We carried out multi-configurational Breit-Pauli DR calculations for silicon-like ions in the independent processes, isolated resonance, distorted wave approximation. Both Δnc = 0 and Δnc = 1 core excitations are included using LS and intermediate coupling schemes.
Results. Results are presented for a selected number of ions and compared to all other existing theoretical and experimental data. The total dielectronic and radiative recombination rate coefficients for the ground state are presented in tabulated form for easy implementation into spectral modelling codes. These data can also be accessed from the Atomic Data and Analysis Structure (ADAS) OPEN-ADAS database. This work is a part of an assembly of a dielectronic recombination database for the modelling of dynamic finite-density plasmas.
Key words: atomic data / atomic processes
© ESO 2018
1 Introduction
The emission of electromagnetic radiation from cosmic plasmas, as a consequence of electron-ion collision processes, reveals information about physical parameters of the plasma such as chemical composition, pressure, electronic or ionic temperature, and density. However, the accuracy of these parameters is strongly influenced by uncertainties in the ionization balance calculations, which are in turn affected by uncertainties in the ionization and recombination rate coefficients. Therefore, it is of fundamental interest to determine accurate rate coefficients for astrophysical and laboratory plasma studies.
Dielectronic recombination (DR) – Burgess (1964, 1965) – is the dominant electron-ion recombination process in most photoionized and (electron) collisionally ionized plasmas. In collisionally ionized plasmas (e.g. stars and supernovae remnants), the ionization occurs due to electrons and ions that are formed at a temperature approximately half of their ionization potential (Bryans et al. 2006). On the other hand, in photoionized plasmas (e.g. H II regions and planetary nebulae), ionization occurs due to photons and ions that are formed at temperatures below the ionization energies (Ferland et al. 1998; Kallman & Bautista 2001). Therefore, the ionization balance is achieved over very different temperature ranges in collisionally ionized and photoionized plasmas. To model the spectral emission, plasma modelling codes, including CLOUDY (Ferland et al. 1998) and XSTAR (Kallman & Bautista 2001), for photoionized plasmas, and the CHIANTI code (Landi et al. 2006), for collisionally ionized plasmas, require accurate DR rate coefficients over a wide range of temperatures to determine the elemental abundances and, therefore, plasma parameters.
In order to address the need for accurate DR rate coefficients, a large collaborative effort was initiated by Badnell et al. (2003) to calculate the total and final-state level-resolved DR rate coefficients from the ground and the metastable states of all ionization stages of all ions up to Zn relevant to the modelling of astrophysical and laboratory plasmas. In a series of papers, multiconfiguration Breit-Pauli (MCBP) calculations have been performed to provide a DR database for all isoelectronic sequences of the first and second row ions and third row ions up through Al -like (Badnell 2006a; Bautista & Badnell 2007; Colgan et al. 2004, 2003; Altun et al. 2004; Zatsarinny et al. 2004b; Mitnik & Badnell 2004; Zatsarinny et al. 2003, 2006, 2004a; Altun et al. 2006, 2007; Abdel-Naby et al. 2012) and also Ar -like (Nikolić et al. 2010). Final-state level-resolved DR rate coefficients are necessary for modelling plasmas within the collisional-radiative framework at densities found in astrophysical plasmas, such as solar flares (>1012 cm−3) (Polito et al. 2016b,a), and in magnetic fusion plasmas for example ITER (1012−1015 cm−3) (Watts et al. 2013), where the coronal approximation is not valid. DR data for initial metastable states are required for modelling plasmas with timescales comparable to the life time of the metastable states. The first unaddressed isoelectronic sequence in the third row is silicon-like, for which no systematic calculations have been performed. Here, we present a reliable DR database for the Si-like isoelectronic sequence.
Bryans et al. (2009a) have demonstrated the effect of inaccuracies in DR data for singly-charged ions in the low-temperature regime of molecular clouds, causing significant differences in the abundances of species found on the surface of dust grains and in the gas-phase. They have used RR rate coefficients of singly-charged ions from the UMIST database (Woodall et al. 2007) in chemical models; however, the origin of this RR data is unclear. There are no other RR data, while DR data exist for P+, S+, Cl+, and Fe+. Our present study of the silicon-like isoelectronic sequence finally provides state-of-the-art calculations of the RR and DR rate coefficients for P+, for instance, that are needed to constrain the chemical models used to study the evolution of dense molecular clouds, protostars, and diffuse molecular clouds. Such studies are in turn important for understanding the origin of the first organic molecules.
Furthermore, the difference in the sulphur abundances in planetary nebulae derived from an ionization correction factor (ICFs), and the spectral emission line measurements from the expected value observed by Henry et al. (2012), constitute the motivation to update the S2+ DR data, as was done for totals by Badnell et al. (2015). Henry et al. (2012) demonstrated how uncertainties in the positions of low-lying resonances affect the low-temperature DR rate coefficients, that in turn affect the elemental abundances in planetary nebulae. The present study extends the previous theoretical work by determining partial as well the total rate coefficients, and including the Δnc = 1 core excitation, in addition to Δnc = 0 core excitation.
Additionally, accurate DR rate coefficients for M-shell Fe12+ are needed to accurately model the absorption features needed to reproduce the so-called unresolved transition array (UTA). This is a series of inner-shell absorption lines at 15−17 Å, caused by 2p → 3d photoabsorption in the X-ray spectrum of Active Galactic Nuclei (AGN), as observed by Chandra and XMM-Newton. The problem has been attributed in part to the underestimated low-temperature DR rate coefficients for M-shell Fe used in the photoionization models (Badnell 2006b). The recent benchmark theoretical and experimental total DR results are presented by Hahn et al. (2014) for M-shell Fe12+ ions.
The remainder of this paper is organized as follows: in Sect. 2 we discuss the theoretical methodology and outline the present calculations. We then present the results for total dielectronic and radiative recombination rate coefficients and compare with earlier theoretical and experimental results in Sect. 3. Finally, we summarize the assembly of final data in Sect. 4.
2 Theory
A detailed description of our theoretical calculations has already been given by Badnell et al. (2003). Here we outline only the main points. The atomic structure and collision code AUTOSTRUCTURE (Badnell 2011) was used to perform DR calculations. A MCBP method is implemented within an independent processes, isolated resonance, distorted-wave (IPIRDW) approximation, whereby radiative and dielectronic recombination processes are treated independently, neglecting interference between the two, which is valid for plasma applications (Pindzola et al. 1992). The code is based on lowest-order perturbation theory, for which both the electron-photon and electron-electron interactions are treated to first order. Energy levels, radiative rates, and autoionization rates were calculated in LS and intermediate coupling (IC) approximations. We note that the spin-independent mass-velocity and Darwin relativistic operators are included in LS coupling, as well as in IC coupling. The wave functions for the N-electron target system are written as a configuration expansion,
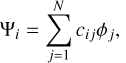 (1)
(1)
where cij are the mixing coefficients that are chosen so as to diagonalize ⟨Ψi|H|Ψj ⟩, where H is the Breit-Pauli Hamiltonian. The set of basis functions are constructed from Slater determinants using the one-electron spin-orbitals.
The dielectronic recombination process for silicon-like ions can be represented schematically as
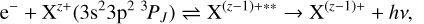 (2)
(2)
where z represents the degree of ionization for the ion X. The basis set consisting of the 3s2 3p2, 3s2 3p 3d, 3s 3p3, 3s 3p2 3d, 3s2 3d2, 3s 3p 3d2, 3p4 and 3p3 3d configurations (assuming a closed shell Ne -like core) was used to define the silicon-like target states, for the (by far dominant) Δnc = 0 core excitation. The one-electron spin-orbitals were obtained using the Thomas-Fermi-Dirac-Amaldi (TFDA) model potential (Eissner & Nussbaumer 1969), and were optimized by varying the scaling parameters λnl so as to reproduce the fine-structure splitting of the 3s23p23PJ levels, to within 0.0005 Ryd compared to NIST. Table 1 lists the optimized scaling parameters for the entire isoelectronic sequence.
The (N + 1)-electron basis was constructed by coupling a valence orbital, nl, or a continuum orbital, ϵl, to the N-electron target configurations, and also included the 3s23p3, 3s2 3p23d, 3s2 3p3d2, 3s 3p4, 3s 3p33d, 3s 3p23d2, 3s2 3d3, 3s 3p3d3, 3p5, 3p4 3d and 3p3 3d2 configurations. Distorted wave calculations were performed to generate the bound nl (n > 3) and continuum orbitals. The wave functions constructed using this (N + 1)-electron basis were used to determine the autoionization and radiative rates, which are then assembled to obtain the final-state level-resolved and total dielectronic recombination rate coefficients for all silicon-like ions.
For the valence electron, n-values were included up to 25, and a quantum defect approximation for high n up to 1000 was used (Badnell et al. 2003). The values for the orbital quantum numbers were included up to l = 8. For intershell (Δnc = 1) core excitation from the n = 3 shell, the N-electron target basis set was comprised of 3s23p2, 3s2 3p3d, 3s 3p3, and 3s 3p23d configurations in addition to configurations arising from 3ℓ → 4ℓ′ excitations (for ℓ = 0 − 1 & ℓ′ = 0 − 3). The (N + 1)-electron target basis was described by coupling a valance orbital 4ℓ′ to the N-electron configurations for (Δnc = 1) core excitation plus either coupling a valence orbital nl, or a continuum orbital ϵl, to the N-electron target configurations. Values of the principal quantum number included were n ≤ 25, and of the continuum/valence electron orbital angular momentum were ℓ′ ≤ 5. A quantum defect approximation is included for 25 < n ≤ 1000.
The partial dielectronic recombination rate coefficient αif from an initial state i to a final, recombined state f is given in the IPIRDW approximation as (Burgess 1964)
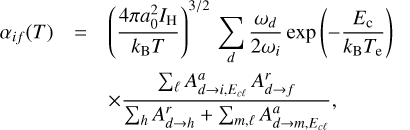 (3)
(3)
where the outer sum is over all accessible (N + 1)-electron doubly excited resonance states d, of statisticalweight ωd, ωi is the statistical weight of the N-electron target state,Aa and Ar are the autoionization and radiative rates (the sums over h and m gives rise to the total widths), and Ec is the energy of the continuum electron, which is fixed by the position of the resonances. Here, IH is the ionization potential energy of the hydrogen atom, kB is the Boltzmann constant, and T is the electron temperature. The total dielectronic recombination rate coefficient is obtained by summing over all the recombined final states f,
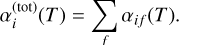 (4)
(4)
Partial and total RR rate coefficients were also computed using the same N- and (N + 1)-electron configurations as for the Δnc = 0 core excitation DR calculations, but with no doubly-excited (resonance) states X(z−1)+**.
Radial scaling parameters for orbitals (1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d and 4f) used in the present study for Δnc = 0 and Δnc = 1 core-excitations in the silicon-like isoelectronic sequence.
Fitting coefficients ci (in cm3 K3∕2 s−1) and Ei (in K) for the total ground-state IC DR rate coefficients.
3 Results
The final-state level-resolved partial dielectronic recombination rate coefficients, from both ground and metastable initial levels, were computed and then tabulated in the ADAS (Summers 2003) adf09 format. The total (Δnc = 0 plus Δnc = 1) intermediate coupling DR rate coefficients were also fitted according to the formula
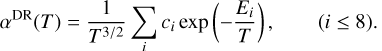 (5)
(5)
The fitting coefficients ci and Ei for DR ratecoefficients from the ground state are listed in Table 2 for the entire silicon-like isoelectronic sequence. Our fits reproduce the actual computed data to better than 5% for all ions over the temperaturerange z2(101−107) K, where z is the residualcharge of the recombining ion. In fact, the accuracy is better than 1% over the collisionally-ionized plasma region.
Also, the total RR rate coefficients were computed, tabulated in ADAS format, and fitted using the formula of Verner & Ferland (1996),
![\begin{equation*} \alpha^{\textrm{RR}}(T) = A \, \sqrt{T_0/T} \, \left[ \left(1 + \sqrt{T/T_{0}} \right)^{1-B} \left(1 + \sqrt{T/T_{1}} \right)^{1+B} \right]^{-1},\end{equation*}](/articles/aa/full_html/2018/02/aa31243-17/aa31243-17-eq6.png) (6)
(6)
where, for low-charge ions, we replace B by (Gu 2003),
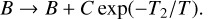 (7)
(7)
Partial RR rate coefficients are tabulated according to the ADAS (Summers 2003) adf48 format. The RR fitting coefficients are also listed in Table 3. These fits are accurate to better than 5% over the temperature range z2(101−107) K.
We compare our present IC total Maxwellian-averaged DR rate coefficients of a selected number of ions along the silicon-like isoelectronicsequence to other available theoretical and experimental results. In particular, we compare to the widely used recommended data of Mewe et al. (1980) and Mazzotta et al. (1998). Mewe et al. (1980) developed a single fitting formula, based on the data of Ansari et al. (1970) and Jacobs et al. (1977), for all ions and for all temperatures. The previously recommended database of Mazzotta et al. (1998) was derived from the calculations of Jacobs et al. (1977, 1979, 1980), which were then fitted by Shull & Van Steenberg (1982), for even numbered nuclei, and interpolated to provide the data forodd numbered nuclei by Landini & Monsignori Fossi (1991). Also, indicated in the figures are the temperatureregions of collisionally-ionized and photoionized plasmas. These temperature ranges are determined for each ion by considering the range of temperatures for which the ion’s fractional abundance is 90% or more of its maximum value. The collisionally-ionized zones were obtained using the calculations of Bryans et al. (2009b), and the photoionized zones have been computed using CLOUDY (Ferland et al. 1998). We note that the DR data used in those Si -like abundance calculations were those of Mazzotta et al. (1998), not including our present DR rate coefficients.
In Fig. 1, we show the total DR rate coefficients for the ground state of S2+. A comprehensive treatment ofS2+ DR for 3 → 3 (Δnc = 0) core excitation has recently been performed by Badnell et al. (2015). The present calculations are performed using the same MCBP IPIRDW approach as in the previous work, but we also include the small contributions from the 3 →4 (Δnc = 1) core excitations, unlike in the previous work. As detailed more fully in the earlier work by Badnell et al. (2015), the DR resonance contributions to the rate coefficient can be classified into one of three categories. First, there are contributions from the well-known dipole resonances (Burgess 1964) – those that accumulate to a dipole-allowed, core-excited S2+ thresholds, such as the 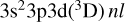 Rydberg series. These give rise to the characteristic high-temperature DR rate coefficient peak at temperatures
Rydberg series. These give rise to the characteristic high-temperature DR rate coefficient peak at temperatures 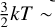 ionization limit.
ionization limit.
As seen in Fig. 1, both MCBP calculations are in good agreement at high temperatures.
The second category of resonance contributions is due to the fine-structure induced, core-excited states, such as the 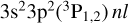 Rydberg series. These resonances only contribute at low energies – below the fine-structure splitting of the Si-like
Rydberg series. These resonances only contribute at low energies – below the fine-structure splitting of the Si-like 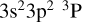 ground term – and therefore the corresponding Rydberg series consist of high-n resonances (22 ≤ n ≤ 32 for all sequences). This latter series yields a DR rate coefficient that peaks (and dominates) at low temperatures
ground term – and therefore the corresponding Rydberg series consist of high-n resonances (22 ≤ n ≤ 32 for all sequences). This latter series yields a DR rate coefficient that peaks (and dominates) at low temperatures  fine-structure splitting.
fine-structure splitting.
The third category of resonances encountered are the so-called “(N + 1)-electron resonances” – low-lying n = 3 dipole resonances such as 3s3p33d, in the case of this sequence. These DR resonance contributions are the most uncertain due to the corresponding uncertainty in energy position, as discussed in the earlier case of S2+ (Badnell et al. 2015). To obtain total DR rate coefficients at 104 K consistent with that required to determine the sulphur abundance in the Orion Nebula, a photoionized plasma, Badnell et al. (2015) shifted the positions of these n = 3 resonances to lower energies. This adjustment was further justified by simpler MCHF structure comparisons for the near-threshold, bound (N + 1)-electron states of S+, indicating that the computed (N + 1)-electron energy positions were indeed higher than the experimental values for bound states (Badnell et al. 2015). For consistency, we make the same shift for S2+ of ΔEN+1 = −0.157 Ryd.
Also in Fig. 1, the present results are compared with other available data including the LS coupling results of Badnell (1991), using AUTOSTRUCTURE, and the LS coupling R-matrix results of Nahar (1995), which include both RR and DR contributions. We note that the recommended data set of Mazzotta et al. (1998) for S2+ appears to use the high-temperature R-matrix results of Nahar (1995).
At this point, it is worth discussing the expected accuracy of our computed DR results, especially as it pertains to the three different categories of resonances. The first dipole core series, as treated in the original Burgess (1964) formulation, peaks at a high temperature given by the Rydberg series limit n →∞ energy positions and core oscillator strengths, the latter being computed fairly accurately in general. Provided that we perform the empirical shift of each core Rydberg limit to the experimental values (Ralchenko et al. 2011), thereby shifting every Rydberg member by the same energy, we expect to minimize the uncertainty in the high-temperature dipole-dominated DR rate coefficient.
In the same manner, the fine-structure resonances, that contribute strongly at lower temperatures, are governed by n →∞ Rydberg series, with limits given by the fine-structure splitting of the S2+ ground state. In fact, the minimum n of each Rydberg series is given by − Z2∕n2 ≈ fine − structuresplitting, giving n ≥ 22 for all series, and minimizing the resonance energy uncertainty. Provided that the calculations reproduce, or empirically shift to, the fine-structure split Si-like experimental energies (Ralchenko et al. 2011), we minimize the uncertainty in these resonance contributions.
The third type of (N + 1)-electron resonance contributions carry the largest uncertainty, as discussed more fully in Badnell et al. (2015) for the case of S2+. This uncertainty in rate coefficient contribution is due to the corresponding, relatively large, uncertainty in the resonance energy positions of the low-lying (n = 3) Rydberg members. However, as we discuss further below, the (N + 1)-electron states all eventually become bound for higher ionization states: only for lower charge states are some of the (N + 1)-electron states autoionizing, thereby contributing to DR. Furthermore, the total uncertainties become negligible at even lower charge-states, as we now demonstrate by looking at the next highest charge states: Cl3+ and Ar4+.
In Fig. 2, we show total DR rate coefficients for the ground state of Cl3+, separating the n = 3 (N + 1)-electron contribution (about 50% of the total for T = 2 × 104 K) from the total. In view of this strong contribution and the uncertainties known to be associated with resonance energy uncertainties here, it is important to try and establish the temperatures where the DR rate coefficients are affected, and by how much. Unfortunately, NIST does not give any autoionizing energies for Cl2+. Furthermore, they give no bound energies for either of the two lowest lying configurations which give rise to autoionizing states (3s2 3p3d2 and 3s 3p33d). Consequently, we can only use observed energies from 3s23p23d to guide us to a plausible shift of the resonances. Even here the doublets and quartets show different levels of agreement and it is only practical to use a single global shift which applies to all resonances. We choose it to be the largest difference, ~ 0.12 Ryd, which is already smaller than the ~0.2−0.4 Ryd case of S+ (Badnell et al. 2015). Thus, we empirically lower the (N + 1)-electron resonances by − 0.12 Ryd and this gives rise to an increase the total DR rate coefficient of ~10% at photoionized plasma temperatures (see Fig. 2). Our present results are also compared to the earlier results of Mazzotta et al. (1998) and Mewe et al. (1980), both of which are based on LS calculations that lack any low-temperature fine-structure DR contributions that are included in our calculations. For comparison, the total RR rate coefficient for Cl3+ is also shown.
In Fig. 3, we show total DR rate coefficients for the ground state of Ar4+, again showing just the contribution from the n = 3 resonances as well. For this higher-ionized system, the 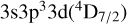 state that dominated the low-T S2+ DR rate coefficient, due to its large oscillator strength and near-threshold positioning, is now bound. However, other n = 3 resonances still contribute to the low-temperature DR – the ionization stage is still relatively low – but their contribution to the total is only about 15% at T = 3 × 104 K. Furthermore, the rate coefficient is found to be fairly insensitive to the uncertainty in n = 3 resonance positions. Lowering them by − 0.12 Ryd only results in an increase of a few percent at photoionized plasma temperatures (too small to be shown separately).
state that dominated the low-T S2+ DR rate coefficient, due to its large oscillator strength and near-threshold positioning, is now bound. However, other n = 3 resonances still contribute to the low-temperature DR – the ionization stage is still relatively low – but their contribution to the total is only about 15% at T = 3 × 104 K. Furthermore, the rate coefficient is found to be fairly insensitive to the uncertainty in n = 3 resonance positions. Lowering them by − 0.12 Ryd only results in an increase of a few percent at photoionized plasma temperatures (too small to be shown separately).
We also compare our results to the previously published final-state level-resolved rate coefficients of Arnold et al. (2015). Although both present and previous calculations used the same methodology, there are some important differences. First, a different basis set of N-electron target configurations was used in the previous work. Second, the previous work also used a different scaling parameter for each orbital whereas the same scaling parameter was used for all the orbitals in the present work, as listed in Table 1. Third, the previous work also shifted the N-electron target energies relative to the NIST values. We see from Fig. 3 that the present DR rate coefficient is less than the previous value by about 50% in the photoionized plasma zone and by about 10% in the collisionally-ionized plasma zone. The low temperature difference is a little large, even allowing for its uncertainty in a low-charge ion. We checked that the use of further observed energies had negligible effect. Instead, it appears (Loch, priv. comm.) that an incorrect input dataset was used by Arnold et al. (2015). The intended dataset gives results much more in line with ours.
As seen in Fig. 3, the recommended data of Mewe et al. (1980) and Mazzotta et al. (1998), based on LS high-temperature calculations, do not reproduce the fine-structure resolved IC DR, for two reasons. First, the fine-structure splitting gives rise to additional Rydberg series near threshold, thereby increasing the low-temperature DR rate coefficient. Second, as discussed in Abdel-Naby et al. (2012), at higher temperatures and for states of sufficiently high n, fine-structure autoionization within terms of doubly-excited states, and subsequent fine-structure autoionization following radiative decay, is responsible for additional DR suppression, giving high-temperature IC results that are lower than the LS ones.
Continuing along the series for higher ionization stages, we note that our findings for K5+ are similar to those for Ar4+ – about 15% contribution from the (N + 1)-electron resonances – while for Ca6+ these resonances contribute at most 5% to the total DR rate coefficient. Higher-charged ions have negligible contribution. Conversely, the (N + 1)-electron resonance contributions for P+ are small as well, about 5%, because the strongest of these resonances are high enough in energy (and remain so under any reasonable shift) that they are dominated by, and masked by, the stronger dipole resonances. Thus, likely only for S2+ (Badnell et al. 2015) do we have a significant uncertainty in the total DR rate coefficients at photoionized plasma temperatures due to the uncertainty in energy positions of the (N + 1)-electron resonances.
In Fig. 4, we compare our intermediate-coupling DR rate coefficients, for Fe12+ forming Fe11+ via 3 → 3 (Δnc = 0) and 3 → 4 (Δnc = 1) core excitations, to experimental measurements, carried out using the heavy-ion Test Storage Ring (TSR) at the Max-Planck Institute for Nuclear Physics in Heidelberg (Hahn et al. 2014). We also compare our present DR data to previous MCBP (AUTOSTRUCTURE) calculations by Hahn et al. (2014), finding a difference of less than 10% in the photoionized plasma region and by about 5% in the collisionally-ionized plasma region. Similar to Hahn et al. (2014), the present theoretical rate coefficient is smaller than the experimental value, by approximately 30% in the photoionized region and 25% in the collisionally ionized region. This somewhat largish discrepancy cannot be explained by any inaccuracies discussed earlier for the three different types of resonances (indeed, all (N + 1)-electron states are strongly bound by Fe12+). Instead, a fourth type of resonance contribution error was discussed by Hahn et al. (2014). At higher ionization stages, the core-excited N-electron states, such as 3s23pnclc (3 < nc < ∞) contribute more to the total DR, and our computational termination at nc = 4 means that 5 ≤ nc < ∞ contributions are neglected. These could account for much of the discrepancy: assuming a pure  scaling beyond nc = 4, the contributions from nc ≥ 5 increase the total DR rate coefficient by 15–25% over 106−109 K. But, it should be noted that increasing Auger suppression with increasing nc can be expected to reduce this amount somewhat. On the other hand, it cannot be ruled out that the experiment is in fact too high by about 25%, which is roughly the total calibration uncertainty in the experiments. Finally, we note also that the previous results of Mazzotta et al. (1998); Mewe et al. (1980), that are based on LS-coupling calculations, do not take into account fine-structure-induced DR and therefore do not show any low-temperature enhancement, as seen in Fig. 4.
scaling beyond nc = 4, the contributions from nc ≥ 5 increase the total DR rate coefficient by 15–25% over 106−109 K. But, it should be noted that increasing Auger suppression with increasing nc can be expected to reduce this amount somewhat. On the other hand, it cannot be ruled out that the experiment is in fact too high by about 25%, which is roughly the total calibration uncertainty in the experiments. Finally, we note also that the previous results of Mazzotta et al. (1998); Mewe et al. (1980), that are based on LS-coupling calculations, do not take into account fine-structure-induced DR and therefore do not show any low-temperature enhancement, as seen in Fig. 4.
In Fig. 5, we show the total DR rate coefficients from metastable as well as ground initial states of Fe12+. We note first that the DR rate coefficients are LS-term dependent. Second, at low temperature there is a significant difference among DR from the three fine-structure split levels 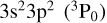 ,
, 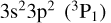 and
and 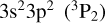 . The
. The 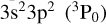 level-resolved DR is enhanced by second and third fine-structure-split Rydberg series near threshold whereas the
level-resolved DR is enhanced by second and third fine-structure-split Rydberg series near threshold whereas the 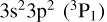 DR has only the second fine-structure-split Rydberg series near threshold, and the
DR has only the second fine-structure-split Rydberg series near threshold, and the 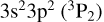 series has no fine-structure-split Rydberg series enhancement near threshold. Also shown in Fig. 5 are the present RR results from both the ground and metastable initial levels of Fe12+.
series has no fine-structure-split Rydberg series enhancement near threshold. Also shown in Fig. 5 are the present RR results from both the ground and metastable initial levels of Fe12+.
We present in Fig. 6 the DR rate coefficients for both Δnc = 0 (3 → 3) and Δnc = 1 (3 → 4) core excitations, for selected ions along the silicon-like sequence. Also shown are the total (Δnc = 0 + Δnc = 1) DR rate coefficients. For low-charged Ar4+, the contribution from 3 → 4 core excitation to the total DR rate coefficient is negligible. Additionally, using a configuration-averaged distorted wave method, Arnold et al. (2015) also showed that the contribution from Δnc = 2 core excitation to the total rate coefficient is 3 to 4 orders of magnitude smaller than the sum of the contributions from Δnc = 0 and Δnc = 1 core excitations. The 3 → 4 core excitation contributions are less than 1% for Ti8+, and 2% for V9+, whereas, for Zn16+, the Δnc = 1 contribution leads to an increase of approximately 15% in the total DR rate coefficient.
Lastly, in Fig. 7, we compare our present Maxwellian-averaged DR rate coefficients (in IC), for the entire silicon-like isoelectronic sequence, to the recommended data of Mazzotta et al. (1998). The recommended data is based-upon calculations that do not take explicit account of fine-structure and therefore do not show DR contributions at low temperatures that arise from fine-structure Rydberg series near threshold. This deficiency becomes greater with increase in the effective charge z. At higher temperatures, the two sets of results differ appreciably, especially for low-z ions. For example, there is a difference of about 50% for P+ and 30% for Cl3+. Also, note that the final results and the fitting coefficients listed in Table 2 correspond to the unshifted calculations.
 |
Fig. 1 Total Maxwellian-averaged DR and RR ground-state rate coefficients for S2+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results (Badnell et al. 2015); f) blue asterisks, LS R-matrix, RR + DR (Nahar 1995); g) black dashed curve with points, LS MCBP results (Badnell 1991). |
 |
Fig. 2 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Cl3+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) black dashed curve with filled circles, present DR rate coefficients omitting n = 3 resonance contributions; f) red dotted-dashed curve with filled triangles, present DR rate coefficients including only the n = 3 resonance contributions; g) brown dashed curve with filled squares, present DR rate coefficients with the n = 3 resonances lowered by − 0.12 Ryd. |
 |
Fig. 3 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Ar4+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results of Arnold et al. (2015). f) black dashed curve with filled circles, present DR rate coefficients omitting n = 3 resonance contributions; g) red dotted-dashed curve with filled triangles, present DR rate coefficients including only the n = 3 resonance contributions. |
 |
Fig. 4 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Fe12+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results presented in Hahn et al. (2014); and f) black dashed curve, experimental measurements (Hahn et al. 2014). |
 |
Fig. 5 Total Maxwellian-averaged DR and RR rate coefficients from the ground ( |
 |
Fig. 6 Total Maxwellian-averaged ground-level DR rate coefficients and the separate contributions from Δnc = 0 and Δnc = 1 core excitations for Ar4+, Ti8+, Fe12+, and Zn16+ ions. |
4 Summary
We have carried-out multi-configuration intermediate-coupling Breit-Pauli calculations for total and partial (final-state level-resolved) DR and RR rate coefficients for all ions from P+ through Zn16+ of the silicon-like isoelectronic sequence. We have compared total dielectronic recombination rate coefficients with other theoretical and experimental results. Good agreement is found at higher temperatures. At lower temperatures that are applicable to photoionized plasmas, our new results include additional DR contributions that were not included in most previous results, and differ markedly from the recommended results of Mazzotta et al. (1998). We have also investigated the contributions from the low-lying (N + 1)-electron resonances to the low-temperature total DR rate coefficient. The uncertainties associated with these contributions are likely significant only for S2+ (Badnell et al. 2015). Fitting coefficients for total DR and RR rate coefficients from the ground state were presented. Partial DR and RR rate coefficients are archived in OPEN-ADAS1 using the ADAS adf09 and adf48 formats, respectively. These data are needed for both astrophysical and fusion plasma modelling and constitute part of a dielectronic recombination database assembly for modelling dynamic finte-density plasmas in general (Badnell et al. 2003).
 |
Fig. 7 Comparison between the present total Maxwellian-averaged IC DR rate coefficients (solid curves) and the recommended data (Mazzotta et al. 1998, dashed curves) for the silicon-like isoelectronic sequence. |
References
- Abdel-Naby, S. A., Nikolić, D., Gorczyca, T. W., Korista, K. T., & Badnell, N. R. 2012, A&A, 537, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altun, Z., Yumak, A., Badnell, N. R., Colgan, J., & Pindzola, M. S. 2004, A&A, 420, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altun, Z., Yumak, A., Badnell, N. R., Loch, S. D., & Pindzola, M. S. 2006, A&A, 447, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altun, Z., Yumak, A., Yavuz, I., et al. 2007, A&A, 474, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansari, S. M. R., Elwert, G., & Mücklich, P. 1970, Z. Naturforsch., 25, 1781 [NASA ADS] [Google Scholar]
- Arnold, I., Thomas, E., Loch, S. D., Abdel-Naby, S., & Ballance, C. P. 2015, J. Phys. B At. Mol. Phys., 48, 175005 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 1991, ApJ, 379, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006a, A&A, 447, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R. 2006b, ApJ, 651, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., O’Mullane, M. G., Summers, H. P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., Ferland, G. J., Gorczyca, T. W., Nikolić, D., & Wagle, G. A. 2015, ApJ, 804, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A., & Badnell, N. R. 2007, A&A, 466, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryans, P., Badnell, N. R., Gorczyca, T. W., et al. 2006, ApJS, 167, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Kreckel, H., Roueff, E., Wakelam, V., & Savin, D. W. 2009a, ApJ, 694, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009b, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1965, ApJ, 141, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Colgan, J., Pindzola, M. S., Whiteford, A. D., & Badnell, N. R. 2003, A&A, 412, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colgan, J., Pindzola, M. S., & Badnell, N. R. 2004, A&A, 417, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eissner, W., & Nussbaumer, H. 1969, J. Phys. B At. Mol. Phys., 2, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Gu, M. F. 2003, ApJ, 590, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, M., Badnell, N. R., Grieser, M., et al. 2014, ApJ, 788, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., Speck, A., Karakas, A. I., Ferland, G. J., & Maguire, M. 2012, ApJ, 749, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Kepple, P. C., & Blaha, M. 1977, ApJ, 211, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Rogerson, J. E., & Blaha, M. 1979, ApJ, 230, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Rogerson, J. E., et al. 1980, ApJ, 239, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Landini, M., & Monsignori Fossi B. C. M. 1991, A&AS, 91, 183 [NASA ADS] [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mewe, R., Schrijver, J., & Sylwester, J. 1980, A&AS, 40, 323 [NASA ADS] [Google Scholar]
- Mitnik, D. M., & Badnell, N. R. 2004, A&A, 425, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nahar, S. N. 1995, ApJS, 101, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolić, D., Gorczyca, T. W., Korista, K. T., & Badnell, N. R. 2010, A&A, 516, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pindzola, M. S., Badnell, N. R., & Griffin, D. C. 1992, Phys. Rev. A, 46, 5725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Polito, V., Del Zanna, G., Dudík, J., et al. 2016a, A&A, 594, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polito, V., Reep, J. W., Reeves, K. K., et al. 2016b, ApJ, 816, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ralchenko, Y., Kramida, A. E., Reader, J., & NIST ASD Team 2011, National Institute of Standards and Technology, http://physics.nist.gov/asd [Google Scholar]
- Shull, J. M., & Van Steenberg M. 1982, ApJS, 48, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, H. P. 2003, ADAS User Manual (v2.6), available from http://www.adas.ac.uk/manual.php [Google Scholar]
- Verner, D. A.,& Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Watts, C., Udintsev, V., Andrew, P., et al. 2013, Nuclear Instruments and Methods in Physics Research A, 720, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A,466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2003, A&A, 412, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K., Badnell, N. R., & Savin, D. W. 2004a, A&A, 426, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2004b, A&A, 417, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Fu, J., et al. 2006, A&A, 447, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Radial scaling parameters for orbitals (1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d and 4f) used in the present study for Δnc = 0 and Δnc = 1 core-excitations in the silicon-like isoelectronic sequence.
Fitting coefficients ci (in cm3 K3∕2 s−1) and Ei (in K) for the total ground-state IC DR rate coefficients.
All Figures
 |
Fig. 1 Total Maxwellian-averaged DR and RR ground-state rate coefficients for S2+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results (Badnell et al. 2015); f) blue asterisks, LS R-matrix, RR + DR (Nahar 1995); g) black dashed curve with points, LS MCBP results (Badnell 1991). |
| In the text | |
 |
Fig. 2 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Cl3+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) black dashed curve with filled circles, present DR rate coefficients omitting n = 3 resonance contributions; f) red dotted-dashed curve with filled triangles, present DR rate coefficients including only the n = 3 resonance contributions; g) brown dashed curve with filled squares, present DR rate coefficients with the n = 3 resonances lowered by − 0.12 Ryd. |
| In the text | |
 |
Fig. 3 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Ar4+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results of Arnold et al. (2015). f) black dashed curve with filled circles, present DR rate coefficients omitting n = 3 resonance contributions; g) red dotted-dashed curve with filled triangles, present DR rate coefficients including only the n = 3 resonance contributions. |
| In the text | |
 |
Fig. 4 Total Maxwellian-averaged DR and RR ground-state rate coefficients for Fe12+: a) black solid curve, previous recommended data of Mazzotta et al. (1998); b) green dashed curve, present MCBP results; c) blue dotted curve, empirical formula of Mewe et al. (1980); d) magenta dotted-dashed curve, present RR rate coefficient; e) red dotted-dashed curve, previous MCBP results presented in Hahn et al. (2014); and f) black dashed curve, experimental measurements (Hahn et al. 2014). |
| In the text | |
 |
Fig. 5 Total Maxwellian-averaged DR and RR rate coefficients from the ground ( |
| In the text | |
 |
Fig. 6 Total Maxwellian-averaged ground-level DR rate coefficients and the separate contributions from Δnc = 0 and Δnc = 1 core excitations for Ar4+, Ti8+, Fe12+, and Zn16+ ions. |
| In the text | |
 |
Fig. 7 Comparison between the present total Maxwellian-averaged IC DR rate coefficients (solid curves) and the recommended data (Mazzotta et al. 1998, dashed curves) for the silicon-like isoelectronic sequence. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.