EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 609 (January 2018) A&A, 609 (2018) A83 Full HTML
Free Access
Issue
A&A
Volume 609, January 2018
Article Number A83
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201731758
Published online 18 January 2018

© ESO, 2018

1. Introduction

Over the last decade, new dedicated transient surveys of the Universe have discovered a multitude of new phenomena. One of the most surprising examples of such new transients is the discovery of superluminous supernovae (SLSNe; Quimby et al. 2011; Gal-Yam 2012) which appear to be long-lived explosions (hundreds of days) with peak magnitudes far in excess of normal supernovae (5–100 times the luminosity of Type Ia and core-collapse supernovae, Gal-Yam 2012; Inserra et al. 2013).

Over the last five years, it has been established that SLSNe come in different types (Gal-Yam 2012; Nicholl et al. 2015; Inserra et al. 2016b) and can be seen to high redshift (z ~ 1−4, Cooke et al. 2012; Howell et al. 2013). The power source for these events remains unclear but the most popular explanation is the rapid spin-down of a magnetar (a highly magnetic neutron star) which can explain both the peak luminosities and the extended light-curve of SLSNe (Kasen & Bildsten 2010; Woosley 2010). Alternatives include possible interactions between the supernova ejecta and the surrounding circumstellar material previously ejected from the massive central star (Chatzopoulos et al. 2013).

With forthcoming surveys like the Zwicky Transient Factory (ZTF; Kulkarni et al. 2012) and the Large Synoptic Survey Telescope (LSST; Ivezic et al. 2008; LSST Science Collaboration et al. 2009), the interest in SLSNe as possible high-redshift cosmological probes has grown due to their high luminosity and possibly increased space density at high redshift (Howell et al. 2013). Recent studies (Inserra & Smartt 2014; Papadopoulos et al. 2015; Chen et al. 2017a) suggest Type Ic SLSNe (namely hydrogen-poor events with similar spectral features as normal Type Ic supernovae, Pastorello et al. 2010) could be standardized in their peak luminosities using empirical corrections similar in spirit to those used in the standardization of Type Ia supernova (Rust 1974; Pskovskii 1977; Phillips 1993; Hamuy et al. 1996; Riess et al. 1996, 1998; Perlmutter et al. 1997; Goldhaber et al. 2001; Guy et al. 2005, 2007; Mandel et al. 2009, 2011). Inserra & Smartt (2014) showed that a correction based on the colour of the SLSN-Ic (over 20 to 30 days past peak in the rest-frame) could reduce the scatter in the peak magnitudes to 0.26 (Table 3 in Inserra & Smartt 2014) thus raising the possibility that such SLSNe could be used as standard candles.

This concept was explored in Scovacricchi et al. (2016) where we investigated the potential of SLSNe-I1 for constraining cosmological parameters. Scovacricchi et al. (2016) found that even the addition of ≃ 100 SLSNe-I to present supernova (SN) samples could significantly improve the cosmological constraints by extending the Hubble diagram into the deceleration epoch of the Universe (i.e. z > 1). Also, this work predicted that LSST could find ~104 SLSNe-I (over 10 yrs) which would constrain Ωm (the density parameter of matter of the Universe) and w (a constant equation-of-state of dark energy) to 2% and 4%, respectively. Such a sample of LSST SLSN-I would also provide interesting constraints on Ωm and w(z) (a varying equation-of-state) that were comparable to that predicted for ESA’s Euclid mission (Laureijs et al. 2011).

Euclid is a 1.2 m optical and near-infrared (NIR) satellite (Laureijs et al. 2011) designed to probe the dark Universe using measurements of weak gravitational lensing and galaxy clustering. Euclid is scheduled for launch in late 2020 and will spend the next six years performing two major surveys, namely a “wide” survey of 15 000 deg2 and a “deep” survey of 40 deg2 at both visual (photometry) and NIR (photometry and grism spectroscopy) wavelengths.

There are proposals to perform a high-redshift Type Ia supernova (SNe Ia) survey with Euclid (see DESIRE by Astier et al. 2014) and WFIRST (Hounsell et al. 2017), which will complement ground-based searches for local and intermediate redshift SNe Ia. DESIRE would be a dedicated 6-month NIR rolling search with Euclid and is predicted to measure distances to 1700 high-redshift SNe Ia (to z ≃ 1.5) thus constraining w to an accuracy of 2%.

In this paper, we study an additional supernova search with Euclid that is different from DESIRE in two ways. First, we only consider using the already planned Euclid surveys, specifically the Euclid Deep Survey (EDS) as it has a planned observing cadence that could be well-suited to the long SLSN light-curves. Secondly, we study the possibility of using SLSNe-I as an additional cosmological probe, which can be seen to higher redshift because of their high luminosities, especially at rest-frame UV wavelengths (although they are not as well-understood as SNe Ia). Therefore, these observations are essentially for free and will be complementary to DESIRE and other Euclid dark energy constraints.

In Sect. 2, we outline the rate of SLSN-I as a function of redshift and what is possible with the EDS, while in Sect. 3 we give an overview of spectroscopic follow-up of Euclid SLSNe. In Sect. 4 we discuss astrophysical uses of the Euclid SLSNe, while in Sect. 5, we construct a mock Hubble diagram using these Euclid SLSNe and study the possible cosmological constraints. We discuss Euclid SLSNe in Sect. 6 and conclude in Sect. 7. Throughout this paper, we assume a fiducial flat ΛCDM cosmology with H0 = 68 km s-1 Mpc-1 and Ωm = 0.3, which is consistent with recent cosmological measurements (e.g. Aubourg et al. 2015).

2. Modelling the rate of SLSN-I

2.1. The observed SLSN-I rate

Despite their intrinsic luminosity, there are only approximately 30 well-studied SLSNe-I presently available in the literature with both spectroscopy and multi-band photometric light-curves (e.g. see SLSN-I collections presented in Inserra & Smartt 2014; Nicholl et al. 2015). However, with forthcoming wide-field imaging surveys (e.g. ZTF, LSST, Euclid), targeting the distant Universe (z> 1), we expect the number of such well-studied SLSNe-I to increase significantly over the next decade.

We focus here on predictions for Euclid. To make such predictions, we need an estimate of the rate of SLSN-I with redshift. Unfortunately there is still uncertainty in the rate of these rare objects especially at high redshift. For example, Quimby et al. (2013) estimates a SLSN-I rate of 32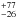+77-26\hbox{$^{+77}_{-26}$} yr-1 Gpc-3 with a weighted mean redshift of z=0.17\hbox{$\overline{z} = 0.17$}. This corresponds to a fraction (~ 10-4) of the volumetric rate of core-collapse SNe (CC-SNe) at the same redshift (consistent with the previous estimate from Quimby et al. 2011). The recent rate measurement of Prajs et al. 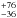(2017) using the first four years of the Canada-France Hawaii Telescope Supernova Legacy Survey (SNLS) finds 91+76-36\hbox{$^{+76}_{-36}$} yr-1 Gpc-3, at a weighted mean redshift of 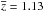z=1.13\hbox{$\overline{z}=1.13$}, thus consistent with Quimby et al. (2013). Between the two measurements there is an increase in the volumetric rate as a function of redshift that is a consequence of the observed star formation history.

However, McCrum et al. (2015) estimate that the SLSN-I rate could be up to ten times lower, based on the Pan-STARRS Medium Deep Survey over the redshift range 0.3 <z< 1.4, while Cooke et al. (2012) obtain an optimistic rate of ~ 200 yr-1 Gpc-3 based on only two SLSNe-I at a weighted redshift of 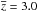z=3.0\hbox{$\overline{z}=3.0$}. The large uncertainties on all these rate measurements allow them to be consistent with each other, demonstrating that further observations are needed to resolve any apparent discrepancies.

In addition, if we note that only one SN of the ≃ 50 gamma-ray burst (GRB) SNe appears to be close to superluminous magnitudes (Greiner et al. 2015; Kann et al. 2016), then the rate of SLSN-I is likely to be smaller than the GRB-SN rate by approximately two orders of magnitude. Assuming a ratio of ≃ 4% between GRB-SN and SN-Ibc (Guetta & Della Valle 2007), and a rate of ≃ 2.5 × 104 yr-1 Gpc-3 for SN-Ibc (from Asiago and Lick surveys, Cappellaro et al. 1999; Li et al. 2011, respectively), the expected rate of SLSN-I would be approximately 10 to 100 objects yr-1 Gpc-3, which provides an independent estimate consistent with Quimby et al. (2013) and Prajs et al. (2017).

thumbnail Fig. 1

Summary of the EDS cadence over the five-year (1825 days) survey. Open symbols refer to the calibration epochs, which are ten per field excluding the Fornax field. Calibration epochs will have the same nominal depth of whole EDS. See Table 1 for further details.

Table 1

Sampling and coverage information of the three fields of the Euclid Deep Survey (EDS).

2.2. Euclid Deep Survey

To calculate the number of likely Euclid SLSNe-I, we need to know the volume sampled by the EDS as a function of epoch. The current EDS will likely comprise of three separate areas (see Scaramella et al., in prep., for further information); one near the north ecliptic pole (EDS-N), one near the south ecliptic pole (EDS-S) and a third overlapping the Chandra Deep Fields South (EDS-Fornax).

EDS-N is presently scheduled for 40 visits over a five year period. The sampling will not be homogeneous with time differences between consecutive visits ranging from 16 to 55 days (excluding the two 240-day gaps at the beginning and ending of the nominal survey). Ten of these 40 visits will be devoted to calibration purposes (covering an area of 20 deg2), while the remaining 30 visit of EDS-N will scan a central 10 deg2. We only consider this central region in this paper.

EDS-S will also have 40 visits over a five year period, but will cover an area of 20 deg2. These observations will be clustered in six-month blocks with an average cadence between visits of 28 days. Every 28 days two visits will be grouped in a three-day window. Discover astronomical transients in a field rich of foreground stars will not be a problem if algorithms using supervized machine learning techniques are employed as done by current transient surveys (e.g. Bloom et al. 2012; Goldstein et al. 2015; Wright et al. 2015).

EDS-Fornax (covering an area of 10 deg2) will be observed 56 times, to compensate for the expected higher background, with a limited visibility. It will be observed every day for a week with gaps of six months between the week of visibility.

We present a summary of these three EDS fields in Fig. 1 and Table 1. For this work, we have ignored the EDS-Fornax because of its low-visibility and therefore, the final areal coverage assumed is 30 deg2 over the first two fields (north central area plus the whole southern area).

thumbnail Fig. 2

Normalized filter transmission of VIS and Y, J, H (NISP).

We assumed a 5σ limiting magnitude of 25.5 for each of the individual EDS visual visits (VIS passband is equivalent to r + i + z passbands, see Fig. 2 and Table 2), while we assumed Y = J = H = 24.05 mag for each Near Infrared Spectrometer and Photometer (NISP) visit of the EDS. These point source values are slightly different from those reported in Astier et al. (2014), but are in agreement with the Euclid science requirements (Laureijs et al. 2011) and the latest estimates of the Euclid performance. We assumed the latest filter transmission curves and quantum efficiencies for VIS (Cropper et al. 2014) and NISP. The filter transmission functions are shown in Fig. 2, and have been implemented in the S3 software package (see Inserra et al. 2016b, for further details on the programmes) for k-corrections. We note that with such a steady cadence, and consistent limit magnitudes per visit, there will always be at least ten epochs for each detected supernova (at any redshift) that can be used as a reference image (e.g. without SN light) for difference imaging.

Table 2

Euclid filters specifications.

2.3. Luminosity function

We adopted a luminosity function with an average light-curve peak of −21.60 ± 0.26r-band magnitude, rising for 25 ± 5 days and declining 1.5 ± 0.3 mag in 30 days (Inserra & Smartt 2014; Nicholl et al. 2015). This has been built fitting literature data (e.g. Inserra et al. 2013; Nicholl et al. 2015) with low-order polynomials (as done in Nicholl et al. 2016) and the magnetar model (Inserra et al. 2013), allowing a reduced χ2 ≲ 5. Such a luminosity function is in agreement, within the uncertainties, with the recent findings of De Cia et al. (2017) and Lunnan et al. (2017). We utilized an empirical template for the spectral energy distribution (SED) of SLSN-I based on 110 rest-frame spectra taken for 20 SLSNe-I spanning a redshift range of 0.1 <z< 1.2 (from 1800 Å to 8700 Å) and covering approximately −20 to 250 days (with respect to peak luminosity) in their light-curve evolution (Gal-Yam et al. 2009; Pastorello et al. 2010; Quimby et al. 2011; Inserra et al. 2013; Nicholl et al. 2013, 2014, 2016; Vreeswijk et al. 2014).

thumbnail Fig. 3

Left: simulated observer-frame light-curve for a z = 2.0 SLSN-I in the four Euclid passbands. The horizontal (dashed) lines represent the assumed 5σ point source limiting magnitudes for each filter as discussed in the text. J and H limiting magnitudes are shifted of 0.05 and 0.10 mag to facilitate the reading. The cross symbols at the top of the panel represent a typical observing cadence for the southern EDS away from the six months gap (including two consecutive observations per passage that are not considered in the rate simulations), which would detect this SLSN four times in three bands. Similarly, the short lines at the top of the panel represent a typical observing cadence for the northern EDS, with four detections in three bands. Right: the same as the left panel but at z = 3.5. In this case both the southern and northern EDS would detect this SLSN three separate times (again excluding double observations within three days of each other). Observed phase is with respect to the observer frame J-band peak.

This template was implemented in the snake software package (Inserra et al. 2016b) to calculate the necessary k-corrections between the assumed Euclid visual and NIR filters and the standard optical rest-frame passbands, namely the SDSS r-band and the two narrow passbands used in Inserra & Smartt (2014) to standardize SLSNe-I (namely, their 4000 and 5200 Å synthetic filters). We use the SDSS r filter as our main reference rest-frame filter for our calculation. Uncertainties on the k-corrections have been evaluated as RMS of the uncertainties on redshift, spectral template and different standard passbands following the methodology of Inserra et al. (2016b). Usually such uncertainties are smaller than 0.05 mag (Kim et al. 1996; Blanton & Roweis 2007; Hsiao et al. 2007; Inserra et al. 2016b). Assuming that the terms leading to the definition of our observed magnitude (m) are uncorrelated, and the uncertainties deriving from the cosmology adopted are negligible, these uncertainties are given by σ(m)2=σ(M)2−4.7(σ(DL)DL)2−σ(A)2−1.2×[(σ(z)z)2+(σ(Lλo)Lλo)2+(σ(Lλr)Lλr)2+(σ(ZPλo)ZPλo)2+(σ(ZPλr)ZPλr)2],\begin{eqnarray} && \sigma (m)^{2} = \sigma (M)^2 - 4.7\left(\frac{\sigma (D_{\rm L})}{D_{\rm L}}\right)^2 -\sigma (A)^2 -1.2 \notag\\[1.5mm] && \times \left[ \left( \frac{\sigma (z)}{z}\right)^2 \!+\! \left( \frac{\sigma (L_{\lambda_{\rm o}})}{L_{\lambda_{\rm o}}}\right)^2 \!+\! \left( \frac{\sigma (L_{\lambda_{\rm r}})}{L_{\lambda_{\rm r}}}\right)^2 \!+\! \left( \frac{\sigma (ZP_{\lambda_{\rm o}})}{ZP_{\lambda_{\rm o}}}\right)^2 \!+\! \left( \frac{\sigma (ZP_{\lambda_{\rm r}})}{ZP_{\lambda_{\rm r}}}\right)^2 \right] , \end{eqnarray}(1)where M refers to the absolute magnitude, DL is the luminosity distance, A is the extinction coefficient, Lλ is the luminosity function in that filter, z the redshift, ZP are the filter zero-points, and o and r refer to the observer and rest-frames, respectively (see Inserra & Smartt 2014; Inserra et al. 2016b). All these uncertainties are included in the uncertainties estimate, with the exception of the uncertainties on the host galaxy extinction, which are usually negligible for SLSNe-I (Inserra & Smartt 2014; Nicholl et al. 2015; Leloudas et al. 2015).

thumbnail Fig. 4

Number of SLSNe-I detected, per redshift bin (Δz = 0.5), during the five years of the EDS (combining both the northern and southern EDS observations). Gold stars denote the “gold sample” (three filter detections for each of three epochs, or 3e3f in legend), while the silver circles are the “silver sample” (two filter detections for each of three epochs, or 3e2f). The error bars are Poisson uncertainties based on the number of SLSNe-I in each bin (Gehrels 1986), while the rates assumed are for our optimistic model (see text). Both gold and silver points are offset of Δz = 0.05 to facilitate the reading.

2.4. Euclid SLSN-I rate

In order to estimate the volumetric rate of SLSN-I in the EDS, we used a model for the evolution of the star-formation rate (SFR) density with redshift (see Hopkins & Beacom 2006), based on the Salpeter initial mass function (IMF) published by Cole et al. (2001), and using the methodology of Botticella et al. (2008). Adopting an IMF and SFR at any redshift then allowed a calculation of the volumetric rate of core-collapse supernova, assuming that all stars above 8 M⊙ produce a SN (the upper mass limit is not important as long as its ≳ 50 M⊙). We then assumed that the ratio between the SLSN-I and CC-SN rate is 10-4 (Quimby et al. 2013; Prajs et al. 2017), which provides a rate per co-moving volume element. We will refer to this rate as the “optimistic” model.

To estimate the systematic uncertainty on this rate, we also re-calculate it adopting a slightly different evolution for the SFR density (Bouwens et al. 2011) as well as the lower ratio of 10-5 between the SLSN-I to CC-SN rates (McCrum et al. 2015). This will be our “pessimistic” model. This approach gives more freedom and allowed us to have better uncertainties in case SLSNe do not follow the SFR of the bulk of the Universe. In fact low-metallicity, faint, galaxies appear to have a much flatter SFR with redshift than the nominal SFR of the Universe (see Heavens et al. 2004). We assume Poisson statistical uncertainties on both estimates. We note that the optimistic set-up is the one consistent with other SLSN-I rate estimates up to redshift z ~ 1 (see Fig. 9 of Prajs et al. 2017, for a comparison) and those at higher redshift (Tanaka et al. 2012, 2013). SLSNe-I host galaxies properties, such as metallicity, star formation rate and stellar mass, do not show any obvious redshift dependence (Lunnan et al. 2014; Leloudas et al. 2015; Chen et al. 2017a) but only a general metallicity threshold (12 + log(O/H)N2< 8.5), which however strongly depends on the diagnostic used (see Chen et al. 2017b, for an in-depth discussion). Hence, we do not expect any significant quantitative change in our assumptions (SFR density and SLSN-I to CC-SN rate) with redshift.

These two models are then used to calculate the number of SLSNe-I, in bins of Δz = 0.5 width, centred on multiples of z = 0.5 up to z = 3.5 which is consistent with the highest SLSN-I redshift observed to date, and likely achievable with Euclid (see Inserra & Smartt 2014).

We then performed 105 Monte Carlo simulations2 of Euclid SLSN-I light-curves for each bin of Δz = 0.5 and placing them at random explosion epochs relative to the EDS observing strategy that is, the survey time, depth, cadence and volume as discussed above. We show in Fig. 3 two examples of such simulated light-curves at z = 2.0 and z = 3.5. During these simulations, we also assumed an average foreground extinction of E(B−V) = 0.02 (see Inserra & Smartt 2014).

Using these simulated light-curves, we then determined which SLSNe-I would be useful for any meaningful astrophysical and cosmological analysis. We therefore defined two sub-sets of SLSN-I using the following selection criteria. First, we defined a “silver sample” that requires each SLSN to be detected (5σ point source) for at least three epochs (3e) in their light-curves in at least two Euclid filters (2f) per epoch (or 3e2f). Second, we defined a “gold sample” which requires a detection (5σ point source) in at least three Euclid filters, each for at least three epoch (3e3f). In all cases, we required at least one of these detections to be before peak brightness. In addition, we only considered epochs that are separated by at least three days to ensure reasonable coverage of the whole light-curve (Fig. 3). We simply ignored all but one epoch of those more closely separated by less than three days. These extra (close) epochs would not provide any additional information in terms of the light curve sampling, and colour evolution at z ≳ 2, but in reality they could be helpful for SN detection (e.g. removing bogus artifacts, asteroids, and cataclysmic variables) and increased signal to noise ratio (S/N).

Moreover, these close epochs (Δt< 3 days) in both EDS-S and EDS-N would be excellent for discovering fast transients such as rapidly evolving SNe (Drout et al. 2014) or observe red kilonovae (e.g. Kasen et al. 2015; Metzger et al. 2015a). The latter are fast transients visible for approximately two weeks as a result of two neutron stars merging and likely producing gravitational waves in the sensitivity region of the LIGO interferometers (strain noise amplitudes below 10-23 Hz−1/2 in the frequency regime 102–103 Hz; Berry et al. 2015; LIGO Scientific Collaboration et al. 2015).

These criteria should be sufficient to efficiently separate SLSNe-I from other transients3, such as active galactic nuclei and high−z lensed SNe Ia because of their characteristic photometric colour evolution (see the colour evolution shown by Inserra et al. 2013; Inserra & Smartt 2014; Nicholl et al. 2015). Also, recent work has shown that the evolution of the luminosity and colour of SLSNe trace a distinctive path through parameter space (see Inserra et al. 2017b), while targeting apparently “hostless” SLSN candidates can also improve the success rate of any spectroscopic follow-up (e.g. McCrum et al. 2015). Finally, SLSNe have been shown to possess similar spectrophotometric evolution up to z ~ 2 (Pan et al. 2017; Smith et al. 2017), which supports our assumption on the luminosity function and our analysis in Sect. 5. Furthermore, requiring a detection in at least two passbands will provide at least one colour measurement which is essential for using the relationship between peak magnitude and colour evolution as discussed in Inserra & Smartt (2014) for standardization. Having three passbands would provide a better estimate of the bolometric light-curve which could further be used to standardize SLSNe-I, for example correlating the spin period of the best-fit magnetar model to the host galaxies metallicity (see Chen et al. 2017a).

In Fig. 4, we show the results of our simulation. When determining the number of SLSNe-I expected from the EDS, we assume that only the northern and southern areas of the EDS (total of 30 deg2) are observed as shown in Fig. 1. In the case of our optimistic model, this provides a yearly volumetric rate of 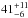41-6+11\hbox{$41^{+11}_{-6}$} yr-1 Gpc-3 for the silver sample (3e2f) and 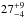27-4+9\hbox{$27^{+9}_{-4}$} yr-1 Gpc-3 for the gold sample (3e3f). Uncertainties are Poisson and have been estimated using Gehrels (1986) for small numbers of events in astrophysics. In addition, uncertainties on the yearly rates at 0.5 <z< 3.5 have been estimated with the same formalism applied to the sum of each bin since the sum of each independent Poisson random variable is Poisson.

We present in Table 3 the expected number of SLSNe-I as a function of redshift for both rates models, while in Fig. 4 we only plot the results of the optimistic model. In total, we predict Euclid will detect ≃ 140 high-quality (gold sample) SLSNe-I up to z ~ 3.5 over the five years of the EDS. On the other hand, the silver sample could deliver an extra 70 SLSNe-I, with respect to the gold, over the same five years. Extending the EDS beyond the nominal five-year duration could add approximately 40 SLSNe-I per year to the sample. If in our optimistic model we increase the detection level from 5σ to 10σ, then the predicted rates would be similar to those for the 5σ pessimistic model. Furthermore, if the limiting magnitude of the VIS filter was less efficient than assumed here, and closer to the initial 24.5 mag limit originally expected, we would see a drop of ~ 7% in our rate.

Table 3

Number of SLSNe-I per year for both samples (silver and gold) and with both rate models (see text).

3. SLSN spectroscopy

Throughout this analysis, we have assumed we know accurately the redshift and identification of the detected SLSN-I events. Such information could be achieved through fitting models of SLSN to the Euclid photometric data as previously done with SNe Ia (e.g. Jha et al. 2007; Guy et al. 2010; Sullivan et al. 2011) or fitting the magnetar model to the multi-colour light-curve (e.g. Prajs et al. 2017). However, these approaches are model-dependent and there are degeneracies in such fitting techniques leading to systematic biases.

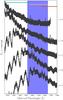thumbnail Fig. 5

Example of an observed spectrum with S ! N ~ 20, R ≃ 350 of a SLSN-I at various redshifts (0.5 <z< 2.5). The spectrum is that of iPTF13ajg at peak epoch (Vreeswijk et al. 2014) with a flux of ~ 10-16 erg s-1 cm-2 Å-1 at Y-band wavelength and at redshift z = 0.5, which should be feasible for the Euclid “blue” grism (see text). The cyan, yellow and red solid lines represent the wavelength regions covered by Euclid VIS, Y and J filters, respectively (we note that VIS and Y are superimposed for 600 Å). The blue region shows the Euclid “blue” grism covering 0.92 to 1.25 microns. The spectra at z> 0.5 show the potential of future facilities (e.g. JWST, E-ELT) and their use in identifying SN features, since they will go deeper and with a better resolution than the Euclid spectrograph.

The logical next step is to secure a spectrum, especially after peak (see Inserra et al. 2017b) for as many of these SLSNe-I as possible to determine both their redshift and classification. This has traditionally been the approach for SNe Ia, but recently the number of detected SN Ia candidates is far beyond our capability to perform real-time spectroscopic follow-up of all these events (see Campbell et al. 2013). For example, the Dark Energy Survey (DES) is now focussed on gaining spectroscopic follow-up for all SN host galaxies which is easier given large multi-object spectrograph (see Yuan et al. 2015). However, such an approach may not work for all SLSNe-I as many of these events happen in low-mass, compact dwarf galaxies (Lunnan et al. 2014).

Fortunately, the rate of new Euclid SLSN detections should be approximately once a week, and each supernova will last for several months in the observer-frame (see Fig. 3). Therefore, it should be feasible to obtain real-time spectroscopic follow-up of these Euclid SLSNe, unlike the LSST SLSN sample where we may find ~ 25 new SLSNe-I per week (Scovacricchi et al. 2016) over the ten years of operations. Also, the intrinsic rate of SLSN-I events should be far in excess of the expected SLSN-II rate, meaning the expected contamination from such events (e.g. for our cosmological analysis) will be minimal, although we note the discovery of more high-redshift SLSNe-II would be of great interest for astrophysical studies.

To assess the feasibility of obtaining spectra of these Euclid SLSNe-I, we use the exposure time simulator of the near-infrared integral-field spectrograph HARMONI (Zieleniewski et al. 2015) planned for the European Extremely Large Telescope (E-ELT). We estimate that an effective exposure time of 900 s would give a S/N of ~20 for an average SLSN-I at z = 2. Such S/N is sufficient to identify a transient as shown in Fig. 5 and by the Public ESO Spectroscopic Survey of Transient Objects (PESSTO; Smartt et al. 2015). Alternatively, it would only require 300 s to achieve a similar S/N for the same SLSN-I using the low-resolution grating on the Near-Infrared Spectrograph (NIRSpec) on the James Webb Space Telescope (JWST). We anticipate similar exposure times for the Wide Field Infrared Survey Telescope (WFIRST), as well as the 30 m Thirty Meter Telescope (TMT) and the 23 m Giant Magellan Telescope (GMT).

On the other hand, it may be more challenging with existing ground-based eight-meter telescopes. For example, we would require a two-hour integration using the Near-Infrared Integral Field Spectrometer (NIFS) on the Gemini telescope, to achieve S/N ~ 5, which is a lower limit for identifying transients object with broad feature like SLSNe-I and secure a redshift.

It may also be possible to obtain some spectral information for these SLSNe-I from the low-resolution (R ≃ 350) Euclid NIR slitless spectroscopy that is planned for the EDS in parallel to the imaging data. The information on the NIR slitless spectroscopy here reported is the latest available to the Euclid consortium and likely to be the final, even though we warn the readers that later changes could always happen. The Euclid NISP instrument has two NIR grisms, namely a “blue” grism covering 0.92 to 1.25 microns and a “red” grism covering wavelengths of 1.25 to 1.85 microns. The EDS slitless spectroscopy strategy may focus primarily on observations with the blue grism with approximately three-quarters of the deep field visits (each of 4 dithers) dedicated to this grism. We expect each visit to reach a limiting flux of 2 × 10-16 erg s-1 cm-2 Å-1 (3.5σ) to match the depth of the Euclid wide survey (for calibration purposes). We estimate that such data may provide spectroscopic information on a live SLSN (as detected in the imaging) to z ≤ 0.5. Better performance could be obtained by re-binning the spectrum as the SLSN-I features are broad and optimally extracting the spectral data using our prior knowledge of a candidate SLSN at that location. In addition, in case of nearby SLSNe, a spectrum observed after peak should contain more information as both the O i and Ca NIR lines will be present in the observed region of a blue NIR grism configuration.

We may also obtain the redshift of a SLSN-I host galaxy through the co-addition of multiple NISP grism spectra, at the known location of the SLSN, to achieve a possible flux limit of 3 × 10-17 erg s-1 cm-2 Å-1 (over a one arcsecond aperture). Many SLSNe-I are located in star-forming dwarf galaxies with strong oxygen nebular emission lines that means we should detect [O iii] to z = 1 in the blue grism for several of the SLSN-I host galaxies (e.g. Leloudas et al. 2015; Perley et al. 2016).

4. Astrophysics from high-redshift SLSNe

The discovery of hundreds of SLSNe-I in the EDS will improve several areas of astrophysics. For example, Euclid photometry and spectroscopy of nearby SLSNe-I will improve our knowledge of their SEDs in the NIR (only up to z = 0.5 objects), where the uncertainties due to extinction are minimized. This would then allow us to compare SLSNe-I with similar photospheric spectra, but different observed colours and continuum slopes, to gain insights into the host galaxy extinction. On the other hand, Euclid will deliver hundreds of SLSNe over a longer redshift baseline than those currently available. This will increase the statistical power providing for a more principled approach in the spectrophotometric analysis. Consequently, it could lead to a better understanding of the mechanism responsible for the luminosity of SLSNe-I, which has been narrowed to an inner engine, spin down of a rapidly rotating magnetar (e.g. Kasen & Bildsten 2010; Woosley 2010; Dessart et al. 2012) or a black hole (Dexter & Kasen 2013) and/or interaction of the SN ejecta with a massive (3−5M⊙) C/O-rich circumstellar medium (e.g. Woosley et al. 2007; Chatzopoulos et al. 2013). We also note that a pair instability explosion (e.g. Kozyreva & Blinnikov 2015) could still be a viable alternative at high redshift after having been disfavoured for SLSNe-I at z ≲ 1.5 (e.g. Nicholl et al. 2013; Smith et al. 2016; Inserra et al. 2016a, 2017a).

Due to their high luminosity, SLSNe-I are also excellent probes of the physical conditions of the gas surrounding the SN, as well as the interstellar medium within the host galaxy interstellar medium. This is possible through the detection of broad UV-absorption lines, which will be redshifted into the NIR wavelength range. For example, elements like Mg, Si, Fe, and Zn can be detected, via narrow absorption lines in the follow-up spectra of SLSN-I, thus allowing us to measure the metal column densities, relative abundances, dust content, ionization state, and kinematics of the gas. First attempts to detect such metal lines in the rest-frame UV of such SLSNe-I have been successful (e.g. Berger et al. 2012; Vreeswijk et al. 2014). Furthermore, any Fe and Ni within 100 parsecs of the SN should be excited via “UV-pumping”, thus providing an estimate of the distance between the SN and any absorbing gas (as achieved for GRBs, e.g. Vreeswijk et al. 2013). This, combined with the velocity information, would provide a novel constraint on the immediate environment, and progenitors, of these SLSNe-I.

In Sect. 2, we estimated the number of SLSNe-I observed by Euclid by assuming they follow the cosmic star-formation history, since these events are proposed to originate from massive stars (e.g. Jerkstrand et al. 2017). Such an assumption will be tested via these Euclid SLSNe-I, especially with those objects beyond z> 1.5, which is currently the limit of the reliability of rate estimates (Prajs et al. 2017). SLSNe-I are associated with low-metallicity, high star-forming galaxies (e.g. Lunnan et al. 2014; Leloudas et al. 2015; Chen et al. 2017a) at all observed redshifts (z< 4; Cooke et al. 2012), hence we do not expect that to change at Euclid SLSNe-I redshifts. This implies that Euclid SLSNe-I will also trace the cosmic chemical enrichment as previously done with CC-SNe (e.g. Strolger et al. 2015).

Furthermore, this large number of Euclid SLSNe-I discovered over a wide redshift range will improve our understanding of stellar explosions and transient events, for example, Euclid could discover interesting objects similar to SN 2011kl (Greiner et al. 2015; Kann et al. 2016; Bersten et al. 2016) and ASASSN-15lh (e.g. Dong et al. 2016; Leloudas et al. 2016; van Putten & Della Valle 2017; Margutti et al. 2017) which achieve similar luminosities as SLSNe, but show different spectrophotometric evolution.

5. SLSN cosmology

5.1. Methodology

Following the work of Scovacricchi et al. (2016), we can also consider the cosmological usefulness of the Euclid SLSNe-I. For this analysis we explored what could be achieved if we were to obtain a sample of 300 Euclid SLSNe-I with the redshift distribution given in Fig. 4. Such an optimistic sample may be possible if we can utilize the additional silver sample (140 + 70) and obtain an extension to the EDS beyond the nominal five-year duration of the Euclid mission, for example like DESIRE. Moreover, we may find even more SLSNe-I given the present uncertainties in the high-redshift SLSN rate, and our assumed luminosity function (which is quite conservative).

We note that, despite such SLSNe-I showing a luminosity function with a gaussian-like distribution (e.g. Inserra & Smartt 2014; Nicholl et al. 2015; Inserra et al. 2017b; Lunnan et al. 2017), current surveys are starting to populate the lower luminosity end creating a continuum in luminosity between normal and superluminous SNe (see De Cia et al. 2017).

We followed the methodology outlined in Scovacricchi et al. (2016) to construct a mock Hubble diagram (redshift-distance relationship) for such a sample. As in Scovacricchi et al. (2016), we include the additional magnitude dispersion of weak gravitational lensing, which will be important for high-redshift objects for example beyond z ≃ 2 (Marra et al. 2013). We also assume that all the SLSNe-I have been successfully classified (see Sect. 3 for discussion of spectroscopic follow-up of these events) and our sample contains negligible contamination (e.g. outliers on the Hubble diagram).

In addition to the high-redshift SLSNe-I, we need to include a low redshift sample to help anchor the Hubble diagram. Therefore, we assumed 50 SLSNe-I, homogeneously distributed over the redshift range 0.1 <z< 0.5 for this local sample. This choice is consistent with Scovacricchi et al. (2016) and is rather conservative given existing samples of low-redshift SLSN-I in the literature and expectations from planned, and on-going, transient searches like ASASSN (Shappee et al. 2014) and ZTF, and spectroscopic follow-up programmes like PESSTO & ePESSTO (Smartt et al. 2015). Within each redshift bin, we assigned the redshift value at random for the number of supernovae given in Table 3.

We combined the SLSN mock Hubble diagram with a DES (see Bernstein et al. 2012) mock sample for SN Ia4. It is composed of 3500 SNe Ia (distributed according to the hybrid-10 strategy in Bernstein et al. 2012) and 300 low-redshift SNe Ia (uniformly distributed for z< 0.1).

We fitted our mock Hubble diagram using the publicly available code cosmomc (July 2014 version, Lewis & Bridle 2002), run as a generic Markov chain Monte Carlo sampler. This allows us to include a custom-made likelihood in the software, 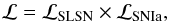ℒ=ℒSLSN×ℒSNIa,\begin{equation} \label{eq:liks} \mathcal{L}=\mathcal{L}_{\rm SLSN}\times \mathcal{L}_{\rm SNIa}, \end{equation}(2)defined as the product of two likelihoods, one for each of the data samples considered here (“SLSN” and “SNIa” hereafter).

Table 4

Our one-sigma predicted cosmological constraints for one parameter (ϵ = Δp/pfid) for various combinations of likely Euclid and DES samples and priors (see text for details).

Both of these likelihoods have the same functional form, ℒ=1(2π)n/2detCexp[−12(ΔμTC-1Δμ)],\begin{equation} \mathcal{L}=\frac{1}{(2\pi)^{n/2}\sqrt{\det C}}\exp \left[-\frac{1}{2} \left(\boldsymbol{\Delta \mu}^T C^{-1} \boldsymbol{\Delta \mu} \right) \right], \end{equation}(3)where Δμ is the n-dimensional vector containing the Hubble residuals (see below) and n is the number of supernovae in that sample. As discussed in Scovacricchi et al. (2016), we neglect the covariance between supernovae (i.e. all the non-diagonal terms are set to be zero) as we expect these to be small compared to the statistical noise of the limited sample sizes and gravitational lensing (see below). We also do not yet have a good understanding of possible systematic uncertainties (e.g. the photometric calibration) but assume they will be sub-dominant given present expertise in calibrating such photometric surveys. Also, the science requirement on the Euclid relative photometry is 0.002 mag, which exceeds the calibration uncertainties with present ground-based large-area surveys.

Hence, each covariance matrix C would reduce to diagonal elements only, giving 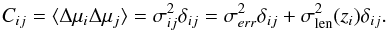Cij=⟨ΔμiΔμj⟩=σij2δij=σerr2δij+σlen2(zi)δij.\begin{equation} C_{ij}=\langle\Delta\mu_i \Delta\mu_j \rangle = \sigma^2 _{ij}\delta_{ij}=\sigma_{err}^2\delta_{ij}+\sigma_{\rm len}^2(z_i)\delta_{ij}. \end{equation}(4)Each measurement then has an uncertainty equal to the sum in quadrature of the data and lensing uncertainties (respectively σerr and σlen(zi), see Sect. 3.2 of Scovacricchi et al. 2016). We assumed that the magnitudes of the SLSN-I population will be standardized using techniques like those outlined in Inserra & Smartt (2014), or more advanced future techniques similar to those now used for SNe Ia (e.g. SALT and BayeSN; Guy et al. 2010; Mandel et al. 2011). To be conservative, for our SLSN-I mock samples, we assumed a dispersion σerr = 0.26 mag, based on the findings of Inserra & Smartt (2014) and following the previous work of Scovacricchi et al. (2016). Specifically, we select this value for σerr from Table 3 of Inserra & Smartt (2014) based on their Δ(400−520) extended SLSN-I sample as this is the most appropriate representation of the corrected peak magnitude root-mean-square that will be available in the future.

For our DES SN Ia mock Hubble diagram we replicated the approach of Scovacricchi et al. (2016), who assumed a redshift dependent σerr, equal to the values published in Bernstein et al. (2012) and reported in Fig. 2 of Scovacricchi et al. (2016). For DES SNe Ia only, we also included σsys = 0.1 mag to reproduce the possible overall effects of systematic uncertainties (see Scovacricchi et al. 2016, for further details).

One systematic uncertainty we must consider is the relative photometric calibration between the local SNe Ia and the more distant SLSN population. Similar to Scovacricchi et al. (2016), we therefore allowed for an unknown offset between the two samples by including a free parameter ξ in each of the two likelihoods. Therefore, the Hubble residual for the generic ith SN is 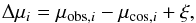Δμi=μobs,i−μcos,i+ξ,\begin{equation} \Delta \mu_i=\mu_{{\rm obs},i}-\mu_{{\rm cos},i}+\xi, \end{equation}(5)where μobs,i is the simulated distance modulus and μcos,i is the theoretical distance modulus using our assumed cosmology.

We then numerically marginalize over this calibration parameter (by doing so, we also re-absorb any difference in H0 with respect to its fiducial value). This approach is not ideal as it treats a possible systematic uncertainty as an additional statistical noise, but given we are still unclear about the accuracy of any cross-calibration of these samples, it is difficult to model otherwise.

5.2. Possible cosmological constraints

We report the cosmological results for our (optimistic) SLSN-I sample in Table 4. We quote the value of the 1σ uncertainties for the free parameters in our fitting (Δp in the table, for a generic parameter p) which are computed by fitting a Gaussian distribution from the one-dimensional posterior distributions. We do not quote the best fit values as they are all consistent with our fiducial cosmology within 2σ. In the same table, we also quote the relative uncertainties ϵ = Δp/pfid, for a generic parameter p with fiducial value pfid. Parameters with a dash symbol (“–”) in Table 3 are considered constant within that fit, and fixed to their fiducial values.

In Table 4, we present results for both a flat ΛCDM model (assuming w = −1) as well as exploring non-zero time derivative of the dark energy equation-of-state parameter, namely w(a) = w0 + wa(1−a) (Chevallier & Polarski 2001), which has traditionally been used to quantify possible evolving DE models (e.g. see Solà et al. 2017; Zhao et al. 2017). Such work should show the importance of obtaining high-redshift distance measurements like those discussed here.

Due to the strong degeneracy between these two dark energy parameters, we therefore include Gaussian priors on Ωm and w0 of width 0.015 and 0.25, consistent with the current uncertainties found by Planck. The use of these priors is indicated in Table 4 with P[Ωm] and P[w0].

In Table 4, we only show our results in combination with the expected DES SN Ia mock sample as the Euclid SLSN-I results on their own are not competitive (due to their relatively small numbers and intrinsic scatter presently assumed). For example, in the case of flat ΛCDM, the Euclid SLSNe-I alone (plus the low-z SLSN-I sample) would constrain Ωm to an accuracy of ~ 15%. This is not competitive with existing SN-only constraints (e.g. Betoule et al. 2014), nor are the results in Table 4 when combined with DES for example 3% uncertainty on Ωm. Again, this is not surprising given the assumed fiducial model, the size of the SLSN-I sample and the assumed uncertainties.

The cosmological constraints get more interesting when we allow w to vary as the importance of the high-redshift SNe come more pronounced. In Table 4, we see that it is possible to improve on the uncertainty of Δwa by adding our 300 SLSNe-I to the existing DES sample (and possible priors from other observations). For example, our overall constraints on the flat w0waCDM model (bottom line of Table 4) are better than the best SN-only constraints available in the literature today (e.g. Table 15 of Betoule et al. 2014), which show an uncertainty of order one for wa using Planck+JLA (and assuming similar weak priors).

We also investigated the possible systematic uncertainty caused by changes in the absolute magnitude of SLSNe-I with redshift due to uncertainties in the k-corrections. We repeated the approach in Scovacricchi et al. (2016) of splitting the Euclid SLSN-I sample into two sub-samples with different normalisation parameters (e.g. different absolute magnitudes). We chose to split the sample at z = 2.5 as this corresponds to the redshift where the broad UV spectral features in the SLSN-I spectrum shift from the Euclid VIS band into the IR bands (see Fig. 5). We then analyzed these two sub-samples together with the low-redshift SLSNe-I and the DES SN Ia mock sample, which also has a free normalization parameter, giving a total of three nuisance parameters in our fitting. We find that both the uncertainties on Ωm and w increase to 10% compared to the values given in Table 4.

The cosmological results in Table 4 could improve in several ways. First, our analysis assumes σerr = 0.26 for the dispersion in peak magnitude for our Euclid SLSNe-I. This is the value obtained by Inserra & Smartt (2014) based on only 14 SLSNe-I available in the literature at the time. If SLSNe-I are standardizable candles, we would expect their standardization to improve in the coming years with on-going surveys and higher quality data on the individual events. In fact, the Euclid SLSN-I sample should provide an important data set for re-visiting the standardization of these events, and one may wish to include the standardization parameters in the cosmological fitting as presently performed for SN Ia cosmology.

Secondly, we have modeled several possible systematic uncertainties (e.g. lensing, calibration) as additional statistical noise. If these uncertainties could be measured, and corrected for, then we would expect the cosmological constraints to again improve compared to those presented in Table 4.

6. Discussion

We present predictions for the rate of SLSN-I detected by the Euclid mission. In Fig. 4, we present the expected number of SLSNe-I in the EDS, as a function of redshift, over the nominal five year mission. It is worth stressing that we predict to find a couple of hundred new SLSNe-I to z ~ 3.5 which will revolutionize our understanding of these enigmatic objects, while providing a new window on the distant Universe. This is possible because of the unique combination of instrumentation available on the Euclid satellite (a wide-field optical and NIR imager) as well as the EDS observing strategy, for example the continuous monitoring of the same field, which minimizes temporal edge effects that may affect ground-based searches. As demonstrated in the large uncertainty on our predictions, these Euclid data will immediately provide a precise determination of the SLSN-I rate (with redshift), thus helping constraint the star-formation history of the Universe at these early epochs. There is no other experiment prior to Euclid that will provide such information on high-redshift SLSNe-I, and therefore it is important to use these unique data to the best of our ability (especially if observed contemporaneously with other facilities like LSST).

In addition to improving our understanding of the astrophysics of these objects, the Euclid SLSN-I sample provides additional cosmological constraints as discussed in Sect. 5. These constraints will be complementary to those planned from Euclid weak gravitational lensing, galaxy clustering and SNe Ia (e.g. DESIRE), as well as probing to higher redshift than SLSN-I samples from LSST. For example, in Scovacricchi et al. (2016), we presented cosmological constraints from an idealised sample of LSST SLSNe-I, but the unavailability of deep NIR imaging over the LSST area will limit the detection of SLSNe beyond z ~ 2. These Euclid SLSNe-I will therefore be unique in allowing us to extend the overall cosmological constraints to z ~ 3.5 thus improving our constraints on possible dynamical DE models (Solà et al. 2017; Zhao et al. 2017). Any additional high-redshift measurements of the expansion history of the Universe are welcome, especially if they come for free from data already planned.

The results of this paper depend on obtaining spectra for as many Euclid SLSNe-I as possible (see Sect. 4). This implies the need for an effective (in terms of purity and completeness) method for identifying as many as “true” SLNSe-I from other types of transients. In the case of objects not matching the conservative selection criteria used to define the golden and silver samples, other methods may be effective such as that presented by D’Isanto et al. (2016). In this case, light-curves are first compressed to a reduced, but extensive, set of statistical features and then classified using the MLPQNA method (Brescia et al. 2014). While this approach has never been applied to the classification of SLSNe-I, it has achieved 96% completeness and 85% purity in classifying SNe Ia in the Catalina Real-Time Transient Survey.

Finally, we raise the possibility of measuring the gravitational lensing of these high-redshift SLSNe-I as we did include it as a likely “noise” term in our analysis above. While the probability of witnessing a strongly lensed SLSN-I (Kelly et al. 2015) will be small, it may be possible to measure the cross-correlation function between the peak, corrected magnitudes of these distant SLSN-I with the foreground large-scale structure as traced by galaxies (Scovacricchi et al. 2017), especially as these Euclid deep fields will become the focus of significant additional observations for example there will likely be overlap with LSST deep drill fields, and possibly WFIRST (Hounsell et al. 2017).

7. Conclusions

We present an analysis of the possible number of superluminous supernovae detected in the Euclid Deep Survey. We show that Euclid should find ≃ 140 high-quality SLSNe-I to z ~ 3.5 over a five year period. An extra ≃ 70 SLSNe-I are possible depending on the quality cuts, while present uncertainties in the rates, luminosity functions, and instrument detection efficiencies may allow many more to be found. These data, especially if also spectroscopically targeted to secure their nature and redshift, will revolutionize the study of SLSNe-I, increasing present samples of high-redshift (z> 2) SLSN-I by two orders of magnitude.

We stress the importance of these Euclid SLSNe-I for the study of supernova astrophysics and the star-formation history of the Universe. Such investigations will be enhanced by follow-up observations by the next generation of large space and ground–based telescopes (E-ELT, LSST, and JWST) and provide excellent targets for these observatories. Euclid will also provide low-resolution NIR grism spectroscopy for some low-redshift SLSNe-I.

We also investigated the possibility of constraining cosmology using these SLSNe-I, when combined with a low-redshift sample of 50 SLSNe-I (from the literature), and the expected cosmological results from DES. In the case of a flat w0waCDM model, our analysis suggests we could obtain an uncertainty of Δwa ~ 0.9 which is an improvement on DES alone result, and the present constraints on this parameterization. Any additional measurements of the high-redshift expansion history of the Universe are invaluable as present baryonic acoustic oscillations observations suggest a possible tension with the standard ΛCDM model (Zhao et al. 2017), either indicating unrecognized systematic uncertainties or dynamical dark energy.

We finish by noting that these Euclid SLSNe-I come “for free” as we have just assumed the latest survey design of the EDS. It is therefore important to prepare the Euclid analysis software pipelines to detect such transients as they will be present in the data. This is a major motivation for this paper, that is, to highlight the urgent need to prepare for such long-lived transients in the Euclid data-stream and be ready to detect them in “real-time” (within days hopefully, but see Inserra et al. 2017b, about SLSN classification in real time) to trigger follow-up observations, for example using JWST which also has a finite lifetime.

1

Throughout this paper, we will use “SLSNe-I” to refer to Type Ic SLSNe as discussed by Inserra et al. (2013). We do not refer further to Type II SLSNe which appear to have a significantly lower rate than SLSNe-I.

2

This level of simulations has been used in previous literature studies (e.g. Prajs et al. 2017) and found to be adequate.

3

Dark Energy Survey, priv. comm.; Angus et al. (in prep.).

4

Details of this mock sample can be found in Sect. 3.2 of Scovacricchi et al. (2016).

Acknowledgments

We thank the internal EC referees (P. Nugent and J. Brichmann) as well as the many comments from our EC colleagues and friends. C.I. thanks Chris Frohmaier and Szymon Prajs for useful discussions about supernova rates. C.I. and R.C.N. thank Mark Cropper for helpful information about the VIS instrument. C.I. thanks the organisers and participants of the Munich Institute for Astro- and Particle Physics (MIAPP) workshop “Superluminous supernovae in the next decade” for stimulating discussions and the provided online material. The Euclid Consortium acknowledges the European Space Agency and the support of a number of agencies and institutes that have supported the development of Euclid. A detailed complete list is available on the Euclid web site (http://www.euclid-ec.org). In particular the Agenzia Spaziale Italiana, the Centre National dEtudes Spatiales, the Deutsches Zentrum für Luft- and Raumfahrt, the Danish Space Research Institute, the Fundação para a Ciênca e a Tecnologia, the Ministerio de Economia y Competitividad, the National Aeronautics and Space Administration, The Netherlandse Onderzoekschool Voor Astronomie, the Norvegian Space Center, the Romanian Space Agency, the State Secretariat for Education, Research and Innovation (SERI) at the Swiss Space Office (SSO), the United Kingdom Space Agency, and the University of Helsinki. R.C.N. acknowledges partial support from the UK Space Agency. D.S. acknowledges the Faculty of Technology of the University of Portsmouth for support during his PhD studies. C.I. and S.J.S. acknowledge funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement No. [291222]. C.I. and M.S. acknowledge support from EU/FP7-ERC grant No. [615929]. E.C. acknowledge financial contribution from the agreement ASI/INAF/I/023/12/0. The work by KJ and others at MPIA on NISP was supported by the Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR) under grant 50QE1202. M.B. and S.C. acknowledge financial contribution from the agreement ASI/INAF I/023/12/1. R.T. acknowledges funding from the Spanish Ministerio de Economía y Competitividad under the grant ESP2015-69020-C2-2-R. I.T. acknowledges support from Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013 and IF/01518/2014. J.R. was supported by JPL, which is run under a contract for NASA by Caltech and by NASA ROSES grant 12-EUCLID12-0004.

References

  1. Astier, P., Balland, C., Brescia, M., et al. 2014, A&A, 572, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Aubourg, É., Bailey, S., Bautista, J. E., et al. 2015, Phys. Rev. D, 92, 123516 [NASA ADS] [CrossRef] [Google Scholar]
  3. Berger, E., Chornock, R., Lunnan, R., et al. 2012, ApJ, 755, L29 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bernstein, J. P., Kessler, R., Kuhlmann, et al. 2012, ApJ, 753, 152 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bersten, M. C., Benvenuto, O. G., Orellana, M., & Nomoto, K. 2016, ApJ, 817, L8 [NASA ADS] [CrossRef] [Google Scholar]
  6. Berry, C. P. L., Mandel, I., Middleton, H., et al. 2015, ApJ, 804, 114 [NASA ADS] [CrossRef] [Google Scholar]
  7. Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bloom, J. S., Richards, J. W., Nugent, P. E., et al. 2012, PASP, 124, 1175 [NASA ADS] [CrossRef] [Google Scholar]
  10. Botticella, M. T., Riello, M., Cappellaro, E., et al. 2008, A&A, 479, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bouwens, R. J., Illingworth, G. D., Labbe, I., et al. 2011, Nature, 469, 504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Brescia, M., Cavuoti, S., Longo, G., et al. 2014, PASP, 126, 783 [Google Scholar]
  13. Campbell, H., D’Andrea, C. B., Nichol, R. C., et al. 2013, ApJ, 763, 88 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cappellaro, E., Evans, R., & Turatto, M. 1999, A&A, 351, 459 [NASA ADS] [Google Scholar]
  15. Chatzopoulos, E., Wheeler, J. C., Vinko, J., Horvath, Z. L., & Nagy, A. 2013, ApJ, 773, 76 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chen, T.-W., Smartt, S. J., Yates, R. M., et al. 2017a, MNRAS, 470, 3566 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chen, T.-W., Schady, P., Xiao, L., et al. 2017b, ApJ, 849, L4 [NASA ADS] [CrossRef] [Google Scholar]
  18. Chevallier, M., Polarski, D., 2001, Int. J. Mod. Phys. D, 10, 213 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cole, S., Norberg, P., Baugh, C. M., et al. 2001, MNRAS, 326, 255 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cooke, J., Sullivan, M., Gal-Yam, A., et al. 2012, Nature, 491, 228 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Cropper, M., Pottinger, S., Niemi, S.-M., et al. 2014, Proc. SPIE, 9143, 91430 [Google Scholar]
  22. De Cia, A., Gal-Yam, A., Rubin, A., et al. 2017, ApJ, submitted [arXiv:1708.01623] [Google Scholar]
  23. Dessart, L., Hillier, D. J., Waldman, R., Livne, E., & Blondin, S. 2012, MNRAS, 426, L76 [NASA ADS] [CrossRef] [Google Scholar]
  24. Dexter, J., & Kasen, D. 2013, ApJ, 772 [Google Scholar]
  25. D’Isanto, A., Cavuoti, S., Brescia, M., et al. 2016, MNRAS, 457, 3119 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dong, S., Shappee, B. J., Prieto, J. L., et al. 2016, Science, 351, 257 [NASA ADS] [CrossRef] [Google Scholar]
  27. Drout, M. R., Chornock, R., Soderberg, A. M., et al. 2014, ApJ, 794, 23 [Google Scholar]
  28. Gal-Yam, A. 2012, Science, 337, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Gal-Yam, A., Mazzali, P., Ofek, E. O., et al. 2009, Nature, 462, 624 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
  31. Goldhaber, G., Groom, D. E., Kimn, A., et al., 2001, ApJ, 558, 359 [NASA ADS] [CrossRef] [Google Scholar]
  32. Goldstein, D. A., D’Andrea, C. B., Fischer, J. A., et al. 2015, AJ, 150, 82 [NASA ADS] [CrossRef] [Google Scholar]
  33. Greiner, J., Mazzali, P. A., Kann, D. A., et al. 2015, Nature, 523, 189 [Google Scholar]
  34. Guetta, D., & Della Valle, M. 2007, ApJ, 657, L73 [NASA ADS] [CrossRef] [Google Scholar]
  35. Guy, J., Astier, P., Nobili, S., Regnault, N., & Pain, R. 2005, A&A, 443, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2438 [NASA ADS] [CrossRef] [Google Scholar]
  39. Heavens, A., Panter, B., Jimenez, R., & Dunlop, J. 2004, Nature, 428, 625 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  40. Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  41. Hounsell, R., Scolnic, D., Foley, R. J., et al. 2017, ArXiv e-prints [arXiv:1702.01747] [Google Scholar]
  42. Howell, D. A., Kasen, D., Lidman, C., et al. 2013, ApJ, 779, 98 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  44. Inserra, C., & Smartt, S. J. 2014, ApJ, 796, 87 [NASA ADS] [CrossRef] [Google Scholar]
  45. Inserra, C., Smartt, S. J., Jerkstrand, A., et al. 2013, ApJ, 770, 128 [NASA ADS] [CrossRef] [Google Scholar]
  46. Inserra, C., Bulla, M., Sim, S. A., & Smartt, S. J. 2016a, ApJ, 831, 79 [NASA ADS] [CrossRef] [Google Scholar]
  47. Inserra, C., Smartt, S. J., Gall, E. E. E., et al. 2016b, ApJ, submitted [arXiv:1604.01226] [Google Scholar]
  48. Inserra, C., Nicholl, M., Chen, T.-W., et al. 2017a, MNRAS, 468, 4642 [NASA ADS] [CrossRef] [Google Scholar]
  49. Inserra, C., Prajs, S., Gutierrez, C. P., et al. 2017b, ApJ, submitted [arXiv:1711.03787] [Google Scholar]
  50. Ivezic, Z., Tyson, J. A., Abel, B., et al. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
  51. Jerkstrand, A., Smartt, S. J., Inserra, C., et al. 2017, ApJ, 835, 13 [NASA ADS] [CrossRef] [Google Scholar]
  52. Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kann, D. A., Schady, P., Olivares E., F., et al. 2016, A&A, submitted [arXiv:1606.06791] [Google Scholar]
  54. Kasen, D., & Bildsten, L. 2010, ApJ, 717, 245 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kasen, D., Fernández, R., & Metzger, B. D. 2015, MNRAS, 450, 1777 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kelly, P. L., Rodney, S. A., Treu, T., et al. 2015, Science, 347, 1123 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kim, A., Goobar, A., & Perlmutter, S. 1996, PASP, 108, 190 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kozyreva, A., & Blinnikov, S. 2015, MNRAS, 454, 4357 [CrossRef] [Google Scholar]
  59. Kulkarni, S. R. 2012, New Horizons in Time-Domain Astronomy, eds. E. Griffin, R. Hanisch, & R. Seaman (Cambridge: Cambridge Univ. Press), IAU Symp., 285, 55 [Google Scholar]
  60. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
  61. Leloudas, G., Schulze, S., Krühler, T., et al. 2015, MNRAS, 449, 917 [NASA ADS] [CrossRef] [Google Scholar]
  62. Leloudas, G., Fraser, M., Stone, N. C., et al. 2016, Nat. Astron., 1, 0002 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lewis, A., Bridle, S., 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
  64. Li, W., Leaman, J., Chornock, R., et al. 2011, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
  65. LIGO Scientific Collaboration, Aasi, J., Abbott, B. P., et al. 2015, Class. Quant. Grav., 32, 074001 [CrossRef] [Google Scholar]
  66. LSST Science book, Abell, P. A., Allison J., Anderson S. F., et al. 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
  67. Lunnan, R., Chornock, R., Berger, E., et al. 2014, ApJ, 787, 138 [NASA ADS] [CrossRef] [Google Scholar]
  68. Lunnan, R., Chornock, R., Berger, E., et al. 2017, ApJ, submitted [arXiv:1708.01619] [Google Scholar]
  69. Mandel, K. S., Wood-Vasey, W. M., Friedman, A. S., & Kirshner, R. P. 2009, ApJ, 704, 629 [NASA ADS] [CrossRef] [Google Scholar]
  70. Mandel, K. S., Narayan, G., & Kirshner, R. P. 2011, ApJ, 731, 120 [NASA ADS] [CrossRef] [Google Scholar]
  71. Margutti, R., Metzger, B. D., Chornock, R., et al. 2017, ApJ, 836, 25 [NASA ADS] [CrossRef] [Google Scholar]
  72. Marra, V., Quartin, M., Amendola, L., 2013, Phys. Rev. D, 88, 063004 [CrossRef] [Google Scholar]
  73. Metzger, B. D., Bauswein, A., Goriely, S., & Kasen, D. 2015a, MNRAS, 446, 1115 [NASA ADS] [CrossRef] [Google Scholar]
  74. McCrum, M., Smartt, S. J., Rest, A., et al. 2015, MNRAS, 448, 1206 [NASA ADS] [CrossRef] [Google Scholar]
  75. Nicholl, M., Smartt, S. J., Jerkstrand, A., et al. 2013, Nature, 502, 346 [NASA ADS] [CrossRef] [Google Scholar]
  76. Nicholl, M., Smartt, S. J., Jerkstrand, A., et al. 2014, MNRAS, 444, 2096 [NASA ADS] [CrossRef] [Google Scholar]
  77. Nicholl, M., Smartt, S. J., Jerkstrand, A., et al. 2015, MNRAS, 452, 3869 [NASA ADS] [CrossRef] [Google Scholar]
  78. Nicholl, M., Berger, E., Smartt, S. J., et al. 2016, ApJ, 826, 39 [NASA ADS] [CrossRef] [Google Scholar]
  79. Pan, Y.-C., Foley, R. J., Smith, M., et al. 2017, MNRAS, 470, 4241 [Google Scholar]
  80. Papadopoulos, A., D’Andrea, C. B., Sullivan, M., et al. 2015, MNRAS, 449, 1215 [NASA ADS] [CrossRef] [Google Scholar]
  81. Pastorello, A., Smartt, S. J., Botticella, M. T., et al. 2010, ApJ, 724, L16 [NASA ADS] [CrossRef] [Google Scholar]
  82. Perley, D. A., Quimby, R., Yan, L., et al. 2016, ApJ, 830, 13 [NASA ADS] [CrossRef] [Google Scholar]
  83. Perlmutter, S., Gabi, S., Goldhaber, G., et al. 1997, ApJ, 483, 565 [NASA ADS] [CrossRef] [Google Scholar]
  84. Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
  85. Prajs, S., Sullivan, M., Smith, M., et al. 2017, MNRAS, 464, 3568 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pskovskii, I. P. 1977, Sov. Astron., 21, 675 [NASA ADS] [Google Scholar]
  87. Quimby, R. M., Kulkarni, S. R., Kasliwal, M. M., et al. 2011, Nature, 474, 487 [NASA ADS] [CrossRef] [Google Scholar]
  88. Quimby, R. M., Yuan, F., Akerlof, C., & Wheeler, J. C. 2013, MNRAS, 431, 912 [NASA ADS] [CrossRef] [Google Scholar]
  89. Riess, A. G., Press, W. H., & Kirshner, R. P. 1996, ApJ, 473, 88 [NASA ADS] [CrossRef] [Google Scholar]
  90. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  91. Rust, B. W. 1974, BAAS, 6, 309 [Google Scholar]
  92. Scovacricchi, D., Nichol, R. C., Bacon, D., Sullivan, M., & Prajs, S. 2016, MNRAS, 456, 1700 [CrossRef] [Google Scholar]
  93. Scovacricchi, D., Nichol, R. C., Macaulay, E., & Bacon, D. 2017, MNRAS, 465, 2862 [CrossRef] [Google Scholar]
  94. Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
  95. Smartt, S. J., Valenti, S., Fraser, M., et al. 2015, A&A, 579, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Smith, M., Sullivan, M., D’Andrea, C. B., et al. 2016, ApJ, 818, L8 [NASA ADS] [CrossRef] [Google Scholar]
  97. Smith, M., Sullivan, M., Nichol, R. C., et al. 2017, ApJ, submitted [Google Scholar]
  98. Solà, J., Gómez-Valent, A., & de Cruz Pérez, J. 2017, ApJ, 836, 43 [CrossRef] [Google Scholar]
  99. Strolger, L.-G., Dahlen, T., Rodney, S. A., et al. 2015, ApJ, 813, 93 [NASA ADS] [CrossRef] [Google Scholar]
  100. Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
  101. Tanaka, M., Moriya, T. J., Yoshida, N., & Nomoto, K. 2012, MNRAS, 422, 2675 [NASA ADS] [CrossRef] [Google Scholar]
  102. Tanaka, M., Moriya, T. J., & Yoshida, N. 2013, MNRAS, 435, 2483 [NASA ADS] [CrossRef] [Google Scholar]
  103. van Putten, M. H. P. M., & Della Valle, M. 2017, MNRAS, 464, 3219 [CrossRef] [Google Scholar]
  104. Vreeswijk, P. M., Ledoux, C., Raassen, A. J. J., et al. 2013, A&A, 549, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Vreeswijk, P. M., Savaglio, S., Gal-Yam, A., et al. 2014, ApJ, 797, 24 [NASA ADS] [CrossRef] [Google Scholar]
  106. Woosley, S. E. 2010, ApJ, 719, L204 [NASA ADS] [CrossRef] [Google Scholar]
  107. Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  108. Wright, D. E., Smartt, S. J., Smith, K. W., et al. 2015, MNRAS, 449, 451 [NASA ADS] [CrossRef] [Google Scholar]
  109. Yuan, F., Lidman, C., Davis, T. M., et al. 2015, MNRAS, 452, 3047 [NASA ADS] [CrossRef] [Google Scholar]
  110. Zhao, G.B., Raveri, M., Pogosian, L., et al. 2017, Nat. Astron., 1, 627 [CrossRef] [Google Scholar]
  111. Zieleniewski, S., Thatte, N., Kendrew, S., et al. 2015, MNRAS, 453, 3754 [CrossRef] [Google Scholar]

All Tables

Table 1

Sampling and coverage information of the three fields of the Euclid Deep Survey (EDS).

In the text
Table 2

Euclid filters specifications.

In the text
Table 3

Number of SLSNe-I per year for both samples (silver and gold) and with both rate models (see text).

In the text
Table 4

Our one-sigma predicted cosmological constraints for one parameter (ϵ = Δp/pfid) for various combinations of likely Euclid and DES samples and priors (see text for details).

In the text

All Figures

thumbnail Fig. 1

Summary of the EDS cadence over the five-year (1825 days) survey. Open symbols refer to the calibration epochs, which are ten per field excluding the Fornax field. Calibration epochs will have the same nominal depth of whole EDS. See Table 1 for further details.

In the text
thumbnail Fig. 2

Normalized filter transmission of VIS and Y, J, H (NISP).
In the text
thumbnail Fig. 3

Left: simulated observer-frame light-curve for a z = 2.0 SLSN-I in the four Euclid passbands. The horizontal (dashed) lines represent the assumed 5σ point source limiting magnitudes for each filter as discussed in the text. J and H limiting magnitudes are shifted of 0.05 and 0.10 mag to facilitate the reading. The cross symbols at the top of the panel represent a typical observing cadence for the southern EDS away from the six months gap (including two consecutive observations per passage that are not considered in the rate simulations), which would detect this SLSN four times in three bands. Similarly, the short lines at the top of the panel represent a typical observing cadence for the northern EDS, with four detections in three bands. Right: the same as the left panel but at z = 3.5. In this case both the southern and northern EDS would detect this SLSN three separate times (again excluding double observations within three days of each other). Observed phase is with respect to the observer frame J-band peak.
In the text
thumbnail Fig. 4

Number of SLSNe-I detected, per redshift bin (Δz = 0.5), during the five years of the EDS (combining both the northern and southern EDS observations). Gold stars denote the “gold sample” (three filter detections for each of three epochs, or 3e3f in legend), while the silver circles are the “silver sample” (two filter detections for each of three epochs, or 3e2f). The error bars are Poisson uncertainties based on the number of SLSNe-I in each bin (Gehrels 1986), while the rates assumed are for our optimistic model (see text). Both gold and silver points are offset of Δz = 0.05 to facilitate the reading.
In the text
thumbnail Fig. 5

Example of an observed spectrum with S ! N ~ 20, R ≃ 350 of a SLSN-I at various redshifts (0.5 <z< 2.5). The spectrum is that of iPTF13ajg at peak epoch (Vreeswijk et al. 2014) with a flux of ~ 10-16 erg s-1 cm-2 Å-1 at Y-band wavelength and at redshift z = 0.5, which should be feasible for the Euclid “blue” grism (see text). The cyan, yellow and red solid lines represent the wavelength regions covered by Euclid VIS, Y and J filters, respectively (we note that VIS and Y are superimposed for 600 Å). The blue region shows the Euclid “blue” grism covering 0.92 to 1.25 microns. The spectra at z> 0.5 show the potential of future facilities (e.g. JWST, E-ELT) and their use in identifying SN features, since they will go deeper and with a better resolution than the Euclid spectrograph.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.