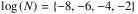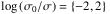| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731540 | |
| Published online | 02 February 2018 | |
Atmospheric thermal tides and planetary spin
I. The complex interplay between stratification and rotation
1 LAB, Université de Bordeaux, CNRS UMR 5804, Université de Bordeaux, Bât. B18N, Allée Geoffroy Saint-Hilaire CS50023, 33615 Pessac Cedex France
e-mail: pierre.auclair-desrotour@u-bordeaux.fr
2 Laboratoire AIM Paris-Saclay, CEA/DRF, CNRS, Université Paris Diderot, IRFU/DAp Centre de Saclay, 91191 Gif-sur-Yvette Cedex, France
e-mail: stephane.mathis@cea.fr
3 LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, UPMC Univ. Paris 6, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
4 IMCCE, Observatoire de Paris, CNRS UMR 8028, PSL Research University, 77 Avenue Denfert-Rochereau, 75014 Paris, France
e-mail: jacques.laskar@obspm.fr
Received: 10 July 2017
Accepted: 28 September 2017
Context. Thermal atmospheric tides can torque telluric planets away from spin-orbit synchronous rotation, as observed in the case of Venus. They thus participate in determining the possible climates and general circulations of the atmospheres of these planets.
Aims. The thermal tidal torque exerted on an atmosphere depends on its internal structure and rotation and on the tidal frequency. Particularly, it strongly varies with the convective stability of the entropy stratification. This dependence has to be characterized to constrain and predict the rotational properties of observed telluric exoplanets. Moreover, it is necessary to validate the approximations used in global modelings such as the traditional approximation, which is used to obtain separable solutions for tidal waves.
Methods. We wrote the equations governing the dynamics of thermal tides in a local vertically stratified section of a rotating planetary atmosphere by taking into account the effects of the complete Coriolis acceleration on tidal waves. This allowed us to analytically derive the tidal torque and the tidally dissipated energy, which we used to discuss the possible regimes of tidal dissipation and to examine the key role played by stratification.
Results. In agreement with early studies, we find that the frequency dependence of the thermal atmospheric tidal torque in the vicinity of synchronization can be approximated by a Maxwell model. This behavior corresponds to weakly stably stratified or convective fluid layers, as observed previously. A strong stable stratification allows gravity waves to propagate, and makes the tidal torque negligible. The transition is continuous between these two regimes. The traditional approximation appears to be valid in thin atmospheres and in regimes where the rotation frequency is dominated by the forcing or the buoyancy frequencies.
Conclusions. Depending on the stability of their atmospheres with respect to convection, observed exoplanets can be tidally driven toward synchronous or asynchronous final rotation rates. The domain of applicability of the traditional approximation is rigorously constrained by calculations.
Key words: hydrodynamics / waves / turbulence / planet-star interactions / planets and satellites: dynamical evolution and stability
© ESO, 2018
1. Introduction
The end of 2016 and the beginning of 2017 have been marked by the discovery of potentially habitable Earth-like exoplanets orbiting two stars that are located in the close neighborhood of the solar system. The first star is Proxima Centauri, where a planet with a minimum mass of 1.3 M⊕ has been detected; this is Proxima b (Anglada-Escudé et al. 2016; Ribas et al. 2016). The second star is the ultra-cool dwarf star Trappist-1, which hosts seven telluric planets of masses between 0.2 M⊕ and 2 M⊕ and radii between 0.7 R⊕ and 1.2 R⊕ (Gillon et al. 2017). Proxima b and Trappist-1 e, f, and g orbit in the habitable zone of their host stars. In addition, they are likely to be covered with an atmosphere like Earth, Venus, or Mars in the solar system. Their habitability is hence strongly constrained by their atmospheric dynamics (i.e., the general circulation and zonal winds), which plays a prominent role in the heat transport and determines their climate and surface temperature.
The atmosphere dynamics is tightly related to the rotational dynamics of planets. For instance, the general circulation of rapidly rotating planets such as Earth is driven by geostrophic flows, while planets close to spin-orbit synchronous rotation are subject to large-scale convective cells that transport heat from the dayside to the nightside (e.g., Leconte et al. 2013). It is thus of great importance to characterize the rotational evolution of the observed rocky exoplanets.
The exoplanets hosted by Trappist-1 are expected to be either tidally synchronized with the star or trapped in a higher-order spin-orbit resonance, since they are submitted to a strong tidal gravitational potential applied on their telluric core (Gillon et al. 2017). However, as noted by Ribas et al. (2016), who studied the rotation of Proxima b, the stellar irradiation can generate thermal atmospheric tides in addition to the standard gravitational tide. Thermal tides have been proved to be able to compensate for the solid tidal torque and to torque the planet away from synchronization. This is the case of Venus, which is maintained in a retrograde rotation state of equilibrium by the competition between solid and atmospheric tides (Gold & Soter 1969; Dobrovolskis & Ingersoll 1980; Correia & Laskar 2001, 2003; Auclair-Desrotour et al. 2017b).
Using a global ab initio modeling, we investigated the role played by the structure and properties of the atmosphere in response to a semidiurnal quadrupolar tidal forcing in a previous study (Auclair-Desrotour et al. 2017a). We showed in particular that stable stratification is able to modify the dependence of the atmospheric tidal torque on the tidal frequency. These results suggest that the Maxwell-like frequency dependence (so called in reference to the Maxwell model, see, e.g., Greenberg 2009; Correia et al. 2014) obtained by early works with parametrized models (Ingersoll & Dobrovolskis 1978; Correia & Laskar 2001) or general circulation models (GCMs; Leconte et al. 2015) corresponds to the tidal response of a neutrally stratified atmosphere with respect to convection. The results also show that a strongly stable stratification tends to annihilate the global tidal bulge by allowing gravity waves to propagate, so that the resulting atmospheric tidal torque becomes negligible. This has large repercussions on the final rotation rate of the planet. In the neutrally stratified case, an asynchronous rotation rate can be reached, while the solid tide dominates in the second case, leading the body to spin-orbit synchronization.
However, these tendencies were obtained by considering asymptotic cases (neutrally slowly rotating and isothermal stably stratified atmospheres), which set the details of the continuous variation of the tidal response with stratification aside. Moreover, the global model used to describe the dynamics of tidal waves in this early work is based upon an approximation on the hierarchy between rotation and stratification, the traditional approximation. It consists of neglecting the latitudinal projection of the rotation vector in the Coriolis acceleration, which allows us to separately integrate the vertical and horizontal structure of the tidal response. The traditional approximation is not valid for all configurations, and its domain of applicability is not clearly established (Gerkema & Zimmerman 2008; Tort & Dubos 2014). Some of the limitations of the traditional approximation have been identified in geophysical and astrophysical fluid dynamics (Gerkema & Shrira 2005). Particularly, the general case is fully 2D, and thus the coordinates cannot be separated (Mathis et al. 2014). Hence, the traditional approximation needs to be validated for thermal atmospheric tides. It is thus necessary to develop a tractable model enabling us to widely explore the possible stratifications and rotations without any approximation on the Coriolis acceleration. Such a model would also allow us to discuss the different tidal regimes, their consequences on the evolution of the rotation rate of a planet, and the possible bias resulting from approximations made in the global modeling.
Therefore, we propose in this study to characterize the behavior of the atmospheric tidal torque with respect to stratification in the framework of a 2D simplified local Cartesian modeling where the effect of rotation is fully taken into account. This approach is based on the early works by Gerkema & Shrira (2005),Mathis et al. (2014), and André et al. (2017), who examined the effect of stratification and rotation on waves propagating within planetary oceans, stars, and gaseous envelopes of giant planets. We generalize their formalism to treat the case of stratified atmospheres with vertically dependent hydrostatic equilibrium structures.
We introduce the physical setup of the local model in Sect. 2 and write the equations describing the dynamics of thermally generated tidal waves in a planetary fluid layer in Sect. 3. Then we derive in Sect. 4 the energy balance associated with a propagating tidal mode. In Sect. 5 analytic solutions are computed in the case of simplified atmospheric models, namely a homogeneous fluid with uniform background distributions and of an isothermal stably stratified atmosphere. In Sect. 6 these solutions are used to discuss the possible tidal regimes and the dependence of the atmospheric tidal torque on stratification in the non-traditional framework. We show that beyond a critical value of the Brunt-Väisälä frequency, this torque becomes negligible. We then illustrate the consequences of this behavior on the planet rotation by computing the evolution of this latter for various stratifications. We end this work with a study of the applicability of the traditional approximation in Sect. 7 that allows us to identify asymptotic regimes where it can be applied. Finally, we give our conclusions in Sect. 8.
2. Physical setup and background structure
Following Gerkema & Shrira (2005) and Mathis et al. (2014), we considered a local volume within a planetary atmospheric layer (Fig. 1). This volume is a Cartesian box of side L such that L ≪ R, R being the planet radius. It is rotating uniformly at the angular velocity Ω. We denote by Ω the corresponding spin vector. The position of the fluid box is located in the corotating frame attached to the body ℛE:{O,XE,YE,ZE}, such that ZE = Ω/ |Ω|, with the usual system of spherical coordinates (r,θ,ϕ), where r stands for the vertical coordinate, θ for the colatitude, and ϕ for the longitude. The associated vectorial basis is denoted 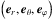 . To study the dynamics of tidal waves inside the box, we used the Cartesian coordinates x (west-east), y (south-north) and z (vertical, positive upward), and the associated basis
. To study the dynamics of tidal waves inside the box, we used the Cartesian coordinates x (west-east), y (south-north) and z (vertical, positive upward), and the associated basis 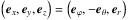 . Finally, the time is denoted t. For convenience, we used the same notations as Gerkema & Shrira (2005) for physical quantities whenever possible.
. Finally, the time is denoted t. For convenience, we used the same notations as Gerkema & Shrira (2005) for physical quantities whenever possible.
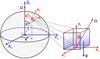 |
Fig. 1 Spherical and Cartesian reference frames and coordinate systems. The vectors Ω and g designate the rotation and the gravity, respectively. |
The structure of the layer is described by the background spatial distributions of gravity g, pressure p0, density ρ0 and temperature T0. To simplify the problem, we assumed that these quantities vary with the vertical coordinate (z) only. This corresponds to ignoring the effects of centrifugal distortion and the day-night variations of the atmosphere. We also introduce the pressure scale height of the fluid, 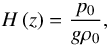 (1)and its Brunt-Väisälä frequency, that is, the frequency characterizing the stability of the vertical entropy stratification, defined as
(1)and its Brunt-Väisälä frequency, that is, the frequency characterizing the stability of the vertical entropy stratification, defined as![\begin{equation} N^2 \left( z \right) = g \left[ \frac{1}{\Gamma_1} \frac{{\rm d} \ln p_0}{{\rm d}z} - \frac{{\rm d} \ln \rho_0}{{\rm d}z} \right], \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq30.png) (2)where Γ1 stands for the first adiabatic exponent (e.g., Gerkema & Zimmerman 2008). We consider in the following that the fluid is a perfect gas, so that Γ1 = 1.4. As the atmosphere is assumed to be in solid rotation with the body, mean flows are ignored in this first paper. However, the internal dissipation due to radiative cooling is taken into account. In the Maxwell approximation mentioned above, the maximum amplitude of the atmospheric torque corresponds to equalizing the tidal period τtide and an effective thermal time associated with internal diffusive and radiative processes τ0 (Leconte et al. 2015; Auclair-Desrotour et al. 2017a). These processes can be described at first order by a Newtonian cooling as in Auclair-Desrotour et al. (2017a; see also Lindzen & McKenzie 1967; Dickinson & Geller 1968). This introduces a parameter for the efficiency of dissipation, the frequency σ0, which is the inverse of the local radiative time of the fluid. Like the other quantities, σ0 can vary along the vertical direction (see, for example, Pollack & Young 1975, for Venus); it was set to a constant value here for the sake of simplicity. The effect of a radiative time varying with altitude on the tidal perturbation has been studied in the framework of the classical theory of atmospheric tides (e.g., Dickinson & Geller 1968; Lindzen & McKenzie 1967).
(2)where Γ1 stands for the first adiabatic exponent (e.g., Gerkema & Zimmerman 2008). We consider in the following that the fluid is a perfect gas, so that Γ1 = 1.4. As the atmosphere is assumed to be in solid rotation with the body, mean flows are ignored in this first paper. However, the internal dissipation due to radiative cooling is taken into account. In the Maxwell approximation mentioned above, the maximum amplitude of the atmospheric torque corresponds to equalizing the tidal period τtide and an effective thermal time associated with internal diffusive and radiative processes τ0 (Leconte et al. 2015; Auclair-Desrotour et al. 2017a). These processes can be described at first order by a Newtonian cooling as in Auclair-Desrotour et al. (2017a; see also Lindzen & McKenzie 1967; Dickinson & Geller 1968). This introduces a parameter for the efficiency of dissipation, the frequency σ0, which is the inverse of the local radiative time of the fluid. Like the other quantities, σ0 can vary along the vertical direction (see, for example, Pollack & Young 1975, for Venus); it was set to a constant value here for the sake of simplicity. The effect of a radiative time varying with altitude on the tidal perturbation has been studied in the framework of the classical theory of atmospheric tides (e.g., Dickinson & Geller 1968; Lindzen & McKenzie 1967).
3. Tidal wave dynamics
The fluid is forced thermally by the perturber with the thermal power per unit mass J. The resulting perturbed quantities are the variations of pressure δp, density δρ, and the velocity field u = (u,v,w). To simplify the equations of dynamics, we used the reduced pressure variations p = δp/ρ0 and the buoyancy b = −gδρ/ρ0 instead of δp and δρ (see, e.g., Gerkema & Shrira 2005). The effect of rotation on the tidal perturbation is taken into account through the Coriolis acceleration. Hence, we introduce the Coriolis parameters f = 2Ωcosθ and 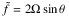 and assume them to be constant in the box, which is the so-called f-plane approximation. We note that f corresponds to the vertical projection of the rotation vector and
and assume them to be constant in the box, which is the so-called f-plane approximation. We note that f corresponds to the vertical projection of the rotation vector and  to its latitudinal component, which is responsible for the coupling of the latitudinal and vertical structures of tidal waves. To make the problem separable and tractable analytically within spherical geometry, it is necessary to assume the traditional approximation, that is, to ignore this term. Here, the simplified Cartesian geometry of the local modeling allows us to conserve the complete Coriolis acceleration that includes terms in
to its latitudinal component, which is responsible for the coupling of the latitudinal and vertical structures of tidal waves. To make the problem separable and tractable analytically within spherical geometry, it is necessary to assume the traditional approximation, that is, to ignore this term. Here, the simplified Cartesian geometry of the local modeling allows us to conserve the complete Coriolis acceleration that includes terms in 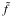 .
.
We assumed that asynchronous rotation rates are possible only in the vicinity of synchronous rotation, in range of forcing periods defined by τtide ~ τ0. This allowed us to ignore the effects of compressibility and to simplify calculations by applying the anelastic approximation (Spiegel & Veronis 1960). Thus, following Mathis et al. (2014), we neglect the contribution of acoustic waves. We note that compressibility can nevertheless contribute to the atmospheric tidal response in a non-negligible way in the regime of rapidly rotating bodies, where horizontally propagating acoustic waves can be generated, the so-called Lamb modes. Finally, we assumed the so-called Cowling approximation (Cowling 1941), which consists of ignoring the perturbation of the self-gravitational potential. The dynamics of the tidally forced fluid response is thus described by the following linearized Navier-Stokes equation 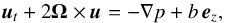 (3)the equation of mass conservation
(3)the equation of mass conservation 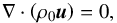 (4)and the equation of energy
(4)and the equation of energy 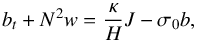 (5)where the subscript t denotes the partial derivative in time,
(5)where the subscript t denotes the partial derivative in time, 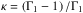 , and σ0b stands for the sink term associated with the Newtonian cooling. Because of the periodicity in time of the tidal forcing (thermal and gravitational), any perturbed quantity q can be expanded as a Fourier series of the form
, and σ0b stands for the sink term associated with the Newtonian cooling. Because of the periodicity in time of the tidal forcing (thermal and gravitational), any perturbed quantity q can be expanded as a Fourier series of the form 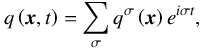 (6)the parameter σ being the tidal frequency of a component and qσ the Fourier coefficient of the expansion. In the following, the superscript σ is omitted in order to lighten expressions. By substituting Eq. (6) in Eqs. (3)–(5), we obtain the system of linearized primitive equations
(6)the parameter σ being the tidal frequency of a component and qσ the Fourier coefficient of the expansion. In the following, the superscript σ is omitted in order to lighten expressions. By substituting Eq. (6) in Eqs. (3)–(5), we obtain the system of linearized primitive equations 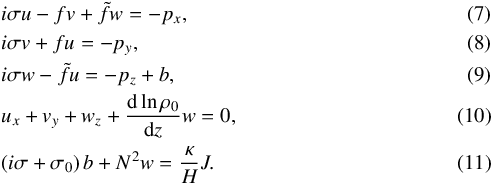 We note that the notations u, v, w, p, and b now refer to the spatial distributions of perturbed quantities.
We note that the notations u, v, w, p, and b now refer to the spatial distributions of perturbed quantities.
We consider waves propagating in the horizontal direction along the vector eα = cosαex + sinαey, α being the angle of the direction of propagation in the (ex,ey) plane. Hence, using the change of variable χ = xcosα + ysinα, the system of Eqs. (7)–(11) can be reduced to a single equation for w, 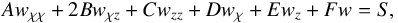 (12)where the subscripts χ and z refer to the horizontal and vertical derivatives, respectively. The coefficients associated with second-order derivatives are expressed as
(12)where the subscripts χ and z refer to the horizontal and vertical derivatives, respectively. The coefficients associated with second-order derivatives are expressed as 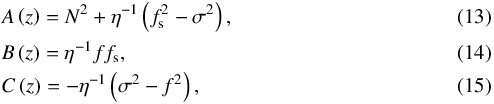 those associated with first-order derivatives as
those associated with first-order derivatives as 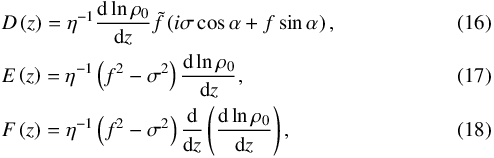 and the source term S due to the thermal forcing is written
and the source term S due to the thermal forcing is written 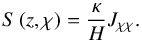 (19)In these expressions, we have introduced the modified Coriolis parameter of Gerkema & Shrira (2005),
(19)In these expressions, we have introduced the modified Coriolis parameter of Gerkema & Shrira (2005),  , and the function
, and the function 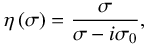 (20)which is such that η = 1 if the radiative cooling is ignored and 0 ≤ |η| < 1 otherwise. In the asymptotic regime dominated by the radiative cooling (|σ/σ0| → 0), η → 0. In the regime where thermal time is far greater than the tidal period (|σ/σ0| → + ∞), η → 1.
(20)which is such that η = 1 if the radiative cooling is ignored and 0 ≤ |η| < 1 otherwise. In the asymptotic regime dominated by the radiative cooling (|σ/σ0| → 0), η → 0. In the regime where thermal time is far greater than the tidal period (|σ/σ0| → + ∞), η → 1.
Hence, by setting σ0 = 0 and a uniform density profile (dlnρ0/ dz = 0), we eliminate terms associated with first-order derivatives and recover the equations given by Gerkema & Shrira (2005).
Following this early work, we seek 2D solutions expressed as ![\begin{equation} w \left( z , \chi \right) = \Psi \left( z \right) e^{i \left[ k_\perp \chi + \delta \left( z \right) \right]}, \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq86.png) (21)where k⊥ stands for the horizontal wavenumber, δ is the function defined as
(21)where k⊥ stands for the horizontal wavenumber, δ is the function defined as 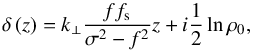 (22)and Ψ the solution of the Schrödinger-like vertical structure equation
(22)and Ψ the solution of the Schrödinger-like vertical structure equation 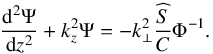 (23)In this equation,
(23)In this equation, 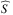 denotes the vertical profile of S resulting from the above separation of coordinates and kz the local vertical wavenumber of the mode, defined by
denotes the vertical profile of S resulting from the above separation of coordinates and kz the local vertical wavenumber of the mode, defined by ![\begin{equation} \begin{array}{lcl} k_z^2 &\!\! =\!\! & \displaystyle k_\perp^2 \left[ \frac{\eta N^2 - \sigma^2}{\sigma^2 - f^2} + \left( \frac{\sigma f_{\rm s}}{\sigma^2 - f^2} \right)^2 \right] \\[0.3cm] & & \displaystyle +\, \frac{{\rm d} \ln \rho_0}{{\rm d}z} \left( k_\perp \frac{\sigma \tilde{f} \cos \alpha}{\sigma^2 - f^2} - \frac{1}{4} \frac{{\rm d} \ln \rho_0}{{\rm d}z} \right) + \frac{1}{2} \frac{{\rm d}^2 \ln \rho_0}{{\rm d}z^2}, \end{array} \label{kz2} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq94.png) (24)while
(24)while 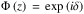 . We recognize in the first term of Eq. (24) the classical vertical wavenumber of gravito-inertial waves. Other terms are associated with the variation of background distributions. The polarization relations giving the vertical profiles of perturbed quantities as functions of Ψ and its first derivative are deduced straightforwardly from primitive equations. Denoting by
. We recognize in the first term of Eq. (24) the classical vertical wavenumber of gravito-inertial waves. Other terms are associated with the variation of background distributions. The polarization relations giving the vertical profiles of perturbed quantities as functions of Ψ and its first derivative are deduced straightforwardly from primitive equations. Denoting by 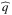 the vertical profile of a quantity q (such that
the vertical profile of a quantity q (such that 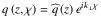 ), we thus obtain for the buoyancy,
), we thus obtain for the buoyancy, ![\begin{equation} \pv{b} \left( z \right) = - \frac{i}{\sigma - i \sigma_0} \left[ \frac{\kappa}{H} \pv{J} - N^2 \Phi \Psi \right], \label{bz} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq99.png) (25)for the pressure,
(25)for the pressure, ![\begin{equation} \pv{p} \left( z \right) = i \frac{f^2 - \sigma^2}{\sigma k_\perp^2} \Phi \left[ \frac{{\rm d} \Psi}{{\rm d}z} + \left( \frac{1}{2} \frac{{\rm d} \ln \rho_0}{{\rm d}z} + \mathcal{A} \right) \Psi \right], \label{pz} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq100.png) (26)and for the components of the velocity field,
(26)and for the components of the velocity field, ![\begin{eqnarray} \label{uz} && \pv{u} \left( z \right) = \frac{i \sigma \cos \alpha + f \sin \alpha}{\sigma k_\perp} \Phi \left[ \frac{{\rm d} \Psi}{{\rm d}z} + \left( \frac{1}{2} \frac{{\rm d} \ln \rho_0}{{\rm d}z} + \mathcal{B} \right) \Psi \right], \\[0.3cm] \label{vz} && \pv{v} \left( z \right) = - \frac{f \cos \alpha - i \sigma \sin \alpha}{\sigma k_\perp} \Phi \left[ \frac{{\rm d} \Psi}{{\rm d}z} + \left( \frac{1}{2} \frac{{\rm d} \ln \rho_0}{{\rm d}z} + \mathcal{C} \right) \Psi \right], \\[0.3cm] \label{wz} && \pv{w} \left( z \right) = \Phi \Psi,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq101.png) with the coefficients
with the coefficients ![\begin{eqnarray} && \mathcal{A} = - k_\perp \frac{\sigma \tilde{f} \cos \alpha}{\sigma^2 - f^2}, \\ && \mathcal{B} = i k_\perp f_{\rm s} \left[ \frac{f}{\sigma^2 - f^2} + \frac{\sin \alpha}{i \sigma \cos \alpha + f \sin \alpha} \right], \\ && \mathcal{C} = i k_\perp f_{\rm s} \left[ \frac{f}{\sigma^2 - f^2} + \frac{\cos \alpha}{f \cos \alpha - i \sigma \sin \alpha} \right]\cdot \end{eqnarray}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq102.png)
4. Energy balance
The vertical profiles of the perturbed quantities being established in Eqs. (25)–(29), we can compute the energy balance and torque associated with the atmospheric tide. The equation for the energy is obtained by multiplying the momentum equation Eq. (3) by u and the equation of buoyancy Eq. (5) by b. We obtain 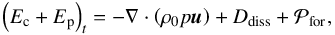 (33)where we have introduced the kinetic energy per unit volume,
(33)where we have introduced the kinetic energy per unit volume, 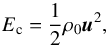 (34)the potential energy per unit volume associated with stratification,
(34)the potential energy per unit volume associated with stratification, 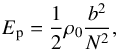 (35)the power dissipated per unit volume by the radiative cooling,
(35)the power dissipated per unit volume by the radiative cooling, 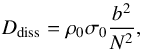 (36)and the power injected per unit volume by the thermal tidal forcing,
(36)and the power injected per unit volume by the thermal tidal forcing, 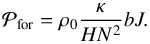 (37)Averaged over time, these quantities become
(37)Averaged over time, these quantities become ![\begin{equation} \begin{array}{ll} \displaystyle E_{\rm c} = \frac{1}{2} \rho_0 \langle \vec{u}^2 \rangle_t, & \displaystyle E_{\rm p} = \frac{1}{2} \frac{\rho_0}{N^2} \langle b^2 \rangle_t, \\[0.3cm] \displaystyle D_{\rm diss} = \frac{\rho_0 \sigma_0}{N^2} \langle b^2 \rangle_t , & \displaystyle \mathcal{P}_{\rm for} = \rho_0 \frac{\kappa}{H N^2} \langle b J \rangle_t, \end{array} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq110.png) (38)where ⟨ ... ⟩ t is the average in time. Finally, we use the identity
(38)where ⟨ ... ⟩ t is the average in time. Finally, we use the identity 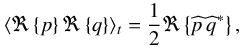 (39)the notations ℜ and ∗ referring to the real part and conjugate of a complex number, respectively. We obtain
(39)the notations ℜ and ∗ referring to the real part and conjugate of a complex number, respectively. We obtain ![\begin{equation} \begin{array}{ll} \displaystyle E_{\rm c} = \frac{1}{4} \rho_0 \left| \pv{\vec{u}} \right|^2, & \displaystyle E_{\rm p} = \frac{1}{4} \frac{\rho_0}{N^2} \left| \pv{b} \right|^2, \\[0.3cm] \displaystyle D_{\rm diss} = \frac{1}{2} \frac{\rho_0 \sigma_0}{N^2} \left| \pv{b} \right|^2 , & \displaystyle \mathcal{P}_{\rm for} = \frac{1}{2} \frac{\rho_0 \kappa}{H N^2} \Re \left\{ \pv{b} \pv{J}^* \right\}. \end{array} \label{energyz} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq115.png) (40)We recall that in these expressions,
(40)We recall that in these expressions, 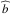 and
and 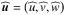 designate the vertical profiles of the complex perturbed quantities that are given by Eqs. (25)–(29).
designate the vertical profiles of the complex perturbed quantities that are given by Eqs. (25)–(29).
Similarly, the tidal torque exerted by the star on the fluid layer with respect to the spin axis of the planet is defined by 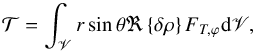 (41)where FT;ϕ is the latitudinal component of the tidal force, ϕ is the longitudinal coordinate, and V is the volume of the fluid shell. This expression can be written as a function of the tidal potential generating the tidal force U, which is such that F = ∇U, and becomes (e.g., Zahn 1966; Auclair-Desrotour et al. 2017a)
(41)where FT;ϕ is the latitudinal component of the tidal force, ϕ is the longitudinal coordinate, and V is the volume of the fluid shell. This expression can be written as a function of the tidal potential generating the tidal force U, which is such that F = ∇U, and becomes (e.g., Zahn 1966; Auclair-Desrotour et al. 2017a) 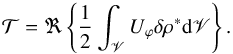 (42)One can note that δρ has two components: the adiabatic component ℜ{δρ}, which is in phase with the tidal potential and does not contribute to the tidal torque, and the dissipative component delayed with respect to the forcing, ℑ{δρ}, the notation ℑ referring to the imaginary part of a complex number. Hence, the equivalent local tidal torque exerted on the fluid box scales as
(42)One can note that δρ has two components: the adiabatic component ℜ{δρ}, which is in phase with the tidal potential and does not contribute to the tidal torque, and the dissipative component delayed with respect to the forcing, ℑ{δρ}, the notation ℑ referring to the imaginary part of a complex number. Hence, the equivalent local tidal torque exerted on the fluid box scales as 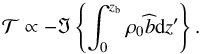 (43)
(43)
5. Simplified atmospheric models
The above equations are formulated in the general case, for any background distribution. In order to analytically explore the parameter domain, we compute in this section analytic solutions of the thermal tide in two simplified cases: in a homogeneous fluid with uniform background distributions, and in an isothermal stably stratified gas. In both cases, we consider a uniform profile of thermal forcing (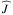 is now a constant) for the sake of simplicity, as done before in the global model (Auclair-Desrotour et al. 2017a). Such a profile physically corresponds to an optically thin atmosphere homogeneous in composition, where the stellar incoming flux is absorbed over the whole depth of the fluid layer. It can also be seen in the general case as a zero-order approximation of the effective energy input per unit mass generating the thermal tide. Assuming
is now a constant) for the sake of simplicity, as done before in the global model (Auclair-Desrotour et al. 2017a). Such a profile physically corresponds to an optically thin atmosphere homogeneous in composition, where the stellar incoming flux is absorbed over the whole depth of the fluid layer. It can also be seen in the general case as a zero-order approximation of the effective energy input per unit mass generating the thermal tide. Assuming 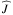 to be constant allows us to reduce the right-hand side of the vertical structure equation (Eq. (23)) to a simple exponential function of the altitude.
to be constant allows us to reduce the right-hand side of the vertical structure equation (Eq. (23)) to a simple exponential function of the altitude.
5.1. In a homogeneous fluid
The simplest case is that of uniform background distributions, which corresponds to the case studied by Gerkema & Shrira (2005). We assume that ρ0, H, and σ0 do not vary with the altitude. As a consequence, the vertical structure equation reduces to ![\begin{equation} \frac{{\rm d}^2 \Psi}{{\rm d}z^2} + k_\perp^2 \left[ \frac{\eta N^2 - \sigma^2}{\sigma^2 - f^2} + \left( \frac{\sigma f_{\rm s} }{\sigma^2 - f^2} \right)^2 \right] \Psi = \frac{k_\perp^2 \kappa \eta \pv{J}}{H \left( \sigma^2 - f^2 \right)} e^{- i \delta_{\rm c} z}, \label{vertical_hom} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq131.png) (44)with
(44)with 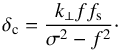 (45)Solving Eq. (44) requires us to choose two boundary conditions. As the guideline of this work is to characterize the atmospheric tidal response of a terrestrial planet, we use an impenetrable rigid-wall condition at z = 0, that is, Ψ = 0. For the upper boundary, following Shen & Zhang (1990), we assume that there is no material escape at the top of the atmosphere. Thus, the obtained solution shall not diverge at z = + ∞. This amounts to eliminating the diverging term of the solution,
(45)Solving Eq. (44) requires us to choose two boundary conditions. As the guideline of this work is to characterize the atmospheric tidal response of a terrestrial planet, we use an impenetrable rigid-wall condition at z = 0, that is, Ψ = 0. For the upper boundary, following Shen & Zhang (1990), we assume that there is no material escape at the top of the atmosphere. Thus, the obtained solution shall not diverge at z = + ∞. This amounts to eliminating the diverging term of the solution, 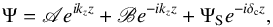 (46)where ΨS is the amplitude of the particular solution, and A and B are integration constants. With the convention ℑ{kz} > 0, it follows that
(46)where ΨS is the amplitude of the particular solution, and A and B are integration constants. With the convention ℑ{kz} > 0, it follows that 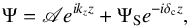 (47)at the upper boundary. Thus, denoting by ν the dimensionless complex factor expressed as
(47)at the upper boundary. Thus, denoting by ν the dimensionless complex factor expressed as 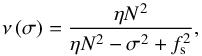 (48)we obtain the solution
(48)we obtain the solution 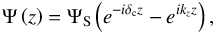 (49)where the constant ΨS is written
(49)where the constant ΨS is written 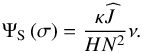 (50)We note that the case ν = 0 corresponds to a neutral stratification (see Eq. (48) with N2 = 0). In this case,
(50)We note that the case ν = 0 corresponds to a neutral stratification (see Eq. (48) with N2 = 0). In this case, ![\hbox{$ \Psi_{\rm S} = \kappa \pv{J}/\left[ H \left( f_{\rm s}^2 - \sigma^2 \right) \right] $}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq148.png) . We then substitute Eq. (49) in Eqs. (25)–(29) and introduce the parameters
. We then substitute Eq. (49) in Eqs. (25)–(29) and introduce the parameters 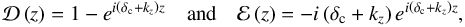 (51)to obtain the vertical profiles of the tidal fluctuation of buoyancy
(51)to obtain the vertical profiles of the tidal fluctuation of buoyancy 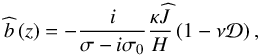 (52)pressure
(52)pressure ![\begin{equation} \pv{p} \left( z \right) = i \frac{f^2 - \sigma^2}{\sigma k_\perp^2} \Psi_{\rm S} \left[ \mathcal{E} + k_\perp \tilde{f} \frac{\sigma \cos \alpha + i f \sin \alpha}{f^2 - \sigma^2} \mathcal{D} \right], \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq151.png) (53)and velocity field
(53)and velocity field ![\begin{eqnarray} && \pv{u} \left (z \right) = i \frac{\cos \alpha}{k_\perp} \Psi_{\rm S} \left[ \mathcal{E} + i k_\perp \frac{\tilde{f} \sin^2 \alpha}{i \sigma \cos \alpha + f \sin \alpha} \mathcal{D} \right], \\ && \pv{v} \left( z \right) = - \frac{f \cos \alpha - i \sigma \sin \alpha}{\sigma k_\perp} \Psi_{\rm S} \left[ \mathcal{E} + i k_\perp \frac{\tilde{f} \sin \alpha \cos \alpha}{f \cos \alpha - i \sigma \sin \alpha} \mathcal{D} \right], \\ && \pv{w} \left( z \right) = \Psi_{\rm S} \mathcal{D} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq152.png) Finally, denoting zb the altitude of the upper boundary and substituting Eq. (52) into Eqs. (40) and (43), we obtain the total averaged dissipated energy per unit area of the
Finally, denoting zb the altitude of the upper boundary and substituting Eq. (52) into Eqs. (40) and (43), we obtain the total averaged dissipated energy per unit area of the 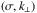 -mode in the fluid Cartesian box,
-mode in the fluid Cartesian box, 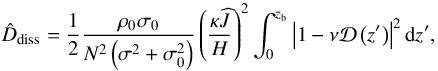 (57)and the dimensionless tidal torque
(57)and the dimensionless tidal torque 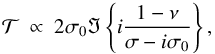 (58)which is normalized so that
(58)which is normalized so that 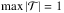 when ν = 0.
when ν = 0.
5.2. In an isothermal atmosphere
The isothermal approximation is the zero-order approximation of the atmospheric structure of terrestrial planets such as Earth. It is also the simplest structure allowing us to examine the repercussions of the variations of background distributions on the tidal response. An isothermal atmosphere is characterized by exponentially decaying density and pressure distributions and a uniform pressure height-scale depending on the temperature. Hence, ρ0 is now given by 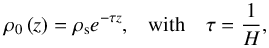 (59)the notations ρs and τ designating the density at the surface of the solid part of the planet and the vertical decaying rate, respectively. Since the density profile follows an exponential law, dlnρ0/ dz = −τ. Therefore, noting that N2 does not vary with the altitude either, we obtain for the vertical structure of tidal waves an equation of the same form as Eq. (44),
(59)the notations ρs and τ designating the density at the surface of the solid part of the planet and the vertical decaying rate, respectively. Since the density profile follows an exponential law, dlnρ0/ dz = −τ. Therefore, noting that N2 does not vary with the altitude either, we obtain for the vertical structure of tidal waves an equation of the same form as Eq. (44), 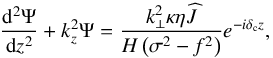 (60)with in this case
(60)with in this case 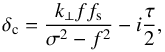 (61)and
(61)and ![\begin{equation} k_z^2 = k_\perp^2 \left[ \frac{\eta N^2 - \sigma^2}{\sigma^2 - f^2} + \left( \frac{\sigma f_{\rm s}}{\sigma^2 - f^2} \right)^2 \right] - \tau k_\perp \frac{\sigma \tilde{f} \cos \alpha}{\sigma^2 - f^2} + \frac{\tau^2}{4}\cdot \label{kz2_iso} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq165.png) (62)Hence, by applying the same boundary conditions as in the previous case, we obtain an analytic solution, which is written similarly as Eq. (49). The parameter ν alone is modified and is written
(62)Hence, by applying the same boundary conditions as in the previous case, we obtain an analytic solution, which is written similarly as Eq. (49). The parameter ν alone is modified and is written 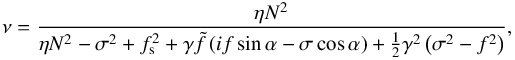 (63)where the parameter γ is defined as
(63)where the parameter γ is defined as 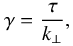 (64)and compares the horizontal wavelength of the mode to the typical scale height of the background vertical distributions. The vertical profiles of perturbed quantities derived from this solution are written for the buoyancy
(64)and compares the horizontal wavelength of the mode to the typical scale height of the background vertical distributions. The vertical profiles of perturbed quantities derived from this solution are written for the buoyancy 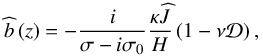 (65)for the pressure
(65)for the pressure ![\begin{equation} \pv{p} \left( z \right) = i \frac{f^2 - \sigma^2}{\sigma k_\perp^2} \Psi_{\rm S} \left[ \mathcal{E} + \left( k_\perp \tilde{f} \frac{\sigma \cos \alpha + i f \sin \alpha}{f^2 - \sigma^2} - \tau \right) \mathcal{D} \right], \label{pressure_iso} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq170.png) (66)and for the velocity field
(66)and for the velocity field ![\begin{eqnarray} \pv{u} \left (z \right) &= & \, i \frac{\cos \alpha}{k_\perp} \Psi_{\rm S} \left[ \mathcal{E} + \left( i k_\perp \frac{\tilde{f} \sin^2 \alpha}{i \sigma \cos \alpha + f \sin \alpha} - \tau \right) \mathcal{D} \right], \\[0.3cm] \pv{v} \left( z \right) &= & - \frac{f \cos \alpha - i \sigma \sin \alpha}{\sigma k_\perp} \Psi_{\rm S} \left[ \mathcal{E} \phantom{\frac{ i k_\perp \tilde{f} \sin \alpha \cos \alpha}{f \cos \alpha - i \sigma \sin \alpha}} \right. \\ && \left. + \left( \frac{ i k_\perp \tilde{f} \sin \alpha \cos \alpha}{f \cos \alpha - i \sigma \sin \alpha}- \tau \right) \mathcal{D} \right], \nonumber \\[0.3cm] \pv{w} \left( z \right)& = & \, \Psi_{\rm S} \mathcal{D} . \end{eqnarray}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq171.png) In these expressions, the parameters
In these expressions, the parameters 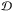 and ℰ are those defined by Eq. (51). Basically, we note that we recover all of the results of the previous case by setting τ = 0 since a uniform density distribution is just the asymptotic limit of an exponentially decaying one with H → + ∞. We finally compute the energy dissipated per unit surface by the radiative cooling in the fluid section
and ℰ are those defined by Eq. (51). Basically, we note that we recover all of the results of the previous case by setting τ = 0 since a uniform density distribution is just the asymptotic limit of an exponentially decaying one with H → + ∞. We finally compute the energy dissipated per unit surface by the radiative cooling in the fluid section 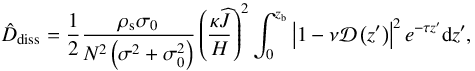 (70)and of the normalized dimensionless tidal torque,
(70)and of the normalized dimensionless tidal torque, 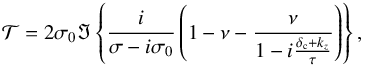 (71)which is obtained in a similar way as Eq. (58) and is such that
(71)which is obtained in a similar way as Eq. (58) and is such that 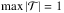 when ν = 0. As noted for other quantities, we easily verify that these two expressions simplify into those obtained in the case of uniform background distributions, that is, Eqs. (57) and (58), respectively, when τ → 0.
when ν = 0. As noted for other quantities, we easily verify that these two expressions simplify into those obtained in the case of uniform background distributions, that is, Eqs. (57) and (58), respectively, when τ → 0.
6. Tidal regimes and their implications on the rotational dynamics of terrestrial planets
In this section, we use the results derived in the framework of our Cartesian model to explore the domain of parameters and understand the behavior of the atmospheric tidal response predicted by the much more complex previous global modelings (Auclair-Desrotour et al. 2017a; Leconte et al. 2015). Particularly, we examine the tidal torque exerted on the atmosphere, which contributes to the evolution of the rotation rate of the planet with the torque resulting from the tidal elongation and the viscous friction of the solid core. In the vicinity of synchronization, the atmospheric and solid tidal torques can balance each other, the first torquing the planet away from synchronous rotation and the second toward it. This can explain the locking of the planet Venus at the observed asynchonous retrograde rotation rate (Gold & Soter 1969; Ingersoll & Dobrovolskis 1978; Dobrovolskis & Ingersoll 1980; Correia & Laskar 2001, 2003).
If the tidal response of the atmosphere is reduced to its non-wavelike part1 (Ogilvie 2013), which is associated with a quadrupolar bulge, the atmospheric tidal torque can be approximated with a Maxwell rheology characterized by the effective radiative frequency of the atmosphere (Ingersoll & Dobrovolskis 1978; Leconte et al. 2015; Auclair-Desrotour et al. 2017a,b), that is, 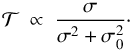 (72)However, Auclair-Desrotour et al. (2017a) pointed out that stable stratification is able to annihilate the tidal torque due to the thermal non-wavelike tide in the vicinity of synchronization because it induces a wavelike tide composed of gravity waves. As a consequence, the planet would be led in this case toward synchronous rotation by the solid tide. To study this effect, the global modeling used in this early study should be completed for two reasons. First, it describes the tidal atmospheric response in a spherical geometry. This tends to dilute the physics into mathematical aspects. Second, it is based upon the traditional approximation, and can be affected by the bias induced by this hypothesis, which we study in the next section. Typically, when 2Ω ≳ N, the traditional approximation can lead us to overestimate the amplitude of the tidal torque, as discussed by Ogilvie & Lin (2004). These authors show that the static approximation, in which the effect of rotation is ignored, is better in this case. Following them, we used this last approximation instead of the traditional approximation to establish the Maxwell law in the global model (Auclair-Desrotour et al. 2017a).
(72)However, Auclair-Desrotour et al. (2017a) pointed out that stable stratification is able to annihilate the tidal torque due to the thermal non-wavelike tide in the vicinity of synchronization because it induces a wavelike tide composed of gravity waves. As a consequence, the planet would be led in this case toward synchronous rotation by the solid tide. To study this effect, the global modeling used in this early study should be completed for two reasons. First, it describes the tidal atmospheric response in a spherical geometry. This tends to dilute the physics into mathematical aspects. Second, it is based upon the traditional approximation, and can be affected by the bias induced by this hypothesis, which we study in the next section. Typically, when 2Ω ≳ N, the traditional approximation can lead us to overestimate the amplitude of the tidal torque, as discussed by Ogilvie & Lin (2004). These authors show that the static approximation, in which the effect of rotation is ignored, is better in this case. Following them, we used this last approximation instead of the traditional approximation to establish the Maxwell law in the global model (Auclair-Desrotour et al. 2017a).
Hence, the local Cartesian modeling developed in the present study allows us to explore the full domain of parameters in rotation and stratification, including taking into account the complete Coriolis acceleration, filtering out complexities due to the spherical geometry, but keeping the key physical ingredients.
Considering the expressions of ν in the two cases treated in the previous section, Eqs. (48) and (63), we recover the asymptotic regimes observed with global modelings. On the one hand, in the convective atmosphere limit (i.e., N2 → 0), ν → 0. The expressions of the tidal torque given by Eqs. (58) and (71) both reduce to Eq. (72), that is, a Maxwell law. On the other hand, in the stably stratified atmosphere limit (N2 → + ∞), ν → 1. Thus, the torque obtained in the case of a uniform background readily tends to zero. The case of the isothermal atmosphere is slightly more complex because we have to take the dependence of the vertical wavelengths of tidal gravito-inertial waves on the tidal frequency into account. Equation (62) shows that 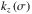 diverges in the vicinity of spin-orbit synchronization (σ = 0), namely kz ∝ |σ2−f2|− 1/2 if |σ| ≫ σ0, and
diverges in the vicinity of spin-orbit synchronization (σ = 0), namely kz ∝ |σ2−f2|− 1/2 if |σ| ≫ σ0, and 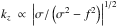 otherwise. As a consequence, |kz/τ| ≫ 1 and the third term associated with the propagation of gravito-inertial waves in Eq. (71) becomes negligible. We identify here how the tidal torque is flattened by the stable stratification. This behavior corresponds to the equilibrium thermal tide of a stably stratified fluid region studied by Arras & Socrates (2010) in the case of fluid extrasolar planets. As demonstrated analytically by Arras & Socrates (2010), the N2ξr/g term of the heat transport equation tends to equalize the heat source term (J) in the equation of energy (Eq. (5)) while σ → 0. This means that the local density decreases generated by the thermal forcing are exactly cancelled by the vertical displacement of denser fluid brought up from below.
otherwise. As a consequence, |kz/τ| ≫ 1 and the third term associated with the propagation of gravito-inertial waves in Eq. (71) becomes negligible. We identify here how the tidal torque is flattened by the stable stratification. This behavior corresponds to the equilibrium thermal tide of a stably stratified fluid region studied by Arras & Socrates (2010) in the case of fluid extrasolar planets. As demonstrated analytically by Arras & Socrates (2010), the N2ξr/g term of the heat transport equation tends to equalize the heat source term (J) in the equation of energy (Eq. (5)) while σ → 0. This means that the local density decreases generated by the thermal forcing are exactly cancelled by the vertical displacement of denser fluid brought up from below.
 |
Fig. 2 Normalized tidal torque as a function of the frequency of the perturber ω = (Ω−norb) /norb for various values of the Brunt-Väisälä frequency from weak to strongly stable stratification, i.e., |
This behavior is illustrated by Figs. 2 and 3, where the case of the stellar semidiurnal thermal tide is examined. The planet is assumed to orbit its host star circularly at the orbital frequency norb, and its equatorial plane is coplanar with the orbital plane, so that the perturbation reduces to the quadrupolar tidal forcing of frequency σ = 2(Ω−norb). We set for the studied mode k⊥ = 2π/λ, with the wavelength λ = 1000 km, so that γ = τ/k⊥ ≫ 1 (asymptotic regime of long wavelengths). The tidal torque is plotted as a function of the normalized apparent orbital frequency of the star in the reference frame in corotation with the planet, namely the normalized tidal frequency ω = (Ω−norb) /norb, for different values of the Brunt-Väisälä frequency from the convective isentropic limit (N = 10-8 s-1) to strongly stable stratification (N = 10-2 s-1). These boundaries are chosen in such way that N ≪ {2Ω,σ,σ0} in the first asymptotic regime and N ≫ {2Ω,σ,σ0} in the other. We recover in the first case (red curve) the Maxwell-like tidal response predicted by early studies (Ingersoll & Dobrovolskis 1978; Correia & Laskar 2001; Auclair-Desrotour et al. 2017a), and in the second (violet curve) the weak torque obtained with the ab initio modeling of Auclair-Desrotour et al. (2017a) that takes tidal gravity waves into account.
Several resonances can be observed in the transition regime. They result directly from the equality of characteristic frequencies of the system (N2, σ, 2Ω), which occurs in the denominator of the parameter ν. They are related to the local nature of the model since their positions depend on the colatitude, and consequently do not exist in the global tidal response, where the tidal equation is integrated over the sphere (Auclair-Desrotour et al. 2017a). However, we have to characterize them here to clarify the tidal torque frequency spectra observed in Fig. 2.
 |
Fig. 3 Normalized tidal torque (left panel) and imaginary part of the surface pressure oscillation (right panel) as functions of the normalized tidal frequency ω = (Ω−norb) /norb (horizontal axis) and Brunt-Väisälä frequency in logarithmic scale (vertical axis). The tidal torque and pressure variations are computed using the functions given by Eqs. (71) and (66), respectively. The torque is normalized by its maximum value in the asymptotic regime of neutral stratification. The imaginary part of pressure oscillations is normalized by its maxima in absolute value. We consider the case of a Venus-like planet with the following set of values: norb = 1.991 × 10-7 s-1, Γ1 = 1.4 (perfect gas), H = 15.9 km, θ = π/ 3, α = 0 (westward propagating wave), σ0 = 7.5 × 10-7 s-1 (Leconte et al. 2015), and k⊥ = 2π/λ with λ = 1000 km. The frequencies ω− and ω+ are the resonant frequencies identified in Sect. 6 (see Eq. (76)). |
In the regime of long wavelengths (γ ≫ 1), the denominator of Eq. (63) can be approximated by 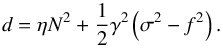 (73)We assume σ0 ≲ σ, which corresponds to the quasi-adiabatic regime (Press 1981; Auclair Desrotour et al. 2015), and substitute σ = 2(Ω−norb) in Eq. (73). Resonances thus correspond to the zeros of the polynomial
(73)We assume σ0 ≲ σ, which corresponds to the quasi-adiabatic regime (Press 1981; Auclair Desrotour et al. 2015), and substitute σ = 2(Ω−norb) in Eq. (73). Resonances thus correspond to the zeros of the polynomial 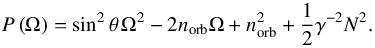 (74)We obtain the roots
(74)We obtain the roots ![\begin{equation} \Omega_{\pm} = \frac{1}{\sin^2 \theta} \left[ n_{\rm orb} \pm \sqrt{n_{\rm orb}^2 \cos^2 \theta - \frac{1}{2} \gamma^{-2} N^2 \sin^2 \theta } \right], \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq219.png) (75)which, expressed in the normalized tidal frequency ω = (Ω−norb) /norb used in Fig. 2, become
(75)which, expressed in the normalized tidal frequency ω = (Ω−norb) /norb used in Fig. 2, become ![\begin{equation} \omega_{\pm} = \frac{\cos \theta}{\sin^2 \theta} \left[ \cos \theta \pm \sqrt{ 1 - \frac{1}{2} \gamma^{-2} \left( \frac{N}{n_{\rm orb}} \right)^2 \tan^2 \theta } \right]. \label{omegapm} \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq220.png) (76)In the limit N2 → 0, they tend to ω− = tan-2θ−1 and ω+ = sin-2θ. As a consequence, ω− = −1 and ω+ = + ∞ at the poles.
(76)In the limit N2 → 0, they tend to ω− = tan-2θ−1 and ω+ = sin-2θ. As a consequence, ω− = −1 and ω+ = + ∞ at the poles.
These features are represented in the right panel of Fig. 3, where the tidal torque is plotted as a function of the tidal frequency (ω) and Brunt-Väisälä frequency in logarithmic scale. Black vertical dashed lines indicate the positions of resonances, while the horizontal dashed line designates the transition between the flat and Maxwell-like regimes for the tidal torque identified above, which corresponds to N ~ {γσ,γf}. For the evolution of planetary systems, this means that rocky planets with an atmospheric Brunt-Väisälä frequency below this critical value are likely to tend toward non-synchronized rotation states of equilibrium, like Venus, while those beyond it will be led toward spin-orbit synchronization, in good agreement with predictions obtained in Auclair-Desrotour et al. (2017a; Sect. 6.3).
In the right panel of Fig. 3, the imaginary part of the surface pressure oscillation is plotted as a function of ω and N. This plot shows that we retrieve the asymptotic behaviors identified for the tidal torque in surface pressure oscillations. In a weakly stratified atmosphere, a net tidal bulge appears, leading to surface pressure oscillations of high amplitude, in agreement with the lag of the bulge. In the strongly stratified regime, pressure oscillations vanish as there is no net tidal bulge anymore. However, we note that 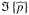 has not the same functional form as the tidal torque. In addition, one should bear in mind that it partly depends on the chosen boundary conditions, which prevents us from proceeding to a more quantitative analysis.
has not the same functional form as the tidal torque. In addition, one should bear in mind that it partly depends on the chosen boundary conditions, which prevents us from proceeding to a more quantitative analysis.
To illustrate the impact of the atmospheric structure on the long-term rotational evolution, we study the evolution of the rotation rate of an idealized Venus-like rocky planet submitted to both atmospheric and solid semidiurnal tides due to a host star. As the goal of these calculations is to isolate the different possible evolutions, we chose simple values of parameters. We used for the solid torque the simplified model expressed as 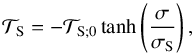 (77)where
(77)where 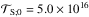 N m designates the amplitude of the torque and σS the effective relaxation frequency of the material composing the rocky core. This model can be interpreted as a zero-order approximation of the Andrade model (Andrade 1910; Efroimsky 2012; Leconte et al. 2015), which describes the forced visco-elastic response of metals and silicates. The relaxation frequency of a rocky planet is usually far lower than the orbital frequency (σS ~ 10-10 s-1; e.g., Efroimsky 2012). Here, we set σS = 10-2norb. In the Andrade model, the decaying rate of the tidal torque is far lower than that of the atmosphere for σ ≫ σS. It is therefore well approximated by a constant in the vicinity of synchronous rotation. Concerning the atmospheric torque, we applied Eq. (71) with the effective radiative frequency σ0 = 3 norb and the amplitude
N m designates the amplitude of the torque and σS the effective relaxation frequency of the material composing the rocky core. This model can be interpreted as a zero-order approximation of the Andrade model (Andrade 1910; Efroimsky 2012; Leconte et al. 2015), which describes the forced visco-elastic response of metals and silicates. The relaxation frequency of a rocky planet is usually far lower than the orbital frequency (σS ~ 10-10 s-1; e.g., Efroimsky 2012). Here, we set σS = 10-2norb. In the Andrade model, the decaying rate of the tidal torque is far lower than that of the atmosphere for σ ≫ σS. It is therefore well approximated by a constant in the vicinity of synchronous rotation. Concerning the atmospheric torque, we applied Eq. (71) with the effective radiative frequency σ0 = 3 norb and the amplitude 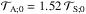 , which was arbitrarily chosen in such way that the final rotation rate corresponds to ω = 4 in case of asynchronous state of equilibrium. The planet was assumed to have the same moment of inertia as Venus, that is, ℐp = 5.88 × 1037 kg m2, and to orbit its host star at the orbital period Porb = 100 d (we recall that norb = 2π/Porb).
, which was arbitrarily chosen in such way that the final rotation rate corresponds to ω = 4 in case of asynchronous state of equilibrium. The planet was assumed to have the same moment of inertia as Venus, that is, ℐp = 5.88 × 1037 kg m2, and to orbit its host star at the orbital period Porb = 100 d (we recall that norb = 2π/Porb).
The equation describing the evolution of the planet’s rotation rate is written 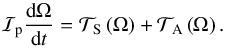 (78)It was integrated over 10 billion years using the ODEX code implemented in the algebraic manipulator TRIP (see Hairer et al. 2000; Gastineau & Laskar 2014), with the initial condition
(78)It was integrated over 10 billion years using the ODEX code implemented in the algebraic manipulator TRIP (see Hairer et al. 2000; Gastineau & Laskar 2014), with the initial condition 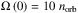 . Simulations were achieved for a wide range of Brunt-Väisälä frequencies N = 10β with β = −7 to β = −3. The results are plotted in Fig. 4 as a function of time.
. Simulations were achieved for a wide range of Brunt-Väisälä frequencies N = 10β with β = −7 to β = −3. The results are plotted in Fig. 4 as a function of time.
We can observe in this figure that rotational evolutions divide into two distinct families. The first family (β ≥ −4), which encompasses strongly stratified cases, is driven by the solid tidal torque alone. In this family, the rotation rate invariably converges toward synchronous rotation (ω = 0). Planets of the second family (β ≤ −5.5) are driven by both solid and atmospheric tidal torques. The evolution rate of their spin varies depending on the strength of the atmospheric tidal torque, which tends to push the planet away from synchronous rotation. They finally reach a stable non-synchronized state of equilibrium corresponding to the frequency where the solid and atmospheric torques exactly balance each other. We can note two evolutions behaving in a different way than those detailed above, namely β = −4.5 and β = −5. These cases are associated with the transition regime. In the first (β = −4.5), a non-synchronized state of equilibrium closer to synchronization is reached, while the rapid evolution of Ω in the second (β = −5) around t = 600 Myr results from one of the resonances studied above (see Eqs. (73) to (76)). We note that the rotation tends toward synchronization in this case.
In the general case, it seems difficult to predict the final rotation rate of the planet using the formula given by Eq. (71). However, it can be done in the asymptotic regime described by the Maxwell model (see, e.g., Auclair-Desrotour et al. 2017b, in the case where the tidal torque of the rocky core is modeled by a Maxwell law). With the law chosen for the tidal torque applied to the rocky core in the present work (Eq. (77)), the frequencies ω± of possible states of equilibrium are expressed as ![\begin{equation} \omega_\pm = \frac{1}{2} \frac{\sigma_0}{n_{\rm orb}} \frac{\mathcal{T}_{\rm A ; 0}}{\mathcal{T}_{\rm S ; 0}} \left[ 1 \pm \sqrt{1 - \left( \frac{\mathcal{T}_{\rm S ; 0}}{\mathcal{T}_{\rm A ; 0}} \right)^2} \right], \end{equation}](/articles/aa/full_html/2018/01/aa31540-17/aa31540-17-eq254.png) (79)although only ω+ corresponds to a stable state leading to an asynchronous final rotation rate.
(79)although only ω+ corresponds to a stable state leading to an asynchronous final rotation rate.
 |
Fig. 4 Evolution of the rotation rate of a Venus-like planet for various Brunt-Väisälä frequencies. The normalized frequency ω = (Ω−norb) /norb is plotted as a function of time (Myr) in logarithmic scale. The Brunt-Väisälä frequency N = 10β is increased from β = −7 (weak stable stratification) to β = −3 (strongly stable stratification) with a step Δβ = 0.5. |
 |
Fig. 5 Relative difference between the parameters νTA and νNTA corresponding to the cases with and without traditional approximation respectively, as a function of the ratio N/σ (horizontal axis) and 2Ω /σ (vertical axis) in logarithmic scales, and for various values of the ratios σ0/σ and γ = τ/k. From left to right, log (γ) = {−2,2}. From bottom to top, |
7. Domain of validity of the traditional approximation
As mentioned in Sect. 3, the traditional approximation consists of ignoring terms involving the factor 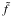 in the momentum equation components, Eqs. (7)–(9). This is convenient to eliminate the coupling between the horizontal and vertical structures of the tidal response induced by the Coriolis acceleration in global modelings (e.g., Chapman & Lindzen 1970; Auclair-Desrotour et al. 2017a). However, the regime of parameters where the approximation is appropriate still remains only partially determined. Early studies generally agree on the fact that the approximation can be applied if 2Ω ≪ σ, that is, in the regime of super-inertial waves, where the fluid tidal response is weakly affected by the rotation of the planet. It has also been shown that the above condition could be extended to 2Ω ≲ σ in the case of a stably stratified fluid (σ ≪ N) (e.g., Friedlander 1987; Mathis et al. 2008; Mathis 2009; Prat et al. 2017).
in the momentum equation components, Eqs. (7)–(9). This is convenient to eliminate the coupling between the horizontal and vertical structures of the tidal response induced by the Coriolis acceleration in global modelings (e.g., Chapman & Lindzen 1970; Auclair-Desrotour et al. 2017a). However, the regime of parameters where the approximation is appropriate still remains only partially determined. Early studies generally agree on the fact that the approximation can be applied if 2Ω ≪ σ, that is, in the regime of super-inertial waves, where the fluid tidal response is weakly affected by the rotation of the planet. It has also been shown that the above condition could be extended to 2Ω ≲ σ in the case of a stably stratified fluid (σ ≪ N) (e.g., Friedlander 1987; Mathis et al. 2008; Mathis 2009; Prat et al. 2017).
We propose here to quantify the conditions of applicability of the traditional approximation by establishing the boundaries of its domain of validity as a function of the characteristic frequencies of the system (i.e., σ, σ0, 2Ω, N) and of the length scale ratio γ.
In light of the expressions of the dissipated power and tidal torque, given in Eqs. (70) and (71), the dimensionless parameter ν introduced in Eqs. (48) and (63) appears as a key parameter to characterize the domain of validity of the traditional approximation. It intervenes in an essential way in 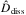 and
and 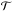 , and contains all the information concerning the hierarchy of characteristic frequencies and control parameters of the system. Therefore, considering that the impact of the traditional approximation on the obtained results is directly related to the variation of ν with
, and contains all the information concerning the hierarchy of characteristic frequencies and control parameters of the system. Therefore, considering that the impact of the traditional approximation on the obtained results is directly related to the variation of ν with 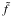 , we adopt as index of validity the normalized relative difference between the parameters νTA and νNTA corresponding to the cases with (
, we adopt as index of validity the normalized relative difference between the parameters νTA and νNTA corresponding to the cases with (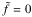 ) and without (
) and without (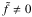 ) the traditional approximation, respectively (the subscripts TA and NTA stand for traditional approximation and no traditional approximation, respectively), which is expressed as
) the traditional approximation, respectively (the subscripts TA and NTA stand for traditional approximation and no traditional approximation, respectively), which is expressed as 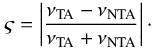 (80)In this approach, the condition of validity of the traditional approximation is ς ≪ 1. Otherwise, neglecting the latitudinal projection of the rotation vector strongly modifies the tidal response, leading to ς ≈ 1, and the traditional approximation should be abandoned.
(80)In this approach, the condition of validity of the traditional approximation is ς ≪ 1. Otherwise, neglecting the latitudinal projection of the rotation vector strongly modifies the tidal response, leading to ς ≈ 1, and the traditional approximation should be abandoned.
The parameter ς is plotted in Fig. 5 as a function of the frequencies ratios N/σ, 2Ω /σ and for asymptotic values of σ0/σ and the length-scale parameter γ = τ/k⊥. Angles are set to θ = π/ 12 and α = π/ 2. The values taken by ς are indicated by colors. Blue regions indicate the domain of parameters where the traditional approximation can be applied (ς ≪ 1), while red regions designate regimes where it is not relevant (ς ≈ 1). Hence, we note that the traditional approximation is appropriate regardless of the hierarchy of characteristic frequencies if the wavelength of the mode is far greater than the pressure height-scale, that is, if γ ≫ 1. The reason is that the term 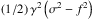 is always far greater in this case than terms associated with the latitudinal component of the Coriolis acceleration in the denominator of ν,
is always far greater in this case than terms associated with the latitudinal component of the Coriolis acceleration in the denominator of ν, 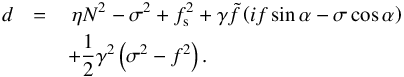 (81)This suggests that the traditional approximation is well adapted to the treatment of the tidal response of thin atmospheres, where the horizontal wavelength of dominating propagating modes is comparable to the radius of the planet in order of magnitude. In the case of small wavelengths (γ ≪ 1), we recover the domain of validity established by early studies: 2Ω ≪ σ if the layer is weakly stably stratified or convective (N ≪ σ), and 2Ω ≲ σ in the case of strongly stable stratification (N ≫ σ). Particularly, the bottom left panel of Fig. 5 shows that the boundary of the validity domain of the approximation corresponds to 2Ω ~ N in the regime of strongly stable stratification, which is in good agreement with the diagnosis reported in Auclair-Desrotour et al. (2017a; Fig. 21). This boundary is slightly modified by the radiative/diffusive cooling (top left panel), with a downward translation of magnitude (1/2)log (σ/σ0) resulting from the equality of the dominating terms of Eq. (81):
(81)This suggests that the traditional approximation is well adapted to the treatment of the tidal response of thin atmospheres, where the horizontal wavelength of dominating propagating modes is comparable to the radius of the planet in order of magnitude. In the case of small wavelengths (γ ≪ 1), we recover the domain of validity established by early studies: 2Ω ≪ σ if the layer is weakly stably stratified or convective (N ≪ σ), and 2Ω ≲ σ in the case of strongly stable stratification (N ≫ σ). Particularly, the bottom left panel of Fig. 5 shows that the boundary of the validity domain of the approximation corresponds to 2Ω ~ N in the regime of strongly stable stratification, which is in good agreement with the diagnosis reported in Auclair-Desrotour et al. (2017a; Fig. 21). This boundary is slightly modified by the radiative/diffusive cooling (top left panel), with a downward translation of magnitude (1/2)log (σ/σ0) resulting from the equality of the dominating terms of Eq. (81): 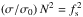 .
.
8. Conclusions
Motivated by the understanding of the role played by thermally forced gravity waves in the atmospheric tidal response of a terrestrial planet submitted to the irradiation of its host star, we have studied the tidal perturbation of a local atmospheric section in solid rotation with the body. In this ab initio approach, inspired by Gerkema & Shrira (2005) and Mathis et al. (2014), the dynamics of tidal waves are reduced to the essentials, which allowed us to conserve the whole physics of tides, and particularly, all the components of the Coriolis acceleration, while avoiding complexities associated with spherical geometry. The goal of this work was to provide a diagnosis of the results obtained in our previous global analytic study (Auclair-Desrotour et al. 2017a) where two asymptotic regimes were identified: a weakly stratified regime inducing a Maxwell-like tidal torque applied on the atmosphere, and a strongly stably stratified regime associated with a weak torque.
We wrote the linearized equations of tides for a fluid section characterized by radial background distributions and dissipative processes modeled with a Newtonian cooling as in Auclair-Desrotour et al. (2017a). We computed analytic solutions describing the forced oscillatory response in two typical cases: a homogeneous fluid with uniform background distributions, and an isothermal atmosphere. In both cases, the tidal torque exerted and the energy dissipated by diffusive/radiative processes were also derived analytically. We showed that tidal regimes are defined by a small number of physical parameters, namely the tidal (σ), inertia (2Ω), Brunt-Väisälä (N), and radiative (σ0) frequencies, and the ratio between the horizontal wavelength of a propagating tidal wave and the pressure height-scale of the fluid (γ).
Considering the semidiurnal stellar tide, we recovered the results obtained with global modelings in early works. The dependence of the tidal torque on the forcing frequency can be described by a Maxwell model in the vicinity of spin-orbit synchronous rotation (Leconte et al. 2015; Auclair-Desrotour et al. 2017a) in the case of weakly stably stratified or convective atmospheres. If the stratification is strong, gravito-inertial waves are generated. This wavelike response breaks the large-scale quadrupolar hydrostatic elongation caused by the stellar heating at zero order, so that there is no net tidal bulge. As a consequence, the amplitude of the tidal torque diminishes and becomes negligible compared to the convective case. This suggests that Venus-like planets with a stably stratified atmosphere are likely to tend toward spin-orbit synchronous rotation, while those with a convective atmosphere rather evolve toward non-synchronized states like Venus, as predicted by the model of Auclair-Desrotour et al. (2017a). Hence, the Cartesian approach allows us to explore the domain of parameters, to confirm the previously identified asymptotic regimes, and to highlight the continuous transition between them. This transition occurs for N ~ {γσ,γσ0}. In the case of Venus itself, the structure of the atmosphere is characterized by a strong negative temperature gradient near the surface of the planet (Seiff et al. 1980). This implies that the densest layers of the atmosphere, which are also the better viscously coupled to the solid part, are neutrally stratified. Hence, our simplified modeling suggests in this case a strong atmospheric torque that agrees with the conclusions of early works that examined the rotation of Venus (e.g., Gold & Soter 1969; Dobrovolskis & Ingersoll 1980; Correia & Laskar 2001; Auclair-Desrotour et al. 2017b).
By isolating in obtained solutions a characteristic scaling parameter (ν), we were also able to delimit the domain of validity of the traditional approximation used in global models as a function of the system’s control parameters, and to characterize the asymptotic regimes. In the short-wavelength approximation, we recovered the domain of validity identified in early studies, namely the validity conditions 2Ω ≪ σ in the case of weakly stratified fluids, and 2Ω ≪ N in the case of strongly stratified fluids (Friedlander 1987; Mathis et al. 2008; Mathis 2009; Auclair-Desrotour et al. 2017a). This domain is slightly modified by dissipative mechanisms in this case. In the long-wavelength asymptotic regime, where the pressure scale height is smaller than the horizontal wavelength of a propagating mode, we found that the Coriolis terms neglected in the traditional approximation do not affect the tidal response, except at the boundary of the inertial regime, defined by 2Ω ~ σ. This result is appropriate to characterize the forced response of the fluid up to meso-scale modes, that is, the application limit of the f-plane approximation used in our modeling. Therefore, the impact of the traditional approximation on global tidal modes should be studied in general with global modelings, as was done by Ogilvie & Lin (2004) in the case of giant planets or Tort & Dubos (2014) for atmospheric dynamics.
However, the local approach developed here still remains an efficient way to peer into the large domain of parameters of atmospheric tidal responses and to clarify the predictions of global modelings obtained with assumptions. It offers a simplified but robust picture of the tidal wave dynamics with the essential physical ingredients. Its predictive power on the rotation state of exoplanets as a function of the convective stability of their atmosphere is of great interest with their probe by forthcoming space missions such as the JWST (Lagage 2015). Such missions will be able to provide constraints on the temperature gradient at different depths in the atmospheres of exoplanets thanks to multiwavelength observations in the near IR. In forthcoming studies, we will complete this picture by including stratified background flows in the Cartesian fluid section. These flows are likely to strongly modify the atmospheric tidal response, but cannot be taken into account directly in global analytic modeling without important mathematical complications.
The separation of the fluid tidal response into non-wavelike and wavelike part was introduced by Ogilvie (2013) in the context of gravitational tides. The non-wavelike part designates the instantaneous global elongation of the atmosphere and the induced large-scale flow, while the wavelike part encompasses the effects of internal waves generated by the forcing and resonances they can induce. In the present work, the term non-wavelike refers to the global elongation of the atmosphere due to the thermal forcing by analogy with the gravitational tidal potential. It is different from the equilibrium tide, however, which designates the tidal response of the fluid in the zero-frequency limit (σ → 0).
Acknowledgments
P. Auclair-Desrotour and S. Mathis acknowledge funding by the European Research Council through ERC grants WHIPLASH 679030 and SPIRE 647383. The authors wish to thank the anonymous referee for helpful suggestions and remarks.
References
- Andrade, E. N. D. C. 1910, Proc. R. Soc. London, Ser. A, 84, 1 [Google Scholar]
- André, Q., Barker, A. J., & Mathis, S. 2017, A&A, 605, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arras, P., & Socrates, A. 2010, ApJ, 714, 1 [Google Scholar]
- Auclair Desrotour, P., Mathis, S., & Le Poncin-Lafitte, C. 2015, A&A, 581, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auclair-Desrotour, P., Laskar, J., & Mathis, S. 2017a, A&A, 603, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auclair-Desrotour, P., Laskar, J., Mathis, S., & Correia, A. C. M. 2017b, A&A, 603, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, S., & Lindzen, R. 1970, Atmospheric tides: Thermal and gravitational (Reidel) [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2001, Nature, 411, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003, J. Geophys. Res. Planets, 108, 5123 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Boué, G., Laskar, J., & Rodríguez, A. 2014, A&A, 571, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Dickinson, R. E., & Geller, M. A. 1968, J. Atmos. Sci., 25, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrovolskis, A. R., & Ingersoll, A. P. 1980, Icarus, 41, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M. 2012, ApJ, 746, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Friedlander, S. 1987, Geophys. J., 89, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Gastineau, M., & Laskar, J. 2014, TRIP 1.3.8, TRIP Reference manual, IMCCE, Paris Observatory, http://www.imcce.fr/trip/ [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005, J. Fluid Mech., 529, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Zimmerman, J. 2008, Lecture Notes, Royal NIOZ, Texel [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gold, T., & Soter, S. 1969, Icarus, 11, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, R. 2009, ApJ, 698, L42 [Google Scholar]
- Hairer, E., Nørsett, S., & Wanner, G. 2000, Solving Ordinary Differential Equations I Nonstiff problems, 2nd edn. (Berlin: Springer) [Google Scholar]
- Ingersoll, A. P., & Dobrovolskis, A. R. 1978, Nature, 275, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Lagage, P.-O. 2015, European Planetary Science Congress 2015, held 27 September–2 October, 2015 in Nantes, France, Online at http://meetingorganizer.copernicus.org/EPSC2015/EPSC2015 [Google Scholar]
- Leconte, J., Forget, F., Charnay, B., et al. 2013, A&A, 554, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., Wu, H., Menou, K., & Murray, N. 2015, Science, 347, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Lindzen, R. S., & McKenzie, D. J. 1967, Pure Appl. Geophys., 66, 90 [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., Neiner, C., & Tran Minh, N. 2014, A&A, 565, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogilvie, G. I. 2013, MNRAS, 429, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., & Young, R. 1975, J. Atmos. Sci., 32, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Prat, V., Mathis, S., Lignières, F., Ballot, J., & Culpin, P.-M. 2017, A&A, 598, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H. 1981, ApJ, 245, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Bolmont, E., Selsis, F., et al. 2016, A&A, 596, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seiff, A., Kirk, D. B., Young, R. E., et al. 1980, J. Geophys. Res., 85, 7903 [Google Scholar]
- Shen, M., & Zhang, C. Z. 1990, Icarus, 85, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, E. A., & Veronis, G. 1960, ApJ, 131, 442 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tort, M., & Dubos, T. 2014, Q. J. R. Meteorolog. Soc., 140, 2388 [Google Scholar]
- Zahn, J. P. 1966, Annales d’Astrophysique, 29, 313 [Google Scholar]
All Figures
 |
Fig. 1 Spherical and Cartesian reference frames and coordinate systems. The vectors Ω and g designate the rotation and the gravity, respectively. |
| In the text | |
 |
Fig. 2 Normalized tidal torque as a function of the frequency of the perturber ω = (Ω−norb) /norb for various values of the Brunt-Väisälä frequency from weak to strongly stable stratification, i.e., |
| In the text | |
 |
Fig. 3 Normalized tidal torque (left panel) and imaginary part of the surface pressure oscillation (right panel) as functions of the normalized tidal frequency ω = (Ω−norb) /norb (horizontal axis) and Brunt-Väisälä frequency in logarithmic scale (vertical axis). The tidal torque and pressure variations are computed using the functions given by Eqs. (71) and (66), respectively. The torque is normalized by its maximum value in the asymptotic regime of neutral stratification. The imaginary part of pressure oscillations is normalized by its maxima in absolute value. We consider the case of a Venus-like planet with the following set of values: norb = 1.991 × 10-7 s-1, Γ1 = 1.4 (perfect gas), H = 15.9 km, θ = π/ 3, α = 0 (westward propagating wave), σ0 = 7.5 × 10-7 s-1 (Leconte et al. 2015), and k⊥ = 2π/λ with λ = 1000 km. The frequencies ω− and ω+ are the resonant frequencies identified in Sect. 6 (see Eq. (76)). |
| In the text | |
 |
Fig. 4 Evolution of the rotation rate of a Venus-like planet for various Brunt-Väisälä frequencies. The normalized frequency ω = (Ω−norb) /norb is plotted as a function of time (Myr) in logarithmic scale. The Brunt-Väisälä frequency N = 10β is increased from β = −7 (weak stable stratification) to β = −3 (strongly stable stratification) with a step Δβ = 0.5. |
| In the text | |
 |
Fig. 5 Relative difference between the parameters νTA and νNTA corresponding to the cases with and without traditional approximation respectively, as a function of the ratio N/σ (horizontal axis) and 2Ω /σ (vertical axis) in logarithmic scales, and for various values of the ratios σ0/σ and γ = τ/k. From left to right, log (γ) = {−2,2}. From bottom to top, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.