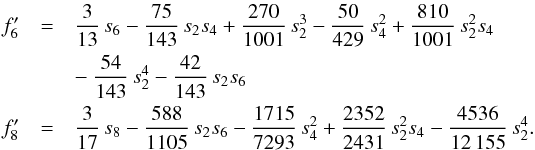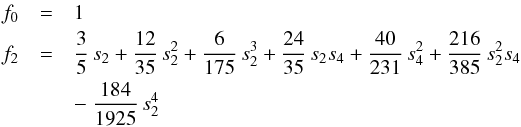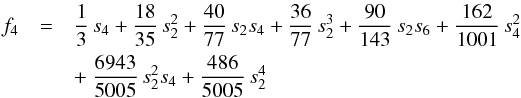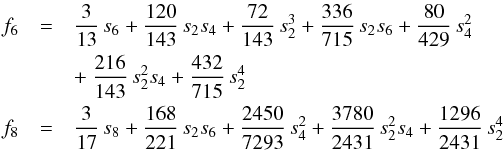© ESO, 2017

1. Introduction

The theory of figures (ToF; Zharkov & Trubitsyn 1978) to third or fourth order, hereafter labeled respectively ToF 3 and ToF 4, is commonly used to compute the gravity field of the gas giant planets in the solar system (e.g., Saumon & Guillot 2004; Helled 2011; Leconte & Chabrier 2012; Nettelmann et al. 2012; Helled & Guillot 2013; Miguel et al. 2016). While a theory to nth order allows for computation of the gravity field in terms of the gravitational harmonics up to J_2n only, Jupiter’s gravity field before the current Juno mission was also measured up to J₆ only. Thus, third or fourth order theories seemed sufficient. Moreover, it is the low-order harmonics J₂ and J₄ that are particularly sensitive to the internal density distribution; they allow for derivation of the interior structure parameters core mass and envelope metallicity. Hence for a long time, the observational data of gravity field theories (e.g., ToF) and planet-interior parameters of interest formed a closed system.

This convenient situation has changed with the arrival of the Juno spacecraft at Jupiter. Juno’s sensitivity limit makes it possible to measure the rigid-rotation contribution to the gravitational harmonics up to J₁₄ (Kaspi et al. 2010). High-order moments yield clues to the properties of the zonal winds as the flows influence the density distribution, which in turn is the source function of the gravitational potential. Differential rotation due to zonal flows is predicted to entirely dominate the J_2n for n ≥ 14, while it is predicted to be within a factor of ten of the prediction for a rigidly rotating planet for J₈−J₁₂ (Hubbard 1999; Kaspi et al. 2010; Cao & Stevenson 2017). Since the wind contribution 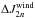$\mathrm{\Delta }{\mathit{J}}_{\mathrm{2}\mathit{n}}^{\mathrm{wind}}$ is obtained by subtracting the theoretical values for a rigidly rotating planet from the observed ones (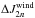${\mathit{J}}_{\mathrm{2}\mathit{n}}^{\mathrm{obs}}\mathrm{=}{\mathit{J}}_{\mathrm{2}\mathit{n}}^{\mathrm{rigid}}\mathrm{+}\mathrm{\Delta }{\mathit{J}}_{\mathrm{2}\mathit{n}}^{\mathrm{wind}}$), it is also important to have accurate knowledge of the rigid-rotation contribution.

For that purpose, Hubbard (2013, hereafter H13), developed the concentric Maclaurin spheroids (CMS) method. This method yields demonstratively good agreement with the exact Bessel solution for an n = 1 polytrope model of Jupiter. Deviations have been found to be about 5 × 10^-5 in J₂ to 2 × 10^-4 in J₂₀ (Wisdom & Hubbard 2016), or to be of the order of 2 × 10^-3 (Cao & Stevenson 2017). However, comparison of the exact Bessel solution to the ToF 3 results (H13; Wisdom 1996) has led to the conclusion that ToF 3 is insufficiently accurate for modeling Jupiter (Wisdom 1996). This raises the question of what accuracy in the low-order moments is desired for inferring Jupiter’s internal density distribution, and which methods can provide that.

Fig. 1 Resulting J2 values of polytropic models of rigidly rotating Jupiter for q = 0.089195487 (left) as in H13 and Wisdom & Hubbard (2016), and for q = 0.088570679 (right) as in Wisdom (1996). Blue symbols: using ToF to fourth order, blue lines: respective fit curves, light blue: same as blue but using ToF 3, red symbols: using CMS method. Reference values are in black; black circle: CMS results of H13 for N = 512, horizontal black lines: unknown value of N, in particular: thick black lines: Bessel/CLC results of Wisdom & Hubbard (2016), thin black lines: ToF 3 results of H13 and Wisdom (1996). The vertical black arrow shows the current Juno uncertainty of J2 (Folkner et al. 2017), here arbitrarily placed. The x-axis is number of radial grid points N.

Fig. 2 Same as Fig. 1 but for J4. The ToF 3 result of Hubbard (2013) exceeds the shown range of J4 values.

The classical view of a Jupiter-like gas giant is that of a well-defined core embedded into an H/He-rich envelope, in which case one can search for the mass of the core and the heavy element mass fraction of the envelope and use the measured planet radius and J₂ value to determine both (Militzer et al. 2008). However, recent gas giant formation models challenge that simple picture. Simultaneous accretion of gas and planetesimals might naturally lead to a gas-enriched, that is, diluted core (Venturini et al. 2016), where the metallicity is predicted to decrease outward as a result of the slow convective timescale compared to the accretion rate during formation (Helled & Stevenson 2017); a diluted core may remain permanent due to the inhibition of convection once a compositional gradient has become established (Vazan et al. 2016). Diluted cores have been found to enhance the predicted atmospheric metallicity of Jupiter models (Fortney & Nettelmann 2010).

In this paper, the uncertainty in the computed values for the low-order harmonics J₂, J₄, J₆ due to application of ToF 3 and ToF 4 is estimated by using the n = 1 polytrope model (Sect. 2); the corresponding uncertainty in the derived core mass and envelope metallicity of Jupiter is estimated in Sect. 3. Finding this uncertainty to be small for ToF 4, I use this method in Sect. 4 to compute physical equations of state (EOS)-based Jupiter models that are designed to match the low-order harmonics J₂ and J₄ from Juno’s first two low-periapse polar orbits around Jupiter (Folkner et al. 2017). Models are presented both for solid cores and for diluted cores, as well as for deep zonal wind corrections as proposed by Cao & Stevenson (2017). For some of the Jupiter models, I compute the high-order moments using the CMS method (Sect. 5), thereby providing the first prediction of the high-order J_2n values for a model of an adiabatic, rigidly rotating Jupiter that matches the measured low-order moments. Conclusions are in Sect. 6. In Appendix A my implementation of the CMS method is validated for the linear density case, while in Appendix B the ToF coefficients are provided up to the fourth order.

2. Polytropic models

In this section, n = 1 polytropic models are computed for GM_J = 12.6686536 × 10¹⁶m³/ s², equatorial radius R_eq = R_J = 71 492 km, and for two different rotation rates as represented by q = 0.0891954870 (Wisdom & Hubbard 2016) and q = 0.08857067907 (Wisdom 1996), where $\mathit{q}\mathrm{=}{\mathit{\omega }}^{\mathrm{2}}{\mathit{R}}_{\mathrm{eq}}^{\mathrm{3}}\mathit{/}\mathit{GM}$. I apply ToF to the third and fourth order as well as the CMS method. For both methods an iterative procedure is required to ensure the total mass is conserved, and that for the thus specified value of K in the polytropic relation P = Kρ² hydrostatic balance holds.

With ToF I calculate the density at grid point i using 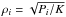${\mathit{\rho }}_{\mathit{i}}\mathrm{=}\sqrt{{\mathit{P}}_{\mathit{i}}\mathit{/}\mathit{K}}$, while with CMS method 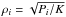${\mathit{\rho }}_{\mathit{i}}\mathrm{=}\sqrt{\mathrm{0.5}\mathrm{(}{\mathit{P}}_{\mathit{i}}\mathrm{+}{\mathit{P}}_{\mathit{i}\mathrm{+}\mathrm{1}}\mathrm{)}\mathit{/}\mathit{K}}$ (H13), except for i = 0 where ρ₀ = P₀ = 0 in their respective units. As I find the dependence on the number of radial grid points, N, to be strong, I plot the resulting values of J₂ (Fig. 1), J₄ (Fig. 2), and J₆ (Fig. 3) against N.

Fig. 3 Same as Figs. 1 and 2 but for J6 and results for different q-values merged into a single panel, distinguished by respectively solid lines/circles and dashed lines/diamonds. The ToF 3 result of Hubbard (2013) exceeds the shown range of J6 values.

Compared to the exact Bessel solution (Wisdom & Hubbard 2016), the CMS method performs best and ToF 3 worst. In particular, ToF 3 underestimates | J₄/ 10^-6 | by one to two times (depending on the implementation) the pre-Juno 1σ error bar of ~2 (Miguel et al. 2016), and therefore predicts a higher atmospheric metallicity for Jupiter than ToF 4 does (Nettelmann et al. 2012).

ToF 4, on the other hand, performs much better: the difference in J₄ to the exact Bessel solution amounts to only about 15% of the total pre-Juno error bar, and the differences in both J₄ and J₆ are still smaller than the uncertainties of the current Juno data. The influence of the error in J₄ due to the application of ToF 4 on the predicted envelope metallicity and core mass of Jupiter can be considered negligible. In the following section, I investigate whether this is also the case for J₂, the error bar of which is 5× the current Juno estimate of 2 × 0.272 × 10^-6 (Fig. 1).

3. Interior models and J₂

The observed value of J₂ allows for insight into the internal structure of Jupiter, as different internal density distributions may yield different values of J₂ to be compared against the observed one. In this section I investigate how sensitive that dependence is. In particular, I consider the resulting uncertainty in the derived core mass (M_core) and atmospheric metallicity (Z_atm) due to the technical uncertainty in J₂, which results from applying ToF 4 to compute the gravitational harmonics. For this purpose, simple models are computed for which I assume a constant metallicity throughout Jupiter’s envelope. Although further details of the procedure do not influence the resulting quantities we are interested in (the uncertainties), I give them for completeness: the envelope is separated into an outer, He-poor part of helium abundance Y_atm = 0.238 in agreement with the Galileo entry probe value, and a He-rich inner envelope that accounts for the remaining helium to yield a total He/H mass ratio of 0.275 in agreement with estimates for the protosolar cloud. The transition takes place at pressure P_trans = 8 Mbar. The envelope adiabat runs through the temperature-pressure point of 423 K at 22 bars as measured by the Galileo entry probe. At the outer boundary at one bar this yields T₁ = 170 K, which I adopt as the outer boundary condition for the Jupiter models. Figure 4 shows the resulting uncertainties in M_core and Z_atm as a function of the assumed value of J₂.

Fig. 4 Uncertainty in the derived values for core mass and atmospheric metallicity due to the assumed uncertainty in J2 for interior models assuming constant envelope-Z. For ΔJ2 about 10 × the current Juno uncertainty, corresponding to 2 × the estimated error from applying ToF 4 (bottom panel) the core mass uncertainty amounts to ~ 0.04 M⊕ (middle panel), while the uncertainty in Zatm is found to be less than 0.0002 (upper panel). These uncertainties are small.

Fig. 5 Same as Fig. 4 but for J4 (lower panel) and J6 (upper panel).

According to Fig. 4, the error in J₂ of about 2 × 10^-4 due to applying ToF 4 maps onto an uncertainty of 0.02 M_⊕ in Jupiter’s core mass and 0.0001 in Z_atm. Furthermore, an uncertainty of 0.1% in J₂ (twice the horizontal length of gray lines) would imply an uncertainty of ~ 0.1 M_⊕ in core mass and 0.0004 in Z_atm. Thus, the uncertainties due to applying ToF 4 can be considered tiny compared to the accuracy in internal structure properties we are interested in, which is about 10% (e.g., ~ 1 M_⊕ in core mass). Moreover, the uncertainty from this source of error is clearly smaller than the uncertainty due to the material input physics like the EOS, which is at best of the order of 1%. Furthermore, the additional error in J₄ and J₆ which results from the uncertainty in J₂ due to applying ToF 4 amounts to only 0.04% for J₄ and 0.03% for J₆ (Fig. 5). From Figs. 4 and 5 I therefore conclude that ToF 4 yields quantitatively useful density distributions for Jupiter.

4. Results for Jupiter

In this section I construct models that aim to match the tight current Juno constraints on J₂ and J₄ and are based on H/He-REOS.3 (Becker et al. 2014, hereafter B14). In Sect. 4.1 I assume rocky cores and rigid rotation, while in Sect. 4.2 I assume diluted cores or take into account the shift due to winds.

4.1. Models with solid cores and rigid rotation

The models in this section are three-layer models and constructed as in Nettelmann et al. (2012), hereafter N12. The only but important difference to the models of Sect. 3 is that three-layer models allow for different heavy element abundances in the two envelopes, so that two free parameters (Z₁ = Z_atm in the outer and Z₂ in the inner envelope) are available for adjusting the two low-order harmonics J₂ and J₄. If this can be achieved and if in addition Z₁ ≥ 2 × solar, consistent with the observed heavy noble gas abundances in Jupiter’s atmosphere, I consider a model as acceptable for Jupiter.

Fig. 6 ToF 4 based three-layer Jupiter models that are designed to match observed J2 and J4 values. This work: black solid, B14: yellow, N12: green. Measured atmospheric particle abundances of the elements as labeled are scaled by their protosolar particle abundance values (Lodders 2003). I use Zsolar = 0.015.

Figure 6 shows these new models as a function of P_trans. They are similar to the ToF 4 based models of N12, who applied H-REOS.2 and He-REOS.1, and of B14 who applied H-REOS.3 and He-REOS.3 as in this work. The biggest differences are the narrower range in possible transition pressure and the lower Z₁ values compared to B14. The latter is mainly a direct consequence of reducing | J₄/ 10^-6 | from 589 to 586.6. The lower Z₁ values also tend to reduce J₂, requiring more heavy elements in the deep interior to compensate for that. Slightly higher Z₂ values then leave less mass to build the core, so that finally a smaller set of models (a smaller range of P_trans values for which M_core ≥ 0) is found. In contrast, the difference between these models and the N12 results was mainly due to differences in the helium EOS at outer envelope pressures. These new results confirm that ab initio H/He-EOSs yield rather low atmospheric metallicities for Jupiter. Compared to ≲ 1 × solar (Hubbard & Militzer 2016; Wahl et al. 2017b), ≲ 2.5 × solar (N12), ≲ 3 × solar (B14), I here obtain Z_atm ≲ 2 × solar, out of which acceptable models have P_trans = 6–7 Mbar.

An inaccuracy in J₄ of about 2.4/600 (0.4%) (compare black and yellow curves in Fig. 6) seems to induce a rather large uncertainty of ΔM_core = 2 M_⊕ in core mass; but a 0.1% uncertainty in J₄ might still lead to ΔM_core = 0.5 M_⊕ for three-layer models. However, this estimate is probably a far upper bound as the models in B14 were computed with a smaller number of grid points of N ~ 2000 compared to ~12 000 in this work.

Fig. 7 (Left panel) Resulting ToF 4-based J6 values of Jupiter models (magenta). The J4 value of these models (magenta, right panel) was adjusted to match the Juno J4 measurement. Black diamonds: Juno measurements, blue error bars: estimated uncertainty due to applying ToF 4 according to Figs. 1–3.

Figure 7 compares the resulting J₆ value of the ToF 4-based Jupiter models that match the Juno J₂ and J₄ values to the Juno measurement of J₆. Models with P_trans = 4–7 Mbar are within the observational uncertainty of J₆, while models with lower transition pressures are within 2σ of the observational uncertainty. The computational error from ToF 4 is much smaller than that.

4.2. Models with diluted cores or zonal winds

Ab initio H/He EOS-based Jupiter models with rock-ice cores and without zonal winds become notoriously low in atmospheric heavy element abundances. On the other hand, diluted cores have been found to enhance Z_atm by up to 50% (Fortney & Nettelmann 2010), while zonal winds directly affect the J₂ and J₄ values to be matched by rigidly rotating models (Militzer et al. 2008; Cao & Stevenson 2017) and thus also influence the derived Z_atm value. While precise predictions on the dynamic contributions ΔJ_2n to the observed values depend on the differential rotation pattern and their mathematical description (Kaspi et al. 2010; Zhang et al. 2015; Cao & Stevenson 2017), it is predicted that the effect on the low-order J_2n increases with the depth of the winds (Kaspi et al. 2010; Cao & Stevenson 2017) and that the effect on the low-order J_2n is small and in the direction of reducing the absolute J_2n values (Hubbard 1999; Kaspi et al. 2010; Cao & Stevenson 2017). Here I calculate Jupiter models as in Sect. 4.1 but by assuming a diluted core of rock mass fraction Z_{3, Rocks} = 0.2, the rest being inner mantle material, and by including zonal wind corrections as proposed by Cao & Stevenson (2017) for half-amplitude width (HAWD) values of 0.8 and 0.9. The latter quantity is defined as the distance to the rotation axis where the azimuthal wind velocity has weakened by a factor of two from its maximum value farther out.

Fig. 8 Jupiter models with diluted cores of central rock mass fraction Z3, Rocks = 0.2 (black dashed) or with zonal winds according to HAWD = 0.9 (solid blue). The solid black curves are the same as in Fig. 6. I use Zsolar = 0.015.

As shown in Fig. 8, the zonal wind corrections lead to lower values in Z₁ and M_core. This is not a surprise, since the absolute values of J₂ and J₄ are reduced and thus demand a smaller mass density in the part of the planet planet where they are most sensitive, which is near P ~ 1 Mbar in the outer envelope. This behavior is in line with the observation of Militzer et al. (2008) who, in order to enhance the resulting envelope Z value, suggest zonal wind effects on J₂ and J₄ in the opposite direction of what zonal wind models that fit the observed wind speeds predict.

For HAWD = 0.8 I do not obtain any acceptable Jupiter model because the ΔJ_2n are too large: both Z₁ and M_core would become negative. For HAWD = 0.9, there is a restricted range of solutions at P_trans = 3–5.5 Mbar, for which Z₁ barely reaches 1.5 × solar. Adiabatic H/He-REOS.3-based Jupiter models thus suggest the vertical extent of the winds to be less than 0.9 R_J (~7000 km).

Assuming a diluted core and adiabatic envelopes, the Z₁ value can be lifted, but only to less than its maximum value obtained for core-less models. The enhancement in Z₁ can indeed reach up to 50% for the largest core mass found here, but then the base Z₁ value is small anyway. Therefore, as Fig. 8 shows, diluted cores do not significantly enhance Z_atm for H/He-REOS-based models, but are helpful for larger core models (Wahl et al. 2017b) such as those obtained with the EOS of Militzer & Hubbard (2013).

5. High-order gravitational harmonics

To compute the high-order gravitational harmonics of models that match the observed Juno values for J₂ and J₄, I use the density distributions of the models from Sect. 4 and apply the CMS method to them¹. For that purpose, I convert the ToF-based density profile as a function of the mean radius of an equipotential surface to a density profile as a function of the equatorial radius of the same equipotential surface using the ToF 4-based figure functions. Then I reduce the number of radial grid points from N ~ 12 000 to N ~ 1000 by assuming a radial spacing that decreases continuously from the middle to the boundaries. At layer boundaries, the jump in density is conserved as illustrated in Fig. 9.

Fig. 9 Conversion of the ToF 4-based density profile (black) to a discrete grid as required by the CMS method, here illustrated for N = 50 (blue) and N = 100 (green).

Finally, Table 1 presents my results for the low- and high-order J_2n values of two models from Sect. 4.1, that is, for P_trans = 3 Mbar (model J17-3a) and 6 Mbar (model J17-6a), and for one model that accounts for deep zonal winds through the corrections to J₂ and J₄ for HAWD = 0.9 from Sect. 4.2 (model J17-4z). Resulting moments of order ≥6 are not affected by the above described procedure within the number of digits given in Table 1. This is shown by model variant (b), where the J₂ value to be fitted was shifted by the difference ToF 4 minus CMS according to model variant (a). The results are compared to the exact polytrope solution (Wisdom & Hubbard 2016), to the DFT-MD-7.13 Jupiter model of Hubbard & Militzer (2016), to the Juno measurements of Folkner et al. (2017), and to the same data but corrected for deep zonal winds as proposed by Cao & Stevenson (2017).

Perhaps most interestingly, the resulting values for J₆ and J₈ for a rigidly rotating Jupiter are within the current Juno observational error bars. This may indicate that the winds are shallow. The J₈ value of model J17-4z is also within the observational error bar and the reduction of its | J₈ | value by a few percent is much less than the few 10% estimate of Cao & Stevenson (2017), whose ΔJ₈ estimate peaks for HAWD = 0.9 compared to deeper (0.8) or shallower (0.975) depths. Furthermore, the high-order J_2n values of n = 1 polytropic Jupiter differ by about 10% from the physical EOS-based Jupiter models. Thus it is important to provide the latter class of models as done in this work and in Hubbard & Militzer (2016).

6. Conclusions

To infer Jupiter’s internal density distribution, the relative accuracy in the computed values of J₂ and J₄ should be of the order of 0.1% (Figs. 4 and 6). According to n = 1 polytropic models, ToF 4 can provide this accuracy, while ToF 3 can do so only for J₂ (Figs. 1 and 2). The error in J₂ (J₄, J₆) due to applying ToF 4, as measured by the difference to the exact solution, is about 5 × (1/2 ×, 1/3 ×) the current Juno uncertainties for these parameters. I conclude that these uncertainties are nevertheless sufficiently small for predicting Jupiter’s internal density distribution. Other uncertainties, such as the thermal state, perhaps as a result of helium rain, may induce larger unknowns in our understanding of Jupiter (Nettelmann et al. 2015; Hubbard & Militzer 2016; Mankovich et al. 2016; Wahl et al. 2017b).

The computed values of J₆ and J₈ of rigidly rotating Jupiter suggest that zonal winds are restricted to regions well above a depth of 7000 km (0.9R_J). Furthermore, application of the more accurate CMS method in combination with the physical EOS H/He-REOS.3 is found to yield higher-order | J_2n | values that are 10% higher than the prediction from the polytropic model (Table 1).

Still, the internal structure of Jupiter remains poorly constrained. Further insight might be gained from a Juno measurement of the fluid Love number k₂ and its consideration in three-dimensional models for the gravity field (Wahl et al. 2017a).

Acknowledgments

I thank Naor Movshovitz for sharing results for linear density models with the CMS method, Ronald Redmer and Ravit Helled for inspiring discussions, and the Referee and the Scientific Editor for helpful comments that improved the paper. This work was supported by the DFG grant NE1734/1-1 of the German Science Foundation.

References

Appendix A: Linear density models with CMS

Hubbard (2013) provides the gravitational harmonics for a linear density model with Jupiter-like parameters and N = 128. I use that model to test my implementation of the CMS method. The agreement is excellent for the given number of digits (seven in H13; see Table A.1). However, a model with only N = 128 is not yet converged as the same linear density model with N = 512 shows. Therefore, in order to obtain this good agreement with the linear density model of H13, I had to choose the spacings in equatorial radius dλ_i and the dimensionless density jumps δ_i exactly as in H13. In particular (N. Movshovitz, pers. comm.), λ₀ = 1, λ_N = 0, δ₀ = δ_N = 0, dλ = 1/(N−1), λ₁ = λ₀ − dλ/ 2, λ_i = λ_i−1−dλ for i> 1, and δ_i = dλ_i for i ≥ 1. All other parameters were chosen as in H13, in particular q = 0.088822426, R_eq = 71 492 km, and GM = 126 686 536km³/ s².

Appendix B: ToF to fourth-order coefficients

I summarize the theory of figures of Zharkov & Trubitsyn (1978) and then give the coefficients up to the fourth order. Consider a spheroidal planet in hydrostatic equilibrium of density distribution ρ(r,ϑ) which is symmetric with respect to the axis of rotation and the equatorial plane. As a result, there is no dependence on azimuthal angle ϕ, and only even indices in the spherical harmonics expansions survive. In this two-dimensional problem, a surface of constant total potential U only depends on polar angle ϑ. Different such surfaces r_l(ϑ) are labeled by the level parameter l. In the ToF method according to Zharkov & Trubitsyn (1978), l is taken to be the mean radius of the respective equipotential surface as defined by the condition of equal volume, 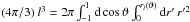$\mathrm{(}\mathrm{4}\mathit{\pi }\mathit{/}\mathrm{3}\mathrm{)}{\mathit{l}}^{\mathrm{3}}\mathrm{=}\mathrm{2}\mathit{\pi }{{}^{\mathrm{\int }}}_{-1}^{\mathrm{1}}\mathrm{d}\cos \mathit{\vartheta }{{}^{\mathrm{\int }}}_{\mathrm{0}}^{{\mathit{r}}_{\mathit{l}}\mathrm{\left(}\mathit{\vartheta }\mathrm{\right)}}\mathrm{d}{\mathit{r}}^{\mathrm{\prime }}\hspace{0.17em}{\mathit{r}}^{\mathrm{\prime }\mathrm{2}}$. Furthermore, any dependence on (r,ϑ) is replaced by dependence on (l,ϑ) through the expansion of r_l(ϑ) into a series of Legendre polynomials P_n(cosϑ) according to 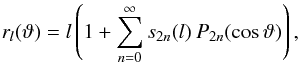${\mathit{r}}_{\mathit{l}}\mathrm{\left(}\mathit{\vartheta }\mathrm{\right)}\mathrm{=}\mathit{l}\left(\mathrm{1}\mathrm{+}\sum _{\mathit{n}\mathrm{=}\mathrm{0}}^{\mathrm{\infty }}{\mathit{s}}_{\mathrm{2}\mathit{n}}\mathrm{\left(}\mathit{l}\mathrm{\right)}{\mathit{P}}_{\mathrm{2}\mathit{n}}\mathrm{\left(}\cos \mathit{\vartheta }\mathrm{\right)}\right)\mathit{,}$(B.1)where the s_2n(l) are the figure functions. The first-order deviation from a spherical shape is described by s₂, while s₀ can be determined with the help of the equal-volume condition to ${\mathit{s}}_{\mathrm{0}}\mathrm{=}\mathrm{-}\frac{\mathrm{1}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{2}}{\mathrm{105}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{-}\frac{\mathrm{1}}{\mathrm{9}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{2}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathit{.}$(B.2)The figure functions s_2n are of nth order except s₀ which is of second order. In the following, I abbreviate the expression in parenthesis in Eq. (B.1) by (1 + Σ) and set μ = cosϑ.

The total potential is composed of the gravitational potential $\mathit{V}\mathrm{\left(}{r}\mathrm{\right)}\mathrm{=}\mathrm{-}\mathit{G}{}^{\mathrm{\int }}\mathrm{d}^{\mathrm{3}}{\mathit{r}}^{\mathrm{\prime }}\mathit{\rho }\mathit{/}\mathrm{|}{{r}}^{\mathrm{\prime }}\mathrm{-}{r}\mathrm{|}$ while the centrifugal potential reads $\mathit{Q}\mathrm{=}\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\omega }}^{\mathrm{2}}{\mathit{r}}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\vartheta }$. 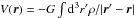In the ToF it is convenient to capture the centrifugal term due to the planetary rotation of angular rotation rate ω by the small parameter 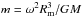$\mathit{m}\mathrm{=}{\mathit{\omega }}^{\mathrm{2}}{\mathit{R}}_{\mathrm{m}}^{\mathrm{3}}\mathit{/}\mathit{GM}$, where R_m is the mean radius of the outermost level surface. After expanding V and Q into series of Legendre polynomials and replacing r by Eq. (B.1), one can write 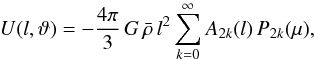$\mathit{U}\mathrm{\left(}\mathit{l,\vartheta }\mathrm{\right)}\mathrm{=}\mathrm{-}\frac{\mathrm{4}\mathit{\pi }}{\mathrm{3}}\hspace{0.17em}\mathit{G}\hspace{0.17em}\mathit{\rho ̅}\hspace{0.17em}{\mathit{l}}^{\mathrm{2}}\sum _{\mathit{k}\mathrm{=}\mathrm{0}}^{\mathrm{\infty }}{\mathit{A}}_{\mathrm{2}\mathit{k}}\mathrm{\left(}\mathit{l}\mathrm{\right)}\hspace{0.17em}{\mathit{P}}_{\mathrm{2}\mathit{k}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\mathit{,}$(B.3)where 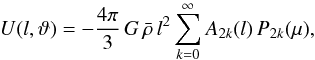denotes the mean density 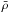$\mathrm{3}\mathit{M}\mathit{/}\mathrm{\left(}\mathrm{4}\mathit{\pi }{\mathit{R}}_{\mathrm{m}}^{\mathrm{3}}\mathrm{\right)}$. On equipotential surfaces, dU/ dθ = 0 and thus A_2k ≡ 0 for k> 0. This property is used to determine the s_2n, while A₀ yields the total potential. One finds $\begin{array}{ccc}{\mathit{A}}_{\mathrm{0}}& \mathrm{=}& \left(\mathrm{1}\mathrm{+}\frac{\mathrm{2}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{4}}{\mathrm{105}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{2}}{\mathrm{9}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{43}}{\mathrm{175}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathrm{-}\frac{\mathrm{4}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{0}}\\ & & \mathrm{+}\left(\mathrm{-}\frac{\mathrm{3}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{12}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{234}}{\mathrm{175}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{24}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{2}}\mathrm{+}\left(\frac{\mathrm{6}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{5}}{\mathrm{9}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{4}}\\ & & \mathrm{+}{\mathit{S}}_{\mathrm{0}}^{\mathrm{\prime }}\mathrm{+}\left(\frac{\mathrm{2}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{2}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{4}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{2}}{\mathrm{25}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\right)\hspace{0.17em}{\mathit{S}}_{\mathrm{2}}^{\mathrm{\prime }}\mathrm{+}(\frac{\mathrm{4}}{\mathrm{9}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\\ & & \mathrm{+}\frac{\mathrm{12}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}){\mathit{S}}_{\mathrm{4}}^{\mathrm{\prime }}\mathrm{+}\frac{\mathit{m}}{\mathrm{3}}\left(\mathrm{1}\mathrm{-}\frac{\mathrm{2}}{\mathrm{5}}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{9}}{\mathrm{35}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{4}}{\mathrm{35}}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{22}}{\mathrm{525}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\right)\mathit{.}\\ & & \end{array}$(B.4)}The functions S_n and 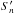${\mathit{S}}_{\mathit{n}}^{\mathrm{\prime }}$ will be defined below.

Appendix B.1: From V to D_n, D$\begin{array}{c}\mathrm{\prime }\\ {n}\end{array}$ and further to S_n, S$\begin{array}{c}\mathrm{\prime }\\ {n}\end{array}$, and J_n

The gravitational potential at a location (r,ϑ) in the planet separates into an external potential r>r′ due to the mass distribution ρ(r′,ϑ′) interior to r and an internal potential r<r′ due to the mass distribution ρ(r′,ϑ′) exterior to r. The multipole expansion of V reads 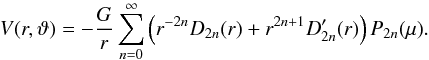$\mathit{V}\mathrm{\left(}\mathit{r,\vartheta }\mathrm{\right)}\mathrm{=}\mathrm{-}\frac{\mathit{G}}{\mathit{r}}\sum _{\mathit{n}\mathrm{=}\mathrm{0}}^{\mathrm{\infty }}\mathrm{\left(}{\mathit{r}}^{\mathrm{-}\mathrm{2}\mathit{n}}{\mathit{D}}_{\mathrm{2}\mathit{n}}\mathrm{\right(}\mathit{r}\mathrm{)}\mathrm{+}{\mathit{r}}^{\mathrm{2}\mathit{n}\mathrm{+}\mathrm{1}}{\mathit{D}}_{\mathrm{2}\mathit{n}}^{\mathrm{\prime }}\mathrm{(}\mathit{r}{\mathrm{\left)}}^{\mathrm{\right)}}{\mathit{P}}_{\mathrm{2}\mathit{n}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\mathit{.}$(B.5)Using Eq. (B.1), the volume integrals D_n of the external and 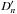${\mathit{D}}_{\mathit{n}}^{\mathrm{\prime }}$ of the internal gravity field expansion take the form²$\begin{array}{ccc}{\mathit{D}}_{\mathit{n}}\mathrm{\left(}\mathit{l}\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{2}\mathit{\pi }}{\mathit{n}\mathrm{+}\mathrm{3}}{\mathrm{\int }}_{\mathrm{0}}^{\mathit{l}}\mathrm{d}{\mathit{l}}^{\mathrm{\prime }}\mathit{\rho }\mathrm{\left(}{\mathit{l}}^{\mathrm{\prime }}\mathrm{\right)}{\mathrm{\int }}_{-1}^{\mathrm{1}}\mathrm{d}{\mathit{\mu }}^{\mathrm{\prime }}\hspace{0.17em}{\mathit{P}}_{\mathit{n}}\mathrm{\left(}{\mathit{\mu }}^{\mathrm{\prime }}\mathrm{\right)}\frac{\mathrm{d}{\mathit{r}}^{\mathit{n}\mathrm{+}\mathrm{3}}}{\mathrm{d}\mathit{l}}\\ {\mathit{D}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{l}\mathrm{\right)}& \mathrm{=}& \\ {\mathit{D}}_{\mathrm{2}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{l}\mathrm{\right)}& \mathrm{=}& \end{array}$(B.6)With z: = l/R_m, their dimensionless form is defined as ${\mathit{S}}_{\mathit{n}}\mathrm{\left(}\mathit{z}\mathrm{\right)}\mathrm{=}\frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }\mathit{\rho ̅}\hspace{0.17em}{\mathit{l}}^{\mathit{n}\mathrm{+}\mathrm{3}}}\hspace{0.17em}{\mathit{D}}_{\mathit{n}}\mathrm{\left(}\mathit{l}\mathrm{\right)}\mathit{,} {\mathit{S}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}\mathrm{=}\frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }\mathit{\rho ̅}\hspace{0.17em}{\mathit{l}}^{\mathrm{2}\mathrm{-}\mathit{n}}}{\mathit{D}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{l}\mathrm{\right)}\mathit{,}$(B.7)and can be written as $\begin{array}{ccc}{\mathit{S}}_{\mathit{n}}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{1}}{{\mathit{z}}^{\mathit{n}\mathrm{+}\mathrm{3}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathit{z}}\mathrm{d}{\mathit{z}}^{\mathrm{\prime }}\frac{\mathit{\rho }\mathrm{\left(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\right)}}{\mathit{\rho ̅}}\hspace{0.17em}\frac{\mathrm{d}}{\mathrm{d}{\mathit{z}}^{\mathrm{\prime }}}\mathrm{\left[}{\mathit{z}}^{\mathrm{\prime }\hspace{0.17em}\mathit{n}\mathrm{+}\mathrm{3}}{\mathit{f}}_{\mathit{n}}\mathrm{\right(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\left)}\mathrm{\right]}\\ {\mathit{S}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{1}}{{\mathit{z}}^{\mathrm{(}\mathrm{2}\mathrm{-}\mathit{n}\mathrm{)}}}{\mathrm{\int }}_{\mathit{z}}^{\mathrm{1}}\mathrm{d}{\mathit{z}}^{\mathrm{\prime }}\frac{\mathit{\rho }\mathrm{\left(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\right)}}{\mathit{\rho ̅}}\hspace{0.17em}\frac{\mathrm{d}}{\mathrm{d}{\mathit{z}}^{\mathrm{\prime }}}\mathrm{\left[}{\mathit{z}}^{\mathrm{\prime }\hspace{0.17em}\mathrm{2}\mathrm{-}\mathit{n}}{\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\right(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\left)}\mathrm{\right]}\\ {\mathit{S}}_{\mathrm{0}}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \end{array}$(B.8)After application of partial integration and assuming dρ/ dz to be finite, the S_n, ${\mathit{S}}_{\mathit{n}}^{\mathrm{\prime }}$ 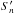adopt the convenient form for numerical evaluation $\begin{array}{ccc}{\mathit{S}}_{\mathit{n}}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \frac{\mathit{\rho }\mathrm{\left(}\mathit{z}\mathrm{\right)}}{\mathit{\rho ̅}}\hspace{0.17em}{\mathit{f}}_{\mathit{n}}\mathrm{\left(}\mathit{z}\mathrm{\right)}\hspace{0.17em}\mathrm{-}\hspace{0.17em}\frac{\mathrm{1}}{{\mathit{z}}^{\mathit{n}\mathrm{+}\mathrm{3}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathit{z}}\frac{\mathrm{d}\mathit{\rho }}{\mathit{\rho ̅}}\hspace{0.17em}{\mathit{z}}^{\mathrm{\prime }\hspace{0.17em}\mathit{n}\mathrm{+}\mathrm{3}}{\mathit{f}}_{\mathit{n}}\mathrm{\left(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\right)}\\ {\mathit{S}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \mathrm{-}\frac{\mathit{\rho }\mathrm{\left(}\mathit{z}\mathrm{\right)}}{\mathit{\rho ̅}}\hspace{0.17em}{\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}\hspace{0.17em}\mathrm{+}\hspace{0.17em}\frac{\mathrm{1}}{{\mathit{z}}^{\mathrm{2}\mathrm{-}\mathit{n}}}\left(\frac{\mathit{\rho }\mathrm{\left(}\mathrm{1}\mathrm{\right)}}{\mathit{\rho ̅}}\hspace{0.17em}{\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathrm{1}\mathrm{\right)}\mathrm{-}{\mathrm{\int }}_{\mathit{z}}^{\mathrm{1}}\frac{\mathrm{d}\mathit{\rho }}{\mathit{\rho ̅}}\hspace{0.17em}{\mathit{z}}^{\mathrm{\prime }\hspace{0.17em}\mathrm{2}\mathrm{-}\mathit{n}}{\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}{\mathit{z}}^{\mathrm{\prime }}\mathrm{\right)}\right)\end{array}$(B.9)with $\begin{array}{ccc}{\mathit{f}}_{\mathit{n}}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{2}\mathrm{(}\mathit{n}\mathrm{+}\mathrm{3}\mathrm{)}}{\mathrm{\int }}_{-1}^{\mathrm{1}}\mathrm{d}\mathit{\mu }{\mathit{P}}_{\mathit{n}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\mathrm{(}\mathrm{1}\mathrm{+}\mathrm{\Sigma }{\mathrm{)}}^{\mathit{n}\mathrm{+}\mathrm{3}}\mathit{,}\\ {\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{2}\mathrm{(}\mathrm{2}\mathrm{-}\mathit{n}\mathrm{)}}{\mathrm{\int }}_{-1}^{\mathrm{1}}\mathrm{d}\mathit{\mu }{\mathit{P}}_{\mathit{n}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\mathrm{(}\mathrm{1}\mathrm{+}\mathrm{\Sigma }{\mathrm{)}}^{\mathrm{2}\mathrm{-}\mathit{n}} \mathrm{(}\mathit{n}\ne \mathrm{2}\mathrm{)}\hspace{0.17em}\mathit{,}\\ {\mathit{f}}_{\mathrm{2}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}& \mathrm{=}& \end{array}$(B.10)By expressing powers of (1 + Σ) in terms of the binomial series expansions, and by further expanding powers of Σ into linear series of Legendre polynomials and by making use of ${{}^{\mathrm{\int }}}_{-1}^{\mathrm{1}}\mathrm{d}\mathit{\mu }{\mathit{P}}_{\mathit{n}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\hspace{0.17em}{\mathit{P}}_{\mathit{m}}\mathrm{\left(}\mathit{\mu }\mathrm{\right)}\mathrm{=}\mathrm{0}$ for n ≠ m, the integrals in Eqs. (B.10) can be solved analytically. 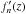The results for f_n(z) and ${\mathit{f}}_{\mathit{n}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{z}\mathrm{\right)}$ are provided in Eqs. (B.16) and (B.17). Accordingly, the integrals S_2n and 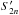${\mathit{S}}_{\mathrm{2}\mathit{n}}^{\mathrm{\prime }}$ are of nth order. Finally, the gravitational harmonics are obtained as ${\mathit{J}}_{\mathrm{2}\mathit{n}}\mathrm{=}\mathrm{-}\mathrm{(}{\mathit{R}}_{\mathrm{m}}\mathit{/}{\mathit{R}}_{\mathrm{eq}}{\mathrm{)}}^{\mathrm{2}\mathit{n}}\hspace{0.17em}{\mathit{S}}_{\mathrm{2}\mathit{n}}\mathrm{(}\mathrm{1}\mathrm{)}\mathit{.}$(B.11)

Appendix B.2: Coefficients in A_2n for computing the s_2n

Below, I give the coefficients that are of fourth order or lower after multiplication with m, S_2n, or 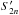${\mathit{S}}_{\mathrm{2}\mathit{n}}^{\mathrm{\prime }}$ as occurring in the respective equations. They were generated by a C++ program written by myself in 2004, 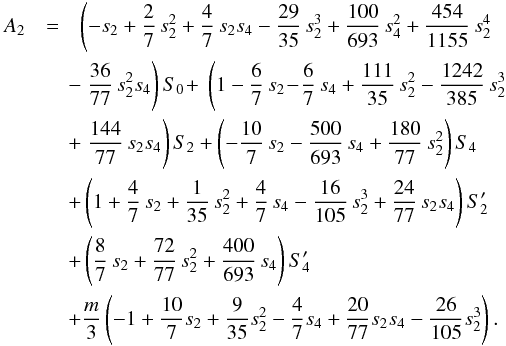$\begin{array}{ccc}{\mathit{A}}_{\mathrm{2}}& \mathrm{=}& (\mathrm{-}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{2}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{4}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{29}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{100}}{\mathrm{693}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{454}}{\mathrm{1155}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\\ & & \mathrm{-}\frac{\mathrm{36}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}){\mathit{S}}_{\mathrm{0}}\mathrm{+}(\mathrm{1}\mathrm{-}\frac{\mathrm{6}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{6}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{111}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{1242}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\\ & & \mathrm{+}\frac{\mathrm{144}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}){\mathit{S}}_{\mathrm{2}}\mathrm{+}\left(\mathrm{-}\frac{\mathrm{10}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{500}}{\mathrm{693}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{180}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\right){\mathit{S}}_{\mathrm{4}}\\ & & \mathrm{+}\left(\mathrm{1}\mathrm{+}\frac{\mathrm{4}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{1}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{4}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{16}}{\mathrm{105}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{24}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{2}}^{\mathrm{\prime }}\\ & & \mathrm{+}\left(\frac{\mathrm{8}}{\mathrm{7}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{72}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{400}}{\mathrm{693}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{4}}^{\mathrm{\prime }}\\ & & \mathrm{+}\frac{\mathit{m}}{\mathrm{3}}\left(\mathrm{-}\mathrm{1}\mathrm{+}\frac{\mathrm{10}}{\mathrm{7}}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{9}}{\mathrm{35}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{4}}{\mathrm{7}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{20}}{\mathrm{77}}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{26}}{\mathrm{105}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\right)\mathit{.}\\ & & \end{array}$(B.12)To lowest order, s₂ ≈ −m/ 3, thus s₂ is of first order in m, 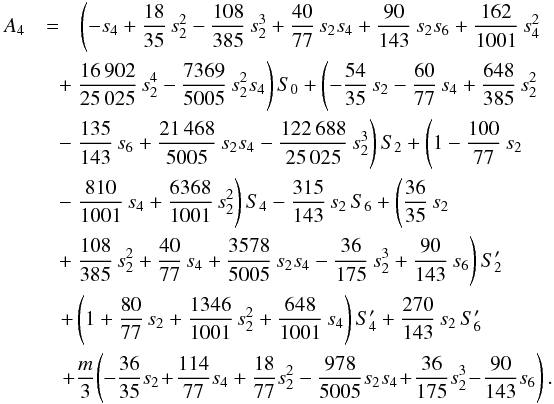$\begin{array}{ccc}{\mathit{A}}_{\mathrm{4}}& \mathrm{=}& (\mathrm{-}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{18}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{108}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{40}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{90}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{162}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\\ & & \mathrm{+}\frac{\mathrm{16}\hspace{0.17em}\mathrm{902}}{\mathrm{25}\hspace{0.17em}\mathrm{025}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathrm{-}\frac{\mathrm{7369}}{\mathrm{5005}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}){\mathit{S}}_{\mathrm{0}}\mathrm{+}(\mathrm{-}\frac{\mathrm{54}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{60}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{648}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\\ & & \mathrm{-}\frac{\mathrm{135}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{21}\hspace{0.17em}\mathrm{468}}{\mathrm{5005}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{122}\hspace{0.17em}\mathrm{688}}{\mathrm{25}\hspace{0.17em}\mathrm{025}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}){\mathit{S}}_{\mathrm{2}}\mathrm{+}(\mathrm{1}\mathrm{-}\frac{\mathrm{100}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\\ & & \mathrm{-}\frac{\mathrm{810}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{6368}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}){\mathit{S}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{315}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\hspace{0.17em}{\mathit{S}}_{\mathrm{6}}\mathrm{+}(\frac{\mathrm{36}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\\ & & \mathrm{+}\frac{\mathrm{108}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{40}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{3578}}{\mathrm{5005}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{36}}{\mathrm{175}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{90}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}){\mathit{S}}_{\mathrm{2}}^{\mathrm{\prime }}\\ & & \mathrm{+}\left(\mathrm{1}\mathrm{+}\frac{\mathrm{80}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{1346}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{648}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{4}}^{\mathrm{\prime }}\mathrm{+}\frac{\mathrm{270}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\hspace{0.17em}{\mathit{S}}_{\mathrm{6}}^{\mathrm{\prime }}\\ & & \mathrm{+}\frac{\mathit{m}}{\mathrm{3}}\left(\mathrm{-}\frac{\mathrm{36}}{\mathrm{35}}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{114}}{\mathrm{77}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{18}}{\mathrm{77}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{978}}{\mathrm{5005}}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{36}}{\mathrm{175}}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{-}\frac{\mathrm{90}}{\mathrm{143}}{\mathit{s}}_{\mathrm{6}}\right)\mathit{.}\\ & & \end{array}$(B.13)To lowest order, s₄ ~ m × s₂, thus s₄ is of second order in m,

$\begin{array}{ccc}{\mathit{A}}_{\mathrm{6}}& \mathrm{=}& (\mathrm{-}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{10}}{\mathrm{11}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{18}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{28}}{\mathrm{55}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{72}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathrm{+}\frac{\mathrm{20}}{\mathrm{99}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\\ & & \mathrm{-}\frac{\mathrm{54}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}){\mathit{S}}_{\mathrm{0}}\mathrm{+}(\mathrm{-}\frac{\mathrm{15}}{\mathrm{11}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{108}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{42}}{\mathrm{55}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{-}\frac{\mathrm{144}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\\ & & \mathrm{+}\frac{\mathrm{216}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}){\mathit{S}}_{\mathrm{2}}\mathrm{+}\left(\mathrm{-}\frac{\mathrm{25}}{\mathrm{11}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{100}}{\mathrm{99}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{270}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\right){\mathit{S}}_{\mathrm{4}}\\ & & \mathrm{+}\left(\mathrm{1}\mathrm{-}\frac{\mathrm{98}}{\mathrm{55}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\right){\mathit{S}}_{\mathrm{6}}\mathrm{+}\left(\frac{\mathrm{10}}{\mathrm{11}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{18}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{36}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{28}}{\mathrm{55}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\right){\mathit{S}}_{\mathrm{2}}^{\mathrm{\prime }}\\ & & \mathrm{+}\left(\frac{\mathrm{20}}{\mathrm{11}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{108}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{80}}{\mathrm{99}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{4}}^{\mathrm{\prime }}\mathrm{+}\left(\mathrm{1}\mathrm{+}\frac{\mathrm{84}}{\mathrm{55}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\right)\hspace{0.17em}{\mathit{S}}_{\mathrm{6}}^{\mathrm{\prime }}\\ & & \end{array}$(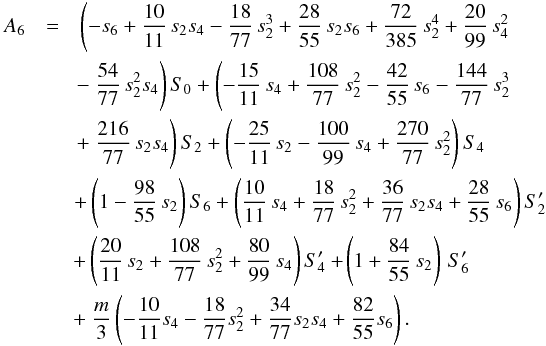B.14)To lowest order, s₆ ~ m × s₄, thus s₆ is of third order in m. 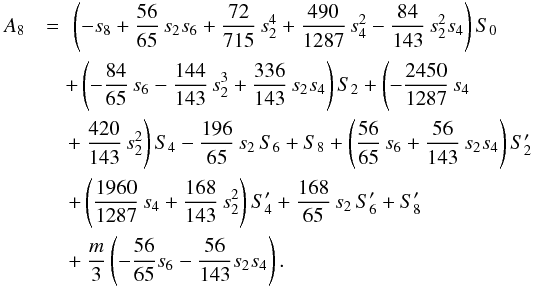$\begin{array}{ccc}{\mathit{A}}_{\mathrm{8}}& \mathrm{=}& \left(\mathrm{-}{\mathit{s}}_{\mathrm{8}}\mathrm{+}\frac{\mathrm{56}}{\mathrm{65}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{72}}{\mathrm{715}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathrm{+}\frac{\mathrm{490}}{\mathrm{1287}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{84}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{0}}\\ & & \mathrm{+}\left(\mathrm{-}\frac{\mathrm{84}}{\mathrm{65}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{-}\frac{\mathrm{144}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{336}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{2}}\mathrm{+}(\mathrm{-}\frac{\mathrm{2450}}{\mathrm{1287}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\\ & & \mathrm{+}\frac{\mathrm{420}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}){\mathit{S}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{196}}{\mathrm{65}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\hspace{0.17em}{\mathit{S}}_{\mathrm{6}}\mathrm{+}{\mathit{S}}_{\mathrm{8}}\mathrm{+}\left(\frac{\mathrm{56}}{\mathrm{65}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{56}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\right){\mathit{S}}_{\mathrm{2}}^{\mathrm{\prime }}\\ & & \mathrm{+}\left(\frac{\mathrm{1960}}{\mathrm{1287}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{168}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\right){\mathit{S}}_{\mathrm{4}}^{\mathrm{\prime }}\mathrm{+}\frac{\mathrm{168}}{\mathrm{65}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\hspace{0.17em}{\mathit{S}}_{\mathrm{6}}^{\mathrm{\prime }}\mathrm{+}{\mathit{S}}_{\mathrm{8}}^{\mathrm{\prime }}\\ & & \end{array}$(B.15)To lowest order, s_2n ~ mⁿ.

Appendix B.3: Coefficients for computing the f_2n and f′_2n

$\begin{array}{ccc}{\mathit{f}}_{\mathrm{0}}& \mathrm{=}& \mathrm{1}\\ {\mathit{f}}_{\mathrm{2}}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{+}\frac{\mathrm{12}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{6}}{\mathrm{175}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{24}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{40}}{\mathrm{231}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{216}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\\ & & \mathrm{-}\frac{\mathrm{184}}{\mathrm{1925}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\end{array}$$\begin{array}{ccc}{\mathit{f}}_{\mathrm{4}}& \mathrm{=}& \frac{\mathrm{1}}{\mathrm{3}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{18}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{40}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{36}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{90}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{162}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\\ & & \mathrm{+}\frac{\mathrm{6943}}{\mathrm{5005}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{486}}{\mathrm{5005}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\end{array}$$\begin{array}{ccc}{\mathit{f}}_{\mathrm{6}}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{13}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{120}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{72}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{+}\frac{\mathrm{336}}{\mathrm{715}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{80}}{\mathrm{429}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\\ & & \mathrm{+}\frac{\mathrm{216}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{432}}{\mathrm{715}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\\ {\mathit{f}}_{\mathrm{8}}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{17}}\hspace{0.17em}{\mathit{s}}_{\mathrm{8}}\mathrm{+}\frac{\mathrm{168}}{\mathrm{221}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{+}\frac{\mathrm{2450}}{\mathrm{7293}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{3780}}{\mathrm{2431}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{1296}}{\mathrm{2431}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\\ & & \end{array}$(B.16)}$\begin{array}{ccc}{\mathit{f}}_{\mathrm{0}}^{\mathrm{\prime }}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{2}}\mathrm{-}\frac{\mathrm{3}}{\mathrm{10}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{2}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{-}\frac{\mathrm{1}}{\mathrm{6}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{6}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{3}}{\mathrm{50}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\\ {\mathit{f}}_{\mathrm{2}}^{\mathrm{\prime }}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}\mathrm{-}\frac{\mathrm{3}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{6}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{36}}{\mathrm{175}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{-}\frac{\mathrm{10}}{\mathrm{231}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{17}}{\mathrm{275}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\\ & & \mathrm{+}\frac{\mathrm{36}}{\mathrm{385}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\\ {\mathit{f}}_{\mathrm{4}}^{\mathrm{\prime }}& \mathrm{=}& \frac{\mathrm{1}}{\mathrm{3}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{9}}{\mathrm{35}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}\mathrm{-}\frac{\mathrm{20}}{\mathrm{77}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{45}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{-}\frac{\mathrm{81}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{1}}{\mathrm{5}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\end{array}$}

$\begin{array}{ccc}{\mathit{f}}_{\mathrm{6}}^{\mathrm{\prime }}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{13}}\hspace{0.17em}{\mathit{s}}_{\mathrm{6}}\mathrm{-}\frac{\mathrm{75}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{+}\frac{\mathrm{270}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{3}}\mathrm{-}\frac{\mathrm{50}}{\mathrm{429}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{810}}{\mathrm{1001}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\\ & & \mathrm{-}\frac{\mathrm{54}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathrm{-}\frac{\mathrm{42}}{\mathrm{143}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\\ {\mathit{f}}_{\mathrm{8}}^{\mathrm{\prime }}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{17}}\hspace{0.17em}{\mathit{s}}_{\mathrm{8}}\mathrm{-}\frac{\mathrm{588}}{\mathrm{1105}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}{\mathit{s}}_{\mathrm{6}}\mathrm{-}\frac{\mathrm{1715}}{\mathrm{7293}}\hspace{0.17em}{\mathit{s}}_{\mathrm{4}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{2352}}{\mathrm{2431}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{2}}{\mathit{s}}_{\mathrm{4}}\mathrm{-}\frac{\mathrm{4536}}{\mathrm{12}\hspace{0.17em}\mathrm{155}}\hspace{0.17em}{\mathit{s}}_{\mathrm{2}}^{\mathrm{4}}\mathit{.}\\ & & \end{array}$(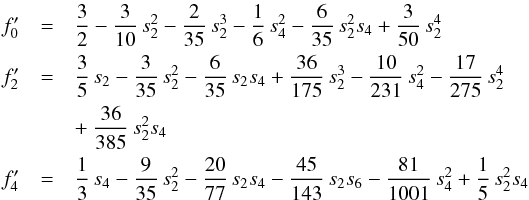B.17)}Numerical values for the s_2n and J_2n for a given barotrope ρ(P) can be obtained through an iterative procedure. For given values of the J_2n and s_2n, which can initially be zero, the density distribution ρ(l) is computed by numerical integration of the hydrostatic balance equation dP/ dl = −ρ(P)dU/ dl using Eq. (B.4), and by integration of the mass conservation equation dm/ dl = 4πl²ρ(l). Given then ρ(l), new figure functions are repeatedly calculated until convergence using Eqs. (B.12) to (B.15), and then the J_2n are calculated using Eq. (B.11). Converged J_2n values for a given barotrope require about six iterations of this procedure.

All Tables

All Figures

Fig. 1 Resulting J2 values of polytropic models of rigidly rotating Jupiter for q = 0.089195487 (left) as in H13 and Wisdom & Hubbard (2016), and for q = 0.088570679 (right) as in Wisdom (1996). Blue symbols: using ToF to fourth order, blue lines: respective fit curves, light blue: same as blue but using ToF 3, red symbols: using CMS method. Reference values are in black; black circle: CMS results of H13 for N = 512, horizontal black lines: unknown value of N, in particular: thick black lines: Bessel/CLC results of Wisdom & Hubbard (2016), thin black lines: ToF 3 results of H13 and Wisdom (1996). The vertical black arrow shows the current Juno uncertainty of J2 (Folkner et al. 2017), here arbitrarily placed. The x-axis is number of radial grid points N.

In the text

	Fig. 2 Same as Fig. 1 but for J4. The ToF 3 result of Hubbard (2013) exceeds the shown range of J4 values.
In the text

	Fig. 3 Same as Figs. 1 and 2 but for J6 and results for different q-values merged into a single panel, distinguished by respectively solid lines/circles and dashed lines/diamonds. The ToF 3 result of Hubbard (2013) exceeds the shown range of J6 values.
In the text

Fig. 4 Uncertainty in the derived values for core mass and atmospheric metallicity due to the assumed uncertainty in J2 for interior models assuming constant envelope-Z. For ΔJ2 about 10 × the current Juno uncertainty, corresponding to 2 × the estimated error from applying ToF 4 (bottom panel) the core mass uncertainty amounts to ~ 0.04 M⊕ (middle panel), while the uncertainty in Zatm is found to be less than 0.0002 (upper panel). These uncertainties are small.

In the text

	Fig. 5 Same as Fig. 4 but for J4 (lower panel) and J6 (upper panel).
In the text

	Fig. 6 ToF 4 based three-layer Jupiter models that are designed to match observed J2 and J4 values. This work: black solid, B14: yellow, N12: green. Measured atmospheric particle abundances of the elements as labeled are scaled by their protosolar particle abundance values (Lodders 2003). I use Zsolar = 0.015.
In the text

	Fig. 7 (Left panel) Resulting ToF 4-based J6 values of Jupiter models (magenta). The J4 value of these models (magenta, right panel) was adjusted to match the Juno J4 measurement. Black diamonds: Juno measurements, blue error bars: estimated uncertainty due to applying ToF 4 according to Figs. 1–3.
In the text

	Fig. 8 Jupiter models with diluted cores of central rock mass fraction Z3, Rocks = 0.2 (black dashed) or with zonal winds according to HAWD = 0.9 (solid blue). The solid black curves are the same as in Fig. 6. I use Zsolar = 0.015.
In the text

	Fig. 9 Conversion of the ToF 4-based density profile (black) to a discrete grid as required by the CMS method, here illustrated for N = 50 (blue) and N = 100 (green).
In the text