| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731281 | |
| Published online | 24 October 2017 | |
Neutron star cooling and the rp process in thermonuclear X-ray bursts⋆
1 SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
e-mail: jeanz@sron.nl
2 University College Utrecht, Utrecht University, 3584 ED Utrecht, The Netherlands
3 School of Physics and Astronomy, Monash University, VIC 3800, Australia
4 Monash Center for Astrophysics, Monash University, VIC 3800, Australia
5 National Space Institute, Technical University of Denmark, Elektrovej 327-328, 2800 Lyngby, Denmark
6 CRESST and X-ray Astrophysics Laboratory NASA/GSFC, Greenbelt, MD 20771, USA
7 Department of Astronomy, University of Maryland, College Park, MD 20742, USA
8 European Space Astronomy Centre (ESA/ESAC), Science Operations Department, 28691 Villanueva de la Cañada, Madrid, Spain
9 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received: 31 May 2017
Accepted: 6 August 2017
When the upper layer of an accreting neutron star experiences a thermonuclear runaway of helium and hydrogen, it exhibits an X-ray burst of a few keV with a cool-down phase of typically 1 min. When there is a surplus of hydrogen, hydrogen fusion is expected to simmer during that same minute due to the rp process, which consists of rapid proton captures and slow β-decays of proton-rich isotopes. We have analyzed the high-quality light curves of 1254X-ray bursts, obtained with the Proportional Counter Array on the Rossi X-ray Timing Explorer between 1996 and 2012, to systematically study the cooling and rp process. This is a follow-up of a study on a selection of 37 bursts from systems that lack hydrogen and show only cooling during the bursts. We find that the bolometric light curves are well described by the combination of a power law and a one-sided Gaussian. The power-law decay index is between 1.3 and 2.1 and similar to that for the 37-bursts sample. There are individual bursters with a narrower range. The Gaussian is detected in half of all bursts, with a typical standard deviation of 50 s and a fluence ranging up to 60% of the total fluence. The Gaussian appears consistent with being due to the rp process. The Gaussian fluence fraction suggests that the layer where the rp process is active is underabundant in H by a factor of at least five with respect to cosmic abundances. Ninety-four percent of all bursts from ultracompact X-ray binaries lack the Gaussian component, and the remaining 6% are marginal detections. This is consistent with a hydrogen deficiency in these binaries. We find no clear correlation between the power law and Gaussian light-curve components.
Key words: X-rays: binaries / X-rays: bursts / stars: neutron / nuclear reactions, nucleosynthesis, abundances
Full Table C.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/606/A130
© ESO, 2017
1. Introduction
The Galaxy is host to at least 100 neutron stars that accrete hydrogen and/or helium from a Roche-lobe overflowing companion star. The hydrogen and helium can burn in an unstable fashion during thermonuclear shell flashes (for reviews, see Lewin et al. 1993; Strohmayer & Bildsten 2006; Galloway et al. 2008). The typical duration is one minute, and the typical frequency is once every few hours. The neutron star photosphere reaches typical temperatures of ~ 107 K, and the thermonuclear runaway expresses itself as a bright X-ray burst, easily detectable from anywhere in the Galaxy.
Thermonuclear X-ray bursts are powered by mainly four nuclear reaction chains (e.g., Fujimoto et al. 1981; Bildsten 1998; José et al. 2010):
-
1.
the CNO cycle (Taam & Picklum 1979), actingon hydrogen forming helium and catalyzed by CNO. The netreaction captures four protons and emits one α particle and two positrons, neutrinos, and photons. It includes two β decays. It may be responsible for ignition at the lowest accretion rates; see Fujimoto et al. (1981) and Peng et al. (2007);
-
2.
the 3α process (Joss 1978), acting on helium forming carbon. It is usually, if not always, responsible for the ignition (i.e., for mass accretion rates higher than 1% of the Eddington limit; Fujimoto et al. 1981);
-
3.
the αp process, acting on products of the previous two chains forming heavier elements. It occurs when the temperature is high enough (> 5 × 108 K) and results from a breakout from the CNO cycle through α-captures by 15O;
-
4.
the rp process, acting on products of the previous chains and any hydrogen that is left from the previous chains (Wallace & Woosley 1981; Schatz et al. 2001). The higher the temperature, the longer the chain of the rp process because the protons need to overcome increasingly higher Coulomb barriers of heavier isotopes. Some branches of the rp process are slow. Although the proton capture rates are high, the β decays are sometimes much slower and constitute bottlenecks in the chain. These are responsible for late nuclear burning in X-ray bursts. Notorious waiting points are at 21Mg, 33Ar, and 48Mn (e.g., Fisker et al. 2008, see also Appendix A) with decay half-lives of up to tens of seconds. Reaction rates in the rp process are sometimes ill-constrained experimentally. The relevance of this for the time profiles of the burst luminosity has recently been assessed by Cyburt et al. (2016, see also Woosley et al. 2004. They found that the uncertainties in the rates of about ten rp and αp reactions introduce significant uncertainty in the time profiles.
The existence of two types of fuel that can burn independently from each other, hydrogen and helium, results in the so-called burning regimes. Through the CNO cycle, hydrogen ignites at lower temperatures and pressures than helium. For T< 8×107 K, the nuclear power of the CNO cycle increases faster with T than the cooling, and a runaway occurs. For higher temperatures, the nuclear power T-dependence levels off to the radiative cooling dependence and the burning becomes continuous. When the burning of a mass parcel of hydrogen is faster than the time for it to reach helium ignition conditions, a thermonuclear flash ignites in a helium-rich/hydrogen-poor environment. At higher accretion rates, ignition conditions are reached faster than it takes for stable hydrogen burning, and the flash occurs in a layer containing hydrogen and helium. This results in three burning regimes (Fujimoto et al. 1981): mixed hydrogen-helium bursts ignited by hydrogen at low accretion rates (regime 3), pure helium bursts at medium accretion rates (regime 2; between 3% and 6% of Eddington for ZCNO = 0.01; Bildsten 1998), and mixed hydrogen-helium ignited by helium at high accretion rates (regime 1). At the highest accretion rates, helium burning may become partially stable (in ’t Zand et al. 2003; Keek & Heger 2016).
For a subset of binaries, the so-called ultracompact X-ray binaries (UCXBs, with orbital periods shorter than 80 min; Nelson et al. 1986), there is a deficiency of accreted hydrogen and the nuclear reactions simplify and become faster. The lack of hydrogen precludes a strong rp process and prolonged burning that would be visible as shoulders in type I X-ray burst decays. Possibly as many as half of all X-ray bursters fall in this category (in ’t Zand et al. 2007). However, the burst rate in these systems is usually rather low (i.e., one every few days or even longer gaps). Most X-ray bursts therefore come from hydrogen-rich systems, and it is expected that all four nuclear reaction chains mentioned at the start of this section occur.
Thermonuclear X-ray bursts were first detected in 1969 (Belian et al. 1972; Kuulkers et al. 2009). The number of detections grew into the hundreds in the mid- to late-1970s (e.g., Grindlay et al. 1976; Lewin et al. 1993) and into the thousands with the advent of X-ray telescopes with large fields of view in the 1990s and onward (e.g., in ’t Zand et al. 2004; Nakagawa et al. 2004; Chelovekov & Grebenev 2011; Jenke et al. 2016) or narrow-field telescopes with observation programs that emphasized accreting neutron stars. The best example of the latter is the high-throughput Proportional Counter Array (PCA) on the Rossi X-ray Timing Explorer (RXTE), which was operational between 1996 and 2012. It detected more than 2200 thermonuclear X-ray bursts with a high throughput (Galloway et al. 2008, 2010).
in ’t Zand et al. (2014) analyzed in detail the light curves of a subset of 37 X-ray bursts that were detected with the PCA. The down selection from more than 2200 to 37 was made in two steps: 1) requiring that the decay, as judged by eye, is smooth; and 2) requiring that the covered dynamic range in flux is wide (more than about 50). This naturally selects hydrogen-poor bursts and UCXBs. The most important result of these authors is that the decay in photon count rate and energy flux can best be modeled by a simple power law (in contrast to the commonly employed exponential decay function), and that the power-law decay index for the energy flux is on average 1.8, with a broad range between 1.3 and 2.4. The most common index of 1.8 is consistent with the electrons carrying most of the heat capacity of the cooling gas. Each burst is consistent with a single power law, which is at odds with the theory presented in this study.
This study is a follow-up of this light curve study of 37 bursts, in which we do not make a selection based on a smooth decay. Therefore, it includes many hydrogen-rich bursts. This 1) provides us with a data set to study the rp process, which because of the waiting points prolongs into the cooling phase; and 2) allows us to study the cooling over many more bursts than 37 after we separate its contribution in the burst decay from that of the rp process. The data set presented by the PCA is the basis of our study. It is the best data set available on X-ray bursts because it is large and provides a wide dynamic range in photon count rates.
In Sects. 2 and 3 we introduce the data of our study and explain how the time histories of the bolometric flux were extracted for each burst. In Sect. 4 we present our approach to modeling the time histories, and in Sect. 5 the results from that modeling, illustrated with histograms and diagrams. In Sect. 6 we discuss these results, while in Sect. 7 we present the conclusions of our study.
2. Data
2.1. Data overview
The PCA, operational from January 1996 to January 2012, consisted of a linear array of five proportional counter units (PCUs) with a total photon-collecting area of 8000 cm2, a bandpass of 2 to 60 keV, and a spectral resolution of about 17% at 6 keV (Jahoda et al. 2006). Each PCU had two proportional counter chambers on top of each other: a top propane layer, and a bottom xenon layer. The xenon layer is the main instrument. The propane layer was used as an anticoincidence counter, although it did occasionally provide scientific value since it extended the bandpass to somewhat lower energies (e.g., Keek 2012). Observations were made with various combinations of PCUs. In general, the average number of active PCUs decreased from five early in the mission to one at the end. The center PCU (number 2, counting from 0) was almost always operational. The PCA electronics typically needed 10 μs to process a single event. For event rates typical for type I bursts (104 s-1), the live time fraction of the PCA was affected by a few percent.
The PCA could be simultaneously read out by six event analyzers (EAs) that could be programmed in any of seven basic read-out modes. One EA always employed the standard-1 mode, yielding photon count rates at 0.125 s resolution for each PCU separately and no photon energy resolution. An often-used mode was the science event mode, which provided the energy information (usually in 64 channels) and timing information (often at 125 μs resolution) for every detected event. Another often-used mode is the good-xenon mode, which provided 0.95 μs time resolution and 256-channel spectra. It was only useful for faint bursts because it more easily overflowed the telemetry than the science event mode. We employed the science event mode because we required an energy resolution that was capable of determining the bolometric flux, and in incidental cases we used the good-xenon mode.
The list of thermonuclear X-ray bursts that RXTE detected was obtained from the Multi-INstrument Burst ARchive (MINBAR; Galloway et al. 2010). In addition to RXTE/PCA data, MINBAR contains the bursts detected with BeppoSAX/WFC (Jager et al. 1997) and the still operational INTEGRAL/JEM-X (Lund et al. 2003). The PCA list in MINBAR consists of 2288 bursts from 60sources (i.e., this is slightly more than half the currently known burster population). Some sources only exhibited one burst in the PCA (e.g., KS 1741-293), while others had close to 400 (e.g., 4U 1636-536). Table 1 lists the burst counts per source (column a).
Sample of 2288 bursts detected with RXTE-PCA from 60 sources (a) and of the selection of 1254 bursts employed in the current study (b).
For a broad perspective of the burst sample and an easy comparison with burst parametrizations elsewhere, we show in Fig. 1 the cumulative distribution of the exponential decay time τ as derived from observed photon rates for all bursts. We included all bad fits since we are only interested in a general picture of timescales and did not draw any further conclusions from these numbers. The most common decay time is 5 s, 50% of all bursts have decay times shorter than 10 s, and 1% have decay times longer than 70 s. The average is 18.9 s.
 |
Fig. 1 Cumulative distribution of exponential decay time τ, as found from fitting Eq. (1)to the photon count rate decay. The employed light curves have 1 s time resolution and concern all RXTE-PCA bursts, except for 181 bursts with insufficient data coverage or almost unconstrained decay times. |
2.2. Data selection
Bursts are often incompletely covered or have signal-to-noise ratios that are too low on the peak fluxes to meaningfully study the decay (i.e., they yield parameter values with large and, thus, indiscriminate uncertainties). We selected only bursts with a continuous data stretch that included the burst start and bursts with relative Poisson errors (after background subtraction) during burst peak better than 5% for one-second exposures. This decreased our sample by roughly 45% to 1254. The number of bursts left per source is specified in Table 1 (column b). Much of the decrease in the sample is due to the many faint bursts on top of a bright persistent flux from IGR J17480-2446 (e.g., Linares et al. 2012), MXB 1730-335 (Bagnoli et al. 2013), 1A 1742-294 (Galloway et al. 2008), Cyg X-2 (e.g., Smale 1998) and GX 17+2 (e.g., Kuulkers et al. 2002). We note that our analysis is biased toward bursts from 4U 1636-536, 4U 1728-34, GS 1826-24, and Aql X-1 because they have the most bursts and the highest signal-to-noise ratio.
3. Spectral analysis
3.1. Approach
Spectra were extracted in fine enough time bins (from 1 s early on in the burst to typically 16 s at the end of the burst) up to mostly 300 s after the burst start time. This 300 s time limit is longer than employed in Galloway et al. (2008), which only covers the brightest portion of the burst (often 30 s and at most out to 150−200 s). The burst start time was determined from the time history of the photon count rate at 1/8 s time resolution; for further details, we refer to the upcoming MINBAR catalog paper (Galloway et al., in prep.). Furthermore, we extracted for each burst a pre-burst spectrum from data taken in the same EA read-out mode and between 100 and 16 s before the burst start, except for a few tens of cases when the data start later than 100 s before the burst start, but before the 16 s mark. All spectra were rebinned such that each spectral bin contained at least 15 photons to ensure applicability of χ2 as the goodness-of-fit parameter. Corrections were applied for the instrument dead time following the prescription from the instrument team1.
The extracted spectra encompass all emission within the field of view and are expected to contain the following components: burst radiation, cosmic X-ray background, particle-induced background, emission from other sources in the field of view, and the non-burst flux from the burst source itself (due to the accretion process). The pre-burst spectrum is considered as one combined measurement of all the components except for the burst radiation. We modeled it through a disk blackbody (Mitsuda et al. 1984) plus power law with the inner disk temperature, photon index, and normalizations of both components as free parameters. Each burst spectrum was modeled by a combination of this pre-burst model and a Planck function for the burst radiation with effective temperature and normalization as free parameters.
It has recently been found that the non-burst accretion flux changes roughly in tandem with the burst flux. in ’t Zand et al. (2013) analyzed the broadband Chandra-PCA spectrum between 0.8 and 20 keV of a very bright burst from SAX J1808.4-3658 and discovered that the spectrum could be satisfactorily modeled if the amplitude of the pre-burst spectrum during the burst was left free to change by a factor of fa while keeping its shape constant. fa was measured to peak at a value of about 30. Worpel et al. (2013, 2015) repeated this exercise on all PCA bursts (approximately the same data set as discussed in the present paper) and found this to be true in general. fa ranges between 1 and a few hundred during the burst peak. When the burst decays, fa generally decreases to approximately unity. There are two interpretations of this “fa effect”: the accretion rate increases in tandem with the burst because of the Poynting-Robertson effect (Worpel et al. 2013, 2015) or a fraction of the burst photons is Compton scattered by an optically thin medium (possibly the accretion disk corona) into the line of sight (in ’t Zand et al. 2013; Keek et al. 2014). Support for scattering and cooling of the corona comes also from measurements at photon energies above 30 keV (e.g., Maccarone & Coppi 2003; Ji et al. 2015; Kajava et al. 2017b).
This fa effect implies that an important choice has to be made in the spectral modeling of the bursts: leave fa free, or keep it fixed at fa = 1. The latter constitutes the traditional method of modeling burst spectra and assumes that the accretion emission is unaffected by the bursts. We chose to perform a full analysis with both methods, showing the results for a free fa in the main part of this paper and those of the fixed fa = 1 in Appendix B. We find that the population-wide perspective of the results is the same, but results on individual sources may differ somewhat.
We applied the fa method in a somewhat different manner than Worpel et al. (2013, 2015). First, we applied a longer exposure time for the pre-burst spectrum of usually 84 s versus 16 s by Worpel et al. (2013, 2015). Second, we fit the same spectral model to all pre-burst spectra, while Worpel et al. fit different models to different bursts. The combination of a disk blackbody and a power law was found to be most generally applicable to all pre-burst spectra, with 63(90)% of all spectra having 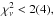 and all burst spectra were finally acceptable. We stress that we employed this model purely empirically and ignored any physical interpretation of it. Third, we did not distinguish between non-burst emission from the burst source and other contributors within the field of view when determining fa, in contrast to Worpel et al. (2013, 2015).
and all burst spectra were finally acceptable. We stress that we employed this model purely empirically and ignored any physical interpretation of it. Third, we did not distinguish between non-burst emission from the burst source and other contributors within the field of view when determining fa, in contrast to Worpel et al. (2013, 2015).
We fit the burst spectra with a combination of the pre-burst model (disk blackbody and power law), fixing its parameters to the pre-burst values and multiplying it with a free constant equal to fa, and a Planck function for the burst radiation with two free parameters (normalization and temperature). The complete model was multiplied with the absorption model for a cold interstellar medium by Morrison & McCammon (1983) and fixing the equivalent hydrogen atom number column density NH per source to the value tabled in Worpel et al. (2013).
A problem with the fa model is (see also Worpel et al. 2015) that the shapes of the blackbody and non-burst spectra are rather similar within the PCA’s 3–20 keV calibrated bandpass, even more so if the statistical quality is not high such as during short exposures. Consequently, there is a coupling between the normalizations of the two components that introduces additional uncertainty in the luminosity of the blackbody component (up to tens of percents according to Worpel et al. 2015). This decreases the diagnostic power of the light-curve analysis and increases the uncertainties of the parameters.
All spectral fits were applied using XSPEC version 12.9.1 (Arnaud 1996) in the calibrated PCA bandpass of 3–20 keV and included a 0.5% systematic uncertainty (Shaposhnikov et al. 2012). A total of more than 35 600 burst spectra were generated. For two-thirds of these spectra, the source was significantly detected in the sense that the flux was at least three times higher than its uncertainty. For these, 4% of the spectral fits had 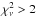 with an average number of degrees of freedom of ⟨ ν ⟩ = 18.7. This percentage is 20 times larger than expected for purely statistical fluctuations. Figure 2 shows the time-resolved spectroscopy of an example burst from GS 1826-24, detected on MJD 51 811.74968 (September 24, 2000, at 17:59:32 UTC) with PCUs 0, 2, and 3.
with an average number of degrees of freedom of ⟨ ν ⟩ = 18.7. This percentage is 20 times larger than expected for purely statistical fluctuations. Figure 2 shows the time-resolved spectroscopy of an example burst from GS 1826-24, detected on MJD 51 811.74968 (September 24, 2000, at 17:59:32 UTC) with PCUs 0, 2, and 3.
From the fitted blackbody parameters, we calculated the bolometric flux. The uncertainty in the bolometric flux was determined by Monte Carlo sampling of the temperature-normalization plane, calculating the bolometric flux for each sample and determining the range of the central 68% values. We note that the bolometric correction, applicable from the 3–20 keV band, is between 1.15 and 1.65 for blackbody temperatures of 3 and 1 keV, respectively.
3.2. Caveats
Our approach to the spectral modeling is, except for the free fa, traditional and effective. Nevertheless, there are some caveats. Foremost, the effective temperature and normalization derived from the blackbody fit are mere proxies for the true effective temperature and emission size. Neutron star surfaces are not blackbodies, but atmospheres that are (nearly) completely ionized and where particularly the hot electrons Comptonize the radiation from below. Furthermore, the atmosphere may contain an increased level of metals that influence the blackbody spectrum through free-free and bound-free electron-ion interactions. Radiation transfer calculations of model atmospheres (London et al. 1986; Madej et al. 2004; Majczyna et al. 2005; Suleimanov et al. 2011, 2012; Nättilä et al. 2015) show that the continuum spectrum may be described by a “diluted” blackbody with a normalization correction factor w (usually w < 1, therefore “diluted”) and a color-correction factor fc (usually fc > 1) to calculate the observed normalization and “color” temperature from the true Planck normalization and effective temperature. If the bolometric flux were unaffected,  would be 1. Nättilä et al. (2015) calculated this number for a variety of metallicities from 1 to 40 times solar plus a pure iron atmosphere, and for gravitational accelerations g between log g = 14.0 and 14.6 for luminosities L between 0.001 and 1 times the Eddington limit LEdd. For Z = Z⊙, we studied
would be 1. Nättilä et al. (2015) calculated this number for a variety of metallicities from 1 to 40 times solar plus a pure iron atmosphere, and for gravitational accelerations g between log g = 14.0 and 14.6 for luminosities L between 0.001 and 1 times the Eddington limit LEdd. For Z = Z⊙, we studied  versus L and find for L> 0.1 LEdd that the trend is consistent with a power-law function with an index of −0.03. We consider this a systematic uncertainty in our cooling power-law decay indices that is due to the blackbody model. Our data also cover the range L< 0.1 LEdd, but we refrained from considering this range because the models show a strong decrease in observed luminosity (and therefore a steepening of the decay), while the data generally do not. Nättilä et al. (2015) attributed this steepening to an opacity that is due to free-free interactions dominating the opacity due to electron scattering.
versus L and find for L> 0.1 LEdd that the trend is consistent with a power-law function with an index of −0.03. We consider this a systematic uncertainty in our cooling power-law decay indices that is due to the blackbody model. Our data also cover the range L< 0.1 LEdd, but we refrained from considering this range because the models show a strong decrease in observed luminosity (and therefore a steepening of the decay), while the data generally do not. Nättilä et al. (2015) attributed this steepening to an opacity that is due to free-free interactions dominating the opacity due to electron scattering.
While leaving fa free improves spectral fits considerably, it is expected that not only the normalization but also the shape of the spectrum of the accretion-induced radiation should change during a burst. If the accretion disk corona is irradiated by the burst photons, its temperature may adjust to the typical temperature of these photons and its spectral shape will change. If the Poynting-Robertson effect is strong, the changing accretion rate is expected to result in variable spectral shapes. We ignored these possibilities because the current spectral model is already rather satisfactory (even in data in a wide bandpass; in ’t Zand et al. 2013). This implies that it is difficult to separate the accretion- and burst-induced spectra from each other, given the limited bandpass and the similar shapes.
We assumed that the burst emission is isotropic. If any anisotropy exists and changes during the burst, this may affect the light curves. However, the few percent anisotropies suggested from burst oscillation measurements (e.g., Watts 2012) are largely averaged out during 1 s time bins by the rotation of the neutron star, which exceeds 10 Hz rotation.
We neglected any absorption features in the burst spectra that might change in amplitude because the ionization degree of the photosphere changes as a result of cooling. Such features have been detected in a few particularly powerful bursts (e.g., Strohmayer & Brown 2002; van Paradijs et al. 1990; in ’t Zand & Weinberg 2010; Keek et al. 2014; Kajava et al. 2017a). However, they make up less than ~ 0.1% of the PCA burst population.
We assumed that the spin of the neutron star has no noticeable effect on the luminosity, either through rotational broadening of spectra by special and general relativistic effects, from an oblateness of the neutron star surface or because burning is confined to changing areas on the neutron star. Bursting neutron star spins are limited to at most 620 Hz, yielding maximum velocities at the equator of 0.1c and an oblateness that is predicted to be a few percent at most (e.g., Bauböck et al. 2012). The implications for the bolometric flux are predicted to be limited to a few percent at most and are constant (e.g., Bauböck et al. 2015).
4. Bolometric light-curve analysis
The goal of our analysis is to model the decay in the bolometric flux of type I X-ray bursts. This bolometric light curve results from the time-resolved spectral modeling discussed in the previous section. In this section we first introduce the approach taken for the light-curve modeling and then discuss a high-quality test case.
4.1. Approach and caveats
The approach that we take to model the bolometric light curves is empirical. Instead of attempting to explain the light curves from first physics principles, which is non-trivial because it involves many different and mutually dependent physical processes whose magnitudes are sometimes ill-constrained (e.g., Woosley et al. 2004; Cyburt et al. 2016), our approach is to apply the simplest mathematical model that is consistent with the data, but has a basic relationship to the physics in terms of the number of components and first-order mathematical forms. Our principal aim is to distinguish the effects of neutron star cooling from those of the rp process. Therefore, our mathematical description consists of two components with different mathematical forms.
Our analysis of the bolometric light curve of each burst consists of the following steps:
-
1.
Double check the start of the burst visually, redetermine starttimes if needed (by at most a few seconds), redefine all times withrespect to this start time.
-
2.
Determine the burst peak flux.
-
3.
Determine the first data point of the decay to be included in fitting the model. This is defined as the last point that drops below 55% of the peak flux (note that the flux may fluctuate and cross the 55% mark multiple times). The 55% mark was evaluated to be the most practical in terms of separation to possible dynamic effects of the emission region (photospheric expansion). Moreover, certain bursts, for instance most from XTE J1814-335 (Strohmayer et al. 2003), clearly have two components: a fast initial spike, and a gradual decrease. The time of this 55% mark is referred to by t0. In 10% of the cases, manual adjustments had to be made to t0 because the light-curve behavior differed near the peak, see Appendix C.
-
4.
Fit the decay data with three models:
-
a.
The traditional two-parameter exponential function
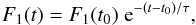 (1)with normalization F1(t0) and exponential decay time τ.
(1)with normalization F1(t0) and exponential decay time τ. -
b.
The two-parameter power law
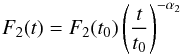 (2)with normalization F2(t0) and decay index α2.
(2)with normalization F2(t0) and decay index α2. -
c.
The four-parameter combination of a power law and a one-sided Gaussian function
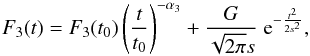 (3)with G the normalization of the Gaussian function and s its standard deviation. The Gaussian function centroid is fixed to the start of the burst t = 0, assuming that the temperature and the hydrogen abundance in the burning layer, and therefore the rp rate, are at a maximum at that time.
(3)with G the normalization of the Gaussian function and s its standard deviation. The Gaussian function centroid is fixed to the start of the burst t = 0, assuming that the temperature and the hydrogen abundance in the burning layer, and therefore the rp rate, are at a maximum at that time.
-
a.
-
5.
Calculate the fluence by adding the integration of the fitteddecay model, from the fit start time to infinity, to the fluences of allthe data points before this until the start of the burst. For the thirdmodel, we separately calculate the fraction f of the Gaussian fluence (G/ 2) to the total fluence.
The functional forms employed in item 4 are motivated by the tradition in burst analyses to model decays with an exponential function, the theoretical expectation that the cooling process follows a power law (Cumming & Macbeth 2004; in ’t Zand et al. 2014), and our goal to model any residuals that look like bumps by the simplest function possible, which is a two-parameter Gaussian function. The choice for a Gaussian function is completely empirical. When we tested this function with theoretical models for the rp process, we found some justification; see Appendix A. It provides a tool to quantify the complex rp process in a straightforward and numerically robust manner that is more or less consistent with the data. The Gaussian amplitude indicates the amount of energy liberated by the rp process, and the Gaussian width its timescale and, thus, nuclear chain length (see below).
 |
Fig. 2 Example of time-resolved spectroscopy of a burst for a burst from GS 1826-24 that was detected at MJD 51 811.750. The typical number of degrees of freedom in these spectral fits is 20. The panels from top to bottom show the time history of the bolometric flux of the best-fit model blackbody, its temperature, its normalization in terms of radius in km of emission sphere when located at 10 kpc distance, the fraction of the time that the detector is susceptible to photon detection (allowing for the detector dead time, see text), the best-fit fa factor, and the reduced chi-squared of the fit. |
We note that we have experimented with several alternatives to the one-sided Gaussian: 1) a Gaussian with a free centroid. This provides somewhat better fits, but the parameters are much more difficult to constrain since this Gaussian has a tendency to fit to any curvature in the observed decay, for instance, the curvatures found later in the burst when variations in the persistent flux may become important. 2) A broken power-law function as a first approximation to a continuously varying power law (e.g., in ’t Zand et al. 2014). This always fits worse. 3) The simplified rp model explained in Appendix A.1, with the parameters amplitude and rp endpoint. We found that this model does not fit the data well because the model timescales are insufficiently long with respect to the data, see also Fig. A.2.
The various decay functions (Eqs. (1)–(3)) in relation to one particular burst are illustrated in Fig. 3 (this is for the same burst whose time-resolved spectroscopy is shown in Fig. 2). The exponential decay is unsatisfactory. The power law even more so, showing a broad excess centered at about 50 s that can be well modeled by including half a Gaussian centered at burst onset. In general, it takes accuracies of a few percent of the peak flux and a dynamic range in excess of a factor of 20 to distinguish the Gaussian component. Therefore it can only be detected with instrumentation with the highest throughput, like the PCA, and not, for instance, with WFC or JEM-X.
We note that best-fit parameters were determined through the Levenberg-Marquardt method (e.g., Bevington & Robinson 1992), with the distinction that G and s were forced to be positive by employing as fitting parameters Gf and sf so that 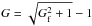 and
and 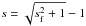 .
.
 |
Fig. 3 Example of a fit to the decay phase of a bolometric light curve of a burst. This is the same burst as in Fig. 2. The top panel shows in logarithmic scale the bolometric flux and the best-fit models for an exponential decay (dashed curve; Eq. (1)), the power law (blue curve; Eq. (2)), and the power-law plus Gaussian function (red curve; Eq. (3)). The second, third, and fourth panels show the residuals with respect to models following Eqs. (1)–(3). The power-law plus Gaussian function is the best model. |
 |
Fig. 4 Application of modeling on the average light curve of 29 RXTE bursts from GS 1826-24 as determined in in ’t Zand et al. (2009). |
In a power law, the applied start time influences the inferred value for α (see Fig. 3 of in ’t Zand et al. 2014). Roughly speaking, an uncertainty of 1 s in the start time translates into an uncertainty of 0.1 in α. We consider the employed start times to be generally more accurate than 1 s. In 0.4% of the cases we manually adjusted the burst start time to accommodate a better fit (see Appendix C).
4.2. High-quality test case
We verified our light-curve modeling on a high-quality test case from the RXTE data archive. GS 1826-24 is a well-documented X-ray burster with highly reproducible bursts and only very slow changes of non-burst emission (Ubertini et al. 1999; Galloway et al. 2004; Heger et al. 2007). in ’t Zand et al. (2009) employed these characteristics to generate a high-quality burst light-curve by averaging PCA/PCU2 data of 29 bursts, to study the tail of these bursts on much longer timescales. We employed our analysis on this very same light curve. The result is shown in Fig. 4. We find that our model 3 is consistent with these data, although there are some small systematic deviations in the data (see bottom panel of figure).
5. Results
 |
Fig. 5 Cumulative distribution for 1254 bursts of |
Figure 5 shows the cumulative distributions of the reduced chi-squared 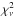 for the three models. We find that the whole burst sample is best fit with the power-law plus Gaussian model and worst fit with the traditional single-exponential function. The distribution for the third model is also closest to the theoretically expected distribution (yellow curve, this is the χ2 distribution for Gaussian statistics assuming 40 degrees of freedom, which is the average value).
for the three models. We find that the whole burst sample is best fit with the power-law plus Gaussian model and worst fit with the traditional single-exponential function. The distribution for the third model is also closest to the theoretically expected distribution (yellow curve, this is the χ2 distribution for Gaussian statistics assuming 40 degrees of freedom, which is the average value).
While the power-law plus Gaussian model is generally the best, it is formally not consistent with the data, given the discrepancy in the cumulative 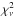 distribution. When fixing fa to 1, this discrepancy worsens. The smaller discrepancy for a free fa may be explained by the aforementioned degeneracy between the persistent and burst spectrum in the 3–20 keV band. The inconsistency of the best-fit model may be partly due to a short-term variability in the spectral shape of the persistent emission. We account for the implied uncertainty by multiplying all associated parameter uncertainties with
distribution. When fixing fa to 1, this discrepancy worsens. The smaller discrepancy for a free fa may be explained by the aforementioned degeneracy between the persistent and burst spectrum in the 3–20 keV band. The inconsistency of the best-fit model may be partly due to a short-term variability in the spectral shape of the persistent emission. We account for the implied uncertainty by multiplying all associated parameter uncertainties with 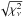 for the power law or the power law plus Gaussian if
for the power law or the power law plus Gaussian if 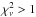 .
.
We review further results through histograms and diagrams. We include only bursts for which the error in the power-law index is smaller than 0.2, the power-law index itself is between 1.0 and 2.5, the error in the Gaussian width s is smaller than 50 s, and the error in the fluence fraction is smaller than 0.1. A final selection was applied by requiring that the burst peak flux is at least 15 times higher than the pre-burst flux. This avoids the worst case of degeneracy between the accretion and burst spectrum, which would affect the calculation of the bolometric burst flux, but remains sensitive enough to detect the Gaussian component. All these filters decrease the sample by approximately half to 501.
Figure 6 shows the histogram of the fitted power-law decay index. The index was taken from the fit with the power law (Eq. (2)) if 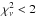 , or from that with the power law plus Gaussian (Eq. (3)) if its
, or from that with the power law plus Gaussian (Eq. (3)) if its 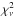 was smaller than that for the fit with the power law. Eighty percent of the decay indices range from roughly 1.3 to 2.1. The average decay index is 1.79 and the rms is 0.31.
was smaller than that for the fit with the power law. Eighty percent of the decay indices range from roughly 1.3 to 2.1. The average decay index is 1.79 and the rms is 0.31.
 |
Fig. 6 Histogram of power-law decay index α (gray shaded) over all acceptably fitting bursts, as found from fitting with Eqs. (2)(α = α2) or (3)(α = α3) when Eq. (2)did not yield a satisfactory fit (i.e., if |
 |
Fig. 7 Histogram of Gaussian width s, as found from fitting with Eq. (3). The peak at 48 s is due to bursts from GS 1826-24, as indicated by the dark gray shaded part of the histogram. Note the cutoff at 60−70 s. |
 |
Fig. 8 Histogram of the fraction f of the fluence contained in the Gaussian component. The peak at 0.6 is due to bursts from GS 1826-24, as indicated by the dark gray shaded part of the histogram. The black histogram blocks are due to bursts from UCXBs at f< 0.3. Note the cutoff beyond the rightmost peak. |
 |
Fig. 9 Diagram of f against s for bursts that fit Eq. (3)best. Indicated in the top right corner are the Spearman rank-order correlation coefficient ρ and the chance probability that ρ is exceeded. |
 |
Fig. 11 Histograms of α for four bursters: two with small variations in persistent flux (4U 1820-30 and GS 1826-24), and two with large variations (4U 1636-536 and 4U 1728-34). 4U 1820-30 has a negligible hydrogen abundance (lower than 10%) in the accreted matter; this is possibly also true for 4U 1728-34. |
Two additional distributions are shown in Fig. 6. The red histogram shows the distribution of the bursts that lack a Gaussian component. There is no qualitative difference with the histogram over all bursts. The average of this distribution is 1.80 and the rms is 0.30. The blue diagram is for all bursts with a significant Gaussian component, with an average of 1.77 and an rms of 0.32. The Kolmogorov-Smirnov test between the data for the red and blue histograms is 0.128;the probability that the value is this high or higher by chance is 3%. The two-sample Anderson-Darling test (Engmann & Cousineau 2011; Pettitt 1976) between both histograms is 1.857 with a chance probability of about 10%. We consider both these tests as insufficient evidence for a difference in the two histograms.
 |
Fig. 12 Diagram for 4U 1636-536 of α against the pre-burst 3–20 keV flux (in units of 10-9 erg cm-2 s-1). |
 |
Fig. 13 Diagram for 4U 1636-536 of α against Sz. The error margins on Sz are fiducial. |
We also separately studied the distribution of power-law indices for all (candidate) UCXBs 4U 0513-40, 2S 0918-549, 4U 1820-30, 4U 1916-05, 4U 1728-34, and 4U 2129+11. We found 108 bursts for these. One hundred and one are best fit with a single power law. The decay index ranges for 80% between 1.4 and 2.1 with an average of 1.94 and an rms of 0.27. These are similar values as for the complete sample, maybe somewhat narrower and steeper.
 |
Fig. 14 Diagram for 4U 1636-536 of f against the parameter SZ. The error margins on Sz are fiducial. |
 |
Fig. 15 Diagram of α against the duration when the power-law flux is above 5% of the peak flux. The red data points refer to bursts from (hydrogen-deficient and, thus, rp-process deficient) UCXBs 4U 0513-40, 2S 0918-549, 4U 1728-34, 4U 1820-30, XB 1916-053, and 4U 2129+12. The blue data points refer to 4U 1636-536 and the orange points to GS 1826-24. This diagram shows the strongest trend in our data with two branches: the short (left) and long branch (right). |
Figure 7 shows the histogram of the fitted values for the width s of the Gaussian component for the bursts that better fit the power law plus Gaussian. The distribution has one large peak at 48 s. This is about half due to bursts from GS 1826-24. The distribution cuts off above 60–70 s, well below the range covered by the data (300 s), with a few detections at large width that have large uncertainties and are associated with bursts with a relatively small Gaussian component (f< 0.1, see Fig. 9).
Figure 8 shows the distribution of the fraction f of the fluence contained in the Gaussian component. This shows that the fluence of the Gaussian is mostly smaller than that of the power-law component. This yields an interesting conclusion about the energy liberated by the rp process, which we discuss in Sect. 6. The distribution is bimodal with a broad component that peaks at f = 0.2 and decreases to almost zero at f = 0.4, and a narrow component centered at f = 0.6. The latter component is again foremost due to GS 1826-24. Both this histogram and that of the width s express the special case of GS 1826-24, which is probably due to its peculiarly constant behavior (see also Ubertini et al. 1999; Galloway et al. 2004; in ’t Zand et al. 2009; Chenevez et al. 2016). Seven out of 108 bursts from UCXBs have a non-zero f value, see Fig. 8. Five are from 4U 1728-34 and one from XB 1916-053 and 4U 0513-40. In all of these cases, the fits with Gaussian components were only marginally better than without. Figure 9 shows a diagram of f versus s. This shows that for each Gaussian width, there is a range of fluence fractions contained in the Gaussian.
An interesting question is whether there is a correlation between α and s or f, because if there were, it would point to a dependence of the cooling on the extent of rp processing. For the same set of bursts, these two parameters are graphed against each other in Fig. 10. There is no obvious correlation with a Spearman rank-order correlation coefficient of ρ = −0.024 and a chance probability of p = 0.72 for this value or larger. The same applies to the dependence between α and f (ρ = −0.119 and p = 0.07). This testifies to a bias-free evaluation of the power law and Gaussian component.
In Fig. 11 we show the distributions of the decay index for four interesting sources with many bursts: GS 1826-24, 4U 1636-536, 4U 1820-30, and 4U 1728-34. Although 4U 1820-30 has considerably fewer bursts than the others, we include it here because it is a confirmed UCXB with a low hydrogen abundance in the accreted gas (Cumming 2003). The distribution is narrow for GS 1826-24, consistent with its constant behavior. The average index is 1.63 and the rms is 0.12(we note that the typical uncertainty in the decay index is of similar magnitude). The distribution for 4U 1636-536 is three times broader and almost equal to that of all bursts. The average index value is 1.82. This source is known to be very variable (e.g., Shih et al. 2011). 4U 1820-30 has a narrow distribution with an average similar to that of 4U 1636-536 (1.90). 4U 1728-34 has an intermediately broad distribution with a steep average index of 2.04.
In Fig. 12 we show the diagram of the decay index of bursts from 4U 1636-536 versus the 3–20 keV flux in the pre-burst spectrum (in units of 10-9 erg cm-2 s-1). There seems to be a trend between the two parameters. Generally, steeper decay indices are found at low pre-burst fluxes. There is a stronger trend if we use Sz instead of pre-burst flux as ordinate, see Fig. 13. Sz is a parameter inferred from the color–color diagram and is interpreted as a better proxy for the mass accretion rate than flux (e.g., Galloway et al. 2008). It is not transferable from source to source, however. There is also a small trend in the diagram of f versus Sz, see Fig. 14. At low Sz values (i.e., smaller than 0.1), there is a shortage of low f< 0.1 values.
Hardly any trends are observed for the Gaussian fluence fraction f (Fig. 14) and the Gaussian width s versus pre-burst flux (not shown).
In Fig. 15 we show the diagram of the decay index versus the duration of the power-law decay, defined as the time that the power-law flux remains above 5% of the peak flux value following the best-fit model for the decay. This diagram is not random; there is a strong correlation between the two parameters. This is probably due to a coupling between these parameters: a shallow decay automatically results in a longer burst duration. It is more interesting that there appear to be two parallel branches. We tested whether they are related to specific types of sources and found that bursts from 4U 1636-536 (the blue data points) spread over both branches, that bursts with a significant Gaussian component also spread over both branches, but that all 108 UCXB bursts except one are on the short branch. It is also noticeable that all bursts from the GS 1826-24 cluster are located on the long (right) branch. The existence of the long branch is related to the fact that a large part of the bursts remains near the peak for some time, even when the Eddington limit is not reached, or has a long rise time. Clear examples of this are bursts from the Rapid Burster (Bagnoli et al. 2013, 2014), GS 1826-24 (see Fig. 2), and 4U 1636-536 (e.g., Zhang et al. 2009).
Many histograms and diagrams show clustering. This may partly be explained by the dominance in the number of bursts from the persistent accretors 4U 1636-536, 4U 1728-34, and GS 1826-24 (see Table 1, column b).
6. Discussion
With reasonable success, we have modeled the decay in bolometric flux of a large sample of thermonuclear X-ray bursts by the combination of a power law with a decay index that is constant over the burst, which we regard as representative of cooling in the neutron star envelope, and a one-sided Gaussian, representative of the rp process. One may question whether these representations are valid since the cooling is expected to be a power law with a varying decay index and the rp process is expected to have more complicated light curves. However, more appropriate functions for the cooling and rp process are difficult, if not impossible, to constrain and distinguish with the best data currently available. Since our simplified modeling does not have these difficulties and is fairly successful, it is interesting to report it and discuss implications, as far as possible.
Recently, Kuuttila et al. (2017) also presented a study of X-ray burst decay in a sample of 540 bursts detected with the PCA. Their focus was on the bursts from 4U 1608-52, 4U 1636-536, 4U 1728-34, 4U 1820-30, and GS 1826-24. This sample pertains to a subset of our sample of 1254 (cf. Table 1). Their data treatment is different from ours, which makes it interesting as a cross check against our results. Basically, the treatment of Kuuttila et al. (2017) follows the fa = 1 method for spectral modeling of the burst spectra, employs the Planck function for the burst emission, and applies a power law to the derived bolometric flux decays with a variable decay index. Complete burst profiles are also included, in contrast to our restriction to fluxes below 55% of the peak. Kuuttila et al. (2017) made no allowance for a second model component next to the power law, like a Gaussian. They found that 1) for the (presumably) H-poor bursts from 4U 1820-30, α has a rather flat profile below about one-third of the peak flux with a value of about 2.0 (cf. Fig. 11); 2) for Eddington-limited bursts (i.e., bursts with photospheric radius expansion or “PRE”) from 4U 1636-526 and 4U 1608-52, the same applies (although at different α values); 3) there are strong α evolutions for all bursts from GS 1826-24 and non-PRE bursts from 4U 1636-536 and 4U 1608-52; 4) below one-third to one-fifth of the peak flux, the α profile is flatter for bursts detected in the hard state than in the soft state. Interestingly, Kuuttila et al. (2017) directly compared the α evolution with the theoretical predictions from in ’t Zand et al. (2014) and found that they are generally inconsistent for fluxes above one-third of the peak flux and marginally consistent below this, with the exception of GS 1826-24, which is strongly inconsistent throughout. In our opinion, both studies (Kuuttila et al. 2017 and ours) show that a large portion of the signal in the decay phase of many bursts is due to rp processing and that the difference between PRE and non-PRE bursts is due to a difference in H abundance in the burning layer. The difference between the two studies, in addition to minor differences in the spectral extraction and modeling we mentioned above, is that we quantitatively attempt to distinguish between the cooling and rp burning. This is only possible, however, if α may be considered constant. In other words, studying the change in power-law decay index precludes the study of the rp process, and vice versa. The exception to this rule is for bursts for which it is more or less certain that there is no H present in the burning layer, like in 4U 1820-30. Kuuttila et al. (2017) found perhaps marginal evidence for α evolution in that source, as judged from their Fig. 3, for the phases where dynamical effects (PRE) are negligible. The difference between soft and hard states is related to our finding of the SZ dependence in our study (Fig. 13).
It may be questioned whether the details of the burst profile are only due to processes within the neutron star or if the burst signal is influenced by the accretion flow. There have been increasing reports of the latter (in ’t Zand et al. 2011, 2013; Chen et al. 2012; Degenaar et al. 2013; Ji et al. 2014b,a; Worpel et al. 2013, 2015), so this is a genuine concern. Fortunately, our attempt to take this into account, through the fa factor, does not make much difference in the results on the distributions of fit parameters (cf. Appendix B). With the assumption that contamination from the accretion flow has been sufficiently taken into account in our analysis, we discuss our findings on cooling and the rp process in the following two subsections.
6.1. Neutron star cooling
The variation in the power-law decay index from burst to burst that we find in this study in 501 bursts (Fig. 6) is similar to the variation found previously in a selection of 37 hydrogen-deficient bursts (in ’t Zand et al. 2014). This implies that the cooling is largely independent of fuel composition or reaction chain. This in turn implies that the variation in the heat capacity of the ashes is small. Furthermore, we find that the broadness of the distribution varies from source to source, with some having a much narrower distribution and others having a distribution almost just as broad as the whole sample, see Fig. 11. It is noticeable that the narrower distributions occur together with rather constant accretion fluxes. This may be related to the fact that the burning regime (see Sect. 1) and ignition depth change when the accretion flux changes. It is also notable that the average index differs from source to source. This is particularly interesting for the three narrow distributions shown in Fig. 11, peaking at α = 1.62, 1.91, and 2.06. This may again be due to systematically different ignition depths. Unfortunately, there is no robust model-independent method to determine the ignition depth for all our bursts to further investigate this dependency.
In Fig. 15 a clear dependence is visible between decay index and power-law duration. The bursts cluster on two branches that each show a decreasing trend of decay index with power-law duration. Figure 15 is a confirmation as well as an elaboration of a tentative finding in Fig. 7 of in ’t Zand et al. (2014). The duration of a burst is rather directly dependent on the ignition depth. The shortest bursts have ignition column depths of about 108 g cm-2. The picture drawn by Fig. 15 is in rough agreement with theoretical expectations (see Fig. 6 in in ’t Zand et al. 2014) that the highest values for α are found in the earliest phases of bursts (i.e., when the burst flux is above 10% of the Eddington limit) with the smallest ignition depth (therefore shortest durations). The reason is that the photons dominate the electrons and ions at shallow depths. We note that we fit only the latter part of the decay, when the flux is half of the peak flux and possibly lower for bursts where part of the flux goes into kinetic energy of a wind. This excludes the high-flux regions (see Fig. 6 in in ’t Zand et al. 2014) where α is steepest and is expected to change the fastest. This may explain partly why our analysis is not sensitive to changes in α. Almost all UCXB, hydrogen-deficient, bursts are on the short branch. Hydrogen-rich bursts spread over both branches. Those that are on the short branch probably burn predominantly helium (in the pure-helium burning regime, see Sect. 1). This shows that hydrogen plays an essential role in generating flat sub-Eddington peaks. We note that if we consider only the blue data points from 4U 1636-536 in Fig. 15, the α versus duration dependence is opposite to that of the general trend. This explains why the diagrams of α and f with SZ or pre-burst flux look counter-intuitive. The reason is that there are two types of bursts emanating from 4U 1636-536: hydrogen-rich and hydrogen-poor bursts. In hydrogen-rich bursts, more photons are produced per gram and the balance favors photons over ions and electrons, and the decay index increases.
The picture drawn here of the power-law component is somewhat confusing. On the one hand, it is unexpected that a single power law describes the cooling of many bursts. This was already clear from the previous study (in ’t Zand et al. 2014). It may be related to the dominance in the heat capacity of one species of particles (ions, electrons, or photons). On the other hand, if a single power-law decay index describes the cooling of neutron stars, why does it differ from burst to burst? The diversity of power-law decay indices over all bursts, also from a single neutron star, seems related to the diversity in accretion flow, see for instance Fig. 13, and as a result, on the diversity of the ignition depth (see above). Possibly, both hands can be joined: the non-detection of decay-index change in single bursts is replaced by a detection of a variation in decay index from burst to burst from the same neutron star.
6.2. rp process
About half of all bursts need the addition of the Gaussian, the others are sufficiently well described by only a power law over a dynamic flux range of, in general, 102. This is partly due to a selection effect: for weaker bursts (intrinsically or because of a relative large burster distance) or for strongly variable accretion radiation, it is more difficult to detect the Gaussian.
In the assumption that the Gaussian is connected to the rp process, its width s is associated with the timescale of the rp process, which has a direct correspondence to the extent of the nuclear chain (see Fig. A.2). The Gaussian width s (Fig. 7) shows a bimodal distribution: a sharp peak at 48 s with a spread of about 10 s and a noisy continuum between 0 and roughly 50 s. Both these components cover about half the population. These timescales are as expected for the rp process, see Fig. A.2, if the nuclear chain extends to at least about 42Ti. This is the first such conclusion drawn from a large observational data study. The peak at 48 s is half due to bursts from GS 1826-24, which is rather stable (in the “hard state”) in its behavior (Ubertini et al. 1999; Galloway et al. 2004; Chenevez et al. 2016), but the other half is due to other bursters.
The histogram of the Gaussian fluence fraction f (Fig. 8) is also bimodal, with a peak at 0.6 due mostly to the reproducible bursts from GS 1826-24 and a continuum extending from 0 to about 0.4. The limited range suggests that there is generally less energy in the rp process than in the 3α burning. This fraction must be related to the abundance of hydrogen and the extent of the rp process. Burning H to Fe yields 5.6 MeV radiative energy per nucleon (where 35% escapes through neutrinos as expected in the rp process, e.g., Fujimoto et al. 1987). Burning He to Fe yields 1.6 MeV per nucleon. The observed fraction of < 0.65 suggests that 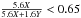 , so
, so 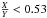 , if X and Y are the mass abundances of hydrogen and helium, respectively. This compares to
, if X and Y are the mass abundances of hydrogen and helium, respectively. This compares to 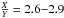 for unprocessed fuel with cosmological or solar abundances. During the Gaussian phase, hydrogen therefore appears to be depleted by a factor of 5 in the burning layer for all bursts from GS 1826-24 and some other bursts from other sources, and at least by a factor of 13 for all other bursts. Hydrogen depletion with respect to the canonical 70% value is probably due to hydrogen burning during the hot CNO cycle or during the initial fast part of the burst (i.e., up to the first waiting point in the rp chain).
for unprocessed fuel with cosmological or solar abundances. During the Gaussian phase, hydrogen therefore appears to be depleted by a factor of 5 in the burning layer for all bursts from GS 1826-24 and some other bursts from other sources, and at least by a factor of 13 for all other bursts. Hydrogen depletion with respect to the canonical 70% value is probably due to hydrogen burning during the hot CNO cycle or during the initial fast part of the burst (i.e., up to the first waiting point in the rp chain).
The histograms of the Gaussian width s and fluence fraction f are dominated by narrow components that are due to the textbook burster GS 1826-24. The burster also distinguishes itself by having the largest and longest Gaussian component, rivaled perhaps only by the Rapid Burster (Bagnoli et al. 2013; in ’t Zand et al. 2017). Other bursts have less hydrogen in the burning layer.
4U 1636-536 is a nice test case for dependencies between burst parameters and the accretion rate because the source has a considerably variable accretion rate and exhibits frequent bursts at many rates. Furthermore, RXTE has a large database on 4U 1636-536. There have been previous interesting studies on this data set, concentrating on the burst oscillation behavior and burst spectral evolution versus accretion rate (e.g., Zhang et al. 2013). We find an interesting dependency (Fig. 14) between the Gaussian fluence fraction and the Sz parameter, which stands for a proxy for the accretion rate. At the low end of the mass accretion rate, we find a substantially larger Gaussian component. This is consistent with the source moving to the so-called burning regime 3 (according to Fujimoto et al. 1981, see Sect. 1) where bursts are ignited in a hydrogen-rich layer. Zhang et al. (2013) find that there is a lack of burst oscillations in this same burning regime.
Ninety-four percent of the bursts from UCXBs clearly lack a significant Gaussian component, and 6% show only a marginally significant detection, which is consistent with the expectation that UCXBs lack hydrogen and the Gaussian being representative of the rp process.
7. Conclusions
Our simplified but successful approach to modeling the decay of thermonuclear shell flashes on accreting neutron stars allows for the following conclusions.
-
1.
Almost all time profiles of X-ray burst bolometric flux can bebetter modeled by the combination of a power law and a one-sidedGaussian function than with an exponential function.
-
2.
No dependency is found between the two light-curve components.
-
3.
Most UCXBs lack significant Gaussian components, which is consistent with it being due to rp burning. The few exceptions are mostly from 4U 1728-34 and are marginal detections.
-
4.
The decay index remains constant within each burst, at least for times when the flux is below 55% of the peak flux.
-
5.
There is no universal power-law decay index; it ranges for 80% between 1.3 and 2.2.
-
6.
There is no unique decay index for any given neutron star, except perhaps for GS 1826-24.
-
7.
The last two points are possibly connected to a spread in ignition depths.
-
8.
The range of decay indices for H-rich systems is similar to that for H-poor systems.
-
9.
GS 1826-24 is an exceptional burster in that it exhibits the largest rp component and the shallowest and most constant decay index.
This investigation was made possible by the high throughput of the PCA instrument on RXTE. It may be verified with the similarly sensitive LAXPC instrument on Astrosat (e.g., Agrawal 2006), provided a similar amount of bursts are observed. A most useful asset in this regard would be an extension of the bandpass toward both lower and higher photon energies and a larger detector effective area. New missions to look forward to in this respect are the NICER mission (e.g. Gendreau et al. 2012; Keek et al. 2016) and the proposed mission concepts LOFT (Feroci et al. 2012; in ’t Zand et al. 2015; Feroci et al. 2016), eXTP (Zhang et al. 2016) and Strobe-X (Ray et al. 2017).
Acknowledgments
We thank Edward Brown and Andrew Cumming for useful discussions and an anonymous referee for suggestions to improve the paper. This paper uses preliminary analysis results from the Multi-INstrument Burst ARchive (MINBAR2), which has received support from the Australian Academy of Science’s Scientific Visits to Europe program, the Australian Research Council’s Discovery Projects and Future Fellowship funding schemes and the European Union’s Horizon 2000 Programme under the AHEAD project (grant agreement No. 654215).
References
- Agrawal, P. C. 2006, Adv. Space Res., 38, 2989 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bagnoli, T., in ’t Zand, J. J. M., Galloway, D. K., & Watts, A. L. 2013, MNRAS, 431, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnoli, T., in ’t Zand, J. J. M., Patruno, A., & Watts, A. L. 2014, MNRAS, 437, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Bauböck, M., Psaltis, D., Özel, F., & Johannsen, T. 2012, ApJ, 753, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bauböck, M., Özel, F., Psaltis, D., & Morsink, S. M. 2015, ApJ, 799, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Belian, R. D., Conner, J. P., & Evans, W. D. 1972, ApJ, 171, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 1992, Data reduction and error analysis for the physical sciences (New York: McGraw-Hill) [Google Scholar]
- Bildsten, L. 1998, in The many faces of neutron stars, eds. A. Alpar, L. Buccheri, & J. van Paradijs (Dordrecht: Kluwer), NATO ASI, 419 [Google Scholar]
- Chelovekov, I. V., & Grebenev, S. A. 2011, Astron. Lett., 37, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-P., Zhang, S., Zhang, S.-N., Li, J., & Wang, J.-M. 2012, ApJ, 752, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Chenevez, J., Galloway, D. K., in ’t Zand, J. J. M., et al. 2016, ApJ, 818, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A. 2003, ApJ, 595, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., & Macbeth, J. 2004, ApJ, 603, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Heger, A., et al. 2016, ApJ, 830, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Miller, J. M., Wijnands, R., Altamirano, D., & Fabian, A. C. 2013, ApJ, 767, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Engmann, S., & Cousineau, D. 2011, J. Appl. Quant. Meth., 6, 1 [Google Scholar]
- Feroci, M., Stella, L., van der Klis, M., et al. 2012, Exp. Astron., 34, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., Bozzo, E., Brandt, S., et al. 2016, in Proc. SPIE, 9905, 99051 [Google Scholar]
- Fisker, J. L., Schatz, H., & Thielemann, F.-K. 2008, ApJS, 174, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Hanawa, T., & Miyaji, S. 1981, ApJ, 247, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Sztajno, M., Lewin, W. H. G., & van Paradijs, J. 1987, ApJ, 319, 902 [CrossRef] [Google Scholar]
- Galloway, D. K., Cumming, A., Kuulkers, E., et al. 2004, ApJ, 601, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D., in ’t Zand, J., Chenevez, J., Keek, L., & Brandt, S. 2010, in 38th COSPAR Scientific Assembly, 6 [Google Scholar]
- Gendreau, K. C., Arzoumanian, Z., & Okajima, T. 2012, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, Proc. SPIE, 8443, 844313 [CrossRef] [Google Scholar]
- Grindlay, J., Gursky, H., Schnopper, H., et al. 1976, ApJ, 205, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Cumming, A., Galloway, D. K., & Woosley, S. E. 2007, ApJ, 671, L141 [NASA ADS] [CrossRef] [Google Scholar]
- in ’t Zand, J. J. M., & Weinberg, N. N. 2010, A&A, 520, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Kuulkers, E., Verbunt, F., Heise, J., & Cornelisse, R. 2003, A&A, 411, L487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J., Verbunt, F., Heise, J., et al. 2004, Nucl. Phys. B Proc. Suppl., 132, 486 [NASA ADS] [CrossRef] [Google Scholar]
- in ’t Zand, J. J. M., Jonker, P. G., & Markwardt, C. B. 2007, A&A, 465, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Keek, L., Cumming, A., et al. 2009, A&A, 497, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Galloway, D. K., & Ballantyne, D. R. 2011, A&A, 525, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Galloway, D. K., Marshall, H. L., et al. 2013, A&A, 553, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Cumming, A., Triemstra, T. L., Mateijsen, R. A. D. A., & Bagnoli, T. 2014, A&A, 562, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Altamirano, D., Ballantyne, D. R., et al. 2015, ArXiv e-print [arXiv:1501.02776] [Google Scholar]
- in ’t Zand, J. J. M., Bagnoli, T., D’Angelo, C., et al. 2017, ArXiv e-print [arXiv:1703.07221] [Google Scholar]
- Jager, R., Mels, W. A., Brinkman, A. C., et al. 1997, A&AS, 125, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Jenke, P. A., Linares, M., Connaughton, V., et al. 2016, ApJ, 826, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, L., Zhang, S., Chen, Y., et al. 2014a, ApJ, 782, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, L., Zhang, S., Chen, Y.-P., et al. 2014b, A&A, 564, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ji, L., Zhang, S., Chen, Y., et al. 2015, ApJ, 806, 89 [NASA ADS] [CrossRef] [Google Scholar]
- José, J., Moreno, F., Parikh, A., & Iliadis, C. 2010, ApJS, 189, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Joss, P. C. 1978, ApJ, 225, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Kajava, J. J. E., Nättilä, J., Poutanen, J., et al. 2017a, MNRAS, 464, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Kajava, J. J. E., Sánchez-Fernández, C., Kuulkers, E., & Poutanen, J. 2017b, A&A, 599, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keek, L. 2012, ApJ, 756, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., & Heger, A. 2016, MNRAS, 456, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., Ballantyne, D. R., Kuulkers, E., & Strohmayer, T. E. 2014, ApJ, 797, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., Wolf, Z., & Ballantyne, D. R. 2016, ApJ, 826, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kuulkers, E., Homan, J., van der Klis, M., Lewin, W. H. G., & Méndez, M. 2002, A&A, 382, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., in ’t Zand, J. J. M., & Lasota, J.-P. 2009, A&A, 503, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuuttila, J., Kajava, J. J. E., Nättilä, J., et al. 2017, A&A, 604, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lampe, N., Heger, A., & Galloway, D. K. 2016, ApJ, 819, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Linares, M., Altamirano, D., Chakrabarty, D., Cumming, A., & Keek, L. 2012, ApJ, 748, 82 [NASA ADS] [CrossRef] [Google Scholar]
- London, R. A., Taam, R. E., & Howard, W. M. 1986, ApJ, 306, 170 [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maccarone, T. J., & Coppi, P. S. 2003, A&A, 399, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madej, J., Joss, P. C., & Różańska, A. 2004, ApJ, 602, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Majczyna, A., Madej, J., Joss, P. C., & Różańska, A. 2005, A&A, 430, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y. E., Yamazaki, T., Suzuki, M., et al. 2004, in Gamma-Ray Bursts: 30 Years of Discovery, eds. E. Fenimore, & M. Galassi, AIP Conf. Ser., 727, 566 [Google Scholar]
- Nättilä, J., Suleimanov, V. F., Kajava, J. J. E., & Poutanen, J. 2015, A&A, 581, A83 [NASA ADS] [EDP Sciences] [Google Scholar]
- Nelson, L. A., Rappaport, S. A., & Joss, P. C. 1986, ApJ, 304, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, F., Brown, E. F., & Truran, J. W. 2007, ApJ, 654, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Pettitt, A. N. 1976, Biometrika, 63, 161 [Google Scholar]
- Ray, P., Wilson-Hodge, C., Gendreau, K., et al. 2017, in APS April Meeting Abstracts [Google Scholar]
- Sakharuk, A., Elliot, T., Fisker, J. L., et al. 2006, in Capture Gamma-Ray Spectroscopy and Related Topics, eds. A. Woehr, & A. Aprahamian, AIP Conf. Ser., 819, 118 [Google Scholar]
- Schatz, H., Aprahamian, A., Barnard, V., et al. 2001, Phys. Rev. Lett., 86, 3471 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shaposhnikov, N., Jahoda, K., Markwardt, C., Swank, J., & Strohmayer, T. 2012, ApJ, 757, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Shih, I. C., Charles, P. A., & Cornelisse, R. 2011, MNRAS, 412, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Smale, A. P. 1998, ApJ, 498, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, New views of thermonuclear bursts, Compact stellar X-ray sources (Cambridge, UK: Cambridge University Press), 113 [Google Scholar]
- Strohmayer, T. E., & Brown, E. F. 2002, ApJ, 566, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Markwardt, C. B., Swank, J. H., & in ’t Zand, J. 2003, ApJ, 596, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., Poutanen, J., & Werner, K. 2011, A&A, 527, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V., Poutanen, J., & Werner, K. 2012, A&A, 545, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E., & Picklum, R. E. 1979, ApJ, 233, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Ubertini, P., Bazzano, A., Cocchi, M., et al. 1999, ApJ, 514, L27 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., Dotani, T., Tanaka, Y., & Tsuru, T. 1990, PASJ, 42, 633 [NASA ADS] [Google Scholar]
- Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Watts, A. L. 2012, ARA&A, 50, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, T. A., Zimmerman, G. B., & Woosley, S. E. 1978, ApJ, 225, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Worpel, H., Galloway, D. K., & Price, D. J. 2013, ApJ, 772, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Worpel, H., Galloway, D. K., & Price, D. J. 2015, ApJ, 801, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, G., Méndez, M., Altamirano, D., Belloni, T. M., & Homan, J. 2009, MNRAS, 398, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, G., Méndez, M., Belloni, T. M., & Homan, J. 2013, MNRAS, 436, 2276 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. N., Feroci, M., Santangelo, A., et al. 2016, in Proc. SPIE, 9905, 99051 [Google Scholar]
Appendix A: Is a Gaussian function a good representation of the rp process?
The one-sided Gaussian is a straightforward mathematical zeroth-order description of the deviations of the bolometric flux time history from power-law decays. The question emerges whether a one-sided Gaussian is a well-motivated zeroth-order representation of the rp process. We investigated this in two ways.
Appendix A.1: Simple nucleosynthesis model for the rp process
We created a simplified model of the rp process, based on the reaction chains as prescribed in Wallace & Woosley (1981) and Schatz et al. (2001). These reaction chains outline which proton captures and beta decays can take place during the rp process. The reaction chain we used was based on the work by Wallace and Woosley for reaction chains with an end point up to 50Fe (see Fig. A.1 of this paper; for longer reaction chains, see Schatz et al. 2001). The full reaction chain we used is presented as the red line in Fig. A.1. There are many points in the reaction chain where both a proton capture and a beta decay are possible. To avoid making our model too complex, at such particular points we ignored the beta decay and assumed that the entirety of the reaction would go through the proton capture. We also assumed a constant high temperature and proton density so that proton capture could be considered instantaneous and the timescales would depend entirely on the beta decay half-lives if no subsequent proton capture is likely (see Table A.1). The simplified model consists of a chain of equations, each calculating the abundance of a beta-decaying isotope per 0.01 s time step. The abundance of each isotope depends on the decay of the previous isotope and on its own decay. We chose 21Mg as the first isotope for our model because it is the first isotope encountering beta decay when the reaction chain breaks out of the CNO cycle for T> 3×108 K, and gave it a starting abundance of 1. We calculated the power associated with each beta decay in keV/s/seed-nucleus by adding the energy Q that is liberated with each proton capture following the beta decay, and multiplying this energy by the number of nuclei that decayed. Table A.1 shows the half-lives of the different isotopes in the reaction chain. We see that there is one decay that has a negative Q associated with it, 71Kr. This is because one of the proton captures following the decay of a 71Kr atom, 72Kr(p, γ)73Rb has a Q of −7121.97 keV. This is the only proton capture in the full reaction chain that has a negative Q. Because so many reactions with a positive Q take place simultaneously, in a real burst there would likely be enough energy available for this capture to take place nevertheless. We convolved the power with a normalized power law with a decay index of 1.6 to account for the fact that the energy released by the rp process first has to travel through the atmosphere before it is emitted by the photosphere and can be measured by our instruments.
Examples of resulting light curves for the simplified rp model are given in Fig. A.2, together with two one-sided Gaussian functions. One has to keep in mind that this figure shows only the output of the rp process, not the output of the cooling after the initial 3α flash. The rp curves show the increase in timescale with the extent of the rp chain. The Gaussian functions are not very good descriptors of the simplified rp process, particularly for the secondary peak at about 100 s, but this peak is rather small and hard to distinguish in the data (and, in fact, not seen in the most sensitive data of a burst with a high rp content, see Fig. 4). Gaussian functions do cover the general trends and provide a tool to quantify the observed timescales. Therefore the timescale measured through the Gaussian function in principle provides a measure for the chain length of the rp process. Combining the timescale measurement with the amplitude provides at least a verification of this chain length.
 |
Fig. A.1 Reaction chain followed in our simplified rp model in red, based on the reaction flows as prescribed by Schatz et al. (2001) and Wallace & Woosley (1981). |
Half-life and energy Q per β+ decay.
 |
Fig. A.2 Nuclear power according to our simplified rp process for end points at 21Mg (dotted curve), 42Ti (dashed), 53Ni and 104Sn (left dash-dotted and right dash-dotted). In these simplified calculations, Q (see Table A.1) is up to 2.4 MeV/nucleon for 53Ni and 2.6 MeV/nucleon for 104Sn. The lines are two examples of one-sided Gaussians with widths of 9 and 50 s. |
 |
Fig. A.3 Fit to KEPLER model 28 (Lampe et al. 2016), showing the effectiveness of the empirical model power-law plus Gaussian function. The model has a metallicity of 2%, a hydrogen content of 70.48%, and an accretion rate of 8.2% of Eddington, so it is expected to have a strong rp tail. Fiducial errors have been applied to calculate the goodness of fit (gof) with the reduced chi-squared formula. The gof numbers have no meaning in an absolute sense but may be compared with each other. |
Appendix A.2: KEPLER models
Lampe et al. (2016) published 465 simulations of thermonuclear X-ray bursts with the KEPLER code (Weaver et al. 1978; Woosley et al. 2004) for various combinations of mass accretion rate, metallicity, and H abundance. The KEPLER code includes an elaborate current nuclear network of 1300 isotopes that models CNO, triple-α, αp, and rp burning. The compositional, temperature, and density changes are tracked one-dimensionally along several zones in the radial direction. Convection and thermohaline mixing are included through one-dimensional prescriptions. Most of the bursts simulated by Lampe et al. (2016) are for accretion rates quite close to the Eddington limit, while our observed bursts are usually far below this. We focused on the 60 simulated bursts that have accretion rates below 10% of the Eddington limit.
Lampe et al. (2016) fit Eq. (2)to their simulated light curves. The decay indices they find are very broadly distributed, between 0.4 and 7.6 for the subset of 60 bursts. Although most bursts are H rich and formally fit unsatisfactorily with a sole power-law function, the indices are much more diverse than we would expect. This appears to be due to features in burst tails that are common in KEPLER simulations but uncommon in observed bursts: flat shoulders that extend up to 200 s and flat peaks extending up to 40 s followed by decays with typical timescales a few times shorter. The latter may be related to an incomplete calculation of radiation pressure effects because all simulated bursts with flat peaks are typically super-Eddington by a factor of 2, while the calculated photospheric radius is not substantially increased. These features render a detailed comparison with the model represented by Eq. (3)less useful. Nevertheless, as an illustration, we fit one simulated burst (model A028) with our empirical model, see Fig. A.3. In this example, the power-law plus Gaussian function is a good fit and the measured power-law index is in the range measured for most real bursts. Peculiarly, the fit with an exponential function is slightly better, while this is almost never the case for real data. This testifies to the limited value of the KEPLER models as a benchmark for our method.
Appendix B: Results for a fixed fa = 1 parameter
 |
Fig. B.1 Cumulative distribution of |
 |
Fig. B.2 Histograms of α for GS 1826-24 for fa = 1. |
 |
Fig. B.4 Histogram of the fraction f of the fluence contained in the Gaussian component for the fa = 1 model. This may be compared to the histogram for the free fa model in Fig. 8. |
We here present some illustrative results of a light-curve analysis with fa = 1. This entails a traditional X-ray burst analysis where a certain pre-burst spectrum is subtracted from burst spectra, and the assumption is that the accretion flow and emission is unaffected by bursts.
Figure B.1 shows the cumulative 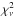 distribution for the fixed fa model and is the equivalent to Fig. 5 for the free fa model. It shows that the fits are substantially worse for a fixed fa model. The main reason is that statistical errors become larger with the additional fa parameter. However, the conclusion is still valid that the power law plus Gaussian best fits the data, followed by the power law and the exponential function.
distribution for the fixed fa model and is the equivalent to Fig. 5 for the free fa model. It shows that the fits are substantially worse for a fixed fa model. The main reason is that statistical errors become larger with the additional fa parameter. However, the conclusion is still valid that the power law plus Gaussian best fits the data, followed by the power law and the exponential function.
Figure B.2 shows the distribution of the power-law index resulting from fa = 1 for GS 1826-24. Of all sources in our sample, GS 1826-24 has the narrowest distribution and is therefore a good illustration of the effect of different choices for fa. For fa = 1, the distribution is somewhat narrower (0.10 versus 0.12) and clusters at a shallower decay index (1.46 versus 1.62). This shallower decay index may be explained as follows. The index becomes steeper for free fa solutions because the low-flux data points carry less weight in the fit because of the larger uncertainties. These low-flux points otherwise tend to pull the power law to shallower decays.
Figure B.3 shows the histogram of the power-law index forthe whole sample. This looks very similar to that for a free fa. The average is 1.78 versus 1.79 for a free fa and the rms is 0.30 versus 0.31.
Figure B.4 shows the histogram of the fluence fraction of the Gaussian. Again, it does not fundamentally differ from that for the free fa model.
Appendix
All 1254 bursts included in our analysis.
Table C.1 is an excerpt of a table that we provide at the CDS3. It lists for each of the 1254 bursts selected for this study the results for models 2 and 3 (Eqs. (2)and (3), respectively), including the goodness of fit 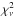 . Furthermore, it lists the manual corrections that were made in incidental cases on the reference time for the bursts, the start time of the burst, and the end time of the burst. These three parameters are only listed when they were different from the nominal values. All results are for a free fa.
. Furthermore, it lists the manual corrections that were made in incidental cases on the reference time for the bursts, the start time of the burst, and the end time of the burst. These three parameters are only listed when they were different from the nominal values. All results are for a free fa.
All Tables
Sample of 2288 bursts detected with RXTE-PCA from 60 sources (a) and of the selection of 1254 bursts employed in the current study (b).
All Figures
 |
Fig. 1 Cumulative distribution of exponential decay time τ, as found from fitting Eq. (1)to the photon count rate decay. The employed light curves have 1 s time resolution and concern all RXTE-PCA bursts, except for 181 bursts with insufficient data coverage or almost unconstrained decay times. |
| In the text | |
 |
Fig. 2 Example of time-resolved spectroscopy of a burst for a burst from GS 1826-24 that was detected at MJD 51 811.750. The typical number of degrees of freedom in these spectral fits is 20. The panels from top to bottom show the time history of the bolometric flux of the best-fit model blackbody, its temperature, its normalization in terms of radius in km of emission sphere when located at 10 kpc distance, the fraction of the time that the detector is susceptible to photon detection (allowing for the detector dead time, see text), the best-fit fa factor, and the reduced chi-squared of the fit. |
| In the text | |
 |
Fig. 3 Example of a fit to the decay phase of a bolometric light curve of a burst. This is the same burst as in Fig. 2. The top panel shows in logarithmic scale the bolometric flux and the best-fit models for an exponential decay (dashed curve; Eq. (1)), the power law (blue curve; Eq. (2)), and the power-law plus Gaussian function (red curve; Eq. (3)). The second, third, and fourth panels show the residuals with respect to models following Eqs. (1)–(3). The power-law plus Gaussian function is the best model. |
| In the text | |
 |
Fig. 4 Application of modeling on the average light curve of 29 RXTE bursts from GS 1826-24 as determined in in ’t Zand et al. (2009). |
| In the text | |
 |
Fig. 5 Cumulative distribution for 1254 bursts of |
| In the text | |
 |
Fig. 6 Histogram of power-law decay index α (gray shaded) over all acceptably fitting bursts, as found from fitting with Eqs. (2)(α = α2) or (3)(α = α3) when Eq. (2)did not yield a satisfactory fit (i.e., if |
| In the text | |
 |
Fig. 7 Histogram of Gaussian width s, as found from fitting with Eq. (3). The peak at 48 s is due to bursts from GS 1826-24, as indicated by the dark gray shaded part of the histogram. Note the cutoff at 60−70 s. |
| In the text | |
 |
Fig. 8 Histogram of the fraction f of the fluence contained in the Gaussian component. The peak at 0.6 is due to bursts from GS 1826-24, as indicated by the dark gray shaded part of the histogram. The black histogram blocks are due to bursts from UCXBs at f< 0.3. Note the cutoff beyond the rightmost peak. |
| In the text | |
 |
Fig. 9 Diagram of f against s for bursts that fit Eq. (3)best. Indicated in the top right corner are the Spearman rank-order correlation coefficient ρ and the chance probability that ρ is exceeded. |
| In the text | |
 |
Fig. 10 Diagram of α3 against s for bursts that fit best Eq. (3)best. |
| In the text | |
 |
Fig. 11 Histograms of α for four bursters: two with small variations in persistent flux (4U 1820-30 and GS 1826-24), and two with large variations (4U 1636-536 and 4U 1728-34). 4U 1820-30 has a negligible hydrogen abundance (lower than 10%) in the accreted matter; this is possibly also true for 4U 1728-34. |
| In the text | |
 |
Fig. 12 Diagram for 4U 1636-536 of α against the pre-burst 3–20 keV flux (in units of 10-9 erg cm-2 s-1). |
| In the text | |
 |
Fig. 13 Diagram for 4U 1636-536 of α against Sz. The error margins on Sz are fiducial. |
| In the text | |
 |
Fig. 14 Diagram for 4U 1636-536 of f against the parameter SZ. The error margins on Sz are fiducial. |
| In the text | |
 |
Fig. 15 Diagram of α against the duration when the power-law flux is above 5% of the peak flux. The red data points refer to bursts from (hydrogen-deficient and, thus, rp-process deficient) UCXBs 4U 0513-40, 2S 0918-549, 4U 1728-34, 4U 1820-30, XB 1916-053, and 4U 2129+12. The blue data points refer to 4U 1636-536 and the orange points to GS 1826-24. This diagram shows the strongest trend in our data with two branches: the short (left) and long branch (right). |
| In the text | |
 |
Fig. A.1 Reaction chain followed in our simplified rp model in red, based on the reaction flows as prescribed by Schatz et al. (2001) and Wallace & Woosley (1981). |
| In the text | |
 |
Fig. A.2 Nuclear power according to our simplified rp process for end points at 21Mg (dotted curve), 42Ti (dashed), 53Ni and 104Sn (left dash-dotted and right dash-dotted). In these simplified calculations, Q (see Table A.1) is up to 2.4 MeV/nucleon for 53Ni and 2.6 MeV/nucleon for 104Sn. The lines are two examples of one-sided Gaussians with widths of 9 and 50 s. |
| In the text | |
 |
Fig. A.3 Fit to KEPLER model 28 (Lampe et al. 2016), showing the effectiveness of the empirical model power-law plus Gaussian function. The model has a metallicity of 2%, a hydrogen content of 70.48%, and an accretion rate of 8.2% of Eddington, so it is expected to have a strong rp tail. Fiducial errors have been applied to calculate the goodness of fit (gof) with the reduced chi-squared formula. The gof numbers have no meaning in an absolute sense but may be compared with each other. |
| In the text | |
 |
Fig. B.1 Cumulative distribution of |
| In the text | |
 |
Fig. B.2 Histograms of α for GS 1826-24 for fa = 1. |
| In the text | |
 |
Fig. B.3 Histograms of α for the fa = 1 model. For a description, see the caption to Fig. 6. |
| In the text | |
 |
Fig. B.4 Histogram of the fraction f of the fluence contained in the Gaussian component for the fa = 1 model. This may be compared to the histogram for the free fa model in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


