EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A137 Full HTML
Free Access
Issue
A&A
Volume 606, October 2017
Article Number A137
Number of page(s) 11
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201730746
Published online 25 October 2017

© ESO, 2017

1. Introduction

Barium stars, CH stars, and carbon-enhanced metal-poor (CEMP) stars with s-process enrichment (CEMP-s) may seem rather distinct objects. Barium stars are G- and K-type giants of roughly solar metallicity with prominent lines of ionized barium and some molecular species of carbon (Bidelman & Keenan 1951). CH stars are somewhat loosely defined as stars whose spectra clearly show the presence of the CH molecule in the photosphere (Keenan 1942; Bond 1974), and are generally subgiants and giants with metallicity around [Fe/H] = −11. And CEMP-s stars are low-metallicity ([Fe/H] ≲ −2) dwarfs and giants with substantial carbon and barium enrichment ([C/Fe] > 1, [Ba/Fe] > 1, and [Ba/Eu] > 0.5; Beers & Christlieb 2005). Nevertheless, all of these objects share notable unifying characteristics: while they display an enrichment in carbon and s-process elements, they are too unevolved to have produced these elements themselves; their radial velocity variations indicate that they all host binary companions (but see Hansen et al. 2016); the mass and luminosity of the companion are consistent with that of a white dwarf (McClure & Woodsworth 1990; Starkenburg et al. 2014; Jorissen et al. 2016; Merle et al. 2016). These characteristics strongly suggest that all these carbon-enriched objects are formed the same way: by binary mass transfer from an asymptotic giant branch (AGB) companion that has since left the AGB and become a white dwarf.

The amount of mass the progenitors of these carbon-enriched stars can accrete must depend on the mass lost by the AGB star and the orbital separation, which sets the mode of mass transfer between wind mass transfer (Han et al. 1995; Pols et al. 2003), wind Roche-lobe overflow (WRLOF; Mohamed & Podsiadlowski 2007; Abate et al. 2013), and Roche-lobe overflow (RLOF; likely of minor importance for these systems as it should in most cases lead to common envelope evolution and result in little accretion by the secondary). But it should also depend on the angular momentum of the material raining down onto the accretor. It seems plausible that, if the accreted material has enough angular momentum to spin the accreting star up to critical rotation, no further accretion can take place before the star either loses the excess angular momentum, or somehow redistributes it in its interior. Packet (1981) estimated analytically that a star needs to accrete only about ten percent of its own mass before it reaches critical rotation. However, the properties of many observed Ba and CEMP-s stars are hard to explain unless they have accreted over 30% of their initial mass (e.g. Miszalski et al. 2013; Abate et al. 2015a,b).

Here we investigate how much mass and angular momentum the supposed progenitors of carbon-enriched stars can accrete before they reach critical rotation. While we do not treat the physics of the accretion process in detail, we consider different accretion rates and values of the specific angular momentum of the accreted material. We thus attempt to deduce if (and what amount of) angular momentum loss is necessary to allow accreting enough mass to explain the chemical abundances of observed CEMP-s and Ba stars. While the focus is mainly on the favourable case of instantaneous redistribution of angular momentum throughout the star, such that uniform rotation is enforced at all times, we also demonstrate the effect of a more realistic treatment of angular momentum redistribution based on the diffusion approximation.

2. Methods

We use the stellar evolution code stars (Eggleton 1971, 1972; Pols et al. 1995; Stancliffe & Eldridge 2009), which has been extended to allow modelling of rotating stars by Potter et al. (2012b,a) based on the work of Endal & Sofia (1976) and Meynet & Maeder (1997).

Stellar rotation is inherently at least a two-dimensional problem. For example, the local gravity geff in a rotating star depends on the angle from the rotation axis θ because of the centrifugal force: 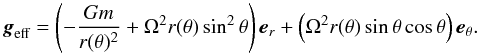geff=(−Gmr(θ)2+Ω2r(θ)sin2θ)er+(Ω2r(θ)sinθcosθ)eθ.\begin{equation} \boldsymbol{g}_{\text{eff}}=\left(-\frac{Gm}{r(\theta)^{2}}+\Omega^{2}r(\theta)\sin^{2}\theta\right)\boldsymbol{e}_{r}+\left(\Omega^{2}r(\theta)\sin\theta\cos\theta\right)\boldsymbol{e}_{\theta}.\label{eq:geff} \end{equation}(1)(Here Ω is the angular velocity, G is the gravitational constant, and m and r are the mass and radial coordinate, respectively.) However, the problem can be kept one-dimensional by formulating the equations of stellar structure on isobaric surfaces SP characterized by radius rP, defined such that 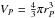VP=43πrP3\hbox{$V_{P}=\frac{4}{3}\pi r_{P}^{3}$} is the volume contained within SP (Meynet & Maeder 1997). Quantities such as temperature and density then represent their averages on an isobar. The radial coordinate rP corresponds to r(θ = θ0 ≈ 54.7°), where sin2θ0 = 2/3. When the star reaches critical rotation (Ω(θ) = Ωc), the radial component of the effective gravity vanishes at the equator (r(π/ 2) = re). At θ0 one has instead (Maeder 2009; Georgy et al. 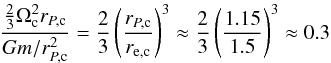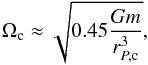2011) 23Ωc2rP,cGm/rP,c2=23(rP,cre,c)3≈23(1.151.5)3≈0.3\begin{equation} \frac{\frac{2}{3}\Omega_{\text{c}}^{2}r_{P,\text{c}}}{Gm/r_{P,\text{c}}^{2}}=\frac{2}{3}\left(\frac{r_{P,\text{c}}}{r_{\text{e,c}}}\right)^{3}\approx\frac{2}{3}\left(\frac{1.15}{1.5}\right)^{3}\approx0.3\label{eq:gcrit} \end{equation}(2)or Ωc≈0.45GmrP,c3,\begin{equation} \Omega_{\text{c}}\approx\sqrt{0.45\frac{Gm}{r_{P,\text{c}}^{3}}},\label{eq:omgc} \end{equation}(3)which we adopt as the condition for critical rotation. This is close to 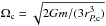Ωc=2Gm/(3rP,c3)\hbox{$\Omega_{\text{c}}=\sqrt{2Gm/(3r_{P,\text{c}}^{3})}$} used by Potter et al. (2012b), to whom we refer for all the details behind the implementation of rotation in the code.

Mass accretion is modelled by simply increasing the mass M of a model at a particular rate Ṁ. The added mass is assigned specific angular momentum ja, so that addition of mass ΔM results in the addition of total angular momentum Ja = jaΔM. To find the upper limit of ΔM for a given value of ja, we set the ZAMS rotation velocity to be small (Ω < 0.01Ωc), so that the initial angular momentum is negligible. The mass is added until 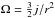Ω=32j/r2\hbox{$\Omega=\frac{3}{2}j/r^{2}$} reaches Ωc anywhere in the model (usually the surface). The added mass is set to have the same composition as the surface at all times, i.e. we ignore composition changes that would surely result from accretion of material from an AGB star near the end of its life. This makes some difference to the angular momentum that a star can accrete (Sect. 3), but none of the conclusions depend on this choice. Furthermore, we assume that the entropy of the added matter is the same as that of the surface at a given time, i.e. no additional energy is deposited in the star by the in-falling matter. As a result of this assumption, we probably underestimate the expansion that results from mass accretion (Prialnik & Livio 1985; Sarna & Ziolkowski 1988; Hosokawa et al. 2010; Haemmerlé et al. 2016). Relaxing this assumption would therefore revise our computed values downwards.

The added angular momentum is instantaneously distributed throughout the star so that uniform rotation results. This gives a plausible upper limit to the amount of material with ja that a star can accrete (Packet 1981). In addition, in some models we follow the internal transport of angular momentum. Potter et al. (2012b) discuss both advective (Zahn 1992; Talon & Zahn 1997) and diffusive (Heger et al. 2000) implementations. We opt here for the diffusive approach, which the stars code is more equipped to handle without additional calibrating constants. Thus meridional circulation is approximated by the Eddington-Sweet circulation (Kippenhahn 1974), and the shear (Zahn 1974; Endal & Sofia 1978), Solberg-Høiland (Wasiutynski 1946), and GSF (Goldreich & Schubert 1967; Fricke 1968) instabilities are all taken into account. For the parameters characterizing the efficiency of rotational mixing, which here only play a minor role because the composition of the accreted material is ignored, we adopt fc = 1/30 and fμ = 0.05, following Heger et al. (2000).

Our models are characterized by the following set of parameters: metallicity Z, initial primary mass MAGB (which here only sets the age at the onset of mass transfer and limits the maximum mass that can be accreted by the secondary to the total amount lost by the primary), initial secondary mass M, mass accretion rate Ṁ, and specific angular momentum of accreted material ja. We restrict ourselves to Z = 10-4 and M ≃ 0.6–0.825 M⊙ for CEMP stars (Abate et al. 2015a,c), and Z = 0.008 and M ≃ 1.0–2.5 M⊙ for Ba stars (e.g. McClure & Woodsworth 1990; Pols et al. 2003; Izzard et al. 2010). The mass accretion rate and specific angular momentum are varied between Ṁ ≃ 10-8–10-5M⊙ yr-1 and ja = (0.2–3) × 1018 cm2s-1. The upper limit of Ṁ is close to typical mass-loss rates of the donor stars near the end of their lives (Vassiliadis & Wood 1993; van Loon et al. 2005; Ramstedt & Olofsson 2014), and the upper limit for ja is comparable to the Keplerian value 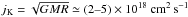jK=GMR≃(2–5)×1018cm2s-1\hbox{$j_{\text{K}}=\sqrt{GMR}\simeq(2\text{--}5)\times10^{18}\ \text{cm}^{2}\thinspace\text{s}^{-1}$} of the different progenitors. At all times we prevent ja from exceeding jK.

3. Results

We have computed the mass ΔM progenitors of carbon-enriched stars can accrete prior to reaching critical rotation (Ω = Ωc) for a range of initial masses of the progenitor M, mass accretion rates Ṁ and specific angular momenta of the added material ja. We now highlight the main features of the models (a summary of all calculations is given in Table A.1).

thumbnail Fig. 1

Mass accreted before critical rotation is reached (relative to initial mass) by uniformly rotating CEMP-s star progenitors for different values of the specific angular momentum of accreted material ja: a) effect of different mass accretion rates in the MAGB = 1 M⊙ case); b) effect of different primary masses (age at the onset of mass transfer) in the Ṁ = 10-8M⊙ yr-1 case. The case of ja = 2 × 1017 cm2 s-1, Ṁ = 10-8M⊙ yr-1 is not shown because in all models ΔM exceeds 0.35 M⊙ (dash-dotted line), at which point the computations were stopped.

Figure 1 shows the amount of mass CEMP-s star progenitors of different masses can add before reaching critical rotation. This amount is a complicated function of the initial structure of the star, the angular momentum of the added material, and the rate at which the material is added. Much of this complexity is an outcome of the response of the star as it gains mass. Thus one crucial parameter is the ratio between the mass accretion timescale τṀ = M/Ṁ (here varied between about 105 and 108 yr) and the thermal adjustment (Kelvin-Helmholtz) timescale τKH of the star (between about 106 and close to 108 yr for the different progenitors). Generally when τṀ ≫ τKH the star is able to stay close to thermal equilibrium, and its global properties change slowly. The star evolves as if replaced at every instant by a slightly more massive and more rapidly rotating star. In this case ΔM depends almost entirely on the angular momentum of the added material alone (this is more clearly seen in Fig. 1b, where Ṁ = 10-8M⊙ yr-1 and τṀ > τKH in all cases).

When τṀ ≲ τKH, the star is driven out of thermal equilibrium, forcing its outer layers to expand while the inner regions are compressed. In this case seemingly minor differences in the initial structure can lead to large differences in the response of the star to mass addition. In particular, the response is related to the convective stability of its outer layers. As long as there is a substantial convective outer region, the star slowly expands and heats up as mass is added. But if in the process of gaining mass convection becomes inefficient and the convective region disappears, the star experiences a brief phase of rapid expansion, during which very little mass (and angular momentum) is accreted (Fig. 2). As the star continues gaining mass, the expansion gradually slows down and the surface layers begin to cool. In stars that initially have a more massive convective region this phase plays a larger role in bringing the star closer to critical rotation, but it also occurs later (Figs. 3 and 4). The result can be a minimum in the ΔM(M) relation, as is the case, e.g. at M ≃ 0.675 M⊙ when ja = 2 × 1017 cm2s-1 (Fig. 1a).

thumbnail Fig. 2

Evolution of the mass distribution in a uniformly rotating model with an initial mass of 0.675 M⊙ when adding matter with ja = 2 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. The light-blue lines show the radius variation with mass in six models from just prior to mass addition to near critical rotation (ΔM ≃ 0.125 M⊙). The black sections of the profiles indicate convective regions. The upper (dark-blue) envelope shows the evolution of the surface radius during mass addition.

thumbnail Fig. 3

Evolution of the radius in uniformly rotating models of the indicated initial masses when adding matter with ja = 2 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. The markers indicate every 10% in Ω/Ωc with the last marker indicating Ω = Ωc. Prior to mass addition the stars have a small outer convective region, which is more massive in less massive stars. The disappearance of this region is followed by a rapid expansion phase, after which the stars are closer to critical rotation. The line corresponding to the M = 0.675 M⊙ case is the same as the upper envelope in Fig. 2.

The evolution of accreting Ba star progenitors is often simpler. Owing to their higher mass the thermal timescale of such stars is about a factor of ten smaller than that of CEMP-s star progenitors. They are thus closer to thermal equilibrium during mass accretion. Furthermore, except in the lowest mass cases (M ≃ 1 M⊙), these stars never have substantial convective envelopes. The disappearance of the convective region and the rapid expansion phase, as observed in the CEMP star case, therefore does not happen in most of these models. Instead the critical rotation rate is reached more gradually, and there is a smaller dependence on Ṁ (Fig. 5).

Packet (1981) presents analytical estimates of the amount of mass a star can accrete when ja = jK. For an initially non-rotating star he finds approximately 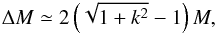ΔM≃2(1+k2−1)M,\begin{equation} \Delta M\simeq2\left(\sqrt{1+k^{2}}-1\right)M,\label{eq:dmp81} \end{equation}(4)where k2 = I/MR2, the square of the normalized gyration radius, characterizes the distribution of mass inside a star with moment of inertia I (a smaller value of k2 corresponds to a steeper, more centrally concentrated mass distribution). While for CEMP-s star progenitors k2 ≃ 0.06–0.12, for Ba star progenitors k2 ≲ 0.05. Thus the value given by Eq. (4)is similar for both sets of progenitors (approximately 0.07–0.09 M⊙). Our computed ΔM values in the ja = jK case are also similar for the two sets, but they are about a factor of two smaller than given by Eq. (4). The difference arises because the response of the star to mass addition (for example, its change in R and k2) is not taken into account by Packet (1981). In particular, k2 decreases during accretion when the outer layers expand (Fig. 2), which implies a lower value of ΔM. Moreover, ΔM shows considerable variation with Ṁ (more so in the CEMP-s star case; Table A.1) because the response of the star depends on the rate at which mass is added.

The distribution of mass in the progenitors of carbon-enriched stars changes during their evolution such that k2 decreases (the stars become more centrally concentrated). As a consequence, the amount of angular momentum the stars can accommodate also decreases over time. Therefore, somewhat more material can be transferred in systems hosting a more massive donor star in which mass transfer occurs earlier (Fig. 1b). But note that we have ignored the composition of the transferred material. Accretion of material with a different composition will alter the opacity, and hence the structure, of the outer layers. The composition will thus also play a role in the response of the star to mass accretion and the amount of mass needed to reach critical rotation. Test models indicate that taking the composition into account can alter ΔM by some ten percent. The effect angular momentum accretion has on the subsequent chemical evolution of carbon-enriched stars is explored in Matrozis & Stancliffe (2017).

thumbnail Fig. 4

Evolution of the surface rotation velocity (starting from Ω/Ωc ≈ 0) for CEMP-s star progenitors of different initial masses when adding mass with ja = 5 × 1017 cm2s-1. The colour coding shows that the disappearance of the convective envelope is accompanied by a rapid expansion phase, during which Ω/Ωc increases.

What is the minimum specific angular momentum that material must have such that accreting it can spin the star up to critical rotation? More explicitly, what is ⟨ j ⟩ when going from J0 = I0Ω0 = 0 to J = IΩc = ⟨ j ⟩ ΔM for large ΔM? Ignoring the change in R and k2 we can crudely estimate that ⟨j⟩≃k2R2(1+MΔM)G(M+ΔM)/R3.\begin{equation} \langle j\rangle\simeq k^{2}R^{2}\left(1+\frac{M}{\Delta M}\right)\sqrt{G\left(M+\Delta M\right)/R^{3}}.\label{eq:jamin} \end{equation}(5)For large ΔM (say ΔM ≃ M) ⟨ j ⟩ ≃ 3k2jK, which for typical values of k2 gives ⟨ j ⟩ ≳ 0.3jK ≃ (5–7) × 1017 cm2s-1 (CEMP stars) and ⟨ j ⟩ ≳ 0.1jK ≃ (5–8) × 1017 cm2s-1 (Ba stars). These values are a bit high (Figs. 1, 6), but give a reasonable estimate when the assumption of a constant radius is closer to being satisfied (e.g. at low accretion rates when thermal equilibrium is maintained). However, models that do swell up can reach critical rotation for even lower values of ja (Fig. 1a).

When the redistribution of angular momentum is not instantaneous, the angular momentum is rapidly distributed only in some outer part of the star (e.g. the convective envelope, when present) instead of throughout, and differential rotation results. One might then expect that generally much less mass is necessary to spin the star up to critical rotation. This is true for ja close to jK (having ja = jK by definition sets the surface to Ω = Ωc). However, when ja is substantially smaller than jK, sometimes even more mass can be added than in the uniformly rotating case (compare Figs. 1a and 7). For example, a M = 0.7 M⊙ CEMP star progenitor rotating uniformly can only add about 0.05 M⊙ of material (when Ṁ = 10-6M⊙ yr-1) with ja = 5 × 1017 cm2s-1 ≃ 0.25jK before reaching critical rotation. But in the differentially rotating case even after adding 0.35 M⊙ no part of the star has reached Ω = Ωc. Figure 8 illustrates why this is the case. When Ω/Ωc reaches unity at the surface in the uniformly rotating case, most of the interior of the star still has Ω/Ωc ≪ 1 (solid black line). If more angular momentum could be stored in the interior, the surface could be prevented from reaching Ωc. This is what happens in the differentially rotating case where more of the angular momentum is stored in the outer 0.1 M⊙ of material at the corresponding time (compare the red lines). By the time 0.35 M⊙ of material have been added (0.35 Myr after the onset of mass accretion) the angular momentum has been transported down to a mass coordinate of m ≃ 0.3 M⊙, and Ω/Ωc> 0.1 in the outer 0.5 M⊙.

4. Discussion

We have stopped the computations and recorded the accreted mass ΔM at the point when the model reaches critical rotation. But this ΔM is subject to change if critical rotation is reached when the star is out of thermal equilibrium. Once accretion stops, the star will attempt to regain equilibrium. Whether the star will tend to spin up or down with respect to the critical rate as it evolves towards equilibrium can be reasonably predicted by comparing ΔM with ΔMTE, the value of ΔM in the case closest to thermal equilibrium (case with the lowest Ṁ).

Models with ΔM < ΔMTE usually experience a phase in which very little mass and angular momentum are accreted while R and Ω/Ωc increase rapidly (Fig. 3). After accretion these stars tend to contract and spin down with respect to the critical rate. After moving away from critical rotation, they could in principle go on to accrete more material (up to about ΔMTE−ΔM such that ΔMfinal ≃ ΔMTE). Conversely, in cases where ΔM > ΔMTE, the stars tend to expand and spin up with respect to the critical rate. Since this is not possible, they must somehow lose angular momentum to return to equilibrium. This could happen by mass shedding (Meynet et al. 2006; Krtička et al. 2011) so that some of the accreted material is, at least temporarily, lost.

The final ΔM thus depends on how the thermal relaxation timescale compares to the accretion timescale. Given the large mass-loss rates near the end of the AGB phase (ṀAGB ≳ 10-5M⊙ yr-1; van Loon et al. 2005; Ramstedt & Olofsson 2014), the mass accretion rate in real systems is likely closer to the higher range of values investigated here (Ṁ ≃ 10− 6...−5M⊙ yr-1, depending on separation). Furthermore, this last stage, during which the AGB star loses most of its envelope, lasts only a small fraction of the overall thermally pulsing AGB lifetime of about 1 Myr (Vassiliadis & Wood 1993; Marigo & Girardi 2007) and is considerably shorter than the thermal timescales of the prospective CEMP and Ba stars. It is thus difficult to envision how the progenitors of carbon-enriched stars could maintain thermal equilibrium (and end up with ΔM ≃ ΔMTE) as they are accreting mass from their AGB companion.

thumbnail Fig. 5

Evolution of the surface rotation velocity (starting from Ω/Ωc ≈ 0) for Ba star progenitors of different initial masses when adding mass with ja = 1 × 1018 cm2s-1. Except for the M = 1 M⊙ case, the outer regions of Ba star progenitors remain radiative at all times.

thumbnail Fig. 6

Mass accreted before critical rotation is reached (relative to initial mass) by uniformly rotating Ba star progenitors for different values of the specific angular momentum of accreted material. For progenitors with M ≥ 1.75 M⊙ addition of material with ja ≤ 5 × 1017 cm2s-1 does not result in critical rotation even for ΔM > 2 M⊙.

thumbnail Fig. 7

Mass accreted before critical rotation is reached (relative to initial mass) by differentially rotating CEMP-s star progenitors for different values of the specific angular momentum of accreted material. Here Ṁ = 10-6M⊙ yr-1. The models were stopped at ΔM = 0.35 M⊙ (dash-dotted line) if critical rotation had not been reached by that point.

thumbnail Fig. 8

Cumulative angular momentum and Ω/Ωc in a M = 0.7 M⊙ model that has added about 0.055 M⊙ of matter with ja = 5 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. For the uniformly rotating model this is just enough to bring it to critical rotation, whereas in the differentially rotating model enough of the angular momentum has been transported to layers deeper in the star (between m ≃ 0.65–0.75 M⊙) to prevent the surface from rotating critically.

We have thus far not discussed the nature of mass transfer. Because RLOF from an AGB star will in most cases be unstable, most carbon-enriched stars probably form through wind mass transfer or WRLOF (Mohamed & Podsiadlowski 2007; Abate et al. 2013). The specific angular momentum of accreted material in the canonical Bondi-Hoyle accretion (Bondi & Hoyle 1944; Edgar 2004) can be less than a few percent of jK (Blondin & Raymer 2012) and would impose no limit on the accreted mass. But because of their slow wind velocities, wind accretion from an AGB star is very different from the Bondi-Hoyle case. As the slowly expanding material cools and falls towards the accretor, it gains angular momentum from Coriolis forces. Once the angular momentum exceeds the local Keplerian value 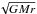GMr\hbox{$\sqrt{GMr}$} (r > R), the material is expected to settle in a disk around the accretor (Eggleton 2006). Both analytical estimates (Soker & Rappaport 2000; Perets & Kenyon 2013) and numerical simulations (e.g. Theuns et al. 1996; Mastrodemos & Morris 1998; de Val-Borro et al. 2009; Huarte-Espinosa et al. 2013; Chen et al. 2017) suggest that disk formation in typical progenitor systems should be common (ja ≃ jK)2.

If the mass accretion in real systems indeed occurs at high rates via a Keplerian disk, our results imply that most CEMP-s (and Ba) star progenitors can gain only up to about ΔM ≃ 0.05 M⊙ even if we assume that the angular momentum is rapidly distributed throughout the star. This is a much smaller amount than the vast majority of CEMP-s stars in the population synthesis calculations of Abate et al. (2015c), who find that the median mass accreted is about 0.15 M⊙ when angular momentum accretion is ignored. Whether accounting for angular momentum accretion would present difficulties explaining the observed fraction of CEMP stars (more than ten percent of all stars with [Fe/H] ≲ −2 are carbon-enhanced; Lucatello et al. 2006; Lee et al. 2013; Placco et al. 2014) would require a careful accounting of the number of systems expected to be lost and gained as a result of severely limiting the accreted masses. Most of the CEMP star progenitors in the simulations of Abate et al. (2015c) have initial masses well below 0.8 M⊙. Stars with larger initial masses (M ≃ 0.8 M⊙) rapidly evolve after accreting a large amount of mass and become white dwarfs. If such stars were not able to gain as much mass, they might be around for long enough to still be observable as CEMP stars. At the same time, some of the lower mass stars, if they were to gain less mass, would no longer be luminous enough to be observable (Abate et al. 2015c). At the moment we can only conclude that angular momentum considerations suggest an initially more massive progenitor population of CEMP-s stars, compared to that found by Abate et al. (2015c).

A more serious issue is that often much higher accreted masses need to be invoked to explain the properties of individual Ba and CEMP stars. For example, Miszalski et al. (2013) require accreting about 0.5 M⊙ onto a M ≃ 1.5 M⊙ (from a primary with initial mass MAGB = 1.8 M⊙), or 0.8 M⊙ onto a M ≃ 2 M⊙ (MAGB = 3 M⊙) star to explain the surface abundances of the Ba star in the planetary nebula Hen 2-39 . Many of the CEMP-s stars considered by Abate et al. (2015a,b) are also best fit with accreted masses in excess of 0.1 M⊙ given the current AGB nucleosynthesis model predictions (Karakas 2010; Lugaro et al. 2012).

In many cases the accreted masses needed to explain the surface chemistry of carbon-enriched stars are a significant fraction of the total mass lost by the AGB star, so the accretor must have captured nearly all of the material entering its Roche lobe. If the star can somehow deal with the angular momentum, this is not implausible. As the inner part of the disk is accreted, the disk spreads outwards to compensate the loss of angular momentum onto the accreting object (Pringle 1981; Lodato 2008). If a disk with initial radius Rd spreads beyond the Roche lobe radius RL, the fraction of material lost that allows the rest to fall to the central object is approximately 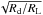Rd/RL\hbox{$\sqrt{R_{\text{d}}/R_{\text{L}}}$} (Lin & Pringle 1976). For disks initially well inside the Roche lobe this is a negligible amount. Furthermore, once the disk spreads enough to approach Rd ≃ RL, tides from the AGB donor (or its remnant) should efficiently transfer angular momentum from the outer disk edge back to the orbit, with little to no mass lost from the Roche volume (Papaloizou & Pringle 1977; Schwarzenberg-Czerny & Rozyczka 1988; Ichikawa & Osaki 1994; Hameury & Lasota 2005)3.

If the star is spun up to critical rotation in the process, it needs to lose angular momentum before it can accrete more of the disk. This could be achieved by depositing the angular momentum back in the disk. Popham & Narayan (1991) show that, once the star approaches critical rotation, outward transport of angular momentum by shear stresses (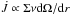\hbox{$\dot{J}\propto\Sigma\nu\mathrm{d}{\Omega}/\mathrm{d}{r}$}, where Σ and ν are respectively the surface density and viscosity of the disk) can dominate the inward transport by accretion (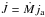\hbox{$\dot{J}=\dot{M}j_{\text{a}}$}), and thus angular momentum can even be removed from the accreting object as it gains mass, if there is sufficient viscous coupling between the star and the disk. This coupling between the accreting star and its disk could also be magnetic in nature. For example, in T Tauri stars (pre-main-sequence stars still surrounded by an accretion disk) the magnetic field of the central star anchors in the disk, which then exerts a negative torque on the star , preventing it from reaching critical rotation (e.g. Armitage & Clarke 1996; Hartmann et al. 1998; Matt & Pudritz 2005b).

Also, some of the energy liberated during accretion could be used to drive strong winds from the stellar surface. Ejecting a mere 10% of the accreted mass would suffice to remove enough angular momentum to prevent critical rotation (Matt & Pudritz 2005a; Dervişoǧlu et al. 2010). However, surface magnetic field strengths in excess of B ~ 100–1000 G are required for this mechanism or disk torques to be effective. While such fields are probably uncommon in the progenitors of carbon-enriched stars, they could perhaps be generated during the accretion if a strong differential rotation results (Dervişoǧlu et al. 2010).

Whatever the mechanism, according to our calculations, for the accreted masses to be large enough to satisfy the chemistry constraints (some tenths of a solar mass), ja must effectively be below about 5 × 1017 cm2s-1 (Figs. 1, 6), or about 10 and 25% of jK for Ba and CEMP stars, respectively. Put differently, above 75% of the angular momentum supplied to the accretor by the disk has to be removed on average.

Nevertheless, the newly born carbon-enriched stars should rotate fairly rapidly after the mass transfer ends. Indeed, a few younger Ba-enriched stars with relatively rapid rotation velocities (tens of km s-1 or more) are known (e.g. Kellett et al. 1995; Jeffries & Smalley 1996; Vennes et al. 1998; Bond et al. 2003; Miszalski et al. 2012), indicating that some angular momentum accretion has occurred. Carbon-enhanced metal-poor dwarfs also rotate more rapidly on average than other metal-poor Halo stars (about 10 and 3 km s-1, respectively; Masseron et al. 2012; Lucatello & Gratton 2003), although the difference is small, which likely points to further angular momentum loss following mass transfer. Given the large amount of time elapsed since mass transfer took place (at least a gigayear)4, magnetic braking seems a plausible candidate for allowing the stars to spin down, assuming it can work in stars with such small convective envelopes (Menv< 10-3M⊙ following mass transfer; Matrozis & Stancliffe 2016).

5. Conclusions

We have calculated in an idealized way the amount of mass that can be added to the progenitors of carbon-enriched (i.e. Ba and CEMP) stars before they are spun up to critical rotation. Material assumed to originate from a Keplerian accretion disk brings the stars to critical rotation after only a few percent of their initial mass is added, even if the angular momentum is allowed to rapidly redistribute throughout the star. If instead the specific angular momentum of the accreted material is a few tenths of the Keplerian value or less, the angular momentum no longer limits the amount of mass that can be added.

Taken at face value, these results have major implications for the progenitor systems of carbon-enriched stars, as many likely do accrete matter through an accretion disk. The large accreted masses inferred from observations of particular Ba and CEMP stars (in some instances comparable to the initial mass of the progenitor) are at odds with our results. However, a way to reconcile them with the necessity of substantial mass accretion would be to invoke some mechanism, such as viscous or magnetic coupling to the accretion disk, that would allow the accreting star to transfer its spin angular momentum back to the orbit with the help of tidal torques from the donor star. In this way the accretor could possibly avoid critical rotation and accrete much more of the material entering its Roche lobe.

1

The relative abundance of element A with respect to element B is [A/B]=logCA(/CB)−logCA(/CB)⊙\hbox{$\text{[A/B]}=\log\left(C_\text{A}/C_\text{B}\right)-\log\left(C_\text{A}/C_\text{B}\right)_{\odot}$} where C is the number or mass fraction.

2

Direct impact (ja < jK) of the transferring material is unlikely because in all but the closest mass ratio binaries the accreting star will be on the main sequence (North & Duquennoy 1991; Böhm-Vitense et al. 2000) and thus well within its Roche lobe. This remains true even if the stars swell up as a result of the accretion.

3

The tidal influence on the accretor itself should be negligible since the timescale for angular momentum transfer from the accretor back to the orbit scales as τsync ~ (R/a)-6 (Zahn 1977), where a ≫ R is the orbital separation.

4

This follows from comparing the lifetime (about 9 Gyr) of the lowest-mass AGB star (MAGB ≃ 0.9 M⊙) that still undergoes third dredge-up at Z ≃ 10-4 (Stancliffe & Glebbeek 2008; Karakas 2010) with the youngest Halo stars (about 10 Gyr). At metallicities characteristic of Ba stars there is no such lower limit.

Acknowledgments

We thank the referee Georges Meynet for valuable comments that have helped improve the presentation and clarity of the paper. We thank Adrian Potter for sharing with us his rotating version of the stars code. We thank Rob Izzard and Zhengwei Liu for illuminating discussions. C.A. acknowledges funding from the Alexander von Humboldt Foundation. R.J.S. is the recipient of a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation.

References

  1. Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Abate, C., Pols, O. R., Izzard, R. G., & Karakas, A. I. 2015a, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015b, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Abate, C., Pols, O. R., Stancliffe, R. J., et al. 2015c, A&A, 581, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Armitage, P. J., & Clarke, C. J. 1996, MNRAS, 280, 458 [NASA ADS] [Google Scholar]
  6. Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bidelman, W. P., & Keenan, P. C. 1951, ApJ, 114, 473 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blondin, J. M., & Raymer, E. 2012, ApJ, 752, 30 [NASA ADS] [CrossRef] [Google Scholar]
  9. Böhm-Vitense, E., Carpenter, K., Robinson, R., Ake, T., & Brown, J. 2000, ApJ, 533, 969 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bond, H. E. 1974, ApJ, 194, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bond, H. E., Pollacco, D. L., & Webbink, R. F. 2003, AJ, 125, 260 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chen, Z., Frank, A., Blackman, E. G., Nordhaus, J., & Carroll-Nellenback, J. 2017, MNRAS, 468, 4465 [NASA ADS] [CrossRef] [Google Scholar]
  14. de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dervişoǧlu, A., Tout, C. A., & Ibanoǧlu, C. 2010, MNRAS, 406, 1071 [NASA ADS] [Google Scholar]
  16. Edgar, R. 2004, New Astron. Rev., 48, 843 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
  18. Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
  19. Eggleton, P. 2006, Evolutionary Processes in Binary and Multiple Stars (Cambridge, UK: Cambridge University Press) [Google Scholar]
  20. Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
  21. Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fricke, K. 1968, ZAp, 68, 317 [Google Scholar]
  23. Georgy, C., Meynet, G., & Maeder, A. 2011, A&A, 527, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571 [NASA ADS] [CrossRef] [Google Scholar]
  25. Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2016, A&A, 585, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Hameury, J.-M., & Lasota, J.-P. 2005, A&A, 443, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Han, Z., Eggleton, P. P., Podsiadlowski, P., & Tout, C. A. 1995, MNRAS, 277, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hansen, T. T., Andersen, J., Nordström, B., et al. 2016, A&A, 588, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
  30. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [NASA ADS] [CrossRef] [Google Scholar]
  32. Huarte-Espinosa, M., Carroll-Nellenback, J., Nordhaus, J., Frank, A., & Blackman, E. G. 2013, MNRAS, 433, 295 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ichikawa, S., & Osaki, Y. 1994, PASJ, 46, 621 [NASA ADS] [Google Scholar]
  34. Izzard, R. G., Dermine, T., & Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Jeffries, R. D., & Smalley, B. 1996, A&A, 315, L19 [NASA ADS] [Google Scholar]
  36. Jorissen, A., Van Eck, S., Van Winckel, H., et al. 2016, A&A, 586, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
  38. Keenan, P. C. 1942, ApJ, 96, 101 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kellett, B. J., Bromage, G. E., Brown, A., et al. 1995, ApJ, 438, 364 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kippenhahn, R. 1974, in Late Stages of Stellar Evolution, eds. R. J. Tayler, & J. E. Hesser, IAU Symp., 66, 20 [Google Scholar]
  41. Krtička, J., Owocki, S. P., & Meynet, G. 2011, A&A, 527, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lee, Y. S., Beers, T. C., Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lin, D. N. C., & Pringle, J. E. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 237 [Google Scholar]
  44. Lodato, G. 2008, New Astron. Rev., 52, 21 [NASA ADS] [CrossRef] [Google Scholar]
  45. Lucatello, S., & Gratton, R. G. 2003, A&A, 406, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
  48. Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin Heidelberg: Springer) [Google Scholar]
  49. Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Masseron, T., Johnson, J. A., Lucatello, S., et al. 2012, ApJ, 751, 14 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mastrodemos, N., & Morris, M. 1998, ApJ, 497, 303 [NASA ADS] [CrossRef] [Google Scholar]
  52. Matrozis, E., & Stancliffe, R. J. 2016, A&A, 592, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Matrozis, E., & Stancliffe, R. J. 2017, A&A, 606, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Matt, S., & Pudritz, R. E. 2005a, ApJ, 632, L135 [NASA ADS] [CrossRef] [Google Scholar]
  55. Matt, S., & Pudritz, R. E. 2005b, MNRAS, 356, 167 [NASA ADS] [CrossRef] [Google Scholar]
  56. McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
  57. Merle, T., Jorissen, A., Van Eck, S., Masseron, T., & Van Winckel, H. 2016, A&A, 586, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Meynet, G., & Maeder, A. 1997, A&A, 321, 465 [NASA ADS] [Google Scholar]
  59. Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Miszalski, B., Boffin, H. M. J., Frew, D. J., et al. 2012, MNRAS, 419, 39 [NASA ADS] [CrossRef] [Google Scholar]
  61. Miszalski, B., Boffin, H. M. J., Jones, D., et al. 2013, MNRAS, 436, 3068 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mohamed, S., & Podsiadlowski, P. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [Google Scholar]
  63. North, P., & Duquennoy, A. 1991, A&A, 244, 335 [NASA ADS] [Google Scholar]
  64. Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
  65. Papaloizou, J., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
  66. Perets, H. B., & Kenyon, S. J. 2013, ApJ, 764, 169 [NASA ADS] [CrossRef] [Google Scholar]
  67. Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
  68. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  69. Pols, O. R., Schröder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pols, O. R., Karakas, A. I., Lattanzio, J. C., & Tout, C. A. 2003, in Symbiotic Stars Probing Stellar Evolution, eds. R. L. M. Corradi, J. Mikolajewska, & T. J. Mahoney, ASP Conf. Ser., 303, 290 [Google Scholar]
  71. Popham, R., & Narayan, R. 1991, ApJ, 370, 604 [NASA ADS] [CrossRef] [Google Scholar]
  72. Potter, A. T., Tout, C. A., & Brott, I. 2012a, MNRAS, 423, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  73. Potter, A. T., Tout, C. A., & Eldridge, J. J. 2012b, MNRAS, 419, 748 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  74. Prialnik, D., & Livio, M. 1985, MNRAS, 216, 37 [NASA ADS] [Google Scholar]
  75. Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
  76. Ramstedt, S., & Olofsson, H. 2014, A&A, 566, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Sarna, M. J., & Ziolkowski, J. 1988, Acta Astron., 38, 89 [NASA ADS] [Google Scholar]
  78. Schwarzenberg-Czerny, A., & Rozyczka, M. 1988, Acta Astron., 38, 189 [NASA ADS] [Google Scholar]
  79. Soker, N., & Rappaport, S. 2000, ApJ, 538, 241 [NASA ADS] [CrossRef] [Google Scholar]
  80. Stancliffe, R. J., & Eldridge, J. J. 2009, MNRAS, 396, 1699 [NASA ADS] [CrossRef] [Google Scholar]
  81. Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
  82. Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  83. Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
  84. Theuns, T., Boffin, H. M. J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  85. van Loon, J. T., Cioni, M.-R. L., Zijlstra, A. A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
  87. Vennes, S., Christian, D. J., & Thorstensen, J. R. 1998, ApJ, 502, 763 [NASA ADS] [CrossRef] [Google Scholar]
  88. Wasiutynski, J. 1946, Astrophys. Norvegica, 4, 1 [NASA ADS] [Google Scholar]
  89. Zahn, J.-P. 1974, in Stellar Instability and Evolution, eds. P. Ledoux, A. Noels, & A. W. Rodgers, IAU Symp., 59, 185 [Google Scholar]
  90. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
  91. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

Appendix A: Additional table

Table A.1

Mass accreted before critical rotation is reached (ΔM) by the different models.

All Tables

Table A.1

Mass accreted before critical rotation is reached (ΔM) by the different models.

In the text

All Figures

thumbnail Fig. 1

Mass accreted before critical rotation is reached (relative to initial mass) by uniformly rotating CEMP-s star progenitors for different values of the specific angular momentum of accreted material ja: a) effect of different mass accretion rates in the MAGB = 1 M⊙ case); b) effect of different primary masses (age at the onset of mass transfer) in the Ṁ = 10-8M⊙ yr-1 case. The case of ja = 2 × 1017 cm2 s-1, Ṁ = 10-8M⊙ yr-1 is not shown because in all models ΔM exceeds 0.35 M⊙ (dash-dotted line), at which point the computations were stopped.
In the text
thumbnail Fig. 2

Evolution of the mass distribution in a uniformly rotating model with an initial mass of 0.675 M⊙ when adding matter with ja = 2 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. The light-blue lines show the radius variation with mass in six models from just prior to mass addition to near critical rotation (ΔM ≃ 0.125 M⊙). The black sections of the profiles indicate convective regions. The upper (dark-blue) envelope shows the evolution of the surface radius during mass addition.
In the text
thumbnail Fig. 3

Evolution of the radius in uniformly rotating models of the indicated initial masses when adding matter with ja = 2 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. The markers indicate every 10% in Ω/Ωc with the last marker indicating Ω = Ωc. Prior to mass addition the stars have a small outer convective region, which is more massive in less massive stars. The disappearance of this region is followed by a rapid expansion phase, after which the stars are closer to critical rotation. The line corresponding to the M = 0.675 M⊙ case is the same as the upper envelope in Fig. 2.
In the text
thumbnail Fig. 4

Evolution of the surface rotation velocity (starting from Ω/Ωc ≈ 0) for CEMP-s star progenitors of different initial masses when adding mass with ja = 5 × 1017 cm2s-1. The colour coding shows that the disappearance of the convective envelope is accompanied by a rapid expansion phase, during which Ω/Ωc increases.
In the text
thumbnail Fig. 5

Evolution of the surface rotation velocity (starting from Ω/Ωc ≈ 0) for Ba star progenitors of different initial masses when adding mass with ja = 1 × 1018 cm2s-1. Except for the M = 1 M⊙ case, the outer regions of Ba star progenitors remain radiative at all times.
In the text
thumbnail Fig. 6

Mass accreted before critical rotation is reached (relative to initial mass) by uniformly rotating Ba star progenitors for different values of the specific angular momentum of accreted material. For progenitors with M ≥ 1.75 M⊙ addition of material with ja ≤ 5 × 1017 cm2s-1 does not result in critical rotation even for ΔM > 2 M⊙.
In the text
thumbnail Fig. 7

Mass accreted before critical rotation is reached (relative to initial mass) by differentially rotating CEMP-s star progenitors for different values of the specific angular momentum of accreted material. Here Ṁ = 10-6M⊙ yr-1. The models were stopped at ΔM = 0.35 M⊙ (dash-dotted line) if critical rotation had not been reached by that point.
In the text
thumbnail Fig. 8

Cumulative angular momentum and Ω/Ωc in a M = 0.7 M⊙ model that has added about 0.055 M⊙ of matter with ja = 5 × 1017 cm2s-1 at a rate of Ṁ = 10-6M⊙ yr-1. For the uniformly rotating model this is just enough to bring it to critical rotation, whereas in the differentially rotating model enough of the angular momentum has been transported to layers deeper in the star (between m ≃ 0.65–0.75 M⊙) to prevent the surface from rotating critically.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.