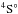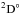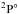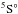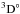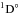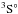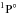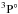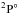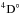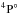| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201731110 | |
| Published online | 04 September 2017 | |
Single and double K-shell resonant photoionization and Auger decay of 1s → 2p excited states of O+–O4+
1 Department of Physics, College of Science, National University of Defense Technology, Changsha Hunan 410073, PR China
e-mail: jlzeng@nudt.edu.cn
2 IFSA Collaborative Innovation Center, Shanghai Jiao Tong University, Shanghai 200240, PR China
3 Graduate school of China Academy of engineering Physics, Beijing 100193, PR China
Received: 4 May 2017
Accepted: 13 June 2017
In this work, single and double photoionization cross sections in the vicinity of 1s → 2p resonances are investigated theoretically for quantum states belonging to the ground and first excited configurations of O+–O4+. R-matrix method has been employed to obtain the single ionization cross section, whereas the double ionization cross sections are obtained by the branching ratios of the direct double Auger decay to the total Auger decay. By analyzing possible double ionization pathways, we conclude that the double photoionization originates predominately from the direct double Auger decay of the K-shell resonant states. Our theoretical work diagnosed the population fraction of the quantum state prepared in a recent experiment and successfully interpreted the experimental observations on both single and double photoionization cross sections.
Key words: atomic data / atomic processes
© ESO, 2017
1. Introduction
The observations from X-ray satellites including Chandra and XMM-Newton have identified a number of intense lines originating from the 1s → 2p transitions in different ionization stages of light elements, in particular oxygen. Oxygen is the third most abundant element in the astrophysical plasmas and it is also abundant in the Earth’s atmosphere. The X-ray photoabsorption in the KLL resonances of O5+ was first detected by the Chandra X-ray Observatory (Lee et al. 2001). Up to now the K-shell absorption lines of oxygen and its ions have been observed in various astrophysical objects (Kallman et al. 2013; Ramírez 2013; Liao et al. 2013; Pinto et al. 2013; Yao et al. 2009).
The observations of K-shell photoabsorption from X-ray satellites motivated both experimental and theoretical investigations on the photoionization (PI) cross sections, which are the basic atomic data to model the astrophysical plasmas and to identify the observed lines. Here we mention relevant work related to O+–O4+. Theoretically, earlier work by Chen et al. (1997, 1988, 1987) investigated the K-shell Auger decay and radiative transitions for the carbon-like and boron-like ions including O2+ and O3+ using the multi-configuration Dirac-Fock (MCDF) approach. For O3+, additional variety of methods such as 1 /Z perturbation theory (Safronova & Shlyaptseva 1999) and the saddle-point-method with R-matrix, complex coordinate rotation methods (Chung 1990; Lin et al. 2001, 2002; Sun et al. 2011, 2013) were used to calculate the Auger resonance energies and widths of K-shell excited states. Later, the K-shell Auger processes of O+–O4+ were investigated by using the R-matrix method (Petrini 1981; Petrini & Da Silva 1996; Zeng et al. 2001, 2004; Zeng & Yuan 2002; Olalla et al. 2002; Pradhan et al. 2003; Garcia et al. 2005), which represent the state-of-the-art ab initio calculations. Experimentally, the relative 1s → 2p resonance PI cross section of O+ was measured by Kawatsura et al. (2002) using the merged-beam technique. Absolute K-shell PI cross sections for boron-like O3+ ions were measured by McLaughlin et al. (2014) employing the ion-photon merged-beam technique at the SOLEIL synchrotron-radiation facility in the photon energy range from 540 to 600 eV with a resolving power ~5000. The key parameters including the resonance energies, natural lifetime widths and resonance strengths of the strong 1s → 2p and the weaker 1s → 3p resonances were determined from the observed K-shell spectra of this ion. All the above theoretical and experimental investigations are devoted to the single PI or single Auger decay processes. Very recently, Bizau et al. (2015) experimentally measured the absolute cross sections for the single and double K-shell PI of O+ and O2+ ions in the 526−620 eV photon energy range by employing the ion-photon merged-beam technique with a high-resolution of resolving power ~5300 at the SOLEIL synchrotron-radiation facility. To the best of our knowledge, however, no theoretical investigations were carried out to the double K-shell PI and double Auger decay of O+–O4+.
In this work, we investigate the 1s → 2p double PI of the quantum states belonging to the ground and the first excited configurations of O+–O4+. We point out that the resonance double PI originates from the direct double Auger decay (DDAD) of the K-shell excited states. By studying the single and double Auger decay rates, the branching ratios (BRs) of DDAD to the total Auger decay are determined. Combining with the single PI cross sections, we obtain the double PI cross sections. Our theoretical results are compared with the experiment of Bizau et al. (2015) and we concluded that the DDAD processes of the final K-shell excited states are the origin of the double PI. We successfully diagnosed the population fraction of the prepared initial state in this experiment and interpreted the experimental results for the first time.
2. Theoretical method
The single PI cross sections were obtained using the R-matrix method (Berrington et al. 1995), which is a powerful tool for analyzing the resonances in the continuum processes. The theoretical background can be found elsewhere (Berrington et al. 1995) and the detailed procedure of the method is described in our previous work (Liu et al. 2014c, 2011, 2013), so we give only an outline here. The basic idea of the R-matrix method is to partition the space into the internal and external regions. In the internal region, the wave function of the (N + 1)-electron system is described as 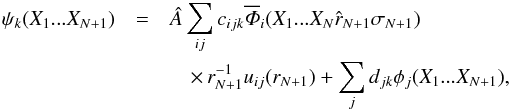 (1)where  is antisymmetrization operator which accounts for the electron exchange between the electrons of the target and the continuum electron. Xm stands for the spatial coordinates (rm) and the spin (σm) of the mth electron. The continuum orbitals uij(r) of the scattered electron are the only terms to be non-zero on the surface of the internal region. In the external region, the exchange interaction between the bound electrons of target and the continuum electron is completely excluded. In both regions, the wave function of target state Φi is expressed in a configuration interaction expansion
(1)where  is antisymmetrization operator which accounts for the electron exchange between the electrons of the target and the continuum electron. Xm stands for the spatial coordinates (rm) and the spin (σm) of the mth electron. The continuum orbitals uij(r) of the scattered electron are the only terms to be non-zero on the surface of the internal region. In the external region, the exchange interaction between the bound electrons of target and the continuum electron is completely excluded. In both regions, the wave function of target state Φi is expressed in a configuration interaction expansion 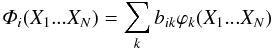 (2)where ϕk is the configuration state function which is constructed from the one-electron orbitals. The configuration interaction expansion allows us to include adequate electron correlations for both the target and (N + 1)-electron system to obtain as accurate results as possible.
(2)where ϕk is the configuration state function which is constructed from the one-electron orbitals. The configuration interaction expansion allows us to include adequate electron correlations for both the target and (N + 1)-electron system to obtain as accurate results as possible.
Theoretical and experimental energies (Kramida et al. 2015) (in eV) for the terms of target states of O2+ and O3+ relative to the ground state in the calculations of PI of O+ and O2+.
Theoretical and experimental energies (Kramida et al. 2015) (in eV) for the terms of target states of O4+ and O5+ relative to the ground state in the calculations of PI of O3+ and O4+.
Single Auger decay (SAD) rates (in s-1), direct double Auger decay (DDAD) rates (in s-1), branching ratios (BR) (%) of DDAD relative to the total Auger process, and the natural lifetime widths (in meV) of the O+1s → 2p excited states.
In this work, the wave functions of the targets were cast as linear combinations of Slater-type orbitals with the appropriate parameters being determined using the CIV3 computer code (Hibbert 1975) except for those orbitals of the ground configurations being taken from Clementi & Roetti (1974). Explicitly, thirteen orbitals (1s, 2s, 2p, 3s, 3p,  ,
,  ,
, 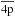 ,
, 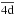 ,
, 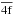 ,
, 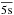 ,
, 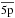 , and
, and 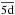 ) were included in the expansion of the wave functions of the target and N + 1 electron system to obtain the photoionization cross section of O+. The wave functions of 3s and 3p orbitals were obtained by optimizing on the 1s22s22p3s
) were included in the expansion of the wave functions of the target and N + 1 electron system to obtain the photoionization cross section of O+. The wave functions of 3s and 3p orbitals were obtained by optimizing on the 1s22s22p3s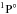 and 1s22s22p3p3P states, respectively. The bar on the orbital indicates that it is a pseudo-orbital. The
and 1s22s22p3p3P states, respectively. The bar on the orbital indicates that it is a pseudo-orbital. The 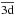 ,
, 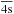 ,
, 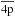 , and
, and 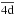 were obtained by optimizing on the 1s22s2p3
were obtained by optimizing on the 1s22s2p3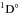 , 1s22s2p3
, 1s22s2p3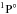 , 1s22s22p21D and 1s22s02p43P states, respectively. The
, 1s22s22p21D and 1s22s02p43P states, respectively. The 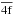 ,
, 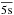 ,
, 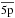 , and
, and 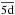 orbitals were obtained by optimizing on the 1s-hole states 1s2s22p3
orbitals were obtained by optimizing on the 1s-hole states 1s2s22p3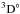 , 1s2s2p43P, 1s2s22p3
, 1s2s2p43P, 1s2s22p3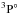 , and 1s2s2p43D, respectively. For the calculations of O2+, O3+ and O4+, we have included ten electron orbitals of 1s, 2s, 2p, 3s, 3p, 3d,
, and 1s2s2p43D, respectively. For the calculations of O2+, O3+ and O4+, we have included ten electron orbitals of 1s, 2s, 2p, 3s, 3p, 3d, 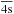 ,
, 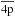 ,
, 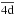 , and
, and 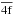 . For the target states of O2+, the wave functions of 3s, 3p and 3d orbitals were obtained by optimizing on the 1s22s23s2S, 1s22s23p
. For the target states of O2+, the wave functions of 3s, 3p and 3d orbitals were obtained by optimizing on the 1s22s23s2S, 1s22s23p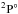 and 1s22s23d2D states, respectively, while the pseudo-orbitals
and 1s22s23d2D states, respectively, while the pseudo-orbitals 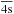 ,
, 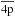 ,
, 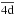 , and
, and 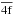 were obtained by optimizing on the 1s22s2p22S, 1s22s2p22P, 1s22s02p3
were obtained by optimizing on the 1s22s2p22S, 1s22s2p22P, 1s22s02p3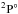 and 1s22s2p22D states. The wave functions of spectroscopic orbitals (2p, 3s, 3p and 3d) of O3+ were optimized on the singlet terms of their respective configurations, whereas those of
and 1s22s2p22D states. The wave functions of spectroscopic orbitals (2p, 3s, 3p and 3d) of O3+ were optimized on the singlet terms of their respective configurations, whereas those of 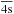 ,
, 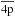 ,
, 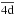 , and
, and 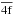 were used to improve the states of 1s22p21S, 1s22s2p
were used to improve the states of 1s22p21S, 1s22s2p , 1s2s22p
, 1s2s22p and 1s2s2p23D, respectively. For the description of the target states of O4+, the wave functions of 2p, 3s, 3p and 3d were determined to represent their only respective spectroscopic term, whereas the pseudo-orbitals
and 1s2s2p23D, respectively. For the description of the target states of O4+, the wave functions of 2p, 3s, 3p and 3d were determined to represent their only respective spectroscopic term, whereas the pseudo-orbitals 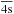 ,
, 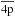 ,
, 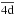 , and
, and 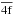 were optimized on the states of 1s2p22S, 1s2s(1S)2p
were optimized on the states of 1s2p22S, 1s2s(1S)2p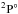 , 1s2p22D and 1s2p22P.
, 1s2p22D and 1s2p22P.
The R-matrix wave function expansion was performed by including 30, 28, 21, and 17 target states for the calculations of photoionization of O+, O2+, O3+, and O4+, respectively. The theoretical energy levels of the target states (relative to their respective ground states) are compared in Tables 1 and 2 with the experimental values (Kramida et al. 2015) for the calculations of PI of O+–O4+. We find good agreement is obtained between the theoretical and experimental results. A large enough boundary has been chosen to ensure that the wavefunction is completely wrapped within the R-matrix sphere. For each angular momentum, the continuum orbitals were expressed as a linear combination of 50 numerical basis functions.
One possible double PI pathway is via the DDAD processes of the final states, where one needs to calculate the DDAD rates to obtain the PI cross section. The theoretical method for the calculations of the DDAD rates has been described in our recent work (Zeng et al. 2013b, 2013a; Liu et al. 2014a). In the second-order perturbation theory, the DDAD rate reads as 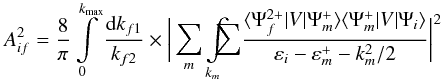 (3)where
(3)where 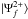 is the wave function of final state after DDAD process with a bound state of the ion plus two continuum electrons. The summation over intermediate states means a summation over all possible bound states of the ionized ion and an integration over a complete set of continuum states of the remaining electron. According to the knock-out (KO) and shake-off (SO) mechanisms (Amusia et al. 1992), the above expression can be simplified as
is the wave function of final state after DDAD process with a bound state of the ion plus two continuum electrons. The summation over intermediate states means a summation over all possible bound states of the ionized ion and an integration over a complete set of continuum states of the remaining electron. According to the knock-out (KO) and shake-off (SO) mechanisms (Amusia et al. 1992), the above expression can be simplified as 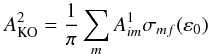 (4)and
(4)and 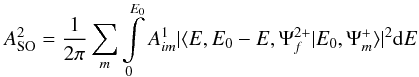 (5)where σmf(ε0) is the cross section of the inelastic scattering of the intermediate Auger electron upon the middle state m to the final one f. The value of ε0 can be determined from the energy conservation relation in the process. The factor of
(5)where σmf(ε0) is the cross section of the inelastic scattering of the intermediate Auger electron upon the middle state m to the final one f. The value of ε0 can be determined from the energy conservation relation in the process. The factor of 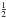 in the SO mechanism is introduced to avoid double counting the contribution of the continuum electrons.
in the SO mechanism is introduced to avoid double counting the contribution of the continuum electrons. 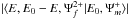 means the overlap integral between the wave functions in the potential field of the initial state and that in the final state with two Auger electrons being ejected. The detailed theoretical methods to calculate single Auger decay rate and electron impact single ionization cross section can be found in references (Gu 2008; Zeng et al. 2014; Liu et al. 2014b, 2015) with the data being obtained by using the Flexible Atomic Code developed by Gu (2008).
means the overlap integral between the wave functions in the potential field of the initial state and that in the final state with two Auger electrons being ejected. The detailed theoretical methods to calculate single Auger decay rate and electron impact single ionization cross section can be found in references (Gu 2008; Zeng et al. 2014; Liu et al. 2014b, 2015) with the data being obtained by using the Flexible Atomic Code developed by Gu (2008).
 |
Fig. 1 Single photoionization (SPI) and double photoionization (DPI) cross sections of the terms |
 |
Fig. 2 As in Fig. 1 but for the terms of 4P, 2D, 2S, and 2P of O+ belonging to the first excited configuration 1s22s2p4. |
 |
Fig. 3 Comparison of theoretical and experimental (Bizau et al. 2015) single photoionization (SPI) and double photoionization (DPI) cross sections of O+. a) SPI cross section compared with the relative measurement of 100 meV BP, b) SPI cross section compared with the absolute measurement of 200 meV BP, and c) DPI cross section compared with the absolute measurement (red open circles) and relative measurement (blue vertical bars) with 200 meV BP. The vertical bars indicate the statistical uncertainties of the experiment. The theoretical cross sections were reconstructed assuming a relative population fraction of 47% for 1s22s22p3 |
For the DDAD processes of K-shell hole states 1s2sx2py of O+ (x + y = 6), O2+ (x + y = 5), O3+ (x + y = 4), and O4+ (x + y = 3), the wave functions of three successive ionization stages are required to obtain the decay rates. For each case, we obtained the optimal radial potential based on the ground configuration of the middle ionization stage to calculate the required wave functions by using the Flexible Atomic Code (Gu 2008). To adequately include the effects of electron correlations, we explicitly considered the configuration interactions among quantum states of single and double electron excitations from the respective ground and first excited configurations of three successive ionization stages to the included orbitals up to 5f for O+ and up to 4f for O2+–O4+. Take O+ to illustrate the details. The optimized radial potential was determined based on the ground configuration 1s22s22p2 of O2+. The interactions among the fine-structure levels of O+ belonging to the following configurations have been included: 1s22s22p3, 1s22s2p4, 1s22s02p5, 1s22s22p2nl, 1s22s2p3nl, 1s22s02p4nl, 1s2s22p4, 1s2s2p5, 1s2s02p6, 1s2s22p3nl, 1s22s22pnln′l′, 1s22s2p2nln′l′, 1s22s02p3nln′l′, 1s2s22p2nln′l′, 1s2s2p3nln′l′, 1s2s02p4nln′l′ (nl, n′l′ = 3s, 3p, 3d, 4s, 4p, 4d, 4f, 5s, 5p, 5d, and 5f). Similar considerations apply for the scale of configuration interaction for two higher ionization stages of O2+ and O3+. The electron impact ionization cross sections from the quantum states of O2+ to those of O3+ given in the list of configurations have been calculated. The dominant channels originate from the single electron ionization processes.
3. Results and discussion
The predominant mechanism of the K-shell resonance double PI is through the DDAD processes of the K-shell excited states for the following reasons. Firstly, there is no possibility for the cascade double PI as the single K-shell excited states have no pathways of cascade double Auger decay. Secondly, the direct double PI is indeed possible, yet the cross section is negligibly trivial. Near the K-shell resonances, the possible channels of direct double PI can originate only from the PI of 2s and 2p electrons, which are further ionized to produce quantum states of two higher ionization stage. However, the cross sections of 2s and 2p electrons are more than four orders of magnitudes smaller than the 1s → 2p resonance PI cross section and thus the contribution of the direct double PI is negligibly small. Therefore the only predominant mechanism for the double PI originates from the DDAD processes of the K-shell excited states.
3.1. N-like O+
The production of the single K-shell resonance PI of N-like O+ relevant to the present work is the inner-shell excited states belonging to the configurations of 1s2s22p4 and 1s2s2p5. The single and direct double Auger decay rates for these K-shell excited states are given in Table 3 along with BRs of the DDAD relative to the total Auger decay. No data on the DDAD rates are available in the literature, to the best of our knowledge and thus we compare the natural lifetime widths with available experimental and theoretical results to evaluate the quality of our theoretical results. Our theoretical natural lifetime widths (fifth column), the measurements of Bizau et al. (2015) (sixth column) and the previous available theoretical results (Zeng et al. 2004; Bizau et al. 2015; Garcia et al. 2005) (seventh column) are given in Table 3. For the quantum state of 1s2s22p42D, two experimental values are given with 159(30) meV being obtained from the resonance of 1s22s22p3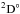 →1s2s22p42D while 80(60) meV from 1s22s22p3
→1s2s22p42D while 80(60) meV from 1s22s22p3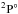 →1s2s22p42D (Bizau et al. 2015). As the final state of the two resonance transitions is the same, the natural lifetime widths should, in principle, be nearly equivalent as the Auger decay rate is much larger than the radiative decay rate. For this state, our theoretical result (140 meV) is within the experimental error of both measured values yet in better agreement with 159(30) meV. Good agreement is also found for the terms of 1s2s22p44P and 1s2s22p42P between our theory and experiment (Bizau et al. 2015). For the term of 1s2s22p42S, however, our theoretical result (154 meV) is much smaller than the experimental value of 430(200) meV, which has a larger error bar. Nevertheless, our predicted natural widths are in reasonable agreement with all available theoretical results reported in the literature (Zeng et al. 2004; Bizau et al. 2015; Garcia et al. 2005).
→1s2s22p42D (Bizau et al. 2015). As the final state of the two resonance transitions is the same, the natural lifetime widths should, in principle, be nearly equivalent as the Auger decay rate is much larger than the radiative decay rate. For this state, our theoretical result (140 meV) is within the experimental error of both measured values yet in better agreement with 159(30) meV. Good agreement is also found for the terms of 1s2s22p44P and 1s2s22p42P between our theory and experiment (Bizau et al. 2015). For the term of 1s2s22p42S, however, our theoretical result (154 meV) is much smaller than the experimental value of 430(200) meV, which has a larger error bar. Nevertheless, our predicted natural widths are in reasonable agreement with all available theoretical results reported in the literature (Zeng et al. 2004; Bizau et al. 2015; Garcia et al. 2005).
Figures 1 and 2 display the single and double 1s → 2p resonance PI cross sections of the terms 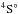 ,
, 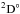 , and
, and 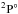 belonging to the ground configuration 1s22s22p3 and terms of 4P, 2P, 2D, and 2S to the first excited configuration 1s22s2p4 of N-like O+. The double PI cross sections are obtained by multiplying the single ionization cross section by the DDAD BRs of the respective final resonance states. The origin of the resonances can easily be identified from the term designations listed in Table 3. The only resonance shown in PI of 1s22s22p3
belonging to the ground configuration 1s22s22p3 and terms of 4P, 2P, 2D, and 2S to the first excited configuration 1s22s2p4 of N-like O+. The double PI cross sections are obtained by multiplying the single ionization cross section by the DDAD BRs of the respective final resonance states. The origin of the resonances can easily be identified from the term designations listed in Table 3. The only resonance shown in PI of 1s22s22p3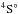 in Figs. 1a, b originates from 1s2s22p44P, the two resonances of 1s22s22p3
in Figs. 1a, b originates from 1s2s22p44P, the two resonances of 1s22s22p3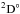 (Figs. 1c, d) from 1s2s22p42D and 1s2s22p42P (dipole selection rule makes transition to 1s2s22p42S forbidden) and the three resonances of 1s22s22p3
(Figs. 1c, d) from 1s2s22p42D and 1s2s22p42P (dipole selection rule makes transition to 1s2s22p42S forbidden) and the three resonances of 1s22s22p3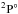 (Figs. 1e, f) from 1s2s22p42D, 1s2s22p42P and 1s2s22p42S, respectively. The only resonance shown in Figs. 2a, b originates from 1s2s(3S)2p5
(Figs. 1e, f) from 1s2s22p42D, 1s2s22p42P and 1s2s22p42S, respectively. The only resonance shown in Figs. 2a, b originates from 1s2s(3S)2p5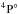 . The origin of other resonances can be similarly determined.
. The origin of other resonances can be similarly determined.
Our theoretical results are helpful to diagnose the population fraction prepared in the initial state of the experiment (Bizau et al. 2015). These authors measured the PI cross sections of N-like O+ with different instrumental broadening with band passes (BP) of 350, 200, and 100 meV in the K-shell resonance PI region. In these experiments, it is well known that considerable population of metastable excited states might be produced (Müller 2015). To interpret the experiment, we first need to diagnose the population fraction in the initial state prepared in the experiment. By carefully comparison of our theoretical work with the experiment, we determined that there are no quantum states belonging to the first excited configuration 1s22s2p4 in the prepared initial state. The initial state originates from the terms of the ground configuration 1s22s22p3 with a population fraction determined to be 47% for 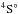 , 31% for
, 31% for 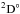 , and 22% for
, and 22% for 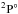 . By utilizing this fraction distribution, the theoretical cross sections for single and double PI were reconstructed in Fig. 3. In this figure we compare our theoretical results with the experiment of Bizau et al. (2015) for the single and double PI cross sections by assuming the above population fraction. For the single PI, two theoretical results are compared with the experimental cross sections obtained with a BP of 100 meV (Fig. 3a) and 200 meV (Fig. 3b). The calculated cross sections have been convolved with a Gaussian profile of 100 and 200 meV full width at half maximum (FWHM) to account for the instrumental broadening. The theoretical cross sections without including the instrumental broadening are also given in Fig. 3a in a dashed line to aid our understanding of the process. We note that the experimental results with 100 meV BP were obtained in the relative mode and the experimental data were normalized to absolute measurement with 200 meV BP. The experimental results for the double PI were recorded in the absolute mode and in the relative mode with a 200 meV BP (Fig. 3c). The vertical bars indicate the statistical uncertainties of the experiment. Five resonances were observed in the experiment for both single and double PI cross sections and they can be identified to be 1s22s22p3
. By utilizing this fraction distribution, the theoretical cross sections for single and double PI were reconstructed in Fig. 3. In this figure we compare our theoretical results with the experiment of Bizau et al. (2015) for the single and double PI cross sections by assuming the above population fraction. For the single PI, two theoretical results are compared with the experimental cross sections obtained with a BP of 100 meV (Fig. 3a) and 200 meV (Fig. 3b). The calculated cross sections have been convolved with a Gaussian profile of 100 and 200 meV full width at half maximum (FWHM) to account for the instrumental broadening. The theoretical cross sections without including the instrumental broadening are also given in Fig. 3a in a dashed line to aid our understanding of the process. We note that the experimental results with 100 meV BP were obtained in the relative mode and the experimental data were normalized to absolute measurement with 200 meV BP. The experimental results for the double PI were recorded in the absolute mode and in the relative mode with a 200 meV BP (Fig. 3c). The vertical bars indicate the statistical uncertainties of the experiment. Five resonances were observed in the experiment for both single and double PI cross sections and they can be identified to be 1s22s22p3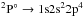 2D,
2D, 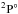 →2P,
→2P, 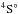 →4P,
→4P, 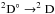 ,
, 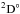 →2P and
→2P and 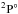 →2S, respectively, from the left to the right of the figure. Excellent agreement is obtained between our theory and the experimental results of relative measurement with 100 meV BP for the single PI process (Fig. 3a). Yet our theoretical single PI cross sections are a little smaller than the experiment of absolute measurement with 200 meV BP for the first (
→2S, respectively, from the left to the right of the figure. Excellent agreement is obtained between our theory and the experimental results of relative measurement with 100 meV BP for the single PI process (Fig. 3a). Yet our theoretical single PI cross sections are a little smaller than the experiment of absolute measurement with 200 meV BP for the first (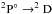 ), second (
), second (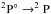 ) and the fifth resonance (
) and the fifth resonance (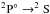 ). For the double PI (Fig. 3c), there is a general good agreement except for the lowest resonance (
). For the double PI (Fig. 3c), there is a general good agreement except for the lowest resonance (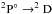 ) located at an energy of 530.1 eV, where the position and shape of this resonance observed in the double PI are different from their measured single PI cross section (Bizau et al. 2015). The reason for this discrepancy is not clear and deserves further inspection.
) located at an energy of 530.1 eV, where the position and shape of this resonance observed in the double PI are different from their measured single PI cross section (Bizau et al. 2015). The reason for this discrepancy is not clear and deserves further inspection.
As discussed in the above, three possible mechanisms contribute to the double PI. The first one is the direct double PI, where two electrons are ejected simultaneously into the continuum, and the second one is the cascade double PI, where two electrons are ejected sequentially. There is no possibility for the cascade double PI near the 1s → 2p resonances and the only channels of the direct double PI are through the ionization of the valence electrons of 2s and 2p, which is also negligibly trivial at the resonance locations. Our work shows that the double PI of 1s → 2p resonances originates predominately from the third mechanism, the DDAD of the K-shell excited states which is a three-electron Auger decay process. From the inspection of Fig. 3c, we can see that this mechanism explains the recent experimental observation of Bizau et al. (2015). The experiment measured ~7% of the decay via double ionization channels relative to that of via single ionization channels (Bizau et al. 2015), which corresponds to ~6.5% of double ionization relative to the total. From inspecting Table 3, we derive the BRs of DDAD relative to the total Auger process being ~5.7% for the K-shell excited terms from the ground configuration of 1s22s22p3, which is close to yet a little smaller than the experimental value of ~6.5%. Considering the general good agreement between the theory and experiment for both the single and double PI cross sections, one of the possible reason of the small difference might be caused by the accuracy of experimental measured natural lifetime widths.
3.2. C-like O2+
For this ion, the final K-shell resonance states of PI are those belonging to the configurations of 1s2s22p3 and 1s2s2p4, whose single and direct double Auger decay rates are listed in Table 4. Compared with the theoretical BRs of ~5.7% for N-like O+, the BRs of C-like O2+ K-shell excited states are more than 50% smaller (~2.6%). The theoretical result is also a little less than the experimental determination of ~3.2% (Bizau et al. 2015). The natural widths of these autoionized states are compared with available experimental (Bizau et al. 2015) and theoretical results (Chen et al. 1997; Zeng et al. 2001; Bizau et al. 2015; Petrini 1981; Olalla et al. 2002; Garcia et al. 2005). Our theoretical widths for the terms of 1s2s22p3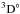 ,
, 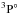 , and
, and 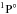 are close to the experimental values (but outside the error bar), yet the discrepancy is a little larger for 1s2s22p3
are close to the experimental values (but outside the error bar), yet the discrepancy is a little larger for 1s2s22p3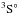 . However, our results are in reasonably good agreement with all other theoretical calculations obtained using the R-matrix method (Zeng et al. 2001; Bizau et al. 2015; Petrini 1981; Olalla et al. 2002; Garcia et al. 2005). The earlier work obtained using MCDF calculations predicted larger values for the terms of 1s2s22p3
. However, our results are in reasonably good agreement with all other theoretical calculations obtained using the R-matrix method (Zeng et al. 2001; Bizau et al. 2015; Petrini 1981; Olalla et al. 2002; Garcia et al. 2005). The earlier work obtained using MCDF calculations predicted larger values for the terms of 1s2s22p3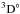 ,
, 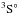 ,
, 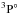 ,
, 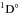 ,
, 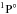 and 1s2s(1S)2p41D, 3P, 1S, and predicted lower values for the terms of 1s2s(3S)2p45P, 3P, 3D, and 3S. Generally speaking, the agreement between our theoretical natural widths and the experimental values for C-like O2+ is not as good as those of O+.
and 1s2s(1S)2p41D, 3P, 1S, and predicted lower values for the terms of 1s2s(3S)2p45P, 3P, 3D, and 3S. Generally speaking, the agreement between our theoretical natural widths and the experimental values for C-like O2+ is not as good as those of O+.
 |
Fig. 4 SPI and DPI cross sections of the terms 1s22s22p23P, 1D, and 1S for O2+. |
 |
Fig. 5 SPI and DPI cross sections of the terms of |
 |
Fig. 6 SPI and DPI cross sections of the terms of |
 |
Fig. 7 Comparison of theoretical and experimental (Bizau et al. 2015) SPI and DPI cross sections of O2+. a) SPI cross section compared with the relative measurement with 110 meV BP, b) DPI cross section (being convolved with a Gaussian profile of 110 and 350 meV FWHM) compared with the absolute measurement with 350 meV BP. The vertical bars indicate the statistical uncertainties of the experiment. The relative population fraction of the initial state were diagnosed to be 71.5% 3P, 19% 1D, and 9.5% 1S of configuration 1s22s22p2. To have the best comparison with the experiment, the theoretical resonance positions have been shifted to lower energy direction according to the experimental results by 1.894 eV for 3P– |
Figure 4 shows the single and double PI cross sections of the terms 3P, 1D, and 1S belonging to the ground configuration 1s22s22p2 of C-like O2+ in the 1s → 2p resonance energy range. Figures 5 and 6 display the single and double PI cross section of the terms 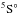 ,
, 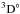 ,
, 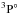 ,
, 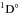 ,
, 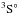 , and
, and 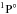 of the first excited configuration 1s22s2p3 of O2+. With the aid of Table 4, we can easily identify the resonances shown in Figs. 4−6 according to the dipole selection rules in the PI processes. We note that the energies of the K-shell excited states given in Tables 3−6 are arranged in an ascending order. Taking Fig. 4 as an example to illustrate the procedure, the three resonances in Plots 4a and 4b are assigned to be 1s2s22p3
of the first excited configuration 1s22s2p3 of O2+. With the aid of Table 4, we can easily identify the resonances shown in Figs. 4−6 according to the dipole selection rules in the PI processes. We note that the energies of the K-shell excited states given in Tables 3−6 are arranged in an ascending order. Taking Fig. 4 as an example to illustrate the procedure, the three resonances in Plots 4a and 4b are assigned to be 1s2s22p3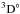 ,
, 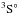 , and
, and 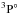 , respectively, from the lower to higher photon energy. The two peaks in Plots 4(c) and 4(d) are identified as 1s2s22p3
, respectively, from the lower to higher photon energy. The two peaks in Plots 4(c) and 4(d) are identified as 1s2s22p3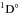 and
and 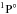 , respectively. The only resonance of the last two plots in Fig. 4 originates from 1s2s22p3
, respectively. The only resonance of the last two plots in Fig. 4 originates from 1s2s22p3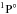 .
.
Figure 7 compares the theoretical single and double PI cross sections of O2+ in the energy range of the 1s → 2p transitions with the experiment of Bizau et al. (2015). The experimental result for the single PI was obtained in a relative mode with a 110 meV BP (Fig. 7a). Double PI cross section was recorded in the absolute mode with a 350 meV BP (Fig. 7b). The vertical bars indicate the statistical uncertainties of the experiment. To interpret the experiment, we diagnosed the relative population fraction of the initial state prepared in the experiment to be 71.5% 3P, 19% 1D, and 9.5% 1S of configuration 1s22s22p2. It is possible that a very small fraction of quantum state 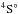 belonging to the excited configuration 1s22s2p3 exist in the experiment. The theoretical cross sections for the single and double PI were reconstructed utilizing this population fraction. In Fig. 7a, the theoretical single PI cross section were convoluted with a Gaussian profile of 110 meV FWHM and then compared with the experiment. Excellent agreement is found between our theory and the experimental result. In Fig. 7b, two theoretical double PI cross sections are given with one being convoluted with a Gaussian profiles of 110 meV FWHM and the other using 350 meV. Comparison shows that better agreement is found between our theoretical result convolved with 110 meV FWHM Gaussian profile and the experimental double PI cross section recorded in the absolute mode with a 350 meV BP. The theoretical results convoluted with 350 meV FWHM are smaller than the peak experiment PI cross sections for all measured resonances.
belonging to the excited configuration 1s22s2p3 exist in the experiment. The theoretical cross sections for the single and double PI were reconstructed utilizing this population fraction. In Fig. 7a, the theoretical single PI cross section were convoluted with a Gaussian profile of 110 meV FWHM and then compared with the experiment. Excellent agreement is found between our theory and the experimental result. In Fig. 7b, two theoretical double PI cross sections are given with one being convoluted with a Gaussian profiles of 110 meV FWHM and the other using 350 meV. Comparison shows that better agreement is found between our theoretical result convolved with 110 meV FWHM Gaussian profile and the experimental double PI cross section recorded in the absolute mode with a 350 meV BP. The theoretical results convoluted with 350 meV FWHM are smaller than the peak experiment PI cross sections for all measured resonances.
For the double PI of O2+ shown in Fig. 7b, one should compare a convoluted theoretical cross section using a width of 350 meV (the reported experimental band pass) with the experimental values. The disagreement between the convoluted theoretical results with a width of 350 meV and the experiment suggests that further work and check are needed to clarify this issue. We do not know the exact reason for the theory-experiment discord. One possibility is that the experimental band pass is actually 110 meV, which is the same with that in the single PI measurement. The more realistic possibility might be that obtaining a weaker double PI cross section of O2+ than that of O+ with a high precision is more challenging. Practical calculations show that the double PI cross section of oxygen ions decreases rapidly with increasing ionization stage.
3.3. B-like O3+ and Be-like O4+
The relevant single and direct double Auger decay rates for the K-shell excited states of B-like O3+ and Be-like O4+ are given in Tables 5 and 6, respectively. It can be seen that the BRs of the DDAD relative to the total Auger decay decrease rapidly with increasing ionization stage of oxygen ions, which reflects the correlation strengths in different charge states. This is evident as effects of electron correlations becomes weaker with the increase of ionization stage. In Tables 5 and 6 we also compare the natural widths with the experimental (McLaughlin et al. 2014) and theoretical results (Chen & Crasemann 1988; Chen & Crasemann 1987; Lin et al. 2001; Lin et al. 2002; McLaughlin et al. 2014; Zeng & Yuan 2002; Pradhan et al. 2003; Garcia et al. 2005; Chen 1985) available in the literature. From the inspection of Table 5, it can be seen that our results are in reasonable agreement with the available theoretical results (Chen & Crasemann 1988, 1987; McLaughlin et al. 2014; Zeng & Yuan 2002; Pradhan et al. 2003; Garcia et al. 2005) except for part of the results obtained by Pradhan et al. (2003). Pradhan et al. (2003) predicted a much smaller lifetime widths for the terms of 1s2s22p2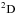 ,
, 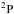 and
and 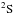 . A good agreement is found for the widths of two terms of 1s2s22p2
. A good agreement is found for the widths of two terms of 1s2s22p2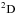 and 1s2s(3S)2p34P◦ between our results and the experiment. There is a large discrepancy for other measured values, in particular for the term of 1s2s22p2
and 1s2s(3S)2p34P◦ between our results and the experiment. There is a large discrepancy for other measured values, in particular for the term of 1s2s22p2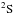 with a theoretical prediction of 125 meV yet the measured value being only 26(22) meV. To the best of our knowledge, no experimental investigations have been reported for Be-like O4+ on the K-shell PI. In general, good agreement is found between the theoretical results (Lin et al. 2001, 2002; Garcia et al. 2005; Chen 1985) of O4+ except for the two terms of 1s2s(3S)2p2
with a theoretical prediction of 125 meV yet the measured value being only 26(22) meV. To the best of our knowledge, no experimental investigations have been reported for Be-like O4+ on the K-shell PI. In general, good agreement is found between the theoretical results (Lin et al. 2001, 2002; Garcia et al. 2005; Chen 1985) of O4+ except for the two terms of 1s2s(3S)2p2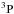 and
and 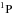 . For 1s2s(3S)2p2
. For 1s2s(3S)2p2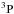 , our theoretical width is only about a half of the calculated value obtained by Chen (1985), while for 1s2s(3S)2p2
, our theoretical width is only about a half of the calculated value obtained by Chen (1985), while for 1s2s(3S)2p2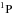 , our result is larger than that of Chen (1985) by 100%.
, our result is larger than that of Chen (1985) by 100%.
 |
Fig. 8 SPI and DPI cross sections of the term of O3+1s22s22p |
 |
Fig. 9 SPI and DPI cross sections of the terms of 4P, 2D, 2P, and 2S belonging to the configuration 1s22s2p2 of O3+. |
 |
Fig. 10 Comparison of theoretical and experimental (in absolute and relative measurement) (McLaughlin et al. 2014) single PI cross sections of O3+. Theoretical cross sections have been convolved with a Gaussian profile of 170 meV FWHM to account for the instrument broadening of 170 meV. The vertical bars indicate the statistical uncertainty of the experiment. The relative population fraction of the initial state was diagnosed to be 82.5% |
 |
Fig. 11 SPI and DPI cross sections of the term of 1S belonging to the ground configuration 1s22s2a), b) and terms of |
Figures 8 and 9 display the single and double 1s → 2p resonance PI cross sections of the term 2P◦ belonging to the ground configuration 1s22s22p and 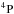 ,
, 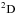 ,
, 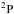 , and
, and 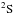 of the first excited configuration 1s22s2p2 of B-like O3+. McLaughlin et al. (2014) measured the absolute cross section of the K-shell single PI of O3+ ions from 540 eV up to 600 eV by employing the ion-photon merged-beam technique at the SOLEIL synchrotron radiation facility with a high resolution of resolving power ~5000. To the best of our knowledge, no experimental results are available in the literature on the double 1s → 2p resonance PI cross sections of O3+. We compare in Fig. 10 our theoretical cross section of single PI in the vicinity of 1s → 2p resonances with the experimental results (McLaughlin et al. 2014) obtained in absolute and relative modes with a 170 meV BP. To reconstruct the theoretical cross section, we assume a relative population fraction of 82.5% 2P◦ of the ground configuration 1s22s22p and 17.5%
of the first excited configuration 1s22s2p2 of B-like O3+. McLaughlin et al. (2014) measured the absolute cross section of the K-shell single PI of O3+ ions from 540 eV up to 600 eV by employing the ion-photon merged-beam technique at the SOLEIL synchrotron radiation facility with a high resolution of resolving power ~5000. To the best of our knowledge, no experimental results are available in the literature on the double 1s → 2p resonance PI cross sections of O3+. We compare in Fig. 10 our theoretical cross section of single PI in the vicinity of 1s → 2p resonances with the experimental results (McLaughlin et al. 2014) obtained in absolute and relative modes with a 170 meV BP. To reconstruct the theoretical cross section, we assume a relative population fraction of 82.5% 2P◦ of the ground configuration 1s22s22p and 17.5% 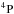 of the excited configuration 1s22s2p2. The theoretical results have been convoluted with a Gaussian profile of 170 meV FWHM to account for the instrumental broadening. It can be seen that excellent agreement is obtained between our theory and the experimental results in relative measurement, while our theoretical cross section is smaller than the absolute measurement.
of the excited configuration 1s22s2p2. The theoretical results have been convoluted with a Gaussian profile of 170 meV FWHM to account for the instrumental broadening. It can be seen that excellent agreement is obtained between our theory and the experimental results in relative measurement, while our theoretical cross section is smaller than the absolute measurement.
The corresponding results for Be-like O4+ are given in Fig. 11 with (a) and (b) referring to the term of 1s22s2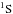 and (c)−(f) to terms of 1s22s2p3P◦ and 1P◦. Again the double PI cross sections are obtained by considering the DDAD BRs of the respective final resonance states. As far as we are aware, no experimental results are available in the literature for both single and double PI cross sections.
and (c)−(f) to terms of 1s22s2p3P◦ and 1P◦. Again the double PI cross sections are obtained by considering the DDAD BRs of the respective final resonance states. As far as we are aware, no experimental results are available in the literature for both single and double PI cross sections.
3.4. Consequences of double PI processes on ionization balance
Interpreting observations of K-shell lines from X-ray satellites and modeling astrophysical processes require knowledge of the underlying charge state distribution (CSD) of the plasma. Previous ionization balance calculations have largely neglected the effects of double PI processes. Experimental and theoretical work indicates that the double ionization cross section can amount to ~7% relative to the single ionization cross section for O+. With increasing ionization stage, the ratio of double to single ionization cross section decreases to ~2.8%, ~1.2%, and ~0.4% for O2+, O3+, and O4+, respectively. Preliminary calculations using the collision-radiative model implemented by the detailed level accounting method (Gao et al. 2013) show that the ion abundances can be modified by about 6% at the most favorable situation by including the double ionization processes. For neutral atoms and in particular negative ions, the influence on their abundances can be larger in ionization balance calculations. Systematic quantitative investigation on the effects of double PI on the CSD is beyond the scope of present work.
4. Conclusion
In conclusion, single and double PI cross sections are investigated for the terms belonging to the ground and first excited configurations of O+-O4+ in the 1s → 2p resonance energy range. In this energy region, the PI cross section is dominated by the 1s → 2p resonances, whereas the continuum background is negligibly small. The double PI originates predominately from the direct double Auger decay of the final resonance states and thus can be obtained by multiplying the single PI cross section by the branching ratio of the direct double Auger decay to the total Auger decay for each channel. For the terms of the ground configuration of O+, this ratio is ~5.7% from our theoretical calculations. It decreases to ~2.6% (O2+), ~1.1% (O3+), and ~0.4% (O4+), respectively, for the terms of respective ground configuration. The population fraction in the initial state of recent experiments on PI of O+–O3+ was diagnosed and our theoretical work successfully interpreted the experimental results for both single and double PI cross sections. Double PI processes will affect the ionization balance in plasmas and the effect on abundances of oxygen ions is evaluated with a collision-radiative model.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant Nos. 11674394 and 11674395.
References
- Amusia, M. Y., Lee, I., & Kilin, V. A. 1992, Phys. Rev. A, 45, 4576 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Berrington, K. A., Eissner, W. B., & Norrington, P. H. 1995, Comput. Phys. Comm., 92, 290 [Google Scholar]
- Bizau, J., Cubaynes, D., Guilbaud, S., et al. 2015, Phys. Rev. A, 92, 023401 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M. H. 1985, Phys. Rev. A, 31, 1449 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, M. H., & Crasemann, B. 1987, Phys. Rev. A, 35, 4579 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, M. H., & Crasemann, B. 1988, Atom. Data Nucl. Data Tables, 38, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M., Reed, K., McWilliams, D., et al. 1997, Atom. Data Nucl. Data Tables, 65, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, K. T. 1990, J. Phys. B Atom. Mol. Phys., 23, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Clementi, E., & Roetti, C. 1974, At. Data Nucl. Data Tables, 14, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, C., Zeng, J., Li, Y., Jin, F., & Yuan, J. 2013, High Energy Density Physics, 9, 583 [Google Scholar]
- Garcia, J., Mendoza, C., Bautista, M., et al. 2005, ApJS, 158, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbert, A. 1975, Comput. Phys. Commun., 9, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T., Evans, D. A., Marshall, H., et al. 2013, ApJ, 780, 121 [Google Scholar]
- Kawatsura, K., Yamaoka, H., Oura, M., et al. 2002, J. Phys. B Atom. Mol. Phys., 35, 4147 [NASA ADS] [CrossRef] [Google Scholar]
- Kramida, A. E., Ralchenko, Y., Reader, J., & NIST ASD Team 2015, NIST Atomic Spectra Database (version 5.3), http://physics.nist.gov/asd. [Google Scholar]
- Lee, J. C., Ogle, P. M., Canizares, C. R., et al. 2001, ApJ, 554, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, J.-Y., Zhang, S.-N., & Yao, Y. 2013, ApJ, 774, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, S.-H., Hsue, C.-S., & Chung, K. T. 2001, Phys. Rev. A, 64, 012709 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Hsue, C.-S., & Chung, K. T. 2002, Phys. Rev. A, 65, 032706 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Gao, C., Zeng, J., & Shi, J. 2011, A&A, 536, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Y., Zeng, J., & Yuan, J. 2013, J. Phys. B Atom. Mol. Phys., 46, 145002 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, P., Liu, Y., Zeng, J., & Yuan, J. 2014a, Eur. Phys. J. D, 68, 214 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, P., Liu, Y., Zeng, J., & Yuan, J. 2014b, Phys. Rev. A, 89, 042704 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Gao, C., Zeng, J., Yuan, J., & Shi, J. 2014c, ApJS, 211, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, P., Zeng, J., Borovik Jr, A., Schippers, S., & Müller, A. 2015, Phys. Rev. A, 92, 012701 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, B., Bizau, J., Cubaynes, D., et al. 2014, J. Phys. B Atom. Mol. Phys., 47, 115201 [Google Scholar]
- Müller, A. 2015, Atoms, 3, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Olalla, E., Wilson, N., Bell, K., Martin, I., & Hibbert, A. 2002, MNRAS, 332, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Petrini, D. 1981, J. Phys. B Atom. Mol. Phys., 14, 3839 [NASA ADS] [CrossRef] [Google Scholar]
- Petrini, D., & Da Silva, E. 1996, Rev. Mex. Astron. Astrofis., 32, 69 [NASA ADS] [Google Scholar]
- Pinto, C., Kaastra, J., Costantini, E., & De Vries, C. 2013, A&A, 551, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pradhan, A. K., Chen, G. X., Delahaye, F., Nahar, S. N., & Oelgoetz, J. 2003, MNRAS, 341, 1268 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ramírez, J. 2013, A&A, 551, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safronova, U., & Shlyaptseva, A. 1999, Phys. Scr., 60, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, Y., Chen, F., & Gou, B. C. 2011, J. Chem. Phys., 135, 124309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sun, Y., Gou, B. C., & Chen, C. 2013, Phys. Rev. A, 87, 032509 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, Y., Schulz, N. S., Gu, M. F., Nowak, M. A., & Canizares, C. R. 2009, ApJ, 696, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., & Yuan, J. 2002, J. Phys. B Atom. Mol. Phys., 35, 3041 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., Yuan, J., & Lu, Q. 2001, J. Phys. B Atom. Mol. Phys., 34, 2823 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., Zhao, G., & Yuan, J. 2004, Eur. Phys. J. D, 28, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, J., Liu, P., Xiang, W., & Yuan, J. 2013a, J. Phys. B Atom. Mol. Phys., 46, 215002 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., Liu, P., Xiang, W., & Yuan, J. 2013b, Phys. Rev. A, 87, 033419 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, J., Liu, L., Liu, P., & Yuan, J. 2014, Phys. Rev. A, 90, 044701 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Theoretical and experimental energies (Kramida et al. 2015) (in eV) for the terms of target states of O2+ and O3+ relative to the ground state in the calculations of PI of O+ and O2+.
Theoretical and experimental energies (Kramida et al. 2015) (in eV) for the terms of target states of O4+ and O5+ relative to the ground state in the calculations of PI of O3+ and O4+.
Single Auger decay (SAD) rates (in s-1), direct double Auger decay (DDAD) rates (in s-1), branching ratios (BR) (%) of DDAD relative to the total Auger process, and the natural lifetime widths (in meV) of the O+1s → 2p excited states.
All Figures
 |
Fig. 1 Single photoionization (SPI) and double photoionization (DPI) cross sections of the terms |
| In the text | |
 |
Fig. 2 As in Fig. 1 but for the terms of 4P, 2D, 2S, and 2P of O+ belonging to the first excited configuration 1s22s2p4. |
| In the text | |
 |
Fig. 3 Comparison of theoretical and experimental (Bizau et al. 2015) single photoionization (SPI) and double photoionization (DPI) cross sections of O+. a) SPI cross section compared with the relative measurement of 100 meV BP, b) SPI cross section compared with the absolute measurement of 200 meV BP, and c) DPI cross section compared with the absolute measurement (red open circles) and relative measurement (blue vertical bars) with 200 meV BP. The vertical bars indicate the statistical uncertainties of the experiment. The theoretical cross sections were reconstructed assuming a relative population fraction of 47% for 1s22s22p3 |
| In the text | |
 |
Fig. 4 SPI and DPI cross sections of the terms 1s22s22p23P, 1D, and 1S for O2+. |
| In the text | |
 |
Fig. 5 SPI and DPI cross sections of the terms of |
| In the text | |
 |
Fig. 6 SPI and DPI cross sections of the terms of |
| In the text | |
 |
Fig. 7 Comparison of theoretical and experimental (Bizau et al. 2015) SPI and DPI cross sections of O2+. a) SPI cross section compared with the relative measurement with 110 meV BP, b) DPI cross section (being convolved with a Gaussian profile of 110 and 350 meV FWHM) compared with the absolute measurement with 350 meV BP. The vertical bars indicate the statistical uncertainties of the experiment. The relative population fraction of the initial state were diagnosed to be 71.5% 3P, 19% 1D, and 9.5% 1S of configuration 1s22s22p2. To have the best comparison with the experiment, the theoretical resonance positions have been shifted to lower energy direction according to the experimental results by 1.894 eV for 3P– |
| In the text | |
 |
Fig. 8 SPI and DPI cross sections of the term of O3+1s22s22p |
| In the text | |
 |
Fig. 9 SPI and DPI cross sections of the terms of 4P, 2D, 2P, and 2S belonging to the configuration 1s22s2p2 of O3+. |
| In the text | |
 |
Fig. 10 Comparison of theoretical and experimental (in absolute and relative measurement) (McLaughlin et al. 2014) single PI cross sections of O3+. Theoretical cross sections have been convolved with a Gaussian profile of 170 meV FWHM to account for the instrument broadening of 170 meV. The vertical bars indicate the statistical uncertainty of the experiment. The relative population fraction of the initial state was diagnosed to be 82.5% |
| In the text | |
 |
Fig. 11 SPI and DPI cross sections of the term of 1S belonging to the ground configuration 1s22s2a), b) and terms of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.