| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201730956 | |
| Published online | 19 September 2017 | |
Linking gamma-ray spectra of supernova remnants to the cosmic ray injection properties in the aftermath of supernovae
1 INAF–Osservatorio Astronomico, Piazza del Parlamento, 1, 90134 Palermo, Italy
e-mail: oleh.petruk@gmail.com
2 Institute for Applied Problems in Mechanics and Mathematics, Naukova Street, 3-b, 79060 Lviv, Ukraine
3 Dipartimento di Fisica e Chimica, Universitá degli Studi di Palermo, Viale delle Scienze, 17, 90128 Palermo, Italy
Received: 7 April 2017
Accepted: 30 June 2017
The acceleration times of the highest-energy particles, which emit gamma-rays in young and middle-age supernova remnants (SNRs), are comparable with SNR age. If the number of particles starting acceleration was varying during early times after the supernova explosion then this variation should be reflected in the shape of the gamma-ray spectrum. We use the solution of the non-stationary equation for particle acceleration in order to analyse this effect. As a test case, we apply our method to describe gamma-rays from IC 443. As a proxy of the IC 443 parent supernova we consider SN1987A. First, we infer the time dependence of injection efficiency from evolution of the radio spectral index in SN1987A. Then, we use the inferred injection behaviour to fit the gamma-ray spectrum of IC 443. We show that the break in the proton spectrum needed to explain the gamma-ray emission is a natural consequence of the early variation of the cosmic ray injection, and that the very-high-energy gamma rays originate from particles which began acceleration during the first months after the supernova explosion. We conclude that the shape of the gamma-ray spectrum observed today in SNRs critically depends on the time variation of the cosmic ray injection process in the immediate post-explosion phases. With the same model, we also estimate the future possibility of detecting gamma-rays from SN 1987A.
Key words: ISM: supernova remnants / supernovae: general / gamma rays: ISM / cosmic rays
© ESO, 2017
1. Introduction
There is a gap in observations which prevents us from seeing how the properties of supernovae (SNe) – asymmetry of explosion, initial structures in the distribution of ions and in the circumstellar medium, and so on – influence their further evolution towards the supernova remnants (SNRs) and how they determine SNR morphologies. Few known supernova events have occurred in our Galaxy during the centuries and so we cannot directly track the development of such objects. Effort is therefore required to look for other possible relationships between SNe and SNRs, which are observed at the present time. One such idea is described here.
Typically, the interpretation of the nonthermal emission from SNRs involves a solution of the steady-state equation for particle acceleration. Time-dependent acceleration however could be important in the analysis of young and middle-aged SNRs because the system eventually has not had enough time to reach the steady-state regime. There are numerical simulations that demonstrate that the particle spectrum is not stationary even in the relatively old SNRs (Brose et al. 2016). The solution of the time-dependent equation demonstrates that the variable injection (fraction of particles which begin acceleration) affects the slope of the power-law part and the shape of the high-energy end of the CR spectrum (Petruk & Kopytko 2016).
Diffusive shock acceleration increases the particle energy by a small amount in each acceleration cycle. In order to reach the high energy, a particle must diffuse around the shock for a long time. Ultrarelativistic electrons lose energy via synchrotron radiation. There is evidence suggesting that in several SNRs their maximum energy is loss-limited. In particular, the loss-limited scenario has been successfully adopted to describe the X-ray spectrum of RX J1713.7-3946 (Zirakashvili & Aharonian 2010; Tanaka et al. 2008), of Tycho (Morlino & Caprioli 2012) and of the nonthermal limbs of SN 1006 (Miceli et al. 2013). At odds with electrons, hadrons do not suffer significant radiative losses and the highest-energy particles are mostly those that have the maximum available time for acceleration; they have to start accelerating very early, around or shortly after the time of supernova explosion. Therefore, the time variation of the number of particles which enter the acceleration during the first decades after the supernova explosion affects the high-energy end of the particle spectrum and thus the hadronic γ-ray emission of SNRs.
In the present paper, we adopt the measurements of the time variation of the radio spectral index in a SN in order to reconstruct the time evolution of the particle-injection efficiency during the early times after the explosion. The extracted dependence is then used to derive the particle momentum distribution and the γ-ray spectrum of a SNR. Here we challenge our method considering the radio observations of SN1987A and the γ-ray spectrum of SNR IC 443.
2. Method
2.1. Time-dependent solution
The distribution of particles in space and momentum with ongoing diffusive shock acceleration is described by the isotropic non-stationary distribution function f(t,x,p). The equation for its evolution is (Skilling 1975; Jones 1990): ![\begin{equation} \pd{f}{t}+u\pd{f}{x}=\pd{}{x}\left[D\pd{f}{x}\right]+\frac{1}{3}\frac{{\rm d}u}{{\rm d}x}p\pd{f}{p}+Q \label{kineq:kineq} , \end{equation}](/articles/aa/full_html/2017/09/aa30956-17/aa30956-17-eq3.png) (1)where t is the time, x the spatial coordinate, p the momentum, D the diffusion coefficient, u the flow velocity in the shock reference frame, and Q the injection term; the velocities of the scattering centres are neglected. We assume the injection to happen at the shock, to be isotropic and monoenergetic with the initial momentum pi:
(1)where t is the time, x the spatial coordinate, p the momentum, D the diffusion coefficient, u the flow velocity in the shock reference frame, and Q the injection term; the velocities of the scattering centres are neglected. We assume the injection to happen at the shock, to be isotropic and monoenergetic with the initial momentum pi:  (2)where the parameter η is the injection efficiency (the density fraction of accelerated particles); actually, it is the amplitude of the efficiency at the saturated level. The term Qt(t) represents the time evolution of the injection (that may be caused by the variation of η or n1). It is unity in the steady-state regime. In the present paper, the indices “1”, “2”, and “o” correspond to upstream, downstream, and to the shock itself.
(2)where the parameter η is the injection efficiency (the density fraction of accelerated particles); actually, it is the amplitude of the efficiency at the saturated level. The term Qt(t) represents the time evolution of the injection (that may be caused by the variation of η or n1). It is unity in the steady-state regime. In the present paper, the indices “1”, “2”, and “o” correspond to upstream, downstream, and to the shock itself.
The test-particle solution of Eq. (1) for the steady-state injection Qt = 1 was derived by Drury (1983), Forman & Drury (1983); the authors additionally assume that the upstream acceleration time 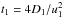 is much higher than the downstream one
is much higher than the downstream one 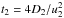 . A more general solution for the time-dependent injection and any relation between t1 and t2 was derived by Petruk & Kopytko (2016). It was shown that if t1/t2 is larger than a few, the difference with the solution obtained for the limit t1 ≫ t2 is negligible. Therefore, for simplicity, we consider t1 ≫ t2 in the present paper. In that case, the particle distribution function at the shock, which satisfies Eq. (1) and accounts for the variable injection Qt(t), is (Petruk & Kopytko 2016)
. A more general solution for the time-dependent injection and any relation between t1 and t2 was derived by Petruk & Kopytko (2016). It was shown that if t1/t2 is larger than a few, the difference with the solution obtained for the limit t1 ≫ t2 is negligible. Therefore, for simplicity, we consider t1 ≫ t2 in the present paper. In that case, the particle distribution function at the shock, which satisfies Eq. (1) and accounts for the variable injection Qt(t), is (Petruk & Kopytko 2016) 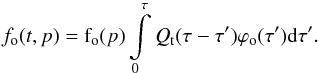 (3)In this expression,
(3)In this expression, 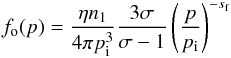 (4)is the solution of the stationary equation,
(4)is the solution of the stationary equation, 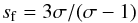 (5)is the spectral index, σ = u1/u2 the shock compression factor and (Forman & Drury 1983; Petruk & Kopytko 2016)
(5)is the spectral index, σ = u1/u2 the shock compression factor and (Forman & Drury 1983; Petruk & Kopytko 2016)  (6)where Hm(x) is the Hermite polynomial, τ = t/t1, ξ(τ) = τ1/2 + A/ (2τ1/2), and A = sf/α, with α being the index in the dependence of the diffusion coefficient on the particle momentum D(p) ∝ pα (the value of α should result in A being an integer).
(6)where Hm(x) is the Hermite polynomial, τ = t/t1, ξ(τ) = τ1/2 + A/ (2τ1/2), and A = sf/α, with α being the index in the dependence of the diffusion coefficient on the particle momentum D(p) ∝ pα (the value of α should result in A being an integer).
At this point we can answer the following questions: Is the time-dependent consideration of the particle acceleration really necessary? And, if so, to what extent? Also, is the steady-state acceleration regime adequate for describing the radio and γ-ray emission? Equation (3) clearly shows that the time-dependent solution equals the steady-state one if the integral over τ is unity. This may happen starting from some τ, if the injection is constant, that is, if Qt = 1. Thus, we may adopt the steady-state description of the particle acceleration whern the following criterion is matched; 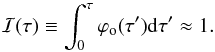 (7)The function ϕo(τ(t,p)) is the two-dimensional probability distribution for particles injected with the momentum pi at the time ti to be accelerated to the momentum p in time t. Let us consider, without loss of generality of the conclusions, an SNR with age tage = 3000 yr and the maximum particle momentum pmax = 104mpc and plot two cross-sections of the 2D distributions ϕo and ℐ: for the fixed momentum p = pmax and for the fixed time t = tage (Fig. 1). Looking at the top axis we see that: i) during the time tage, most of the particles (maximum of ϕo) are accelerated to the momentum (marked by the dotted vertical line a) somehow larger than pmax (which is marked by the dotted vertical line b); and ii) particles with momenta smaller than the threshold momentum ≈pmax/ 3 (marked by the vertical line c) may be described by the steady-state solution. The bottom axis in Fig. 1 demonstrates that: i) most particles are accelerated to the momentum pmax during the time (vertical line a) which is somehow smaller than tage (vertical line b); ii) the acceleration regime for particles around the maximum momentum is not yet steady-state because ℐ(pmax) = 0.6 for the time tage; and iii) the acceleration of particles with momentum p = pmax may be considered to be steady-state after the threshold time (vertical line c), which is about three times larger than tage.
(7)The function ϕo(τ(t,p)) is the two-dimensional probability distribution for particles injected with the momentum pi at the time ti to be accelerated to the momentum p in time t. Let us consider, without loss of generality of the conclusions, an SNR with age tage = 3000 yr and the maximum particle momentum pmax = 104mpc and plot two cross-sections of the 2D distributions ϕo and ℐ: for the fixed momentum p = pmax and for the fixed time t = tage (Fig. 1). Looking at the top axis we see that: i) during the time tage, most of the particles (maximum of ϕo) are accelerated to the momentum (marked by the dotted vertical line a) somehow larger than pmax (which is marked by the dotted vertical line b); and ii) particles with momenta smaller than the threshold momentum ≈pmax/ 3 (marked by the vertical line c) may be described by the steady-state solution. The bottom axis in Fig. 1 demonstrates that: i) most particles are accelerated to the momentum pmax during the time (vertical line a) which is somehow smaller than tage (vertical line b); ii) the acceleration regime for particles around the maximum momentum is not yet steady-state because ℐ(pmax) = 0.6 for the time tage; and iii) the acceleration of particles with momentum p = pmax may be considered to be steady-state after the threshold time (vertical line c), which is about three times larger than tage.
In summary, the time-scale for the steady acceleration until pmax is a few times larger than the SNR age. Therefore, if injection is constant, it is mandatory to consider the time-dependent acceleration for particles with the highest momenta, and these particles are actually those emitting γ-rays in SNRs. If injection varies with time, the time-dependent regime has to be adopted for all particles which start acceleration before the injection reaches the level Qt = 1.
 |
Fig. 1 Probability ϕo (red solid line) and the integral ℐ (blue dashed line) versus time for the fixed momentum p = pmax (bottom horizontal axis) and versus particle momenta for the fixed time t = tage (top horizontal axis). Numbers on the horizontal axes correspond to the particular choice of tage = 3000 yr, pmax = 104mpc and α = 1. The meaning of the dotted vertical lines is explained in the text. |
2.2. Our approach
The solution given by Eq. (3) allows us to consider effects of the variable injection on the spectrum of accelerated particles and on their nonthermal emission.
Our approach is the following. We use properties of some supernova observed in the present epoch to reconstruct the early evolution of some supernova remnant, assuming that they have similar evolution during the first years after SN event.
Namely, we start from the observations of the time variation of the radio spectral index αr in the SN. This index is known to be αr = (s−3)/2 where s is the spectral index of the particle distribution fo. Thus, at the first step, we find the function Qt(τ) by solving the integro-differential equation 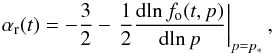 (8)where fo(t,p) is given by (3), αr(t) are taken from observations and p∗ is the particle momentum which gives the maximum contribution to emission at the observational frequency. As a result, we uncover how the injection efficiency evolved during the early times after the SN explosion.
(8)where fo(t,p) is given by (3), αr(t) are taken from observations and p∗ is the particle momentum which gives the maximum contribution to emission at the observational frequency. As a result, we uncover how the injection efficiency evolved during the early times after the SN explosion.
At the second step, we use this function Qt(τ) as an input to Eq. (3), in order to model the particle spectrum fo(t∗,p) in the SNR at the present time t∗. Having the particle spectrum, we calculate the nonthermal emission of the SNR, in particular, its γ-ray spectrum.
There is a property noted by Petruk & Kopytko (2016) which essentially simplifies the first step. Namely, if the injection term is of the form Qt ∝ τβ, then the spectral index of the radio emitting electrons in SNRs is approximately 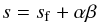 (9)(for details see Appendix A). We use this relation to reconstruct Qt(t) without solving Eq. (8). In fact, we derive the time series of different βi from the observed series of αri and approximate Qt(t) by a complex piecewise function. The normalisation of this function comes from the condition that Qt = 1 in the steady-state part.
(9)(for details see Appendix A). We use this relation to reconstruct Qt(t) without solving Eq. (8). In fact, we derive the time series of different βi from the observed series of αri and approximate Qt(t) by a complex piecewise function. The normalisation of this function comes from the condition that Qt = 1 in the steady-state part.
The solution is expressed in Eq. (3) through the unitless time τ which, in fact, is a function of t and p. Therefore, we need two scaling rules, in order to convert between the physical and normalised values. The first rule is obviously 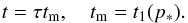 (10)The second rule is given by the definition of τ written for a general p in the form
(10)The second rule is given by the definition of τ written for a general p in the form 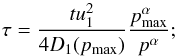 (11)it follows from here that
(11)it follows from here that 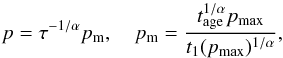 (12)where tage is the SNR age and pmax is the maximum momentum of accelerated particles in the SNR whose spectrum we would like to explain. The value of t1(pmax) is a rough estimate of the acceleration time to reach the momentum pmax. Since the time available is limited by the age of SNR then t1(pmax) ≃ tage and therefore pm ≃ pmax.
(12)where tage is the SNR age and pmax is the maximum momentum of accelerated particles in the SNR whose spectrum we would like to explain. The value of t1(pmax) is a rough estimate of the acceleration time to reach the momentum pmax. Since the time available is limited by the age of SNR then t1(pmax) ≃ tage and therefore pm ≃ pmax.
In the present paper, we set σ = 4 that corresponds to the unmodified shock and α = 1 which is relevant to the Bohm-like diffusion.
3. Ongoing acceleration in SN1987A and the γ-ray spectrum of IC 443
The described approach is adopted in the present paper to the supernovae 1987A and the supernova remnant IC 443. SN1987A is a type II supernova (Lyman et al. 2014) and IC 443 is generally expected to also be from the type II SN. The initial arguments for this were based on SNR location in the star-forming region and the association with a neutron star and its pulsar-wind nebula (Bocchino & Bykov 2001; Olbert et al. 2001; Gaensler et al. 2006; Swartz et al. 2015). The low Fe and high Mg abundance (Troja et al. 2008), as well as the position of the centroid of the Fe Kα emission (Yamaguchi et al. 2014) found by observing X-rays from IC 443, strengthen this view. As discussed below, our results also support the core-collapse scenario for this SNR.
3.1. Radio index of SN1987A
3.1.1. Radio index and injection
Evolution of the radio spectral index in SN1987A is presented by Zanardo et al. (2010), from ATCA observations during the period between 1517 and 8014 days after explosion (Fig. 2 – filled circles with errors). The spectral index does not reach the saturated value (something close to the canonical 0.5) yet, thus the injection in SN1987A is not in the steady state. In order to trace a possible future evolution of the spectral index, we extrapolate the linear fit of the data up to the time when the spectral index becomes 0.5 and then keep it constant (black circles without errors), as shown in Fig. 2.
 |
Fig. 2 Evolution of the radio spectral index as observed by Zanardo et al. (2010) during the period between 1517 and 8014 days after explosion (filled circles with errors), extrapolation (black circles without errors) of the linear fit (black line; from the same reference) up to the value αr = 0.5; then the constant αr is assumed. The red solid line represents the spectral index αr calculated by Eq. (8) with the dependence Qt(t) derived from the observed αr with the simple approximate formula (9); this Qt(t) is shown in Fig. 3. Green dashed line represents the case of the steady-state injection. |
 |
Fig. 3 Time dependence of injection term. Blue circles correspond to the days of the radio observations. A red solid line traces the function Qt(t) derived as described in Sect. 2 from the observations during the period between 1517 and 8014 days after explosion and from the extrapolation of αr after the 8014th day. As for the behaviour of the injection term before day 1517, we adopt a simple approximation as described in the text, with βx = 0.8 and dx = 100. Green dashed line represents the case of the steady-state injection. The thin black line is the function Qt = lg(t/ 950). |
At the first step, the time-dependence of the injection term is derived from αr with the use of the approximate formula (9), as described in the previous section (Fig. 3). It is interesting that the derived function Qt(t) looks smooth despite the noisy behaviour of the radio index. In particular, during most of the observational period, it may approximately be traced by the simple dependence Qt = lg(t/ (950 days)). This means that Qt is sensitive to the average global shape of the radio index evolution. All short-time features, which may depend on the details of the blast wave interaction with nonuniformities of the circumstellar medium, do not significantly affect the shape of Qt.
SN1987A was invisible in radio before day 1200 (Zanardo et al. 2010). Therefore, we describe the behaviour of Qt(t) at earlier times with a simple approximation: it is steady-state from the beginning up to day dx and then Qt(t) ∝ tβx after this day until day 1450; then it follows the dependence from observations. The values of the parameters βx and dx are determined ad hoc, from the requirement to provide an acceptable fit of the γ-ray spectrum of IC 443. It is worth mentioning that there are also detailed radio observations of SN1987A during the first months after the explosion (from February to September, e.g. Ball et al. 2001) that are useful for the studies of the flux evolution. Papers that report the radio spectral index, which is of interest for our purposes, (Turtle et al. 1987; Storey & Manchester 1987) demonstrated that the radio spectrum at this early stage is affected by the free-free absorption and the synchrotron self-absorption that makes it impossible to use these data in the solution of the Eq. (1), which does not account for these effects.
In order to check the accuracy of our approach, we calculated the spectral index αr from the full Eq. (8) using derived Qt. One can see in Fig. 2 (solid red line) that we restore even the small-scale features of the original observational data, meaning that our approximate approach based on Eq. (9) is relatively accurate and robust.
3.1.2. What could be the reason for the injection behaviour?
Though it is not necessary for the purpose of the present paper – which consists in derivation of the time-dependence of the injection from observations and in its use in modelling the γ-ray emission – we investigate the reason for the obtained time dependence of the injection efficiency.
It is clear from observations that SN1987A may not be approximated by an emitting sphere (e.g. Ng et al. 2013; Zanardo et al. 2013). The accurate analysis of the radio observations in the Fourier space (Ng et al. 2008, 2013) reveals that the radio emission arises from a ring-like structure. Detailed 3D numerical models of SN1987A (Potter et al. 2014; Orlando et al. 2015) supported this fact and have demonstrated that this emitting torus is a consequence of the interaction of the supernova shock with the H ii region with density a few orders of magnitude higher than in the blue super-giant wind where the rest of the SN evolves. Figure 4 illustrates a sketch of the ambient medium structure and Fig. 5 shows the 3D rendering of the post-shock density as derived from the model which explains the temporal and spatial properties of the X-ray emission from SN1987A (Orlando et al. 2015)1. In order to quantify the changes of the thickness of the emitting ring, Ng et al. (2008, 2013) introduced the half-opening angle θ (see our Fig. 4) and derived its temporal evolution (shown by the black dots with errors in Fig. 6). Actually, the thickness of the H ii region in the 3D numerical model of Orlando et al. (2015) fits well the evolution of θ (shown by the red solid line in Fig. 6). The thickness of the H ii region is approximated by the function h(r) = 0.25((r−rHii) /rm)0.25 pc where r is the distance from the explosion site in the equatorial plane, rHii = 0.08 pc is the inner radius of the H ii region, and the scale rm = 3 pc.
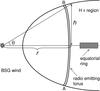 |
Fig. 4 Structure of the ambient medium around SN1987A in the 3D numerical model from Orlando et al. (2015). The shock is almost plane-parallel between points A and B because it decelerates in the dense medium of the H ii region. |
 |
Fig. 5 3D volumetric rendering of the density in the numerical model of SN1987A Orlando et al. (2015), at 15 yr (around Day 5500) after the supernova explosion. The three panels show the rendering at three different angles (see upper left corner of each panel) between the line of sight and the axis of the H ii region surrounding SN1987A. The colour-scale is normalised to the maximum value in each panel. |
From the same 3D numerical model, besides h, we can calculate the average characteristics of the shocked flow, namely, the shock radius R, the pre-shock flow velocity u1 and the post-shock density of plasma n2 which is proportional to the pre-shock density n1. With these data, we may calculate the time evolution of the product 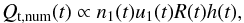 (13)which is an approximate measure of the particle flux through the (increasing) shock surface.
(13)which is an approximate measure of the particle flux through the (increasing) shock surface.
We considered two cases, namely, a uniform H ii region with and without a denser equatorial ring inside. In order to mimic these two configurations with our single simulation, we have averaged the values in the cross-section in the equatorial plane (the black line in Fig. 7) and in a plane inclined by few degrees (the red line in Fig. 7) in order to simulate the situation when the shock does not interact with the dense equatorial ring in the nebula around SN1987A. Both the black and the red lines follow the “observational” trend during the time when the shock propagates in the uniform H ii region. Interestingly, it seems that the equatorial ring in the circumstellar medium does not contribute to the particle injection and to the radio emission (only the red line follows the blue dots after Day 5500). This is in agreement with the results of Potter et al. (2014): blue and green lines on their Fig. 11, which represent the model accounting for the equatorial ring, do not follow the observed evolution of the radio flux after Day 5500 when the shock encounters the equatorial ring.
An important property is revealed by Fig. 7: The “observed” Qt (blue dots) follows the product n1u1Rh derived from the numerical simulations (lines). This means that the fraction of particles injected into the Fermi acceleration process seems to be approximately the constant fraction of the particles entering the shock front. In turn, the flux of incoming particles changes during the radio observation period, mostly (see inset in Fig. 7) due to the shock surface increase.
All SNRs expand very rapidly (“explosively”) at the early times. In this sense, the derived dependence Qt on time is “general”: it arises mainly from increasing surface of the blast wave (common for all SNRs) and does not depend significantly on individual properties of SNe, at least during the first ~ 30 yr of evolution. In order to strengthen this conclusion even more, we calculated the flux through the shock of SN 1987A either assuming a cylindrical expansion (namely assuming the flux proportional to Rhu1) of the remnant (red solid line in Fig. 7) or a spherical expansion (flux proportional to R2u1; red dashed line). The former assumption is motivated by the cylindrical geometry of the blast wave evident from both observations and modelling of this SNR (see Fig. 5). The second assumption is the most common for the expansion of SN blast waves. Figure 7 shows that the two cases differ by no more than ≈20% and both follow the same general trend. Thus, we conclude that the particular geometry of SN 1987A does not affect the generality of our analysis.
In fact, the increase of shock surface only plays a prominent role in the evolution of injection during the early phases of SNRs and becomes weaker at later times. The common scheme of SNR evolution is that the shock moves freely after the explosion (with roughly constant velocity), so that u1 = const., R = u1t. Then the shock decelerates in the later adiabatic stage and the Sedov solutions give u1 ∝ t− 3/2, R ∝ t2/5. As a result, the dependence of the volume on time is: R2u1 ∝ t2 during the free expansion, and R2u1 ∝ t1/5 during the adiabatic phase. In other words, the effects on the flux increase is significantly reduced for SNRs that are not very young.
In our case, Fig. 3 demonstrates that Qt reaches unity and is constant shortly after Day 104 (i.e. sometime after 30 yr). In the case Qt = const., our approach predicts that the injection does not affect the spectrum slope of the particles incoming after this time and therefore their distribution function has the classic test-particle shape p− sf (see Eqs. (4) and (9): constant Qt means β = 0). This is true for all momenta except the highest ones, because the highest-energy particles are those injected at the earliest times (they need more time for acceleration) when injection (number of particles starting accelerations) was smaller. Figure 8 illustrates how the particle spectra evolve with time.
 |
Fig. 6 Temporal evolution of the half-opening angle θ (black dots with errors) derived by analysis of observations (Ng et al. 2013) and from the 3D numerical model Orlando et al. (2015, red solid line). |
 |
Fig. 7 Temporal evolution of the injection efficiency derived from the radio spectral index (blue dots) and from the 3D model of SN1987A (Orlando et al. 2015). The black (red) line represents Qt,num and corresponds to the case where the dense equatorial ring in the circumstellar nebula around SN1987A is accounted (neglected). The thick parts of the lines correspond to the time when the shock propagates in the uniform H ii region. The volume increase per unit time was calculated as Rhu1 for the solid lines and as R2u1 for the dashed line. The rapid increase in the black line shortly after Day 5000 corresponds to the shock interaction with the dense equatorial ring in the nebula around the SN. The rapid increase and following decrease of the red line right after the Day 6000 is due to the few ejecta clumps which protrude the forward shock and causes an artificial increase of the post-shock density and velocity around this time. Inset: evolution of different characteristics, in arbitrary units. This plot corresponds to the red line on the main figure. One can see that the main contribution to the evolution of Qt,num comes from the surface increase, R·h. |
Finally, it is worth emphasising that our solution (3) of Eq. (1) is obtained for the constant velocity u1. However, comparing Eqs. (2) and (13), we see that the velocity variation is accounted in our solution through the term Qt. In addition, the timescale of velocity change is small compared to the particle acceleration rate. We expect therefore that our solution restores the main features in the particle spectrum while the time variation of velocity in other terms of Eq. (1) provide only the higher order corrections.
 |
Fig. 8 Particle spectra at 30 and 3000 yr calculated with Eq. (3) and the dependence Qt(t) shown in Fig. 3. Bottom axis is for protons and the upper one is for electrons, under the condition that both populations have the same maximum momentum (parameters used are listed in the caption to Fig. 9). |
3.2. γ-rays from IC 443
Once we have the evolution of injection in a supernova from the radio observations, we may proceed to the second step, namely, to use the derived Qt in order to calculate the particle spectrum and to simulate the γ-ray spectrum from IC 443. In doing so, we assume that the injection of electrons and protons has the same time dependence (as in Fig. 3) and that the particle escape is negligible.
Gamma-ray spectrum of IC 443 (Fig. 9) is measured by the Fermi observatory (Ackermann et al. 2013), MAGIC (Albert et al. 2007) and VERITAS (Acciari et al. 2009). The rapid decrease of the flux at energies below ~ 200 MeV discovered by Ackermann et al. (2013) is a sign of the hadronic γ-ray emission.
With our model, we confirm the hadronic origin of the γ-rays from IC 443. Our fit is shown by the red solid line in Fig. 9. Though the data on αr are fluctuating, the derived dependence Qt(t) and the γ-ray spectrum are rather smooth.
Interpretation of the γ-ray spectrum of IC 443 by Ackermann et al. (2013, their Fig. 3) has required the introduction of an ad-hoc artificial spectral break in the proton spectrum around the proton energy 0.2 TeV. We obtain such a break (though at a somehow lower energy, 50 GeV (it is around p/mpc ≃ 50 in Fig. 8, red line) as a natural consequence of the time-dependent particle injection into the time-dependent acceleration.
It is worth emphasising that the behaviour of the term Qt is only strictly determined by the radio observations between days 1517 and 8014 after explosion. Figure 9 clearly shows that this is exactly the period which is necessary to confirm that this break in the γ-ray spectrum is due to the injection variation: Increasing photon energy corresponds to the change in Qt from a more or less steady value after ~ 104 days to the approximate behaviour Qt = lg(t/ 950) during the period of the radio observations. The actual behaviour of the radio index after day 8014 influences the part of the γ-ray spectrum below 2 GeV. Our fit follows the observed spectrum on the smaller photon energies. Therefore, our assumption about the steady-state injection after ~ 104 days seems to be justified. On the other hand, our choice of the approximation Qt ∝ tβx and the parameters βx, dx, which determine the behaviour of Qt before day ≈1500 is less sure. These were chosen, rather arbitrarily, from the condition to trace the shape of the γ-ray spectrum above ~20 GeV.
 |
Fig. 9 Gamma-ray spectrum of IC 443. The Fermi data are shown in red, MAGIC in blue and VERITAS in green dots with errors. Our fit is shown by the solid red line. The distribution of the parental protons is shown by the red line in Fig. 8. The emission and the particle spectra are calculated with the scales tm = 60 days and pm = 9.5 × 103mpc as well as the values of dx = 100 days and βx = 0.8; the last two parameters determine the fit of the γ-ray spectrum above 20 GeV. The emission spectrum for the same case but with the steady injection is shown by the green dashed line. The green dotted lines represent the spectra with the artificial injection terms which are the same as Qt but zero before day 100 (the rightmost line), before day 1517 (middle line) and before day 8014 (the leftmost line). The γ-ray spectrum is calculated following the recipe of Aharonian & Atoyan (2000) with the cross-section for the pion production from Kelner et al. (2006); such an approach is very accurate for γ-rays with energies below a few TeV (Kelner et al. 2006). |
It is apparent from Fig. 9 that the steady injection (Fig. 9, green dashed line) cannot fit the observed γ-ray spectrum in IC 443. The variation of the injection efficiency at the early times affects the energy distribution of γ-rays in SNR to a large extent.
Which time periods are important in formation of certain portions of the γ-ray spectrum? The highest-energy protons require the longest time for acceleration. Therefore, the higher the photon energy, the earlier the times when the emitting particles were injected. It can be seen from Eqs. (10) and (12) that the injection time and the momentum of particles at the present epoch are related as ti = (p/pm)− αtm. It is not so easy to relate the injection time to the energy of γ-rays. In order to answer the above question, we also calculated the γ-ray spectra for the three artificial injection terms: They are the same as Qt(t) but zero before day 100, day 1517 and day 8014, respectively. These spectra are shown by the green dotted lines in Fig. 9. In order to make the situation even more transparent, we use vertical lines to mark the photon energies where the contributions to the flux from the particles injected before these days become higher than 10% (present time is about Day 11 000).
One can see for example that the change of the red line slope around the photon energy 0.3 TeV (Fig. 9) is due to the switch from Qt ∝ tβx to the steady injection at dx = 100. Thus, all the TeV hadronic γ-rays from young and middle-age SNRs observed by the ground-based Cherenkov telescopes are from the protons injected mostly during the first months after SN explosion. The photon energy just below 20 GeV corresponds to the time when the observations of the radio index were started. The energy about 2 GeV, near the point where all lines converge, corresponds to the last days of the radio data that we used. Thus, the γ-spectrum above 1 GeV is determined by the injection during the first 20 yr of SN evolution.
Clearly, the time dependence of injection at early times is very important in shaping the γ-ray spectra of SNRs.
3.3. Can SN1987A be visible in the future in hadronic gamma-rays?
Above, we have adopted SN1987A as a proxy for the IC 443 supernova. Naturally, we may use Qt extracted from the evolution of the radio index in SN1987A to also estimate the visibility of SN1987A in hadronic γ-rays in the near future.
The amplitude of the γ-ray spectrum is proportional to the product of the accelerated ncr and the target npp proton densities ncrnpp. Fermi LAT has not yet detected SN1987A, therefore the density around SN1987A is smaller than the density around IC 443. The age of SN1987A is tsn87a ≃ 0.01tIC 443. We consider two possible cases depending on the acceleration rate in SN 1987A.
Case A. The acceleration rate in SN1987A is the same as in IC 443 (Fig. 10 upper plot). Let us consider an “optimistic” value of the target protons in SN1987A npp,sn87a ≃ 0.03npp,ic443 which could allow it to be detectable by Fermi in a few years. The upper plot in Fig. 10 demonstrates that, even if SN1987A is detected in GeV γ-ray range, there is no chance of seeing the hadronic TeV γ-rays from SN1987A in the near future, also by CTA. This is because the available time (age of SN1987A) is not enough to accelerate protons to the energies which allow them to emit TeV γ-rays.
Case B. Acceleration in SN1987A is faster than in IC 443 (Fig. 10 lower plot). The right-hand portion of the γ-ray spectrum scales with time as t/tacc ∝ tV2/D where tacc is the acceleration time-scale. In order for t/tacc to be larger in SN1987A, there must be a smaller diffusion coefficient and a larger shock velocity, in order to provide 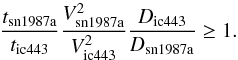 (14)Thus, if Fermi detects SN1987A in a few years and
(14)Thus, if Fermi detects SN1987A in a few years and 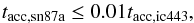 (15)then SN1987A should be detectable in future by CTA (Fig. 10 lower plot; here we used the “optimistic” value of density npp,sn87a ≃ 0.005npp,ic443).
(15)then SN1987A should be detectable in future by CTA (Fig. 10 lower plot; here we used the “optimistic” value of density npp,sn87a ≃ 0.005npp,ic443).
 |
Fig. 10 Hadronic γ-ray spectrum of SN1987A (green line). Also shown are: instrument sensitivities (Funk & Hinton 2013), the upper limits on the γ-ray flux after 7 yr of Fermi observations (orange, Ackermann et al. 2016) and after 210 h of HESS observations (blue, H.E.S.S. Collaboration 2015). The estimate of the upper limit for observations by CTA (grey) is obtained by scaling of the HESS upper limit. The spectrum of IC 443 (red line from Fig. 9) is also shown for comparison. The upper and lower plots correspond to the γ-ray spectrum of SN1987A in the cases A and B described in the text. |
4. Conclusions
We present an approach which could be a powerful tool for understanding the evolution of SNe as well as the γ- and non-thermal X-rays from SNRs.
We outline the methodology and prove its validity with a clear test case, namely, the pair of SNRs, SN1987A and IC 443. The radio spectrum of the former is free of the self-absorption during the period of observations while the γ-spectrum of the later is hadronic in origin and is not affected by the radiative losses.
We apply temporal evolution of the injection efficiency derived from the observed radio index of SN1987A to IC 443. Is it correct to relate two different objects by the same function Qt, especially because the progenitor of SN1987A is believed to be rather peculiar? We stress that Qt, as it is shown in Sect. 3.1, depends on the average global trend in the evolution of the radio spectral index and is almost insensitive to the details which reflect the detailed configuration of the circumstellar medium around SN1987A. The main reason of the injection variation, as is demonstrated in Sect. 3.1, is the increase of the surface of SN (i.e. more particles cross the shock with a chance to be accelerated). Furthermore, the observed evolution of the radio index, as is confirmed by the numerical model, corresponds to the period of time when the shock was in the nearly uniform H ii region. We conclude therefore that the details of the configuration of the nebula around SN1987A are not effective in determination of the function Qt. In addition, relatively good correspondence between the radio data of SN1987A and the derived γ-ray spectrum of IC 443 could be considered as a sign of similarities between the two remnants, SN1987A and IC 443. To conclude, since the main factor in the early evolution of the injection efficiency is the increase of the size of the very young remnant, the adoption of the Qt behaviour extracted from SN1987A could therefore have general applicability, not strictly to SNR with exactly the same progenitor.
There are two basic results. First, the break in the proton spectrum in SNR IC 443 around the proton energy 50 GeV and the corresponding decrease of its γ-ray spectrum after ~ 2 GeV are, as proved by the radio observations of SN1987A, a consequence of the injection efficiency evolution during the supernova stage. Second, the shape of the γ-ray spectrum of IC 443 at the photon energies above 20 GeV results in a guess about a possible evolution of the injection in SN1987A before it becomes visible for the radio telescopes. Namely, the value βx = 0.8, which fits this part of the γ-ray spectrum of IC 443, corresponds to the radio index 0.9 during the unobserved period of SN1987A, which is a reasonable index for supernovae.
We confirm the finding of Ackermann et al. (2013); namely, that γ-rays from IC 443 are of the hadronic origin. We found that the break in the proton spectrum around 50 GeV (which is needed to explain the observed γ-ray spectra) naturally originates from the time-dependent injection during the early stage of the remnant evolution. It is interesting that there is also evidence for the same breaks in the proton spectra in the SNR W44 (Ackermann et al. 2013), W51C (Abdo et al. 2009; Jogler & Funk 2016) and W49B (Abdalla et al. 2017). These four SNRs also exhibit the specific hadronic low-energy cutoff in the γ-ray spectra (below ~ 200 MeV) and are generally believed to be the remnants of the core-collapse SNe as well.
There is a model for the origin of this proton spectrum break developed in the framework of the stationary particle acceleration (Uchiyama et al. 2010; Cardillo et al. 2016). However, it does not simultaneously explain, the radio index variation at the supernova stage. Our scenario is in agreement with a general expectation that γ-rays from SNRs like IC 443 originate in the nearby molecular clouds. The clouds provide the target protons which generate γ-rays in interactions with the bullet protons which are accelerated by the SNR shock. In this framework, the γ-ray spectrum naturally reflects the momentum distribution of incoming relativistic protons (the bullets), not the particles in a cloud. The approach developed by Uchiyama et al. (2010), Cardillo et al. (2016) is completely alternative to ours; the shock re-accelerates the pre-existing cosmic rays. The early development of the particle acceleration during the SN stage is unimportant in this scenario.
The early time-dependent injection could explain both the shape of the γ-ray spectrum of SNR and the time evolution of the radio index in SN. An alternative scenario for deviations of the synchrotron spectral indices in SNRs from the canonical value 0.5 is the effect of the efficient non-linear particle acceleration; in this case, the shock compression factor σ is modified. In particular, the non-stationary numerical model which accounts for the back-reaction of relativistic particles could also explain the evolution of the radio spectral index in SN1987A (though with a lower accuracy, cf. Fig. 3 in Berezhko et al. 2015,and our Fig. 2)together with the variable injection (dashed line in Fig. 3 in Berezhko et al. 2015). The shock modification provides the second order corrections to the test-particle results. Our analytical description being test-particle in its nature catches the main trends and, due to its relative simplicity, clearly demonstrates that the observations of the radio spectral index evolution in SN1987A as well as the γ-ray spectrum of IC 443 do not agree with the constant injection rate. Indeed, why should the injection be the same during different epochs and under different conditions? We stress that in the present paper we do not model the temporal evolution of the injection efficiency but derive it from observations of the radio index. Any model of the evolution of the radio emission should take the variable injection into account.
It is worth noting once more that our solution of the time-dependent acceleration equation also considers, for the first time, the time-dependent injection (the original studies assume the steady-state injection, see Drury 1983 for the test-particle regime and Blasi et al. 2007 for the non-linear acceleration). The new effect in the present paper (change of the particle spectrum slope due to the variable injection) is simply a consequence of the non-stationary particle injection into the non-stationary acceleration. The steady-state acceleration equation cannot catch the same effect even if the injection is time-dependent because the variable injection in this case affects the only normalisation of the particle spectrum, Eq. (4), through the factor η, – but not its slope.
In summary, i) the time-scale for steady acceleration to pmax is larger than an SNR age; ii) it is obligatory therefore to consider the non-stationary particle spectrum for models of the γ-ray emission; and iii) interpretation of the hard γ-ray spectra should take into account the evolution of the particle injection during the first months after the supernova event. Furthermore, this is the point where SNe are linked to SNRs; information necessary to understand the γ-ray spectra of SNRs could be extracted from present-day radio observations of SNe. The opposite is also true; actually, the γ-ray spectrum of an SNR sheds light on its own first months after the supernova explosion.
At this point, our use of the Eq. (1), which describes the plane shock, is justified: we divide the thin emitting cylinder on a number of sectors and consider the shock to be plane-parallel in each sector.
Acknowledgments
We would like to thank G. Zanardo for the radio data on the spectral index evolution in SN1987A. This work is supported by the PRIN INAF 2014 grant “Filling the gap between supernova explosions and their remnants through magnetohydrodynamic modeling and high performance computing”. We acknowledge that the results in Sect. 3.1 have been achieved with the software developed in part by the U.S. Department of Energy supported Advanced Simulation and Computing/Alliance Center for Astrophysical Thermonuclear Flashes at the University of Chicago, using the PRACE Research Infrastructure resource MareNostrum III based in Spain at the Barcelona Supercomputing Center (PRACE Award N.2012060993). We acknowledge the CINECA Awards N.HP10BI36DG, 2012 and HP10CKMKX1, 2016 for the availability of high-performance computing resources and support.
References
- Abdalla, H., Ackermann, M., Ajello, M., et al. 2017, A&A, in press, DOI: 10.1051/0004-6361/201527843 [Google Scholar]
- Abdo, A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V., Aliu, E., Arlen, T., et al. 2009, ApJ, 698, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Albert, A., Atwood, W. B., et al. 2016, A&A, 586, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., & Atoyan, A. 2000, A&A, 362, 937 [NASA ADS] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 664, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, L., Crawford, D., Hunstead, R., Klamer, I., & McIntyre, V. 2001, ApJ, 549, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E., Ksenofontov, L., & Völk, H. 2015, ApJ, 810, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Amato, E., Caprioli, D., et al. 2007, MNRAS, 375, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchino, F., & Bykov, A. 2001, A&A, 376, 248 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brose, R., & Telezhinsky, P. M. 2016, A&A, 593, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardillo, M., Amato, E., & Blasi, P. 2016, A&A, 595, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Forman, M., & Drury, L. 1983, Proc. 18th ICRC, 2, 267 [Google Scholar]
- Funk, S., & Hinton, J. 2013, Astropart. Phys., 43, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B., Chatterjee, S., Slane, P. O., et al. 2006, ApJ, 648, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration 2015, Science, 347, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Jogler, T., & Funk, S. 2016, ApJ, 816, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, F. 1990, ApJ, 361, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S., Aharonian, F., & Bugayov, V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J., Bersier, D., & James, P. 2014, MNRAS, 437, 3848 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Bocchino, F., Decourchelle, A., et al. 2013, A&A, 556, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlino, G., & Caprioli, D. 2012, A&A, 538, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ng, C.-Y., Gaensler, B., Staveley-Smith, L., et al. 2008, ApJ, 684, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C.-Y., Zanardo, G., Potter, T., et al. 2013, ApJ, 777, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Olbert, C., Clearfield, C., Williams, N., Keohane, J., & Frail, D. 2001, ApJ, 554, L205 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, S., Miceli, M., Pumo, M., & Bocchino, F. 2015, ApJ, 810, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Petruk, O., & Kopytko, B. 2016, MNRAS, 462, 3104 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, T., Staveley-Smith, L., & Reville, B., et al. 2014, ApJ, 794, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, M., & Manchester, R. 1987, Nature, 329, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Swartz, D., Pavlov, G. G., Clarke, T., et al. 2015, ApJ, 808, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., Uchiyama, Y., Aharonian, F. A., et al. 2008, ApJ, 685, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Bocchino, F., Miceli, M., & Reale, F. 2008, A&A, 485, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turtle, A., Campbell-Wilson, D., Bunton, J., et al. 1987, Nature, 327, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Blandford, R., Funk, S., Tajima, H., & Tanaka, T. 2010, ApJ, 723, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Badenes, C., Petre, R., et al. 2014, ApJ, 785, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Zanardo, G., Staveley-Smith, L., Ball, L., et al. 2010, ApJ, 710, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Zanardo, G., Staveley-Smith, L., Hg, C.-Y., et al. 2013, ApJ, 767, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V., & Aharonian, F. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Note on Eq. (8)
Let us consider the injection term in the form Qt ∝ τβ. The distribution function ϕo(τ) given by Eq. (6) (Fig. A.1 red line) has a prominent maximum around τ∗ ≈ 0.7α-1 (the numerically evaluated values of τ∗ are 0.70 for α = 1, 1.6 for α = 1/2 and 2.6 for α = 1/3). After substitution Eq. (3) with ϕo(τ′) ≈ δ(τ′−τ∗), we obtain, for τ>τ∗, that fo(t,p) ∝ p− sf(τ(t,p)−τ∗)β. The spectral index of the particle spectrum is defined as 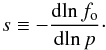 (A.1)Taking this derivative, with the use of the property dτ/τ = −αdp/p, we have
(A.1)Taking this derivative, with the use of the property dτ/τ = −αdp/p, we have 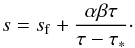 (A.2)Radio emitting electrons in evolved SNe and SNRs have typically large τ (due to small p and large t). For such τ ≫ τ∗, Eq. (A.2) transforms to Eq. (9); this is demonstrated also by the blue solid line in Fig. A.1.
(A.2)Radio emitting electrons in evolved SNe and SNRs have typically large τ (due to small p and large t). For such τ ≫ τ∗, Eq. (A.2) transforms to Eq. (9); this is demonstrated also by the blue solid line in Fig. A.1.
We consider the observations of SN1987A from t = 1517 day and the scale tm = 60 days. Therefore, the use of Eq. (9) in the present paper is justified since we consider τ ≥ 25 and the value of τ∗ = 0.7 has a negligible effect in Eq. (A.2).
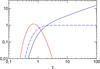 |
Fig. A.1 The same as Fig. 1 versus the dimensionless time τ. The blue dashed line represents the integral in Eq. (3) with Qt = 1 and the solid blue line gives the same integral with Qt = τ0.7. |
All Figures
 |
Fig. 1 Probability ϕo (red solid line) and the integral ℐ (blue dashed line) versus time for the fixed momentum p = pmax (bottom horizontal axis) and versus particle momenta for the fixed time t = tage (top horizontal axis). Numbers on the horizontal axes correspond to the particular choice of tage = 3000 yr, pmax = 104mpc and α = 1. The meaning of the dotted vertical lines is explained in the text. |
| In the text | |
 |
Fig. 2 Evolution of the radio spectral index as observed by Zanardo et al. (2010) during the period between 1517 and 8014 days after explosion (filled circles with errors), extrapolation (black circles without errors) of the linear fit (black line; from the same reference) up to the value αr = 0.5; then the constant αr is assumed. The red solid line represents the spectral index αr calculated by Eq. (8) with the dependence Qt(t) derived from the observed αr with the simple approximate formula (9); this Qt(t) is shown in Fig. 3. Green dashed line represents the case of the steady-state injection. |
| In the text | |
 |
Fig. 3 Time dependence of injection term. Blue circles correspond to the days of the radio observations. A red solid line traces the function Qt(t) derived as described in Sect. 2 from the observations during the period between 1517 and 8014 days after explosion and from the extrapolation of αr after the 8014th day. As for the behaviour of the injection term before day 1517, we adopt a simple approximation as described in the text, with βx = 0.8 and dx = 100. Green dashed line represents the case of the steady-state injection. The thin black line is the function Qt = lg(t/ 950). |
| In the text | |
 |
Fig. 4 Structure of the ambient medium around SN1987A in the 3D numerical model from Orlando et al. (2015). The shock is almost plane-parallel between points A and B because it decelerates in the dense medium of the H ii region. |
| In the text | |
 |
Fig. 5 3D volumetric rendering of the density in the numerical model of SN1987A Orlando et al. (2015), at 15 yr (around Day 5500) after the supernova explosion. The three panels show the rendering at three different angles (see upper left corner of each panel) between the line of sight and the axis of the H ii region surrounding SN1987A. The colour-scale is normalised to the maximum value in each panel. |
| In the text | |
 |
Fig. 6 Temporal evolution of the half-opening angle θ (black dots with errors) derived by analysis of observations (Ng et al. 2013) and from the 3D numerical model Orlando et al. (2015, red solid line). |
| In the text | |
 |
Fig. 7 Temporal evolution of the injection efficiency derived from the radio spectral index (blue dots) and from the 3D model of SN1987A (Orlando et al. 2015). The black (red) line represents Qt,num and corresponds to the case where the dense equatorial ring in the circumstellar nebula around SN1987A is accounted (neglected). The thick parts of the lines correspond to the time when the shock propagates in the uniform H ii region. The volume increase per unit time was calculated as Rhu1 for the solid lines and as R2u1 for the dashed line. The rapid increase in the black line shortly after Day 5000 corresponds to the shock interaction with the dense equatorial ring in the nebula around the SN. The rapid increase and following decrease of the red line right after the Day 6000 is due to the few ejecta clumps which protrude the forward shock and causes an artificial increase of the post-shock density and velocity around this time. Inset: evolution of different characteristics, in arbitrary units. This plot corresponds to the red line on the main figure. One can see that the main contribution to the evolution of Qt,num comes from the surface increase, R·h. |
| In the text | |
 |
Fig. 8 Particle spectra at 30 and 3000 yr calculated with Eq. (3) and the dependence Qt(t) shown in Fig. 3. Bottom axis is for protons and the upper one is for electrons, under the condition that both populations have the same maximum momentum (parameters used are listed in the caption to Fig. 9). |
| In the text | |
 |
Fig. 9 Gamma-ray spectrum of IC 443. The Fermi data are shown in red, MAGIC in blue and VERITAS in green dots with errors. Our fit is shown by the solid red line. The distribution of the parental protons is shown by the red line in Fig. 8. The emission and the particle spectra are calculated with the scales tm = 60 days and pm = 9.5 × 103mpc as well as the values of dx = 100 days and βx = 0.8; the last two parameters determine the fit of the γ-ray spectrum above 20 GeV. The emission spectrum for the same case but with the steady injection is shown by the green dashed line. The green dotted lines represent the spectra with the artificial injection terms which are the same as Qt but zero before day 100 (the rightmost line), before day 1517 (middle line) and before day 8014 (the leftmost line). The γ-ray spectrum is calculated following the recipe of Aharonian & Atoyan (2000) with the cross-section for the pion production from Kelner et al. (2006); such an approach is very accurate for γ-rays with energies below a few TeV (Kelner et al. 2006). |
| In the text | |
 |
Fig. 10 Hadronic γ-ray spectrum of SN1987A (green line). Also shown are: instrument sensitivities (Funk & Hinton 2013), the upper limits on the γ-ray flux after 7 yr of Fermi observations (orange, Ackermann et al. 2016) and after 210 h of HESS observations (blue, H.E.S.S. Collaboration 2015). The estimate of the upper limit for observations by CTA (grey) is obtained by scaling of the HESS upper limit. The spectrum of IC 443 (red line from Fig. 9) is also shown for comparison. The upper and lower plots correspond to the γ-ray spectrum of SN1987A in the cases A and B described in the text. |
| In the text | |
 |
Fig. A.1 The same as Fig. 1 versus the dimensionless time τ. The blue dashed line represents the integral in Eq. (3) with Qt = 1 and the solid blue line gives the same integral with Qt = τ0.7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


