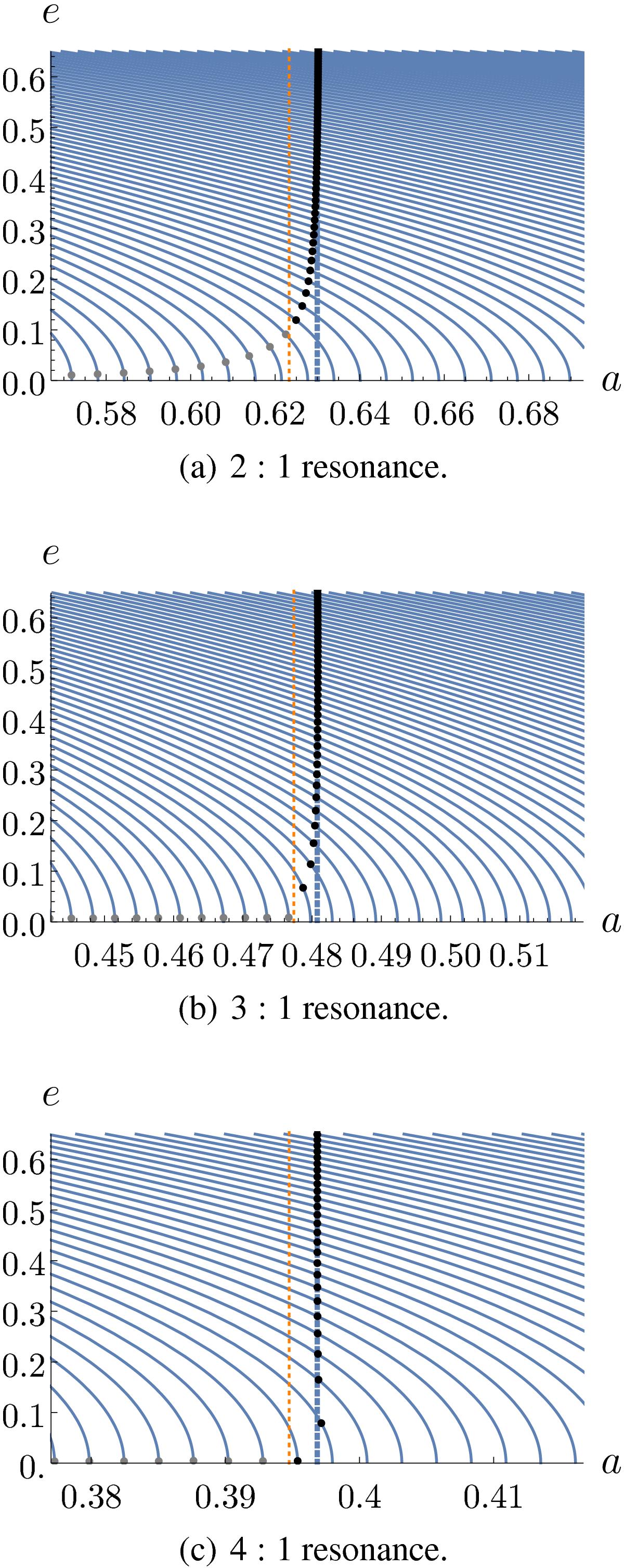
Level curves of N on the (a,e) plane for the case of the 2:1, 3:1, and 4:1 resonances with a′ = 1 AU for the perturber (in units where ). The solid lines depict Eq. (3.4), where the numerical value of N increases from left to right. The vertical thick dashed lines indicate the location of exact Keplerian resonance, a_res = a′(k/k′)^{2 / 3}. The dots represent the equilibrium values for the eccentricity and the semi-major axis on different level curves of N, while the arbitrary value of ϖ remains fixed. Here we used e′ = 0.2 and μ = 10^-3. We note that the equilibrium points deviate away from exact resonance at low eccentricities, which is particularly evident in the case of first-order resonances (the 2:1 resonance in this case; see text for details). Since this deviation is linked to a faster precession of the pericentre ϖ = − p, the value of e at which this effect becomes higher than yields a lower bound in e above which our approach is valid. The orange dashed line indicates a deviation from the exact resonance of this amount. We thus colour-coded the equilibrium points using black for those that fall above this lower limit in eccentricity, and grey for those that fall below it: for the latter, the fast change in p does not allow us to consider the pair (N,p) as slowly evolving variables.