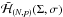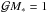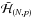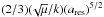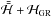| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 12 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201730936 | |
| Published online | 01 September 2017 | |
Extreme secular excitation of eccentricity inside mean motion resonance
Small bodies driven into star-grazing orbits by planetary perturbations⋆
1 Laboratoire Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, CS 34229 06304 Nice, France
e-mail: gabriele.pichierri@oca.eu
2 Cornell Center for Astrophysics and Planetary Science, Department of Astronomy, Cornell University, Ithaca, NY 14853, USA
Received: 4 April 2017
Accepted: 1 May 2017
Context. It is well known that asteroids and comets fall into the Sun. Metal pollution of white dwarfs and transient spectroscopic signatures of young stars like β-Pic provide growing evidence that extra solar planetesimals can attain extreme orbital eccentricities and fall into their parent stars.
Aims. We aim to develop a general, implementable, semi-analytical theory of secular eccentricity excitation of small bodies (planetesimals) in mean motion resonances with an eccentric planet valid for arbitrary values of the eccentricities and including the short-range force due to General Relativity.
Methods. Our semi-analytic model for the restricted planar three-body problem does not make use of series expansion and therefore is valid for any eccentricity value and semi-major axis ratio. The model is based on the application of the adiabatic principle, which is valid when the precession period of the longitude of pericentre of the planetesimal is much longer than the libration period in the mean motion resonance. In resonances of order larger than 1 this is true except for vanishingly small eccentricities. We provide prospective users with a Mathematica notebook with implementation of the model allowing direct use.
Results. We confirm that the 4:1 mean motion resonance with a moderately eccentric (e′ ≲ 0.1) planet is the most powerful one to lift the eccentricity of planetesimals from nearly circular orbits to star-grazing ones. However, if the planet is too eccentric, we find that this resonance is unable to pump the planetesimal’s eccentricity to a very high value. The inclusion of the General Relativity effect imposes a condition on the mass of the planet to drive the planetesimals into star-grazing orbits. For a planetesimal at ~ 1 AU around a solar mass star (or white dwarf), we find a threshold planetary mass of about 17 Earth masses. We finally derive an analytical formula for this critical mass.
Conclusions. Planetesimals can easily fall into the central star even in the presence of a single moderately eccentric planet, but only from the vicinity of the 4:1 mean motion resonance. For sufficiently high planetary masses the General Relativity effect does not prevent the achievement of star-grazing orbits.
Key words: celestial mechanics / planets and satellites: dynamical evolution and stability / minor planets, asteroids: general / white dwarfs / methods: analytical
The Mathematica notebook is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/605/A23
© ESO, 2017
1. Introduction
Over the last 30 yr it has become clear that planetary perturbations can force asteroids into such highly eccentric orbits that they collide with the Sun. There is also growing evidence that planetesimals may fall into their parent stars or suffer tidal disruption.
In the solar system, Sun-grazing long-period comets (e.g. the famous Kreutz group; Marsden 1967) have been known for a long time, but these objects are expected to come from the Oort cloud on orbits that are already highly eccentric, which means that planetary perturbations only play a minor role in driving their final Sun-grazing eccentricities. But in 1994, Farinella et al. (1994), following the evolution of the known near-Earth objects with numerical simulations, discovered that asteroids frequently collide with the Sun. The original source of near-Earth asteroids is the asteroid belt, so in this case planetary perturbations must play a major role in removing the object’s initial angular momentum. Mean motion resonances with Jupiter and a secular resonance with Saturn were identified as the main mechanisms capable of pushing the asteroid’s eccentricity to high values, far more effective than planetary close encounters. Gladman et al. (1997), again with numerical simulations, showed that more than 70% of the objects initially in the ν6 secular resonance with Saturn or the 3:1 mean motion resonance with Jupiter eventually collide with the Sun.
The collision of small bodies with the central star is not an oddity of our solar system. Ferlet et al. (1987) and Lagrange et al. (1987) proposed that the red-shifted Ca II and NA I absorption lines observed in β Pictoris were due to infalling evaporating bodies (see also Beust et al. 1989, 1990, 1991). The frequency of such events, on a characteristic timescale of a few years, suggests that the infalling bodies were on short-period orbits, similar to asteroids or short-period comets in the solar system. In recent years, many more young star systems have been observed to possess Doppler-shifted, transient absorption line features similar to β Pic, suggesting that infalling small bodies may be a common phenomenon (e.g. Sorelli et al. 1996; Welsh & Montgomery 2013; Greaves et al. 2016).
Additional evidence for planetesimals falling into the central star comes from the atmospheric pollution in heavy elements observed in white dwarfs (see Farihi 2016 for a review). Spectroscopic studies of a large sample of cool, hydrogen-rich white dwarfs has established a minimum frequency of 30% for the pollution phenomenon in these objects (Zuckerman et al. 2003; Koester et al. 2014). In cold white dwarfs, heavy elements should rapidly sink (Fontaine & Michaud 1979; Vauclair & Fontaine 1979) leaving behind only hydrogen or helium. Thus, external sources must be responsible for any photospheric metals. The most commonly accepted explanation is that these metals originate from tidally disrupted planetesimals (Debes & Sigurdsson 2002; Jura 2003). In essence, planetesimals perturbed into highly eccentric orbits pass within the stellar Roche limit (which is of the order of the solar radius R⊙) and are torn apart by gravitational tides; subsequent collisions reduce the fragments to dust; the latter produce an infrared excess and slowly rain down onto the stellar surface, which generates the observed atmospheric pollution. Obviously, for this model to work, planetesimals have to be “pushed” by planetary perturbations to achieve orbits that are eccentric enough to pass within ~ R⊙ from the star. Given the ubiquity of the white dwarf pollution phenomenon, a robust mechanism of extreme eccentricity excitation of planetesimals is needed (e.g. Bonsor et al. 2011; Debes et al. 2012; Petrovich & Muñoz 2017). These astrophysical contexts have revived the interest in mean motion resonances with eccentric planets as a generic mechanism for pumping the eccentricities of small bodies from ~ 0 to ~ 1, i.e. for driving planetesimals into the central star.
Analytic celestial mechanics shows that mean motion resonances with a planet on a circular orbit only cause an oscillation of the small body’s semi-major axis coupled with a moderate oscillation of the eccentricity and with the libration of the angle kλ − k′λ′ (where λ and λ′ are the mean longitudes of the small body and of the planet, respectively, and the integer coefficients k and k′ define the k′:k resonance; Henrard & Lemaitre 1983; Lemaitre 1984). However, if the perturbing planet has a finite eccentricity, inside a mean motion resonance there can be a dramatic secular evolution; the eccentricity of the small body can undergo large excursions correlated with the precession of the longitude of perihelion (Wisdom 1985, 1983; Henrard & Caranicolas 1990).
These pioneer works used a series expansion of the Hamiltonian in power laws of the eccentricities of the perturbed body (e) and of the planet (e′), and focused specifically on the case of the 3:1 resonance with Jupiter. A few years later, Moons & Morbidelli (1993, 1995) developed a semi-analytic study of the dynamics in mean motion resonances using a first-order expansion in e′ but no series expansions in e. This way, they were able to follow the evolution of the small body to arbitrarily high eccentricities. This approach is valid only for small values of e′ and moreover for e>e′. Motivated by the Farinella et al. (1994) numerical results, Moons and Morbidelli focused on the specific case of the solar system, including the effects of Saturn on the orbital evolution of Jupiter in addition to their combined perturbation to the asteroid. In this framework, they established the existence of overlapping secular resonances inside the 4:1, 3:1, 5:2, and 7:3 mean motion resonances, which can push the eccentricity of the small body to unity.
In a more general context, Beust & Morbidelli (1996) investigated the secular dynamics in mean motion resonances with a single planet with various (albeit moderate) eccentricities. Again, they considered an expansion in e′ to the first order, and no expansion in the eccentricity of the perturbed body. Of all the resonances, they found that 4:1 is the most powerful in pushing the eccentricity of the small body from ~ 0 to ~ 1, provided that e′ ≳ 0.05. In contrast, the 3:1 resonance only generates large oscillations in the eccentricity of the small body, but they are insufficient to produce star-grazing orbits, at least for planet eccentricities up to 0.1. Because of the linear expansion in e′, Beust & Morbidelli (1996) could not determine the threshold planetary eccentricity that generates the star-grazing phenomenon for small bodies initially on quasi-circular orbits in the 3:1 resonance.
In this paper we revisit the problem of the eccentricity evolution of small bodies inside mean motion resonances with an eccentric planet using a semi-analytic approach. In order to go beyond the works cited above, we do not expand the Hamiltonian in the eccentricity of either the small body or the perturber. In this way, our study is valid for all eccentricities and also in the e<e′ regime. Our work is not the first to avoid expansions in e′ (e.g. Beaugé et al. 2006; Michtchenko et al. 2006; Sidorenko 2006). We use the adiabatic principle (already invoked in Wisdom 1985) to disentangle the motion related to the libration of kλ − k′λ′ from the secular motion relating eccentricity and longitude of perihelion. To remain relatively simple, our analysis is performed in the limit of small amplitude of libration in the mean motion resonance.
The paper is structured as follows. In Sect. 2, we develop the analytic formalism for the study of the secular dynamics at the core of mean motion resonances, without series expansions. This results in the averaged Hamiltonian with two degrees of freedom (2.10). In Sect. 3 we lay out the method for studying the dynamics given by the averaged Hamiltonian, using the theory of adiabatic invariance; we also discuss the limit of validity of this method. In Sect. 4 we also include a post-Newtonian term, describing the fast precession of the longitude of perihelion at large eccentricity due to General Relativity. Our results are presented in Sect. 5. We first neglect the effect of General Relativity; in this case the secular evolution is independent of the planet’s mass, and only the timescale of the secular evolution depends on it. We focus in particular on the 4:1, 3:1, and 2:1 resonances, and for each of these resonances we evaluate what planetary eccentricities are needed to lift bodies from initially quasi-circular orbits to star-grazing ones, if it is ever possible. When this is the case, we then introduce the post-Newtonian correction, which makes the secular dynamics at high eccentricity dependent on the planetary mass. Thus, we determine – for the resonances and the planetary eccentricities previously considered – the minimal planetary mass required to achieve the star-grazing phenomenon. In addition, we provide supplementary material available at the CDS: a Mathematica notebook implementing our model so that the reader can compute the secular dynamics in the desired resonances with the desired planets. The conclusions of this work are summarized in Sect. 6.
2. Planetary Hamiltonian
We start with the Hamiltonian for the restricted planar three-body problem. By denoting with x = (x,y) and v = (vx,vy) the Cartesian coordinates and momenta of the perturbed test particle (“small body”), and using a prime for the perturber (“planet”), the Hamiltonian reads: 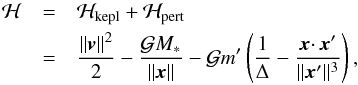 (2.1)where M∗ is the mass of the star, m′ is the mass of the perturber, and Δ = ∥ x − x′ ∥ is the distance between the test particle and the perturber (Murray & Dermott 2000). The perturber is assumed to follow a given Keplerian orbit, so x′ is a function of time. In terms of orbital elements, the Cartesian coordinates are given by
(2.1)where M∗ is the mass of the star, m′ is the mass of the perturber, and Δ = ∥ x − x′ ∥ is the distance between the test particle and the perturber (Murray & Dermott 2000). The perturber is assumed to follow a given Keplerian orbit, so x′ is a function of time. In terms of orbital elements, the Cartesian coordinates are given by 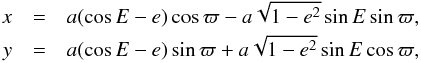 (2.2)where a is the semi-major axis, e is the eccentricity and E is the eccentric anomaly of the perturbed particle, and similar (primed) equations and orbital parameters for the perturber (Murray & Dermott 2000).
(2.2)where a is the semi-major axis, e is the eccentricity and E is the eccentric anomaly of the perturbed particle, and similar (primed) equations and orbital parameters for the perturber (Murray & Dermott 2000).
We introduce the canonical modified Delaunay action-angle variables (Λ,P,λ,p), given by  (2.3)where λ is the mean longitude, ℓ = E − esinE is the mean anomaly, and ϖ is the longitude of pericentre of the test mass. In order to make the system autonomous, we extend the phase space by introducing for the perturber
(2.3)where λ is the mean longitude, ℓ = E − esinE is the mean anomaly, and ϖ is the longitude of pericentre of the test mass. In order to make the system autonomous, we extend the phase space by introducing for the perturber 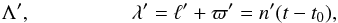 (2.4)where
(2.4)where 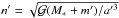 is the mean motion of the perturber. We assume that the perturber does not precess, so without loss of generality we set ϖ′ = 0. Now the autonomous Hamiltonian of the system reads
is the mean motion of the perturber. We assume that the perturber does not precess, so without loss of generality we set ϖ′ = 0. Now the autonomous Hamiltonian of the system reads ![\begin{eqnarray} \Ha(\LAMBDONA,\P, \LAMBDONA',\LAMBDA,\p, \LAMBDA') &= &-\frac{\GravC ^2 M_*^2}{2 \LAMBDONA^2} + \N' \LAMBDONA' \notag\\[3mm] &&+\Ha_{\rm pert}(\LAMBDONA,\P,\LAMBDA,\p, \LAMBDA'; e', \VARPI' = 0), \end{eqnarray}](/articles/aa/full_html/2017/09/aa30936-17/aa30936-17-eq36.png) (2.5)where the perturbation part ℋpert is to be written in terms of the newly defined variables. We note that it depends parametrically on the arbitrary values of e′ and ϖ′ = 0.
(2.5)where the perturbation part ℋpert is to be written in terms of the newly defined variables. We note that it depends parametrically on the arbitrary values of e′ and ϖ′ = 0.
We now consider the test particle to be close to an inner mean motion resonance with the outer perturber. In other words, we assume kn − k′n′ ~ 0, where 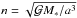 is the mean motion of the test particle for some positive integers k, k′, such that k′>k. In order to study the resonant dynamics, it is possible to introduce a set of canonical resonant action-angle variables:
is the mean motion of the test particle for some positive integers k, k′, such that k′>k. In order to study the resonant dynamics, it is possible to introduce a set of canonical resonant action-angle variables: 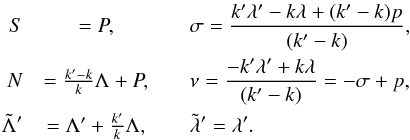 (2.6)The historical reason for adopting these variables is that for e′ = 0 there is no harmonic term in ν in the Hamiltonian and thus N is a constant of motion. The reason why the critical resonant angle σ is not simply defined as k′λ′ − kλ + (k′ − k)p is explained in Lemaitre (1984) and is due to the d’Alembert rules: the coefficient of the terms cos [ l(k′λ′ − kλ + (k′ − k)p) ] in the Fourier expansion of the perturbing Hamiltonian is proportional to el | k′ − k | for small values of e. Thus, for small eccentricities the Hamiltonian is a polynomial expression in ecosσ and esinσ, and the apparent singularity at e = 0 can be removed.
(2.6)The historical reason for adopting these variables is that for e′ = 0 there is no harmonic term in ν in the Hamiltonian and thus N is a constant of motion. The reason why the critical resonant angle σ is not simply defined as k′λ′ − kλ + (k′ − k)p is explained in Lemaitre (1984) and is due to the d’Alembert rules: the coefficient of the terms cos [ l(k′λ′ − kλ + (k′ − k)p) ] in the Fourier expansion of the perturbing Hamiltonian is proportional to el | k′ − k | for small values of e. Thus, for small eccentricities the Hamiltonian is a polynomial expression in ecosσ and esinσ, and the apparent singularity at e = 0 can be removed.
Using the variables (2.6), the Keplerian part of the Hamiltonian takes the form ![\begin{eqnarray} \Ha_{\rm kepl}(\SS, \NN, \tilde\LAMBDONA')& = &-\GravC^2 M_*^2 \frac{ (k'-k)^2}{2 k^2 (\NN-\SS)^2} \notag \\ &&+\N'\left[ \tilde\LAMBDONA' - \frac{k'}{(k'-k)}(\NN-\SS)\right]. \label{eq:KeplerianHamiltonianInResonantVariables} \end{eqnarray}](/articles/aa/full_html/2017/09/aa30936-17/aa30936-17-eq53.png) (2.7)At this point, we average the Hamiltonian over the fast angles. From a computational point of view, a remark is in order. The Cartesian components given in (2.2)are expressed in terms of the eccentric anomalies E, E′. Thus, it would be necessary to invert Kepler’s equation λ − ϖ = ℓ = E − esinE to obtain E = E(λ), and similarly for E′ = E′(λ′). If e′ is not too large, the latter inversion is not problematic. However the eccentricity e of the test particle can reach high values, and solving the Kepler equation for the test particle becomes numerically cumbersome. Therefore, it is advisable to retain the dependence on the eccentric anomaly E, use the differential relationship dλ = (1 − ecosE)dE, and integrate over E instead. This is more convenient because the dependence of λ on E is given through Kepler’s equation by an explicit formula. We also note that λ is related to λ′ through σ by λ′ = [ (kλ − (k′ − k)(p − σ) ] /k′. In summary, using the resonant relationship and Kepler’s equation one obtains E′ from λ′, λ′ from λ, and λ from E, so that the averaging on E eliminates the short periodic dependence of the Hamiltonian. By doing so, the canonical angle λ′ vanishes from the averaged Hamiltonian, and
(2.7)At this point, we average the Hamiltonian over the fast angles. From a computational point of view, a remark is in order. The Cartesian components given in (2.2)are expressed in terms of the eccentric anomalies E, E′. Thus, it would be necessary to invert Kepler’s equation λ − ϖ = ℓ = E − esinE to obtain E = E(λ), and similarly for E′ = E′(λ′). If e′ is not too large, the latter inversion is not problematic. However the eccentricity e of the test particle can reach high values, and solving the Kepler equation for the test particle becomes numerically cumbersome. Therefore, it is advisable to retain the dependence on the eccentric anomaly E, use the differential relationship dλ = (1 − ecosE)dE, and integrate over E instead. This is more convenient because the dependence of λ on E is given through Kepler’s equation by an explicit formula. We also note that λ is related to λ′ through σ by λ′ = [ (kλ − (k′ − k)(p − σ) ] /k′. In summary, using the resonant relationship and Kepler’s equation one obtains E′ from λ′, λ′ from λ, and λ from E, so that the averaging on E eliminates the short periodic dependence of the Hamiltonian. By doing so, the canonical angle λ′ vanishes from the averaged Hamiltonian, and 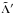 becomes a constant of motion, so that the term
becomes a constant of motion, so that the term 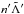 can be dropped from (2.7).
can be dropped from (2.7).
Proceeding this way, we have that 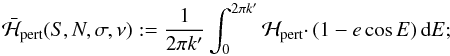 (2.8)it is important to note that we integrate over E from 0 to 2πk′ instead of just 2π because only after k′ revolutions of the test particle around the star (which correspond to k revolutions of the outer perturber) does the system attain the initial configuration, thus recovering the complete periodicity of the Hamiltonian. The integral (2.8)can be solved numerically. In our code we use a Mathematica function with an imposed relative accuracy of 10-10. For the Keplerian part we just write
(2.8)it is important to note that we integrate over E from 0 to 2πk′ instead of just 2π because only after k′ revolutions of the test particle around the star (which correspond to k revolutions of the outer perturber) does the system attain the initial configuration, thus recovering the complete periodicity of the Hamiltonian. The integral (2.8)can be solved numerically. In our code we use a Mathematica function with an imposed relative accuracy of 10-10. For the Keplerian part we just write 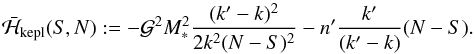 (2.9)The averaged Hamiltonian then becomes
(2.9)The averaged Hamiltonian then becomes 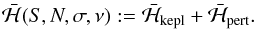 (2.10)This two degree of freedom system is not integrable in general, unless further approximation is made.
(2.10)This two degree of freedom system is not integrable in general, unless further approximation is made.
3. Studying the averaged Hamiltonian
We now intend to study quantitatively the dynamics given by the Hamiltonian (2.10). This can be seen as an integrable system (i.e. the Keplerian part), to which a small perturbation of order μ = m′/M∗ ≪ 1 is added.
We begin by noticing that 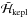 only depends on N − S, so it is convenient to introduce the canonical variables
only depends on N − S, so it is convenient to introduce the canonical variables 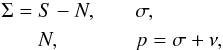 (3.1)making
(3.1)making 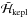 a function of Σ alone. The location of exact resonance is given by the value Σ = Σres such that
a function of Σ alone. The location of exact resonance is given by the value Σ = Σres such that 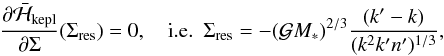 (3.2)which is simply n = nres = (k′/k)n′. The expansion of
(3.2)which is simply n = nres = (k′/k)n′. The expansion of 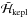 in ΔΣ = Σ − Σres starts with a quadratic term in ΔΣ. Since the perturbation
in ΔΣ = Σ − Σres starts with a quadratic term in ΔΣ. Since the perturbation 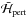 is a function of (Σ,N,σ,p) and is of order μ, the dynamics in the canonical pair of variables (Σ,σ) near Σres is equivalent to that of a pendulum with Hamiltonian of the form (ΔΣ)2 + μcosσ, so its frequency is of order
is a function of (Σ,N,σ,p) and is of order μ, the dynamics in the canonical pair of variables (Σ,σ) near Σres is equivalent to that of a pendulum with Hamiltonian of the form (ΔΣ)2 + μcosσ, so its frequency is of order  . On the other hand, the dynamics in the canonical pair (N,p) is slower, with a characteristic frequency of order μ. We can therefore apply the adiabatic principle and study the dynamics in (Σ,σ) with fixed (N,p), and then the dynamics in (N,p) keeping constant the action integral
. On the other hand, the dynamics in the canonical pair (N,p) is slower, with a characteristic frequency of order μ. We can therefore apply the adiabatic principle and study the dynamics in (Σ,σ) with fixed (N,p), and then the dynamics in (N,p) keeping constant the action integral 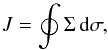 (3.3)which is the adiabatic invariant of the dynamics (Henrard 1993).
(3.3)which is the adiabatic invariant of the dynamics (Henrard 1993).
We now explain this procedure in more detail. Once the values of N and p have been fixed, 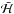 reduces to a one degree of freedom Hamiltonian in (Σ,σ) and parametrized by (N,p), which we denote by
reduces to a one degree of freedom Hamiltonian in (Σ,σ) and parametrized by (N,p), which we denote by 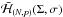 . This Hamiltonian is therefore integrable, so we can study its dynamics by plotting its level curves. We note however that by fixing N we can obtain Σ from e and vice versa, so we can also use (ecosσ,esinσ) as independent variables. Although these variables are not canonical, they have the already mentioned advantage that for small e the Hamiltonian is a polynomial in (ecosσ,esinσ), so the level curves do not have a singularity at e = 0. In addition, the plot of the level curves does not require the use of canonical variables. We show examples of these plots in the case of the 4:1 resonance in Fig. 1.
. This Hamiltonian is therefore integrable, so we can study its dynamics by plotting its level curves. We note however that by fixing N we can obtain Σ from e and vice versa, so we can also use (ecosσ,esinσ) as independent variables. Although these variables are not canonical, they have the already mentioned advantage that for small e the Hamiltonian is a polynomial in (ecosσ,esinσ), so the level curves do not have a singularity at e = 0. In addition, the plot of the level curves does not require the use of canonical variables. We show examples of these plots in the case of the 4:1 resonance in Fig. 1.
 |
Fig. 1 Level plots of the Hamiltonian |
In principle, the dynamics can be studied for any value of J. Once the cycle of 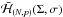 corresponding to the considered value of J through (3.3)is identified, the full Hamiltonian
corresponding to the considered value of J through (3.3)is identified, the full Hamiltonian 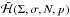 is averaged over the cycle, as explained in Henrard (1993), leading to a new one degree of freedom Hamiltonian
is averaged over the cycle, as explained in Henrard (1993), leading to a new one degree of freedom Hamiltonian 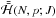 . This Hamiltonian is integrable, and the resulting dynamics in (N,p) describes the secular evolution of the small body inside the mean motion resonance with the perturber.
. This Hamiltonian is integrable, and the resulting dynamics in (N,p) describes the secular evolution of the small body inside the mean motion resonance with the perturber.
In this paper we vastly simplify this procedure by limiting ourselves to the case J → 0, i.e. the limit of small libration amplitude in the mean motion resonance. In this limit, the cycle in (Σ,σ) described by 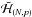 shrinks to the stable equilibrium point. Thus, there is no need to average the full Hamiltonian over a cycle:
shrinks to the stable equilibrium point. Thus, there is no need to average the full Hamiltonian over a cycle: 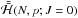 is obtained by evaluating
is obtained by evaluating 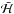 on the stable equilibrium point of
on the stable equilibrium point of 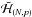 in the variables e and σ. We note that by having fixed N, we are effectively linking the semi-major axis a to the eccentricity e, via the relation
in the variables e and σ. We note that by having fixed N, we are effectively linking the semi-major axis a to the eccentricity e, via the relation 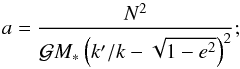 (3.4)therefore, we recover the equilibrium values aeq of the semi-major axis as well.
(3.4)therefore, we recover the equilibrium values aeq of the semi-major axis as well.
We show an example of this calculation in Fig. 2, for the 2:1, 3:1, and 4:1 resonances. It is worth pointing out that the equilibrium points in the (e,a) diagram deviate away from the Keplerian resonant value ares = a′(k/k′)2 / 3 as e → 0. This is especially evident in the case of first-order resonances, | k − k′ | = 1. In this case, for e>e′ the main harmonic in the Hamiltonian is ecosσ, i.e. 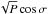 , from (2.3)and expansion for small e. Because ṗ = ∂ℋ /∂P, this harmonic gives
, from (2.3)and expansion for small e. Because ṗ = ∂ℋ /∂P, this harmonic gives 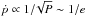 , which grows considerably as e approaches zero; therefore, in order to maintain
, which grows considerably as e approaches zero; therefore, in order to maintain ![\hbox{$\dot\SIGMA = [k'\dot\LAMBDA'-k\dot\LAMBDA+(k'-k)\dot\p]/(k'-k)\sim 0$}](/articles/aa/full_html/2017/09/aa30936-17/aa30936-17-eq119.png) , it is necessary to have
, it is necessary to have 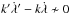 i.e. a/a′ ≁ (k/k′)(2 / 3). For resonances of order | k′ − k | > 1 the main harmonic in the Hamiltonian for e>e′ is e| k′ − k |cosσ, i.e. P| k′ − k | / 2cosσ. Therefore, the first derivative in P is not singular for
i.e. a/a′ ≁ (k/k′)(2 / 3). For resonances of order | k′ − k | > 1 the main harmonic in the Hamiltonian for e>e′ is e| k′ − k |cosσ, i.e. P| k′ − k | / 2cosσ. Therefore, the first derivative in P is not singular for 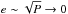 . However, for e<e′ the main harmonic dependent on e is e′ | k′ − k | − 1ecos [ (k′ − k)σ − (k′ − k − 1)(p + ϖ′) ], which gives a contribution to ṗ proportional to 1 /e, and the same reasoning applies. Indeed, in the case of inner mean motion resonance, aeq always attains values that are slightly less than the Keplerian ares as e → 0, as shown in Fig. 2. We must note, however, that the deviation of the equilibrium points away from the resonant value ares indicates a rapid precession of the pericentre ϖ. This means that our assumption that p and N remain constant is no longer valid. It breaks down when their motion evolves with a frequency of order
. However, for e<e′ the main harmonic dependent on e is e′ | k′ − k | − 1ecos [ (k′ − k)σ − (k′ − k − 1)(p + ϖ′) ], which gives a contribution to ṗ proportional to 1 /e, and the same reasoning applies. Indeed, in the case of inner mean motion resonance, aeq always attains values that are slightly less than the Keplerian ares as e → 0, as shown in Fig. 2. We must note, however, that the deviation of the equilibrium points away from the resonant value ares indicates a rapid precession of the pericentre ϖ. This means that our assumption that p and N remain constant is no longer valid. It breaks down when their motion evolves with a frequency of order 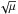 , i.e. of the same order as the frequency of the Σ,σ evolution. When
, i.e. of the same order as the frequency of the Σ,σ evolution. When 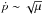 , the equilibrium semi-major axis of the test particle deviates from the Keplerian value by the amount of order
, the equilibrium semi-major axis of the test particle deviates from the Keplerian value by the amount of order 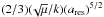 . Thus, we can determine the lower limit in eccentricity for the validity of our approach as the value of e at which the equilibrium point aeq deviates away from ares by more than this quantity. In this paper, we will focus mainly on resonances of order higher than 1 because they are much more efficient in pushing the eccentricity e from ~ 0 to ~ 1 (see Sect. 5). In this case, for e<e′ our approach is valid down to very small values of the eccentricity.
. Thus, we can determine the lower limit in eccentricity for the validity of our approach as the value of e at which the equilibrium point aeq deviates away from ares by more than this quantity. In this paper, we will focus mainly on resonances of order higher than 1 because they are much more efficient in pushing the eccentricity e from ~ 0 to ~ 1 (see Sect. 5). In this case, for e<e′ our approach is valid down to very small values of the eccentricity.
 |
Fig. 2 Level curves of N on the (a,e) plane for the case of the 2:1, 3:1, and 4:1 resonances with a′ = 1 AU for the perturber (in units where |
We have implemented this scheme in a Mathematica notebook, which is made available at the CDS. Let us now briefly explain the steps in our calculation, which ultimately yields the level curves of the Hamiltonian 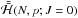 on the (ecosϖ,esinϖ) plane, thereby describing the secular evolution of the small body inside the mean motion resonance with the perturber, in the limit of J = 0. First, we consider a fixed value of N = N∗. For some given value of ϖ, we can find the (stable) equilibrium point in the (ecosσ,esinσ) plane in the following manner. If ϖ = ϖ0 = 0, the Hamiltonian (2.10)contains only cosines of (k′ − k)σ (and its multiples) so that its extrema in σ are found at 2πl/ (k′ − k) and (2πl + π) / (k′ − k), l ∈Z. Taking for example σ = σ0 = 0, ± π, we can write the Hamiltonian (2.10)as
on the (ecosϖ,esinϖ) plane, thereby describing the secular evolution of the small body inside the mean motion resonance with the perturber, in the limit of J = 0. First, we consider a fixed value of N = N∗. For some given value of ϖ, we can find the (stable) equilibrium point in the (ecosσ,esinσ) plane in the following manner. If ϖ = ϖ0 = 0, the Hamiltonian (2.10)contains only cosines of (k′ − k)σ (and its multiples) so that its extrema in σ are found at 2πl/ (k′ − k) and (2πl + π) / (k′ − k), l ∈Z. Taking for example σ = σ0 = 0, ± π, we can write the Hamiltonian (2.10)as 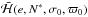 and we can find its maximum as a function of the eccentricity. The fact that
and we can find its maximum as a function of the eccentricity. The fact that 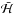 , as a function of e, must have a maximum at the resonance can be seen from Eq. (2.9), which clearly has a maximum in Σ = S − N at Σres (defined in Eq. (3.2)). Then, because
, as a function of e, must have a maximum at the resonance can be seen from Eq. (2.9), which clearly has a maximum in Σ = S − N at Σres (defined in Eq. (3.2)). Then, because 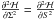 and S is monotonic in e,
and S is monotonic in e, 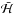 must have a maximum in e. We call emax the value of the eccentricity for which
must have a maximum in e. We call emax the value of the eccentricity for which 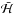 is maximal. We must now check that this is in fact the stable equilibrium point, i.e. that in σ0 the function
is maximal. We must now check that this is in fact the stable equilibrium point, i.e. that in σ0 the function 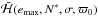 of σ has a maximum (and not a minimum). If this is not the case, we can repeat the calculation with σ = π/ (k′ − k),π/ (k′ − k) + π. Although in principle the maximum in σ could be away from this axis (because of the higher order harmonics in (k′ − k)σ), in practice in all the cases we studied this procedure effectively yields, for the given value of N = N∗ and for ϖ = ϖ0 = 0, the stable equilibrium point in (e,σ), denoted by (eeq,σeq). We note from Fig. 1 that eeq increases with the value N∗.
of σ has a maximum (and not a minimum). If this is not the case, we can repeat the calculation with σ = π/ (k′ − k),π/ (k′ − k) + π. Although in principle the maximum in σ could be away from this axis (because of the higher order harmonics in (k′ − k)σ), in practice in all the cases we studied this procedure effectively yields, for the given value of N = N∗ and for ϖ = ϖ0 = 0, the stable equilibrium point in (e,σ), denoted by (eeq,σeq). We note from Fig. 1 that eeq increases with the value N∗.
Following the procedure described above, we can assign to the Hamiltonian 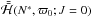 the value
the value 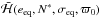 on the point (eeqcosϖ0,eeqsinϖ0). We also note that from the equilibrium value eeq, it is possible to obtain the corresponding aeq through Eq. (3.4). When ϖ is not zero, the diagram in the (ecosσ,esinσ) plane is, to a good approximation1 for most values of e, simply rotated by a quantity related to ϖ, so that the equilibrium values of the eccentricity and the semi-major axis do not change substantially, but only σeq changes (see Fig. 1). This way, it is possible to obtain the equilibrium value for σ by finding the maximum in σ of the function
on the point (eeqcosϖ0,eeqsinϖ0). We also note that from the equilibrium value eeq, it is possible to obtain the corresponding aeq through Eq. (3.4). When ϖ is not zero, the diagram in the (ecosσ,esinσ) plane is, to a good approximation1 for most values of e, simply rotated by a quantity related to ϖ, so that the equilibrium values of the eccentricity and the semi-major axis do not change substantially, but only σeq changes (see Fig. 1). This way, it is possible to obtain the equilibrium value for σ by finding the maximum in σ of the function 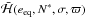 for the fixed value of ϖ. It is worth noticing that in order to assign to the point (eeqcosϖ,eeqsinϖ) the appropriate value of the Hamiltonian, we are only interested in the
for the fixed value of ϖ. It is worth noticing that in order to assign to the point (eeqcosϖ,eeqsinϖ) the appropriate value of the Hamiltonian, we are only interested in the ![\hbox{$\max_{\SIGMA\in[0,2\pi]}\bar\Ha(e_{\rm eq}, \NN^*, \SIGMA,\VARPI)= \max_{\SIGMA\in[0,2\pi/(k'-k)]}\bar\Ha(e_{\rm eq}, \NN^*, \SIGMA,\VARPI)$}](/articles/aa/full_html/2017/09/aa30936-17/aa30936-17-eq174.png) for the fixed value of ϖ, not in the actual value σeq of σ where the maximum is attained. However, we need to check that σeq changes smoothly with N∗ and ϖ. If this were not the case, a bifurcation would occur, which would invalidate the assumption that the amplitude of libration remains small. We have checked that this happens only in the case of the 3:1 resonance in a point on the ϖ = 0 axis (e.g. at e ≃ 0.35 in Fig. 7b). We note that this point is never crossed during the secular evolution because it appears as a centre of libration.
for the fixed value of ϖ, not in the actual value σeq of σ where the maximum is attained. However, we need to check that σeq changes smoothly with N∗ and ϖ. If this were not the case, a bifurcation would occur, which would invalidate the assumption that the amplitude of libration remains small. We have checked that this happens only in the case of the 3:1 resonance in a point on the ϖ = 0 axis (e.g. at e ≃ 0.35 in Fig. 7b). We note that this point is never crossed during the secular evolution because it appears as a centre of libration.
By letting N vary, i.e. effectively by allowing eeq to vary, we obtain the level curves of the Hamiltonian 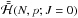 in the variables (ecosϖ,esinϖ). We present several examples in Sect. 5, where we show level curves of
in the variables (ecosϖ,esinϖ). We present several examples in Sect. 5, where we show level curves of 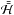 for different resonances and different values of e′.
for different resonances and different values of e′.
4. Effect of short-range forces
When the eccentricity of the test mass reaches values close to 1, so that the osculating ellipse becomes narrower and narrower, the periapsis distance from the star aperi = a(1 − e) becomes considerably small. At this point, the effect of various short-range forces may become important and must be considered. One such short-range force arises from General Relativity, with the post-Newtonian contribution to the test particle’s Hamiltonian given by 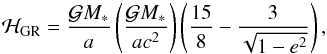 (4.1)where c is the speed of light (Krivov 1986). We note that the 15/8 term only gives the General Relativity correction to the mean motions, while the 1/
(4.1)where c is the speed of light (Krivov 1986). We note that the 15/8 term only gives the General Relativity correction to the mean motions, while the 1/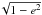 term gives the correction to the precession of the pericentre. Since we are only interested in the latter and we have averaged over the mean motion, we drop the former. Another short-range force arises from the rotational bulge of the central star, with the Hamiltonian given by
term gives the correction to the precession of the pericentre. Since we are only interested in the latter and we have averaged over the mean motion, we drop the former. Another short-range force arises from the rotational bulge of the central star, with the Hamiltonian given by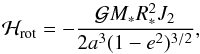 (4.2)where R∗ is the stellar radius, and
(4.2)where R∗ is the stellar radius, and 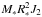 is the rotation-induced quadruple moment of the star. To assess the importance of these short-range forces, we compare ℋGR and ℋrot to Φ0, the characteristic tidal potential produced by the planetary perturber on the test particle,
is the rotation-induced quadruple moment of the star. To assess the importance of these short-range forces, we compare ℋGR and ℋrot to Φ0, the characteristic tidal potential produced by the planetary perturber on the test particle, 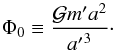 (4.3)We find
(4.3)We find 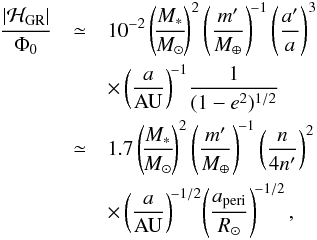 (4.4)
(4.4)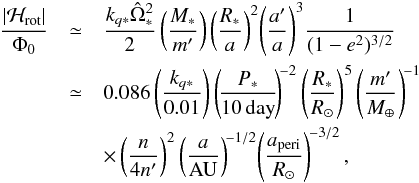 (4.5)where aperi = a(1 − e), and we use
(4.5)where aperi = a(1 − e), and we use 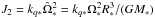 , with Ω∗ = 2π/P∗ the stellar rotation rate. Clearly, for most main-sequence stars (with P∗ ≳ 2 days) and white dwarfs, | ℋrot | is negligible compared to | ℋGR |. We neglect ℋrot in the remainder of this paper.
, with Ω∗ = 2π/P∗ the stellar rotation rate. Clearly, for most main-sequence stars (with P∗ ≳ 2 days) and white dwarfs, | ℋrot | is negligible compared to | ℋGR |. We neglect ℋrot in the remainder of this paper.
It is straightforward to include ℋGR into the scheme outlined in Sect. 3 as we simply need to add the value ℋGR(aeq,eeq) to the value of the planetary Hamiltonian. This could change the dynamics of the system considerably at sufficiently high eccentricity. In fact, up to this point, the perturber’s mass (rescaled by the star’s mass) μ has played a role in setting the amplitude of libration in Σ (or a, e) in the Hamiltonian 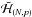 , and in setting the frequency of libration around the stable equilibrium point. However, the dynamics described by
, and in setting the frequency of libration around the stable equilibrium point. However, the dynamics described by 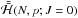 does not depend on the perturber’s mass because both N and p appear only in the part of the Hamiltonian derived from
does not depend on the perturber’s mass because both N and p appear only in the part of the Hamiltonian derived from 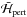 , where μ is a multiplying parameter. Thus, the evolution of e as a function of ϖ = − p does not depend on μ, only the timescale of this evolution does (and scales as 1 /μ).
, where μ is a multiplying parameter. Thus, the evolution of e as a function of ϖ = − p does not depend on μ, only the timescale of this evolution does (and scales as 1 /μ).
With the addition of the General Relativity term in the Hamiltonian, the dynamical behaviour of the system will in general depend on μ. Indeed, ℋGR is independent of μ, and is dependent on N: 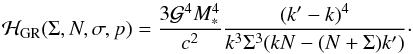 (4.6)Thus, the actual evolution of N (i.e. of eeq if J = 0) as a function of p (i.e. ϖ) depends on the value of μ.
(4.6)Thus, the actual evolution of N (i.e. of eeq if J = 0) as a function of p (i.e. ϖ) depends on the value of μ.
Another way to understand this is that the General Relativity potential has the effect of keeping the eccentricity constant while the pericentre ϖ=− p precesses (because 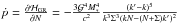 <0 while Ṅ=0,
<0 while Ṅ=0, 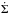 =0). In contrast, in the restricted three-body problem (see previous section) the precession of the pericentre is coupled with the variation in the eccentricity. Since the mass of the perturber μ appears in the planetary potential as a multiplicative factor in the perturbation, but not in the General Relativity potential, it will play the role of a parameter regulating which of the two dynamics in the (ecosϖ,esinϖ) plane is dominant. The smaller μ is, the more the General Relativity contribution will prevail, and the less efficient the planet will be in pumping the eccentricity of the test particle; the bigger μ is, the less the ℋGR contribution will be apparent.
=0). In contrast, in the restricted three-body problem (see previous section) the precession of the pericentre is coupled with the variation in the eccentricity. Since the mass of the perturber μ appears in the planetary potential as a multiplicative factor in the perturbation, but not in the General Relativity potential, it will play the role of a parameter regulating which of the two dynamics in the (ecosϖ,esinϖ) plane is dominant. The smaller μ is, the more the General Relativity contribution will prevail, and the less efficient the planet will be in pumping the eccentricity of the test particle; the bigger μ is, the less the ℋGR contribution will be apparent.
5. Results
In Figs. 3–5 we show the level curves of the Hamiltonian 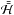 (see Sect. 3) on the (ecosϖ,esinϖ) plane for the 2:1, 3:1, and 4:1 resonances, respectively, with low values of the eccentricity of the perturber, e′ = 0.05 and e′ = 0.1. The General Relativity effect is not included in these figures. The white shaded disks centred at the origin (barely visible in Fig. 5) indicate the regions where the adiabatic method is not valid (see Sect. 3); in these regions our calculations do not necessarily reflect the true dynamics of the system.
(see Sect. 3) on the (ecosϖ,esinϖ) plane for the 2:1, 3:1, and 4:1 resonances, respectively, with low values of the eccentricity of the perturber, e′ = 0.05 and e′ = 0.1. The General Relativity effect is not included in these figures. The white shaded disks centred at the origin (barely visible in Fig. 5) indicate the regions where the adiabatic method is not valid (see Sect. 3); in these regions our calculations do not necessarily reflect the true dynamics of the system.
 |
Fig. 3 Level curves of the Hamiltonian |
 |
Fig. 5 Same as Fig. 3, but for the 4:1 mean motion resonance with an outer perturber. In contrast to Figs. 3 and 4, orbits with small initial eccentricities can be driven to e ~ 1. |
We note in Fig. 5 how even for low values of e′ the 4:1 resonance is extremely effective in driving the eccentricity of the test particle from e ~ 0 to e ~ 1. Indeed, there is only a small portion of the phase space that allows orbits starting with low eccentricities to circulate near the origin (e = 0). In the case of e′ = 0.05 only some orbits with moderate initial eccentricities, i.e. e> 0.2 and initial ϖ ~ 0, actually librate around the stable equilibrium point at ϖ = 0, e ~ 0.4, while for e′ = 0.1, all orbits sufficiently distant from the origin eventually end up at e ~ 1. This is not the case for the other resonances. For the 2:1 resonance, we see from Fig. 3 that all orbits with initial eccentricities up to ~ 0.4 and ~ 0.3, for e′ = 0.05 and e′ = 0.1, respectively, remain confined around the equilibrium point near the origin. Another equilibrium point is present at e ~ 0.7, ϖ = 0, implying that whatever the initial values of ϖ even a higher initial eccentricity is not enough to push the test particle to a star-grazing orbit. Indeed, the presence of the separatrix (shown as a black dashed curve) does not allow any orbit with initial eccentricity lower than ~ 0.9 to move farther away from the origin. In the case of the 3:1 resonance, Fig. 4 shows that eccentricities lower than 0.4 for e′ = 0.05 and 0.2 for e′ = 0.1 remain small, because the level curves librate around ϖ = 0. For e′ = 0.05 a separatrix bounds the maximum attainable eccentricity as in the 2:1 resonance. This confirms the results in Beust & Morbidelli (1996).
 |
Fig. 6 Level plots of the Hamiltonian |
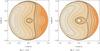 |
Fig. 8 Same as Fig. 6, but for the 4:1 mean motion resonance with an outer perturber. In contrast to Fig. 5, orbits with initial e ~ 0 do not experience extreme eccentricity excitation. |
 |
Fig. 9 Level curves of the Hamiltonians |
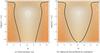 |
Fig. 10 Same as in Fig. 9, except for μ = 5 × 10-5. In this case, a test mass starting at ϖ = 0 and e = 0.05 can fall into the star even considering the General Relativity contribution. The level curves of the purely planetary Hamiltonian do not change with different values of μ: as explained in the text, here μ only plays the role of setting the timescales of the evolution of the test particle, not the evolution itself. |
Figures 6–8 depict our results for high values of the perturber’s eccentricity, e′ = 0.2 and e′ = 0.3. We find that for the 2:1 and 3:1 resonances, even these higher values of e′ are not sufficient to generate star-grazing objects from e ~ 0. Although for some initial configurations it is possible to observe an excitation in the eccentricity (see e.g. the case of the 3:1 resonance in Fig. 7a, where particles with e ~ 0.2 and ϖ = π may indeed reach e ~ 1), a modest/high initial eccentricity of the test particle is needed in order to eventually reach a value close to 1. On the other hand, Fig. 8 shows that when the perturber’s eccentricity is too high, the capability of the 4:1 resonance to raise the eccentricity of the test particle from ~ 0 to ~ 1 is diminished. In all cases (Figs. 6–8), a separatrix confines all orbits close to the origin. We note that this separatrix occupies the region where the adiabatic method remains valid (see Sect. 3), i.e. outside the white shaded region in each plot. Therefore, any orbit with a small initial eccentricity remains confined to low values of e.
As we noted in Sect. 4, when the eccentricity of the test particle reaches sufficiently high values, the effect of the General Relativity term becomes important, and the mass parameter μ plays a crucial role in shaping the dynamics of the system. Led by our results shown in Figs. 3–8, we restrict ourselves to the case of a test particle in the 4:1 mean motion resonance with the outer perturber, and we study the critical value μcrit needed such that the periapsis distance aperi = a(1 − e) reaches sufficiently small values, e.g. the radius of the central star or the star’s Roche limit (which is ~ R⊙, for white dwarfs and asteroids with internal density about a few g / cm3).
In Fig. 9 we show the level curves of the Hamiltonian 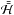 with e′ = 0.1, on the (ϖ,log aperi) plane, both with and without the addition of the General Relativity contribution, for the case of μ = 3×10-6. Here we choose the resonance location of the test particle ares at 1 AU. We can clearly see that while in the purely planetary case the resonance is capable of pushing a test mass with a small initial eccentricity e ~ 0.05 into a star-grazing orbit, this does not hold true when ℋGR is introduced. In Fig. 10 we repeat the calculation, this time with μ = 5 × 10-5 and the same values for ares = 1 AU and e′ = 0.1, and we see that even with the General Relativity contribution, test particles with initial small eccentricities are just about able to reach aperie ~ R⊙. Because the thick curve in Fig. 10b is almost tangent to the bottom of the figure at ϖ = π, we deduce that the critical mass to achieve star-grazing orbits for this choice of a′ and e′ is close to 5×10-5 solar masses.
with e′ = 0.1, on the (ϖ,log aperi) plane, both with and without the addition of the General Relativity contribution, for the case of μ = 3×10-6. Here we choose the resonance location of the test particle ares at 1 AU. We can clearly see that while in the purely planetary case the resonance is capable of pushing a test mass with a small initial eccentricity e ~ 0.05 into a star-grazing orbit, this does not hold true when ℋGR is introduced. In Fig. 10 we repeat the calculation, this time with μ = 5 × 10-5 and the same values for ares = 1 AU and e′ = 0.1, and we see that even with the General Relativity contribution, test particles with initial small eccentricities are just about able to reach aperie ~ R⊙. Because the thick curve in Fig. 10b is almost tangent to the bottom of the figure at ϖ = π, we deduce that the critical mass to achieve star-grazing orbits for this choice of a′ and e′ is close to 5×10-5 solar masses.
The critical perturber mass 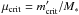 can be estimated as follows. For a test particle near a given mean-motion resonance (4:1) with an external perturber (of given m′,a′,e′), the “secular” planetary Hamiltonian can be written schematically as
can be estimated as follows. For a test particle near a given mean-motion resonance (4:1) with an external perturber (of given m′,a′,e′), the “secular” planetary Hamiltonian can be written schematically as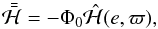 (5.1)where
(5.1)where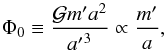 (5.2)and
(5.2)and 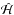 is dimensionless. We note that in the above equation, a is really a0 = a′/ 42 / 3 (the value of a in exact Keplerian resonance with the perturber). We assume that the test mass starts with an initial eccentricity e0 ≪ 1 at ϖ = 0. Its maximum eccentricity
is dimensionless. We note that in the above equation, a is really a0 = a′/ 42 / 3 (the value of a in exact Keplerian resonance with the perturber). We assume that the test mass starts with an initial eccentricity e0 ≪ 1 at ϖ = 0. Its maximum eccentricity 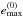 (achieved at ϖ = π) is determined by
(achieved at ϖ = π) is determined by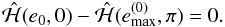 (5.3)The superscript “(0)” in
(5.3)The superscript “(0)” in 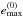 indicates that this maximum eccentricity is obtained without any short-range force effect.
indicates that this maximum eccentricity is obtained without any short-range force effect.
Now we consider how ℋGR affects emax. We write 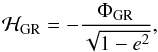 (5.4)with
(5.4)with 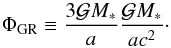 (5.5)Again, starting with an initial eccentricity e0 ≪ 1 at ϖ = 0, the maximum eccentricity emax of the test mass (achieved at ϖ = π) is estimated by
(5.5)Again, starting with an initial eccentricity e0 ≪ 1 at ϖ = 0, the maximum eccentricity emax of the test mass (achieved at ϖ = π) is estimated by 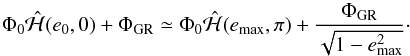 (5.6)Assuming 1 − emax ≪ 1, Eq. (5.6) becomes
(5.6)Assuming 1 − emax ≪ 1, Eq. (5.6) becomes 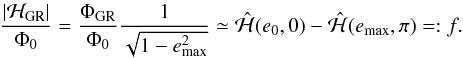 (5.2)This shows that emax depends on various parameters through the ratio
(5.2)This shows that emax depends on various parameters through the ratio 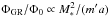 .
.
Setting a(1 − emax) = Rcrit in Eq. (5.7), we obtain the critical perturber mass 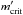 that allows the test particle to reach a certain pericentre distance Rcrit:
that allows the test particle to reach a certain pericentre distance Rcrit: 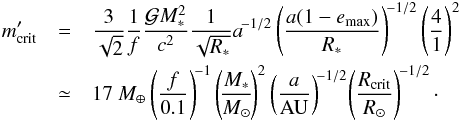 (5.8)It is important to note that f in general depends on emax and thus is a complicated function of (Rcrit/a). However, we can calculate its numerical value in the case depicted in Figs. 9 and 10, where we obtain f ~ 0.1.
(5.8)It is important to note that f in general depends on emax and thus is a complicated function of (Rcrit/a). However, we can calculate its numerical value in the case depicted in Figs. 9 and 10, where we obtain f ~ 0.1.
6. Conclusions
In this paper, we have revisited the problem of resonant dynamics inside mean motion resonances in the restricted planar three-body problem in order to determine to what extent planetary perturbations can effectively drive small bodies into highly eccentric orbits, and cause them to fall into the star or suffer tidal disruption. While most previous works employed series expansion of the Hamiltonian in powers of the eccentricities or were limited by a first-order development in e′ to the case of e>e′ and small e′ (where e′ and e are the eccentricities of the planetary perturber and the test particle, respectively), we do not perform any expansions, thus making our results valid for a wider range of orbital configurations. We make use of the principle of adiabatic invariance to reduce the two degree of freedom Hamiltonian (2.10)to the integrable Hamiltonian 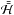 , which we study in the limit of vanishing amplitude of libration of k′λ′ − kλ in the k′:k = 2:1, 3:1 and 4:1 mean motion resonances. We confirm the results of Beust & Morbidelli (1996), and show that for small e′ (≲ 0.1) the 2:1 and 3:1 resonances are not able to push test particles in initially nearly circular orbits into star-grazing trajectories (Figs. 3, 4), while the 4:1 resonance is extremely effective (Fig. 5). Moreover, we find that a higher value of e′ (=0.2–0.3) does not change this picture for the 2:1 and 3:1 resonances (Figs. 6, 7), but makes the 4:1 resonance less effective by generating a larger stable region of circulation around e ~ 0 (Fig. 8). Finally, in the cases where the resonance is strong enough to generate star-grazing objects, we include the General Relativity contribution to the Hamiltonian, which causes a fast precession of the pericentre while keeping the eccentricity constant, thereby suppressing the effectiveness of the planet’s perturbation to generate extreme eccentricities (Fig. 9). While the planetary mass only sets the timescales of the secular eccentricity evolution when the General Relativity effect is neglected, we note that it now plays an important dynamical role, as it regulates the relative contribution of the purely Newtonian evolution and the impact of the post-Newtonian term. We then obtain, for a specific choice of semi-major axis and eccentricity of the perturber, an estimate on the minimum planetary mass needed to drive eccentricity growth of the test particle from ~ 0 to ~ 1. An approximate analytic expression for this critical mass is also obtained. In addition, we make available a Mathematica notebook which implements the calculations outlined in the paper to allow the interested reader to examine the effect of secular dynamics inside mean motion resonances for other applications.
, which we study in the limit of vanishing amplitude of libration of k′λ′ − kλ in the k′:k = 2:1, 3:1 and 4:1 mean motion resonances. We confirm the results of Beust & Morbidelli (1996), and show that for small e′ (≲ 0.1) the 2:1 and 3:1 resonances are not able to push test particles in initially nearly circular orbits into star-grazing trajectories (Figs. 3, 4), while the 4:1 resonance is extremely effective (Fig. 5). Moreover, we find that a higher value of e′ (=0.2–0.3) does not change this picture for the 2:1 and 3:1 resonances (Figs. 6, 7), but makes the 4:1 resonance less effective by generating a larger stable region of circulation around e ~ 0 (Fig. 8). Finally, in the cases where the resonance is strong enough to generate star-grazing objects, we include the General Relativity contribution to the Hamiltonian, which causes a fast precession of the pericentre while keeping the eccentricity constant, thereby suppressing the effectiveness of the planet’s perturbation to generate extreme eccentricities (Fig. 9). While the planetary mass only sets the timescales of the secular eccentricity evolution when the General Relativity effect is neglected, we note that it now plays an important dynamical role, as it regulates the relative contribution of the purely Newtonian evolution and the impact of the post-Newtonian term. We then obtain, for a specific choice of semi-major axis and eccentricity of the perturber, an estimate on the minimum planetary mass needed to drive eccentricity growth of the test particle from ~ 0 to ~ 1. An approximate analytic expression for this critical mass is also obtained. In addition, we make available a Mathematica notebook which implements the calculations outlined in the paper to allow the interested reader to examine the effect of secular dynamics inside mean motion resonances for other applications.
Acknowledgments
G.P. wishes to thank Clément Robert for the valuable advice in improving the readability of the Mathematica code. D.L. acknowledges support by the NASA grants NNX14AG94G and NNX14AP31G, and by a Simons Fellowship in Theoretical Physics from the Simons Foundation. He also thanks the Laboratoire Lagrange OCA for hospitality.
References
- Beaugé, C., Michtchenko, T. A., & Ferraz-Mello, S. 2006, MNRAS, 365, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., & Morbidelli, A. 1996, Icarus, 120, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., Lagrange-Henri, A. M., Vidal-Madjar, A., & Ferlet, R. 1989, A&A, 223, 304 [NASA ADS] [Google Scholar]
- Beust, H., Vidal-Madjar, A., Ferlet, R., & Lagrange-Henri, A. M. 1990, A&A, 236, 202 [Google Scholar]
- Beust, H., Vidal-Madjar, A., Ferlet, R., & Lagrange-Henri, A. M. 1991, A&A, 241, 488 [NASA ADS] [Google Scholar]
- Bonsor, A., Mustill, A. J., & Wyatt, M. C. 2011, MNRAS, 414, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Debes, J. H., & Sigurdsson, S. 2002, ApJ, 572, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Debes, J. H., Walsh, K. J., & Stark, C. 2012, ApJ, 747, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G. 1967, AJ, 72, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Farihi, J. 2016, New Astron. Rev., 71, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., Froeschle, C., Froeschle, C., et al. 1994, Nature, 371, 315 [Google Scholar]
- Ferlet, R., Vidal-Madjar, A., & Hobbs, L. M. 1987, A&A, 185, 267 [Google Scholar]
- Fontaine, G., & Michaud, G. 1979, ApJ, 231, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B. J., Migliorini, F., Morbidelli, A., et al. 1997, Science, 277, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Greaves, J. S., Holland, W. S., Matthews, B. C., et al. 2016, MNRAS, 461, 3910 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M. 2003, ApJ, 584, L91 [Google Scholar]
- Henrard, J. 1993, The Adiabatic Invariant in Classical Mechanics, Dynamics Reported (Springer), 117 [Google Scholar]
- Henrard, J., & Caranicolas, N. D. 1990, Celest. Mech. Dyn. Astron., 47, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Henrard, J., & Lemaitre, A. 1983, Celest. Mech., 30, 197 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Koester, D., Gänsicke, B. T., & Farihi, J. 2014, A&A, 566, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V. 1986, Sov. Astron., 30, 224 [NASA ADS] [Google Scholar]
- Lagrange, A. M., Ferlet, R., & Vidal-Madjar, A. 1987, A&A, 173, 289 [NASA ADS] [Google Scholar]
- Lemaitre, A. 1984, Celest. Mech., 32, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Ferraz-Mello, S. 2006, Celest. Mech. Dyn. Astron., 94, 411 [Google Scholar]
- Moons, M., & Morbidelli, A. 1993, Celest. Mech. Dyn. Astron., 57, 99 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moons, M., & Morbidelli, A. 1995, Icarus, 114, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar System Dynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Petrovich, C., & Muñoz, D. J. 2017, ApJ, 834, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Sidorenko, V. V. 2006, Cosmic Res., 44, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Sorelli, C., Grinin, V. P., & Natta, A. 1996, A&A, 309, 155 [NASA ADS] [Google Scholar]
- Vauclair, G., & Fontaine, G. 1979, ApJ, 230, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., & Montgomery, S. 2013, PASP, 125, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1985, Icarus, 63, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1983, Icarus, 56, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Koester, D., Reid, I. N., & Hünsch, M. 2003, ApJ, 596, 477 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Level plots of the Hamiltonian |
| In the text | |
 |
Fig. 2 Level curves of N on the (a,e) plane for the case of the 2:1, 3:1, and 4:1 resonances with a′ = 1 AU for the perturber (in units where |
| In the text | |
 |
Fig. 3 Level curves of the Hamiltonian |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for the 3:1 mean motion resonance with an outer perturber. |
| In the text | |
 |
Fig. 5 Same as Fig. 3, but for the 4:1 mean motion resonance with an outer perturber. In contrast to Figs. 3 and 4, orbits with small initial eccentricities can be driven to e ~ 1. |
| In the text | |
 |
Fig. 6 Level plots of the Hamiltonian |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for the 3:1 mean motion resonance with an outer perturber. |
| In the text | |
 |
Fig. 8 Same as Fig. 6, but for the 4:1 mean motion resonance with an outer perturber. In contrast to Fig. 5, orbits with initial e ~ 0 do not experience extreme eccentricity excitation. |
| In the text | |
 |
Fig. 9 Level curves of the Hamiltonians |
| In the text | |
 |
Fig. 10 Same as in Fig. 9, except for μ = 5 × 10-5. In this case, a test mass starting at ϖ = 0 and e = 0.05 can fall into the star even considering the General Relativity contribution. The level curves of the purely planetary Hamiltonian do not change with different values of μ: as explained in the text, here μ only plays the role of setting the timescales of the evolution of the test particle, not the evolution itself. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.