| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201630026 | |
| Published online | 20 September 2017 | |
Charged-particle acceleration in a reconnecting current sheet including multiple magnetic islands and a nonuniform background magnetic field
1 Yunnan Observatories, Chinese Academy of Sciences, Kunming, 650216 Yunnan, PR China
e-mail: liyan821@ynao.ac.cn
2 Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
3 Center for Astronomical Mega-Science, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, 100012 Beijing, P.R. China
4 School of Tourism and Geography, Yunnan Normal University, 650031 Kunming, PR China
Received: 8 November 2016
Accepted: 14 June 2017
Context. Charged particles are accelerated to high energies in solar flares. Although we know that magnetic reconnection is an efficient mechanism in generating energetic particles, the detailed role it plays in accelerating particles is still unknown.
Aims. We investigate particle acceleration by magnetic reconnection in the current sheet, including multiple islands and a guide field.
Methods. The long current sheet produced by the disruption in the corona magnetic field is usually not stable to various plasma instabilities, among which the tearing mode is the most important, and magnetic islands start to form in the current sheet when these instabilities develop. Two reverse processes are typically observed in the sheet: cascading of large islands to smaller ones, and merging of small islands into larger ones. Coalescent reconnection consequently takes place between two adjacent islands when merging occurs. The electric field induced by the coalescent reconnection is opposite to the electric field of the primary large-scale reconnection. We studied particle acceleration in such a current sheet and examined in detail the dynamic properties of electrons and protons in the current sheet through test particle approach.
Results. We found that some particles can be accelerated to high energies in a very short time, and some particles (near the coalescence reconnection site) are accelerated and decelerated back and forth by the primary and secondary electric fields. Particle motions show two distinct types along different trajectories: some particles are trapped around magnetic islands, and some escape from the current sheet mainly along open field lines. With the presence of a guide field, protons and electrons are found to eventually move in different directions. The energy spectra for both species follow a double power-law shape. The softer components of the power-law spectrum are due to the particles that are trapped and circulate around magnetic islands, while the particles that escape and are partly trapped contribute to the harder component of the spectrum. Finally, we also investigated the influences of the parameters for the reconnection process on the spectral feature.
Key words: acceleration of particles / magnetic reconnection / Sun: flares
© ESO, 2017
1. Introduction
Solar flares are the manifestation of the energy release process in the solar corona, and a large fraction of the released energy is transferred into energetic ions and electrons (Lin et al. 1976, 2003; Priest & Forbes 2000; Emslie et al. 2004), and references therein). The physics of the acceleration of a large number of charged particles to high energy still remains an open question, although many different mechanisms have been studied (e.g., see Zharkova et al. 2011, for a review). It is widely accepted that magnetic reconnection plays a significant role in converting magnetic energy into heating, the bulk motion of the plasma, and particle acceleration (Priest & Forbes 2000; Biskamp 2000). The strong induced electric field in the magnetic reconnection region is very efficient in directly accelerating charged particles during solar flares.
In general, a test-particle approach had been used to investigate particle acceleration by magnetic reconnection. Some authors studied the situation in a steady-state electromagnetic field topology, using analytical methods or numerical integration of test particles: direct electric field acceleration has commonly been investigated in the framework of reconnecting current sheet (Martens 1988; Martens & Young 1990; Litvinenko 1996; Zharkova & Gordovskyy 2004), or in X-type (namely X-point) magnetic configurations with or without a guide field (Bulanov 1980; Bruhwiler & Zweibel 1992; Mori et al. 1998; Browning & Vekstein 2001; Heerikhuisen et al. 2002; Wood & Neukirch 2005; Zharkova & Gordovskyy 2005; Hannah & Fletcher 2006; Li & Lin 2012; Li et al. 2013). The 3D spine and fan reconnection regime has also been investigated (Dalla & Browing 2005; Dalla & Browing 2008). On the other hand, laboratory experiments have been carried out to study the magnetic reconnection process in a solar flare with powerful lasers. A recent experiment by Zhong et al. (2016) showed that relativistic electrons with energies of up to MeV were detected along the magnetic separatrices that bound the reconnection outflow. In these works, the acceleration of charged particles is mainly studied by examining particle orbits (trajectories) and the final kinetic energy distribution of particles. These simulations and experiments confirmed that the acceleration by the electric field induced by reconnection is an efficient mechanism for accelerating charged particles that may account for the hard X-ray and even γ-ray emissions in solar flares.
In a typical eruptive process, on the other hand, as indicated by both observations and theories, the reconnecting current sheet tends to separate into several reconnection sites that develop multiple X- and O-points, which include closed field lines in a magnetic island (e.g., see Lazarian & Vishniac 1999; Ko et al. 2003; Lin et al. 2005, 2007, 2009; Bemporad 2008; Shen et al. 2011; Mei et al. 2012). In such a configuration, one magnetic island is bounded by two X-points at each side. Motions of particles in such a current sheet inevitably interact continuously with these small structures. Particles are usually trapped in a magnetic island and continue to gain energy by repetitively crossing the X-point, although the reconnecting electric field is relatively weak inside magnetic islands (e.g., see also discussions of Scholer & Jamitzky 1987; Gordovskyy et al. 2010). Li & Lin (2012) showed that protons and electrons can be accelerated to energies of up to several MeV, and they are typically efficiently accelerated when multiple X-points appear as a result of the tearing mode instability.
Recently, multi-island coalescence starts to enjoy considerable attention. In this process, two magnetic islands merge into a larger island. This has been reported and studied through both theories and numerical simulations (Biskamp & Welter 1980; Pritchett 2007; Barta et al. 2011; Shen et al. 2011). When the coalescence takes place, an electric field, opposite to the large-scale electric field in the background, is induced nearby the merging point of the two islands. Kliem (1994) used multi-island coalescence to study the effect of the fragmentation of the 2D reconnecting current sheet on the acceleration of particles, and showed that particles could be accelerated to near-relativistic energy within short time. Oka et al. (2010) performed 2D particle-in-cell (PIC) simulations of multi-island coalescence without a guide field. They found that the secondary induced electric field plays an important role in accelerating electrons.
In the present work, we investigate the acceleration of electrons and protons as island coalescence takes place. For this, we assume that a guide field exists in the direction of the induced electric field, which is commonly assumed to play an important role in particle acceleration (Litvinenko 1996; Zharkova & Gordovskyy 2004). In our simulation, the test particle approach was used to calculate particle trajectories, which is still vital, especially when there are fewer accelerated particles than particles that are sent into the reconnecting region, and a large-scale model is considered (Zharkova et al. 2011). Then the obtained particle trajectories are used to deduce the energy spectrum of the particles in order to extend our previous works by comparing differences among these works, to cover a wider range of parameters, and to demonstrate the robustness of the acceleration process in this current sheet configuration, which could be applied to more complex situations in the future as well.
In the next section, we briefly describe the particle acceleration model and formulae we used in the calculations. The results are given and are further analyzed in Sect. 3. Conclusions and a short discussion are presented in Sect. 4.
2. Model description and computation setup
Because the timescale of the particle acceleration is shorter than that of the magnetic reconnection process and the change in the induced electric field, we consider the electromagnetic field to be static or quasi-static in the process of particle acceleration. In this case, we use the configuration of a reconnecting current sheet given by Zwingmann (1983) to investigate the kinematic and dynamic behaviors of accelerated electrons and protons. In his work, the self-consistent theory of the quiet magnetotail is extended to the 2D static equilibrium configuration with arbitrary variations along the tail axis. Zwingmann (1983) investigated the influence of boundary conditions that caused the equilibrium configuration to form the oscillatory structures (magnetic islands) within the current sheet. On the other hand, a similar phenomenon can also be observed in a typical solar eruptive process, and the relevant numerical experiments show that the reconnecting current sheet tend to separate into many magnetic islands as a result of the tearing mode instability (Furth 1963; Priest & Forbes 2000).
In the solution of Zwingmann (1983), the magnetic island gradually grew with the increase of x (see Fig. 1 in this article). For the magnetic field of the solar atmosphere, the magnetic field gradually weakens with height, and the expansion of the magnetic island in the current sheet occurs, therefore the magnetic island is larger at large distance from the Sun. In the solution of the Grad-Shafranov equation described by Biskamp (1993), on the other hand, the size of the magnetic island is the same, that is, the current sheet has a periodical structure, and the arrangement of the magnetic island is also regular. Such a magnetic field configuration may be applicable to a small-scale current sheet with a uniform magnetic field distribution in the uniform background field, but it is not as good as the Zwingmann structure for large-scale current sheets with a variable background field. In addition, particle acceleration in a current sheet with regularly arranged structures has been studied in previous works (Kliem 1994; Li & Lin 2012), and we do not duplicate this here. We therefore choose the Zwingmann model here to study the particle acceleration process in a current sheet with a more practical magnetic configuration, and try to obtain more realistic results.
 |
Fig. 1 Panel a: Configuration of the magnetic field with oscillatory structures. Panel b: Diagram of the enlarged coalescence reconnecting current sheet. The arrows imply the the motion direction of the plasma bulk flow. The position of the primary magnetic reconnection is indicated by thick arrows, and the position of the coalescence magnetic reconnection is shown by thin arrows. Panel c: The electric field varies along the x-direction. |
In the model of Zwingmann (1983), the magnetic flux function is A(x,z) = A0(x,z) − δAl(x,z), where A0(x,z) is for the initial equilibrium configuration, and Al(x,z) presents an oscillating feature, with δ being a small constant (δ ≪ 1) that works as a perturbation to the equilibrium configuration A0(x,z). The magnetic configuration governed by A(x,z) is in the zx-plane, including a current sheet that extends along the x-axis from x = 0 to Lx0, which represents the right-hand boundary of the computation domain, and A0(x,z) is imposed as a Dirichlet boundary condition for solving the Laplace equation governing A0(x,z). In the z-direction, perpendicular to the current sheet, the perturbation Al(x,z) ceases at a location far away from the current sheet, for instance, z = Lz0. Normalizing the magnetic field B0 to the background field far from the current sheet and the length to the half-thickness of the current sheet Lth, we obtain an expression for the reconnecting configuration in equilibrium that is given by ![\begin{equation} \label{eq:B0 field} A_{0}(x,z)=\ln \{\cosh[F(x)z]\}-\ln [F(x)], \end{equation}](/articles/aa/full_html/2017/09/aa30026-16/aa30026-16-eq17.png) (1)where F(x) is an arbitrary positive function for the current sheet, with its scale length Lx much larger than Lth. In our calculation, it is convenient to take the form of power law for it, such as
(1)where F(x) is an arbitrary positive function for the current sheet, with its scale length Lx much larger than Lth. In our calculation, it is convenient to take the form of power law for it, such as 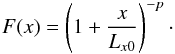 (2)Zwingmann (1983) stated that the value of p does not play a role in governing the particular results he wished to establish in his paper, that is to say, it is not essential to know the precise value of p. We note that the number of magnetic islands that we consider depends on the size of the calculation domain. We take p = 0.6 in this work as an example, which corresponds to the case that four magnetic islands appear in the calculation domain. The purpose of choosing p = 0.6 is twofold. First, enough magnetic islands appear in the current sheet for us to be able to study the interaction of energetic particles with the magnetic island and also the effect of this interaction on the final energy as well as the spectrum of particles. Second, a typical coalescence process of magnetic islands is allowed to take place in the current sheet, and we can thus investigate the effect of the coalescence on the acceleration process and on the final energy spectrum of particles.
(2)Zwingmann (1983) stated that the value of p does not play a role in governing the particular results he wished to establish in his paper, that is to say, it is not essential to know the precise value of p. We note that the number of magnetic islands that we consider depends on the size of the calculation domain. We take p = 0.6 in this work as an example, which corresponds to the case that four magnetic islands appear in the calculation domain. The purpose of choosing p = 0.6 is twofold. First, enough magnetic islands appear in the current sheet for us to be able to study the interaction of energetic particles with the magnetic island and also the effect of this interaction on the final energy as well as the spectrum of particles. Second, a typical coalescence process of magnetic islands is allowed to take place in the current sheet, and we can thus investigate the effect of the coalescence on the acceleration process and on the final energy spectrum of particles.
Adding a small perturbation Al to A0 invokes oscillations of A in space, and function Al has to vanish far away from the current sheet in z-direction (namely Al = 0) because A needs to satisfy the Dirichlet boundary condition. After several straightforward algebra (we refer to Zwingmann 1983, for more details), we obtain function Al![\begin{eqnarray} && A_{l}(x,z)=\sum \limits_{m=1}^{\infty}\frac{\sin [(2m-1)\pi G(x)/G(L_{x0})]}{2m-1}\nonumber~~~~~~~~~~~~~~~~~~~~~~~\\ &\times& \left\{-\frac{1}{[(2m-1)\pi/G(L_{x0})]^{2}-1}\cdot \frac{1}{\cosh [F(x)z]} \phantom{\sum \limits_{n=1}^{\infty} \frac{\beta_{n}^{2}\{\tanh[F(x)z]\cdot\sin[\beta_{n}F(x)z]-\beta_{n}\cdot\cos[\beta_{n}F(x)z]\}}{ {\{[\frac{2m-1}{G(L_{x0})}\pi]^{2}+\beta_{n}^{2}\}}\cdot [\frac{L_{z0}(1+\beta_{n}^{2})}{2L}-\frac{1}{1+\beta_{n}^{2}}]\cdot \sinh(\frac{\beta_{n}\pi}{2}) }}\nonumber\right. \\ && \left. +\sum \limits_{n=1}^{\infty} \frac{\beta_{n}^{2}\{\tanh[F(x)z]\cdot\sin[\beta_{n}F(x)z]-\beta_{n}\cdot\cos[\beta_{n}F(x)z]\}}{ {\left\{\left[\frac{2m-1}{G(L_{x0})}\pi\right]^{2}+\beta_{n}^{2}\right\}}\cdot \left[\frac{L_{z0}(1+\beta_{n}^{2})}{2L}-\frac{1}{1+\beta_{n}^{2}}\right]\cdot \sinh\left(\frac{\beta_{n}\pi}{2}\right) }\right\}, \end{eqnarray}](/articles/aa/full_html/2017/09/aa30026-16/aa30026-16-eq26.png) (3)with
(3)with ![\begin{equation} \label{eq:G(x)} G(x)=\int\limits_{0}^{x}F(x){\rm d}x=\frac{L_{x0}}{1-p}\left[\left(1+\frac{x}{L_{x0}}\right)^{1-p}-1\right], \end{equation}](/articles/aa/full_html/2017/09/aa30026-16/aa30026-16-eq27.png) (4)and
(4)and ![\begin{equation} \label{eq:beta} \beta_{n}=\tan(\beta_{n}L_{z0})[\tanh(L_{z0})]. \end{equation}](/articles/aa/full_html/2017/09/aa30026-16/aa30026-16-eq28.png) (5)For δ = 0.1, the magnetic flux function is A = A0 − 0.1Al, and the oscillatory structure of the equilibrium possesses its most prominent feature. As shown in Fig. 1a, multiple X-points and magnetic islands are displayed in the configuration. Coalescent reconnection can therefore take place between every two adjacent islands. As indicated by Fig. 1b, the coalescence takes place between the first and second islands, and between the third and fourth islands, respectively. The arrows in the figure indicate the motion direction of the plasma bulk flow.
(5)For δ = 0.1, the magnetic flux function is A = A0 − 0.1Al, and the oscillatory structure of the equilibrium possesses its most prominent feature. As shown in Fig. 1a, multiple X-points and magnetic islands are displayed in the configuration. Coalescent reconnection can therefore take place between every two adjacent islands. As indicated by Fig. 1b, the coalescence takes place between the first and second islands, and between the third and fourth islands, respectively. The arrows in the figure indicate the motion direction of the plasma bulk flow.
We also add a uniform guide field ξ in the y-direction to represent the component of the magnetic field in the direction of the induced electric field that is ubiquitous in reality and plays an important role in particle acceleration (see also Litvinenko 1996; Zharkova & Gordovskyy 2004; Li & Lin 2012; and Zhong et al. 2016). Here ξ is a constant with values in the range from 0 to 1, and ξB0 determines the strength of the guide field. Therefore, the normalized total magnetic field in the system studied here has the form 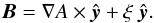 (6)We here follow Kliem (1994) and set the electric field configuration so as to include the coalescence of magnetic islands in the reconnection process. Strictly speaking, the induced electric field in the magnetic reconnection process should be self-consistently deduced from Ohm,s law E = ηj − v × B according to the magnetic field structure and the plasma property of the actual process. However, it is hard to obtain an analytic expression for functions of v and η because it is difficult to deduce the analytic solution and because the numerical simulation is complex. This makes it almost (if not completely) impossible to obtain an entirely self-consistent electromagnetic field distribution for the reconnection process around the current sheet.
(6)We here follow Kliem (1994) and set the electric field configuration so as to include the coalescence of magnetic islands in the reconnection process. Strictly speaking, the induced electric field in the magnetic reconnection process should be self-consistently deduced from Ohm,s law E = ηj − v × B according to the magnetic field structure and the plasma property of the actual process. However, it is hard to obtain an analytic expression for functions of v and η because it is difficult to deduce the analytic solution and because the numerical simulation is complex. This makes it almost (if not completely) impossible to obtain an entirely self-consistent electromagnetic field distribution for the reconnection process around the current sheet.
The main goal of this work is to capture the main characteristics of particle accelerations in the coalescent magnetic reconnection process. Because the acceleration timescale is shorter than the reconnection timescale, we are allowed to choose an electromagnetic field configuration that can approximately describe the coalescence of magnetic islands in magnetic reconnection, to investigate the acceleration and kinetic behaviors of charged particles in such a current sheet. In a forthcoming paper, we will adopt the self-consistent electromagnetic field distribution from the full magnetohydrodynamic (MHD) numerical simulation, and study the particle acceleration in a more self-consistent framework. In this case, the electric field has the form (Fig. 1c) ![\begin{equation} \label{eq:E} \vec{E}= -E_{0}\{0.6 \times \cos[1.2xF(x)/2]-0.4\} ~ \vec{\hat{y}}. \end{equation}](/articles/aa/full_html/2017/09/aa30026-16/aa30026-16-eq39.png) (7)The coalescence of two magnetic islands clearly leads to the secondary reconnection process, in which the induced electric filed is opposite to the primary field that is induced by the large-scale reconnection process. This electric field allows net acceleration or deceleration to take place for charged particles that move around, trapped in the islands. The electromagnetic field configuration used in this work (Eqs. (1)through (7)) is not exactly self-consistent because ∇ × E ≠ 0 in our calculations, which implies ∂B/∂t ≠ 0, but we expect to reveal the qualitative feature of particle trajectories including meander and drift motions on which the acceleration is based. Furthermore, the time that an electron (a proton) is efficiently accelerated in the current sheet is about 10-5 (10-3) s, which is shorter than the time interval of several minutes in which the electromagnetic field evolves in the reconnection process. This means that the electromagnetic configuration can be taken to be static in the particle acceleration process.
(7)The coalescence of two magnetic islands clearly leads to the secondary reconnection process, in which the induced electric filed is opposite to the primary field that is induced by the large-scale reconnection process. This electric field allows net acceleration or deceleration to take place for charged particles that move around, trapped in the islands. The electromagnetic field configuration used in this work (Eqs. (1)through (7)) is not exactly self-consistent because ∇ × E ≠ 0 in our calculations, which implies ∂B/∂t ≠ 0, but we expect to reveal the qualitative feature of particle trajectories including meander and drift motions on which the acceleration is based. Furthermore, the time that an electron (a proton) is efficiently accelerated in the current sheet is about 10-5 (10-3) s, which is shorter than the time interval of several minutes in which the electromagnetic field evolves in the reconnection process. This means that the electromagnetic configuration can be taken to be static in the particle acceleration process.
Now we study the particle acceleration in the electromagnetic field described by Eqs. (1) through (7). The trajectory of a particle with a rest mass m and an electric charge q is governed by the following relativistic motion equations  where r and v (v = p/mγ) are the position and the velocity vectors of the particle, respectively, and γ = 1 /
where r and v (v = p/mγ) are the position and the velocity vectors of the particle, respectively, and γ = 1 /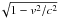 is the Lorentz factor. We note that collisions among particles are neglected in the equations. In addition to the normalization of the lengths to Lth and the magnetic fields to B0, we further normalize the electric field to E0, and the time to τe,p = me,p/qB0 for electrons and protons, respectively, which is the charged-particle gyration period associated with the magnetic field B0.
is the Lorentz factor. We note that collisions among particles are neglected in the equations. In addition to the normalization of the lengths to Lth and the magnetic fields to B0, we further normalize the electric field to E0, and the time to τe,p = me,p/qB0 for electrons and protons, respectively, which is the charged-particle gyration period associated with the magnetic field B0.
The thickness of the reconnecting current sheet in a solar eruption is still an open question, although recent observations indicated that the thickness of the current sheet that is developed in the solar eruption could reach up to several 104 km or even a few times 105 km (e.g., see the review by Lin et al. 2015). Therefore we here follow Kliem (1994) and Gordovskyy et al. (2010), taking a similar half-thickness Lth = 100 m, which could be the scale of some local structures inside a large-scale current sheet, as discussed by Lin et al. (2015). On the other hand, because A0 needs to fulfill the linear Dirichlet boundary condition far away from the current sheet in the z-direction, we take a normalized Lz0 = 10 in our calculations. The length of the domain in the x-direction is taken as Lx0 = 10π, which means that the length of a current sheet is larger than its thickness.
We used a fourth-order Runge-Kutta-Fehlberg (RKF45) scheme to solve Eqs. (8)and (9). For the electromagnetic field configuration we used, the dimensionless size of the calculation domains is 0 ≤ x ≤ Lx0 and − 1 ≤ z ≤ 1. In our calculations, approximately 5 × 106 test particles are initially uniformly distributed within this domain. Considering the symmetry of the system with respect to the y-axis, we assume that the initial position of all particles has y = 0 with no loss of generality. Each calculation was run until a test particle crossed one of the four domain boundaries (namely x = 0, x = Lx0, and z = ± 1). Furthermore, if a test particle remained in the domain more than 2600 τe for electrons and 200 τp for protons, the corresponding calculation ended. The final energy of particles obtained from the acceleration process was taken as its kinetic energy: Ek = mc2(γ − 1), and the behavior of Ek is the main goal of this work.
3. Results
In this part of our work, we investigate the kinematic and dynamic behaviors of electrons and protons that are accelerated by the electromagnetic field that is described by Eqs. (6) and (7), with the corresponding magnetic configuration displayed in Fig. 1. With the parameters for the electromagnetic field and the current sheet given, we are able to study the trajectories of the particles for different initial locations, the particle energy spectra, and the dependence of energies on these parameters.
3.1. Trajectories of protons and electrons
With B0 = 10 G, ξ = 1, E0 = 5 V/cm, and Lth = 100 m, several test particle trajectories are plotted in Figs. 2 and 3 for electrons and protons, respectively. Each colored curve is for a particle that starts to be accelerated from the location denoted by a solid dot. The curves in Figs. 2a, 3a and 2b, 3b are for the projections of trajectories on the xz- and xy-plane, and the change in the energy of several particles versus time is shown in Figs. 2c and 3c.
 |
Fig. 2 Kinematics and dynamic of a randomly chosen sample of accelerated electrons. Panel a: Projection of electron trajectories onto the xz-plane, b) projection of the trajectories onto the xy-plane, and c) variations of the electron energies versus time for ξ = 1. Particles that start to be accelerated from different locations are displayed, and the initial location of each particle is denoted by the solid dot in plane a) and b). |
We note that electrons and protons basically move along the magnetic field lines (Figs. 2a and 3a). The reconnection process leads to the formation of two regions: open and closed field lines. Thus, trajectories of electrons and protons have two different forms: some electrons and protons on open field lines travel a fairly long distance in the x-direction, oscillate in the z-direction, and eventually leave the acceleration region; some particles are trapped in closed magnetic features (O-points), and pass by the X-points along the field lines at either side of the nearby O-points several times (circulating in the xz-plane), as can be seen from the zigzag orbits in Figs. 2b and 3b.
With the existence of the guide field, the accelerated particles moving along open field are found to proceed along different directions, such that electrons in the z> 0 semi-space have positive vx components, and those that have negative vx components are located in the z< 0 semi-space; while protons move in opposite direction. On the other hand, the trapped particles circulate in different directions around magnetic islands: electrons move clockwise, and protons move anticlockwise. At the same time, Figs. 2b and 3b show that the motion of energetic electrons is in the positive y-direction, and energetic protons move in the negative y-direction. These motion characteristics signify the separation of electrons from protons over the scale of the current sheet in the acceleration by the electric field.
On the other hand, the coalescence of two adjacent magnetic islands leads to the secondary reconnection process, in which the induced electric filed is opposite to the primary field that was induced by the large-scale reconnection process. As particles enter the secondary reconnection region, they are decelerated by the secondary electric field. This means that when some particles enter and leave this region back and forth, they undergo a bounce-back process and repeatedly gain and lose energy (see the short trajectories in Figs. 2b and 3b and the oscillating curves in Figs. 2c and 3c), and the net energy gain of these particles is finally not apparent. In an evolving background magnetic field, we would expect some of these particles to become liberated through the field line motions. However, because the acceleration timescale is shorter than the MHD timescale, a reversible bouncing process is in fact unlikely to occur on the acceleration timescale. As described in Figs. 2b and 3b, some particles in circular orbits move a longer distance in the y-direction than those that leave the current sheet along the field lines, which indicates that these particles that are trapped by the magnetic islands obtain more energy.
3.2. Spectra of the particle energy
We now investigate the energy spectrum of electrons and protons through calculating the final energy of these particles. With the parameters as given before, the distribution of particle numbers versus the final energy is shown as a double logarithmic plot in Fig. 4. Apparently, both electrons and protons can be accelerated to higher energies and possess a similar manifestation: most particles remain in the low-energy region, while a small group of particles are accelerated to high energies. There are also noticeable differences in the higher energy part, however, where the spectrum does not show a single power-law profile. Instead, a double power-law distribution is the common feature, and the transition between the low- and high-energy parts is sharp. We fit these profiles to double power-law spectra, with the two power-law components with indices of γ1 = 1.86 (harder component) and γ2 = 8.27 for electrons (softer component), and γ1 = 0.97 and γ2 = 7.04 for protons, respectively.
 |
Fig. 4 Energy spectra of electrons and protons for ξ = 1. |
Figures 5a and 5b display the final energy of electrons and protons versus time. The energetic particles either eventually leave the current sheet or are trapped in the acceleration region longer than τe = 2600 or τp = 200 when the acceleration ends. These two figures also show that almost 38% of electrons and 65% of protons leave the acceleration region before the end of the calculation. This implies that protons leave the acceleration region more easily than electrons. Of those that remain in the acceleration region, 22% of all electrons and 18% of all protons are thermal, and the remaining particles are eventually accelerated to high energies, but they do not leave the current sheet when the calculation stopped. The particles left in the acceleration region obtain more energy.
 |
Fig. 5 Final energy of electrons a) and protons b) versus the time that the particles remain in the computational domain. Each dot represents a single particle. |
The escaped particles underwent two phase stages: a rising and a decaying phase. In the rising phase, the net acceleration was dominant, which led to a final energy gain of some particles that apparently exceeded their initial energy. Many particles quickly left the current sheet in this stage after the apparent energy gain. This shows that at this stage, the particles rapidly obtained energy and were obviously accelerated. In the decaying phase, on the other hand, deceleration became dominant. If the particles remained inside the current sheet, they then moved in the reversed electric field and were subject to deceleration, lost a portion of their energy, and were delayed in escaping from the acceleration region. The more they lost, the later they left. This indicates that the time that the particles remain in the acceleration region and the total energy that they eventually gain are governed by the paths along which they move and the regions in which they remain during the time that they are in the current sheet.
From comparing Figs. 3–5, we see that some trapped particles can reach higher energies than those that escaped, therefore we understand that the higher energy component of the power-law spectrum represents the particles that are trapped in the magnetic islands, while the escaping and partly trapped particles contribute to the lower energy component of the spectrum.
Observations showed that the double power-law spectral profile also occurred in some flares (e.g., see Lin et al. 2003; Holman et al. 2003). Turkmani et al. (2006) studied the particle acceleration in a stochastic current sheet and obtained the distribution function of accelerated particles, which consists of a clear double power-law pattern. The double power-law distribution apparently displays a knee-like feature that suggests a sudden drop in the number of high-energy particles, therefore two power indices are deduced. Figure 4 shows that the corresponding energy of the knee is about 583 keV and 2721 keV for the electron and the proton, respectively. In our model, the physics behind the double power-law could be related to the structure of the magnetic field as shown in Figs. 2 and 3, such that particles trapped and rotating around the magnetic islands have on average much higher energy; the guide field may also help the particle to remain longer in the acceleration region and obtain more energy. The coexistence of the primary and secondary induced electric fields may play an important role in not only accelerating some particles to the near-relativistic speed to excite the X-ray emission, but also in causing the trapped particles to are differently displaced in y-direction and to obtain different energies, although they are accelerated in the same time interval. The discrepancy between the manifestations of different energies in electrons and protons is also observed, most likely as a result of the difference in mass of the proton and the electron, which leads to different acceleration processes for electrons and protons.
 |
Fig. 6 Variation in electron and proton energy spectra a)–f), spectrum indices γ1 and γ2g, h, j, k), and the energy of the knee i, l) with different guide fields. Corresponding ξ values are shown in the panels. |
3.3. Dependence of the energy spectrum on various parameters
According to Eqs. (8) and (9), the energy obtained eventually is determined jointly by the electric field, the magnetic field, and combinations of the other parameters. To have a clearer and more quantitative scenario for this dependence, we now separately investigate the effect of the guide field and the electric field, with the other parameters fixed.
3.3.1. Effect of the guide field
We studied six cases with ξ increasing from 0 to 1, while the other parameters Lth = 100 m, B0 = 10 G, and E0 = 5 V/cm were fixed. The energy spectra of the accelerated particles are plotted in Figs. 6a–f for electrons and protons, which show that the energy spectra have the form of a double power-law spectrum for both electrons and protons.
We note that the number of electrons that are accelerated to high energies obviously increases with ξ, such that only about 2.7% of electrons are accelerated to energies 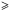 20 keV for ξ = 0, while about 29% are accelerated for ξ = 1. On the other hand, different from behaviors of the electrons, the acceleration rate of the protons (>200 keV) is about 18.8%, and its dependence on the guide field is not apparent.
20 keV for ξ = 0, while about 29% are accelerated for ξ = 1. On the other hand, different from behaviors of the electrons, the acceleration rate of the protons (>200 keV) is about 18.8%, and its dependence on the guide field is not apparent.
 |
Fig. 7 Energy spectra of electrons and protons for different values of the electric field (a)–(d). Variations in the spectrum indices γ1 and γ2(e)–(i) and the energy of the knee (g),(j) versus the electric field for electrons and protons, respectively. |
Figure 6 also indicates that the maxima of the final energy and the knee of the double power-law spectrum both vary with ξ. The effect of ξ on these two fields for electrons is more apparent than for protons. With the increase of ξ, the maximum energy of the electrons increases from 100 keV to more than 700 keV. Correspondingly, the spectrum knee for electrons shifts toward the higher energy as the guide field ranges from 0 to 1. For the protons, on the other hand, the maximum energy remains almost unchanged, and the spectrum knee changes slightly with the guide field. This indicates that the effect of the guide field on the proton acceleration is not apparent.
At the same time, we separately fit the spectrum profile to the power-law curve according to the location of knee, and obtained spectrum indices γ1 and γ2. The dependence of γ1 and γ2 on ξ is displayed in Figs. 6g and h, and in Figs. 6j and k for electrons and protons, respectively. For electrons, we note that the increase in ξ not only causes the energy gain of the electrons to increase, but it also causes a change in the energy spectrum indices of the particles. It can be seen that index γ1 increases steadily with ξ ranging from 0 to 1, but γ2 shows the opposite behavior. However, the dependence of the spectrum indices on ξ for the protons is different, such that γ1 and γ2 manifest an oscillating behavior in the range from 0.85 to 1 and from 6.8 to 7.1, respectively. On the other hand, the relationship between the corresponding energy of the knee and ξ is plotted in Fig. 6i for electrons. The energy of the knee moves toward the high energy regime as ξ increases. The dependence of the knee on ξ for protons is plotted in Fig. 6l, which shows that the variation in knee energy is weakly related to ξ.
As described above, we have shown changes in the energy spectrum of particles, spectrum indices, and the corresponding energy of the knee versus the guide field. From Figs. 2 and 3, particle trajectory calculations may provide some explanation for the dependence of the particle acceleration on the guide field. The stronger ξ yields that more electrons can remain in the current sheet longer and obtain sufficient net acceleration before they eventually leave the current sheet or at the end of calculation, hence the number of electrons accelerated to high energies and the maximum energy of the electron distinctly increases with ξ. However, the mass of the protons is higher than that of the electron, so that the proton acceleration is not sensitive to the guide field. Therefore the total number and the maximum energy of the accelerated protons do not display an apparent change with the strength of the guide field.
3.3.2. Effect of the electric field
The induced electric field in the reconnection process has a direct influence on the particle energy gain. Since E0 changes, the overall motion pattern of the particle and the final energy change as well. Martens (1988) analyzed the effective resistivity in a reconnection region, and gave an electric field strength of around 10 V/cm. On the other hand, Foukal & Behr (1995) calculated an upper limit to the electric field in a particular flare of about 35 V/cm according to the Stark effect on broadening spectral lines by the turbulent electric field, while the strongest electric field so far reported is 45 V/cm (Xu et al. 2004). Therefore, it is worth determining the effect of the induced electric field on the dynamical properties of energetic particles.
With B0 = 10 G, ξ = 1, and Lth = 100 m, Figs. 7a–d show the energy spectra for different values of the electric field. Not surprisingly, electrons and protons can be accelerated to higher energies, and the knee of the double power-law curves also moves to high energy as E0 increases (Figs. 7g and j). Thus, the fraction of accelerated electrons from the thermal energy to energies ≥20 keV at E0 = 1 V/cm is approximately 4.5%, and this fraction increases to about 39.5% as E0 = 20 V/cm. The corresponding fraction of the proton energy exceeding 200 keV changes from 1.2% to 43%.
The spectrum indices γ1 and γ2 are also found to vary with the electric field. In the case of an electric field of intermediate strength (E0 = 1 V/cm), the indices γ1 and γ2 are 3.1 and 6.39 for electrons and 1.44 and 4.12 for protons, respectively. In the case of a strong electric field (E0 = 20 V/cm), γ1 tends to become harder than the field in the weak E0, but γ2 shows an apparent increase with E0. In other words, since E0 governs the overall motion pattern of the particle, the decrease in E0 not only causes the particle energy gain to reduce, but also causes a change in hardness of the particle energy spectrum.
4. Discussions and conclusions
We here investigated the acceleration process of charged particles in a reconnecting current sheet where a guide field exists and magnetic island coalescence occurs. Using the test-particle method, we considered several properties of the accelerated particles, which include particle trajectories, the energy spectra, and the dependence of these parameters on the guide field and the induced electric field.
The trajectories of particles showed that some electrons and protons circulate around the magnetic island (O-point), the others in the open magnetic field travel a fairly long distance and eventually leave the acceleration region. For protons and electrons in an open magnetic field, different accelerated particles leave the acceleration region along the different directions when a guide field is present, as confirmed by laboratory experiments (e.g., see Zhong et al. 2016). The trapped particles circulate around different pitch angles in the magnetic island: the electrons move clockwise, and the protons anticlockwise. This suggests that the accelerated electrons and protons in reconnecting current sheets separate.
Our results imply that the fine structures inside the sheet are also governing features of the particle energy spectrum. We found that these X- and O-points help some particles to become trapped in the acceleration region for the maximum acceleration, and they increase the efficiency of the acceleration significantly. The final energy of the particles is proportional to the distance they move in the direction E0. The resulting energy spectrum of protons and electrons has the form of a double power-law shape, and the softer part of the spectrum comes from the particles that are trapped in the magnetic islands, while escaping and partly trapped particles contribute the harder component of the spectrum.
We also investigated how parameters such as the guide field and electric field affect the spectral profile: γ1 decreases with a larger electric field E0, but γ2 increases with E0. With ξ ranging from 0 to 1, we noted that the index γ1 of the electrons increases steadily with ξ, while γ2 shows an apparent decrease with ξ; and for the protons, both γ1 and γ2 show an oscillating behavior. On the other hand, the acceleration rate of electrons increases with larger E0 and ξ; while the acceleration rate of proton increases sharply with E0, but the fraction of the accelerated protons remains roughly unchanged with ξ.
As discussed by Wood & Neukirch (2005), a significant difficulty in the study of particle acceleration is the problem of the total number of particles that are accelerated. The reason is that the production rate of energetic particles is very low, which makes it difficult it to have enough particles that are accelerated to high energy. Recently, Krucker et al. (2010) showed that all electrons in the above the loop-top source seem to be accelerated, suggesting that all the electrons could be accelerated in the current sheet by magnetic reconnection. Raymond (2012) also pointed out that the acceleration must be very efficient, up to 50%, in terms of the fraction of electrons in the reconnection region that undergo acceleration. For the single X-point configuration, our previous results indicated that the fraction of the accelerated protons and electrons was much smaller than 10% (e.g., see Li & Lin 2012). In the present work, the maximum acceleration rate could reach up to 40%. This implies that small-scale structures in the reconnection region play an important role in enhancing the acceleration efficiency.
Finally, we need to note here that the motion of protons and electrons in different directions may produce an electric current distribution that distorts the original magnetic field configuration, and charge separation will generate an additional electric field. This effect will partly eliminate the induced electric field and affect the acceleration process, which is not considered in this work. Because of the very short distance of the particle acceleration in the coronal environment, the radiation loss is not included in our calculations. Finally, it is also important to point out that the electromagnetic field configuration considered here is only a special case, and even somehow artificial. We might not be able to describe the electromagnetic field inside the current sheet in reality for the time being, in which the structure of the electromagnetic field should possess much more complex features and properties. The purpose of this work is to investigate the effect of the internal structures of the current sheet on the particle acceleration process, including particle trajectory and energy spectra. We offer our results as an attempt to further our understanding of the particle acceleration during the multi-island coalescence and the explosive energy release phenomenon. In the future, we will consider the particle acceleration in an electromagnetic field that is produced through an MHD simulation in a more self-consistent sense.
Acknowledgments
This work was supported by Program 973 grant 2013CBA01503, NSFC grants 11203069, 11273055, 11333007, 11403100, 11573064, CAS grants XDB09040202 and QYZDJ-SSW-SLH012, the key Laboratory of Solar Activity grant KLSA201409. The authors gratefully acknowledge the computing time granted by the Yunnan Observatories, provided at the facilities of the Yunnan Observatories Supercomputing Platform, and the NSFC-Guangdong Joint Fund (the Second Phase) of NSFC 2015-463.
References
- Barta, M., Buchner, J., Karlicky, M., & Skala, J. 2011, ApJ, 737, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bemporad, A. 2008, ApJ, 689, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Biskamp, D. 1993, Nonlinear Magnetohydrodynamics (New York: Cambridge University Press) [Google Scholar]
- Biskamp, D. 2000, Magnetic Reconnection in Plasmas (New York: Cambridge University Press) [Google Scholar]
- Biskamp, D., & Welter, H. 1980, Phys. Rev. Lett., 44, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, P. K., & Vekstein, G. E. 2001, J. Geophys. Res., 106, 18677 [NASA ADS] [CrossRef] [Google Scholar]
- Bruhwiler, D. L., & Zweibel, E. G. 1992, J. Geophys. Res., 97, 10825 [NASA ADS] [CrossRef] [Google Scholar]
- Bulanov, S.V. 1980, Sov. Astron. Lett., 6, 206 [NASA ADS] [Google Scholar]
- Dalla, S., & Browing, P. K. 2005a, A&A, 436, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalla, S., & Browing, P. K. 2005b, A&A, 491, 289 [Google Scholar]
- Emslie, A. G., Kucharek, H., & Dennis, B. R. 2004, J. Geophys. Res., 109, A10104 [NASA ADS] [CrossRef] [Google Scholar]
- Foukal, P., & Behr, B. 1995, Sol. Phys., 156, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Furth, H. P., Killeen, J., Rosenbluth, M. N., et al., 1963, Phys. Fluids, 6, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2010, ApJ, 720, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Hannah, I. G., & Fletcher, L. 2006, Sol. Phys., 236, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Litvinenko, Y. E., & Craig, I. J. D. 2002, ApJ, 566, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B. 1994, ApJS, 90, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Ko, Y.-K., Raymond, J. C., Lin, J., Lawrence, G., Li, J., & Fludra, A. 2003, ApJ, 594, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Hudson, H. S., Glesener, L., et al. 2010, ApJ, 714, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., & Lin, J. 2012, Sol. Phys., 279, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Winter, H. D., Murphy, N. A., Lin, J., & Wu, N. 2013, Publ. Astron. Soc. Jpn., 65, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Ko, Y.-K., Sui, L., et al. 2005, ApJ, 622, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Li, J., Forbes, T. G., Ko, Y.-K., Raymond, J. C., & Vourlidas, A. 2007, Astrophys. Lett., 658, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Li, J., Ko, Y.-K., & Raymond, J. C. 2009, ApJ, 693, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Murphy, N. A., Shen, C., et al. 2015, Space Sci. Rev., 194, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Krucker, S., & Hurford, G. J., et al. 2003, ApJ, 595, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 1996, ApJ, 462, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Martens, P. C. H. 1988, Astrophys. Lett., 330, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Martens, P. C. H., & Young, A. 1990, ApJS, 73, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, Z., Shen, C., Wu, N., Lin, J., Murphy, N. A., & Roussev, I. I. 2012, MNRAS, 425, 2824 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, K. I., Sakai, J. I. & Zhao, J. 1998, ApJ, 494, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, M., Phan, T.-D., Krucker, S., Fujimoto, M., & Shinohara, I. 2010, ApJ, 714, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2000, Magnetic Reconnection: MHD Theory and Applications (Cambridge, England: Cambridge University Press) [Google Scholar]
- Pritchett, P. L. 2007, Phys. Plasmas, 14, 052102 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J.C., Krucker, S., Lin, R. P., & Petrosian, V. 2012, Space Sci. Rev., 173, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, C. C., Lin, J., & Murphy, N. A. 2011, ApJ, 737, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Scholer, M., & Jamitzky, F. 1987, J. Geophys. Res., 92, 12181 [NASA ADS] [CrossRef] [Google Scholar]
- Turkmani, R., Cargill, P. J., Galsgaard, K., Vlahos, L., & Isliker, H. 2005, A&A, 449, 749 [Google Scholar]
- Wood, P., & Neukirch, V. 2005, Sol. Phys., 226, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Cao, W., Liu, C., et al. 2004, Astrophys. Lett., 607, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2004, ApJ, 604, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, MNRAS, 356, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Arzner, K., Benz, A. O., et al. 2011, Space Sci. Rev., 159, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zwingmann, W. 1983, J. Geophys. Res., 88, 9101 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, J. Y., Lin, J., Li, Y. T., et al. 2016, ApJS, 225, 30 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Panel a: Configuration of the magnetic field with oscillatory structures. Panel b: Diagram of the enlarged coalescence reconnecting current sheet. The arrows imply the the motion direction of the plasma bulk flow. The position of the primary magnetic reconnection is indicated by thick arrows, and the position of the coalescence magnetic reconnection is shown by thin arrows. Panel c: The electric field varies along the x-direction. |
| In the text | |
 |
Fig. 2 Kinematics and dynamic of a randomly chosen sample of accelerated electrons. Panel a: Projection of electron trajectories onto the xz-plane, b) projection of the trajectories onto the xy-plane, and c) variations of the electron energies versus time for ξ = 1. Particles that start to be accelerated from different locations are displayed, and the initial location of each particle is denoted by the solid dot in plane a) and b). |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for protons. |
| In the text | |
 |
Fig. 4 Energy spectra of electrons and protons for ξ = 1. |
| In the text | |
 |
Fig. 5 Final energy of electrons a) and protons b) versus the time that the particles remain in the computational domain. Each dot represents a single particle. |
| In the text | |
 |
Fig. 6 Variation in electron and proton energy spectra a)–f), spectrum indices γ1 and γ2g, h, j, k), and the energy of the knee i, l) with different guide fields. Corresponding ξ values are shown in the panels. |
| In the text | |
 |
Fig. 7 Energy spectra of electrons and protons for different values of the electric field (a)–(d). Variations in the spectrum indices γ1 and γ2(e)–(i) and the energy of the knee (g),(j) versus the electric field for electrons and protons, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


