| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201730435 | |
| Published online | 05 July 2017 | |
Fully self-consistent thermal evolution studies of rotating neutron stars
1 Instituto de Física, Universidade Federal Fluminense 20420 Niteroi RJ Brazil
e-mail:
negreiros@if.uff.br
2 FIAS, Goethe University, Ruth Moufang Str. 1, 60438 Frankfurt, Germany
3 Department of Physics, San Diego State University, 5500 Campanile Drive, San Diego, California 92182, USA
4 Center for Astrophysics and Space Sciences, University of California, San Diego, La Jolla, CA 92093, USA
Received: 13 January 2017
Accepted: 14 April 2017
In this work we study the thermal evolution of rotating, axis-symmetric neutron stars, which are subjected to structural and compositional changes during spin-down. Our aim is to go beyond standard thermal evolution calculations where neutron stars are considered spherically-symmetric and with a static, “frozen-in” composition. Building on previous work, we carry out fully self-consistent thermal evolution calculations where the neutron star has an axis-symmetric, time-dependent structure. Such an approach allows us to consider, during the thermal evolution, changes of the star’s geometry as well as its microscopic particle population. As a proof-of-concept, we study the thermal evolution of a neutron star subjected to magnetic braking spin-down. We show that the spin-evolution, combined with the accompanying structural and compositional changes lead to a substantially distinct thermal evolution scenario.
Key words: stars: neutron / stars: evolution / stars: rotation
© ESO, 2017
1. Introduction
In the traditional approach, the thermal evolution of neutron stars is treated under the assumption that the star is spherically symmetric and with a “frozen-in” structure/composition (Page et al. 2006, 2004; Tsuruta & Cameron 1965; Yakovlev & Pethick 2004; Negreiros et al. 2010), i.e., a snapshot of the neutron star is taken at the beginning of the thermal evolution and assumed to be constant throughout cooling. In practical terms that means that the particle composition, as well as macroscopic properties such as gravitational mass and radius are all assumed to be constant throughout the cooling era (that may be as long as 107 years). There are, however, many circumstances in which such assumptions may no longer be valid. Magnetic fields, for example are known to break the spherical symmetry of a neutron stars (Page et al. 2004; Cardall et al. 2001). Even if the magnetic field is not strong enough to alter the macroscopic properties of the object, it may alter the thermal conductivity such that the thermal energy transport is no longer spherically symmetric (Geppert et al. 2004; Hui & Cheng 2004). Rotation is also known to break spherical symmetry (Weber et al. 2009; Komatsu et al. 1989; Cook et al. 1992; Negreiros et al. 2010). Furthermore, neutron stars undergoing spin-down due to magnetic braking (for example) may experience an increase in density and undergo particle re-population making the assumption of a frozen-in composition invalid (Negreiros et al. 2013). Strong magnetic field evolution, accretion and many other scenarios may lead to a neutron star whose structure and composition are evolving through time, warranting thus a new approach to the thermal evolution of neutron stars, one that can take into account not only the breaking of spherical symmetry, but also the possibility of an evolving structure/composition. The work presented in Aguilera et al. (2008) as well as Negreiros et al. (2012) represented initial efforts to go beyond the traditional spherical symmetry standpoint and consider axis-symmetric cooling. The work in (Negreiros et al. 2013), in addition, has considered the effects of particle re-population on the thermal evolution of neutron stars, although on a spherically symmetric approximation. Our purpose with this work is to present a new approach to the thermal evolution of neutron stars, one that is able to handle a dynamic structure and composition, as well as an axis-symmetric structure. For that purpose we will, as a proof of concept, study the thermal evolution of spinning-down neutron stars, in which spin evolution is a result of magnetic braking. We note that in the magnetic braking model typical magnetic field strengths are relatively weak, such that we can safely neglect its influence on the structure and thermal evolution of the star, as is the case in this work. We note, however, that there are other scenarios in which the magnetic field is strong enough to play a role both on the stellar structure and thermal evolution (such as magnetars, for instance). In this work we do not consider such cases, although we could, in principle, deal with any axis-symmetric neutron star undergoing a structure/composition evolution (as long as it is in a quasi-static regime). We intend to pursue such scenarios in future works.
2. Spinning-down neutron stars
For the purpose of this article we investigate the thermal evolution of neutron stars undergoing spin-evolution due to magnetic braking. Under this assumption the spin-down rate of the object is given by: 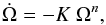 (1)where Ω denotes the neutron star rotational frequency, and K and n are constants (Glendenning 1996) that depend on the moment of inertia and surface magnetic field of the neutron star. For a neutron star that spins down solely due the emission of magnetic dipole radiation we find n = 3 (Glendenning 1996). For this work, we limit our study to neutron stars with intermediary values of K, in the range 10-18 s ≤ K ≤ 10-15 s. It is important to note that, as mentioned above, K depends on the moment of inertia of the star and, as such, is expected to vary during the spin-down. For the traditional magnetic braking model, however, such changes are not taken into account. Following the “proof-of-concept” spirit of this work, we stick to the traditional braking model, and consider a constant value for K in the aforementioned range. One must keep in mind, however, that a strict treatment must consider the changes in moment of inertia resulting from the spin-evolution. This will be investigated in future work.
(1)where Ω denotes the neutron star rotational frequency, and K and n are constants (Glendenning 1996) that depend on the moment of inertia and surface magnetic field of the neutron star. For a neutron star that spins down solely due the emission of magnetic dipole radiation we find n = 3 (Glendenning 1996). For this work, we limit our study to neutron stars with intermediary values of K, in the range 10-18 s ≤ K ≤ 10-15 s. It is important to note that, as mentioned above, K depends on the moment of inertia of the star and, as such, is expected to vary during the spin-down. For the traditional magnetic braking model, however, such changes are not taken into account. Following the “proof-of-concept” spirit of this work, we stick to the traditional braking model, and consider a constant value for K in the aforementioned range. One must keep in mind, however, that a strict treatment must consider the changes in moment of inertia resulting from the spin-evolution. This will be investigated in future work.
In Fig. 1 we show the frequency evolution for neutron stars with the aforementioned properties and initial frequency of Ω = 500 Hz, which will be considered in this work.
 |
Fig. 1 Frequency evolution for neutron stars undergoing magnetic braking, with n = 3 and a range of different K values. |
In order to accurately calculate the thermal evolution of such neutron stars one also needs to properly describe its macroscopic properties. For such, we solve Einstein’s equation for a rigidly rotating neutron star, whose metric is given by Weber (1999), Glendenning (1996) and references therein  (2)where ν, φ, Nϕ and ω are metric functions that depend only on the coordinates r and θ. Einstein’s equations for such metric are solved numerically, coupled to the hydrostatic equilibrium condition, and with source terms given by that of a perfect fluid. The numerical scheme used is one based on the KEH (Stergioulas & Friedman 1995; Komatsu et al. 1989; Cook et al. 1992) approach. Evidently, we are interested in the thermal evolution of spinning-down neutron stars, that is, with a structure that changes over time. We assume here that the structural changes take place in a quasi-static regime, such that we can ignore the time dependence of the metric. That is a reasonable approach, since the relaxation times of the spin-down model we are using are of the order of 102−6 years.
(2)where ν, φ, Nϕ and ω are metric functions that depend only on the coordinates r and θ. Einstein’s equations for such metric are solved numerically, coupled to the hydrostatic equilibrium condition, and with source terms given by that of a perfect fluid. The numerical scheme used is one based on the KEH (Stergioulas & Friedman 1995; Komatsu et al. 1989; Cook et al. 1992) approach. Evidently, we are interested in the thermal evolution of spinning-down neutron stars, that is, with a structure that changes over time. We assume here that the structural changes take place in a quasi-static regime, such that we can ignore the time dependence of the metric. That is a reasonable approach, since the relaxation times of the spin-down model we are using are of the order of 102−6 years.
One also needs an equation of state to fully describe the neutron star. Great efforts have been made towards the accurate description of the micro-physics inside a neutron star (Akmal et al. 1998; Alcock et al. 1986; Alford et al. 2005; Baym et al. 1971; Dexheimer et al. 2013; Dexheimer & Schramm 2010; Glendenning 1996, 1985, 1995; Lattimer & Prakash 2007; Negreiros et al. 2010; Weber 1999, 2005; Weber et al. 2007), however, much is still unknown. For the purpose of this study it is sufficient to use a non-linear relativistic mean-field equation of state (parameter set G300) (Glendenning 1989), which reproduces the properties of nuclear matter at saturation density (Weber 1999; Glendenning 1996, 1989). We save the study of more sophisticated EoS under our approach for future investigations.
 |
Fig. 2 Mass as a function of central density. The blue and magenta curves depict sequences of constant baryonic mass of 1.6 and 1.8 solar masses, which are limited by the spherically symmetric stellar sequence (Ω = 0) and the Kepler sequence (Ω = ΩK). Such curves represent the evolutionary path taken by isolated neutron stars during their spin-evolution (and the corresponding increase in central density). |
Figure 2 displays the different possible stable configurations of two neutron stars, with baryonic masses of 1.8 and 1.6 solar masses, described by the aforementioned microscopic model. In addition, this figure also shows sequences of stars with constant baryonic mass (1.6 and 1.8 solar masses), which represent the paths taken for isolated stars with the corresponding baryonic mass during their spin evolution. Such sequences are limited by the Kepler frequency ΩK, given by 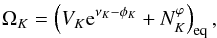 (3)where νK, φK and
(3)where νK, φK and 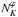 are the corresponding metric functions evaluated at the Kepler frequency, VK is the fluid element velocity at which mass shedding starts to take place at the equator, thus terminating stable rotating configurations. This quantity is written as
are the corresponding metric functions evaluated at the Kepler frequency, VK is the fluid element velocity at which mass shedding starts to take place at the equator, thus terminating stable rotating configurations. This quantity is written as 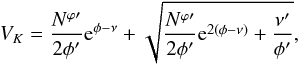 (4)and needs to be solved self-consistently with Einstein’s equation and the hydrostatic equilibrium condition. Note that in Eq. (4) a prime indicates differentiation with respect to the radial coordinate r.
(4)and needs to be solved self-consistently with Einstein’s equation and the hydrostatic equilibrium condition. Note that in Eq. (4) a prime indicates differentiation with respect to the radial coordinate r.
It is important to recall that each stellar configuration depicted in the constant baryonic mass sequence of Fig. 2 corresponds to a star with different frequency. This is shown in Fig. 3 in which we see that differently than for the gravitational mass, that changes very little with frequency, as the stellar frequency decreases, the object gets considerably more dense, which will be reflected in the particle composition and the thermal properties, as was discussed in Negreiros et al. (2013).
 |
Fig. 3 Frequency as a function of central stellar density for the constant baryonic mass sequences shown in Fig. 2. Stable neutron stars exist only in the unshaded area. |
3. Axis-symmetric thermal evolution
We now turn our attention to the thermal evolution of the stars studied in the previous sections. The description of the thermal evolution of general relativistic, axis-symmetric neutron stars was given in Negreiros et al. (2012), in which the thermal evolution of (stationary) axis-symmetric relativistic stars was investigated. It was shown that the cooling equations for a neutron star with an axis-symmetric metric/structure is given by (in the case of rigid rotation)  where α−β = ω,
where α−β = ω,  , with Hi being the ith component of the heat flux;
, with Hi being the ith component of the heat flux; 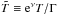 , with T being the temperature; κ is the thermal conductivity; CV is the specific heat; ϵ is the neutrino emissivity; and the Lorentz factor Γ ≡ (1−U2)− 1/2, where U is the proper velocity with respect to a zero angular momentum observer, given by U = (Ω−Nϕ)eφ. In this work we follow the ground work laid out in Negreiros et al. (2012) and proceed to calculate the thermal evolution of neutron stars undergoing spin-down, as described in Sect. 2. For that purpose we solve the thermal evolution Eqs. (7), updating at each time step the macroscopic and microscopic components according to the spin-evolution. As discussed in Negreiros et al. (2013), the compression that follows spin-down may be enough to change the microscopic properties (particle population, Fermi momentum, etc.) of the neutron stars, impacting directly the cooling of such objects. We can thus expect that the effects of spin-down on cooling will be two-fold: due to the microscopic changes that incur as a result of compression, and due to the macroscopic changes resulting from the modification of the space-time.
, with T being the temperature; κ is the thermal conductivity; CV is the specific heat; ϵ is the neutrino emissivity; and the Lorentz factor Γ ≡ (1−U2)− 1/2, where U is the proper velocity with respect to a zero angular momentum observer, given by U = (Ω−Nϕ)eφ. In this work we follow the ground work laid out in Negreiros et al. (2012) and proceed to calculate the thermal evolution of neutron stars undergoing spin-down, as described in Sect. 2. For that purpose we solve the thermal evolution Eqs. (7), updating at each time step the macroscopic and microscopic components according to the spin-evolution. As discussed in Negreiros et al. (2013), the compression that follows spin-down may be enough to change the microscopic properties (particle population, Fermi momentum, etc.) of the neutron stars, impacting directly the cooling of such objects. We can thus expect that the effects of spin-down on cooling will be two-fold: due to the microscopic changes that incur as a result of compression, and due to the macroscopic changes resulting from the modification of the space-time.
We note that for our cooling simulations we have considered all neutrino emission processes that may occur inside the neutron star, including the direct and modified Urca processes, Bremsstrahlung, and pair breaking/formation. A review of such processes may be found in Yakovlev & Pethick (2004), Page et al. (2004, 2006). Furthermore, we have also considered neutron superfluidity (triplet in the core and singlet in the crust) as well as proton superconductivity (singlet).
We show in Fig. 4 different snapshots of the temperature distribution inside a MB = 1.6 solar masses neutron star, with an initial frequency of 500 Hz and K = 1.0 × 10-15 s.
 |
Fig. 4 Temperature profiles of a neutron star with MB = 1.6 solar masses, spinning-down (due to magnetic braking) from an initial frequency of 500 Hz and with K = 1.0 × 10-15 s. The figures above represent different stages of the thermal evolution of the neutron star, i.e. 0.1 (a), 10 (b), 25 (c) , and 105(d) years after birth. |
One can clearly see in Figs. 4 the temperature and structure evolving as the star spins/cool down. We see that during this process the star gradually regains its spherical shape. This, as discussed before, causes the star to increase its density, which in turn may affect the microscopic composition, leading then to modification of the microscopic thermal processes as well as anisotropic heat propagation, as can be seen in Fig. 4. We note that the modification in heat propagation arises from two sources: 1) the increase in density and subsequent modification of microscopic properties; and 2) the change of the space-time.
An interesting avenue of study that this approach to the thermal evolution of neutron stars opens is the investigation of the distribution of microscopic, temperature-dependent properties inside an axis-symmetric neutron star. We can, for instance, investigate the pairing gap distribution inside the neutron star during its spin-evolution. The pairing gap depends on the temperature and on the Fermi momentum of the particles. Both these quantities change during the spin/thermal evolution. We illustrate, for instance, how the pairing gap for the neutron triplet (present in the core, and especially important for the modeling of the thermal evolution of Cas A; see Shternin et al. 2011; Page et al. 2011; Negreiros et al. 2013; Ho & Heinke 2009) changes during the spin/thermal evolution. We emphasize that both the thermal evolution and the spin-down affect the pairing, one due to the lowering of the temperature, and the other due to the increase in density. The pairing gap distribution inside of the cooling neutron star at different time snapshots and for K = 1.0 × 10-15 s are shown in Fig. 5.
 |
Fig. 5 Neutron triplet GAP distribution (Δ /κT) for different times in the thermal evolution with K = 1.0 × 10-15 s. The GAP distribution are for neutron stars 60 (a), 105 (b), 820 (c) and 105(d) years after birth. |
As illustrated in Fig. 5, one can see the effect that the spin-down combined with the thermal evolution has on the pair formation. Differently than the traditional spherically symmetric thermal evolution, where the spatial distribution of the pairs is fixed and their gaps increase as the star cools down, in our study we show that the spatial distribution is also modified, as it should be, due to the dynamic behavior of the particle densities during spin-down. As the pairing is of paramount importance for the cooling (Yakovlev & Pethick 2004; Page et al. 2004, 2006), we should not neglect the importance of the structure evolution (due to spin-down or otherwise) on the cooling of neutron stars.
Finally we compare the polar/equatorial surface temperature evolution with that of a spherically symmetric star. We do that for neutron stars with different values for the constant K, representing different rates of frequency spin-down.
As expected, Figs. 6−9 show that the polar/equatorial temperatures tend towards that of a spherically symmetric star as the object spins down. This happens more or less quickly according to the spin-down rate of the object. For instance, objects with K = 1.0 × 10-15 (associated with a faster spin-down) exhibit the behavior of spherically symmetric stars after ages of about 100 years, whereas stars with K = 1.0 × 10-18 (that have slower spin-down) have a distinct behavior, with the pole and equator exhibiting slightly different temperatures until ~ 105 years.
Our study also provides the possibility to study how the temperature of the star (at the equator for instance) varies with the frequency. We show this in Fig. 10, where the equatorial temperature is shown as a function of the stellar frequency. It is important to note that even though in Fig. 10 we have shown the temperature as a function of frequency, this could have just as well be any other quantity that affects the structure of the star over time. For instance, a magnetic field that deforms the star and is evolving over time, thus changing the star’s geometry, such that we could in principle determine the dependence of the surface temperature as a function of the magnetic field. Furthermore in our study, we consider that the thermal evolution is affected by the spin evolution (as it should be) but not the other way around (which does not necessarily need to be case). One could envision a scenario in which changes in the thermal evolution could affect the spin evolution as well (see for instance Ho & Andersson 2012). Such scenario could also be investigated within our approach.
In addition to Fig. 10, we can combine the dependence of the temperature on time and frequency in one figure, representing a three dimensional track of how the equator temperature evolves with time and frequency. This is shown in Fig. 11.
Finally, we briefly address the possibility of heating. As mentioned before we consider that the spin-evolution takes place adiabatically, so that the metric may be considered static at each step of the evolution. Evidently, we could not hope to model violent effects such as collapse into black holes or neutron star mergers within our approach, nor it is our aim, since we are mostly concerned with long-term thermal and spin properties. Nonetheless, depending on the spin evolution mechanism there could be a gradual release of heat that may affect the thermal evolution. For the case studied here (spin-down due to magnetic braking) the amount of heat is negligible, as, in the magnetic braking model, the emission of magnetic dipole radiation is powered by the loss of rotational energy. This does not have to be the case, however. Heat could have different sources, like the magnetic field for example. In a model where the magnetic field is buried within the crust (Viganò & Pons 2012; Bernal et al. 2013; Muslimov & Page 1995) and grows over time, there could be a considerable amount of heat there, and as such it could affect the thermal evolution. We hope to apply our approach to scenarios such as this in future investigations.
 |
Fig. 6 Surface polar/equatorial temperatures as a function of time for the thermal evolution with K = 1.0 × 10-15 s. Also shown is the temperature evolution of the equivalent spherically symmetric neutron star with a “frozen-in” composition. |
4. Conclusions
In this work we have presented a self-consistent calculation of the thermal evolution of an axis-symmetric neutron stars with a dynamic structure/composition. This research is the culmination of previous works in which these two processes were treated separately. As a proof-of-concept we have studied the thermal evolution of a neutron star that is undergoing spin-down due to magnetic braking. We have considered a star with baryon masses of M/M⊙ = 1.6, in which we assumed to begin their thermal/rotational evolution with rotational frequency of Ω = 500 Hz, and undergoing different spin-down evolution (as determined by the parameters K). By taking into account a frequency-dependent stellar structure, and solving the thermal balance/transport equations of a general relativistic axis-symmetric star we were able to obtain a completely self-consistent simulation of the thermo-rotational evolution of such object. We have shown the temperature evolution inside the star and at its surface, as well as the overall change in the stellar structure. We stress that within our approach to the thermal evolution of neutron stars, we can take into account effects that cannot be considered in the traditional spherically symmetric, “frozen-in” composition. To illustrate that we have shown that the neutron triplet (3P2) pairing gap distribution inside of the evolving star is substantially different than that of spherically symmetric neutron stars. In order to understand effects such as this one must take notice that two factors affect the microscopic and transport properties of a neutron star: temperature and density. In traditional calculations, transport properties only evolve dynamically due to the temperature evolution. In our approach we could consider modifications on transport and thermal properties brought on by dynamical structure evolution (in addition to the thermal changes). For instance, in the case we considered, the pairing gaps inside of a neutron star depend on the temperature and on the density. Therefore, we had a competing phenomena: the increase in density favors the weakening of the gaps, whereas the cool down acts to strengthen it. This illustrates the importance of a self-consistent treatment of the thermal and structure evolution of neutron stars, since most of their properties are intrinsically connected and feed back into each other.
 |
Fig. 10 Equatorial temperature as a function of stellar frequency for the different spin-down evolutions studied in this paper, which are represented by the different values of K. |
 |
Fig. 11 3D path of the temperature as it evolves with time and frequency for the different values of K studied (the vertical stems are exhibited only to aid visualization). |
We believe that we have taken an important step to build upon the study of the cooling of neutron stars, whose current understanding we owe to the efforts of many scientists. We hope that with our approach we can provide the community with a new way to calculate the thermal evolution of neutron stars, that can just as well deal with spherically symmetric-static stars, and more sophisticated, axis-symmetric, dynamic structure scenarios, such as the one investigated here. In the future we aim to go beyond the thermo-rotational model we studied in this paper, and explore more sophisticated situations. We are particularly interested in situations that would benefit from the departure of traditional spherical calculations. Particularly interesting are phenomena involving the magnetic field, since it is known to break the spherical symmetry, as well as influence composition/structure. Furthermore, the presence of a magnetic field, even if not strong enough to affect the structure, may alter the thermal conductivity, leading to anisotropic heat transfer, thus warranting axis-symmetric thermal calculations. Another possible scenarios of interest would be formation of thermo-rotational vortexes in superfluid matter, as well as the spin-up of neutron stars due to accretion. We believe that we have the tools necessary to tackle such problems (and others) in the future.
Acknowledgments
F.W. is supported by the National Science Foundation (USA) under Grant PHY-1411708. S.S. acknowledges access to the computer facilities of the CSC Frankfurt. R.N. acknowledges financial support from the CAPES and CNPq.
References
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008, A&A, 486, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Farhi, E., & Olinto, A. 1986, ApJ, 310, 261 [Google Scholar]
- Alford, M., Braby, M., Paris, M., & Reddy, S. 2005, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
- Bernal, C. G., Page, D., & Lee, W. H. 2013, ApJ, 770, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Cardall, C. Y., Prakash, M., & Lattimer, J. M. 2001, ApJ, 554, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1992, ApJ, 398, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Dexheimer, V. A., & Schramm, S. 2010, Phys. Rev. C, 81, 045201 [NASA ADS] [CrossRef] [Google Scholar]
- Dexheimer, V., Steinheimer, J., Negreiros, R., & Schramm, S. 2013, Phys. Rev. C – Nucl. Phys., 87, 015804 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., Küker, M., & Page, D. 2004, A&A, 426, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glendenning, N. 1985, ApJ, 293, 470 [Google Scholar]
- Glendenning, N. K. 1989, Nucl. Phys. A, 493, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. 1995, ApJ, 450, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. 1996, Compact Stars, Nuclear Physics, Particle Physics and General Relativity (New York, USA: Springer-Verlag) [Google Scholar]
- Ho, W. C., & Andersson, N. 2012, Nature Phys., 8, 787 [Google Scholar]
- Ho, W. C. G., & Heinke, C. O. 2009, Nature, 462, 71 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hui, C. Y., & Cheng, K. S. 2004, ApJ, 608, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989, MNRAS, 237, 355 [NASA ADS] [Google Scholar]
- Lattimer, J., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A., & Page, D. 1995, ApJ, 440, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Negreiros, R., Dexheimer, V. A., & Schramm, S. 2010, Phys. Rev. C, 82, 035803 [NASA ADS] [CrossRef] [Google Scholar]
- Negreiros, R., Schramm, S., & Weber, F. 2012, Phys. Rev. D, 85, 104019 [NASA ADS] [CrossRef] [Google Scholar]
- Negreiros, R., Schramm, S., & Weber, F. 2013, Phys. Lett. B, 718, 1176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
- Stergioulas, N., & Friedman, J. L. 1995, ApJ, 444, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuruta, S., & Cameron, A. G. W. 1965, Nature, 207, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Viganò, D., & Pons, J. A. 2012, MNRAS, 425, 2487 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, F. 1999, Pulsars as astrophysical laboratories for nuclear and particle physics (Bristol, UK: Institute of Physics) [Google Scholar]
- Weber, F. 2005, Prog. Part. Nucl. Phys., 54, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, F., Negreiros, R., Rosenfield, P., & Stejner, M. 2007, Prog. Part. Nucl. Phys., 59, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, F., Negreiros, R., & Rosenfield, P. 2009, in Neutron Stars and Pulsars (Berlin, Heidelberg: Springer) [Google Scholar]
- Yakovlev, D., & Pethick, C. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Figures
 |
Fig. 1 Frequency evolution for neutron stars undergoing magnetic braking, with n = 3 and a range of different K values. |
| In the text | |
 |
Fig. 2 Mass as a function of central density. The blue and magenta curves depict sequences of constant baryonic mass of 1.6 and 1.8 solar masses, which are limited by the spherically symmetric stellar sequence (Ω = 0) and the Kepler sequence (Ω = ΩK). Such curves represent the evolutionary path taken by isolated neutron stars during their spin-evolution (and the corresponding increase in central density). |
| In the text | |
 |
Fig. 3 Frequency as a function of central stellar density for the constant baryonic mass sequences shown in Fig. 2. Stable neutron stars exist only in the unshaded area. |
| In the text | |
 |
Fig. 4 Temperature profiles of a neutron star with MB = 1.6 solar masses, spinning-down (due to magnetic braking) from an initial frequency of 500 Hz and with K = 1.0 × 10-15 s. The figures above represent different stages of the thermal evolution of the neutron star, i.e. 0.1 (a), 10 (b), 25 (c) , and 105(d) years after birth. |
| In the text | |
 |
Fig. 5 Neutron triplet GAP distribution (Δ /κT) for different times in the thermal evolution with K = 1.0 × 10-15 s. The GAP distribution are for neutron stars 60 (a), 105 (b), 820 (c) and 105(d) years after birth. |
| In the text | |
 |
Fig. 6 Surface polar/equatorial temperatures as a function of time for the thermal evolution with K = 1.0 × 10-15 s. Also shown is the temperature evolution of the equivalent spherically symmetric neutron star with a “frozen-in” composition. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for a thermal evolution with K = 1.0 × 10-16 s. |
| In the text | |
 |
Fig. 8 Same as Fig. 6 except but for a thermal evolution with K = 1.0 × 10-17 s. |
| In the text | |
 |
Fig. 9 Same as Fig. 6 but for a thermal evolution with K = 1.0 × 10-18 s. |
| In the text | |
 |
Fig. 10 Equatorial temperature as a function of stellar frequency for the different spin-down evolutions studied in this paper, which are represented by the different values of K. |
| In the text | |
 |
Fig. 11 3D path of the temperature as it evolves with time and frequency for the different values of K studied (the vertical stems are exhibited only to aid visualization). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


