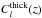EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 602 (June 2017) A&A, 602 (2017) A72 Full HTML
Free Access
Issue
A&A
Volume 602, June 2017
Article Number A72
Number of page(s) 8
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/201730399
Published online 15 June 2017

© ESO, 2017

1. Introduction

Cosmology is entering the era of wide and deep surveys of galaxies, such as, for example, with the Dark Energy Spectroscopic Instrument (DESI; Levi et al. 2013), the Large Synoptic Survey Telescope (LSST; Ivezic et al. 2008), and the Euclid satellite (Laureijs et al. 2011), in order to investigate the mechanisms of cosmic acceleration (for a review see Weinberg et al. 2013). Cosmological models can be tested, that is, compared against actual measurements, by studying the statistical properties of galaxy clustering. Several methods exist for this, the most classical ones computing correlations in real (Landy & Szalay 1993) or Fourier space (Feldman et al. 1994). However, for wider and deeper surveys, one may also try to condense the clustering information into redshift bins (“shells”) and compute the auto- and cross-correlations between redshift shells (Asorey et al. 2012). This is known as tomography, and allows for a more precise understanding of potential systematic errors in different redshift regions. Several studies compare the merits of this kind of approach with the more classical ones (Asorey et al. 2012, 2014; Di Dio et al. 2014; Nicola et al. 2014; Lanusse et al. 2015) and try to optimize the binning to keep most of the cosmological information. All previous studies have been based on the Fisher formalism, which considers observables as Gaussian; unrepresentative, however, of real life data.

To go on further and prepare the future tomographic analyses, one needs to implement a full pipeline and test the method with, for instance, a Monte-Carlo Markov chain (MCMC) exploration of the cosmological parameter space. But there is a technical bottleneck; running a typical MCMC algorithm in cosmology is already very lengthy and requires computing typically a few 105 models. Each model is the result of a numerical code that solves the cosmological equations (known as “Boltzmann solvers”), such as CLASS1 (Blas et al. 2011), which takes typically 5–10 s on eight cores. Today this amounts to several days of computation.

For a tomographic method, one further needs to transform the output of the Boltzmann solver, the matter power spectrum, into the observable space, represented as Cℓ(zi,zj) angular power spectra between two redshift shells located at zi and zj. This transformation is numerically challenging because of overlapping integrals between very oscillating spherical Bessel functions.

One then often makes use of the Limber’s approximation, which essentiallyreplaces the Bessel functions by a single Dirac value. However, as we show here, this leads to a poor approximation for auto-correlations and may even be incorrect for cross-correlations, since it cannot capture any anti-correlation.

We therefore address here the issue of accurately and quickly computing the integrals required to derive the correlations between tomographic bins. Our goal, in computational terms, is that this computation be faster than one typical Boltzmann code computation time, that is, essentially at or below the 1s level (on eight cores). Another aspect of this work is to provide a stand-alone library that offers a generic interface where the user can plug any matter power spectrum. This is a different approach from CLASSgal (Di Dio et al. 2013) which also provides some theoretical computations related to tomography that are deeply rooted within the CLASS software.

The integrals defining the Cℓ(zi,zj) angular power spectra are introduced in Sect. 2. In Sect. 3 we detail the algorithm implemented in Angpow, while we address some numerical tests in Sect. 4. Section 5 provides insight into the code design and we conclude in Sect. 6.

2. The position of the problem

Our aim is to compute the angular over density power spectrum Cℓ(z1,z2) as a cross-correlation between two z-shells with mean values (z1,z2) and also the auto-correlation Cℓ(z1) with z1 = z2, taking into account, in both cases, possible redshift selection functions. Following notations of reference (Di Dio et al. 2013), for a couple of redshift (z1,z2) one computes Cℓ(z1,z2) according to Cℓ(z1,z2)=2π∫0∞ dkk2P(k)Δℓ(z1,k)Δℓ(z2,k),\begin{equation} C_{\ell}(z_1, z_2) = \frac{2}{\pi} \int_0^\infty \dx k\ k^2\ P(k) \Delta_{\ell}(z_1, k)\Delta_{\ell}(z_2, k) \label{eq-cl-def} , \end{equation}(1)with on one hand P(k) the non-normalized primordial power spectrum, and on the other hand, Δℓ(z,k), a general function used to describe physical processes down to redshift z (Di Dio et al. 2013; Bonvin & Durrer 2011). At the lowest order, Δℓ(z,k) can be expressed as the product of the bias b and a growth factor D(z,k) to account for matter density contribution: Δℓmat.(z,k)=bD(z,k)jℓ(k r(z)),\begin{equation} \Delta^{\mrm{mat.}}_{\ell}(z, k) = b D(z,k) j_{\ell}(k\,r(z)) \label{eq-DeltaFunc-def} , \end{equation}(2)where jℓ(x) is a first kind spherical Bessel function of parameter ℓ, and r(z) is the radial comoving distance of the shell located at redshift z.

For thick redshift shells, one introduces two normalized redshift selection functions W1(z;z1,σ1) and W2(z′;z2,σ2) around z1 and z2 with typical width σ1 and σ2, respectively. Then, one extends Eq. (1)by Cℓthick(z1,z2;σ1,σ2)=2π”0∞ dz dz′W1(z;z1,σ1)W2(z′;z2,σ2) ×∫0∞ dkk2P(k)Δℓ(z,k)Δℓ(z′,k).\begin{eqnarray} C^{\mrm{thick}}_{\ell} (z_1, z_2;\sigma_1, \sigma_2) &=& \frac{2}{\pi} \iint_0^\infty \dx z \dx z^\prime \ W_1(z; z_1, \sigma_1) W_2(z^\prime; z_2, \sigma_2)\notag \\ &&\quad \times \int_0^\infty \dx k\ k^2\ P(k) \Delta_{\ell}(z, k)\Delta_{\ell}(z^\prime, k). \end{eqnarray}(3)It is convenient to introduce the auxiliary function justified in the following section fℓ(z,k)≡2πkP(k)Δℓ(z,k)=2πkP(k){bD(z,k)jℓ(k r(z))+... }=2πkP(k)D(z,k)2{bjℓ(k r(z))+... }≡\begin{eqnarray} f_\ell(z,k) &\equiv& \sqrt{\frac{2}{\pi}}\ k \sqrt{P(k)} \ \Delta_{\ell}(z, k) \notag \\ &=& \sqrt{\frac{2}{\pi}}\ k \sqrt{P(k)} \left\{ \vphantom{\sqrt{P(k)}}b D(z,k) j_{\ell}(k\,r(z)) + \dots\right\}\notag \\ &=& \sqrt{\frac{2}{\pi}}\ k \sqrt{P(k)D(z,k)^2} \left\{ \vphantom{\sqrt{P(k)}} bj_{\ell}(k\,r(z)) + \dots\right\} \notag \\ &\equiv& \sqrt{\frac{2}{\pi}}\ k \sqrt{P(k,z)}\ \widetilde{\Delta}_\ell(z,k), \label{eq-fell-func} \end{eqnarray}(4)where we have used the factorization of the growth factor D(k,z) from the matter density contribution to introduce the notation P(k,z) and 􏽥Δℓ(z,k)\hbox{$\widetilde{\Delta}_\ell(z,k)$}. The dots signify that other contributions may be introduced as the redshift distortions and lensing effects that we ignore here for simplicity. Then, Cℓthick(z1,z2;σ1,σ2)=”∞0dzdz′W1(z;z1,σ1)W2(z′;z2,σ2)\begin{eqnarray} C^{\mathrm{thick}}_{\ell} (z_1, z_2;\sigma_1, \sigma_2) & = &\iint_0^\infty \mathrm{d} z \mathrm{d} z^\prime \ W_1(z; z_1, \sigma_1) W_2(z^\prime; z_2, \sigma_2)\notag \\ &&\quad \times \int_0^\infty \mathrm{d} k\ f_{\ell}(z, k) f_{\ell}(z^\prime, k). \label{eq-clz1z2-obs} \end{eqnarray}(5)The auto-correlation is a particular case where the redshift selection function W2(z′;z2,σ2) is reduced to W1(z′;z1,σ1) and we can use a single W function, which leads to Cℓthick(z1;σ1)=”∞0 dz dz′W(z;z1,σ1)W(z′;z1,σ1)\begin{eqnarray} C^{\mrm{thick}}_{\ell}(z_1 ;\sigma_1) &= & \iint_0^\infty \dx z\ \dx z^\prime\ W(z; z_1, \sigma_1) W(z^\prime; z_1, \sigma_1)\notag \\ &&\quad \times \int_0^\infty \mathrm{d} k\ f_{\ell}(z, k) f_{\ell}(z^\prime, k). \label{eq-clz1-obs} \end{eqnarray}(6)To account for infinite redshift precision at z = z1, the use of a Dirac selection function for W yields Cℓδ(z1)=2π∫0∞ dkk2P(k,z1)􏽥Δℓ2(z1,k).\begin{equation} C^{\delta}_{\ell}(z_1) = \frac{2}{\pi} \int_0^\infty \dx k\ k^2 P(k,z_1) \widetilde{\Delta}^2_{\ell}(z_1, k). \label{eq-clz1-delta} \end{equation}(7)Angpow is designed to efficiently compute these Cℓ expressions once one provides access to the power spectra P(k,z), the ˜Δℓ(z,k)\hbox{$ \tilde{\Delta}_{\ell}(z, k)$} extra function, and the cosmological distance r(z). To simplify the notation, we do not write the width σ of the selection functions if not explicitly needed.

3. A brief description of the computational algorithm

The redshift integral computations of Eq. (5)can be conducted in practice inside the rectangle [z1min,z1max] × [z2min,z2max] given by the W selection functions using a Cartesian product of a one-dimensional (1D) quadrature defined by the set of sample nodes zi and weights wi. In practice, we use the Clenshaw-Curtis quadrature. The corresponding sampling points (z1i,z2j) are weighted by the product wiwj using the 1D quadrature sample points and weights on both redshift regions with i = 0,...,Nz1−1 and j = 0,...,Nz2−1. Then, one gets the following approximation: Cℓthick(z1,z2)≈∑i=0Nz1−1∑j=0Nz2−1wiwjW1(zi,z1)W2(zj,z2)􏽢Pℓ(ri,rj)\begin{equation} C^{\mrm{thick}}_{\ell}(z_1, z_2) \approx \sum_{i=0}^{N_{{z}_1}-1}\sum_{j=0}^{N_{{z}_2}-1} w_i w_j W_1(z_i,z_1)W_2(z_j,z_2) \widehat{P}_\ell(r_i,r_j) \label{eq-cross-zquadra} \end{equation}(8)with the notations zi = z1i, zj = z2j and ri = r(z1i), rj = r(z2j) and 􏽢Pℓ(zi,zj)=∫0∞ dkfℓ(zi,k)fℓ(zj,k),\begin{equation} \widehat{P}_\ell(z_i,z_j) = \int_0^\infty \dx k\ f_\ell(z_i,k) f_\ell(z_j,k) , \end{equation}(9)defined with the fℓ(z,k) function of Eq. (4).

We use a piecewise integration over a user-defined range [kmin,kmax] such that 􏽢Pℓ(zi,zj)≈∑p=0Nk−1Iℓ(kpℓ,kp+1ℓ;zi,zj),\begin{equation} \widehat{P}_\ell(z_i,z_j) \approx \sum_{p=0}^{N_\mrm{k}-1} I_\ell(k^\ell_p,k^\ell_{p+1};z_i,z_j) , \end{equation}(10)where the kpℓ\hbox{$k^\ell_p$} bounds are related to the roots of jℓ(x) noted qℓp and the user-defined number of roots qℓp per sub-interval [kpℓ,kp+1ℓ]\hbox{$[k^\ell_p, k^\ell_{p+1}]$} (see Appendix A). Then, Eq. (8)may be rewritten as  Cℓthick(z1,z2)≈∑i=0Nz1∑j=0Nz2wiwjW1(zi,z1)W2(zj,z2)  ×∑p=0Nk−1Iℓ(kpℓ,kp+1ℓ;zi,zj).\begin{eqnarray} \begin{split} C^{\mrm{thick}}_{\ell}(z_1, z_2) \approx \sum_{i=0}^{N_{\mrm{z}_1}}\sum_{j=0}^{N_{\mrm{z}_2}} & w_i w_j W_1(z_i,z_1)W_2(z_j,z_2) \\ &\qquad \times \ \sum_{p=0}^{N_\mrm{k}-1} I_\ell(k^\ell_p,k^\ell_{p+1};z_i,z_j). \end{split} \end{eqnarray}(11)The integral Iℓ(kpℓ,kp+1ℓ;ri,rj)\hbox{$I_\ell(k^\ell_p,k^\ell_{p+1};r_i,r_j)$} defined as Iℓ(kpℓ,kp+1ℓ;ri,rj)=∫kpℓkp+1ℓ dkfℓ(k,zi)fℓ(k,zj),\begin{equation} I_\ell(k^\ell_p,k^\ell_{p+1};r_i,r_j) = \int_{k^\ell_p}^{k^\ell_{p+1}} \dx k\ f_\ell(k, z_i) f_\ell(k, z_j) \label{eq-I-integ-cross}, \end{equation}(12)is computed using the 3C-algorithm of appendix A. Investigating the different steps of the algorithm, one notices that the sampling of the function fℓ(k,zi) along the k axis for a given [kpℓ,kp+1ℓ]\hbox{$[k^\ell_p, k^\ell_{p+1}]$} interval depends on zi but is independent from zj and vice versa for the fℓ(k,zj) function (those samplings are independent from zi). So, one may proceed to k-sampling before performing the double sum over (i,j), which is particularly efficient as the CPU bottleneck is the computation of the spherical Bessel function jℓ. Angpow uses a spherical Bessel function implementation based on Numerical Recipes (Press et al. 1992). The brute force Cartesian quadrature evolves as O(Nz1 × Nz2), while the optimized version reduces the CPU times scaling to O(Nz1 + Nz2). Therefore, as a matter of efficiency, it is more appropriate to exchange the order of the p and (i,j) summations leading to Cℓobs(z1,z2)≈∑p=0Nk−1∑i=0Nz1∑j=0Nz2wiwjW(zi,z1) ×W(zj,z2)Iℓ(kp,kp+1;zi,zj).\begin{eqnarray} C^{\mrm{obs}}_{\ell}(z_1, z_2) &\approx& \sum_{p=0}^{N_\mrm{k}-1} \sum_{i=0}^{N_{\mrm{z}_1}}\sum_{j=0}^{N_{\mrm{z}_2}} w_i w_j W(z_i,z_1)\notag \\ &&\quad \times W(z_j,z_2) I_\ell(k_p,k_{p+1};z_i,z_j). \end{eqnarray}(13)As a first hint for the 3C-algorithm, we use typically 28−29 polynomial approximations for ℓmax ≈ 500–1000 of the fℓ(k,ri) and fℓ(k,rj) functions, 100 spherical Bessel roots per sub-interval, 99-point Clenshaw-Curtis quadrature nodes, and weights for z integration in case of σ = 0.02.

4. Numerical tests

4.1. Comparison with other codes

We proceed now to a numerical comparison of the estimation of Cℓ(z1) and Cℓ(z1,z2) computed by CLASSgal (Di Dio et al. 2013) and Mathematica (Wolfram Research Inc. 2016) with Dirac redshift selection functions. Concerning CLASSgal (v1.1.3), we have started with the provided explanatory.ini file where we have modified the cosmological parameters to: h = 0.679, Ωb = 0.0483, Ωcdm = 0.2582 and Ωk = Ωfld = 0. We have also set k_scalar_max_tau0_over_l_max to fix the upper bound of the k-integration taking into account the maximal ℓ value and the redshift mean value. Concerning Angpow we have taken advantage of the possibility to read an external file produced by CLASSgal as an input P(k) computed at z = 0 in association to the growth function computed internally given by Lahav et al. (1991), Carroll et al. (1992). Finally, to avoid the Limber’s approximation for CLASSgal, we have set the “Limber” threshold much higher than the ℓ upper limit.

thumbnail Fig. 1

Comparison of the computations of the Cℓδ(z=1)\hbox{$C_\ell^{\delta}(z=1)$} given by Angpow, Mathematica, and CLASSgal for a Dirac selection function with kmax = 10 Mpc-1.

thumbnail Fig. 2

Computations of Clδ(z)\hbox{$C_l^{\delta}(z)$} with Dirac selections centered at z ∈ {0.85,1.00,1.15} with Angpow alone and Clthick(z)\hbox{$C_l^{\mrm{thick}}(z)$} with Angpow and CLASSgal using a Gaussian selection function with mean z = 1, a width of σ = 0.3, and a redshift cut at ± 5σ (in all cases kmax = 0.44 Mpc-1). For Angpow we use the power spectrum produced by CLASSgal and we have varied the redshift grid sampling resolution from 9 × 9 to 159 × 159 points to reach the converged result (blue curve) in good agreement with the CLASSgal result (cyan points). Comparing the Clδ(z=1)\hbox{$C_l^{\delta}(z=1)$} to the Clthick(z=1,σ=0.3)\hbox{$C_l^{\mrm{thick}}(z=1,\sigma=0.3)$} results we measure the effect of self-cross-correlation inside a thick redshift shell which washes out the matter fluctuation contrast.

Results of the auto-correlation Cℓδ(z)\hbox{$C_\ell^{\delta}(z)$} computations at z = 1 using Dirac selection functions are shown in Fig. 1. As the three softwares use the same primordial power spectrum, all the results agree with one other within a maximal relative error of 0.06% on the whole ℓ range.

thumbnail Fig. 3

Comparison between Angpow (red/orange points) and CLASSgal (black points) for several cross-correlation spectra with Gaussian (σ = 0.01) selection and kmax = 1 Mpc-1. The orange points are used to emphasize negative Cℓ.

The Cℓthick(z)\hbox{$C_\ell^{\mrm{thick}}(z)$} auto-correlation computation within a thick redshift band, selected by a Gaussian of mean z = 1 and σ = 0.03 cut at ± 5σ, has been used as a test bench. But, for this test we have neglected the Mathematica software, which is too slow, and have restricted testing to comparison of Angpow to CLASSgal. Figure 2 shows computation results. The orange, violet, and red curves are produced by Angpow using Dirac selection function in the range ± 5σ around the mean redshift z = 1, while the green, forest green, purple, and blue curves are results of the above mentioned Gaussian selection function but sampled using different grid sizes: 9 × 9, 19 × 19, 39 × 39 and 159 × 159 Clenshaw-Curtis sample points. As the number of points, or equivalently the quadrature order, increases, the Cℓthick(z)\hbox{$C_\ell^{\mrm{thick}}(z)$} computation converges towards the CLASSgal result (cyan points). We also address the cross-correlation computations performed by Angpow and CLASSgal (Cℓthick(z1,z2)\hbox{$C_\ell^{\mrm{thick}}(z_1,z_2)$}) using Gaussian selection functions (σ = 0.01 and a ± 5σ cut). The results are shown in Fig. 3. One should not be surprised by negative values since we are cross-correlating two different quantities. In both tests we have used the power spectrum computed at z = 0 by CLASSgal as input to Angpow. The agreement between the two software codes is very good, keeping the relative residuals at values less than 0.02%.

4.2. Note on Limber’s approximation

The Angpow library can also be used to compute, if desired, the first order Limber’s approximation (Loverde & Afshordi 2008). In such an approximation, the spherical Bessel function is formally reduced to jℓ(x)≈π2ℓ+1δD(x−(ℓ+12))·\begin{equation} j_\ell(x) \approx \sqrt{\frac{\pi}{2\ell +1}} \delta^D\left(x-\left(\ell+\frac{1}{2}\right)\right)\cdot \label{eq-jlx-Limber} \end{equation}(14)In such conditions, the product kr(z) is constrained, and if one uses the following notation for the comoving distance computation with dH = c/H0, the Hubble distance (H0 = 100h km s-1 Mpc-1 and c the speed of light) and E(z), the dimensionless Hubble parameter, r(zℓ(k))=l+1/2k=dH∫0zℓ(k) dzE(z)·\begin{equation} r(z_\ell(k)) = \frac{l+1/2}{k} = d_\mrm{H}\int_0^{z_\ell(k)} \frac{\dx z}{E(z)}\cdot \end{equation}(15)Then, Eq. (5)is transformed to the following expression  Cℓthick(z1,z2;σ1,σ2)≈2dH2(2ℓ+1)∫0∞ dkW1(zℓ(k);z1,σ1)×W2(zℓ(k);z2,σ2)E2(zℓ(k))P(k,zℓ(k)).\begin{eqnarray} \begin{split} C_{\ell}^{\mrm{thick}}(z_1, z_2; \sigma_1, \sigma_2) &\approx \frac{2}{d_\mrm{H}^2(2\ell+1)} \int_0^\infty \dx k\ W_1(z_\ell(k); z_1, \sigma_1) \\& \times W_2(z_\ell(k); z_2, \sigma_2) E^2(z_\ell(k)) P(k,z_\ell(k)). \label{eq-Cl-limber} \end{split} \end{eqnarray}(16)This integral can be computed using a divide-and-conquer recursive method with the Gauss-Kronrod quadrature (Laurie 1997). The Gauss sample points are a subset of the Gauss-Kronrod sample points and can easily be used to set up an error estimate to drive the recursive algorithm.

Looking at Eq. (16) one realizes that all the terms are positive, indicating that such approximation is not suitable for cross-correlation where Cℓ(z1,z2) is not guaranteed to be positive as can be explicitly seen in Fig. 3. We have proceeded to the computation of Cℓ(z) in the case of a Gaussian selection function of mean z = 1 and σ = 0.03 for both Angpow and CLASSgal, with/without the Limber’s approximation. The results are shown in Fig. 4. The two software codes agree very well and show that the Limber’s approximation can give sizeable errors compared to the exact computation; of the order of the cosmic variance in the given example. So, this Limber’s approximation, even if it runs 100 times faster than the exact computation, should then be used with extreme care not only for cross-correlation but also for auto-correlation.

thumbnail Fig. 4

Comparison of the computations of the Cℓthick(z)\hbox{$C_\ell^\mrm{thick}(z)$} given by Angpow and CLASSgal either with the Limber’s approximation or the exact computation.

4.3. Correlations in real space

Angpow can also quickly compute the correlation function in real space from the power spectrum C(θ;z1,z2)=14π∑ℓ=0ℓmax(2ℓ+1)˜Cℓ(z1,z2)Pℓ(cosθ),\begin{equation} \label{eq:ctheta} C(\theta; z_1, z_2)=\frac{1}{4\pi} \sum_{\ell=0}^{\ell_\mrm{max}} (2\ell+1) \tilde{C}_{\ell}(z_1, z_2) P_\ell(\cos \theta) , \end{equation}(17)where Pℓ denotes the ℓth order Legendre polynomial. Because the Cℓ(z1,z2) values are generally cut at a given ℓmax, one needs to introduce an apodization to avoid ringing due to a sharp cut-off. We introduce a Gaussian one (which is the smoothest in both real and harmonic spaces) as in Di Dio et al. (2013) so that the ˜Cℓ(z1,z2)\hbox{$ \tilde{C}_{\ell}(z_1, z_2) $} term in Eq. (17)is ˜Cℓ(z1,z2)=Cℓ(z1,z2)e−ℓ(ℓ+1)/ℓa2.\begin{equation} \tilde{C}_{\ell}(z_1, z_2) = C_{\ell}(z_1, z_2 )e^{-\ell(\ell+1)/\ell_{\rm a}^2}. \end{equation}(18)The apodization length ℓa may depend on the signal but for the standard cosmology shown here (around z = 1) we noticed that using la ≃ 0.4ℓmax gives good results. Correlations in real space are generally easier to comprehend as is shownin Fig. 5, which represents the analogue of Fig. 3 but in real space. Here one may identify a peak, named the “Baryonic Acoustic Oscillation” (e.g., Weinberg et al. 2013) that decreases in the cross-correlation when the distance between shells increases and is finally washed out.

thumbnail Fig. 5

Cross-correlations in real space corresponding to the spectra shown on Fig. 3. The points show where the function was evaluated.

4.4. Speed tests

Angpow is designed and written in C++ and parallelization is achieved through OpenMP. To qualify the code we provide four input parameter files and their corresponding outputs obtained in one of our runs. In all tests, we used a ΛCDM reference cosmology, a P(k) at z = 0 provided by CLASSgal, ℓmax = 1000, a 3C-algorithm with 29 Chebyshev polynomial order, and 100 roots per sub-k-interval:

  • Test 1:

    auto-correlation with a Dirac selection function at z = 1 and kmax = 10 Mpc-1;

  • Test 2:

    cross-correlation with two Dirac selection functions at z = 1 and z = 1.05 and kmax = 10 Mpc-1;

  • Test 3:

    auto-correlation with a Gaussian selection function with (zmean = 1, σz = 0.02, 5σz-cut) and kmax = 1 Mpc-1 and a radial quadrature based on Npts = 139 sample points;

  • Test 4:

    cross-correlation with two Gaussian selection functions with (zmean,1 = 0.90, zmean,2 = 1.00) both with (σz = 0.02, 5σz-cut) and kmax = 1 Mpc-1 and a radial quadrature based on Npts = 139 sample points.

We have tested the code both on laptop (Linux, MacOSX) as well as on Computer Center (CCIN2P3 in France and NERSC in the USA). We use OpenMP to distribute the computation of a given Cℓ on a single thread. Table 1 gives Central Processing Unit (CPU) execution times averaged over ten processes. The code wall time decreases reasonably well with the number of threads and a wall time at the \hbox{$\mathcal{O}$}(1s) level can be reached to reconstruct these accurate spectra. Such performances are much higher than those obtained with CLASSgal when not using the Limber approximation. For example, on our Test-3 setup, running the latter takes about 15s (on 16 threads), which is to be compared to about 0.5s in Table 1.

Table 1

Wall time (in seconds) measured at CCIN2P3 (on Intel Xeon CPU E5-2640 v3 processors) for the test benches described in the text, according to the number of OpenMP threads used.

thumbnail Fig. 6

Evolution of the wall time with respect to the width of the selection function (σ) illustrated in the condition of Test 3 and using 16 threads. In the upper scale of the frame is shown an indication of the radial_order used to sample the along the z direction for a given σ (see Sect. 5).

Figure 6 shows the dependence of the wall time with respect to the width of the selection function (σ) in the conditions of Test 3 using 16 threads. For a given σ, we have chosen the minimal radial_order value such that the relative accuracy on the Cℓ is of the order of 0.01% compared to a computation with a much larger radial_order value (see Sect. 5). If one uses a looser criteria on the accuracy of the Cℓ or if the number of sigma is lower than 5, then one may use a lower radial_order and gain on the wall time.

5. Code design and input parameters

Angpow is written in C++ which allows both good CPU performances and keeps the code flexible. A front end interface to Python is also foreseen and the code is distributed publicly2. The angpow.cc file is an example of the library usage to perform Cℓ and C(θ) computations. We also provide the limber.cc file if one wants to test the Limber’s approximation (Sect. 4.2). The different files are located in self-explained directories: src, inc/Angpow, lib, data. Finally, a README file provides details for the installation and build procedures.

The two main classes Pk2Cl and KIntegrator (located in angpow_pk2cl.h and angpow_kinteg.h files) are generic codes using abstract base classes. They define interface to the power spectrum function P(ℓ,k,z) (class PowerSpecBase), the generalisation of P(k,z) used in Eq. (5); to the comoving distance computation r(z) (class CosmoCoorBase); and to the radial/redshift selection functions W(z) (class RadSelectBase). The user can derive their own concrete classes to access a third party library or use the ones implemented by default. For instance, we have implemented a file access to a (k,P(k))-tuple saved by the CLASSgal output. In this implementation, we have coded the growth factor defined in Lahav et al. (1991), Carroll et al. (1992) as minimal ˜Δℓ(z,k)\hbox{$\tilde{\Delta}_\ell(z,k)$} function (Eq. (2)).

To run the executable, one provides an ascii file defining the input parameters that drive the computational conditions of the algorithm and define the I/O locations. Some ready-made input parameter files are also provided (angpow_bench<n>.ini) as well as the Cℓ output files (angpow_bench<n>_cl.txt.REF) corresponding to the icpc outputs of Table 1.

Among the different input parameters some are more sensitive than others, as those that deal with the radial/redshift 1D quadrature and the 3C algorithm. Here is a closer look at these parameters:

  • cl_kmax: this is the maximal value of k in the k-integral. We have not set up an internal algorithm to determine this upper bound. As a hint, one may consider a relation with the factor ℓmax/r(zmin). The lower bound on k is internally fixed using the cut-off xmin(ℓ) defined as x < xmin(ℓ) ⇔ jℓ(x) < cut (see the input parameters jl_xmin_cut and Lmax_for_xmin set as default to 5 × 10-10 and 2000, respectively).

  • radial_order: if noted n, this fixes the number of sample points along one z direction, that is, Npts = 2n−1. The accuracy on the selection function as well as the CPU increase with n but we keep a O(n) complexity of the k-sampling (see Fig. 6);

  • chebyshev_order: if noted N, this fixes the degree d of the Chebyshev polynomial approximation of the fℓ(k,zi) and fℓ(k,zj) functions (Eq. (4)); that is, d = 2N. Keeping the same degree of approximation for both functions guarantees a power of 2 for the product approximation. Even if not mandatory, this helps in getting CPU performance for the DCT-I transform (using the FFTW library). When ℓmax increases it may be worth updating this parameter by 1 unit step. For ℓmax = 500chebyshev_order is set to 8 by default. Increasing the angular spectrum computation up to ℓmax = 1000 keeping this default value leads to absolute error of the order of 10-6 for Tests 1 and 2 and 5 × 10-10 for Test 3 and 4, then to get better accuracy in this case we use chebyshev_order = 9.

  • n_bessel_roots_per_interval: this is the number of Bessel roots qℓp used to define the bounds of the integral Iℓ(kpℓ,kp+1ℓ;ri,rj)\hbox{$I_\ell(k^\ell_p,k^\ell_{p+1};r_i,r_j)$} (Eq. (12)). By default it is set to 100. There is an interplay with the chebyshev_order parameter as a lower n_bessel_roots_per_interval value is coherent with a lower chebyshev_order.

  • total_weight_cut and deltaR_cut: these two threshold parameters are used to avoid unnecessary 3C algorithm processing (especially for the k-sampling of the fℓ(k,zi) or fℓ(k,zj) functions). So, we do not consider a couple (zi,zj) for which either the product wiwjW(zi,z1)W(zj,z2) is too low (total_weight_cut cut) or the radial distance | r(zi)−r(zj) | is too large to produce a sizeable contribution to the final Cℓ. The deltaR_cut cut is in Mpc units and is used in conjunction with has_deltaR_cut set to 1. These two threshold parameters depend on the use case under consideration and for preliminary tests we recommend to set both total_weight_cut and has_deltaR_cut to 0.

6. Summary and outlooks

We have set up a fast and generic software to compute the tomographic Cℓ(z1,z2) with redshift selection functions. Angpow is versatile enough to accept user-defined matter power spectrum P(k), transfer functions ˜Δℓ(k,z),\hbox{$\tilde{\Delta}_\ell(k,z),$} and cosmology. The code provides an accurate computation of the auto and cross-correlation power spectra, checked by comparison with other codes, which is fast enough to be included inside MCMC cosmology softwares. The rapidity of the software relies on the use of the 3C-algorithm, adapted to the computation of integrals over spherical Bessel functions, while other codes rely on the Limber’s approximation. We emphasize that the Limber’s approximation can lead to incorrect Cℓ(z1,z2), especially in the case of cross-correlations, as Limber’s Dirac functions cannot model the interferences between two spherical Bessel functions at different redshifts.

This code is thus fast and accurate enough to be used to test cosmological parameters, and perform tomographic analysis of the galaxy distribution. The definition of the ˜Δℓ(k,z)\hbox{$\tilde{\Delta}_\ell(k,z)$} function is general and can accept zero order function as ˜Δℓmat(k,z)\hbox{$\tilde{\Delta}^{\rm mat}_\ell(k,z)$}, but also relativistic corrections such as the redshift space distortions or the gravitational lensing; despite these corrections, it can also contain spherical Bessel functions (see e.g., Di Dio et al. 2013). Because Angpow provides the correct angular power spectra for cross-correlations, it can be a key tool to perform an integrated approach to cosmology, as advertised in Nicola et al. (2016). In particular, we propose this tool for deriving the auto- and cross-correlation angular power spectra for galaxy clustering, but also with angular power spectra from cosmic shear and the cosmological microwave background.

Angpow is publicly available3 and can be interfaced to other codes; a Python interface is foreseen. At the moment the code only accepts two redshift bins but soon it will be generalized to any number of bins. Feedback from Angpow users would be greatly accepted.

Acknowledgments

The authors want to thank M. Reinecke who kindly provided pieces of the code, and J. D. McEwen for fruitful discussion on the Chebyshev transform.

References

  1. Asorey, J., Crocce, M., Gaztañaga, E., & Lewis, A. 2012, MNRAS, 427, 1891 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asorey, J., Crocce, M., & Gaztañaga, E. 2014, MNRAS, 445, 2825 [NASA ADS] [CrossRef] [Google Scholar]
  3. Baszenski, G., & Tasche, M. 1997, Linear Algebra and its Application, 252, 1 [CrossRef] [Google Scholar]
  4. Blas, D., Lesgourgues, J., & Tram, T. 2011, JCAP, 2011, 034 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonvin, C., & Durrer, R. 2011, Phys. Rev. D, 84, 063505 [NASA ADS] [CrossRef] [Google Scholar]
  6. Carroll, S. M., Press, W. H., & Turner, E. L. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
  7. Di Dio, E., Montanari, F., Lesgourgues, J., & Durrer, R. 2013, JCAP, 11, 044 [CrossRef] [Google Scholar]
  8. Di Dio, E., Montanari, F., Durrer, R., & Lesgourgues, J. 2014, JCAP, 1, 042 [CrossRef] [Google Scholar]
  9. Feldman, H. A., Kaiser, N., & Peacock, J. A. 1994, ApJ, 426, 23 [NASA ADS] [CrossRef] [Google Scholar]
  10. Frigo, M., & Johnson, S. G. 2005, special issue on “Program Generation, Optimization, and Platform Adaptation, Proc. IEEE, 93, 216 [Google Scholar]
  11. Giorgi, P. 2012, IEEE Trans. Comput., 61, 780 [CrossRef] [Google Scholar]
  12. Glasser, M. L., & Montaldi, E. 1993, ArXiv e-prints [arXiv:math/9307213] [Google Scholar]
  13. Ivezic, Z., Tyson, J. A., Abel, B., et al. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
  14. Lahav, O., Lilje, P. B., Primack, J. R., & Rees, M. J. 1991, MNRAS, 251, 128 [NASA ADS] [CrossRef] [Google Scholar]
  15. Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lanusse, F., Rassat, A., & Starck, J.-L. 2015, A&A, 578, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
  18. Laurie, D. P. 1997, Math. Comput., 466, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  19. Levi, M., Bebek, C., Beers, T., et al. 2013, ArXiv e-prints [arXiv:1308.0847] [Google Scholar]
  20. Loverde, M., & Afshordi, N. 2008, Phys. Rev. D, 78, 123506 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lucas, S., & Stone, H. 1995, J. Comput. Appl. Math., 64, 217 [CrossRef] [Google Scholar]
  22. Nicola, A., Refregier, A., Amara, A., & Paranjape, A. 2014, Phys. Rev. D, 90, 063515 [NASA ADS] [CrossRef] [Google Scholar]
  23. Nicola, A., Refregier, A., & Amara, A. 2016, Phys. Rev. D, 94, 083517 [NASA ADS] [CrossRef] [Google Scholar]
  24. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C, 2nd edn.: The Art of Scientific Computing (New York: Cambridge University Press) [Google Scholar]
  25. Waldvogel, J. 2006, BIT Numerical Mathematics, 46, 195 [CrossRef] [Google Scholar]
  26. Weinberg, D. H., Mortonson, M. J., Eisenstein, D. J., et al. 2013, Phys. Rep., 530, 87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  27. Wolfram Research Inc. 2016, Mathematica 11.0, Champaign, Illinois, USA [Google Scholar]

Appendix A: Clenshaw-Curtis-Chebyshev algorithm (3C-algorithm)

Each integral type of Eq. (12)involves the product of “highly” oscillatory functions. The purpose of this section is not to provide a review of all the integration methods used in the different fields of physics to tackle such a difficult task. To focus on our case, where we have to deal with (at least) the product of spherical Bessel functions, the authors point out that the reader may find either specific integral solving rules as in Glasser & Montaldi (1993) or general methods as in Lucas & Stone (1995). However we need a precise and also very fast method. We cannot rely on methods that solve the problem of a product of spherical Bessel functions multiplied by a regular function. In fact, both the primordial power spectrum and the extension beyond the matter density ˜Δmat.(z,k)\hbox{$\tilde{\Delta}^{\mrm{mat.}}(z,k)$} may show oscillation features in the form of derivative of spherical Bessel functions. So, we have searched and found a general method that meets our requirements of precision and speed.

Equation (12)is a special case of the following generic integral after a proper change of variable I=∫-11 dxf(x)g(x).\appendix \setcounter{section}{1} \begin{equation} I = \int_{-1}^1 \dx x f(x) g(x). \end{equation}(A.1)To get an approximate value of this integral, we use in this section the Clenshaw-Curtis quadrature at order Ncc (noting h = f × g): I≈∑k=0Nccwkf(xk)g(xk)=∑k=0Nccwkh(xk),\appendix \setcounter{section}{1} \begin{equation} I \approx \sum_{k=0}^{N_{\mrm{cc}}} w_k f(x_k)g_(x_k) = \sum_{k=0}^{N_{\mrm{cc}}} w_k h(x_k) \label{eq-CC-productInt} , \end{equation}(A.2)where the sampling points are defined as xk = coskπ/Ncc (k = 0,...,Ncc) and the corresponding weights wk are addressed later in the section. But, if the functions f and g have a highly oscillatory behavior, one needs, in principle, to use large values of Ncc to reach a sufficient accuracy level. In that case, dealing with the above sum may not be computationally efficient. The idea is then to use Chebyshev series to approximate both functions f and g. Then, one performs the product of both Chebyshev series, which is also a Chebyshev series but with a higher order, and finally one uses a fast Clenshaw-Curtis weights computation to perform the last weighted sum. We briefly describe those steps leaving the details of the demonstration that the interested reader can find in Baszenski & Tasche (1997).

Let fN be a polynomial approximation of f of degree N−1. We expend fN onto the following basis of the first kind of Chebyshev polynomials { Tn;n = 0,...,N−1 } which have the property Tn(cosθ) = cosnθ: fN(x)=a02+∑k=1N−1akTk(x).\appendix \setcounter{section}{1} \begin{eqnarray} f_N(x) = \frac{a_0}{2}+\sum_{k=1}^{N-1} a_k T_k(x). \end{eqnarray}(A.3)To determine the ak coefficients one uses the following sampling vector f(N)=(f(tμ(N)))T with tμ(N)≡cosμπN;μ=0,...,N,\appendix \setcounter{section}{1} \begin{equation} \mbb{f}^{(N)} =( f( t_\mu^{(N)}))^T\qquad \mrm{with} \qquad t_\mu^{(N)} \equiv \cos \frac{\mu \pi}{N};\; \mu=0,\dots,N , \end{equation}(A.4)of length N + 1 and related to the vector a(N) = (a0,...,aN−1,0)T by the linear algebra relation a(N)=2NCNI f(N),\appendix \setcounter{section}{1} \begin{equation} \mbb{a}^{(N)} = \frac{2}{N}\mbb{C}^I_N\, \mbb{f}^{(N)} \label{eq-aCoeff} , \end{equation}(A.5)with CNI\hbox{$\mbb{C}^I_N$} being a discrete cosine transform of type-I (DCT-I) matrix of dimension (N + 1)2. Similarly, we note gM a polynomial approximation of g of degree M−1 from which we determine the sampling vector g(M) using the sample points tμ(M)\hbox{$t_\mu^{(M)}$}. The coefficient vector b(M) = (b0,...,bM−1,0)T is related to g(M) using a relation similar to Eq. (A.5), namely b(M)=2MCMI g(M).\appendix \setcounter{section}{1} \begin{equation} \mbb{b}^{(M)} = \frac{2}{M}\mbb{C}^I_M\, \mbb{g}^{(M)}. \label{eq-bCoeff} \end{equation}(A.6)By combining the polynomial approximations fN and gM, the function h is then approximated by a Chebyshev series of degree N + M−2 with coefficient vector c(P) of length P + 1 with P ≥ N + M−1. Using a relation of type Eq. (A.5), the vector c(P) is related to the sampling vector h(P)=(h(tμ(P)))T;μ=0,...,P.\appendix \setcounter{section}{1} \begin{equation} \mbb{h}^{(P)} = \left(h\left(t_\mu^{(P)}\right)\right)^T;\; \mu=0,\dots,P. \end{equation}(A.7)To get h(P) it is not necessary to compute c(P) and proceed to an inversion of a DCT-I matrix. The key point is that if we note ⊙ , the component-wise multiplication, one has h(P)=f(P)⊙g(P).\appendix \setcounter{section}{1} \begin{equation} \mbb{h}^{(P)} = \mbb{f}^{(P)} \odot \mbb{g}^{(P)} . \end{equation}(A.8)Moreover, f(P) (g(P)) is obtained from a(N) (b(M)) of length N + 1 (M + 1) by an extension to a larger vector at least of length N + M noted ˜a(P)\hbox{$\tilde{\mbb{a}}^{(P)}$} (˜b(P)\hbox{$\tilde{\mbb{b}}^{(P)}$}) by appending with zeros: ˜a(P)=(a(N),0,...,0),˜b(P)=(b(M),0,...,0).\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{\mbb{a}}^{(P)} &=& (\mbb{a}^{(N)}, 0, \dots, 0), \nonumber \\ \tilde{\mbb{b}}^{(P)} &=& (\mbb{b}^{(M)}, 0, \dots, 0). \end{eqnarray}(A.9)Then, the sampling vector used in Eq. (A.2)where one identifies Ncc = P is determined by h(Ncc)=(CNccI ˜a(Ncc))⊙(CNccI ˜b(Ncc)),\appendix \setcounter{section}{1} \begin{equation} \mbb{h}^{(N_{\mrm{cc}})} = \left(\mbb{C}^I_{N_{\mrm{cc}}}\, \tilde{\mbb{a}}^{(N_{\mrm{cc}})}\right) \odot \left(\mbb{C}^I_{N_{\mrm{cc}}}\, \tilde{\mbb{b}}^{(N_{\mrm{cc}})}\right) \label{eq-hSample} , \end{equation}(A.10)using CNccI\hbox{$\mbb{C}^I_{N_{\mrm{cc}}}$} the DCT-I matrix of dimension (Ncc + 1)2 and the inversion property (CPI)-1=(2/P)CPI\hbox{$(\mbb{C}^I_P)^{-1}=(2/P) \mbb{C}^I_P$}. In some sense, for both f and g approximation sampling vectors, we have performed a Chebyshev basis change to a larger parameter space compatible with the polynomial degree involved in the product f(N) × g(M).

The second key point is that the Clenshaw-Curtis weights associated to h(Ncc) in Eq. (A.2)can also be computed with a DCT-I transform from the vector (2 /Ncc)(1,0,−1/3,0,−1/15,...,((−1)k + 1)/2(1−k2),... ) of length Ncc + 1 (Waldvogel 2006) (the normalization depends on the exact definition of the DCT-I used).

So, to perform the integral given by Eq. (A.2), one needs 4 + 1 DCT-I transforms, 1 for the Clenshaw-Curtis weights and 4 to transform the Chebyshev coefficients vectors. The DCT-I transform may be implemented using O(nlog n) efficient algorithm, for example, the FFTW library (Frigo & Johnson 2005) used by Angpow. Angpow uses a power of 2 for N, M, and also P (keeping P ≥ N + M−1) for a fast implementation. The 3C-algorithm is a special case of a more general class of algorithms dealing with the product of polynomials. We note that according to reference (Giorgi 2012) an even faster algorithm (although moderate) might be implemented in a future version of Angpow if necessary. We note finally that this general method can be applied to use cases beyond the power spectrum computation in other fields of interest.

All Tables

Table 1

Wall time (in seconds) measured at CCIN2P3 (on Intel Xeon CPU E5-2640 v3 processors) for the test benches described in the text, according to the number of OpenMP threads used.

In the text

All Figures

thumbnail Fig. 1

Comparison of the computations of the Cℓδ(z=1)\hbox{$C_\ell^{\delta}(z=1)$} given by Angpow, Mathematica, and CLASSgal for a Dirac selection function with kmax = 10 Mpc-1.
In the text
thumbnail Fig. 2

Computations of Clδ(z)\hbox{$C_l^{\delta}(z)$} with Dirac selections centered at z ∈ {0.85,1.00,1.15} with Angpow alone and Clthick(z)\hbox{$C_l^{\mrm{thick}}(z)$} with Angpow and CLASSgal using a Gaussian selection function with mean z = 1, a width of σ = 0.3, and a redshift cut at ± 5σ (in all cases kmax = 0.44 Mpc-1). For Angpow we use the power spectrum produced by CLASSgal and we have varied the redshift grid sampling resolution from 9 × 9 to 159 × 159 points to reach the converged result (blue curve) in good agreement with the CLASSgal result (cyan points). Comparing the Clδ(z=1)\hbox{$C_l^{\delta}(z=1)$} to the Clthick(z=1,σ=0.3)\hbox{$C_l^{\mrm{thick}}(z=1,\sigma=0.3)$} results we measure the effect of self-cross-correlation inside a thick redshift shell which washes out the matter fluctuation contrast.
In the text
thumbnail Fig. 3

Comparison between Angpow (red/orange points) and CLASSgal (black points) for several cross-correlation spectra with Gaussian (σ = 0.01) selection and kmax = 1 Mpc-1. The orange points are used to emphasize negative Cℓ.
In the text
thumbnail Fig. 4

Comparison of the computations of the Cℓthick(z)\hbox{$C_\ell^\mrm{thick}(z)$} given by Angpow and CLASSgal either with the Limber’s approximation or the exact computation.
In the text
thumbnail Fig. 5

Cross-correlations in real space corresponding to the spectra shown on Fig. 3. The points show where the function was evaluated.

In the text
thumbnail Fig. 6

Evolution of the wall time with respect to the width of the selection function (σ) illustrated in the condition of Test 3 and using 16 threads. In the upper scale of the frame is shown an indication of the radial_order used to sample the along the z direction for a given σ (see Sect. 5).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.