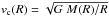| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201628319 | |
| Published online | 22 March 2017 | |
Forming disk galaxies in major mergers
II. The central mass concentration problem and a comparison of GADGET3 with GIZMO
Aix-Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, UMR 7326, 13388 Marseille, France
e-mail: sergey.rodionov@lam.fr
Received: 16 February 2016
Accepted: 28 December 2016
Context. In a series of papers, we study the major merger of two disk galaxies in order to establish whether or not such a merger can produce a disk galaxy.
Aims. Our aim here is to describe in detail the technical aspects of our numerical experiments.
Methods. We discuss the initial conditions of our major merger, which consist of two protogalaxies on a collision orbit. We show that such merger simulations can produce a non-realistic central mass concentration, and we propose simple, parametric, active galactic nuclei (AGN)-like feedback as a solution to this problem. Our AGN-like feedback algorithm is very simple: at each time-step we take all particles whose local volume density is above a given threshold value and increase their temperature to a preset value. We also compare the GADGET3 and GIZMO codes, by applying both of them to the same initial conditions.
Results. We show that the evolution of isolated protogalaxies resembles the evolution of disk galaxies, thus arguing that our protogalaxies are well suited for our merger simulations. We demonstrate that the problem with the unphysical central mass concentration in our merger simulations is further aggravated when we increase the resolution. We show that our AGN-like feedback removes this non-physical central mass concentration, and thus allows the formation of realistic bars. Note that our AGN-like feedback mainly affects the central region of a model, without significantly modifying the rest of the galaxy. We demonstrate that, in the context of our kind of simulation, GADGET3 gives results which are very similar to those obtained with the PSPH (density independent SPH) flavor of GIZMO. Moreover, in the examples we tried, the differences between the results of the two flavors of GIZMO – namely PSPH, and MFM (mesh-less algorithm) – are similar to and, in some comparisons, larger than the differences between the results of GADGET3 and PSPH.
Key words: Galaxy: kinematics and dynamics / methods: numerical
© ESO, 2017
1. Introduction
A number of observational works have argued that a large fraction of present-day spiral galaxies have experienced a major merger event during the last 8 Gyr (e.g., Hammer et al. 2005, 2009a,b; Puech et al. 2012). This has motivated a number of numerical simulations modeling the merging and its remnant. However, most dynamical simulations of major mergers between two spiral galaxies made so far have initial conditions where each galaxy has the properties of nearby disk galaxies, with, in the best cases, an enhanced gas fraction to mimic disk galaxies at intermediate redshifts (Barnes 2002; Springel & Hernquist 2005; Cox et al. 2006; Hopkins et al. 2009, 2013; Lotz et al. 2010; Wang et al. 2012; Borlaff et al. 2014; Querejeta et al. 2015; Governato et al. 2009). Merger remnants from such simulations have, in general, a B/T (bulge to total stellar mass) ratio that is too high to adequately represent spiral galaxies. This can be easily explained assuming that a disk can be formed only from the gas that survived the merger (Hopkins et al. 2009). In order to have a small B/T ratio, it is necessary that a large fraction of gas survives the merger event. For example, in the most favorable case of 100% gaseous progenitors, for B/T ~ 0.3, at least 70% of the gas must survive the merger. But this is relatively difficult to accomplish if all the gas is initially in the disk. The surface density of the gas in such gas-rich progenitors is high, so if we simply adopt the Kennicutt-Schmidt law, we find that the star-formation efficiency will be great (i.e., the gas consumption time-scale will be small). Moreover, star formation will be strongly enhanced during the merger event (Larson & Tinsley 1978). As a consequence, a significant fraction of the gas will not survive the merging, and will turn into stars before its end, which will lead to high B/T fraction.
In Athanassoula et al. (2016, hereafter A16), we proposed a more realistic setup for the dynamical study of a major merger event between two spiral galaxies, introducing gas in the form of a gaseous halo, existent in each of the protogalaxies. We thus collide not a couple of fully evolved local spiral galaxies, but a couple of protogalaxies, consisting of only dark matter and gas halos. Each protogalaxy, after 1–2 Gyr of evolution in isolation, resembles an intermediate-redshift disk galaxy, while after 8–10 Gyr of evolution, it resembles a present-day spiral galaxy (see A16 and Appendix A). In the current article, the second of a series, we discuss in detail the technical aspects of our numerical experiments. In Sect. 2, we describe the initial conditions for our simulations, while in Appendix A we discuss the evolution of individual protogalaxies in isolation. In Sect. 3, we demonstrate why we need active galactic nuclei (AGN)-like feedback in our models, describe the adopted feedback, and test it. In Sect. 4, we compare results of our simulations calculated using either GADGET3 or GIZMO codes. We conclude in Sect. 5.
2. Simulations
2.1. Initial conditions
2.1.1. Individual protogalaxies
In all our simulations, individual protogalaxies are initially spherical and composed of a dark matter (DM) halo and a gaseous halo, of masses MDM and Mgas, respectively. Stars do not exist in the initial conditions, but form during the evolution. To within a multiplicative constant, the type of functional form for the density of both the DM and the gaseous halo is 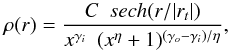 (1)where r is the spherical radius, x = r/rs, and rs and rt are characteristic radii of the halo that can be considered as measures of the scale length and the tapering radius, respectively. The constants γi, γo, and η characterize the radial density profile and C is a global multiplicative constant to set the total mass to the desired value. For the DM, in this article, we use γi = 1, γo = 3, and η = 1, which corresponds, up to the truncation, to Navarro-Frenk-White (NFW) models (Navarro et al. 1996, 1997). For the gas, we have γi = 0, γo = 2, and η = 2 (Beta model for β = 2/3, e.g., Miller & Bregman 2015, and references therein). All parameters for each model discussed here can be found in Appendix B.
(1)where r is the spherical radius, x = r/rs, and rs and rt are characteristic radii of the halo that can be considered as measures of the scale length and the tapering radius, respectively. The constants γi, γo, and η characterize the radial density profile and C is a global multiplicative constant to set the total mass to the desired value. For the DM, in this article, we use γi = 1, γo = 3, and η = 1, which corresponds, up to the truncation, to Navarro-Frenk-White (NFW) models (Navarro et al. 1996, 1997). For the gas, we have γi = 0, γo = 2, and η = 2 (Beta model for β = 2/3, e.g., Miller & Bregman 2015, and references therein). All parameters for each model discussed here can be found in Appendix B.
The halo component was built as a spherical isotropic system in equilibrium with the total potential including gas, using the distribution function technique (Binney & Tremaine 2008, Sect. 4.3). For this, we used the program mkhalo written by W. Dehnen (McMillan & Dehnen 2007), which is part of the NEMO tool box (Teuben 1995). We also have the possibility to add a spin to the halo. The fraction of particles with a positive sense of rotation is given by the parameter fpos. In cases with no net rotation fpos = 0.5, while if all particles rotate in the positive (negative) sense this parameter is equal to 1 (–1).
The gaseous component was constructed as follows. For each gas particle, all velocities except the tangential velocity vφ were set to zero. The tangential velocity was set to the value of 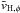 , the mean tangential velocity in the halo at the location of the gas particle. This value can be calculated directly from the distribution function of the halo. First, at a given spherical radius r, we calculate
, the mean tangential velocity in the halo at the location of the gas particle. This value can be calculated directly from the distribution function of the halo. First, at a given spherical radius r, we calculate  , the mean of the module of the velocity vector.
, the mean of the module of the velocity vector. 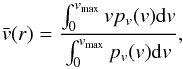 (2)where
(2)where 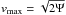 is the maximal velocity at a given radius r, Ψ is the negative of the total gravitational potential at a given radius, pv(v) ~ v2DF(Ψ(r)−v2/ 2) is the probability density of v at a given radius and DF is the distribution function (Binney & Tremaine 2008, Sect. 4.3). It is easy to prove that in 3D space, if we start from an isotropic system and add rotation by changing the fraction of particles with positive and negative sense of rotation (by introducing fpos), the mean of the tangential velocity
is the maximal velocity at a given radius r, Ψ is the negative of the total gravitational potential at a given radius, pv(v) ~ v2DF(Ψ(r)−v2/ 2) is the probability density of v at a given radius and DF is the distribution function (Binney & Tremaine 2008, Sect. 4.3). It is easy to prove that in 3D space, if we start from an isotropic system and add rotation by changing the fraction of particles with positive and negative sense of rotation (by introducing fpos), the mean of the tangential velocity  .
.
It would have been possible to add spin to the system in a different way. For example fpos in the halo does not have to be constant and could be set as a function fpos(R,z), where R is the cylindrical radius. Also, rotation in the gas could be set as completely independent of the rotation in the halo.
The internal energy of each gaseous particle is calculated so that it is in hydrostatic equilibrium in the halo + gas potential, taking into account the spin, if it exists. In the case without rotation, from the condition of hydrostatic equilibrium and assuming that the pressure is zero at infinity, we have: 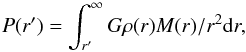 (3)where M(r) is the total mass inside a sphere with radius r, and ρ(r) and P(r) are the density and pressure, respectively, of the gas at a given radius. From the pressure, assuming the condition of ideal gas, we can calculate the specific internal energy u = P/ (ρ (γ−1)), where γ is the adiabatic index (in all our simulations, we set γ = 5/3, which corresponds to mono-atomic gas).
(3)where M(r) is the total mass inside a sphere with radius r, and ρ(r) and P(r) are the density and pressure, respectively, of the gas at a given radius. From the pressure, assuming the condition of ideal gas, we can calculate the specific internal energy u = P/ (ρ (γ−1)), where γ is the adiabatic index (in all our simulations, we set γ = 5/3, which corresponds to mono-atomic gas).
Whenever present, the spin is taken into account using the following simple approximation. We derive the thermal energy in the polar regions up from Eq. (3), and calculate the thermal energy in the equatorial region ue from the pressure: 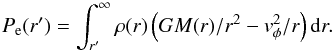 (4)We interpolate the thermal energy as, u = kup + (1−k)ue, where k = | θ | /(π/ 2), and θ is the angle between a given direction and the equatorial plane. However, we should note that in all models considered here, the correction for the spin is almost negligible and it would be enough to use Eq. (3) without any corrections.
(4)We interpolate the thermal energy as, u = kup + (1−k)ue, where k = | θ | /(π/ 2), and θ is the angle between a given direction and the equatorial plane. However, we should note that in all models considered here, the correction for the spin is almost negligible and it would be enough to use Eq. (3) without any corrections.
Models constructed in such a way are in equilibrium if the gas is adiabatic (i.e., without cooling and feedback). During the runs, however, the gas will cool radiatively and, getting out of equilibrium, fall inwards. In Appendix A we discuss the evolution of such protogalaxies in detail.
2.1.2. Collisions
In all cases considered here, we have mergers between two equal-mass galaxies. However, cases with unequal galaxies can be easily created in our framework, and they will be discussed in following articles.
Each of the two protogalaxies is initially created with Z as rotation axis. After that, they can be arbitrary orientated, which, in general, gives us two Euler angles per protogalaxy. Let the plane of the collisional orbit be the X−Y plane. We describe this orbit by an initial separation in phase space x0, y0, vx,0, vy,0. In some cases, we choose the initial separation from a two-body problem (assuming that all the mass of the protogalaxies is concentrated in two points), setting the desired orbit eccentricity, initial separation, and distance in pericenter. See all the parameters of the models discussed here in Appendix B.
2.2. Code
We use a version of GADGET3 including gas and its physics (Springel 2005). The stars and the dark matter are followed by N-body particles and gravity is calculated with a tree code. The code uses an improved SPH method (Springel & Hernquist 2002) and sub-grid physics (Springel & Hernquist 2003). We use the same parameters for the sub-grid physics as Springel & Hernquist (2003), which were calibrated with Kennicutt’s law (Kennicutt 1998).
Except for test simulations, we use a softening length of 25 pc for the gas and stars and of 50 pc for the halo, a 0.005 relative accuracy of the force, and the GADGET opening criterion 1, that is, a relative criterion that tries to limit the absolute truncation error of the multiple expansion for every particle-cell interaction1. We also use the GADGET system of units; that is, the unit of length is 1 kpc, the unit of mass is 1010M⊙, and the unit of velocity is 1 km s-1. We continued all simulations up to 10 Gyr.
3. Central mass concentration in merger models
3.1. Models without AGN-like feedback
3.1.1. The central mass concentration problem
As shown in A16 and the following papers, our simulations can make galaxies whose properties are generally in good agreement with those of real galaxies. Such comparisons include face-on and edge-on morphologies, radial density profiles, finding type II profiles with inner and outer disk scale lengths, and break radii in good agreement with those observed, etc. We also find good agreement with observations for vertical density profiles and thick disk properties, as well as for a number of kinematic properties. In particular, their rotation curves are flat, as observed by Bosma (1981).
 |
Fig. 1 Central part of the circular velocity profiles for models mdf018 (high resolution model), mdf225 (low resolution model), and mdf214 (low resolution models with two times bigger softening) at times 2.5, 5, 7.5, and 10 Gyr. This is calculated from the total mass distribution, assuming spherical symmetry. |
However, our models without AGN feedback have one notable problem, concerning the very central part of the disk. During the collision, the models form an extremely dense, and, as we discuss below, non-realistic central mass concentration (CMC). This central mass concentration can be better seen on the circular velocity profile vc(R)2.
Let us consider a typical example of a model without AGN: mdf018. All parameters of this model can be found in Appendix B. This model is the non-AGN analog of mdf732, which was thoroughly analyzed in A16. In Fig. 1 (red line), we show the central part of the vc(R) profiles at different times for mdf018. At t = 2.5 Gyr, that is, approximately 1 Gyr after the merger, the central bump on vc(R) is very high, and reaches almost 360 km s-1 (see Fig. 1).
The strong central peak on vc(R) is unrealistic by itself. The circular velocity curves of the models can be compared with observed HI or Hα rotation curves. Central bumps on rotation curves may appear in real galaxies, but are considerably smaller (e.g., Sofue et al. 1999). Another problem with the strong central peaks on vc(R) concerns bars. Our simulations show that such a strong central peak stops, or delays beyond 10 Gyr, the formation of a bar (see also A16), while approximately two thirds of disk galaxies have bars (Buta et al. 2015). Bumps of similar size did also appear in cosmological simulations until relatively recently, but have been lately strongly diminished by increasing the feedback (see Brooks & Christensen 2016, for a review). We will follow a similar route (see Sect. 3.2), but before doing so, we would like to continue the discussion of CMCs in a model without an AGN.
3.1.2. Demise of the CMC in low-resolution models
In Fig. 1, we can see that during the evolution, the central bump on the vc(R) profile in mdf018 becomes less and less prominent with time, and at t = 10 Gyr it has only a maximum of 260 km s-1. One can suggest that this is due to two-body relaxation (Binney & Tremaine 2008). In order to demonstrate this, we consider two low-resolution test models, each with ten times less particles than mdf018 (see Appendix B). One model (mdf225) has the same gravitational softening as mdf018: 50 pc for the halo, and 25 pc for gas and stars. The other model (mdf214) has double this softening: 100 pc for the halo, and 50 pc for gas and stars. All parameters, except the number of particles and the softening lengths, are identical to those of mdf018. Low-resolution models with the same gravitational softening (mdf225) at t = 2.5 Gyr have a central peak on vc(R) with almost the same maximum as in the high-resolution model mdf018 (see Fig. 1, green line). Nevertheless, during the evolution, the central bump decreases much faster than in mdf018, and by t = 10 Gyr, the low resolution model mdf225 has no central bump on vc(R) at all. This fits well with the fact that the relaxation time is smaller for a smaller number of particles. Low-resolution models with a softening twice as big (mdf214), at t = 2.5 Gyr, have a central peak significantly less pronounced on vc(R), which is expected due to the decreased spacial resolution. During the evolution, however, the central bump on vc(R) decreases slower than in low-resolution simulations with a smaller softening (mdf225), which is also expected, because the relaxation time is bigger for a bigger softening (Athanassoula et al. 2001; Rodionov & Sotnikova 2005). This analysis argues that the lowering of the central peak on vc(R) in the high-resolution model mdf018 is due, at least partly, to the two-body relaxation.
As a result, we can expect that higher-resolution simulations, namely with a greater number of particles and smaller softening, will make the problem with CMC even worse, because a smaller softening will make the peak on vc(R) higher, and a bigger number of particles will prevent its attenuation with time. On the other hand, smaller resolution spuriously diminishes the problem (see Fig. 1, for two low-resolution models, mdf214 and mdf225). This means that, in sufficiently low-resolution models, one will not have problems with a non-realistic CMC. Of course, decreasing the resolution cannot be considered as a solution to the high central concentration problem.
3.2. AGN-like feedback. How we will proceed
One could expect that adding AGN feedback would solve, or at least alleviate, the problem with the central peak in the circular velocity profile. However, an AGN is not trivial to model. There are inherent difficulties in understanding both the accretion into the central black hole (BH; Hopkins & Quataert 2010) and the subsequent energetic feedback (King 2003; Wurster & Thacker 2013). Moreover, we obviously do not have enough resolution to model these two processes directly.
Nevertheless, there are several AGN feedback algorithms (see, for example, a comparative study of Wurster & Thacker 2013, and papers by Dubois et al. 2010; Blecha et al. 2013; Volonteri et al. 2015; Gabor et al. 2016). Usually, such algorithms include the explicit calculation of the accretion onto the black hole (thus the evolution of the mass of the black hole), its movement (advection), and the merging of black holes in cases of collisional simulations. But here we propose a much simpler and less ambitious approach. We do not aim to calculate the evolution of the super-massive black holes; we only want to remove non-physical central mass concentrations in our models by adding physically motivated feedback. One way to proceed in such a situation is to introduce some kind of subgrid-physics model and “calibrate” it with observations.
 |
Fig. 2 Comparison of various radial profiles for the stellar component of five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3), and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), all at t = 10 Gyr. From left to right and top to bottom: surface density, median of the absolute value of z, which is a good approximation for thickness (Sotnikova & Rodionov 2006), mean value of the azimuthal velocity and radial velocity dispersion. The inlay in the upper left panel shows the surface density in the innermost region (within 3 kpc). |
Our intent was to include, in our model, a simple, parametric, AGN-like feedback with the following properties:
-
Being simple.
-
Being able to solve the problem with the central peak in the circular velocity profile.
-
Allowing the formation of a bar.
-
Being physically plausible, thus injecting a reasonable amount of energy in the central region of the galaxy.
-
Influencing mainly the central region of the model.
The last point requires some explanation. It is commonly believed that AGN feedback could be quite strong and, presumably, be able to significantly quench star formation in the entire galaxy (Springel et al. 2005; Di Matteo et al. 2005; Bundy et al. 2008), thereby influencing more than just the central region of the galaxy. However, as we mentioned before, there are a lot of fundamental difficulties in proper modeling of AGN feedback. So, if we include an AGN-feedback that modifies the entire galaxy in our model, we will need to calibrate it with some observations, which is not trivial. Because of this, we have decided that it would be reasonable, as a first step, to include an AGN-like feedback that mainly influences the central region of the model, and barely affects the outer parts.
3.3. Description of our AGN-like feedback
Our AGN-like feedback is based on two parameters: a volume density threshold ρAGN, and a temperature TAGN. More specifically, at every time step, we give internal energy to the gas particles whose local volume density is larger than the threshold ρAGN, by increasing their temperature to TAGN. The density threshold is chosen so as to ensure that the particles are located in the center-most region.
In our algorithm, we do not have a single particle representing the black hole, so we do not directly follow the mass of the BH. We can, however, calculate the BH mass from the feedback energy by, in some sense, inverting the formalism described in Springel et al. (2005). We take the same value as Springel et al. (2005) for the radiative efficiency of the BH, ϵr = 0.1, and the fraction of radiative luminosity ϵf = 0.05, which can couple thermally to the surrounding gas. Consequently: 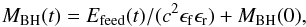 (5)where MBH(t) is the BH mass at a given time t, and Efeed(t) is the cumulated feedback energy up to time t. We stress that in the basic version of our feedback algorithm (without Eddington limit), we do not need to know MBH in the algorithm itself.
(5)where MBH(t) is the BH mass at a given time t, and Efeed(t) is the cumulated feedback energy up to time t. We stress that in the basic version of our feedback algorithm (without Eddington limit), we do not need to know MBH in the algorithm itself.
The Eddington limit can be added as an option. It requires three new free parameters: ϵr, ϵf, and MBH(0). Knowing MBH(t), we can calculate the Eddington luminosity as: 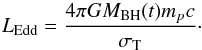 (6)From this, we can calculate the energy available for the feedback for the current time-step dt as EEdd = LEdd·dt·ϵf. We then calculate Ereq, the energy required to heat all particles with ρ>ρAGN up to a temperature of TAGN. If Ereq>EEdd, we heat particles with a probability p = EEdd/Ereq. This way, we statistically obey the Eddington limit. For further discussion of the Eddington limit see Sect. 3.5.
(6)From this, we can calculate the energy available for the feedback for the current time-step dt as EEdd = LEdd·dt·ϵf. We then calculate Ereq, the energy required to heat all particles with ρ>ρAGN up to a temperature of TAGN. If Ereq>EEdd, we heat particles with a probability p = EEdd/Ereq. This way, we statistically obey the Eddington limit. For further discussion of the Eddington limit see Sect. 3.5.
3.4. Models with and without AGN-like feedback
Here we compare five models; all of them have identical parameters, except for the AGN-like feedback parameters;
-
mdf018: Model without AGN-like feedback
-
mdf789: TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3;
-
mdf732: TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3;
-
mdf788: TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3;
-
mdf791: TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3.
The remaining parameters are given in Appendix B.
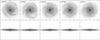 |
Fig. 3 Face-on (upper row) and edge-on (lower row) views of the stars component for five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3), and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), from left to right, respectively, and all at t = 10 Gyr. The size of each square box corresponds to 50 kpc. |
 |
Fig. 4 Circular velocity profiles for five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3) and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), at 5 (left) and 10 (right panel) Gyr. |
At t = 10 Gyr, all these models are very similar. Their radial surface density profiles are virtually identical, except for the innermost region where models with no or weak feedback (mdf018, mdf789, and mdf791) have a steeper cusp than the others (Fig. 2). It is the extra density in their cusps that is responsible for the steep maximum in the circular velocity curve, already discussed in Sect. 3.1.1. Kinematic profiles including the mean azimuthal velocity and the radial velocity dispersion profiles are also very similar (Fig. 2). However, comparing face-on views, we see differences in morphology (Fig. 3). Despite the fact that azimuthally averaged profiles are very similar, in the outer part of the models, we can see relatively strong differences in the shape of the spiral structure. These differences are partly due to the transient nature of the spirals, but we can not exclude that they are also partly due to differences in the central part. Anyway, the spiral structure has often been referred to as “the frosting on the cake”. Below, we will discuss the central part of the models.
 |
Fig. 5 Comparison of circular velocity profiles (at 5 and 10 Gyr) for models with and without Eddington limits. The upper row shows two models with Eddington limit (mdf732 TAGN = 1 × 107 K and mdf751 TAGN = 1.5 × 107 K) and one model without Eddigton limit (mdf726 TAGN = 1 × 107 K). The lower panels also display three models: two with Eddigtion limit (mdf737 TAGN = 2 × 107 K, and mdf780 TAGN = 2.5 × 107 K) and one model without (mdf730 TAGN = 2 × 107 K). |
First, let us analyze the model without AGN (mdf018). As already discussed in Sect. 3.1.1, during the collision, an extremely dense and presumably non-realistic CMC is created. This can be better seen on the circular velocity profile (vc(R)) and is very prominent at t = 5 Gyr (see Fig. 4 for the model without AGN, mdf018). At t = 10 Gyr, this peak is less prominent, which could partly be due to the numerical two-body relaxation, but a part of it, albeit small, could perhaps also reflect true two-body relaxation, as in globular clusters. Because of this strong central mass concentration, we do not have a bar in this model (model mdf018, without AGN, see Fig. 3).
Let us now consider a sequence of models with fixed ρAGN, and increasing TAGN: mdf789 (TAGN = 5 × 106 K), mdf732 (TAGN = 1 × 107 K), and mdf788 (TAGN = 2 × 107 K). This can be considered as a sequence with increasing feedback strength. The weak AGN in mdf789 (TAGN = 5 × 106 K) manages to only partly remove the very dense CMC (see Fig. 4, t = 5 Gyr), which, however, is still relatively prominent, and at t = 10 Gyr, the vc profile is similar to that of mdf018 (Fig. 4, t = 10 Gyr). At this time, we do have a bar, but it is quite small, with a semi-major axis of approximately 1.5 kpc at 10 Gyr (see Fig. 3 for mdf789). In mdf732, we increase TAGN to 107 K, and in this model, the central bump on the vc profile is much less prominent, which allows the formation of a bigger bar with a semi-major axis of approximately 3 kpc (see Figs. 4 and 3 for mdf732). A further increase of TAGN to 2 × 107 in mdf788 fully removes the central bump on vc, but the bar size in this model is similar to mdf732 (TAGN = 1 × 107 K). We must note that one can expect the relation between the bar and the AGN to be more complicated than a simple linear correlation, and that a strong AGN, by shuffling material in the central region, could, in some cases, delay or even prevent the formation of a bar (the analysis of this subject is beyond the scope of this article). We note that mdf732 is one of our reference models and was thoroughly analyzed in A16.
Our last model to compare is mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), which is similar to mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), but has a ρAGN twice as high as the others. We can see that by increasing ρAGN, we decrease the efficiency of the AGN and make this model very similar to mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3, see Figs. 3 and 4). This can be easily understood because an increase in ρAGN means that fewer particles will have their thermal energy increased and thereby the total feedback will be smaller.
The vertical thickness is a further noticeable difference between the models with and without AGN (see Fig. 2). In the very central region (less than 2 kpc), the difference in the thickness is due to the presence of a bar, and particularly to the boxy/peanut bulge associated to it. But the differences outside the bar region are more difficult to explain. The model with a very weak AGN (mdf789), beyond the bar region, is approximately in between the model without AGN and the rest of the models. Presumably it is somehow connected to the very dense central mass concentration but the exact mechanism which causes such a difference is not clear for us yet.
In general, we can say that our simple AGN-like feedback is exactly what we wanted it to be. It introduces the desired considerable changes in the central part of the model, as aimed for, and only relatively small ones in the rest of the galaxy. More specifically, it solves the problem with the central peak of the vc profile, and allows the formation of the bar.
3.5. Models with and without Eddington limit
The main reason for including the Eddington limit in an AGN feedback model is to make sure that the amount of feedback energy is reasonable. There is, however, both observational and theoretical evidence for the possibility of supercritical accretion (King 2003; Sa¸dowski et al. 2014). So even from a general point of view, including Eddington limits may not be obligatory in order to be physically reasonable.
Here we will show that in our simple, parametric, AGN-like feedback model, the Eddington limit can be almost fully compensated by varying TAGN.
Let us compare three models. These models have identical parameters, except for TAGN and the Eddington limit:
-
mdf732, with Eddington limit,TAGN = 1 × 107 K;
-
mdf751, with Eddington limit, TAGN = 1.5 × 107 K;
-
mdf726, without Eddington limit, TAGN = 1 × 107 K.
The remaining parameters for these models are given in Appendix B.
 |
Fig. 6 Comparison of circular velocity profiles for G3, PSPH, and MFM models at t = 2.5 Gyr (left panels) and t = 10 Gyr (right panels). The upper row compares models without AGN and the lower row compares models with AGN. |
All three models are very similar, although there is a small difference in the mass distribution in the central part (see upper panels of Fig. 5). If we compare mdf732 and mdf726, which differ only in the presence, or absence of the Eddington limit, we can see that in a model without Eddington limit (mdf732), the AGN is somewhat less efficient and the central bump on the circular velocity profile is more prominent, which is expected because of the Eddington limit. However, when we make a simulation with Eddington limit, but increase the value of TAGN by 50%, we fully compensate for the presence of the Eddington limit (see model mdf751 in Fig. 5).
Let us consider another set of three models:
-
mdf737, with Eddington limit,TAGN = 2 × 107 K;
-
mdf780, with Eddington limit, TAGN = 2.5 × 107 K;
-
mdf730, without Eddington limit, TAGN = 2 × 107 K.
The remaining parameters for these models are given in Appendix B.
These models have a more eccentric orbit and a larger initial separation than the previous ones. This leads to a greater amount of low-angular-momentum gas in the central part, immediately after the collision, and consequently requires a more energetic AGN (bigger TAGN) in order to remove the central peak in the circular velocity profile and make the bar formation possible. Nevertheless, this does not change the conclusion of this section. If we compare models with and without the Eddington limit, but with the same TAGN, then we observe that the former has a larger central bump (compare mdf737, which has an Eddington limit, to mdf730, which does not, in the lower panels of Fig. 5). It is, however, possible to compensate for this by simply increasing TAGN (see mdf780 with Eddington limit and TAGN = 2.5 × 107 K vs. mdf730 without Eddington limit and TAGN = 2 × 107 K in lower panels of Fig. 5). Thus, it is possible to compensate for the effect of the Eddington limit on the circular velocity curve by varying the AGN-like feedback parameters.
4. Comparison with GIZMO
4.1. Introductory remarks
The GIZMO simulation code (Hopkins 2013, 2014, 2015) is a fork of GADGET3 (hereafter G3), using the same MPI parallelization, domain decomposition, gravity solvers, and so on. However, in contrast to G3, GIZMO offers several hydrodynamical solvers for the user to choose from. In this article, we compare the three solvers, which are briefly described below (see Hopkins 2015, Sect. 4.1, for more information).
-
TSPH (“Traditional” SPH): this is the same, entropy conserving,density-driven formulation of SPH as the one in G3. (Springel &Hernquist 2002).
-
PSPH: this is a density independent version of SPH (Hopkins 2013). It also includes a better treatment of the artificial viscosity term (Cullen & Dehnen 2010), as described in Hopkins (2013, Sect. 3.1).
-
MFM (Meshless Finite-Mass): Lagrangian formulation of mesh-free algorithm that conserves particle masses (Hopkins 2015).
Phase boundaries, such as, for example, those between the hot gas in the halo and the much colder gas in the disk, or those around cold dense clumps of gas in the hot halo can be better handled by PSPH or MFM, than by TSPH or G3 (see Hopkins 2015, and references therein).
Since our aim here is to see how results will change with different hydro-solvers, we keep the same subgrid physics.
The main difference we found between G3 and PSPH/MFM is in the hot gaseous halo. This has small gaseous clumps in the simulation run with G3, which are either absent, or much less prominent in the PSPH or MFM runs (see also Torrey et al. 2012; Hayward et al. 2014). However, in our project, we are mostly interested in the properties of the remnant. Therefore, in this comparative study, we will focus on the properties of the final galaxy.
4.2. Simulations without AGN-like feedback
We first compared G3 to TSPH and, as expected, we found no differences. We will thus not discuss TSPH further here.
Let us now compare three simulations of major mergers without AGN. All three simulations were run with the same parameters, those of mdf018 (see Appendix B), except for the softening, which is 50 pc for both dark matter and baryons, but with a different hydrodynamical solver. We also used the same subgrid physics in all three cases. Thus, the only difference is the hydro-solvers. These three runs are mdf624 (run with G3), mdi101 (run with GIZMO/PSPH), and mdh101 (run with GIZMO/MFM).
 |
Fig. 7 Comparison of various radial profiles for G3, PSPH, and MFM models. The upper row shows models without AGN and the lower row models with AGN. In each row, from left to right: surface density, median of the absolute value of z, which is a good approximation for thickness (Sotnikova & Rodionov 2006) and mean value of the azimuthal velocity. |
Comparisons are made in the upper panels of Figs. 6 (for the circular velocity curves) and 7 (for the projected surface density, the vertical thickness, and the mean tangential velocity of the stars). In the former, we see that at t = 2.5 Gyr, all three runs have a very strong CMC; that of the MFM run being somewhat stronger than the other two. Nevertheless, in all three cases, the peak is considerably higher than 300 km s-1, for a velocity of the flat part of the circular velocity curve of approximately 200 km s-1. By t = 10 Gyr, this CMC has considerably decreased, as expected (see Sect. 3.1.1), but still has a maximum of approximately 250 km s-1, still giving an unrealistic shape of the circular velocity curve, although much less so than that at t = 2.5 Gyr. In general, the G3 and the PSPH runs give very similar results, in most cases differing by approximately no more than the plotting accuracy. On the other hand, MFM gives somewhat higher values, corresponding to a somewhat higher mass. We note that the CMC found in these runs, which have no AGN-like feedback, is sufficient to prohibit bar formation, or at least to delay it beyond the 10 Gyr over which we make the comparisons.
In the upper left panel of Fig. 7, we compare the radial projected surface density profiles, as obtained at t = 10 Gyr for the three simulations. It is clear that the inner disk scale length (i.e., the scale length of the part of the disk which is within the break in the projected surface density, around R = 17 kpc) is approximately the same for all three models. The outer disk scale length is approximately the same for models G3 and PSPH, while for MFM it is somewhat smaller, leading to a faster drop in the surface densities in the outer disk region (i.e., the part of the disk beyond the break). The middle panel compares the radial profile of a measure of the stellar disk vertical thickness, namely the azimuthal averaged median of the absolute value of the z coordinates of all stellar particles (Sotnikova & Rodionov 2006). The three methods give similar results, and, although the differences are larger than what we found for the circular velocities and the projected surface densities, they are still relatively small, especially taking into account that dist thickness is very sensitive to numerical effects (Rodionov & Sotnikova 2013). We also note that in this plot, the MFM does not stand out as being further apart from the other two runs.
Finally the rightmost panel compares the radial profiles of the three mean stellar tangential velocity radial profiles. Here, again, the G3 and the PSPH are very similar and the MFM differs somewhat more, but never by too much.
 |
Fig. 8 Comparison of the baryonic mass (gas + stars), within a sphere of 30 kpc radius as a function of time for G3, PSPH, and MFM models. The left panel is for simulations without AGN-like feedback and the right one with it. |
A further comparison is given in Fig. 8, where we present the evolution of the baryonic mass (gas + stars) inside a sphere of radius 30 kpc with time. We can see that in the MFM model, gas accretes on the disk somewhat faster than in the PSPH and G3 models. As a result, at t = 10 Gyr, the disk in the MFM models is approximately 12% more massive. There is also some difference between the G3 and the PSPH models, but this is much smaller than the difference between the MFM and the other two models. Indeed, at t = 10 Gyr, the difference between G3 and PSPH amounts to only approximately 4% of the baryonic mass. These differences in accretion rate could explain the corresponding differences between the three circular velocity curves discussed above.
4.3. Simulations with AGN-like feedback
Here, we again first compared G3 with GIZMO in the case of the same hydro solver (G3 vs. TSPH). We found that, with the same parameters, our AGN-like feedback is slightly less efficient in TSPH runs than in G3 runs. It should be noted that even with the TSPH hydro solver, GIZMO is not identical to G3 (Hopkins 2015, Sect. F1). Nevertheless, this difference can be easily compensated for by tuning the feedback parameters, and we do so in the following.
Let us now compare three other runs, identical to the three compared in the previous subsections, but now including the proposed AGN-like feedback.
-
mdf627: run with GADGET3.TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3, with Eddigton limit.
-
mdh115: run with GIZMO/PSPH. TAGN = 1 × 107 K, ρAGN = 0.75 M⊙/pc3, without Eddigton limit.
-
mdi115: run with GIZMO/MFM. TAGN = 1 × 107 K, ρAGN = 0.75 M⊙/pc3, without Eddigton limit.
These simulations were run with 50 pc softening for both dark matter and baryons. The remaining parameters are those of mdf018 (see Appendix B).
The results are again compared in Figs. 6 and 7, but now in the lower panels. We note that in all three cases this feedback leads to a realistic circular velocity curve with no strong CMC, contrary to what we found in runs with no AGN-like feedback, which all had strong CMCs. Furthermore, we witnessed that, with the demise of the CMC, bars form in all three cases under consideration. In fact, it is due to these bars that there is a maximum of the disk thickness in the central region for all three models (lower middle panels of Fig. 7). Considering all the comparisons globally, we see that in the case with AGN-like feedback, the MFM differs from the other two more than in the cases without AGN-like feedback. The results of runs with G3 and PSPH are again very close to each other, similarly to cases without AGN-like feedback.
5. Summary and conclusions
In this paper, we discuss, in detail, the technical aspects of our wet major merger simulations, where we collide two idealized protogalaxies. In Sect. 2.1, we describe the initial conditions of our simulations. Each protogalaxy is initially spherical and consists of a dark matter halo and a gaseous halo. Spin is added to the system. In Appendix A, we demonstrate that in isolation their evolution resembles the evolution of disk galaxies; after 1–2 Gyr they tend to be similar to intermediate redshift disks and after 10 Gyr they resemble present day spirals.
For the simulations, we use the GADGET3 code (Springel 2005) with star-formation and feedback modeled by sub-grid physics (Springel & Hernquist 2003). We demonstrate that, without any additional feedback, our major merger models have a very compact and massive CMC (see Sect. 3.1). This leads to an unphysically high central peak of the circular velocity profile. Moreover, this compact and massive CMC prevents the formation of a bar, while approximately two thirds of real disk galaxies have bars. We demonstrate that low resolution can, in some cases, artificially mask this problem. In models with a small number of particles, a very compact CMC will be relatively quickly attenuated by two-body relaxation, and bigger gravitational softening will make CMC less compact from the beginning. Of course, we cannot consider decreasing the resolution as a “solution” to the problem. We note that higher resolution, namely a larger number of particles and a smaller softening, will make the CMC problem even more acute.
We solve the problem of the compact CMC by adding simple AGN-like feedback: at every time step we give internal energy to the gas particles whose local volume density is larger than the threshold ρAGN by increasing their temperature to TAGN. We demonstrate that this simple AGN-like feedback is able to solve the problem with the central peak on the circular velocity profile, making this profile very realistic, and allowing bar formation. We also show that our AGN-like feedback mainly changes the central region of the disk without significantly modifying the rest of the model.
As an option, in our AGN-like feedback, we have an Eddington limit (see Sect. 3.3). However, we demonstrate that the absence or presence of the Eddington limit in the models we have considered so far can be compensated, at least as far as the mass and velocity distributions are concerned, by changing the TAGN parameter. This, together with observational and theoretical evidence of the possibility of supercritical accretion (King 2003; Sa¸dowski et al. 2014), argues that one is not obliged to include an Eddington limit in the AGN-like feedback described here in order to obtain models with realistic density and velocity profiles. They can, however, prove useful if one wants to set reasonable limits to the energy injected into the central regions.
We have also compared results of our simulations calculating with three different hydro-solvers: traditional SPH (G3 or TSPH in the GIZMO code), density independent SPH (PSPH, GIZMO code), and Lagrangian formulation of mesh-free algorithm, which conserves particle masses (MFM, GIZMO code). We found that for the specific results we are interested in, namely properties of major merger remnants, G3, and PSPH give, in all cases we tried, very similar results, and one can use either of the two codes. Moreover, the differences between MFM and PSPH are similar, and, in some comparisons, even bigger than the differences between PSPH and G3.
See GADGET manual, http://www.mpa-garching.mpg.de/gadget/users-guide.pdf
Acknowledgments
We thank P. Hopkins and V. Springel for providing us with the versions of GIZMO and GADGET used here, and for useful discussions. We also thank an anonymous referee for comments that helped improve the presentation of this paper. We acknowledge financial support from CNES (Centre National d’Études Spatiales, France) and from the EU Programme FP7/2007-2013/, under REA grant PITN-GA-2011-289313. We also acknowledge HPC resources from GENCI/TGCC/CINES (Grants x2013047098 and x2014047098) and from Mesocentre of Aix-Marseille-Universite (program DIFOMER).
References
- Athanassoula, E., Vozikis, C. L., & Lambert, J. C. 2001, A&A, 376, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanassoula, E., Rodionov, S. A., Peschken, N., & Lambert, J. C. 2016, ApJ, 821, 90 (A16) [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics (Princeton University Press) [Google Scholar]
- Blecha, L., Loeb, A., & Narayan, R. 2013, MNRAS, 429, 2594 [NASA ADS] [CrossRef] [Google Scholar]
- Borlaff, A., Eliche-Moral, M. C., Rodríguez-Pérez, C., et al. 2014, A&A, 570, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosma, A. 1981, AJ, 86, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., Broadhurst, T. J., & Franx, M. 2004, ApJ, 611, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A., & Christensen, C. 2016, Galactic Bulges, 418, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Georgakakis, A., Nandra, K., et al. 2008, ApJ, 681, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., Sheth, K., Athanassoula, E., et al. 2015, ApJS, 217, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, T. J., Jonsson, P., Primack, J. R., & Somerville, R. S. 2006, MNRAS, 373, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Cullen, L., & Dehnen, W. 2010, MNRAS, 408, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Mobasher, B., Dickinson, M., et al. 2007, ApJ, 654, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dubois, Y., Devriendt, J., Slyz, A., & Teyssier, R. 2010, MNRAS, 409, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Vollbach, D. R., Foster, E. R., & Ferguson, T. E. 2005, ApJ, 634, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C., Dickinson, M., Giavalisco, M., et al. 2004, ApJ, 600, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Gabor, J. M., Capelo, P. R., Volonteri, M., et al. 2016, A&A, 592, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Brook, C. B., Brooks, A. M., et al. 2009, MNRAS, 398, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Flores, H., Puech, M., et al. 2009a, A&A, 507, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Flores, H., Yang, Y. B., et al. 2009b, A&A, 496, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayward, C. C., Torrey, P., Springel, V., Hernquist, L., & Vogelsberger, M. 2014, MNRAS, 442, 1992 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F. 2013, MNRAS, 428, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F. 2014, GIZMO: Multi-method magneto-hydrodynamics+gravity code, Astrophysics Source Code Library [Google Scholar]
- Hopkins, P. F. 2015, MNRAS, 450, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009, ApJ, 691, 1168 [Google Scholar]
- Hopkins, P. F., Cox, T. J., Hernquist, L., et al. 2013, MNRAS, 430, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2003, ApJ, 596, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., & Tinsley, B. M. 1978, ApJ, 219, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2010, MNRAS, 404, 590 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J., & Dehnen, W. 2007, MNRAS, 378, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. J., & Bregman, J. N. 2015, ApJ, 800, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Hammer, F., Hopkins, P. F., et al. 2012, ApJ, 753, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Querejeta, M., Eliche-Moral, M. C., Tapia, T., et al. 2015, A&A, 573, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodionov, S. A., & Sotnikova, N. Y. 2005, Astron. Rep., 49, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Rodionov, S. A., & Sotnikova, N. Y. 2013, MNRAS, 434, 2373 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, M., Puech, M., Hammer, F., Rothberg, B., & Flores, H. 2012, MNRAS, 421, 2888 [NASA ADS] [CrossRef] [Google Scholar]
- Sądowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, 439, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y., Tutui, Y., Honma, M., et al. 1999, ApJ, 523, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Sotnikova, N. Y., & Rodionov, S. A. 2006, Astron. Lett., 32, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Springel, V., & Hernquist, L. 2005, ApJ, 622, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Teuben, P. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, APS Conf. Ser., 77, 398 [Google Scholar]
- Torrey, P., Vogelsberger, M., Sijacki, D., Springel, V., & Hernquist, L. 2012, MNRAS, 427, 2224 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Capelo, P. R., Netzer, H., et al. 2015, MNRAS, 449, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Hammer, F., Athanassoula, E., et al. 2012, A&A, 538, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wurster, J., & Thacker, R. J. 2013, MNRAS, 431, 2513 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Isolated models
 |
Fig. A.1 Upper row: cumulative mass of accreted gas as a function of time for three isolated models of different initial spin: a) shows accretion into 30 kpc sphere and b) shows accretion into the disk region with R< 30 kpc and | z | < 2 kpc. Lower panels: c) fraction of gas fgas = Mgas/ (Mgas + Mstars) inside the disk region defined by R< 30 kpc and | z | < 2 kpc as a function of time and d) stellar mass as a function of time. |
Here we consider the evolution of three isolated protogalaxies with different fpos parameters (see Sect. 2.1.1).
-
1.
idf407 – fpos = 0.6.
-
2.
idf401 – fpos = 0.7.
-
3.
idf413 – fpos = 0.8.
The remaining parameters are identical for these models and they are given in Appendix B.
The initial conditions for our protogalaxies are, by construction, in equilibrium for adiabatic gas (see Sect. 2.1.1). But, in our simulations, the gas is cooling radiatively during the evolution and, getting out of equilibrium, falls inwards. Because gas has angular momentum, it forms a gaseous disk in the central parts, which, due to star formation, develops a stellar disk component.
Before discussing the accreted gas, we need to choose regions for which we will calculate this accretion. We consider two regions: a sphere of radius 30 kpc, and a pill-box shaped disk region with R < 30 kpc and | z | < 2 kpc, where R is the cylindrical radius. In our three models, only very few stars were formed outside this disk region (approx. 1.5%), and even less outside the 30 kpc sphere (approx. 0.1%). In Fig. A.1a we show the cumulative mass of gas accreted onto the 30 kpc sphere as a function of time, and in Fig. A.1b we show the cumulative mass of gas accreted onto the disk region with R < 30 kpc and | z | < 2 kpc. The mass of gas accreted onto a given region was calculated as the mass of baryons (gas + stars) which, at least once, were inside this region before time t. Actually, relatively few baryons leave the considered regions after they are in, so if we simply use here the mass of gas+stars inside the given region, the results will be very similar. As can be seen from these figures, the accretion depends very little on the amount of angular momentum (fpos parameter). The cumulative accretion onto the 30 kpc sphere for the first 7 Gyr of evolution is almost identical for our three models, while after this time there is slightly less accretion for models with higher angular momentum (bigger fpos). But when we consider accretion onto the disk itself (Fig. A.1b), the situation is different. At intermediate times, gas accretes slightly faster onto the disk region for models with higher angular momentum. However, overall there is little difference, and we can conclude that the accretion rate is practically independent on fpos. However, models with smaller angular momentum form stars more efficiently, as should be expected, because they form more compact disks. As a result, the gas fraction in the disk (Fig. A.1c), and the stellar mass (Fig. A.1d), depend on fpos. Models that at a given time have a smaller angular momentum (smaller fpos) have greater stellar masses and smaller fractions of the gas in the disk region.
 |
Fig. A.2 Radial stellar surface density profiles for three isolated models for times 1, 2, 5, and 10 Gyr. |
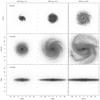 |
Fig. A.3 Face-on view at t = 2 Gyr (upper row), face-on view at t = 10 Gyr (middle row), and edge on view (lower row) at t = 10 Gyr for three isolated models: idf407 (fpos = 0.6, left column), idf401 (fpos = 0.7, middle column) and idf413 (fpos = 0.8, right column). |
In Fig. A.2, we show the surface density profile for three models considered at different moments of time. We can see that disks grow inside-out, and at initial stages, they are significantly smaller than at t = 10 Gyr (see also Fig. A.3). At initial stages, our models are more clumpy and their surface density profiles are, in general, further away from exponential compared to later stages (t = 10 Gyr). This, together with the fact that at early stages the disks in our models are more gas rich (see Fig. A.1c), makes them similar to disks in intermediate redshift galaxies, which are considerably smaller, more perturbed, and have higher gas fractions than disks in local spiral galaxies (Bouwens et al. 2004; Ferguson et al. 2004; Elmegreen et al. 2005; Erb et al. 2006; Dahlen et al. 2007; Leroy et al. 2008; Daddi et al. 2010; Tacconi et al. 2010; Rodrigues et al. 2012; Genzel et al. 2015, etc.). At t = 10 Gyr, our models resemble local disk galaxies. They have type II exponential surface density profiles (down-bending) and a fraction of gas of approximately 10–20% (see Fig. A.1c).
Appendix B: Parameters of the models
All models considered in this article have the same masses for the protogalaxies: MDM = 35 × 1010M⊙ and Mgas = 5 × 1010M⊙ (see Sect. 2.1.1). The mass of the gas and stellar particles is mg = 5 × 104M⊙, and the mass of the DM particles is mDM = 2 × 105M⊙. Consequently, each protogalaxy has 106 gas particles and 1.75 × 106 halo particles. There is an exception for two low resolution models considered in Sect. 3.1 (mdf214, mdf225), which have protogalaxies with ten times less particles. The parameter fpos is fixed to 0.6 for all models with the exception of two isolated models (for idf401 fpos = 0.7 and for idf413 fpos = 0.8 see Appendix A), where we wanted to examine the effect of fpos on the final density distribution.
In all merger models, the two protogalaxies have their rotation axis parallel to each other and perpendicular to the orbit of collision (see Sect. 2.1.2). Here we have two types of collisional orbits: o1 and o2, whose parameters are given in Table B.1. We note that o2 values were obtained using the two-body problem with the following parameters: eccentricity ϵ = 0.99, initial separation ri = 200 kpc and distance at pericenter rp = 2 kpc.
In Table B.2, we present, for all models used here, the corresponding collisional orbits and the parameters of the AGN-like feedback. All models with Eddington limits were calculated with ϵr = 0.1 and ϵf = 0.05, and only the initial mass of the BH MBH(0) is given in Table B.2 (see Sect. 3.3).
Parameters of the collisional orbits.
Parameters of the models.
All Tables
All Figures
 |
Fig. 1 Central part of the circular velocity profiles for models mdf018 (high resolution model), mdf225 (low resolution model), and mdf214 (low resolution models with two times bigger softening) at times 2.5, 5, 7.5, and 10 Gyr. This is calculated from the total mass distribution, assuming spherical symmetry. |
| In the text | |
 |
Fig. 2 Comparison of various radial profiles for the stellar component of five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3), and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), all at t = 10 Gyr. From left to right and top to bottom: surface density, median of the absolute value of z, which is a good approximation for thickness (Sotnikova & Rodionov 2006), mean value of the azimuthal velocity and radial velocity dispersion. The inlay in the upper left panel shows the surface density in the innermost region (within 3 kpc). |
| In the text | |
 |
Fig. 3 Face-on (upper row) and edge-on (lower row) views of the stars component for five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3), and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), from left to right, respectively, and all at t = 10 Gyr. The size of each square box corresponds to 50 kpc. |
| In the text | |
 |
Fig. 4 Circular velocity profiles for five models with different AGN feedback parameters: mdf018 (no AGN), mdf789 (TAGN = 5 × 106 K, ρAGN = 1 M⊙/pc3), mdf732 (TAGN = 1 × 107 K, ρAGN = 1 M⊙/pc3), mdf788 (TAGN = 2 × 107 K, ρAGN = 1 M⊙/pc3) and mdf791 (TAGN = 1 × 107 K, ρAGN = 2 M⊙/pc3), at 5 (left) and 10 (right panel) Gyr. |
| In the text | |
 |
Fig. 5 Comparison of circular velocity profiles (at 5 and 10 Gyr) for models with and without Eddington limits. The upper row shows two models with Eddington limit (mdf732 TAGN = 1 × 107 K and mdf751 TAGN = 1.5 × 107 K) and one model without Eddigton limit (mdf726 TAGN = 1 × 107 K). The lower panels also display three models: two with Eddigtion limit (mdf737 TAGN = 2 × 107 K, and mdf780 TAGN = 2.5 × 107 K) and one model without (mdf730 TAGN = 2 × 107 K). |
| In the text | |
 |
Fig. 6 Comparison of circular velocity profiles for G3, PSPH, and MFM models at t = 2.5 Gyr (left panels) and t = 10 Gyr (right panels). The upper row compares models without AGN and the lower row compares models with AGN. |
| In the text | |
 |
Fig. 7 Comparison of various radial profiles for G3, PSPH, and MFM models. The upper row shows models without AGN and the lower row models with AGN. In each row, from left to right: surface density, median of the absolute value of z, which is a good approximation for thickness (Sotnikova & Rodionov 2006) and mean value of the azimuthal velocity. |
| In the text | |
 |
Fig. 8 Comparison of the baryonic mass (gas + stars), within a sphere of 30 kpc radius as a function of time for G3, PSPH, and MFM models. The left panel is for simulations without AGN-like feedback and the right one with it. |
| In the text | |
 |
Fig. A.1 Upper row: cumulative mass of accreted gas as a function of time for three isolated models of different initial spin: a) shows accretion into 30 kpc sphere and b) shows accretion into the disk region with R< 30 kpc and | z | < 2 kpc. Lower panels: c) fraction of gas fgas = Mgas/ (Mgas + Mstars) inside the disk region defined by R< 30 kpc and | z | < 2 kpc as a function of time and d) stellar mass as a function of time. |
| In the text | |
 |
Fig. A.2 Radial stellar surface density profiles for three isolated models for times 1, 2, 5, and 10 Gyr. |
| In the text | |
 |
Fig. A.3 Face-on view at t = 2 Gyr (upper row), face-on view at t = 10 Gyr (middle row), and edge on view (lower row) at t = 10 Gyr for three isolated models: idf407 (fpos = 0.6, left column), idf401 (fpos = 0.7, middle column) and idf413 (fpos = 0.8, right column). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.