| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527553 | |
| Published online | 12 April 2017 | |
Thermal emission in the early afterglow of gamma-ray bursts from their interaction with supernova ejecta
1 International Center of Relativistic Astrophysics Network (ICRANet), Piazza della Repubblica 10, 65122 Pescara, Italy
e-mail: veresh@icra.it
2 Dipartimento di Fisica, Università degli Studi di Roma “Sapienza”, P.le Aldo Moro 5, 00185 Roma, Italy
Received: 14 October 2015
Accepted: 1 January 2017
Context. A thermal X-ray component is observed in the early afterglow of some gamma-ray bursts. Possible explanations include shockwave breakout, relativistic photosphere, or emission from cocoon. The difficulties of these models are discussed.
Aims. We propose an alternative model that attributes such a thermal component to the interaction of the gamma-ray burst outflow with a baryonic material near the gamma-ray burst source.
Methods. The analytic model is based on relativistic energy-momentum conservation and a diffusion model for photons. The kinematic and observational properties of the supernova ejecta after the interaction are derived. In particular, the temperature and the duration of the thermal emission are obtained.
Results. The model is applied to a prototypical GRB 090618 and other gamma-ray bursts associated with supernovae having thermal emission in the early afterglow. The mass of the baryonic material is found to be a few 10-4M⊙, indicating that this material can be a small fraction of the supernova ejecta.
Key words: X-rays: general / radiation mechanisms: thermal
© ESO, 2017
1. Introduction
A thermal X-ray component is observed in the early afterglow of some gamma-ray bursts (GRBs), such as GRB 060729, 081007, 090618, and 130427A; see (Page et al. 2011; Sparre & Starling 2012; Starling et al. 2012; Ruffini et al. 2014, 2015) for more examples. Different origins of this component were proposed in the literature, but consensus has not been reached. The traditional shockwave breakout model (Campana et al. 2006; Waxman et al. 2007; Li 2007) has difficulties in generating the observed high luminosity in a distant radius, and especially the required long duration of the order of hundreds to thousands of seconds (Ghisellini et al. 2007; Starling et al. 2012). Friis & Watson (2013) link the afterglow thermal radiation to the prompt phase via photospheric emission from the jet, but the observed cooling of thermal components in the afterglow is too fast to be interpreted as part of the photospheric emission; see an example in Fig. 4 below. Pe’er et al. (2006) interpret the thermal emission as coming from a hot plasma “cocoon” emerging when the GRB jet breaks out from the progenitor star, but this model requires unusually high Lorentz factors (approx. 10) of the cocoon, and unusually large radius (1013 cm).
In this paper, we provide a comprehensive interpretation of the thermal component in the early afterglow, affiliating it to the interaction of GRB outflow with a part of the baryonic shell surrounding the GRB source. We focus on the particular paradigm of “binary-driven hypernovae” (BdHNe); see Ruffini et al. (2014, 2016), for example, and references therein. Within this paradigm, such a shell is interpreted as supernova (SN) ejecta. BdHN occurs in an ultra-compact binary system composed of a FeCO core and a neutron star (NS); when the FeCO core explodes as a supernova (SN), the companion NS accretes a part of the SN ejecta and gravitationally collapses to a black hole (BH), resulting in emission of a GRB with isotropic energy Eiso> 1052 erg; for details see Rueda & Ruffini (2012), Ruffini et al. (2014, 2016). Within this paradigm, the mechanisms of GRB energy engine and explosive dynamics in the prompt phase are described by the fireshell model; see Ruffini et al. (2009), for example, and references therein. Such an outflow GRB then interacts with the rest of the supernova ejecta, accelerating and heating it. As a consequence, the supernova ejecta expand mildly relativistically and emit the thermal radiation.
To observe a thermal component, some conditions are required due to the capacity of satellites. The flux of a thermal component must be sufficient and the ratio of thermal flux to total flux prominent; these two conditions are not easily reached, especially for high-redshift GRBs. In addition, most of the GRBs only have observations of X-ray afterglow from Swift-XRT, which covers energy of photons from 0.3 keV to 10 keV, corresponding to the temperature between ~0.1 keV and ~3 keV. Practically, for most GRBs, Swift-XRT does not provide precise data in its high-energy tail, thus the temperature we can measure confidently is limited to between ~0.1 keV and ~1.5 keV. We found five GRBs associated to a SN with known redshifts and observed a thermal component in the early afterglow.
The content of this paper is organized as follows. In Sect. 2, a physical scenario is outlined. In Sect. 3, we solve the equations of relativistic energy-momentum conservation in order to recover the amount of thermal energy and the velocity of the shell after the collision with the GRB outflow. The photon diffusion is also considered in this section. In Sect. 4, we compute the resulting temperature and estimate the optical depth of the shell. We apply the model in Sect. 5 and consider the cases of three family 2 GRBs with different magnitudes of energy, including the prototype GRB 090618. We also make a comparison to three family 1 GRBs. We then compare our results with those in the literature before presenting our conclusions.
2. The scenario
The presence of the baryonic material in the vicinity of the GRB source is expected in many GRB models. In our scenario, the thermal component in the early afterglows of some GRBs is attributed to the interaction of the GRB outflow with this baryonic material.
In particular, within the BdHN model, baryons may form part of SN ejecta. In the BdHN scenario, the induced gravitational collapse of the NS to a BH occurs after the SN explosion (Rueda & Ruffini 2012). The binary stars in the BdHN model have very small orbital separation, typically <1010 cm (Fryer et al. 2014). Consequently the travel time of the SN ejecta needed to reach the NS is as short as approximately 10 s. The time delay between the SN explosion and BH formation comprises this travel time as well as the time needed for the NS to accrete sufficient mass to undergo gravitational collapse (Fryer et al. 2014). The delay between the SN explosion and the BH formation in this model is of the order of 50 s (Izzo et al. 2012). From the observational point of view, the supernova in the optical band is detected days after the GRB; see, for example, (Woosley & Bloom 2006; Hjorth & Bloom 2012) for reviews. Given that the typical velocities of the SN ejecta are larger than 0.1c (Bufano et al. 2012), the interaction between the GRB outflow and SN ejecta should occur at distances larger than R> 1011 cm, at least an order of magnitude larger than the orbital separation in the binary. Then R is also considered to be approximately the distance between the shell and the GRB source.
One can assume that the SN ejecta represents a massive optically thick shell located at the radius R from the SN source when it is hit by the GRB outflow. The GRB outflow is energetic enough that it penetrates the SN ejecta. The prompt radiation is emitted at larger radii, above the photospheric radius, typically 1012 cm (see, for example, Vereshchagin 2014), well above the SN ejecta.
Here, we approximate the total energy of GRB outflow E as the observed isotropic energy Eiso. This energy is mainly the kinetic energy of baryons Ek and the energy of photons Eγ, so we assume E = Ek + Eγ. Thermal energy of baryons can be safely neglected. As long as baryons are ultra-relativistic, they carry kinetic energy Ek = γMbc2 and momentum γMbc, where Mb is rest mass of baryons, c is the speed of light, and γ is their bulk Lorentz factor. Hence, the total energy of GRB outflow is E and total momentum is E/c.
We neglect both the initial kinetic energy of the massive shell as well as its internal energy. This assumption is justified as long as SN ejecta are initially non-relativistic. Indeed, typical SN Ibc ejecta velocities are below 0.1c (Cano 2013).
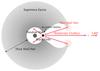 |
Fig. 1 Cartoon illustrating the binary system left after the explosion of the SN and formation of the GRB. GRB outflow collides with the SN ejecta and interacts with baryonic material on its way out to the distant observer. |
The massive shell may not fully cover the sphere, also the GRB outflow may be jetted, therefore in the following, we only consider the interacting part; see Fig. 1 involving a portion of the shell with area 4πϵR2 and the associated mass M = ϵMs; the energy of GRB outflow interacting with this portion of the shell E = ϵEiso, where ϵ is a fractional factor and Ms is the mass of the spherical shell. For brevity, in the following, when we mention the shell, we are referring to the interacting part of the shell.
3. Velocity and internal energy
Interaction transfers energy and momentum from the GRB outflow to the clumps of the shell. Energy-momentum conservation reads 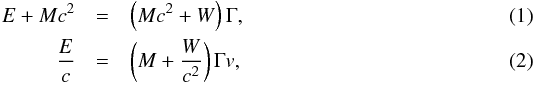 where Γ = [1−(v/c)2]− 1/2 is the Lorentz factor of the radial motion of the shell, W is internal energy, and M is the mass of the baryonic shell. These equations can be used to find the internal energy and the velocity of the shell after the interaction.
where Γ = [1−(v/c)2]− 1/2 is the Lorentz factor of the radial motion of the shell, W is internal energy, and M is the mass of the baryonic shell. These equations can be used to find the internal energy and the velocity of the shell after the interaction.
In order to solve Eqs. (1) and (2), we introduce the new variables 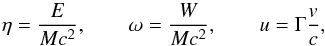 (3)and we rewrite the energy-momentum conservation
(3)and we rewrite the energy-momentum conservation  The solution to this system reads
The solution to this system reads 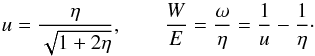 (6)In non-relativistic and ultra-relativistic asymptotics, respectively, the solution becomes
(6)In non-relativistic and ultra-relativistic asymptotics, respectively, the solution becomes 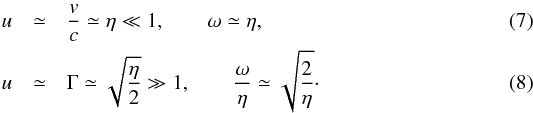 This solution is illustrated in Fig. 2.
This solution is illustrated in Fig. 2.
 |
Fig. 2 Two functions are shown: the dimensionless velocity parameter u = Γv/c of the shell after the interaction with the GRB outflow (thick), as a function of the parameter η = E/ (Mc2), as well as the ratio between the internal energy and the initial energy (thin), ω/η = W/E, as a function of the same parameter η. The dotted (dashed) line shows the non-relativistic (ultra-relativistic) asymptotics for u, while the dash-dotted line shows the ultra-relativistic asymptotics for W/E. |
These results imply the following. On the one hand, when the energy E is much less than the rest mass of the shell, E ≪ Mc2, most of the energy is transferred into internal energy W ≃ E, and the resulting velocity of the shell is non-relativistic, v/c ≃ E/ (Mc2). On the other hand, for E ≫ Mc2 , the transfer of momentum is inefficient. We have 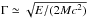 and
and 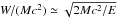 . The shell is accelerated to ultra-relativistic velocity, but some energy goes into internal energy as well.
. The shell is accelerated to ultra-relativistic velocity, but some energy goes into internal energy as well.
 |
Fig. 3 Ratio between internal (dashed) and kinetic (solid) energy of the shell to initial energy E (dotted) after the interaction. In the non-relativistic case with η ≪ 1, all the energy of the GRB outflow is transformed into internal energy (heat) of the baryonic shell. In the ultra-relativistic case with η ≫ 1, the energy of the GRB outflow is transformed mostly into kinetic energy of the shell. |
This internal energy can then be transferred into kinetic energy during the acceleration phase; see below.
In Fig. 3, we present the ratio between internal and kinetic energy of the shell to initial energy E of the GRB outflow, computed after the interaction. One can see that in the non-relativistic case, with E ≪ Mc2, all the energy of the GRB outflow is transformed into internal energy of the massive shell. In contrast, in the ultra-relativistic case, with E ≫ Mc2, the energy of the GRB outflow is transformed mostly into kinetic energy of the shell. We notice a striking similarity with the corresponding diagram for the energies emitted in the P-GRB and in the extended afterglow in units of the total energy of the plasma within the fireshell model; see, for example, Fig. 5 in (Ruffini et al. 2009).
3.1. Acceleration
If the shell is spherical and it remains opaque after the interaction, the internal energy of the shell is transformed into its kinetic energy. This energy transformation results in expansion with acceleration (Piran 1999; Ruffini et al. 2000). At the phase of acceleration, the radial momentum is not conserved, and Eq. (2) in the above set cannot be used. The final velocity after the acceleration phase can be found from the energy conservation alone, namely from Eq. (1). If the shell is spherically symmetric, assuming all energy is ultimately transferred into kinetic energy of the shell (W ≪ Mc2) from the energy conservation, Eq. (1), one has 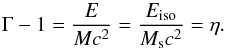 (9)Again, in non-relativistic and ultra-relativistic asymptotics, respectively, one finds
(9)Again, in non-relativistic and ultra-relativistic asymptotics, respectively, one finds  As a matter of fact, the values of velocity (Lorentz factor) after the interaction are always smaller than the final values, reached after the acceleration phase.
As a matter of fact, the values of velocity (Lorentz factor) after the interaction are always smaller than the final values, reached after the acceleration phase.
We note that in the derivation in this Section, we never used the condition W ≪ Mc2. This condition is valid in the context of GRBs, as baryons never reach relativistic temperatures after collision, kT ≪ mpc2.
4. Temperature and optical depth
The co-moving temperature of the shell Tc is found from the condition 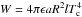 . The observed temperature for the source with angle ϑ with respect to the line of sight is
. The observed temperature for the source with angle ϑ with respect to the line of sight is 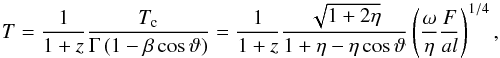 (12)where F = ϵEiso/(4πϵR2) = Eiso/(4πR2) is isotropic energy flux, and z is cosmological redshift of the source. This expression gives, respectively, in non-relativistic and ultra-relativistic asymptotics
(12)where F = ϵEiso/(4πϵR2) = Eiso/(4πR2) is isotropic energy flux, and z is cosmological redshift of the source. This expression gives, respectively, in non-relativistic and ultra-relativistic asymptotics ![\begin{eqnarray} T & \simeq&\left( \frac{F}{al}\right) ^{1/4},\qquad E\ll Mc^{2},\label{TNR}\\ T & \simeq&2\Gamma\left[ \frac{F}{al}\left( \frac{2}{\eta}\right)^{1/2}\right] ^{1/4},\qquad E\gg Mc^{2},\label{TUR} \end{eqnarray}](/articles/aa/full_html/2017/04/aa27553-15/aa27553-15-eq61.png) where in Eq. (14), we assume that the source is near the line of sight. We reiterate here that the GRB outflow penetrates the massive shell through holes and its emission reaches the distant observer.
where in Eq. (14), we assume that the source is near the line of sight. We reiterate here that the GRB outflow penetrates the massive shell through holes and its emission reaches the distant observer.
The shell will emit photons from its photosphere. The case of ultra-relativistic photosphere with Γ ≫ 1 is treated in (Ruffini et al. 2013); see, also, the recent review (Vereshchagin 2014). From now on, we assume that the photosphere is not ultra-relativistic. We still retain fully relativistic expression (12). The validity of the treatment in the previous section requires that the shell is opaque; its optical depth τ is large. The latter is given by 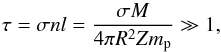 (15)where σ is the Thomson cross-section, mp is proton mass, and Z is atomic number.
(15)where σ is the Thomson cross-section, mp is proton mass, and Z is atomic number.
The emission from the photosphere occurs due to radiative diffusion from the interior of the shell. The emission lasts until all energy diffuses out from the shell. The characteristic diffusion time from a clump with a given thickness is 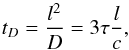 (16)where D = c/ (3σn) is the diffusion coefficient for photons. Since τ ≫ 1, we have l ≪ ctD. The density decrease in diffusion coefficient due to expansion of the shell can be neglected if the diffusion time is less than the dynamical time of expansion R/v, namely if
(16)where D = c/ (3σn) is the diffusion coefficient for photons. Since τ ≫ 1, we have l ≪ ctD. The density decrease in diffusion coefficient due to expansion of the shell can be neglected if the diffusion time is less than the dynamical time of expansion R/v, namely if 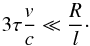 (17)In the opposite case, one must consider the effects of expansion and the thermal spreading of the baryonic shell after interaction with photons on the diffusion time. For the ultrarelativistic case of diffusion, we refer to (Ruffini et al. 2013) and for thermal spreading we refer to (Ruffini et al. 2014). In any case, this effect reduces the diffusion time.
(17)In the opposite case, one must consider the effects of expansion and the thermal spreading of the baryonic shell after interaction with photons on the diffusion time. For the ultrarelativistic case of diffusion, we refer to (Ruffini et al. 2013) and for thermal spreading we refer to (Ruffini et al. 2014). In any case, this effect reduces the diffusion time.
Note that Eqs. (8) and especially (14) are relevant in the context of the fireshell model (Ruffini et al. 2009) as they describe the values of the Lorentz factor of the pair-electromagnetic-baryon (PEMB) pulse and its temperature at the moment after the collision of the pair-electromagnetic (PEM) pulse with the baryonic remnant. The asymptotic expression (11) describes the Lorentz factor of the PEMB pulse under the condition η< 104.
5. Application
From the observation, one can derive the isotropic energy via the observed flux and redshift, and by fitting the light curve and spectra, one can obtain the evolution of temperature from thermal emission, as well as the velocity of expansion. In practice, the satellites do not cover the whole energy band; we can only find given temperatures with given duration. The Swift-XRT is the most widely used instrument for detecting the GRB afterglow; it covers 0.3 ~ 10 KeV. In other words, by analyzing the data from Swift-XRT, we can only infer the thermal temperature in soft-X-ray band, and the corresponding duration. For example, in Fig. 7 of (Ruffini et al. 2015), the temperature of blackbody radiation from 196 s to 461 s is clearly within the scope of Swift-XRT; temperature decreases along the time. Therefore, here, we adopt three parameters Eiso, tD, and u given by the observations. Then, we deduce the temperature using the above equations for the comparison with the observational one. It is convenient to rewrite Eq. (12) using Eqs. (6) and (16) as 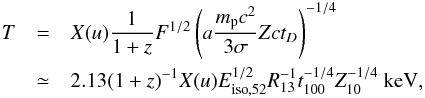 (18)where E52 = E/ 1052 erg, R13 = R/ 1013 cm, t100 = tD/ 100 s, Z10 = Z/ 10,
(18)where E52 = E/ 1052 erg, R13 = R/ 1013 cm, t100 = tD/ 100 s, Z10 = Z/ 10, ![\begin{eqnarray} X & =&\frac{1}{\sqrt{u}}\frac{1}{\sqrt{1+u^{2}}-u\cos\vartheta}\left(\frac{u+\sqrt{1+u^{2}}-1}{2u^{2}+2u\sqrt{1+u^{2}}+1}\right) ^{1/4}\\ & =&\left\{\begin{array}[c]{cc} u^{-1/4}, & u\ll1,\\[2mm] 2^{3/4}u^{1/4}, & u\gg1 \end{array} \right. \nonumber \end{eqnarray}](/articles/aa/full_html/2017/04/aa27553-15/aa27553-15-eq84.png) (19)is a slowly varying function of u, which decreases as u− 1/4 for u< 1 and increases as u1/4 for u> 1, with X(u = 1,ϑ = 0) ≈ 1.7.
(19)is a slowly varying function of u, which decreases as u− 1/4 for u< 1 and increases as u1/4 for u> 1, with X(u = 1,ϑ = 0) ≈ 1.7.
In fact, in most cases, the thermal component in soft X-ray contains a small fraction of the GRB energy; see Table 1. The baryonic shell may not necessarily be spherically symmetric as we assumed; clumps may have different thickness. The thinner clumps have earlier emission with higher temperature, and vice versa. The small ratio between thermal energy in X-ray and GRB energy can be explained assuming a small ratio of the total surface of relatively thin baryonic clumps to the total spherical area at that radius. Naturally, in the BdHN paradigm, these thin clumps are accumulated around the accreting source, the progenitor of GRB.
5.1. The case of GRB 090618
A thermal component has been inferred from observations of the early X-ray afterglow in GRB 090618. Following (Izzo et al. 2012) and (Ruffini et al. 2014), we summarize the parameters:
-
isotropic energy of GRBEiso = 2.9 × 1053 erg;
-
redshift z = 0.54;
-
observed duration of the thermal component in the early afterglow, t = 73 s;
-
observed temperature T is decreasing from 0.62 keV to 0.14 keV.
In the model described above, we neglected the initial kinetic energy of the shell and assumed that the interaction between the GRB outflow and the shell results in two effects: heating of the shell and its acceleration. The parameters of the shell were inferred from observations (Ruffini et al. 2014):
-
radius R = 2.6 × 1012 cm;
-
velocity v/c ≃ 0.49.
These parameters are relatively close to those discussed above. The observed trend of decreasing temperature can be explained by the expansion of the shell, neglected in our simplified treatment in Sect. 4. Given relativistic velocities of the shell, neither non-relativistic nor ultra-relativistic approximations can be used to infer the parameters of the clump. Instead, the full analytic solution (6) must be used. Therefore, from Eq. (6), we determine η = 0.95, then from Eq. (3) it follows that Ms = 0.17 M⊙, then the optical depth of the clump is found from Eq. (15), that is, Zϵτ = 1.6 × 106, then the length of the clump is obtained from Eq. (16), giving 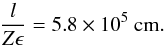 (20)With these parameters, the constraint Eq. (17) is not satisfied, as both terms appear to be almost equal. This implies that the observed temperature should be less than the one estimated below.
(20)With these parameters, the constraint Eq. (17) is not satisfied, as both terms appear to be almost equal. This implies that the observed temperature should be less than the one estimated below.
It is clear from Fig. 3 that, with these parameters, the energy of GRB outflow is divided almost equally between kinetic energy of the shell and its internal energy.
Assuming that the shell is composed of radioactive elements produced at the SN explosion, the atomic number should be approximately Z = 26; Eq. (18) gives a temperature of 6.9 keV, which is a factor ~10 higher than the one observed. Clearly, in our simplified treatment, this coincidence is remarkable. In fact, we assumed that the temperature and density distribution in the shell are uniform. However, realistic temperature and density profiles will give a smaller temperature at the photosphere, compared to the temperature in the interior of the shell.
Our model predicts that in the non-relativistic case (η ≲ 1) practically all the kinetic energy of the GRB outflow is transferred into internal energy of the baryonic shell, namely W ≃ E. In the case of GRB 090618, we have W ≃ E/ 2. However, the total energy in the thermal component is estimated to be only Ebb = 9 × 1050 erg. This can be explained if only a small fraction (ϵ ≃ 0.0031) of the GRB outflow actually interacts with thin baryonic clumps. We highlight that our model is also valid without imposing the spherical symmetry. This implies that the mass of thin baryonic material that emits thermal radiation seen in the early afterglow is M ~ 5 × 10-4M⊙. This is the lower limit to the total mass of baryonic material around the source. The rest of the material could be much more massive and thicker. This model also could explain unusual parameters of SN ejecta inferred from observations of the bump in the light curve at t ~ 106 s.
If the GRB outflow is spherical, interaction of this outflow with the main (thick) part of the SN ejecta (see Fig. 1), which contains most of the mass, will increase the internal energy, thus contributing to the bolometric luminosity of the optical SN light curve. This effect could explain why the nickel mass inferred from the optical luminosity by a single star collapsar model of GRB-SN connection is systematically higher than in normal type Ib/c SNe (Cano 2013).
This interpretation also provides a way to solve the puzzle of energy requirement in the GRB-SN connection, that for a GRB with very high energy, the isotropic energy of GRB 130427A, for example, is more than 1054 erg, and in the framework of a single star collapsar, the rest of the energy can hardly push the progenitor’s outer shell and generate a successful SN, but from the observation, the ejecta from the SN associated with GRBs has high velocity (Cano 2013), approximately 2.5 times the velocity of normal type Ib/c SN ejecta. This contradiction can easily be resolved considering the energy transfer from GRB outflow to SN ejecta, the kinetic energy of SN ejecta between GRB-associated SN and normal SN has a marked difference of approximately 1052 erg, which is similar to the GRB energy.
 |
Fig. 4 Temperature and radius of the thermal component in the prompt emission (gray points) and in the afterglow (blue points), plotted in the observer’s frame. Upper: single power-law fitting of the temperature in the prompt emission (dashed line, power-law index ~−0.5) clearly shows its extrapolation lays much higher than the temperature in the afterglow (power-law index ~−2). Bottom: radius in the afterglow (~1012 cm) is much larger than the radius in the prompt emission (109–1010 cm). The value of temperature and radius in the prompt emission are reproduced from (Izzo et al. 2012). |
For GRB 090618, the thermal component with decreasing temperature in the range 10–100 keV within the first 50 s is observed, as shown in Fig. 4. As can be seen from the figure, the thermal component in the early afterglow does not follow the same power law behavior. Moreover, the temperature here decreases much steeper than t− 2/3−t− 1/2, as observed in the prompt emission of many GRBs (Ryde & Pe’er 2009). This consideration supports the idea that the thermal component in the early afterglow has a different origin: in this article this component is attributed to the collision of GRB outflow and a baryonic shell.
Observational parameters and deduced temperatures of five SN-associated GRBs, assuming Z = 30.
5.2. More examples
We consider five GRBs (see Table 1); all of them show supernova signal; either from the spectral aspect, or a bump in the optical light-curve is detected. Only the prominent part of the thermal radiation is observed due to the capacity of satellites. Therefore, the time tD from the observation should be shorter than the real thermal emission time. However, it is reasonable to employ the observed tD as an approximation since a great fraction of the total thermal energy is released during tD.
In the table, only three GRBs have isotropic energy larger than Eiso> 1052 erg, and they are interpreted as BdHNs; see (Pisani et al. 2016).
Table 1 shows the observational parameters and the temperature deduced from Eq. (18), and the ratio (defined as ϵ) of observed total thermal energy Ebb in the early X-ray afterglow versus isotropic energy. We notice that temperature, radius, and velocity in the table are the averaged value, since not all the GRBs provide adequate data to perform precisely time-resolved analyses. For energetic GRBs with Eiso> 1052 erg, common patterns are found, as radius increases while temperature decreases within the duration tD, shown in Fig. 4, taking GRB 090618 as an example. This is in agreement with Eq. (18).
The temperatures deduced are universally higher than the observed ones, and a trend that the deduced temperature increases along with the observed temperature can be found. These results are in agreement with our expectations, as Eq. (18) depicts the average temperature measured in the interior of the shell. More precise work shall introduce a temperature distribution profile, and a steep gradient of temperature always exists at the outer edge, which emits thermal photons. A detailed simulation will be given elsewhere.
In GRBs 100418A and 0810007, reported in Table 1, the thermal component is observed, but the radius of emission does not change with time, that is, velocity is consistent with zero. Our model assumes that the baryonic shell is moving after the interaction with the outflow, and it cannot be applied to such cases. It is interesting to note that the isotropic energy of both GRBs is lower than 1052 erg.
6. Comparison with previous works
Several scenarios are suggested in the literature for the explanation of the thermal component observed in the early afterglows of some GRBs.
The shockwave breakout in the supernova naturally produces thermal emission; see, for example, (Campana et al. 2006; Waxman et al. 2007; Li 2007). However, this emission is too weak to explain the observed high luminosity in a distant radius (Bayless et al. 2015). Moreover, the duration of the shockwave breakout event is inconsistent with the observed long duration in the order of hundreds to thousands of seconds (Ghisellini et al. 2007; Starling et al. 2012).
Friis & Watson (2013) link the thermal radiation observed in the early afterglow to the prompt phase via photospheric emission from the jet. However, the observed temperature of the thermal component in the early afterglow decreases much steeper than t− 2/3−t− 1/2, as observed in the prompt emission of many GRBs (Ryde & Pe’er 2009), so it cannot be interpreted as part of the photospheric emission; see also (Larsson et al. 2015), who reached the same conclusion for GRB 101219b.
Some authors interpret the thermal emission observed in some GRBs as coming from a hot plasma “cocoon” emerging when the GRB jet breaks out from the progenitor star, Pe’er et al. (2006), Suzuki & Shigeyama (2013), Piro et al. (2014). However, the observed energies, radii, and expansion velocities are difficult to explain with this model (Friis & Watson 2013). Unlike the cocoon scenario (Pe’er et al. 2006), where the cocoon is entrained by the mild-relativistic jet propagating inside the star, in our scenario, the baryonic shell interacts with the ultra-relativistic outflow composed of baryons and associated electrons, as well as photons. The outflow is accelerated to ultra-relativistic velocity in the region that is evacuated by the accretion process, see Fig. 1.
Some authors (Granot et al. 2003) discuss refreshed shocks as the origin of re-brightening in the afterglow light curve. In that scenario, the kinetic energy of the central engine is dissipated in shock waves, produced in optically thin medium. The non-thermal emission in this model is generated within the standard relativistic shock model with synchrotron emission from electrons having power law distribution in energy moving in a magnetic field; see, for example, (Kumar & Piran 2000). In contrast, in our scenario, the optical depth at which the GRB outflow interacts with the baryonic material is high enough, such that the emitted photons have sufficient time to thermalize before escaping the plasma. This is why the internal energy, generated during the interaction, is emitted in the form of thermal radiation, rather than non-thermal radiation proposed by Granot et al. (2003).
7. Conclusions
The observed parameters of the thermal component in the early afterglow in GRB 090618 are reproduced by considering the interaction of the GRB outflow with the part of the SN ejecta having a mass of 10-4M⊙ and a thickness of 107 cm. Similarly, the parameters of associated baryonic shells are also obtained for another two GRBs, namely 060729 and 130427A.
Our results suggest an alternative explanation of the observed thermal signal in the early afterglow for GRBs with isotropic energies above 1052 erg. We propose that this thermal component is produced by the interaction of the GRB outflow with part of the SN ejecta, which is accelerated and heated. Instead, for weaker GRBs with isotropic energies below 1052 erg, we found that the thermal component is emitted by a source with velocity consistent with zero. These results are in agreement with the classification of GRBs proposed by Ruffini et al. (2016).
Our approach also offers natural solutions to the difficulties existing in the collapsar model by interpreting the observed high velocity, high kinetic energy and high mass of SN ejecta in the SN-GRB connections by transferring energy from GRB outflow to SN ejecta in the binary progenitor.
Acknowledgments
We thank the anonymous referee for his remarks and suggestions, which allowed us to improve the presentation of our results.
References
- Bayless, A. J., Even, W., Frey, L. H., et al. 2015, ApJ, 805, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bufano, F., Pian, E., Sollerman, J., et al. 2012, ApJ, 753, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Mangano, V., Blustin, A. J., et al. 2006, Nature, 442, 1008 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cano, Z. 2013, MNRAS, 434, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Friis, M., & Watson, D. 2013, ApJ, 771, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Rueda, J. A., & Ruffini, R. 2014, ApJ, 793, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., & Tavecchio, F. 2007, MNRAS, 382, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Nakar, E., & Piran, T. 2003, Nature, 426, 138 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hjorth, J. & Bloom, J. S. 2012, in The Gamma-Ray Burst – Supernova Connection (Cambridge: Cambridge University Press), 169 [Google Scholar]
- Izzo, L., Ruffini, R., Penacchioni, A. V., et al. 2012, A&A, 543, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumar, P., & Piran, T. 2000, ApJ, 535, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Larsson, J., Racusin, J. L., & Burgess, J. M. 2015, ApJ, 800, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X. 2007, MNRAS, 375, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Starling, R. L. C., Fitzpatrick, G., et al. 2011, MNRAS, 416, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Pe’er, A., Meszaros, P., & Rees, M. J. 2006, ApJ, 652, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 1999, Phys. Rep., 314, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, L., Troja, E., Gendre, B., et al. 2014, ApJ, 790, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Pisani, G. B., Ruffini, R., Aimuratov, Y., et al. 2016, ApJ, 833, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Rueda, J. A., & Ruffini, R. 2012, ApJ, 758, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Salmonson, J. D., Wilson, J. R., & Xue, S.-S. 2000, A&A, 359, 855 [NASA ADS] [Google Scholar]
- Ruffini, R., Aksenov, A. G., Bernardini, M. G., et al. 2009, in Cosmology and Gravitation: XIII Brazilian School on Cosmology and Gravitation (XIII BSCG), AIP Conf. Proc. 1132, 199 [Google Scholar]
- Ruffini, R., Siutsou, I. A., & Vereshchagin, G. V. 2013, ApJ, 772, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Muccino, M., Bianco, C. L., et al. 2014a, A&A, 565, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruffini, R., Siutsou, I. A., & Vereshchagin, G. V. 2014b, New Astron., 27, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Wang, Y., Enderli, M., et al. 2015, ApJ, 798, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Rueda, J. A., Muccino, M., et al. 2016, ApJ, 832, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, F., & Pe’er, A. 2009, ApJ, 702, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., & Starling, R. L. C. 2012, MNRAS, 427, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Page, K. L., Pe’er, A., Beardmore, A. P., & Osborne, J. P. 2012, MNRAS, 427, 2950 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, A., & Shigeyama, T. 2013, ApJ, 764, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Vereshchagin, G. V. 2014, Int. J. Mod. Phys. D, 23, 30003 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E., Mészáros, P., & Campana, S. 2007, ApJ, 667, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observational parameters and deduced temperatures of five SN-associated GRBs, assuming Z = 30.
All Figures
 |
Fig. 1 Cartoon illustrating the binary system left after the explosion of the SN and formation of the GRB. GRB outflow collides with the SN ejecta and interacts with baryonic material on its way out to the distant observer. |
| In the text | |
 |
Fig. 2 Two functions are shown: the dimensionless velocity parameter u = Γv/c of the shell after the interaction with the GRB outflow (thick), as a function of the parameter η = E/ (Mc2), as well as the ratio between the internal energy and the initial energy (thin), ω/η = W/E, as a function of the same parameter η. The dotted (dashed) line shows the non-relativistic (ultra-relativistic) asymptotics for u, while the dash-dotted line shows the ultra-relativistic asymptotics for W/E. |
| In the text | |
 |
Fig. 3 Ratio between internal (dashed) and kinetic (solid) energy of the shell to initial energy E (dotted) after the interaction. In the non-relativistic case with η ≪ 1, all the energy of the GRB outflow is transformed into internal energy (heat) of the baryonic shell. In the ultra-relativistic case with η ≫ 1, the energy of the GRB outflow is transformed mostly into kinetic energy of the shell. |
| In the text | |
 |
Fig. 4 Temperature and radius of the thermal component in the prompt emission (gray points) and in the afterglow (blue points), plotted in the observer’s frame. Upper: single power-law fitting of the temperature in the prompt emission (dashed line, power-law index ~−0.5) clearly shows its extrapolation lays much higher than the temperature in the afterglow (power-law index ~−2). Bottom: radius in the afterglow (~1012 cm) is much larger than the radius in the prompt emission (109–1010 cm). The value of temperature and radius in the prompt emission are reproduced from (Izzo et al. 2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


