| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629806 | |
| Published online | 21 February 2017 | |
Asteroseismology of ZZ Ceti stars with fully evolutionary white dwarf models
I. The impact of the uncertainties from prior evolution on the period spectrum
1 Grupo de Evolución Estelar y Pulsaciones. Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
2 Instituto de Astrofísica La Plata (IALP – CONICET), Paseo del Bosque s/n, 1900 La Plata, Buenos Aires, Argentina
3 Departamento de Astronomia, Universidade Federal do Rio Grande do Sul, Av. Bento Goncalves 9500, 91501-970 Porto Alegre, RS, Brazil
e-mail: fdegeronimo@fcaglp.unlp.edu.ar
Received: 28 September 2016
Accepted: 28 November 2016
Context. ZZ Ceti stars are pulsating white dwarfs with a carbon-oxygen core build up during the core helium burning and thermally pulsing Asymptotic Giant Branch phases. Through the interpretation of their pulsation periods by means of asteroseismology, details about their origin and evolution can be inferred. The whole pulsation spectrum exhibited by ZZ Ceti stars strongly depends on the inner chemical structure. At present, there are several processes affecting the chemical profiles that are still not accurately determined.
Aims. We present a study of the impact of the current uncertainties of the white dwarf formation and evolution on the expected pulsation properties of ZZ Ceti stars.
Methods. Our analysis is based on a set of carbon-oxygen core white dwarf models with masses 0.548 and 0.837 M⊙ that are derived from full evolutionary computations from the ZAMS to the ZZ Ceti domain. We considered models in which we varied the number of thermal pulses, the amount of overshooting, and the 12C(α,γ)16O reaction rate within their uncertainties.
Results. We explore the impact of these major uncertainties in prior evolution on the chemical structure and expected pulsation spectrum. We find that these uncertainties yield significant changes in the g-mode pulsation periods.
Conclusions. We conclude that the uncertainties in the white dwarf progenitor evolution should be taken into account in detailed asteroseismological analyses of these pulsating stars.
Key words: asteroseismology / stars: evolution / white dwarfs / stars: oscillations
© ESO, 2017
1. Introduction
White dwarf (WD) stars are the final result of the evolution of low- and intermediate-mass (up to ~10.6 M⊙, Woosley & Heger 2015) stars. A carbon-oxygen core composition, which is expected in most WDs, is the result of He burning in the core of progenitor stars. The exact proportions of the resulting carbon-oxygen composition is a key factor that determines the cooling properties of the emerging WDs. In addition, the precise shape of the chemical abundance distribution is critical for the pulsational properties of these stars.
ZZ Ceti (or DAV) variable stars are pulsating WDs with H-rich atmospheres. Located in a narrow instability strip with effective temperatures between 10 500 K and 12 500 K (Fontaine & Brassard 2008; Winget & Kepler 2008; Althaus et al. 2010b), ZZ Ceti stars constitute the most numerous class of compact pulsators. These stars are characterized by multimode photometric variations caused by non-radial, g-mode pulsations of low degree (ℓ ≤ 2) with periods between 70 and 1500 s and amplitudes up to 0.30 mag. These pulsations are thought to be excited by both the κ−γ mechanism acting on the base of the H partial ionization zone (Dolez & Vauclair 1981; Winget et al. 1982) and the “convective driving” mechanism (Brickhill 1991; Goldreich & Wu 1999; Saio 2013). Since the discovery of the first ZZ Ceti star, HL Tau 76 by Landolt (1968), a continuous effort has been made to model the interior of these variable stars.
The comparison of the observed pulsation periods in WD with the periods computed from appropriate theoretical representative models allows us to infer details about the origin and evolution of the progenitor star (Fontaine & Brassard 2008; Winget & Kepler 2008; Althaus et al. 2010b). In particular, asteroseismological analysis of ZZ Ceti stars provides strong constraints on the stellar mass, thickness of the outer envelopes, core chemical composition, and stellar rotation rates (e.g., Romero et al. 2012). In addition, ZZ Ceti asteroseismology is a valuable tool for studying axions (Isern et al. 1992, 2010; Bischoff-Kim et al. 2008; Córsico et al. 2012, 2016) and crystallization (Montgomery et al. 1999; Córsico & Althaus 2004; Córsico et al. 2005; Metcalfe et al. 2004; Kanaan et al. 2005; Romero et al. 2013).
There are two main approaches adopted for WD asteroseismology. The first employs static stellar models with parametrized chemical profiles. This approach has the advantage that it allows a full exploration of the parameter space to find an optimal seismic model (Bischoff-Kim & Østensen 2011; Bischoff-Kim et al. 2014; Giammichele et al. 2014, 2016). The other approach uses fully evolutionary models resulting from the complete evolution of the progenitor star, from the zero age main sequence (ZAMS) to the WD stage (Romero et al. 2012, 2013). This approach involves the most detailed and updated input physics, in particular regarding the internal chemical structure, which is a crucial aspect for correctly disentangling the information encoded in the pulsation patterns of variable WDs. This method has been successfully applied in different classes of pulsating WDs (see Romero et al. 2012, 2013, in the case of ZZ Ceti stars). However, asteroseismological inferences based on this approach do not take the current uncertainties either in the modeling or input physics of WD progenitors into account. An assessment of the impact of these uncertainties on the pulsation periods of ZZ Ceti stars, constitutes the core feature of the present paper.
In this regard, several important uncertainties linked to WD prior evolution exist that should be explored. As is well known, the exact proportions of the carbon-oxygen composition of the WD core constitute a key factor that strongly impacts the cooling properties of the emerging WDs. In addition, the precise shape of the chemical abundance distribution is critical for the pulsational properties of WDs. The main uncertainty affecting the carbon-oxygen chemical profiles and the cooling times in WDs is related to the 12C(α,γ)16O reaction rate. Salaris et al. (2010) studied the differences found in cooling times that arise from uncertainties in several processes during the pre-WD evolution, and found that the changes in cooling times associated with the 12C(α,γ)16O reaction rate was of about 7%. More recently, Fields et al. (2016) have carried out an extensive study of the impact of uncertainties in several reaction rates during core H and He burning on important stellar parameters, such as mass, age, carbon-oxygen central abundances, and central density. These investigators found that uncertainties in the 12C(α,γ)16O and 14N(p,γ)15O are dominant. Another uncertain process that modifies the chemical structure is overshooting (OV). The precise size of the convective core and mixing regions are currently one of the major uncertainties affecting the computations of stellar structure and evolution. In particular, the amount of OV considered during core He burning is not completely known and strongly modifies the internal carbon-oxygen profile, mass of the convective core, and temperature stratification. Current uncertainties in physical processes operative during the thermally pulsing asymptotic giant branch (TP-AGB) phase also leave their signature in the final chemical abundance distribution expected in WDs. In particular, the outermost-layer chemical stratification of the WD core is built up during the TP-AGB phase and depends strongly on the occurrence of OV and mass loss during this stage. In particular, the mass of the intershell rich in He and C that is left by the short-lived He flash convective zone depends on both the amount of OV and the number of thermal pulses (TP) which is determined by the poorly constrained efficiency of mass loss (Karakas & Lattanzio 2014).
In this paper, we assess the impact of the main uncertain processes in the evolutionary history of the progenitors on the chemical profiles and pulsation period spectrum of ZZ Ceti stars. In particular, we focus on the effects of OV during the core He burning stage, the occurrence and number of TP in the AGB phase, and the uncertainties in the 12C+ α reaction rate. To this end, we computed evolutionary sequences from the ZAMS through the TP-AGB stage following the evolution of the remnant star to the WD state until the domain of the ZZ Ceti instability strip. The sequences are characterized by progenitor masses of 1.5 and 4 M⊙ with initial metallicity of Z = 0.01.
This paper is organized as follows: in Sect. 2 we introduce the numerical tools employed, the input physics assumed in the evolutionary calculations as well as the pulsation code employed. In Sect. 3 we present our results. Finally, in Sect. 4 we conclude the paper by summarizing our findings.
2. Computational tools
2.1. Evolutionary code and input physics
The DA WD evolutionary models calculated in this work were generated with the LPCODE evolutionary code, which produces detailed WD models based on updated physical description (Althaus et al. 2005, 2010a; Ronedo et al. 2010; Romero et al. 2012; Miller Bertolami 2016). We employed LPCODE to study different aspects of the evolution of low-mass stars (Wachlin et al. 2011; Althaus et al. 2013, 2015), formation of horizontal branch stars (Miller Bertolami et al. 2008), extremely low mass WDs (Althaus et al. 2013), AGB, and post-AGB evolution (Miller Bertolami 2016). The main physical ingredients of LPCODE relevant to this work are: i) the standard mixing-length theory with the free parameter α = 1.61 was adopted for pre-WD stages; ii) diffusive OV during the evolutionary stages prior to the TP-AGB phase was allowed to occur following the description of Herwig et al. (1997). We adopted f = 0.016 for all sequences, except when indicated. Overshooting is relevant for the final chemical stratification of the WD (Prada Moroni & Straniero 2002; Straniero et al. 2003); iii) breathing pulses, which occurs at the end of core He burning, were suppressed (see Straniero et al. 2003, for a discussion on this topic); iv) LPCODE considers a simultaneous treatment of non-instantaneous mixing and burning of elements. Our nuclear network accounts explicitly for the following 16 elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne, and 34 thermonuclear reaction rates (Althaus et al. 2005); v) gravitational settling and thermal and chemical diffusion were taken into account for 1H, 3He, 4He,12C,13C, 14N, and 16O (Althaus et al. 2003); vi) during the WD phase, chemical rehomogenization of the inner carbon-oxygen profile induced by Rayleigh-Taylor (RT) instabilities was implemented following Salaris et al. (1997); vii) for the high-density regime characteristic of WDs, we used the equation of state of Segretain et al. (1994), which accounts for all the important contributions for both the liquid and solid phases.
 |
Fig. 1 Upper panels: inner O, C and He abundance distribution in terms of the outer mass fraction for the two stellar models considered in our analysis at Teff ~ 12 000 K. 0TP refers to the expected chemical profiles resulting from a progenitor before the occurrence of the first TP (red dashed line). 3TP corresponds to the case of the chemical profiles resulting from a progenitor at end of the third TP (black solid line). |
We computed the evolution of our sequences throughout all the evolutionary stages of the WD progenitor, including the stable core He burning and the TP-AGB and post-AGB phases. The LPCODE has been compared against other WD evolution code, showing 2% differences in the WD cooling times that come from the different numerical implementations of the stellar evolution equations (Salaris et al. 2013).
2.2. Pulsation code
For the pulsation analysis presented in this work, we employed the LP-PUL adiabatic non-radial pulsation code described in Córsico & Althaus (2006) coupled to the LPCODE evolutionary code. LP-PUL solves the full fourth-order set of real equations and boundary conditions governing linear, adiabatic, and non-radial stellar pulsations. The pulsation code provides the eigenfrequency ωℓ,k, where k is the radial order of the mode, and the dimensionless eigenfunctions y1,...,y4. The LP-PUL code computes the periods (Πℓ,k), rotation splitting coefficients (Cℓ,k), oscillation kinetic energy (Kℓ,k), and weight functions (Wℓ,k). The expressions to compute these quantities can be found in the Appendix of Córsico & Althaus (2006). The Brunt-Väisälä frequency (N) is computed as (Tassoul et al. 1990) 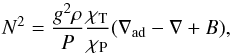 (1)where
(1)where 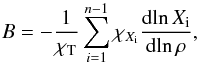 (2)is the Ledoux term and contains the contribution coming from the chemical composition changes, and
(2)is the Ledoux term and contains the contribution coming from the chemical composition changes, and ![\begin{equation} \chi_{\rm T} = \left [\frac{\partial\! \ln P}{\partial T} \right ]_{\rho},~ \chi_{\rho} = \left [\frac{\partial\! \ln P}{\partial \rho} \right ]_{\rm T},~ \chi_{X_i} = \left [\frac{\partial\! \ln P}{\partial X_i} \right]_{\rho, {\rm T}, X_{j \neq i}}\cdot \end{equation}](/articles/aa/full_html/2017/03/aa29806-16/aa29806-16-eq42.png) (3)
(3)
3. Pulsational analysis
In this section we study the uncertainties during the prior evolution of the progenitor star that affects the chemical structure of the emerging WDs and their pulsation period spectra. In particular, we explore
-
1.
The occurrence of TP during the AGB phase of the progenitorstar.
-
2.
The occurrence of OV during core He burning.
-
3.
The 12C(α,γ)16O reaction rate.
We concentrate on template models characterized by M⋆ = 0.548,0.837 M⊙, with an H-envelope mass of MH ~ 4 × 10-6M⋆ at Teff ~ 12 000 K, and considered the pulsation period spectrum for modes with ℓ = 1.
 |
Fig. 2 Inner He abundance distribution in terms of the outer mass for models at the ZZ Ceti stage for which the progenitor experienced no TP (0TP), three TP (3TP), and ten TP (10TP) models. The intershell region is eroded completely for the massive model. |
In Fig. 1 we show the internal chemical profiles and the logarithm squared Brunt-Väisälä frequency in terms of the outer mass fraction for both models at the ZZ Ceti domain. Our models are characterized by three chemical transition regions from center to the surface: a chemical interface of C and O, a double-layered chemical structure involving He, C, and O, and an interface of He/H. The existence of these three transition zones induces bumps in the shape of the Brunt-Väisälä frequency, which strongly affects the whole structure of the pulsation spectrum of the star, in particular the mode-trapping properties (Brassard et al. 1992; Bradley 1996; Córsico et al. 2002). These features play a crucial role, acting as filters by trapping the mode oscillation energy close to the surface, or confining this oscillation energy in the core.
Next, we compare the pulsation properties of the models considered for each case. Since the models compared have the same stellar mass1, effective temperature and mass of the H envelope, the differences found in the pulsation properties are strictly due to the differences in the chemical structure resulting from different kinds of progenitor evolution.
3.1. Occurrence of TP in AGB
In this section we explore the impact on the chemical profiles when the progenitor evolves through the TP-AGB phase. Because during this phase a pulse-driven convection zone develops, the building of an intershell region and a double-layered chemical structure is expected at the bottom of the He buffer. The size of this region decreases with the number of TP, i.e., as the star evolves through the TP-AGB, as a consequence of the He-burning shell. The number of TP experienced by the progenitor star is uncertain and depends on the rate at which mass is lost during the TP-AGB phase, on the initial metallicity of progenitor star, as well as, to a lesser extent, on the occurrence of extra mixing in the pulse-driven convection zone (Herwig 2000). To quantify the impact of all these uncertainties on the pulsational properties of ZZ Ceti stars, we explored the situation in which the progenitor experiences three and ten TP (hereinafter referenced as 3TP and 10 TP models) by forcing the departure from the TP-AGB phase at specific stages. In addition, we considered the extreme situation in which the star is forced to abandon the AGB phase before the occurrence of the first TP (hereinafter referred to as 0TP model).
 |
Fig. 3 Period differences (with fixed radial order k) in terms of k between the 0TP and 3TP models (black dashed line) and between the 10TP and 3TP models (black solid line) for the M⋆ = 0.548 M⊙ and M⋆ = 0.837 M⊙ WD models (left and right panels, respectively). |
In Fig. 1 we show the chemical profiles (upper panel) for the most abundant elements, and the logarithm of the squared Brunt-Väisälä (B-V) frequency (lower panel) in terms of the outer mass. As mentioned, the evolution through the TP-AGB leaves its signature on the chemical profile of our models with the formation of an intershell region rich in He and C at the bottom of the He buffer. The presence of C in the intershell region stems from the short-lived convective mixing that has driven the C-rich zone upward during the peak of the He pulse on the AGB (Althaus et al. 2010a). As we mentioned, the size of this intershell region depends on the number of TP experienced by the star, decreasing as the number of TP increases (see later in this Section). For the low-mass models, we find that this intershell region formed at the TP-AGB is expected to survive when the stars reach the ZZ Ceti phase. On the other hand, for more massive stars we do not expect this region to be present at the ZZ Ceti stage. This is because the diffusion processes acting during the WD cooling phase are more efficient for massive stars, thus completely eroding it (Althaus et al. 2010a). The impact on the chemical structure, and in consequence, on the B-V frequency, is more pronounced for the less massive model (see lower panels of Fig.1). The results for the 0TP model are shown with dashed red lines in the upper panels of Fig. 1. In this case, no intershell region is expected. In the case of the 10TP model sequence, the intershell region becomes less massive, and it is removed by diffusion by the time the ZZ Ceti stage is reached more easily than in the case of the 3TP model. This is borne out by Fig. 2, which depicts the He abundance distribution below the envelope of the emerging WD.
 |
Fig. 4 Same as Fig. 1, but for models at the third TP calculated with an OV parameter f = 0.016 (3TP) and with f = 0 (3TP-NOV) during core He burning. |
The impact of considering different numbers of TP on the period spectrum of the models can be seen in Fig. 3. In this plot, we show the resulting period differences (ΔPk ≡ Pk,0TP−Pk,3TP) between the 0TP and 3TP models (solid line and filled circles) and the period differences (ΔPk ≡ Pk,10TP−Pk,3TP) between the 10TP and 3TP models (dashed line and empty circles) as a function of the radial order k. We found that the resulting changes in the periods (at fixed k) are more pronounced in the case of the less massive model. These substancial variations, of as high as 22 s, are not solely due to the intershell region (or the overall shape of the profile), but are also due to the shift outward of the core/He main chemical transition region.
Not surprisingly, the expectation for the massive model are markedly different. Indeed, in this case the period differences are on average between 2 and 3 s, with some modes reaching period differences as high as ~8 s. These smaller changes resulting in the case of the massive model are due to the slight differences found in chemical profiles. In fact, no intershell is expected to occur at the ZZ Ceti domain.
3.2. Occurrence of OV during core He burning
The occurrence of extra mixing episodes during core He burning strongly affects the final shape of the carbon-oxygen core. To quantify the impact of the occurrence of core OV on the period spectrum of ZZ Ceti stars, we considered the extreme situation in which no OV is allowed during the core He burning (3TP-NOV model). We compared this situation to the template 3TP model, which, as we mentioned, takes OV during core He burning into account.
We start by examining Fig. 4, which shows the inner chemical profiles at the ZZ Ceti stage. Models with OV are characterized by lower central C abundances. This is because the ingestion of fresh He in a C-rich zone favors the consumption of C via the reaction 12C+ α with the consequent increase of 16O. This change in the central value of C and O does not modify the B-V frequency (lower panel). However, the B-V frequency is notoriously affected by the steep variation in the carbon-oxygen profile at −log (1−Mr/M⋆) ~ 0.4 left by core OV. The resulting differences in the value of the periods are shown in Fig. 5. We find that OV introduces absolute differences of 2 to 5 s on average, which is markedly lower than the period differences resulting from uncertainties in the TP-AGB phase. Also, the average of the period differences resulting from OV are similar for both stellar masses.
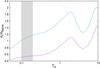 |
Fig. 6 Ratio between the Kh and Nacre, and Kl an Nacre reaction rates (upper and lower curves, respectively) as a function of temperature. Gray region denotes the typical temperatures expected during the core He burning. |
3.3. Uncertainties in the 12C(α,γ)16O reaction rate
 |
Fig. 7 Same as Fig. 1 but for models computed with three different 12C+ α reaction rates: Angulo et al. (1999; Nacre, black solid line), the higher (KH), and the lower (KL) reaction rates from Kunz et al. (2002; red dashed and blue dashed lines, respectively). |
 |
Fig. 8 Same as Fig. 3 but for the period differences between Kh and Nacre models, (black dashed line) and Kl and Nacre models (black solid line). |
To determine the impact of the uncertainties in the 12C+ α reaction rate, we computed the core He burning phase of the progenitors by considering three different values for the 12C(α,γ)16O reaction rate; we followed the evolution until the progenitor experienced several TP in the AGB-TP phase. We considered the reaction rates provided by Angulo et al. (1999) (Nacre, our reference model), and the extreme high and low values from Kunz et al. (2002) (Kh and Kl models, respectively). These high and low values are derived by the authors from the uncertainty for the recommended rate listed in that work. The use of these extreme values for this reaction rate allows us to account for the uncertainties in the carbon-oxygen chemical profiles of WD. In Fig. 6 we plot the temperature dependence of the ratio between the Kh and Nacre, and Kl an Nacre reaction rates. For core He burning temperatures (~2 × 108 K, gray zone), σKl/σNacre ~ 0.55 and σKh/σNacre ~ 1.1. The impact on the chemical profiles at the ZZ Ceti stage is depicted in Fig. 7. We found differences in the carbon-oxygen abundances, the location of the O/C and O/C/He chemical transitions, and the abundances of the intershell region. As expected, the 16O abundance is larger for the models computed with the Kh reaction rate. Models that were computed assuming the Nacre and Kh reaction rates exhibit very similar chemical structures. Differences in the B-V frequency are found at the carbon-oxygen and triple transition (see lower panels of Fig. 7).
The resulting impact on the pulsation periods can be seen in Fig. 8, in which we plot the differences between the periods predicted by the Kh and Nacre models (dashed line and empty circles) and the differences predicted by the Kl and Nacre models (solid line and filled circles). Low-order modes are, in general, more affected when the Kl reaction rate is assumed. In particular, for the 0.548 M⊙ model, appreciable differences are expected for both low and high radial-order modes, with maximum differences of | ΔP | ~ 11 s. By contrast, in the case of the massive model, small period differences are found for modes with radial orders k< 23, independent of the adopted rate, with a maximum of |ΔP| ~ 5 s. These small variations found in low-order modes reflect the much smoother behavior of the chemical profile at the outermost part of the carbon-oxygen core in the case of the massive model. But, for radial orders k> 23, appreciable differences are found, reaching |ΔP| ~ 18 s at most. The appreciable differences found for modes with radial orders k> 23 stems from the fact that some modes of high radial order k are sensitive to the chemical structure of the core.
4. Summary and conclusions
In this paper, we studied the impact of uncertainties from progenitor evolution on the pulsational properties of ZZ Ceti WD stars. We focused on the occurrence of TP in the AGB stage, the occurrence of OV during the core He burning and also the uncertainties in the 12C(α,γ)16O reaction rate. Our models were derived from the full and complete evolution from the ZAMS, through the TP-AGB. Evolution of our model sequences was followed to the domain of ZZ Ceti stars, for which we computed the adiabatic g-mode pulsation properties. We computed various sets of models in which we varied the amount of OV during core He burning, the 12C(α,γ)16O reaction rate, and the occurrence and number of TP during the TP-AGB phase.
We found that whether or not progenitor evolves through the TP-AGB phase makes an important point as far as the pulsational properties at the ZZ Ceti stage are concerned. In particular, we found that the resulting changes in the periods (at fixed k) are more pronounced in the case of the less massive model, with period differences on average between 5 and 10 s. However, for massive models, the period differences are markedly smaller (~2–3 s). This is mainly because the shift of the core/He main chemical transition is less pronounced and the double layered chemical structure buildup during the last TP on the AGB, which impacts the period spectrum of pulsating WDs (Althaus et al. 2010a), is completely eroded by element diffusion in the massive WDs (M⋆ ≳ 0.80 M⊙) by the time the domain of the ZZ Ceti stars is reached.
On the other hand, the occurrence of OV during the core He burning leaves imprints on the Brunt-Väisälä frequency, resulting in absolute differences of 2 to 5 s on average in the pulsation periods, as compared with the situation in which OV is disregarded. This conclusion is the same regardless of the stellar mass.
Finally, uncertainties related with the 12C+ α reaction rate affects both O, C, and He abundances and the location of the chemical transitions. In the case of less massive models, the changes in period induced by these different chemical structures amount to, at most, | ΔP | ~ 11 s for some specific modes. For our massive model, period differences are relevant only for k ≥ 20 modes. The period differences resulting from uncertainties of the 12C+ α reaction rate are less relevant than the period differences inflicted by uncertainties in OV during core He burning and by the occurrence of TP.
We conclude that the current uncertainties in the chemical profiles of WDs, resulting from the progenitor evolution, impact the pulsational period spectrum of ZZ Ceti stars. In this paper, we quantified the magnitude of this impact for the first time. The amount of the resulting period changes is larger than the typical uncertainties of the observed periods and also higher than the typical accuracy of the period-to-period fits of Romero et al. (2012) which is, on average, less than 3.5 s. However, we stress that the differences of the periods we found must be considered as upper limits, since they correspond to extreme uncertainties in prior evolution. In addition, the largest period differences are found to occur only at certain specific modes rather than at the whole period spectrum. Anyway, these uncertainties should be taken into account in any asteroseismological analysis of ZZ Ceti stars. We defer an assessment of this issue to a future work.
Acknowledgments
We acknowledge the valuable comments of our referee that improved the original version of this paper. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR and by the PIP 112-200801-00940 grant from CONICET. This research has made use of NASA Astrophysics Data System.
References
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010a, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010b, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., & Østensen, R. H. 2011, ApJ, 742, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., Montgomery, M. H., & Winget, D. E. 2008, ApJ, 675, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., Østensen, R. H., Hermes, J. J., & Provencal, J. L. 2014, ApJ, 794, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A. 1996, ApJ, 468, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., & Hansen, C. J. 1992, ApJS, 80, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Brickhill, A. J. 1991, MNRAS, 251, 673 [NASA ADS] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2004, A&A, 428, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Benvenuto, O. G., & Serenelli, A. M. 2002, A&A, 387, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Montgomery, M. H., García-Berro, E., & Isern, J. 2005, A&A, 429, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., et al. 2012, MNRAS, 424, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Romero, A. D., Althaus, L. G., et al. 2016, J. Cosmology Astropart. Phys., 7, 036 [Google Scholar]
- Dolez, N., & Vauclair, G. 1981, A&A, 102, 375 [NASA ADS] [Google Scholar]
- Fields, C. E., Farmer, R., Petermann, I., Iliadis, C., & Timmes, F. X. 2016, ApJ, 823, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Fontaine, G., Brassard, P., & Charpinet, S. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 285 [Google Scholar]
- Giammichele, N., Fontaine, G., Brassard, P., & Charpinet, S. 2016, ApJS, 223, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Wu, Y. 1999, ApJ, 511, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Isern, J., Hernanz, M., & García-Berro, E. 1992, ApJ, 392, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Althaus, L. G., & Córsico, A. H. 2010, A&A, 512, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanaan, A., Nitta, A., Winget, D. E., et al. 2005, A&A, 432, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Landolt, A. U. 1968, ApJ, 153, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Montgomery, M. H., & Kanaan, A. 2004, ApJ, 605, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, M. H., Klumpe, E. W., Winget, D. E., & Wood, M. A. 1999, ApJ, 525, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., et al. 2012, MNRAS, 420, 1462 [Google Scholar]
- Romero, A. D., Kepler, S. O., Córsico, A. H., Althaus, L. G., & Fraga, L. 2013, ApJ, 779, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H. 2013, in EPJ Web Conf., 43, 05005 [Google Scholar]
- Salaris, M., Domínguez, I., García-Berro, E., et al. 1997, ApJ, 486, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., Pietrinferni, A., Kowalski, P. M., & Isern, J. 2010, ApJ, 716, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O., Domínguez, I., Imbriani, G., & Piersanti, L. 2003, ApJ, 583, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., van Horn, H. M., Tassoul, M., et al. 1982, ApJ, 252, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2015, ApJ, 810, 34 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Upper panels: inner O, C and He abundance distribution in terms of the outer mass fraction for the two stellar models considered in our analysis at Teff ~ 12 000 K. 0TP refers to the expected chemical profiles resulting from a progenitor before the occurrence of the first TP (red dashed line). 3TP corresponds to the case of the chemical profiles resulting from a progenitor at end of the third TP (black solid line). |
| In the text | |
 |
Fig. 2 Inner He abundance distribution in terms of the outer mass for models at the ZZ Ceti stage for which the progenitor experienced no TP (0TP), three TP (3TP), and ten TP (10TP) models. The intershell region is eroded completely for the massive model. |
| In the text | |
 |
Fig. 3 Period differences (with fixed radial order k) in terms of k between the 0TP and 3TP models (black dashed line) and between the 10TP and 3TP models (black solid line) for the M⋆ = 0.548 M⊙ and M⋆ = 0.837 M⊙ WD models (left and right panels, respectively). |
| In the text | |
 |
Fig. 4 Same as Fig. 1, but for models at the third TP calculated with an OV parameter f = 0.016 (3TP) and with f = 0 (3TP-NOV) during core He burning. |
| In the text | |
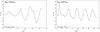 |
Fig. 5 Same as Fig. 3 but for the 3TP and 3TP-NOV models shown in Fig. 4. |
| In the text | |
 |
Fig. 6 Ratio between the Kh and Nacre, and Kl an Nacre reaction rates (upper and lower curves, respectively) as a function of temperature. Gray region denotes the typical temperatures expected during the core He burning. |
| In the text | |
 |
Fig. 7 Same as Fig. 1 but for models computed with three different 12C+ α reaction rates: Angulo et al. (1999; Nacre, black solid line), the higher (KH), and the lower (KL) reaction rates from Kunz et al. (2002; red dashed and blue dashed lines, respectively). |
| In the text | |
 |
Fig. 8 Same as Fig. 3 but for the period differences between Kh and Nacre models, (black dashed line) and Kl and Nacre models (black solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


