EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 598 (February 2017) A&A, 598 (2017) A75 Full HTML
Free Access
Issue
A&A
Volume 598, February 2017
Article Number A75
Number of page(s) 6
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201629361
Published online 03 February 2017

© ESO, 2017

1. Introduction

The collision processes of light elements H (D), He, and Li play a dominant role in the chemistry of the early universe and in the formation of first cosmological objects (Lepp et al. 2002). Lithium abundances in stellar atmospheres are the key observational parameters, providing information about the stellar evolution (Lambert 1993; Carlsson & Shchukina 1994). The abundances of Li, Li+ and Li− in the early universe are on the order of 10-10, 10-11 and 10-18, respectively (Palla et al. 1995; Stancil et al. 1996). The lithium chemistry in the recombination era of the universe was analyzed in detail in Stancil et al. (1996, 1998), and Galli & Palla (1998). Despite its small abundance, the Li− ion can still play a significant role in the overall chemistry of the early universe due to the highly diffuse nature of its weakly bound electron, which has a binding energy of 0.6180492 eV (Gunnar et al. 1996). Recently, the nonradiative charge transfer process Li− + H → Li + H− has been studied by the quantum-mechanical molecular orbital close coupling (QMOCC) method and it was found that in the temperature range 103−106 K its rate coefficient increases from ~ 10-12 cm3 s-1 to 10-7 cm3 s-1.In the present article we study, via a fully quantum mechanical approach, the radiative charge transfer (RCT) and radiative association (RA) processes in the Li− + H collision system

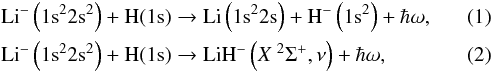\begin{eqnarray} && {\rm {Li}^{-}\left(1s^22s^2\right)+H(1s)\rightarrow \text{Li} \left(1s^22s\right)+H^{-}\left(1s^2\right)}+\hbar\omega, \label{chargetransfer} \\ && {\rm \text{Li}^{-}\left(1s^22s^2\right)+H(1s)} \rightarrow \text{LiH}^{-}\left(X\text{ }^2\Sigma^+, \nu\right)+\hbar\omega, \label{association} \end{eqnarray}where ν denotes the vibrational state of LiH− in its ground electronic state.

To the best of our knowledge these processes have not been studied before. The article is organized as follows. In Sect. 2 we briefly outline the theoretical methods used for the description of processes (1) and (2). In Sect. 3 we present and discuss the results of our electronic structure and scattering calculations. Finally, a brief summary is given in Sect. 4. Atomic units are used in remainder of this article, unless explicitly indicated otherwise.

2. Theoretical methods

2.1. The fully quantum mechanical method

The fully quantum mechanical method for calculation of RCT is described in detail in Stancil & Zygelman (1996) and Zygelman & Dalgarno (1988) and for the radiative association in Zygelman & Dalgarno (1990), Zygelman et al. (1998), and da Silva Jr et al. (2015). Here we give only a brief outline. After decomposing the continuum wave functions of the system in its initial (A) and final (X) state of reaction (1) into partial waves with angular momenta J and J′, respectively, the RCT cross section can be derived in the form σRCT=83(πkA)2∫0ωmaxω3c3∑J[JMJ,J−12(kA,kX)\begin{eqnarray} \sigma ^{\rm RCT}& =& \frac{8}{3}\left(\frac{\pi }{k_{A}}\right){}^2\int _0^{\omega _{\mathrm{\max} }}\frac{\omega ^3}{c^3}\sum _J [JM_{J,J-1}^2(k_{A},k_{X}) \nonumber \\ && +\,(J+1)M_{J,J+1}^2(k_{A},k_{X})]{\rm d}\omega. \label{3} \end{eqnarray}(3)Where the selection rule J′ = J ± 1 has been taken into account, c is speed of light, ω is the angular frequency of the emitted photon limited to ωmax by the maximum energy in the exit channel, kA and kX are the initial and final momenta, respectively, MJJ′ is the transition matrix coupling the initial and final molecular reaction states, MJJ′(kX,kA)=∫∞0dRfJ′X(kXR)D(R)fJA(kAR)\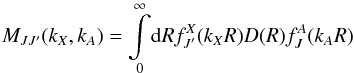begin{equation} M_{JJ'}(k_{X},k_{A})=\underset{0}{\overset{\infty }{\int }}{\rm d}Rf_{J'}^{X}(k_{X}R)D(R)f_J^A(k_{A}R) \label{4} \end{equation}(4)where D(R) is the dipole moment and kA and kX are given by 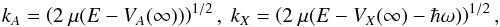kA=(2μ(E−VA(∞)))1/2,kX=(2μ(E−VX(∞)−ħω))1/2,\begin{equation} k_{A}=\left(2~\mu (E-V_{A}(\infty ))\right)^{1/2},\text{ }k_{X}=\left(2~\mu (E-V_{X}(\infty )-\hbar \omega) \right)^{1/2}, \label{5} \end{equation}(5)where E is the center-of-mass collision energy, VA and VX are the adiabatic potential energies of the initial and final molecular state, respectively, μ is the reduced mass of colliding system and R is the internuclear distance. The partial wave functions 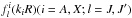fli(kiR)(i=A,X;l=J,J′)\hbox{$f_l^i(k_i R)(i=A,X;l=J,J')$} satisfy the homogeneous radial equation (d2dR2−l(l+1)R2−2μ[Vi(R)−Vi(∞)−ki2])fli(kiR)=0\begin{equation} \left(\frac{{\rm d}^2}{{\rm d}R^2}-\frac{l(l+1)}{R^2}-2\mu \left[V_i(R)-V_i(\infty )-k_i^2\right]\right)f_l^i(k_iR)=0 \label{6} \end{equation}(6)with the asymptotic (kiR → ∞) condition 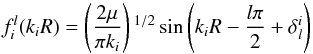fil(kiR)=(2μπki)1/2sin(kiR−lπ2+δli)\begin{equation} f_i^l(k_iR)=\left(\frac{2\mu }{\pi k_i}\right){}^{1/2}\sin \left(k_iR-\frac{l\pi }{2}+\delta _l^i\right) \label{7} \end{equation}(7)where 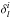δli\hbox{$\delta_l^i$} is the phase shift. The radiative association cross section is given by (da Silva Jr et al. 2015) 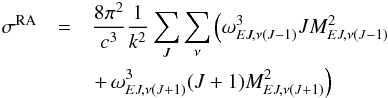σRA=8π2c31k2∑J∑ν(ωEJ,ν(J−1)3JMEJ,ν(J−1)2\begin{eqnarray} \sigma^{\rm RA}& = &\frac{8\pi ^2}{c^3}\frac{1}{k^2}\sum _J \sum _\nu \left(\omega_{{E}J,\nu(J-1)}^3JM_{{E}J,\nu(J-1)}^2\right. \nonumber \\ && \left. + \,\omega_{{E}J,\nu(J+1)}^3(J+1) {M_{{E}J,\nu(J+1)}^2}\right) \label{8} \end{eqnarray}(8)where k(= kA) and J are the wave number and the total angular momentum of the initial continuum state A with energy E, ν and J′(J′ = J ± 1) are the vibrational and rotational quantum numbers of the final bound electronic state X, respectively. The transition dipole moment MJ′,J is given again by Eq. (4) in which now the wave function 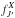fJ′X\hbox{$f_{J^{\prime}}^{X}$} describes a bound rovibrational state (ν,J′) in the potential well of ground electronic state X2Σ+ of the LiH− molecular ion with binding energy Eν,J′ and is normalized to unity. The energy of emitted photon is ħω = E + ΔE−Eν,J′ where ΔE is the energy difference between the VA(R) and VX(R) adiabatic potential energies. The partial wave function in the entrance channel 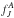fJA\hbox{$f_{J}^{A}$} satisfies Eq. (6) with the normalization form (7).

2.2. Optical-potential and semiclassical methods for radiative decay

The optical potential approach (Stancil & Zygelman 1996; Zygelman & Dalgarno 1988) is used to calculate the total collision induced radiative decay cross section, that is the sum of RCT and radiative association cross sections. In this approach the transition (decay) probability is represented by the imaginary part of a complex optical potential. The Jth partial scattering wave function 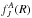fJA(R)\hbox{$f_{J}^A(R)$} in the entrance channel (A) is obtained by solving the Schrödinger equation [−12μd2dR2+J(J+1)2μR2+VA(R⇀)−E]FJA(R⇀)=i2A(R)FJA(R⇀)\begin{equation} \left[-\frac{1}{2\mu }\frac{{\rm d}^2}{{\rm d}R^2}+\frac{J(J+1)}{2\mu R^2}+V_{A}(\overset{\rightharpoonup }{R})-E\right]F_J^A(\overset{\rightharpoonup }{R})=\frac{i}{2}A(R)F_J^A(\overset{\rightharpoonup }{R}) \label{9} \end{equation}(9)where E is the collision energy and A(R) is the total collision induced radiative decay probability given by (Stancil & Zygelman 1996; Zygelman & Dalgarno 1988)

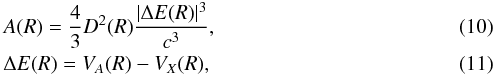\begin{eqnarray} && A(R)=\frac{4}{3}D^2(R)\frac{|\Delta E(R)|^3}{c^3}, \label{10} \\ && \Delta E(R)=V_{A}(R)-V_{X}(R), \label{11} \end{eqnarray}where VA(R), VX(R), and D(R) have the same meanings as before. The collision induced radiative decay cross section is given as (West et al. 1982; Cohen & Bardsley 1978; Zhao et al. 2004) σ(E)=πkA2∑J∞(2J+1)[1−exp(−4ηJ)],\begin{equation} \sigma (E)=\frac{\pi }{k_{A}^2}\sum _J^{\infty } (2J+1)[1-\exp (-4\eta _J)], \label{12} \end{equation}(12)where ηJ is the imaginary part of the phase shift for the Jth partial wave of the radial Schrödinger equation which in the distorted-wave approximation is given by (Stancil & Zygelman 1996; Cohen & Bardsley 1978) ηJ=π2∫0∞dR|FJA(kAR)|2A(R),\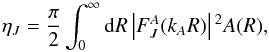begin{equation} \eta _J=\frac{\pi }{2}\int _0^{\infty }{\rm d}R\left|F_J^A(k_{A}R)\right|{}^2A(R), \label{13} \end{equation}(13)and kA=2μ[E−VA(∞)].\begin{equation} k_{A}=\sqrt{2\mu [E-V_{A}(\infty )]}. \label{14} \end{equation}(14)For high collision energies the number of angular momenta contributing to the sum (11) becomes very large and, using the classical relation between the angular momentum and the impact parameter, the summation over J in Eq. (11) can be replaced by integration over the impact parameter. 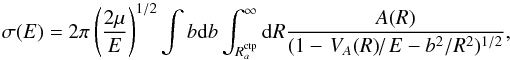Using further the Jeffreys-Wentzel-Kramers-Brillouin (JWKB) approximation for the phase shifts, one obtains the semiclassical expression for the radiative decay cross section (Chen 1967; Mizuno & Chen 1971)σ(E)=2π(2μE)1/2∫bdb∫Ractp∞dRA(R)(1−VA(R)/E−b2/R2)1/2,\begin{equation} \sigma (E)=2\pi \left(\frac{2\mu }{E}\right)^{1/2}\int b{\rm d}b\int _{R_a^{\rm ctp}}^{\infty }{\rm d}R\frac{A(R)}{(1-\left.V_{A}(R)\right/E-b^2/R^2){}^{1/2}}, \label{15} \end{equation}(15)where b is the impact parameter and 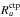Ractp\hbox{$R_{a}^{\rm ctp}$} is the classical turning point in the incoming channel. This formula has been used to calculate many cross sections of the radiative processes (Dalgarno et al. 1990; Andreazza et al. 1995; Bates 1951). For large energies (E ≥ VA), the integral is nearly energy independent and σ(E) varies as E− 1/2.

3. Results and discussions

3.1. Molecular structure calculations

In our previous work (Wu et al. 2016), the potential energy curves used in the scattering calculations have been calculated with the multireference single and double excitation configuration interaction (MRD-CI) method (Buenker & Phillips 1985; Stefan & Buenker 1995). In Fig. 1, the potential energy curves VX(R) and VA(R) of 12Σ+ and 22Σ+ molecular states, corresponding to the exit and entrance channels of reactions (1) and (2), respectively, are plotted for the range of internuclear distances R = 0.2−20au. It can be observed that at small internuclear distances these potentials exhibit rather deep potential wells with depths of about 2.156 eV and 1.670 eV and the equilibrium positions of 3.15 au and 3.05 au, respectively. The maximum height of the potential at R ≈ 6 au is about 0.4178 eV above the dissociation limit. The long range multipole interaction between colliding particles plays an important role in the collision processes for very low collision energies. Beyond R = 50 au, the potentials of the 12Σ+ and 22Σ+ states are described by the long-range interaction V(L)(R)=−12[C4R4+C6R6+C8R8]+E∞\begin{equation} V_\mathrm(L)(R)=-\frac{1}{2}\left[\frac{C_4}{R^4}+\frac{C_6}{R^6}+\frac{C_8}{R^8}\right]+E_{\infty } \label{longrange} \end{equation}(16)where C4,C6 and C8 are the dipole, quadrupole, and octupole polarizabilities of Li−(1s22s2) and H (1s) (Puchalski et al. 2011), respectively, and E∞ is the separated atom energy. The sharp change of the R behavior of the potential energy curve of the 22Σ+ state at R~ 6 au is because it has avoided crossing, at this internuclear distance, the potential energy curve of the 32 ∑ + state that asymptotically correlates with the H(1s) + Li−(1s22s2p03P°) configuration (Wu et al. 2016). The existence of this barrier in the potential of the entrance channel has significant effects on the cross sections of considered collision processes.

thumbnail Fig. 1

Adiabatic potential energy curves for HLi− as a function of internuclear distance R.

The dipole transition matrix element D(R) between 12Σ+ and 22Σ+ molecular states of HLi− as a function of internuclear distance R is plotted in Fig. 2. It exhibits a broad peak at internuclear distances around R ~ 12.5 au beyond which it rapidly decreases. The contribution of the dipole transition moment from the short R region (R < 7 au) to the final cross sections is expected to be very small.

thumbnail Fig. 2

Dipole transition matrix element between the 12Σ+ and 22Σ+ states of HLi−.

Table 1

Binding energies of vibrational levels in the potential well of the 22Σ+ state of HLi−.

The binding energies of vibrational levels in the potential well of the ground electronic state 22Σ+ of HLi−, obtained by solving the corresponding Schrödinger equation, are given in Table 1. The potential well of this state accommodates 41 vibrational levels.

3.2. Cross-section results

Using the expressions for the cross sections of RCT, radiative association (RA) and radiative decay processes given in Sect. 2 and the molecular structure results of the preceding subsection, we performed the cross-sections calculations and the results are presented in Fig. 3. The fully quantal calculations were performed in the energy range 10-10−10 eV, while the semiclassical and optical potential calculations were performed in the 10-4−10 eV energy range. In Fig. 3 the cross section for the nonradiative charge transfer (NRCT) from (Wu et al. 2016) is also shown for comparison. The figure shows that in the energy region below ~ 1 eV the RA cross section is larger than the RCT cross section (by two orders of magnitude for E< 10-3 eV), while for higher energies the opposite is true. The RA cross section becomes larger than the NRCT cross section for energies below ~ 10-4 eV. In the overlapping energy range the optical potential and semiclassical decay cross sections coincide with the sum of the fully quantal RA and RCT cross sections, except for the absence of any resonant structure in the semiclassical cross section in the 0.2−2 eV energy range. The most remarkable features of quantum mechanical RA and RCT cross sections in Fig. 3 are the sharp resonances in the energy range 0.2−2 eV and the few broad resonances in the energy region below ~ 10-5 eV. Similar resonant structures are also present in the quantal NRCT cross section and were discussed in detail in Wu et al. (2016). The origin of these resonances in the cross sections is the formation of quasi-bound states of the colliding system in the effective potential of the initial molecular state A2Σ+, 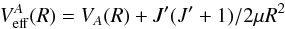VeffA(R)=VA(R)+J′(J′+1)/2μR2\begin{equation} V_{\rm eff}^A(R)=V_{A}(R)+J'(J'+1)/2\mu R^2 \label{eff-potential} \end{equation}(17)in which the colliding system temporarily resides (thus increasing the radiative decay probability).

The sharp cross-section peaks correspond to shape resonances formed below the top of the barrier of effective potential, while the broad resonances in the region below 10-5 eV are caused by the nonmonotonic behavior of the long- range potential (17) containing three contributions. The width of the resonant peak in the cross section is inversely proportional to the lifetime of the quasi-bound state. With increasing J the repulsive part of the potential 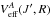VeffA(J′,R)\hbox{$V_{\rm eff}^A(J^\prime,R)$} becomes increasingly more dominant and at certain 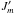Jm′\hbox{$J^\prime_m$} the effective potential attains an inflection point (at some R = Rm) and cannot support any bound state with the further increase of J′ or E. For energies above 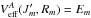VeffA(Jm′,Rm)=Em\hbox{$V_{\rm eff}^A (J^\prime_m, R_m) = E_m$}, the shape resonances in the cross section disappear. It should be noted that resonances have a quantum mechanical origin and cannot be described by the semiclassical radiative decay method.

thumbnail Fig. 3

Total cross sections for radiative decay, radiative association, radiative charge transfer and nonradiative charge transfer in Li− + H collisions.

thumbnail Fig. 4

Total and ν-resolved radiative association cross sections in the Li− + H collisions.

thumbnail Fig. 5

Total and ν-resolved radiative association cross sections in the Li− + H collisions.

thumbnail Fig. 6

Radiative charge transfer cross section in the resonant energy region.

Table 2

Energies, widths, and lifetimes of resonant states in the A2Σ+ potential.

In Figs. 4 and 5 we show vibrationally resolved cross sections for the radiative association to vibrational levels of the ground state X2Σ+ with ν = 34–38 (panel a), ν = 9–14 (panel b), ν = 1–15 (panel a) and ν = 0–11 (panel b) in the energy ranges 10-10−10-3, 0.2−0.5, 0.5−1.0 and 1.0−1.5 eV, respectively. The total RA cross section in these energy ranges is also shown. The resonant peaks are labeled by the quantum numbers (ν, J) of the rovibrational state in the effective potential of A2Σ+ state. It is observed that by increasing the collision energy, the partial waves with high angular momentum dominantly contribute to the radiative association that populates the lower vibrational states of HLi−. In Fig. 4a, the broad resonances below E = 10-5 eV are not related to quasi-bound states in the main effective potential well of the upper state A2Σ+, but rather to the very shallow potential wells at large internuclear distances formed as result of superposition of the three terms of the multipole long-range potential (17), and their J values are very small. Figure 5 illustrates the rapid decrease of the cross section and the disappearance of its resonant structure for sufficiently high J values, indicating the reduction of quasi-bound states in the potential well of the effective potential of initial state. In Fig. 6 we show the RCT cross section in the resonant region 0.7−1.8 eV. The strongest resonances appear in the energy range 1.0−1.5 eV and involve high angular momenta (J = 50−73).

In order to determine the resonance peaks exactly, the complex absorbing potential combined with the MRDCI method (Riss & Meyer 1993; Peng et al., in prep.) was used to compute the resonance positions Er and widths Γ and the results obtained are shown in Table 2. The dissociation limit of the upper A state is used as the zero of the real energy part Er. It can be observed that the collision energies equal to the real-energy portion of the complex energy of that resonance state and the lifetime of these resonance states are on the order of 10-11−10-14 s, except the resonance state of (ν = 9,J = 10), for which the lifetime is about 1.92 × 10-8 s.

3.3. Reaction rate coefficients

We calculated the reaction rate coefficients for the radiative and nonradiative processes by averaging the cross sections shown in Fig. 3 over the Maxwellian velocity distribution; these reaction rate coefficients are plotted as a function of temperature T in Fig. 7. With increasing the temperature, the rate coefficients for radiative processes increase and attain their maxima in the regions around 4 × 103 K for RA and 3 × 104 K for RCT with maximum values of ~ 8 × 10-16 cm3 s-1 and ~ 2 × 10-15 cm3 s-1, respectively. The figure shows that for T< 4 × 103 K the RA rate coefficient is larger than that for the RCT process (by two orders of magnitude for T< 10 K), while for higher temperatures the opposite is true. The maximum value of the rate coefficient for the nonradiative charge transfer occurs at 3 × 106 K and amounts to ~ 9 × 10-8 cm3 s-1. The NRCT rate coefficient, however, decreases much more rapidly with the temperature decrease than the rate coefficients for the RA and RCT processes, and below ~ 0.3 K the RA rate coefficient becomes larger than that for the NRCT process. In the temperature region below ~ 0.3 K the radiative association is the dominant process in Li− + H collisions.

4. Conclusions

The fully quantum, optical potential, and semiclassical methods are employed to calculate the radiative association, RCT, and radiative decay cross sections in Li− + H collisions in the 10-10−10 eV energy range. In the energy region below ~ 0.8 eV the radiative association is the dominant radiative process, while above this energy the RCT dominates. A prominent feature of considered radiative processes is the appearance of resonant structures in the energy region below ~ 2 eV. In the energy range 0.2−2 eV the narrow resonances are associated with the formation of quasi-bound states in the effective potential of the entrance channel of RCT and RA reactions (shape resonances). The broad resonances in the energy region below ~ 10-5 eV are associated with the nonmonotonic character of the long-range part of the potential of initial molecular state.

The vibrationaly resolved RA cross sections were also calculated. It is observed that with increasing the collision energy the partial waves with high angular momentum contribute dominantly to the radiative association, which populates the lower vibrational states of LiH−(X2Σ+). For a given vibrational level ν, the resonances disappear for energies higher than certain 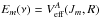Em(ν)=VeffA(Jm,R)\hbox{$E_m(\nu) =V_{\rm eff}^A(J_m,R)$} value, indicating that the effective potential of the entrance channel has reached its inflection point R = Rm.

thumbnail Fig. 7

Rate coefficients as a function of temperature for the radiative decay, radiative association, radiative charge transfer and nonradiative charge transfer processes in Li− + H collisions.

The total rate coefficients for the RCT and RA reactions were also calculated. It is shown that RA rate coefficient is

larger than that for the nonradiative RCT for temperatures below 0.3 K, where the RA becomes the dominant process in Li− + H collisions.

Acknowledgments

This work was supported by the National Basic Research program of China under Grant No. 2013CB922200, the Science Challenge Program and the National Natural Science Foundation of China under Grant Nos. 11474032, 11474033 and 11534011.

References

  1. Andreazza, C. M., Singh, P., & Sanzovo, G. 1995, ApJ, 451, 889 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bates, D. R. 1951, MNRAS, 111, 303 [NASA ADS] [CrossRef] [Google Scholar]
  3. Buenker, R. J., & Phillips, R. A. 1985, J. Mol. Struct.: Theochem, 123, 291 [Google Scholar]
  4. Chen, J. C. Y. 1967, Phys. Rev., 156, 12 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cohen, J. S., & Bardsley, J. N. 1978, Phys. Rev. A, 18, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  6. Dalgarno, A., Du, M. L., & You, J. H. 1990, ApJ, 349, 675 [NASA ADS] [CrossRef] [Google Scholar]
  7. da Silva Jr, H., Raoult, M., Aymar, M., & Dulieu, O. 2015, New J. Phys., 17, 045015 [NASA ADS] [CrossRef] [Google Scholar]
  8. Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
  9. Gunnar, H., Hanstorp, D., Kiyan, I., et al. 1996, Phys. Rev. A, 53, 4127 [CrossRef] [PubMed] [Google Scholar]
  10. Lambert, D. L. 1993, Phys. Scr., 1993, 186 [NASA ADS] [CrossRef] [Google Scholar]
  11. Lepp, S., Stancil, P. C., & Dalgarno, A. 2002, J. Phys. B: At. Mol. Opt. Phys., 35, 57 [Google Scholar]
  12. Carlsson, M., Rutten, J. B., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
  13. Mizuno, J., & Chen, J. C. Y. 1971, Phys. Rev. A, 4, 1500 [NASA ADS] [CrossRef] [Google Scholar]
  14. Palla, F., Galli, D., & Silk, J. 1995, ApJ, 451, 44 [NASA ADS] [CrossRef] [Google Scholar]
  15. Puchalski, M., Kędziera, D., & Pachucki, K. 2011, Phys. Rev. A, 84, 052518 [NASA ADS] [CrossRef] [Google Scholar]
  16. Riss, U. V., & Meyer, H. D. 1993, J. Phys. B: At. Mol. Opt. Phys., 26, 4503 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  17. Stancil, P. C., & Zygelman, B. 1996, ApJ, 472, 102 [NASA ADS] [CrossRef] [Google Scholar]
  18. Stancil, P. C., Lepp, S., & Dalgarno, A. 1996, ApJ, 458, 40 [Google Scholar]
  19. Stancil, P. C., Lepp, S., & Dalgarno, A. 1998, ApJ, 509, 1 [NASA ADS] [CrossRef] [Google Scholar]
  20. Stefan, K., & Buenker, R. J. 1995, J. Chem. Phys., 103, 5613 [NASA ADS] [CrossRef] [Google Scholar]
  21. West, B. W., Lane, N. F., & Cohen, J. S. 1982, Phys. Rev. A, 26, 3164 [NASA ADS] [CrossRef] [Google Scholar]
  22. Wu, Y., Lin, X. H., Yan, B., Wang, J. G., & Janev, R. K. 2016, J. Phys. B: At. Mol. Opt. Phys., 49, 035203 [NASA ADS] [CrossRef] [Google Scholar]
  23. Zhao, L. B., Stancil, P. C., Gu, J. P., et al. 2004, ApJ, 615, 1063 [NASA ADS] [CrossRef] [Google Scholar]
  24. Zygelman, B., & Dalgarno, A. 1988, Phys. Rev. A, 38, 1877 [NASA ADS] [CrossRef] [Google Scholar]
  25. Zygelman, B., & Dalgarno, A. 1990, ApJ, 365, 239 [NASA ADS] [CrossRef] [Google Scholar]
  26. Zygelman, B., Stancil, P. C., & Dalgarno, A. 1998, ApJ, 508, 151 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Binding energies of vibrational levels in the potential well of the 22Σ+ state of HLi−.

In the text
Table 2

Energies, widths, and lifetimes of resonant states in the A2Σ+ potential.

In the text

All Figures

thumbnail Fig. 1

Adiabatic potential energy curves for HLi− as a function of internuclear distance R.
In the text
thumbnail Fig. 2

Dipole transition matrix element between the 12Σ+ and 22Σ+ states of HLi−.
In the text
thumbnail Fig. 3

Total cross sections for radiative decay, radiative association, radiative charge transfer and nonradiative charge transfer in Li− + H collisions.
In the text
thumbnail Fig. 4

Total and ν-resolved radiative association cross sections in the Li− + H collisions.
In the text
thumbnail Fig. 5

Total and ν-resolved radiative association cross sections in the Li− + H collisions.
In the text
thumbnail Fig. 6

Radiative charge transfer cross section in the resonant energy region.
In the text
thumbnail Fig. 7

Rate coefficients as a function of temperature for the radiative decay, radiative association, radiative charge transfer and nonradiative charge transfer processes in Li− + H collisions.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.