| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629360 | |
| Published online | 13 February 2017 | |
Reanalysis of high-resolution XMM-Newton data of V2491 Cygni using models of collisionally ionized hot absorbers
Department of Physics, Middle East Technical University, Dumlupınar Bulvarı, 06800 Ankara, Turkey
e-mail: solen@astroa.physics.metu.edu.tr; cigdem.gamsizkan@gmail.com
Received: 20 July 2016
Accepted: 21 October 2016
Aims. We model spectral absorption features in data of the high-resolution XMM-Newton Reflection Grating Spectrometer.
Methods. We performed X-ray spectral analysis and modeling using the SRON software SPEX version 2.05.04.
Results. We present a reanalysis of data obtained with the XMM-Newton Reflection Grating Spectrometer of the classical nova V2491 Cyg from two different pointings, 40 d and 50 d after outburst. We aim to model absorption components in the high-resolution spectra independently of the continuum model. To model the complex absorption, we used hot collisionally ionized (in equilibrium) absorber models along with interstellar absorption (of gas and dust origin separately) that we discuss in the light of observations. For an adequate approximation and to facilitate the fitting procedures, we used a blackbody model for the continuum. We find blackbody temperatures in the range 61–91 eV (slightly variable over the two observations) that yield a white dwarf (WD) mass of 1.15–1.3 M⊙ assuming this range is the maximum temperature achieved during the H-burning phase. Our fits model the ionized absorption features simultaneously, thus calculating a global velocity shift for the absorption component in the data originating from the nova wind and/or ejecta as a result of collisionally ionized hot absorption. We derive two different hot-absorber components from our fits with blueshifts yielding 2900–3800 km s-1 for the first (day 40) and 2600–3600 km s-1 for the second observation 50 days after outburst that are consistent with ejecta or wind speeds. The two collisionally ionized hot-absorption components have temperatures kT1 ≃ 1.0−3.6 keV and kT2 ≃ 0.4−0.87 keV with rms velocities σv1 ~ 872 km s-1 and σv2 ~ 56 km s-1. These are consistent with shock temperatures in the X-ray wavelengths. V2491 Cyg shows signature of H-burning with underabundant carbon C/C⊙ = 0.3−0.5, and enhanced nitrogen N/N⊙ = 5−7 and oxygen O/O⊙ = 16−43. The high oxygen overabundance hints at a C–O WD. We find the equivalent hydrogen column density of the hot collisionally ionized (in equilibrium) absorbers in a range (0.6–18.0) × 1023 cm-2 and (2.0–5.3) × 1023 cm-2 on days 40 and 50 after outburst, respectively. Our fits yield the most adequate 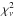 (range 1.8–2.9) currently obtained for the modeling of high-resolution X-ray data of V2491 Cyg. An additional photoionized absorber (third intrinsic absorber component) originating in the shell or the ejecta improves the model fits with
(range 1.8–2.9) currently obtained for the modeling of high-resolution X-ray data of V2491 Cyg. An additional photoionized absorber (third intrinsic absorber component) originating in the shell or the ejecta improves the model fits with 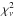 in a range 1.7–2.5, but shows only (1–0.1)% of the absorption by the collisionally ionized hot gas. Our analysis reveals a second blackbody component on day 50 with an effective temperature of 120–131 eV and an effective radius of about 10% of the WD, which may indicate the onset of magnetic accretion.
in a range 1.7–2.5, but shows only (1–0.1)% of the absorption by the collisionally ionized hot gas. Our analysis reveals a second blackbody component on day 50 with an effective temperature of 120–131 eV and an effective radius of about 10% of the WD, which may indicate the onset of magnetic accretion.
Conclusions. Our work on data of the XMM-Newton Reflection Grating Spectrometer yields two main hot collisionally ionized (in equilibrium) absorber components with different temperatures, rms velocities, and equivalent column densities originating in the shocked fast-moving ejecta and/or the wind. These two components may be the reason for the complex absorption spectra of V2491 Cyg, as a result of high- and low-density regions with different turbulent conditions and temperatures in the ejecta and/or the wind, indicating the inhomogeneity (e.g., oxygen-dense regions) and mixed morphology of the outflow.
Key words: X-rays: stars / stars: individual: V2491 Cyg / binaries: general / novae, cataclysmic variables / stars: abundances / stars: winds, outflows
© ESO, 2017
1. Introduction
Classical novae (CNe) outbursts occur in cataclysmic variable (CV) systems on the surface of the WD as a result of an explosive ignition of accreted material (thermonuclear runaway) causing the ejection of 10-7 to 10-3M⊙ of material at velocities of up to several thousand kilometers per second (Shara 1989; Livio 1994; Starrfield et al. 2012; Bode & Evans 2008).
After the initial expansion phase of the outburst, the velocity of the material in deeper zones of the envelope drops quickly, and a hydrostatic equilibrium is established (Shara 1989; Bode & Evans 2008). A gradual hardening of the stellar remnant spectrum with time past visual maximum is expected consistent with H-burning at constant bolometric luminosity and decreasing photospheric radius, as the envelope mass is depleted. This residual hydrogen-rich envelope matter is mainly consumed by H-burning and wind-driven mass loss. The emission from the remnant WD is a blackbody-like stellar continuum. As the stellar photospheric radius decreases during the constant bolometric luminosity phase, the effective photospheric temperature increases (up to values in the range 1–10 × 105 K), and the peak of the stellar spectrum is shifted from visual to ultraviolet and to the X-ray energy band, where the H-burning finally turns off (e.g., MacDonald & Vennes 1991; Balman et al. 1998; Kahabka et al. 1999; Balman & Krautter 2001; Ness et al. 2003, 2007; Orio et al. 2002, 2003; Nelson et al. 2008; Page et al. 2010; Rauch et al. 2010; Osborne et al. 2011; Tofflemire et al. 2013; Henze et al. 2014; Page et al. 2015). This constitutes the soft X-ray component (0.1–1.0 keV, 124.0–12.4 Å) that is detected during the nova outbursts.
CNe are also detected in the hard X-rays (above 0.5 keV, shorter than 24.8 Å) during the outburst stage as a result of shocked plasma emission in the accretion process, wind outflow, wind-wind, and/or blast wave interactions (e.g., O’Brien et al. 1994; Krautter et al. 1996; Balman et al. 1998; Mukai & Ishida 2001; Orio et al. 2001; Ness et al. 2003, 2009; Hernanz & Sala 2002, 2007; Sokoloski et al. 2006; Page et al. 2010; Chomiuk et al. 2014; Orio et al. 2015). Recurrent novae (RNe) are a type of CNe with outbursts occurring at intervals of several decades (Webbink et al. 1987; Hachisu & Kato 2001; Bode & Evans 2008).
In this paper, we reanalyze the XMM-Newton Reflection Grating Spectrometer (RGS) data of the classical nova V2491 Cyg. The high-resolution nova spectra show the existence of absorption features in the X-ray wavelengths. We assume that there is complex absorption of interstellar, photospheric, and of collisionally and/or photoionized gas origin that is due to moving material in the line of sight from a nova wind and/or ejecta. Our main aim is to model the absorption components detected in the high-resolution spectra independently of the continuum model and compare the photoionized warm and collisionally ionized hot absorber gas in this system. In addition to deriving the absorption properties, we obtain abundances of elements in the ejecta or nova wind. In comparison with previous modeling of individual absorption features with Gaussians, non-local thermodynamic equilibrium (NLTE) static atmosphere models, NLTE expanding atmosphere models, or intrinsic photoionized warm absorber models, we use collisionally ionized absorber models that we discuss in the light of observations. We compare the results obtained with the same XMM-Newton RGS data that we analyze here using photoionized warm absorber models as described in Pinto et al. (2012) with the hot collisionally ionized (in equilibrium) absorber model fits for V2491 Cyg using SPEX software. We caution that we use a blackbody model for the continuum (as was used in Pinto et al. 2012), which means that we may miss some photospheric absorption features.
Nova V2491 Cyg was discovered in April 2008 at about 7.7 mag on CCD frames in white light (Nakano et al. 2008). Munari et al. (2011) calculated the time to decay by two magnitudes of 4.8 days, making this nova a very fast nova similar to V838 Her and V2487 Oph. V2491 Cyg has been classified as a He/N nova based on photometric and spectroscopic results (Lynch et al. 2008; Helton et al. 2008). The spectra have very broad lines with complex profiles and high expansion velocities (~4000–6000 km s-1; Lynch et al. 2008; Tomov et al. 2008). V2491 Cyg shows hard and soft X-ray components during the outburst stage (analysis can be found in Page et al. 2010; Ness et al. 2011). Ibarra et al. (2009) showed that V2491 was a persistent X-ray source using archival ROSAT, XMM-Newton, and Swift data during its quiescent phase before the optical outburst. Takei et al. (2011) revealed early nonthermal emission from the nova during the outburst stage and found that accretion is re-established as early as day 50 (also plausibly day 40) after outburst. Recently, observations of the source more than two years after the outburst indicate that the quiescent source is a bright hard X-ray emitter including a blackbody emission component with 77 eV effective temperature, indicating the characteristics of a soft intermediate polar (magnetic) type CV (Zemko et al. 2015).
2. Data and observations
The XMM-Newton Observatory (Jansen et al. 2001) has three 1500 cm2 X-ray telescopes each with a European Photon Imaging Camera (EPIC) at the focus. Two of the telescopes have metal oxide semiconductor (MOS) CCDs (Turner et al. 2001), and the third uses pn CCDs (Strüder et al. 2001) for data recording. There are also two reflection grating spectrometers (den Herder et al. 2001) located behind two of the telescopes. V2491 Cyg was observed (pointed archival observation, OBSID = 0552270501) for an exposure of 39.2 ks between 2008 May 20 UT 14:03:53 and 2008 May 21 UT 00:59:28 (~40 d after outburst). The second pointed archival observation (OBSID = 0552270601) was obtained between 2008 May 30 08:21:01 and 2008 May 30 16:40:40 for an XMM-Newton exposure of 29.8 ks (~50 d after outburst). Both observations used all the EPIC cameras with different modes, but in this study we use the RGS data to obtain the high-resolution spectra for our analysis purpose.
The RGS observations were carried out using the standard high event rate with SES spectroscopy mode for readout. For the analysis, the science analysis software (SAS) version 14.0.0 was used, and we reprocessed the data using the XMM-SAS routine rgsproc. Source and background counts for the RGS data were extracted using the standard spatial and energy filters for the source position, which defines the spatial extraction regions as well as the wavelength zero point. rgsproc allows the user to restrict the processing to an enumerated subset of exposures within the observation and an enumerated set of reflection orders. From the first to the fifth stage, it performs basic calibrations on the events in separate CCD event lists and then gathers them in a combined event list. A source-specific aspect-drift correction is performed and the channel grids are defined for events and exposures allowing filtering of data (to correct or to remove what is unusable, e.g., bad-pixel correction). The fourth and fifth stages produce spectra and generate response matrices for the designated primary source. The sixth stage produces light curves. Following this, we derived spectra for different orders of RGS1 and RGS2 and generated light curves. In addition, we used the SAS task rgsfluxer to obtain fluxed spectra between 5–38 Å with 3400 bins as is required for the SPEX software. In addition, we used the event files and determined times of low background from the count rate on CCD 9 (which is closest to the optical axis). The final exposure times and net count rates showed that there were no sporadic high background events in our data, and since the nova was bright in both observations, we did not include any corrections for flares. Figure 1 shows the light curves of the first and second observations (RGS1 data) with a bin time of 100 s. Following the analysis by Ness et al. (2011) and Pinto et al. (2012), we selected the three different count rate regions in the light curve of the first observation as labeled in the figure (i.e., regions 1–3) to investigate the nature and effect of the variation seen in the light curve on the produced spectra from the given regions. The second observation did not show any major variation, thus the entire event file was used for the analysis. Next, we extracted the events from the event files by filtering on time for the first observation (regions 1–3) and then re-run rgsproc and rgsfluxer to produce appropriate response matrices and fluxed spectra.
 |
Fig. 1 XMM-Newton RGS1 light curve (LC) of V2491 Cyg. First observation (40 d after outburst) is on the left and the second observation is on the right (50 d after outburst). The three different count rate regions are labeled 1, 2, and 3 on the LC of the first observation as assumed in the spectral analysis. |
3. Analysis and results
3.1. Photoionized and collisionally ionized absorber models
SPEX is a software package (version 2.05.04; Kaastra et al. 1996) optimized for the analysis and interpretation of high-resolution cosmic X-ray spectra. The software is especially suited for fitting spectra obtained by current X-ray observatories such as XMM-Newton, Chandra, and Suzaku. It is maintained by SRON (HEA Division, Netherlands Institute for Space Research).
We obtained a similar model description to Pinto et al. (2012) to fit both sets of the nova data (first and second observation) in order to compare the different ionized absorber components in the system. There are two main models in SPEX that can be used to model ionized intrinsic absorption; one of them is the xabs (used by Pinto et al. 2012), and the other is the Hot model used in this study. The xabs model of SPEX calculates the warm, photoionized absorption by a thin slab composed of different ions located between the ionizing source and the observer. The xabs model assumes a small angle subtended by the slab at the source so that only absorption and scattering out of the line of sight by the slab are considered. The processes taken into account are the continuum and the line absorption by the ions and scattering out of the line of sight by the free electrons in the slab. The transmission, T, of the slab is calculated as T = exp [−τc−τl−τe]. Here τc and τl are the total continuum and line optical depth, respectively, and τe is the electron-scattering optical depth. For τe the classical Thomson approximation is valid below 10 keV (longer than 1.24 Å). Most continuum opacities are taken from Verner & Yakovlev (1995), while line opacities and wavelengths for most ions are taken from Verner et al. (1996) and abundances are calculated using Lodders & Palme (2009) (see the details and additional references in the SPEX user’s manual). τl is a function of v and σv, which are free parameters of xabs. v is the average systematic velocity shift of the absorber, in km s-1. Negative and positive values of v correspond to blue- and redshifts, respectively. σv is the turbulent velocity broadening of the absorber in km s-1, defined as 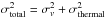 , where σtotal is the total width of a line and σthermal the thermal contribution. The relative column densities of the ions are calculated through a photoionization model introducing two free parameters:
, where σtotal is the total width of a line and σthermal the thermal contribution. The relative column densities of the ions are calculated through a photoionization model introducing two free parameters: 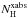 and ξ.
and ξ. 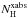 is the equivalent hydrogen column density of the ionized absorber in units of atoms cm-2. ξ is the ionization parameter of the absorber defined as ξ = L/ner2, where L is the luminosity of the ionizing source, ne the density of the plasma, and r the distance between the slab and the ionizing source. ξ is expressed in units of erg cm s-1. Codes such as XSTAR (Kallman & Bautista 2001) or CLOUDY (Ferland 2003) are used for the broadband ionizing continuum from infrared to hard X-rays where the ionic column densities of a photoionized slab are precalculated for different values of ξ and used in the fitting procedure with SPEX. During the fitting process, SPEX reads in the grid of precalculated ionic column densities and finds the best set and the best-fit values for
is the equivalent hydrogen column density of the ionized absorber in units of atoms cm-2. ξ is the ionization parameter of the absorber defined as ξ = L/ner2, where L is the luminosity of the ionizing source, ne the density of the plasma, and r the distance between the slab and the ionizing source. ξ is expressed in units of erg cm s-1. Codes such as XSTAR (Kallman & Bautista 2001) or CLOUDY (Ferland 2003) are used for the broadband ionizing continuum from infrared to hard X-rays where the ionic column densities of a photoionized slab are precalculated for different values of ξ and used in the fitting procedure with SPEX. During the fitting process, SPEX reads in the grid of precalculated ionic column densities and finds the best set and the best-fit values for 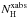 and ξ.
and ξ.
 |
Fig. 2 RGS1+2 fluxed spectrum of V2491 Cyg fitted in the range 7–14.4 Å using the plasma emission model Cie and the cold Hot-ISM absorption model. A blackbody model of emission was also used as an additive model for the second-observation spectrum. The left- and right-hand panels show the fit to the fluxed spectrum of region 3 and second-observation data, respectively. |
Spectral parameters obtained from the composite model fits including two Hot absorber models to the RGS spectrum of V2491 Cyg.
Spectral parameters obtained from the composite model fits including two Hot absorber and one xabs models to the RGS spectra of V2491 Cyg.
To compare with the analysis using xabs models, we here focus mainly on the Hot model within SPEX that assumes a collisional ionization (equilibrium) absorber model instead of the photoionized absorber model. This model calculates the transmission of a plasma in collisional equilibrium with cosmic abundances. For a given temperature and abundances, the model calculates the ionization balance and then determines all ionic column densities by scaling the prescribed hydrogen column density. Using these column densities, the transmission of the plasma is calculated by multiplying the transmission of the individual ions. The transmission assumes both continuum and line opacity. Most continuum opacities are taken from Verner & Yakovlev (1995), while line opacities and wavelengths for most ions are taken from Verner et al. (1996) and abundances are calculated using Lodders & Palme (2009). This model mimics neutral plasma transmission at about 0.0005 keV (6000 K), which we used to model the gas component of the interstellar absorption. It also has free parameters similar to those of the xabs model, such as velocity shift v and turbulent velocity broadening σv, together with the equivalent hydrogen column density 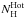 and kT, the temperature of the absorber in keV.
and kT, the temperature of the absorber in keV.
3.2. XMM-Newton RGS spectrum of V2491 Cyg
As outlined in Sect. 2.0, we analyzed the data using SAS version 14.0.0 and produced RGS1-2 spectra and relevant response matrices using rgsproc and rgsfluxer for different spectral orders. Some spectral analysis checks were performed using XSPEC (Arnaud 1996) version 12.9.0, and the main analyses were conducted with the SPEX software package (Kaastra et al. 1996) version 2.05.04. To perform the analysis with SPEX, RGS1 and RGS2 first-order spectra were combined by using the tasks rgsfluxcombine and rgsfmat within SPEX. The fluxed spectra were created between 5–38 Å with 3400 bins. In general, the spectra between 7–38 Å (0.3–1.8 keV) were used for the fitting process and the data were binned by a factor of 4 between 7–11 Å and by a factor 2 for 11–38 Å. The detailed description of the emission and absorption lines and edges can be found in Ness et al. (2011) and Pinto et al. (2012).
Our main aim is to study the complex absorption properties in the high-resolution X-ray spectra of classical and recurrent novae, and our target in this work is V2491 Cyg. To compare with the absorption modeling used in Pinto et al. (2012), who used the photoionized absorber model xabs, we used the absorption model Hot, which is a collisionally ionized (in equilibrium) absorber model in the SPEX software package. Since a comparative study with the xabs models would require that the data are analyzed and fitted in the same manner as in Pinto et al. (2012), except for the photoionized absorber models. We used a composite model that includes a blackbody model Bb for the continuum and a plasma emission model in collisional equilibrium Cie for the excess in the harder X-ray band together with two Hot absorber models, one Amol model for the dust absorption (Pinto et al. 2010) in the line of sight, and finally another Hot model with a very low temperature (~1 eV) that would mimic the cold gas absorption in the interstellar medium. We followed a fitting procedure similar to Pinto et al. (2012). First the harder X-ray band data (7–14.4 Å) was fitted with the Cie model together with the cold Hot (Hot-ISM) absorber model for the gas in the interstellar medium to determine the abundances separately from the other absorber models using the fluxed spectrum of region 3 and the second observation. An additional blackbody model Bb was added in the fitting process for the second observation to account for the long-wavelength excess. When the additional blackbody model was not included, the 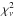 of the fit was 2.15 and not acceptable. Figure 2 shows the fitted models to the two data sets. We find that the spectral parameters of this blackbody emission are different than the main blackbody model parameters of the stellar remnant presented in Table 1 (and Table 2). The normalization is (2.0–4.0) × 1015 cm2, the temperature is (120–131) eV, and the luminosity is 6.0 × 1035 erg s-1. However, inclusion of this component in the fitting procedure in the total RGS band 7–38 Å does not affect the spectral parameters in Table 1 (and Table 2), particularly the main stellar remnant emission, and it only improves the fits at about 93% confidence level. The spectral parameters of this new blackbody component remain similar at the 90–95% confidence level when fitted in the 7–14 Å or 7–38 Å energy range. We elaborate on this component in the discussion section.
of the fit was 2.15 and not acceptable. Figure 2 shows the fitted models to the two data sets. We find that the spectral parameters of this blackbody emission are different than the main blackbody model parameters of the stellar remnant presented in Table 1 (and Table 2). The normalization is (2.0–4.0) × 1015 cm2, the temperature is (120–131) eV, and the luminosity is 6.0 × 1035 erg s-1. However, inclusion of this component in the fitting procedure in the total RGS band 7–38 Å does not affect the spectral parameters in Table 1 (and Table 2), particularly the main stellar remnant emission, and it only improves the fits at about 93% confidence level. The spectral parameters of this new blackbody component remain similar at the 90–95% confidence level when fitted in the 7–14 Å or 7–38 Å energy range. We elaborate on this component in the discussion section.
 |
Fig. 3 RGS1+2 fluxed spectrum of V2491 Cyg using region 1 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
 |
Fig. 4 RGS1+2 fluxed spectrum of V2491 Cyg using region 2 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
 |
Fig. 5 RGS1+2 fluxed spectrum of V2491 Cyg using region 3 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
 |
Fig. 6 RGS1+2 fluxed spectrum of V2491 Cyg obtained from the second observation fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
The Ne and Mg abundances from these fits above (i.e., using region 3 and second-observation spectra) were fixed together with the vmic parameter for the fits using fluxed spectra of regions 1 and 2. We note that the free fits yield very similar abundances of Ne and Mg for the second observation. Following this, first the fluxed spectrum of region 3 was fitted with the composite model Hot-ISM×(Cie+(Hot-1×Hot-2)×(Bb)), and when the fit converged, the multiplicative model Amol was added and a final fit was performed: Amol×Hot-ISM×(Cie+ (Hot-1×Hot-2)×(Bb)). Next, the elemental abundances derived for the Hot absorber models using the fit to the fluxed spectrum of region 3 were fixed for all the fits to the fluxed spectra of regions 1, 2, and the second observation assuming that the abundances in the ejecta and/or the wind will stay the same in the short duration of the X-ray observation, and that the second observation was made only ten days after the first observation. The fitted fluxed spectra of V2491 Cyg are shown in Figs. 3–6, where Figs. 3–5 show regions 1, 2, and 3 as labeled in Fig. 1 (left panel) for the first observation. Figure 6 is the spectral fit to the fluxed spectrum of the second observation. The resulting spectral parameters from fits with the composite model using the collisionally ionized (in equilibrium) hot-absorber models are listed in Table 1. All abundances are given in solar units. The error ranges of the spectral parameters are given at the 90% confidence level for a single parameter (Δχ2 = 2.71). The degrees of freedom are taken in accordance with the fits of Pinto et al. (2012) for comparison. However, we assumed abundances in solar units, which takes H as the reference element instead of using oxygen as the reference.
We find that our fits yield 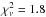 –2.9 (for about 1440 degrees of freedom) using the collisionally ionized hot intrinsic absorber models for the classical nova V2491 Cyg. Given the
–2.9 (for about 1440 degrees of freedom) using the collisionally ionized hot intrinsic absorber models for the classical nova V2491 Cyg. Given the 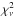 values, the collisionally ionized absorber models yield considerably better fits to these data sets of V2491 Cyg than the photoionized absorber fits in Pinto et al. (2012), which have
values, the collisionally ionized absorber models yield considerably better fits to these data sets of V2491 Cyg than the photoionized absorber fits in Pinto et al. (2012), which have 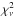 in a range 2.3–7.0 for about 1470 degrees of freedom. Other modeling using expanding atmosphere models (van Rossum & Ness 2010) yielded very high values of
in a range 2.3–7.0 for about 1470 degrees of freedom. Other modeling using expanding atmosphere models (van Rossum & Ness 2010) yielded very high values of 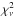 not given in the paper and the NLTE static atmosphere fits in Ness et al. (2011) had a
not given in the paper and the NLTE static atmosphere fits in Ness et al. (2011) had a 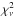 range of 2.2–21.8 for about 5600 degrees of freedom. We note that the comparison with the results of Pinto et al. (2012) using the photoionized absorbers indicates that particularly for spectral fits to regions 1 and 3, where the count rates are the highest, inclusion of the collisionally ionized hot absorbers improves the fits to a good extent, the improvements of spectral fits for region 2 and the second-observation data with the lowest count rate are much less obvious. This might be caused by the high count rate data showing the absorption and emission features (along with a strong continuum) more prominently, which allows for a better fitting of the detailed models using the high spectral resolution data. Such high spectral resolution data with low count rates have increased statistical errors, with the detailed spectral features more smeared out or less visible (with weaker continuum), it does not allow for the fit quality to appropriately differentiate between several models. However, in all four spectra that we fitted, we have better
range of 2.2–21.8 for about 5600 degrees of freedom. We note that the comparison with the results of Pinto et al. (2012) using the photoionized absorbers indicates that particularly for spectral fits to regions 1 and 3, where the count rates are the highest, inclusion of the collisionally ionized hot absorbers improves the fits to a good extent, the improvements of spectral fits for region 2 and the second-observation data with the lowest count rate are much less obvious. This might be caused by the high count rate data showing the absorption and emission features (along with a strong continuum) more prominently, which allows for a better fitting of the detailed models using the high spectral resolution data. Such high spectral resolution data with low count rates have increased statistical errors, with the detailed spectral features more smeared out or less visible (with weaker continuum), it does not allow for the fit quality to appropriately differentiate between several models. However, in all four spectra that we fitted, we have better 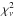 values than achieved through the intrinsic photoionized absorber fits in Pinto et al. (2012). An F-test (within XSPEC) can be performed to test the significance of the improvement in these fits with respect to the photoionized absorber fits in Pinto et al. (2012). A comparison of the χ2 and degrees of freedom of each fit for regions 1–3 shows that the F-test probability ranges between 3 × 10-26−6 × 10-270, which is a value of 1- (confidence level). Thus, the improvement is much better than 10σ, where 3σ significance would have F-test probability of ~0.003. However, the F-test for the fits to the lowest count rate data (the second observation) gives a probability of 0.4 (about 60% confidence level), which yields an improvement of only around 1σ for the collisionally ionized absorber fits over the photoionized absorber fits.
values than achieved through the intrinsic photoionized absorber fits in Pinto et al. (2012). An F-test (within XSPEC) can be performed to test the significance of the improvement in these fits with respect to the photoionized absorber fits in Pinto et al. (2012). A comparison of the χ2 and degrees of freedom of each fit for regions 1–3 shows that the F-test probability ranges between 3 × 10-26−6 × 10-270, which is a value of 1- (confidence level). Thus, the improvement is much better than 10σ, where 3σ significance would have F-test probability of ~0.003. However, the F-test for the fits to the lowest count rate data (the second observation) gives a probability of 0.4 (about 60% confidence level), which yields an improvement of only around 1σ for the collisionally ionized absorber fits over the photoionized absorber fits.
In addition, we tested the possibility of having a third absorber by adding another Hot model to the fits in Table 1 and tested the significance of this component by applying an F-test. We find that the fits to the data of regions 1, 2, and the second observation yield an improvement of χ2 values at a confidence level lower than 30%. However, an F-test for the fit of the spectrum of region 3 resulted in a probability of 5 × 10-8, yielding an improvement over 5σ.
Our original idea, as described in the Introduction section, was a composite model with complex absorption of interstellar, photospheric, and collisionally ionized and/or photoionized gas originating from the moving material in the line of sight from a nova wind or ejecta. As a result, our goal was to model the absorption components detected in the high-resolution spectra independently of the continuum model (i.e., mainly stellar remnant emission) and compare the photoionized warm and collisionally ionized hot absorber gas. Thus, we next employed the xabs model for the third absorber in V2491 Cygni (Amol×Hot-ISM×(Cie+(Hot-1×Hot-2×xabs)×(Bb))). This composite model implies that there is some absorption from photoionized gas along with the main absorbers that are collisionally ionized. For this additional model, we used a grid of ionic column densities for xabs calculated using the CLOUDY software assuming an ionizing continuum of blackbody radiation at 65 eV (7.8 × 105 K) chosen in accordance with our analysis. The resulting fits show that all the 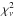 values except for the region 2 fit (F-test probability is 0.005, yielding an improvement at 99.5% confidence level) are improved over 10σ significance (using F-test the probability is 3.2 × 10-12−6.9 × 10-47). These improved fits are given in Table 2. We note here that the spectral parameters (in Tables 1 and 2) of the main stellar remnant emission (Bb), plasma emission Cie, the interstellar dust Amol, and Hot-ISM gas absorption remain consistent within 90–95% confidence level errors.
values except for the region 2 fit (F-test probability is 0.005, yielding an improvement at 99.5% confidence level) are improved over 10σ significance (using F-test the probability is 3.2 × 10-12−6.9 × 10-47). These improved fits are given in Table 2. We note here that the spectral parameters (in Tables 1 and 2) of the main stellar remnant emission (Bb), plasma emission Cie, the interstellar dust Amol, and Hot-ISM gas absorption remain consistent within 90–95% confidence level errors.
Finally, we note that Pinto et al. (2012) have attempted to use stellar atmosphere models instead of blackbody models using particular CNO abundances along with the complex absorption model they used. They report that such models only resulted in higher 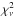 values and have not improved the fits at all.
values and have not improved the fits at all.
4. Discussion
In a nova explosion, convection and radiation pressure leads to the ejection of the envelope material, forming an optically thick or thin shell through which the high-energy photons produced by the nuclear burning have to travel. The resulting spectrum is an atmospheric spectrum originating from the photosphere with a blackbody-like continuum and superimposed absorption lines as detected by the X-ray grating data (in addition to the hard X-ray component originating from the ejecta and/or winds). In the X-ray spectral analysis of novae data, first attempts to derive spectral parameters were made using blackbody models indicating or yielding super-Eddington luminosities for the stellar remnant (see, Oegelman et al. 1993). To overcome the super-Eddington luminosity problem and to incorporate the abundance and ionization edge effects of C–O and O–Ne core WDs, local thermodynamic equilibrium (LTE) models were used with the ROSAT and BeppoSAX data, and successful results were achieved (e.g., Balman et al. 1998; Kahabka et al. 1999; Balman & Krautter 2001). However, these data had crude spectral resolution, and only after obtaining stellar remnant spectra with the X-ray gratings was the very detailed structure with emission and absorption features recovered. After this, a few attempts to derive spectral parameters from the stellar remnants have been made using hydrostatic NLTE atmosphere models (Orio et al. 2002; Nelson et al. 2008; Rauch et al. 2010; Osborne et al. 2011; Ness et al. 2011; Tofflemire et al. 2013) that would account for the absorption edges or lines from a static atmosphere. However, the detailed structure in the spectra was very difficult to model, and results yielded best approximations to the observed spectra with high 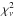 values in the fitting process. In addition, most absorption features showed blueshifts in the spectra (e.g., Ness et al. 2003, 2007) that were not modeled by the NLTE static atmosphere models, where only the static photospheric absorption lines were taken into account (for the analysis of the spectra using static atmospheres, the spectra themselves had to be shifted for a fixed blueshift).
values in the fitting process. In addition, most absorption features showed blueshifts in the spectra (e.g., Ness et al. 2003, 2007) that were not modeled by the NLTE static atmosphere models, where only the static photospheric absorption lines were taken into account (for the analysis of the spectra using static atmospheres, the spectra themselves had to be shifted for a fixed blueshift).
To compensate for the inadequacies, the stellar atmosphere code PHOENIX (Hauschildt & Baron 1999, 2004) was adjusted to model NLTE expanding atmosphere models, a hybrid atmosphere model that is hydrostatic at the base with an expanding envelope at the top. Expansion is attained by an optically thick wind from the remnant. These models have been used to fit the detailed spectral data with yet again best approximations yielding estimated spectral parameters (e.g., Petz et al. 2005; van Rossum & Ness 2010). van Rossum (2012) presented a new set of expanding NLTE atmosphere models with better quality fit approximations, but still with solar composition models. One important outcome of this modeling was that dynamic models resulted in lower effective temperatures for the remnant WD in comparison with the static models. This is largely due to existing edges and lines being too strong in the static case than the expanding envelope case where features were weak. This can cause the static models to measure higher temperatures than normal to account for the harder X-ray tails in the observed spectra (van Rossum & Ness 2010; van Rossum 2012).
Our approach is to mainly model the absorption components in the X-ray spectroscopic data. This is an independent approach regarding the choice of the continuum emission, with the atmosphere models being expanding or static. We assume a simple continuum model, a blackbody emission model together with a plasma emission model (collisional equilibrium), so that the complicated absorption models are thoroughly investigated. We note that a blackbody model does not include absorption features that could exist in the stellar atmosphere emission, thus we miss some of the atmospheric absorption features. We note that SPEX software does not have user-defined models (version 2.05.04), and we therefore have no means of publicly adding atmosphere models to use within the software. We model the blueshifted absorption features in the line of sight as in a nova wind or expanding ejecta. We inferred, for this case of V2491 Cyg, two main collisionally ionized hot absorbers and an additional photoionized component along with absorption from interstellar neutral hydrogen column density of cold gas and dust (separately) in the line of sight. We compared and contrasted our results with the spectral parameters from different modeling that exists in the literature, particularly with Pinto et al. (2012), who have analyzed the same data using only photoionized absorbers.
In comparison with the modeling using three photoionized absorption components reported by Pinto et al. (2012), our fits yield better 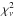 (with similar degrees of freedom) for regions 1–3 and the second observation (see Tables 1 and 2). Our findings on the plasma continuum emission parameters using the Cie model, and the absorption properties using the Hot-ISM, and Amol dust absorption models are similar to the results of Pinto et al. (2012). We assume that the difference in the quality of the fits has to do with the assumption of the used intrinsic absorption models. We therefore suggest that the main absorber in V2491 Cyg is associated with the shocked and collisionally ionized nova ejecta and the wind, which would also be consistent with the high velocity blueshifts and turbulent line broadening that we obtained from our fits. An additional photoionized warm absorber model improves the fits, indicating that there is also some contribution to the complex absorption from photoionized gas in the wind, expanding shell or ejecta.
(with similar degrees of freedom) for regions 1–3 and the second observation (see Tables 1 and 2). Our findings on the plasma continuum emission parameters using the Cie model, and the absorption properties using the Hot-ISM, and Amol dust absorption models are similar to the results of Pinto et al. (2012). We assume that the difference in the quality of the fits has to do with the assumption of the used intrinsic absorption models. We therefore suggest that the main absorber in V2491 Cyg is associated with the shocked and collisionally ionized nova ejecta and the wind, which would also be consistent with the high velocity blueshifts and turbulent line broadening that we obtained from our fits. An additional photoionized warm absorber model improves the fits, indicating that there is also some contribution to the complex absorption from photoionized gas in the wind, expanding shell or ejecta.
The best-fit model for V2491 Cyg using optically thick wind models to fit the X-ray, near-infrared, and optical light curves finds 1.3 ± 0.02M⊙ for a chemical composition of X = 0.20, Y = 0.48, XCNO = 0.2, XNe = 0.1, and Z = 0.02 (Hachisu & Kato 2010). The fits with the blackbody emission model to the Swift spectra yield blackbody temperatures on day 39 of 36–40 eV (4.3–4.8 × 105 K), on day 53 of 73–83 eV (8.8–10.0 × 105 K), and on day 80–109 of 76–81 eV (9.1–10.0 × 105 K) (Page et al. 2010). The XMM-Newton data used in our work are obtained on day 40 and 50, for which we derive a blackbody temperature of 61–91 eV (7.3–10.1 × 105 K) and 69–85 eV (8.3–10.0 × 105 K), respectively. These ranges have remained the same, but narrowed down slightly to 62–85 eV for day 40 and 78–82 to day 50 when an additional xabs model was introduced. The value (blackbody temperature) for day 40 is higher than the value obtained from Swift on day 40, but is in accordance with the Swift value obtained for day 53. Our effective temperature values are higher than the effective temperature of 6 × 105 K obtained from the best-fit approximations to the XMM-Newton data (day 50) using expanding NLTE atmosphere models (van Rossum & Ness 2010). In comparison with the fits using NLTE static atmosphere models where effective temperatures of (9.6–10.5) × 105 K are achieved (Ness et al. 2011), our temperatures are lower, including the best-fit values. The temperature ranges obtained using the fits with photoionized absorbers are 81–123 eV for day 40 and 94–96 eV (9.6–10.5 × 105 K) for day 50 (Pinto et al. 2012), which are high in general. Our fitted results with the two Hot models for a collisionally ionized (in equilibrium) absorber yield abundances of C/C⊙ = 0.3–0.5, O/O⊙ = 28–43, and N/N⊙ = 5–7. When we introduce the third photoionized absorber component, the abundance of the carbon and nitrogen remains the same, but the oxygen abundance becomes O/O⊙ = 15–17. These values are determined from material in absorption. We find that carbon is subsolar and N supra-solar, consistent with the effects of H-burning (i.e., depletion of C and enhancement of N). The high oxygen content hints at the existence of an underlying C–O WD. Munari et al. (2011) calculated elemental abundances of V2491 Cyg using ground-based optical observations. They found Fe/Fe⊙ = 0.6, O/O⊙ = 4.3, N/N⊙ = 59, and Ne/Ne⊙ = 6.5. van Rossum & Ness (2010) have only assumed solar abundances for simplicity while working with the NLTE expanding atmosphere models, and Ness et al. (2011) have found consistent fits using static NLTE atmosphere models with fixed abundances where the oxygen abundance was in a range O/O⊙ = 10–30. This latter model has similar abundances to what we derived in this study.
In addition to the effective temperatures of the blackbody emission, we can derive the effective radius of the blackbody-emitting region to infer the WD radius. The normalization of the blackbody model fits in Tables 1 and 2 is equal to 4πR2. As a result, the effective radius limits are in a range (32–39) × 108 cm for the region1 data, (12–29) × 108 cm for the regions 2, 3 on day 40 and (2.8–7.5) × 108 cm on day 50 (within the 90% confidence error ranges). The addition of a third absorber component xabs slightly modifies these ranges to (27–30) × 108 cm for the region 1 data, (17–20) × 108 cm for regions 2 and 3 on day 40 and (2.8–4.9) × 108 cm on day 50. The progressive change (getting smaller in time) of radius by a factor of about 5–10 (within errors) in about 10 days is notable. Such a fast decrease in effective stellar remnant radius by about a factor of 2–3 within a week was detected for the moderately fast nova V1974 Cyg (N Cyg 1992) (Balman et al. 1998). Balman et al. (1998) also noted radii in excess of 1 × 109 cm, hinting at a bloated WD during the early H-burning phases of the outburst. The effective blackbody temperatures that are in a range 61–91 eV (taking the widest range from Tables 1 and 2) on day 40 and 50 constrain the WD mass in a range 1.15–1.3 M⊙, which is consistent with the fast nature of the nova. For this calculation we assumed that the temperature range is the maximum temperature achieved by the H-burning WD and used Eq. (3) in Balman et al. (1998), which relates maximum effective temperature with WD mass. We underline that the radius range for the stellar remnant on day 50 shows the desired range for the radius of a C–O WD, which is (2.8−4.5) × 108 cm for the mass range of 1.15–1.3 M⊙ (Hamada & Salpeter 1961; Panei et al. 2000). Our model fits predict super-Eddington luminosities (see Tables 1 and 2) as found in all blackbody model fits, in general. The SPEX assumes a given distance to the source fixed in the fitting procedure, 10.5 kpc (Darnley et al. 2011); a smaller distance will decrease these luminosity values further. A recent distance estimate toward this source is 2.1–3.5 kpc (Özdönmez et al. 2016), which yields a decrease by a factor of 10–25 in the luminosities, reducing our values to the Eddington limit.
We find an interstellar neutral hydrogen column density (in the line of sight, using the Hot-ISM model) for V2491 Cyg of about (3.2–4.2) × 1021 cm-2 for day 40 and (2.2–2.7) × 1021 cm-2 for day 50 from our fits (see Tables 1 and 2). We used the colden1 and nhtot2 interactive program to calculate the column density of hydrogen in the direction of V2491 Cyg. The colden program uses the databases of Stark et al. (1992) and Dickey & Lockman (1990), and nhtot the database from Willingale et al. (2013). The resulting values are (3.8–5.5) × 1021 cm-2, in very good agreement with our findings. Our values are also similar to the values measured from the Swift data (Page et al. 2010). We note that the Amol model fits measure the dust content in the line of sight toward the nova in a range (0.1–2.5) × 1017 cm-2 for the oxygen molecule and (4.64–8.3) × 1017 cm-2 for the water ice. The amount of dust absorption seems to correlate with the variation seen in the LC of the first observation where the low-count-rate region 2 of regions 1–3 shows more dust absorption. The second observation that has the lowest count rate has a dust absorption similar to that of region 2 as far as the oxygen molecule and water ice are concerned. The two collisionally ionized (in equilibrium) hot-absorber components show an equivalent column density of hydrogen in a range (0.6–5.0) × 1023 cm-2 for day 40 and (1.7–3.0) × 1023 cm-2 for day 50 for the first Hot component (see Table 1). We find progressively lower absorption in this component from region 1 to region 3 of the LC (within errors) for the fits presented in Table 1. The second Hot component yields (1.6–18) × 1023 cm-2 for day 40 and (4.6–5.3) × 1023 cm-2 for day 50. The second Hot component has a lower column density at the lowest-count-rate region 2 and the second observation (see Table 1). When we include the additional xabs model in the fitting procedure as displayed in Table 2, the ranges of the column density of the first Hot component diminishes to (0.05–0.4) × 1023 cm-2 for day 40 and (0.14–0.9) × 1023 cm-2 for day 50. The second Hot component shows equivalent hydrogen absorption in a range (0.2–1.6) × 1023 cm-2 for day 40 and (0.6–0.8) × 1023 cm-2 for day 50, which are also lower than the fitted parameters in Table 1. There does not seem to be a strong variation pattern in the range of the equivalent column density of hydrogen for the Hot components over the four spectra fitted. The column density is progressively lower for the first Hot component in Table 1 for day 40. Table 2 indicates that this component shows a higher column density by only about a factor of 2 for the data sets of region 2 and the second observation, where the count rates are the lowest. The second Hot component does not indicate a particular trend. The additional warm absorber component indicates the complexity of the absorption processes and shows that some photoionized absorption is also at work in the wind, expanding shell or ejecta. Table 2 shows that the photoionized absorption is (1.3–4.3)× 1020 cm-2 for day 40 and (0.5–0.7) × 1020 cm-2 for day 50. These values are lower than the interstellar column density of the hydrogen gas in the line of sight, and they comprise about (1–0.1)% absorption relative to the collisionally ionized gas in absorption.
As a result, we suggest that the large-scale variation of the LC of the first observation is due to the changes in the blackbody component parameters and intrinsic to the stellar remnant source itself. However, the changes in the absorption of the Hot-1 component should also be noted. As the effective temperatures increase and/or the effective radius is large, the count rates increase, and when the radius and temperature decrease and/or change, the count rates change as the flux is altered (see Tables 1 and 2). We note that Takei et al. (2011) found that accretion is re-established by day 50 (second observation) and even plausibly by day 40 (see also Page et al. 2010). Some effects of rekindled sporadic accretion onto the surface of the H-burning WD may cause the variations seen in the LC on day 40 (first observation). Moreover, we have recovered a second blackbody emission component in the spectral fitting of the second observation on day 50 with a blackbody temperature of 120–131 eV and an emitting effective radius of (1.3–1.8) × 107 cm calculated from the normalization of the fitted model (see Sect. 3.2). Inclusion of this component in the fits (in Table 2) for the second observation on day 50 decreases the 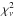 to 1.97. The effective radius is consistent with structures on an accretion disk or is about 10% of the size of the WD calculated from the fits for day 50, which may be consistent with accretion hot spots on intermediate polar CVs. The temperature and the emitting radius of the second blackbody component support the magnetic nature of the system as revealed by Zemko et al. (2015) and that accretion could have been established by day 50 (Takei et al. 2011).
to 1.97. The effective radius is consistent with structures on an accretion disk or is about 10% of the size of the WD calculated from the fits for day 50, which may be consistent with accretion hot spots on intermediate polar CVs. The temperature and the emitting radius of the second blackbody component support the magnetic nature of the system as revealed by Zemko et al. (2015) and that accretion could have been established by day 50 (Takei et al. 2011).
We find self-consistent moving absorber velocities from blueshifts in a range 3097–3812 km s-1 (Hot-1) and 2845–3250 km s-1 (Hot-2) for day 40 (see Table 1). Table 2 shows similar ranges of absorber velocities for this component. On day 50 the two collisionally ionized absorber fits yield velocities 3517–3586 km s-1 (Hot-1) and 2590–2683 km s-1 (Hot-2) by fitting all the absorption lines simultaneously. These ranges are slightly altered for the second observation as 2730–2914 km s-1 (Hot-1) and 3660–3735 km s-1 (Hot-2) when the additional xabs model is added. These velocities are in accordance with the wind or ejecta expansion velocities (see Introduction). We note that absorption from slower material is evident in the second observation on day 50. The additional photoionized absorber has velocities calculated from the blueshift of the lines in the global fit in a range 2645–3113 km s-1 for region 1, 750–2387 km s-1 for region 2, and 2924–3015 km s-1 for region 3 (day 40). On day 50 the range is 3009–3254 km s-1. The location is similar in the shell or ejecta given the derived velocities in Table 2. Assuming the definition ξ = L/nr2 with Eddington luminosities and using the equivalent hydrogen densities in Table 2, the absorber can be located (i.e., r) in the wind, expanding shell or ejecta for all four fits (see also Sect. 3.1).
The blueshifts measured from simple fits to individual lines are found to be in excess of 3000 km s-1 (Ness et al. 2011). In addition, Ribeiro et al. (2011) determined two components in the ejected material by fitting the Hubble Space Telescope (HST) imaging data. They found polar blobs with speeds (3100–3600) km s-1 and an equatorial ring or belt with (2600–2700) km s-1 for the first 100 d of the outburst. These are consistent with our blueshifted Hot-1 and Hot-2 absorber component velocities where the contribution from the equatorial belt or ring becomes more evident by day 50.
To assess the origins of the absorbers (collisionally ionized or photoionized), we need to consider the ejecta or the wind by day 40 and 50 for V2491 Cyg. The plasma temperature obtained from the Swift data on day 39 is 1.0–2.5 keV (1.2–3.0 × 107 K) and on day 53, it is 1.8–4.0 keV (2.2–4.8 × 107 K) (for details of the Swift results, see Page et al. 2010). These values indicate that the X-ray emission originates in shocked fast-moving ejecta. The two Hot components of the collisionally ionized absorber models show temperatures at around 1.1–3.6 keV (day 40) and 1.3–2.0 keV (day 50) for the first Hot component. A temperature range of 0.5–1.0 keV (day 40) and 0.4–0.9 keV (day 50) are derived for the second Hot component (Tables 1 and 2 show similar or overlapping ranges). These temperatures are consistent with the collisionally ionized hot shocked fast-moving ejecta as detected by Swift. We note that the hard X-ray component of V2491 Cyg as detected by Swift is modeled by only a single component, and an existence of different X-ray emission components for the hard component is not considered because of the moderate spectral resolution. For example, there might be a component from wind-wind interactions or circumstellar interaction with different temperatures and evolution. Moreover, a component arising from the wind-driven mass-loss may exist (e.g., shocks within winds due to instabilities) with lower X-ray temperatures and luminosity. It is important to clarify that the 0.2 keV temperature we derive for the collisionally ionized plasma continuum emission (Cie) could be a component within the hard X-ray component. A 0.2 keV temperature is consistent with shock temperatures for stellar winds (e.g., ≤1 keV (≤1.2 × 107 K) in general: Owocki & Cohen 1999). However, the luminosity of this continuum component is high compared with the Swift hard X-ray component, which has a maximum at 3 × 1034 erg s-1 (Page et al. 2010). This may be because the fitted blackbody component results in super-Eddington luminosities with a plausibly inadequate hard X-ray tail to model the spectrum, and as a result, the modeling does not predict the correct luminosities.
We find that the turbulent velocity broadening is in a range 740–897 km s-1 (day 40) and 100–132 km s-1 (day 50) for the first Hot component. This value is 9–62 km s-1 (day 40) and 52–67 km s-1 (day 50) for the second Hot absorber model component. The ranges are similar when an additional xabs model is added to the fits for the first Hot absorber model, and the ranges are <50 km s-1 (day 40) and <17 km s-1 (day 50) for the second Hot absorber component. The turbulent velocity broadening ranges for the third additional photoionized absorber component are 31–174 km s-1 for region 1, not well constrained for region 2, and 44–63 km s-1 for region 3 (day 40). On day 50 the range is 137–273 km s-1. The values for turbulent velocity broadening suggest that the locations of the first and second collisionally ionized absorber are different. It is an indication that the flow (of the ejecta and/or wind) is inhomogeneous, with locations of different densities, turbulent characteristics, and temperatures.
We stress that the X-ray absorption in classical or recurrent novae spectra during the outburst stage is complicated, with several different components such as photospheric, warm photoionized absorption and hot collisionally ionized absorption originating from a nova wind and/or ejecta along with the interstellar absorption from gas and dust in the line of sight toward the system. Using stellar atmosphere models with photospheric absorption, expanding atmospheres or photoionized absorber models alone (as used in the literature), have been inadequate for modeling the high-resolution X-ray spectra, which clearly shows that the modeling needs to be improved. We plan to extend our analysis to other existing data on novae and possible super-soft X-ray sources to study how complex absorption affects X-ray spectra and how the stellar continuum is shaped during the course of the outburst evolution. We also aim to use plausible different continuum models as in stellar atmosphere models.
Acknowledgments
The authors thank an anonymous referee for the critical reading of the manuscript and valuable remarks that have improved it. S.B. and C.G. acknowledge support from TÜBİTAK, The Scientific and Technological Research Council of Turkey, through project 114F351.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Balman, Ş., & Krautter, J. 2001, MNRAS, 326, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Balman, Ş., Krautter, J., & Ögelman, H. 1998, ApJ, 499, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, M. F., & Evans, A. 2008, in Classical Novae (Cambridge University Press) [Google Scholar]
- Chomiuk, L., Nelson, T., Mukai, K., et al. 2014, ApJ, 788, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Darnley, M. J., Ribeiro, V. A. R. M., Bode, M. F., & Munari, U. 2011, A&A, 530, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ferland, G. J. 2003, ARA&A, 41, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2010, ApJ, 709, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Hamada, T., & Salpeter, E. E. 1961, ApJ, 134, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2004, A&A, 417, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helton, L. A., Woodward, C. E., Vanlandingham, K., & Schwarz, G. J. 2008, Central Bureau Electronic Telegrams, 1379 [Google Scholar]
- Henze, M., Ness, J.-U., Darnley, M. J., et al. 2014, A&A, 563, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernanz, M., & Sala, G. 2002, Science, 298, 393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hernanz, M., & Sala, G. 2007, ApJ, 664, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Ibarra, A., Kuulkers, E., Osborne, J. P., et al. 2009, A&A, 497, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, eds. K. Yamashita, & T. Watanabe, 411 [Google Scholar]
- Kahabka, P., Hartmann, H. W., Parmar, A. N., & Negueruela, I. 1999, A&A, 347, L43 [NASA ADS] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Krautter, J., Oegelman, H., Starrfield, S., Wichmann, R., & Pfeffermann, E. 1996, ApJ, 456, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 1994, in Saas-Fee Advanced Course 22: Interacting Binaries, eds. S. N. Shore, M. Livio, E. P. J. van den Heuvel, H. Nussbaumer, & A. Orr, 135 [Google Scholar]
- Lodders, K., & Palme, H. 2009, in 72nd Annual Meeting of the Meteoritical Society, Meteoritics and Planetary Science Suppl. Ser., 72, 5154 [Google Scholar]
- Lynch, D. K., Russell, R. W., Rudy, R. J., Woodward, C. E., & Schwarz, G. J. 2008, IAU Circ., 8935 [Google Scholar]
- MacDonald, J., & Vennes, S. 1991, ApJ, 373, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., & Ishida, M. 2001, ApJ, 551, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Siviero, A., Dallaporta, S., et al. 2011, New Astron., 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, S., Beize, J., Jin, Z.-W., et al. 2008, IAU Circ., 8934 [Google Scholar]
- Nelson, T., Orio, M., Cassinelli, J. P., et al. 2008, ApJ, 673, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Starrfield, S., Burwitz, V., et al. 2003, ApJ, 594, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Starrfield, S., Beardmore, A. P., et al. 2007, ApJ, 665, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Drake, J. J., Starrfield, S., et al. 2009, AJ, 137, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Osborne, J. P., Dobrotka, A., et al. 2011, ApJ, 733, 70 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, T. J., Lloyd, H. M., & Bode, M. F. 1994, MNRAS, 271, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Oegelman, H., Orio, M., Krautter, J., & Starrfield, S. 1993, Nature, 361, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Parmar, A., Benjamin, R., et al. 2001, MNRAS, 326, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Parmar, A. N., Greiner, J., et al. 2002, MNRAS, 333, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Hartmann, W., Still, M., & Greiner, J. 2003, ApJ, 594, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Rana, V., Page, K. L., Sokoloski, J., & Harrison, F. 2015, MNRAS, 448, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, J. P., Page, K. L., Beardmore, A. P., et al. 2011, ApJ, 727, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Cohen, D. H. 1999, ApJ, 520, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Özdönmez, A., Güver, T., Cabrera-Lavers, A., & Ak, T. 2016, MNRAS, 461, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Osborne, J. P., Evans, P. A., et al. 2010, MNRAS, 401, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Osborne, J. P., Kuin, N. P. M., et al. 2015, MNRAS, 454, 3108 [NASA ADS] [CrossRef] [Google Scholar]
- Panei, J. A., Althaus, L. G., & Benvenuto, O. G. 2000, A&A, 353, 970 [NASA ADS] [Google Scholar]
- Petz, A., Hauschildt, P. H., Ness, J.-U., & Starrfield, S. 2005, A&A, 431, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, C., Kaastra, J. S., Costantini, E., & Verbunt, F. 2010, A&A, 521, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, C., Ness, J.-U., Verbunt, F., et al. 2012, A&A, 543, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Orio, M., Gonzales-Riestra, R., et al. 2010, ApJ, 717, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, V. A. R. M., Darnley, M. J., Bode, M. F., et al. 2011, MNRAS, 412, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M. 1989, PASP, 101, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloski, J. L., Luna, G. J. M., Mukai, K., & Kenyon, S. J. 2006, Nature, 442, 276 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stark, A. A., Gammie, C. F., Wilson, R. W., et al. 1992, ApJS, 79, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Starrfield, S., Iliadis, C., Timmes, F. X., et al. 2012, Bull. Astron. Soc. India, 40, 419 [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takei, D., Ness, J.-U., Tsujimoto, M., et al. 2011, PASJ, 63, S729 [NASA ADS] [Google Scholar]
- Tofflemire, B. M., Orio, M., Page, K. L., et al. 2013, ApJ, 779, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Tomov, T., Mikolajewski, M., Ragan, E., Swierczynski, E., & Wychudzki, P. 2008, ATel, 1475 [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rossum, D. R. 2012, ApJ, 756, 43 [NASA ADS] [CrossRef] [Google Scholar]
- van Rossum, D. R., & Ness, J.-U. 2010, Astron. Nachr., 331, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109 [Google Scholar]
- Verner, D. A., Verner, E. M., & Ferland, G. J. 1996, At. Data Nucl. Data Tables, 64, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F., Livio, M., Truran, J. W., & Orio, M. 1987, ApJ, 314, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Zemko, P., Mukai, K., & Orio, M. 2015, ApJ, 807, 61 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectral parameters obtained from the composite model fits including two Hot absorber models to the RGS spectrum of V2491 Cyg.
Spectral parameters obtained from the composite model fits including two Hot absorber and one xabs models to the RGS spectra of V2491 Cyg.
All Figures
 |
Fig. 1 XMM-Newton RGS1 light curve (LC) of V2491 Cyg. First observation (40 d after outburst) is on the left and the second observation is on the right (50 d after outburst). The three different count rate regions are labeled 1, 2, and 3 on the LC of the first observation as assumed in the spectral analysis. |
| In the text | |
 |
Fig. 2 RGS1+2 fluxed spectrum of V2491 Cyg fitted in the range 7–14.4 Å using the plasma emission model Cie and the cold Hot-ISM absorption model. A blackbody model of emission was also used as an additive model for the second-observation spectrum. The left- and right-hand panels show the fit to the fluxed spectrum of region 3 and second-observation data, respectively. |
| In the text | |
 |
Fig. 3 RGS1+2 fluxed spectrum of V2491 Cyg using region 1 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
| In the text | |
 |
Fig. 4 RGS1+2 fluxed spectrum of V2491 Cyg using region 2 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
| In the text | |
 |
Fig. 5 RGS1+2 fluxed spectrum of V2491 Cyg using region 3 of the LC (first observation) fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
| In the text | |
 |
Fig. 6 RGS1+2 fluxed spectrum of V2491 Cyg obtained from the second observation fitted with the composite model described in the text using the Hot model in SPEX (see Table 1). Certain detected blueshifted absorption lines are labeled with dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


