| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628893 | |
| Published online | 02 February 2017 | |
Galactic winds and the origin of large-scale magnetic fields
1 School of Mathematics, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
e-mail: david.moss@manchester.ac.uk
2 Department of Physics, Moscow University, 119992 Moscow, Russia
Received: 10 May 2016
Accepted: 17 October 2016
Context. Observations of dwarf galaxies suggest the presence of large-scale magnetic fields. However the size and slow rotation of these galaxies appear insufficient to support a mean-field dynamo action to excite such fields.
Aims. Here we suggest a new mechanism to explain large-scale magnetic fields in galaxies that are too small to support mean-field dynamo action. The key idea is that we do not identify large-scale and mean magnetic fields. In our scenario the magnetic structures originate from a small-scale dynamo which produces small-scale magnetic field in the galactic disc and a galactic wind that transports this field into the galactic halo where the large turbulent diffusion increases the scale and order of the field. As a result, the magnetic field becomes large-scale; however its mean value remains vanishing in a strict sense.
Methods. We verify the idea by numerical modelling of two distinct simplified configurations, a thin disc model using the no-z approximation, and an axisymmetric model using cylindrical r,z coordinates.
Results. Each of these allows reduction of the problem to two spatial dimensions. Taken together, the models support the proposition that the general trends will persist in a fully 3D model. We demonstrate that a pronounced large-scale pattern can develop in the galactic halo for a wide choice of the dynamo governing parameters.
Conclusions. We believe that our mechanism can be relevant to explaining the presence of the fields observed in the halos of dwarf galaxies, and maybe elsewhere. We emphasize that detailed modelling of the proposed scenario needs 3D simulations, and adjustment to the specific dynamo governing parameters of dwarf galaxies.
Key words: galaxies: magnetic fields / galaxies: dwarf / dynamo
© ESO, 2017
1. Introduction
A variety of celestial bodies, such as galaxies, stars and planets contain large magnetic fields (e.g. Rüdiger et al. 2013). The conventional mechanism believed to be responsible for their origin is a dynamo, driven by differential rotation and the mirror-asymmetric motions of an electrically conducting medium. This kind of dynamo action results in mean magnetic field generation and the large-scale (regular)1 magnetic field of these objects is identified with this mean field. Of course, many details of the mechanism remain debatable. However models of dynamo generation for specific celestial bodies are gradually becoming more realistic.
The mean field dynamo mechanism is a threshold phenomenon, so dynamo drivers have to be strong enough to overcome various magnetic field losses. The strength of dynamo action, measured by a dimensionless number (the dynamo number) is determined partially by the size of the body in question. Celestial bodies are much larger than laboratory devices and magnetic field excitation by a dynamo occurs much more easily in celestial bodies than in the laboratory.
There are however celestial bodies that are relatively small and rotate slowly compared with other bodies of similar type, and nevertheless contain large-scale magnetic fields. Dwarf galaxies which are substantially smaller than spiral galaxies and nevertheless demonstrate the presence of large-scale magnetic fields, e.g. by showing polarized synchrotron emission; Chyży et al. (2016) provide a straightforward example (NGC 2976). The important point here is that dynamo action in spiral galaxies is believed (e.g. Beck et al. 1996) to be slightly supercritical (i.e. the dynamo number is slightly larger than its critical value). It is natural to expect the dynamo number in dwarf galaxies to be several times smaller than that in spirals, and so below the threshold value, implying that the conventional dynamo explanation for large-scale magnetic field generation becomes difficult to maintain (e.g. Mao et al. 2008).
Of course, estimates of the strengths of dynamo drivers in galaxies are far from precise and it is possible to play with numbers in an attempt to resolve the problem. In particular, Chyży et al. (2016) show how this might be achieved in the case of NGC 2976. In spite of the fact that the dynamo active region is supposed to be located within a galactocentric radius of 2 kpc (compared with about 10 kpc in spiral galaxies) and that the rotation velocity is taken as 71 km s-1 (against 250 km s-1 in spirals), they found the intensity of dynamo action (measured by the dynamo number) to be about half that in the Milky Way, but still larger than the critical value at which dynamo generation occurs. An important role in their estimate is played by the fact that a cosmic ray driven dynamo (Hanasz et al. 2009; Gaensler et al. 2005; Kepley et al. 2010; Mao et al. 2012) is modelled. Another attempt of this kind was made by Siejkowski et al. (2014) who emphasized that “the environment of a dwarf galaxy is unfavourable for the large-scale dynamo action because of the very slow rotation that is required to create the regular component of the magnetic field”, but who however argue that the intensity of dynamo drivers in dwarfs might be still sufficient for dynamo action. We recognize the possibilty, however the doubts suggested by Shukurov (2007) concerning the efficiency of dynamo action in dwarfs still persist, and it looks desirable to have an alternative mechanism available to explain the origin of ordered magnetic field in dwarf galaxies.
The aim of this paper is to suggest such an alternative approach to the problem. The key idea here is that we do not now identify the large-scale magnetic field of a body with the mean field obtained by averaging taken over an ensemble of turbulent (convective) motions. Another important point is that generation of mean magnetic field is not the only possibility for dynamo action in a turbulent conducting medium. The additional mechanism is the small-scale (or turbulent) dynamo (e.g. Zeldovich et al. 1990; and in particular it operates in supersonic situations, e.g. Federrath et al. 2014). Differential rotation and/or mirror asymmetry are not required, and turbulent (or convective) motions alone are sufficient. The small-scale dynamo mechanism produces magnetic fields with zero mean. The spatial scale of such fields is comparable with the basic scale of turbulence in the domain where the dynamo action occurs – hence the term small-scale dynamo. This small-scale dynamo is not so dependent on the size of the body, and it looks plausible that it could be efficient in dwarf galaxies as well as in spirals.
 |
Fig. 1 Stationary magnetic field distributions for several models, all Rα = 1,Rω = 7.5,Ru = 120. a) ηh = 25; b) ηh = 50; c) ηh = 1; d) the model shown in panel a) with the field smoothed over a scale 0.1 Rdisc. |
A further important detail of the mechanism proposed below is that a galactic wind can transport small-scale magnetic field into the media surrounding the disc of dwarf galaxies. The diffusivity of the turbulent medium surrounding the disc is believed to be substantially larger than that in the disc (e.g. Beck et al. 1996) and the spatial scale of any magnetic field transported by the wind from the disc will become substantially larger. Such a field remains a field with zero mean in sense that it is determined by an interplay of random factors. However it will appear as a large-scale field on the scale of galactic discs. Because we see only snapshots of magnetic field distributions such a field would be referred to as large-scale from the observational viewpoint. We attempt to illustrate these ideas by computing two quite distinct dynamo models, using first the thin disc (no-z) approximation (Sects. 2 and 3), and then by assuming axisymmetry (Sect. 4).
We emphasize that we are not attempting to model dwarf galaxies (or any other specific class of object) explicitly. The aim of this paper is to demonstrate the idea by simple models that contain the basic features of the proposed mechanism. Thus we have not adapted our models to the specific quantities (dynamo numbers, dimensions) relevant to dwarf galaxies, leaving this to a later paper, and concentrate here on proof of concept. Correspondingly, we do not attempt to give here a review of the properties of these objects.
 |
Fig. 2 Evolution of Fourier components m = 0,1,2 for: a) the external field of the model of Fig. 1a with ηh = 25; b) the internal field of this model; c) the external field of the model shown in Fig. 1c (ηh = 1). In each case the upper panel shows the power in mode m = 0, and the lower panel that in modes m = 1,2 (solid and broken curves respectively). |
2. Thin disc dynamo model
As a basis for our modelling we consider a thin rotating disc (the centre plane of the disc is z = 0) which represents the disc of a dwarf galaxy. The magnetic field evolution in the disc and its surrounding is described using the no-z dynamo model (Moss 1995), which deals with the horizontal magnetic field components Bx and By as functions of x,y, while the component Bz perpendicular to the disc can be estimated from the solenoidality condition. The no-z model has been shown to give a reasonable approximation for modelling of magnetic fields in disc galaxies and, being two-dimensional, allows extensive modelling using reasonably limited computational facilities.
We assume that the disc rotates differentially, and that the rotation curve is asymptotically flat, as is typical for spiral galaxies. An additional dynamo driver, mirror asymmetric turbulence, is also formally present, parametrized by the α-effect. The turbulent diffusivity η is assumed to be larger in the galactic halo than in the disc. The dynamo drivers are chosen to be slightly subcritical so that the magnetic field prescribed as an initial condition decays with time and is, in fact, irrelevant to the final outcome.
The additional factor governing magnetic field evolution, the small-scale dynamo, is parametrized by magnetic field injections distributed randomly in Nspot “hotspots” (star forming regions) in the disc, which sporadically supply small-scale magnetic field. The injection time scale is taken to be of order 10 Myr. The hotspots are relocated randomly at intervals comparable to the rotation period of the disc. We verified that the injections and magnetic field losses rapidly result in a statistical steady state magnetic field distribution. This distribution appears as a random field in the disc. We note that details of this mechanism are irrelevant here: we just need ongoing excitation of small-scale magnetic field. Motivation and further details are given in Moss et al. (2012).
The simplest model of a wind is homogeneous and directed along the x-axis. Such a wind could originate from the motion of the galaxy through the intergalactic medium. We can model this explicitly. Another possible origin is associated with supernova explosions and galactic fountains from strong starburst activity in the galaxy. In this case the wind would be expected to be approximately orthogonal to the disc plane. Initially we attempt to assess this by studying the effects of a radial wind in the disc plane. Thus this model of this wind is not fully realistic: it is assumed to flow in the disc plane and not approximately perpendicular to it. This unrealistic feature is necessary to retain the 2D formulation of the problem: we do not see why changing the wind direction would destroy the basic effect that we wish to illustrate. However, to address this issue we also use another simplification of the dynamo problem, assuming that the magnetic field is axially symmetric and ignoring the azimuthal coordinate (Sect. 4) – the “r,z problem”. Of course, this approach has its separate limitations and inconsistencies.
Various components of the thin disc model have been explored in several recent papers (e.g. Moss et al. 2012, 2015) and have been shown to give realistic magnetic field configurations: here we combine all the above elements for the first time to study the effects of a wind on the small-scale field. The axisymmetric model in r,z coordinates has a long history in studying galactic magnetic fields.
3. Results: no-z model
The strength of the dynamo drivers is measured by the conventional dynamo numbers Rα = α0h/η0, Rω = Ω0h2/η0, Nspot, Binj0 the rms amplitude of the injected field, and Ru = u0h/η0 the magnetic Reynolds number of the wind. Here α0,η0 are the uniform values of α,η in the disc, h = 0.05Rdisc is the uniform disc thickness taken where Rdisc is the disc radius. Ω0 is the central angular velocity and u0 is a reference velocity. ηh is the ratio of the external diffusivity to η0 at large distances from the disc.
For most of our models we choose subcritical values for the mean-field dynamo, Rα = 1, Rω = 7.5, Ru = 120. We set Nspot = 200, and take Binj0 to be the equipartition field strength, and study the development of large-scale magnetic structures in the medium surrounding the disc.
The first three panels of Fig. 1 show the statistically steady magnetic field configurations obtained with a radial wind with speed proportional to radius for various choices of ηh – see the captions. The fourth panel demonstrates that the effect of spatial smoothing hardly alters the distribution of external field shown in Fig. 1a. Of course, these figures are just snapshots taken from fluctuating distributions – as indeed are the observed fields.
We verified that the large-scale configurations is robust to changes in numerical resolution, and that the form of the final configuration is unaltered when the mean field dynamo is absent (i.e. Rα = 0) – as the mean field dynamo is subcritical in the previous models its long term influence is negligible.
 |
Fig. 3 The model with a uniform wind in the x-direction, ηh = 25,Ru = 120: a) the statistically steady field; b) evolution of Fourier components of the external field; c) the evolution of the global magnetic energy. |
In Fig. 2 we show the evolution of the lower Fourier-analysed components of the external and internal fields for the model of Fig. 1a, and the external field of the model of Fig. 1c – these are typical. Here we also show the time evolution of the global magnetic energy – the cases with a radial wind appear very similar. The spikes correspond to the small-scale field injections.
We define the power in the m = 0 part of the field by the global integral 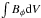 , and that in the azimuthal mode m> 0 by
, and that in the azimuthal mode m> 0 by 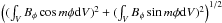 . Thus the power in m = 0 can take negative values, that in higher modes is positive definite.
. Thus the power in m = 0 can take negative values, that in higher modes is positive definite.
Finally we present in Fig. 3 the corresponding results for a model with a uniform wind in the x-direction. Now the external field is displaced to one side of the disc. Here we also show in panel 3c the time evolution of the global magnetic energy in this case – the examples with radial wind are very similar. The spikes correspond to the discrete field injections
We learn from Fig. 2 what happens during the formation of large-scale patterns in the galactic halo. Indeed, we see that the mode m = 0 becomes about 3 times larger in the external parts of the galaxy (i.e. in the halo) than in the galactic disc. This large-scale field fluctuates in time and is in this sense a field with zero mean. The large-scale component m = 0 is present in the disc as well. However the field injections are random and have zero mean. Presumably, these effects occur because Nspot is quite, but not very large.
4. Axisymmetric model in (r, z) coordinates
The experiments described in Sect. 3 using the thin disc, no-z approximation provide strong evidence that the proposed mechanism can work in that geometry. However, in the specific context of ordered magnetic field above the discs of dwarf galaxies, it might be preferable to use a more directly applicable geometry. (Although, as we point out in Sect. 3, that geometry can be directly relevant to a galaxy moving through an external medium, as described in Moss et al. 2014.) Thus in this section we study an axisymmetric galaxy model, represented in cylindrical polar coordinates (r,φ,z) with no φ-dependence. The code used is basically that of Moss et al. (1998), and subsequently adapted for use in Moss et al. (2016).
In these experiments we implement the same random field injection mechanism as in the no-z model of Sect. 2, with the hotspots now being at randomly allocated points in r,z. Of course, this model also has its own obvious deficiencies, notably that the “turbulence” is now necessarily axisymmetric, but we feel that the results of this section combined with those of Sect. 3 can contribute to the case for the more general relevance of the mechanism.
 |
Fig. 4 Stationary magnetic field distributions for the axisymmetric model in r,z coordinates for Ru = 0,1,5,10 respectively. The extent of the magnetic field in the region surrounding the disc increases with Ru. |
Our standard disc semi-thickness h = λR has λ = 0.04 (so with R = 10 kpc, h = 400 pc), and the computational grid covers rmin ≤ r ≤ 1.0, −zmax ≤ z ≤ zmax, with rmin = 0.05,zmax = 0.3333 in units of the galactic radius. The diffusivity increases asymptotically by a factor of 30 with | z |, and we study a model with no alpha-effect, i.e. Rα = 0, and take Rω = 10. The random field injections are described by the same parameters as before: Nspot,rspot,dtinj, and the interval between rerandomizations of the spot locations, Tspot = 0.3. First we display in Fig. 4a the statistically steady field without any bulk velocity present. A maybe somewhat surprising feature is the apparent presence of semi-ordered “vortices” in the instantaneous mature fields. We attribute this feature to the intervals between relocation of the hotspots being much longer than the field injection intervals (i.e. Tspot ≫ dtinj), so there is sufficient time for diffusion at the boundaries between these sites to allow the instantaneously stronger hotspots to dominate. The height of the disc may also play a role – it is known that in spherical thin shell αΩ mean field dynamos that there is a tendency for cells to form with aspect ratio O(1). In support of this hypothesis we note two subsidiary experiments.
-
1.
With just an initial injection of field and no subsequentadditions, the field of course decays. However after some time the(much weakened) field structure reduces to that of just 3 or4 vortices.
-
2.
If the relocation interval Tspot is made slightly shorter than the injection interval dtinj, the effect almost vanishes.
We now introduce a bulk velocity directed out of the disc. For demonstration purposes (and simplicity) we take a velocity purely in the z-direction, uz = Rutanh(z/h(r)) (where of course h(r) = const. here). For simplicity, as the model does not involve any mixing of poloidal and toroidal magnetic fields, below we discuss only the poloidal field component. We show in Figs. 4b,c,d the steady state field with Ru = 1,5,10 respectively. The main features, i.e. the presence of ordered field above the disc, appear after a relatively short time, certainly by τ< 2. We note that the results are substantially similar with Ru> 0 and Tspot ≲ dtinj.
We also experimented with changing the disc height, and with changing the number of hotspots. There was little or no qualitative change in the results. As might be expected, the magnetic field patterns in the halo region near to the disc become more pronounced as Ru increases, i.e. with increasing wind velocity. Effects are still very small for Ru = 1, but the scale of the field exterior to the disc reaches a third of the disc radius with Ru = 10. We note that marked large-scale structures are produced for significantly smaller values of Ru in this case than in the no-z problem of Sect. 3, but it should be remembered that the displacement of the structures from the disc is substantially larger in the no-z case. Again, these figures represent just instantaneous states of a fluctuating field distribution.
 |
Fig. 5 Stationary magnetic field distributions for the axisymmetric model in r,z coordinates with Nspot = 400,rspot = 0.005 and a) Ru = 0; b)Ru = 25. |
To avoid the possibility that the out-of-disc field is just an artifact of the particular implementation of the introduction of the random field, we also experimented with random injection parameters that give smaller scale disorder, rspot = 0.005,Nspot = 400. The statistically steady field in the absence of a bulk velocity, i.e. with Ru = 0, is shown in Fig. 5a. In panel b of this figure we show the statistically steady field when Ru = 25. It can be seen that results are quantitatively similar to those obtained previously, albeit using a somewhat larger (but still plausible) value of Ru.
For the models with Nspot = 100 discussed above, the ratio of the rms poloidal field in the halo (0.08 ≤ z ≤ zmax) to that in the disc is also calculated. These values are plotted in Fig. 6. Unsurprisingly the ratio increases with the value of Ru. An important effect appears to be amplification of the halo field by stretching by the z-dependent wind. The small non-zero value when Ru = 0 arises purely from the large diffusion coefficient above the disc. (Any small fluctuations are manifestations of the stochastic nature of the model.)
We feel that these results, taken with those of Sect. 3, provide support for the operation of the effect discussed independently of the particular geometry in which the model is embedded.
5. Discussion and conclusions
We have presented several numerical models of large-scale magnetic patterns generated by wind transport of randomly distributed small-scale magnetic field present in the galactic disc. Even if the large-scale dynamo in the disc remains subcritical (or equivalently is absent), the overall magnetic field distribution rapidly reaches a statistically steady state which resembles a large-scale field distribution in the regions external to the disc (the “galactic halo”). Amplification caused by stretching by a spatially dependent wind may also play a role. We believe that this scenario could be relevant to producing large-scale magnetic fields in dwarf galaxies, and potentially explain certain observations of these objects (Chyży et al. 2016). Note that Drzazga et al. (2016), when discussing observations of a dwarf galaxy NGC 2976 performed in order to isolate a large-scale magnetic pattern, discussed the necessity of a mechanism similar to that one suggested here.
 |
Fig. 6 Ratio of rms poloidal field in 0.08 ≤ z ≤ zmax to that in the disc as a function of Ru for the models with Nspot = 100. |
Possibly, this scenario (combined with conventional large-scale dynamo action) could also be useful for explaining some magnetic field structures in stellar atmospheres.
We stress that strictly speaking the magnetic field generated in our modelling in the outermost parts of dwarf galaxies will still have a vanishing mean. However this fact is mainly of mathematical interest because we only see snapshots of magnetic field distributions. The magnetic field mean will vanish after averaging over a substantial time interval, but the length of this interval is huge compared to the lifetime of human beings and substantial even compared to galactic timescales.
We note that in the thin disc model of Sect. 3 the large-scale pattern is displaced from the disc as far as distances comparable with the disc radius. The displacement is large because the wind modelled is quite fast (Ru = 120 corresponds to u0 = 160 km s-1 if Ω0h = 10 km s-1). Plausibly the actual wind velocity is several times smaller and so, correspondingly, would be the displacement. The point however is that if we consider displacement of the large-scale field pattern in the direction orthogonal to the disc then a displacement by 1/5 of the galactic radius seems sufficient, as galactic discs are thin compared to their radii. This is supported by the models of Sect. 4. In Sect. 3 we enhanced the effect to make it pronounced while retaining the 2D format of the problem.
Presumably, the effect observed depends on the number of injections being quite, but not very, large. In this sense the effect discussed looks similar to the proposed explanation for the presence of a nonvanishing magnetic moment during solar magnetic field inversions (Moss et al. 2013). This magnetic moment randomly migrates from being almost parallel to the rotation axis to being almost antiparallel (Pipin et al. 2014). The net magnetic moment appears due to the finite number of active regions. We agree that if the number of injection sites were much larger and, certainly if anywhere near to comparable with, say, Avogadro’s number, the resulting large-scale pattern would be averaged out.
We also note that the mechanism that we suggest has some features in common with that suggested by Chakrabarti et al. (1994) which, however, is addressed to a different astrophysical situation (see also Cho 2014). A related mechanism, in which turbulent diffusion plays an important role, was discussed in a galactic context by Blackman (1998).
Our simulations are intended only as a demonstration of a physical effect, and are not specifically directed to modelling any specific object or particular type of galaxy. Thus we have not attempted to model observational consequences of the models, such as polarization patterns. Such an undertaking would require much more computationally demanding 3D modelling and corresponding adjustment of physical parameters, and would need to be addressed separately. We note however that our results appear broadly compatible with what is known about magnetic fields in dwarf galaxies. We are content here to demonstrate what we feel may be an interesting physical process.
Acknowledgments
D.S. is grateful to RFBR for financial support under grant 15-02-01407. Useful discussions with Olga Silchenko are acknowledged. Comments from an anonymous referee were valuable.
References
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, E. G. 1998, ApJ, 496, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., Rosner, R., & Vainshtein, S. I. 1994, Nature, 368, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J. 2014, ApJ, 797, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., Drzazga, R. T., Beck, R., et al. 2016, ApJ, 819, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Drzazga, R. T., Chyży, K. T., Heald, G. H., Elstner, D., & Gallagher, J. S. 2016, A&A, 589, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federrath, C., Schober, J., Bovino, S., & Schleicher, D. R. G. 2014, ApJ, 797, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Science, 307, 1610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hanasz, M., Wóltański, D., & Kowalik, K. 2009, ApJ, 706, L15 [Google Scholar]
- Kepley, A. A., Mühle, S., Everett, J., et al. 2010, ApJ, 712, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Stanimiroviċ, S., et al. 2008, ApJ, 688, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., McClure-Griffiths, N. M., Gaensler, B. M., et al. 2012, ApJ, 759, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1995, MNRAS, 275, 191 [NASA ADS] [Google Scholar]
- Moss, D., Shukurov, A., Sokoloff, D., Berkhuijsen, E. M., & Beck, R. 1998, A&A, 335, 500 [NASA ADS] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Kitchatinov, L. L., & Sokoloff, D. 2013, A&A, 550, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2014, A&A, 566, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Stepanov, R., Krause, M., Beck, R., & Sokoloff, D. 2015, A&A, 578, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Mikhailov, E., Silenko, O., et al. 2016, A&A, 592, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pipin, V. V., Moss, D., Sokoloff, D., & Hoeksema, J. T. 2014, A&A, 567, A90 [Google Scholar]
- Rüdiger, G., Kitchatinov, L. L., & Hollerbach, R. 2013, Magnetic Processes in Astrophysics: Theory, Simulations, Experiments (Wiley-VCH) [Google Scholar]
- Siejkowski, H., Otmianowska-Mazur, K., Soida, M., et al. 2014, A&A, 562, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shukurov, A. 2007, in Mathematical Aspects of Natural Dynamos, eds. E. Dormy, & A. M. Soward (Boca Raton, FL: CRC Press), 313 [Google Scholar]
- Zeldovich, Ya. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1990, The Almighty Chance (Singapore: World Scientific) [Google Scholar]
All Figures
 |
Fig. 1 Stationary magnetic field distributions for several models, all Rα = 1,Rω = 7.5,Ru = 120. a) ηh = 25; b) ηh = 50; c) ηh = 1; d) the model shown in panel a) with the field smoothed over a scale 0.1 Rdisc. |
| In the text | |
 |
Fig. 2 Evolution of Fourier components m = 0,1,2 for: a) the external field of the model of Fig. 1a with ηh = 25; b) the internal field of this model; c) the external field of the model shown in Fig. 1c (ηh = 1). In each case the upper panel shows the power in mode m = 0, and the lower panel that in modes m = 1,2 (solid and broken curves respectively). |
| In the text | |
 |
Fig. 3 The model with a uniform wind in the x-direction, ηh = 25,Ru = 120: a) the statistically steady field; b) evolution of Fourier components of the external field; c) the evolution of the global magnetic energy. |
| In the text | |
 |
Fig. 4 Stationary magnetic field distributions for the axisymmetric model in r,z coordinates for Ru = 0,1,5,10 respectively. The extent of the magnetic field in the region surrounding the disc increases with Ru. |
| In the text | |
 |
Fig. 5 Stationary magnetic field distributions for the axisymmetric model in r,z coordinates with Nspot = 400,rspot = 0.005 and a) Ru = 0; b)Ru = 25. |
| In the text | |
 |
Fig. 6 Ratio of rms poloidal field in 0.08 ≤ z ≤ zmax to that in the disc as a function of Ru for the models with Nspot = 100. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


