| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629618 | |
| Published online | 11 January 2017 | |
Measurement of the X-ray proper motion in the south-east rim of RX J1713.7−3946
1 Laboratoire AIM, IRFU/SAp – CEA/DRF – CNRS – Université Paris Diderot, Bât. 709, CEA-Saclay Gif-sur-Yvette Cedex France
e-mail:
fabio.acero@cea.fr
2 Department of Physics, Faculty of Science & Engineering, Chuo University, 1-13-27 Kasuga, Bunkyo, 112-8551 Tokyo, Japan
3 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
Received: 30 August 2016
Accepted: 18 November 2016
We report on the first proper motion measurement in the supernova remnant RX J1713.7−3946 using the XMM-Newton X-ray telescope on a 13 yr time interval. This expansion measurement is carried out in the south-east region of the remnant, where two sharp filament structures are observed. For the outermost filament, the proper motion is 0.75+0.05-0.06 ± 0.069syst arcsec yr-1 which is equivalent to a shock speed of ~3500 km s-1 at a distance of 1 kpc. In contrast with the bright north-west region, where the shock is interacting with the border of the cavity, the shock in the south-east region is probably expanding in the original ambient medium carved by the progenitor and can be used to derive the current density at the shock and the age of the remnant. In the case where the shock is evolving in a wind profile (ρ ∝ r− s, s = 2) or in a uniform medium (s = 0), we estimate an age of ~2300 yr and ~1800 yr respectively for an ejecta power-law index of n = 9. The specific case of an ejecta power-law index of n = 7, and s = 0, yields an age of ~1500 yr, which would reconcile RX J1713.7−3946 with the historical records of SN 393. In all scenarios, we derive similar upstream densities of the order of 0.01 cm-3, compatible with the lack of thermal X-rays from the shocked ambient medium.
Key words: ISM: supernova remnants / ISM: individual objects: RX J1713.7-3946 / X-rays: ISM
© ESO, 2017
1. Introduction
Shell-like X-ray synchrotron emission in supernova remnants (SNRs) is the evidence that electrons can be accelerated to very high energies (up to 100 TeV) at the shock. All such SNRs are young (t< 5000 yr) and exhibit high shock speeds (Vsh> 2000 km s-1). These are ideal conditions in which diffusive shock acceleration can take place. Therefore, these sources provide the best targets to study the detailed physics of cosmic ray (CR) acceleration in SNRs.
While very young historical SNRs, e.g. Tycho, Kepler, SN 1006 typically show a mix of both synchrotron and thermal emission (from ejecta and shocked ambient medium), some slightly older SNRs, e.g. RX J1713.7−3946, Vela Jr and HESS J1731-347, exhibit spectra dominated by X-ray synchrotron emission. Despite a decade of search, no thermal X-ray emission was detected in any of these SNRs until Katsuda et al. (2015) recently reported the first detection of thermal X-rays from the central region of RX J1713.7−3946, which probably originates from shocked ejecta, rather than shocked interstellar medium (ISM). The measured abundance ratio suggest that the progenitor of RX J1713.7−3946 was a relatively low-mass star (<20 M⊙), consistent with the estimate of 12–16 M⊙ (Cassam-Chenaï et al. 2004) based on the effect of stellar winds of the progenitor star on the surrounding medium.
 |
Fig. 1 Left panel: exposure corrected and background subtracted count map in the 0.6–6 keV energy band of the 2015 XMM-Newton observation. The image is smoothed with a Gaussian of 20 arcsec kernel radius. The red contours are the results of the Canny edge detection algorithm discussed in the main text. The white boxes represent the regions used to extract the radial profiles shown in Fig. 2 and the white and red crosses the 2002 and 2015 pointing positions. Right panel: edges detected in the 2002 (black) and 2015 (red) observations. The point sources discussed in the image registration process are labeled Src 1 to Src 6. |
RX J1713.7−3946 is the brightest SNR at TeV energies and is considered the prototypical CR accelerator. Despite clear evidence of efficient electron acceleration from X-ray synchrotron, it is unclear whether γ-rays originate from accelerated hadrons (dominating the Galactic CR composition) or electrons. GeV observations with Fermi-LAT show a hard spectrum (Γ = 1.50 ± 0.11, Abdo et al. 2011) that is incompatible with purely hadronic γ-rays stemming from a canonical E-2 proton population, but can be represented by inverse Compton (IC) emission from CR electrons up to TeV energies.
However, while IC γ-ray emission is dominant, this does not mean that there is no hadron acceleration in RX J1713.7−3946 since we see indirect evidence in other SNRs of efficient hadronic acceleration through other means, e.g. highly amplified magnetic fields and back-reaction of energetic hadrons (Parizot et al. 2006; Miceli et al. 2012). Detailed modeling of CR acceleration coupled to the SNR evolution has been performed by Ellison et al. (2010) and been fit to X-ray and γ-ray data. The lack of thermal X-rays implies a low density (<0.05 cm-3, Ellison et al. 2010) that suppresses hadronic γ-rays. Using these models with a known value of the ambient density enables us to provide actual measurements and no longer upper limits on the fraction of kinetic energy that is transferred to accelerated hadrons in RX J1713.7−3946; a key parameter in understanding the role of SNRs as Galactic CR accelerators. As no thermal X-ray emission from shocked ISM is seen, detecting proper motion in X-rays remains the best hope for constraining the ambient density and the age of this remnant. In addition, while the SNR is commonly associated with the historical supernova SN 393 (Wang et al. 1997), this association has been debated by Fesen et al. (2012) and shock speed measurements can help to estimate the SNR age.
To obtain a clean measurement of proper motion, a sharp filament is needed. These types of features are not present in the bright, most studied, north-west region of the remnant. By inspecting the full mosaic provided by XMM-Newton (Fig. 1 of Acero et al. 2009), we found promising filaments in the south-east (SE). The shock front in the SE region is the most distant shock from the central compact object (indicating the initial location of the supernova). The shock in this region is probably still evolving in the original cavity carved by the wind of the massive progenitor, enabling us to directly probe the cavity density and the age of the SNR.
2. Data reduction
 |
Fig. 2 Radial profiles, Cstat maps and Cstat radial contribution from the outer region (top panel) and inner region (bottom panel) defined in Fig. 1. The right panels show the cumulative statistics radial contribution (ΔCstat = C0(r)−Cbestfit(r)) taken at the best-fitted amplitude and where C0(r) is the Cstat radial contribution at a 0 arcsec model shift. |
The SE region of the SNR was observed by XMM-Newton on March 14 2002 for 13.7 ks but was affected by solar flares resulting in a useful exposure time of 11.7 and 5.7 ks for MOS and pn respectively. The deep 82 ks observation (64.1/48.0 ks for MOS and pn respectively after screening) obtained on March 11, 2015 provides high statistics and a 13-yr leverage to study the proper motion of the rim.
For the image generation and the radial profiles, the instrumental background was derived from the filter wheel closed data provided by the XMM-Newton Science Operation Center1.
The 0.6–6 keV energy range was chosen since there is little emission below 0.6 keV and the instrumental background starts to dominate above 6 keV. The background subtracted and exposure corrected MOS + pn image in the 0.6–6 keV energy range (shown in Fig. 1, left) clearly reveals several sharp filaments. The exact shape and edge position of the filaments is not easy to determine by eye, which hampers a proper definition of regions parallel to the shock to extract radial profiles. To guide our region definition, we used a Canny edge detection algorithm, which is commonly used in image processing. The first step of this algorithm is a Gaussian filtering to reduce the image noise. Then the intensity gradients in the image are computed and potential edges are thinned down to 1-pixel curves. Finally edges pixels are filtered using an hysteresis thresholding on the gradient magnitude. We used the Canny edge implementation provided in the scikit-image2 Python library (van der Walt et al. 2014) applied to the background subtracted, exposure corrected, count map. In the Gaussian filtering step, the width was set to 20 arcsec radius and the edges are stable when changing the width of the Gaussian in the filtering step. The resulting edges are shown as a contour on Fig. 1 and perfectly outline the shape of the filaments, even in faint regions where the filament fades out. Based on the edge images shown in Fig. 1 (right), two main structures labeled outer region and inner region (towards the inside of the SNR which are probably due to projection effects) were identified as promising regions to investigate the filament’s proper motion. The inclination of the box regions was chosen to be parallel to the shock edge and the width was chosen so that the shock edge is approximately planar within the regions.
While the 2002 and 2015 observations were carried out with the same position angle, the two pointing positions are separated by 2.7 arcmin (see crosses in Fig. 1). The peak of the sharp inner filament is almost equidistant to the two pointing positions and is not affected by changes in PSFs in 2002 and 2015 (same off-axis angle). The outer filament is respectively located at 6.5 arcmin from the 2002 pointing position and 4.3 arcmin from the 2015 pointing position. We investigated the evolution of the PSF as a function of off-axis angle using the XMM-Newton calibration file (XRT*_XPSF_0014.CCF) for a reference energy of 1.5 keV. The FWHM for our off-axis angle configuration (4.3 arcmin and 6.5 arcmin) corresponds to 5.9 arcsec and 6.3 arcsec respectively. This very small difference in PSF slightly changes the way the shock front is smoothed but, at the first order, does not affect the localisation of the peak.
The 2002 and 2015 observations were searched for common registration sources and six candidate X-ray point sources were found (Sources 1–6 are shown in Fig. 1, right). Whenever the sources were covered by archival Chandra observations, we confirmed that they were point-like in nature (Sources 1–3). Sources 2–4 have optical counterparts and, while Sources 3 and 4 have measured proper motions (from the PPMXL catalog, Roeser et al. 2010), the displacement remains <0.5 arcsec over our 13-yr period. Sources 5A (detected in 2002) and 5B (detected in 2015) are separated by 25 arcsec and are probably two independent variable sources. We ruled out a source with a high proper motion since source 5B is detected by Chandra in 2000 and 2009 at a position that is compatible with the one obtained by XMM-Newton in 2015. Source 5A is not detected in the 2000 nor in the 2009 Chandra observation. Source 6 has an optical counterpart with high proper motion (PMDec = −120 mas yr-1, and PMRA = 17 mas yr-1), which amounts to an apparent displacement of 1.6 arcsec over 13 yr and is not used in our alignment process. Since the 2015 observation is much deeper, we used the 2015 position of Sources 1−4 (obtained with the XMM-Newton SAS tool edetect_chain) as reference to align the astrometry of the 2002 observation, using the SAS tool eposcorr. After alignment, the mean 2002–2015 residual offset of the four registration sources is 0.9 arcsec, which we consider as our systematic uncertainty.
To avoid any pixelization effect for the rapidly changing profile of the filament, we extracted the source radial profiles with a 2 arcsec binning directly from the event lists and only from the MOS instrument that has a smaller camera pixel size (1.1 arcsec) compared to pn (4.1 arcsec). Removing pn from the 2002 observation (our limiting factor) only discards 5.7 ks of observation (11.7 ks of MOS remaining). The instrumental background and the exposure profiles were extracted directly from the filter wheel closed images and the exposure maps. The point sources were removed from the event lists, the exposure maps, and the background maps. As a result, we obtained three radial profiles (count, exposure, and instrumental background profiles) for each observation and for each MOS camera.
3. Analysis
Best-fitted expansion parameters.
To estimate the proper motion between the two epochs, we built a shock profile model based on the 2015 high statistic observation (assuming no errors), which is then compared to the 2002 profile. The latter profile is in counts and is the sum of the MOS1 and MOS2 camera. We note that the number of counts for some bins of the 2002 radial profile falls below 25 counts/bins and we have therefore used Cash statistics (Cstat, Cash 1979) rather than the χ2 estimator. A count profile model and the associated Cstat value is calculated as a function of a Shift (in arcsec) and Amplitude (the ratio of the 2002 to 2015 profile) parameters. The Cstat value C is calculated as 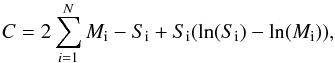 (1)where Mi is the predicted number of counts in bin i and Si the observed number of counts in bin i in the 2002 observation. The model M is calculated for each pair of parameters and provides the expected number of counts, taking into account the observational conditions of the 2002 observation (exposure and instrumental background profile):
(1)where Mi is the predicted number of counts in bin i and Si the observed number of counts in bin i in the 2002 observation. The model M is calculated for each pair of parameters and provides the expected number of counts, taking into account the observational conditions of the 2002 observation (exposure and instrumental background profile): 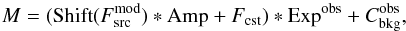 (2)where
(2)where 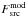 represents the vignetting-corrected, background-subtracted flux profile from the 2015 model observation. Fcst is the astronomical background flux, measured upstream of the SNR shock for r< 75 arcsec in the outer region (see Fig. 2, top, left panel). The parameters Expobs and
represents the vignetting-corrected, background-subtracted flux profile from the 2015 model observation. Fcst is the astronomical background flux, measured upstream of the SNR shock for r< 75 arcsec in the outer region (see Fig. 2, top, left panel). The parameters Expobs and 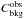 represent the 2002 exposure and instrumental background profiles. We note that the amplitude and shift parameters are applied only to
represent the 2002 exposure and instrumental background profiles. We note that the amplitude and shift parameters are applied only to 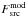 not to shift or amplify the instrumental background or any exposure related features. The resulting 2D Cstat maps are shown in the middle panels of Fig. 2, and a 1D profile as a fit of the shift alone is shown in the right panels. The best-fit results are listed in Table 1. In both regions, no significant change in brightness is observed (Amplitude is compatible with unity) and for a distance of 1 kpc, the corresponding shock speed is respectively 2880 ± 240stat ± 330syst km s-1 and
not to shift or amplify the instrumental background or any exposure related features. The resulting 2D Cstat maps are shown in the middle panels of Fig. 2, and a 1D profile as a fit of the shift alone is shown in the right panels. The best-fit results are listed in Table 1. In both regions, no significant change in brightness is observed (Amplitude is compatible with unity) and for a distance of 1 kpc, the corresponding shock speed is respectively 2880 ± 240stat ± 330syst km s-1 and 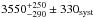 km s-1 for the inner and outer regions.
km s-1 for the inner and outer regions.
4. Discussion
The measurements of the X-ray expansion rate in the SE region can be used to estimate the age of the SNR since the shock there is probably still evolving in the cavity carved by the progenitor and has not yet encountered denser material similar to that in the bright north-west region. The age t and the radius R can be related via the expansion parameter m as R ∝ tm, where the age can be derived as 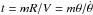 . The value of the expansion parameter ranges from m = (n−3)/(n−s) in the ejecta dominated phase to m = 2/(5−s) in the Sedov-Taylor phase, where n and s are the ejecta and ambient medium density profile indices (ρ(r) ∝ r− n,s). For the values n = 9 and s = 2 (the shock is evolving in the wind of the progenitor star), m = 0.86/0.66 in the ejecta dominated/Sedov-Taylor phase, respectively.
. The value of the expansion parameter ranges from m = (n−3)/(n−s) in the ejecta dominated phase to m = 2/(5−s) in the Sedov-Taylor phase, where n and s are the ejecta and ambient medium density profile indices (ρ(r) ∝ r− n,s). For the values n = 9 and s = 2 (the shock is evolving in the wind of the progenitor star), m = 0.86/0.66 in the ejecta dominated/Sedov-Taylor phase, respectively.
In the outer and inner region, we obtain very similar values of 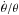 (see Table 1) suggesting a projection effect for the inner shock. For simplicity, we use the value from the outer shock propagating in the plane of the sky, where
(see Table 1) suggesting a projection effect for the inner shock. For simplicity, we use the value from the outer shock propagating in the plane of the sky, where 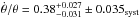 kyr-1 or
kyr-1 or 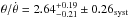 kyr.
kyr.
With the previously derived values of θ, 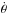 , and m and without any assumptions on the ambient density nor on the distance to the SNR, we can constrain the age of the SNR to be 1760 yr in the Sedov-Taylor phase and 2270 yr in the ejecta dominated phase (2170 yr if n = 7).
, and m and without any assumptions on the ambient density nor on the distance to the SNR, we can constrain the age of the SNR to be 1760 yr in the Sedov-Taylor phase and 2270 yr in the ejecta dominated phase (2170 yr if n = 7).
The characteristic transition timescale between the ejecta dominated and ambient medium dominated phase is given by Eq. (24) of Tang & Chevalier (2016). For n = 9 and s = 2, a reasonable ejecta mass of 10 M⊙, an explosion energy of 1051 erg, and an ambient density of 0.05 cm-3, ttran is 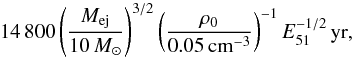 (3)where ρ0 is the density given at a reference radius R0 = 9.6 pc (the radius of the SE rim at 1 kpc) and ρ = ρ0(R/R0)-2. Therefore, in the case of RX J1713.7−3946, the SNR is still in the ejecta dominated phase.
(3)where ρ0 is the density given at a reference radius R0 = 9.6 pc (the radius of the SE rim at 1 kpc) and ρ = ρ0(R/R0)-2. Therefore, in the case of RX J1713.7−3946, the SNR is still in the ejecta dominated phase.
 |
Fig. 3 Left panel: ejecta mass distribution as a function of age and density assuming equality in Eq. (4). For each point of the grid, the swept-up mass in the equation is derived by computing the shock radius using evolution equations for a supernova explosion energy of 1051 erg, n = 9, and s = 2. The white region indicates the excluded parameter space, where the ejecta mass becomes negative. Middle panel: using the ejecta distribution previously derived, the same explosion energy, and ejecta and density profile indices, the ratio Rsh/Vsh is obtained and shown here as the distance independent ratio |
To investigate the age and the ambient density parameters in more detail, the shock evolution equations of Tang & Chevalier (2016), which provide a better accuracy than the Truelove & McKee (1999) solutions for s = 2, are used. Based on the size of the cavity carved by the progenitor star, Cassam-Chenaï et al. (2004) estimated a progenitor zero-age main sequence (ZAMS) mass of 12–16 M⊙.
The shock in the SE is probably still propagating in the stellar wind since no shock-cloud interaction is detected in 12CO observations of this region (Fukui et al. 2012) and the SE rim has the lowest absorption column density (Sano et al. 2015). In this scenario, the swept-up mass Msw in the cavity is related to the mass loss of the progenitor (Msw<Mmassloss). Starting from an initial progenitor mass of Mzams = 14M⊙, the ejecta mass remaining after the mass lost in the wind is 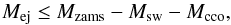 (4)where for s = 2,
(4)where for s = 2, 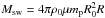 (μ is the mean atomic mass and mp the proton mass), and Mcco is the mass of the central compact object (1.4 M⊙). We note that the shock in the south east region is probably not far from the cavity boundary (implying Msw ~ Mmassloss) since the shock in the north west is thought to already be interacting with the border of the cavity (Fukui et al. 2012).
(μ is the mean atomic mass and mp the proton mass), and Mcco is the mass of the central compact object (1.4 M⊙). We note that the shock in the south east region is probably not far from the cavity boundary (implying Msw ~ Mmassloss) since the shock in the north west is thought to already be interacting with the border of the cavity (Fukui et al. 2012).
For an explosion energy of E = 1051 erg, and n = 9 and s = 2, the shock radius is computed using evolution equations as a function of the SNR age and wind density, which is used to estimate the swept-up mass in the cavity. The ejecta mass distribution (Fig. 3, left panel) is then derived assuming the equality in Eq. (4). We note that high density values are excluded since the swept-up mass cannot be larger than the progenitor mass (Msw<Mzams−Mcco).
Using the ejecta mass distribution and the same supernova explosion parameters, Rsh and Vsh are obtained from evolution equations and expressed independently of the SNR distance as 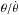 for each age and ambient density shown in Fig. 3 (middle panel). The X-ray measurement of this ratio (
for each age and ambient density shown in Fig. 3 (middle panel). The X-ray measurement of this ratio (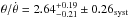 kyr) is shown as a white contour and leads to a SNR age3 of 2250 ± 170stat ± 200syst yr. We note that if the measured proper motion was smaller, the age estimate would increase.
kyr) is shown as a white contour and leads to a SNR age3 of 2250 ± 170stat ± 200syst yr. We note that if the measured proper motion was smaller, the age estimate would increase.
For a fixed age of 2250 yr, the constraints that we can obtain on the wind density depend on the explosion energy and the physical radius of the SNR. To explore those dependencies, we computed the radius of the SNR (or its distance for a fixed angular size of θ = 0.55°) as a function of the explosion energy and the wind density, as shown in the right-hand panel of Fig. 3. For a given distance, an upper-limit of the explosion energy can be derived (E< 1051 erg at 1 kpc) since the energy cannot be too high to match the SNR radius. For a certain given distance and explosion energy, there are two possible density solutions (a low ρ/high Mej and a high ρ/low Mej configuration) that can reproduce the SNR radius for a given age.
At a distance of 1 kpc and E = 0.95 × 1051 erg (the maximum value allowed), the corresponding wind density is ρ0 = ρ = 0.01 cm-3 (as R0 was fixed at 9.6 pc; the radius at 1 kpc). For those parameters, the corresponding swept-up mass is 4 M⊙ and the ejecta mass is 9 M⊙ and the SNR is therefore still in the ejecta dominated evolution phase. The reported mass loss of 4 M⊙ is higher than expected for a single progenitor with an initial mass of 14 M⊙ (about 1–1.5 M⊙, see Fig. 19 of Sukhbold et al. 2016). If the progenitor evolved in a binary system, the companion could have increased the mass loss by stripping the envelope. It is, however, not clear if this is the case for RX J1713.7−3946 since Katsuda et al. (2015) have not found the remaining companion.
While the mass loss and ejecta mass are obtained assuming the equality in Eq. (4), the ejecta mass could, in fact, be lower since the shock has not fully reached the border of the cavity (implying Msw<Mmassloss) or because the initial progenitor is lower than 14 M⊙. To test this effect, we fixed the ejecta mass to 2 M⊙ (as estimated for CasA SNR by Hwang & Laming 2012) for all ages and densities. For this much smaller value, the remnant has just started its transition to the Sedov phase and, by using the same method as shown in Fig. 3 (middle panel), an age of ~2100 yr is derived.
The age of 2250 ± 170stat ± 200syst yr derived in the previous paragraph is in tension with the association of RX J1713.7−3946 with SN 393. We note that the age of the SNR can be significantly reduced assuming a constant density distribution in the cavity. This is plausible for a wind configuration, where the shock would pass little time in the steep (s = 2) wind profile, and very quickly afterwards evolve in the uniform shocked wind region (s = 0). For E = 1051 erg, d = 1 kpc, Mzams = 14 M⊙, s = 0 and n = 9, and Msw = 4/3πρμmpR3, we obtain t = 1760 ± 130stat ± 150syst yr and, using the same procedure as described in the previous paragraphs, we here obtain two possible density solutions, ρ = 0.01/0.07 cm-3. The higher density solution is however excluded by the upper-limit of 0.02 cm-3 based on the lack of thermal X-rays in the SE region (region 1 in Fig. 8 of Cassam-Chenaï et al. 2004). For ρ = 0.01 cm-3, Msw = 2.5 M⊙ for an ejecta mass of 10 M⊙ and the SNR is still in the ejecta dominated phase.
For the ejecta index n = 7 and Mzams = 14 M⊙, we obtain anage of 1520 ± 110stat ± 140syst yr, in agreement with an association with SN 393 and a density ρ = 0.01/0.09 cm-3 (the latter being excluded by the lack of thermal X-rays) for a distance of 1 kpc and E = 1051 erg. In this same configuration, it is interesting to note that, if the initial progenitor mass is significantly reduced (Mzams = 9 M⊙), the maximum explosion energy allowed at 1 kpc is E = 0.8 × 1051 erg (0.6 if d = 0.9 kpc) for a corresponding density of ρ = 0.02 cm-3. A lower explosion energy can reduce the visual brightness (see, e.g. Morozova et al. 2015) which could help to reconcile the apparent discrepancy noted by Fesen et al. (2012) between an expected visually bright supernova (–3.5 to –5.0 mag) and the historical Chinese record of SN 393 describing a rather faint guest star.
The decrease in 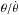 being slow in Fig. 3 (middle panel), we used the mean value of 2250 yr.
being slow in Fig. 3 (middle panel), we used the mean value of 2250 yr.
Acknowledgments
We acknowledge the use of several open-source libraries for Python, including Numpy, Matplotlib, and Astropy.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ballet, J., Decourchelle, A., et al. 2009, A&A, 505, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 427, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, D. C., Patnaude, D. J., Slane, P., & Raymond, J. 2010, ApJ, 712, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Kremer, R., Patnaude, D., & Milisavljevic, D. 2012, AJ, 143, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, Y., Sano, H., Sato, J., et al. 2012, ApJ, 746, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., & Laming, J. M. 2012, ApJ, 746, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Acero, F., Tominaga, N., et al. 2015, ApJ, 814, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Bocchino, F., Decourchelle, A., et al. 2012, A&A, 546, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morozova, V., Piro, A. L., Renzo, M., et al. 2015, ApJ, 814, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Sano, H., Fukuda, T., Yoshiike, S., et al. 2015, ApJ, 799, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Tang, X., & Chevalier, R. A. 2016, ArXiv e-prints [arXiv:1607.06391] [Google Scholar]
- Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., et al. 2014, PeerJ, DOI: 10.7717/peerj.453 [Google Scholar]
- Wang, Z. R., Qu, Q.-Y., & Chen, Y. 1997, A&A, 318, L59 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panel: exposure corrected and background subtracted count map in the 0.6–6 keV energy band of the 2015 XMM-Newton observation. The image is smoothed with a Gaussian of 20 arcsec kernel radius. The red contours are the results of the Canny edge detection algorithm discussed in the main text. The white boxes represent the regions used to extract the radial profiles shown in Fig. 2 and the white and red crosses the 2002 and 2015 pointing positions. Right panel: edges detected in the 2002 (black) and 2015 (red) observations. The point sources discussed in the image registration process are labeled Src 1 to Src 6. |
| In the text | |
 |
Fig. 2 Radial profiles, Cstat maps and Cstat radial contribution from the outer region (top panel) and inner region (bottom panel) defined in Fig. 1. The right panels show the cumulative statistics radial contribution (ΔCstat = C0(r)−Cbestfit(r)) taken at the best-fitted amplitude and where C0(r) is the Cstat radial contribution at a 0 arcsec model shift. |
| In the text | |
 |
Fig. 3 Left panel: ejecta mass distribution as a function of age and density assuming equality in Eq. (4). For each point of the grid, the swept-up mass in the equation is derived by computing the shock radius using evolution equations for a supernova explosion energy of 1051 erg, n = 9, and s = 2. The white region indicates the excluded parameter space, where the ejecta mass becomes negative. Middle panel: using the ejecta distribution previously derived, the same explosion energy, and ejecta and density profile indices, the ratio Rsh/Vsh is obtained and shown here as the distance independent ratio |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


